Combining the small-x evolution and DGLAP for description of inclusive photon induced processes

Abstract

We study amplitudes of the inclusive photon induced high-energy processes: elastic Compton scattering off hadrons and photoproduction. Although description of these amplitudes includes both non-perturbative and perturbative contributions, QCD factorization makes possible to study them separately. Throughout the present paper we focus on the perturbative amplitudes and study such amplitudes in all available in the literature forms of QCD factorization: Collinear, $K_T$ and Basic. As a result, we obtain expressions for the perturbative Compton amplitudes, which can be used at arbitrary x and $Q^2$ in any form of QCD factorization. Putting $Q^2 = 0$ in those expressions allows us to obtain expressions for the perturbative components of the photoproduction amplitudes. The small-x asymptotics of the Compton amplitudes in any form of QCD factorization are of the Regge type, with the Reggeon being a double-logarithmic (non-BFKL) contribution to Pomeron.

1 Introduction

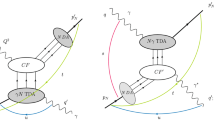
Photon induced inclusive processes such as Deep-Inelastic Scattering (DIS), Photoproduction and Diffractive Deep-Inelastic Scattering (DDIS) are the objects of intensive experimental and theoretical investigation. Theoretical studying these processes is based on the concept of QCD factorization which makes possible to separate perturbative and non-perturbative contributions. There are several forms/types of QCD factorization in the literature. Firstly, there is Collinear factorization [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. Secondly, there is the more general $K_T$ factorization suggested in Refs. [15,16,17]. The third, the most general, type of QCD factorization is basic factorization suggested in Refs. [18, 19]. In any of those factorizations the approximation of the single-parton photon–hadron interactions is used and as a result, the subjects of consideration are represented through convolutions of perturbative and non-perturbative objects connected by two-parton intermediate states. For instance, representation of the amplitude T of the elastic forward Compton scattering off a hadron in any type of QCD factorization is depicted in Fig. 1.

Fig. 1

QCD factorization of amplitude T. The dashed lines denote virtual photons with momentum q, the horizontal straight lines correspond to the incoming hadron with momentum p, the vertical straight lines stand for intermediate quarks and the wavy lines denote intermediate gluons with momentum k. The upper blobs denote DIS off partons, they are described with Perturbative QCD while the lowest blobs are non-perturbative

In the analytical form, QCD factorization of T is generically written as follows:

$$\begin{aligned} T = T_q \otimes \Phi _q + T_g \otimes \Phi _g, \end{aligned}$$

(1)

where $T_q$ and $T_g$ are the perturbative amplitudes of the elastic Compton scattering off a quark and gluon respectively. Non-perturbative blobs $\Phi _q$ and $\Phi _g$ denote distributions of those partons in the hadrons. The notations $\otimes$ refer to integrations over momentum k of any parton in the two-quark and two-gluon intermediate states. The specific form of the integrations as well as a parametrization of momentum k of the intermediate partons depend on the type of chosen factorization.¹ Amplitudes $T_{q,g}$ as well as amplitudes $\Phi _{q,g}$ are also given by expressions depending on the type of factorization. In the present paper we focus on the perturbative amplitudes $T_{q,g}$. In any specific type of factorization, there are kinematic regions where amplitudes $T_{q,g}$ are given by essentially different expressions. Such regions are:

• Region A. Large x and large $Q^2$: $(x \sim 1) \bigotimes (Q^2 \gg \mu ^2)$.

• Region B. Small x and large $Q^2$: $(x \ll 1)\bigotimes (Q^2 \gg \mu ^2)$.

• Region C. Small x and small $Q^2$: $(x \ll 1)\bigotimes (Q^2 < \mu ^2)$.

• Region D. Large x and small $Q^2$: $(x \sim 1)\bigotimes (Q^2 < \mu ^2)$.

We have used above the conventional notations: $Q^2 = - q^2$, with q being the external photon momentum, and $x = Q^2/w$, where $w = 2pq$, with p being the momentum of the incoming/outgoing parton. The parameter $\mu$ is associated with the factorization scale. Besides, it plays the role of the infrared (IR) cut-off in Collinear, $K_T$ and basic factorizations, when the double-logarithmic (DL) contributions to amplitudes $T_{q,g}$ are accounted for. The physical meaning of $\mu$ for the parton distributions $\Phi _{q,g}$ in $K_T$ factorization and its role in transition from $K_T$ factorization to Collinear factorization were considered in Refs. [18, 19]. Now let us consider the status of knowledge of amplitudes $T_{q,g}$ in the Regions A–D.

The region A is the DGLAP applicability region, so expressions for $T_{q,g}$ in this region are provided by the DGLAP evolution equations [20,21,22,23]. Such expressions can easily be found in the literature. They account for logarithms of $Q^2$ but neglect total resummations of logarithms of x because such logarithms are unessential in Region A.

Description of $T_{q,g}$ in the small-x region B in the double-logarithmic approximation (DLA) in the framework of Collinear factorization was obtained in Refs. [24, 25]. In particular, it was shown in Refs. [24, 25] that the small-x asymptotics of $T_{q,g}$ exhibits a new, DL contribution to Pomeron. In contrast, double-logarithmic expressions for $T_{q,g}$ in region B in $K_T$ factorization have not been obtained. We do it in the present paper, using the same method as in Refs. [24, 25]: constructing and solving Infrared Evolution Equations (IREE).² Then we obtain expressions for $T_{q,g}$ which combine DL and non-DL contributions available in DGLAP, so these expressions can universally be used at large $Q^2$ and arbitrary x (i.e. in the region $\mathbf{A} \oplus \mathbf{B}$) in Collinear, $K_T$ and basic factorizations.

Extending expressions for $T_{qg}$ to low $Q^2$ was suggested in Ref. [27] for Collinear factorization. In the present paper we generalize this extension to the cases of $K_T$ and basic factorizations, obtaining thereby expressions which can universally be used at arbitrary x and $Q^2$ in any form of QCD factorization.

Putting $q^2 = 0$ in Eq. (1), one arrives at the photoproduction amplitudes $A_{\gamma }$:

$$\begin{aligned} A_{\gamma } \equiv T|_{q^2 = 0}. \end{aligned}$$

(2)

Combining it with Eq. (2) leads to the factorized form of $A_{\gamma q}$:

$$\begin{aligned} A_{\gamma } = A_{\gamma q} \otimes \Phi _q + A_{\gamma g} \otimes \Phi _g. \end{aligned}$$

(3)

Fig. 2

Graphs for the parton–parton amplitudes

The Optical theorem relates the amplitude $A_{\gamma }$ to the total cross section of photoproduction. Using the expressions for $T_{qg}$ at low $Q^2$ allows us to obtain expressions for the perturbative amplitudes $A_{\gamma q}, A_{\gamma g}$ first in Collinear and then in the other forms of QCD factorization.

Our paper is organized as follows: in Sect. 2 we remind results of Refs. [24, 25] for amplitudes $T_{q,g}$ in Region B in Collinear factorization and extend $T_{q,g}$ to Regions A,C,D, obtaining explicit expressions for $T_{q,g}$ which can be used at any x and $Q^2$. Then we briefly discuss the small-x asymptotics of $T_{q,g}$, their applicability region the power $Q^2$-corrections to $T_{q,g}$ in the low-$Q^2$ region C. In Sect. 3 we study amplitudes $T_{q,g}$ in $K_T$-factorization. This type of factorization involves dealing with essentially off-shell external partons, which brings a new technical problem which is absent in Collinear factorization: there is no universal description of $T_{q,g}$ in Region B at at arbitrary virtualities of the external partons. We deal with this problem also by constructing and solving appropriate IREEs. In Sect. 4 we consider the photoproduction amplitudes in Collinear, $K_T$ and basic factorizations. Finally, Sect. 5 is for concluding remarks.

2 Compton amplitudes in Collinear factorization

Equation (1) for Collinear factorization takes the following form:

$$\begin{aligned} T^{(col)}= & {} \int _x^1 \frac{d \beta }{\beta }\left[ T^{(col)}_q(x/\beta ,Q^2/\mu ^2) \Phi ^{(col)}_q (\beta ,\mu ^2)\right. \nonumber \\&\left. + T^{(col)}_g(x/\beta ,Q^2/\mu ^2) \Phi ^{(col)}_g (\beta ,\mu ^2)\right] , \end{aligned}$$

(4)

where the superscript $``col''$ refers to Collinear factorization and $\beta$ is the longitudinal fraction of momentum k in Fig. 1. We start with considering amplitudes $T^{(col)}_{q,g}$ in region B and then extend these expressions to regions A,C,D.

2.1 Amplitudes $T^{(col)}_{q.g}$ in region B

Perturbative amplitudes $T^{(col)}_{q,g}$ in region B were calculated in Refs. [24, 25] in the double-logarithmic approximation (DLA) and the cases of fixed and running $\alpha _s$ were investigated separately. Amplitudes $T^{(col)}_{q,g}$ were in Refs. [24, 25] represented as follows:

$$\begin{aligned} T^{(col)}_q (x/\beta , Q^2/\mu ^2)= & {} \int _{-\imath \infty }^{\imath \infty } \frac{d \omega }{2 \imath \pi } \left( x/\beta \right) ^{-\omega } \xi ^{(+)} (\omega ) F^{(col)}_q (\omega , y), \nonumber \\ T^{(col)}_g (x/\beta , Q^2/\mu ^2)= & {} \int _{-\imath \infty }^{\imath \infty } \frac{d \omega }{2 \imath \pi } \left( x/\beta \right) ^{-\omega } \xi ^{(+)} (\omega ) F^{(col)}_g (\omega ,y),\nonumber \\ \end{aligned}$$

(5)

with $\mu$ being the factorization scale. The logarithmic variable y in Eq. (5) is related to $Q^2$:

$$\begin{aligned} y = \ln (Q^2/\mu ^2) \end{aligned}$$

(6)

and $\xi ^{(+)} (\omega )$ is the positive signature factor:

$$\begin{aligned} \xi ^{(+)} (\omega ) = - \left( e^{-\imath \pi \omega } + 1\right) /2. \end{aligned}$$

(7)

The signature factor $\xi ^{(+)} (\omega )$ guarantees that $T_{q,g}$ are invariant with respect to permutation of the incoming and outgoing external photons. The integral representation (5) is the asymptotic form of the Sommerfeld-Watson transform but it is frequently addressed as the Mellin transform. Throughout the paper we will name $T_{q,g}$ the Mellin amplitudes. Explicit expressions for the Mellin amplitudes $F^{(col)}_{q,g}$ in the region B are:

$$\begin{aligned}&F^{(col)}_q = C_q^{(+)} e^{\Omega _{(+)} y} + C_q^{(-)} e^{\Omega _{(-)} y}, \nonumber \\&F^{(col)}_g = C_g^{(+)} e^{\Omega _{(+)} y} + C_g^{(-)} e^{\Omega _{(-)} y}. \end{aligned}$$

(8)

Obtained in Refs. [24, 25] expressions for $\Omega _{(\pm )}, C_q^{(\pm )}$ and $C_g^{(\pm )}$ can be found in Appendix B where they are expressed through the on-shell parton–parton amplitudes $A_{rr'}$ ($r,r' = q,g$). Graphs for amplitudes $A_{rr'}$ are depicted in Fig. 2.

The Mellin transform for the parton–parton amplitudes is similar to the one in Eq. (5):

$$\begin{aligned} A_{rr'} (s/\mu ^2) = \int _{-\imath \infty }^{\imath \infty } \frac{d \omega }{2 \imath \pi } \left( s/\mu ^2\right) ^{\omega } \xi ^{(+)} (\omega ) f_{rr'} (\omega ). \end{aligned}$$

(9)

Technically, it is more convenient to use the Mellin amplitudes $h_{rr'}$ which are proportional to $f_{rr'}$:

$$\begin{aligned} h_{rr'}(\omega ) = f_{rr'}(\omega )/(8 \pi ^2). \end{aligned}$$

(10)

Explicit expression for amplitudes $h_{rr'}$ can be found in Appendix A. Let us discuss Eq. (8). It is easy to see that its structure exhibits a distinct similarity to the structure of the DGLAP description of $F^{(col)}_{q,g}$, which is especially obvious when the approximation of fixed $\alpha _s$ is used:

$$\begin{aligned} F^{DGLAP}_q= & {} \hat{C}_q^{(+)} e^{\gamma _{(+)}^{DGLAP} y} + \hat{C}_q^{(-)} e^{\gamma _{(-)}^{DGLAP} y}, \nonumber \\ F^{DGLAP}_g= & {} \hat{C}_g^{(+)} e^{\gamma _{(+)}^{DGLAP} y} + \hat{C}_g^{(-)} e^{\gamma _{(-)}^{DGLAP} y}. \end{aligned}$$

(11)

Indeed, the factors $\Omega _{(\pm )}$ in the exponents of Eq. (8) are new anomalous dimensions instead of $\gamma ^{DGLAP}_{(\pm )}$ in Eq. (11) while the factors $C_g^{(\pm )}, C_q^{(\pm )}$ are new coefficient functions instead of the DGLAP coefficient functions $\hat{C}^{(\pm )}_{q,g}$. However in contrast to DGLAP, the coefficient functions and the anomalous dimensions in (8) are calculated with the same means and they include the total resummations of the DL contributions. The both coefficient functions and anomalous dimensions in (8) are made of amplitudes $h_{rr'}$. When the partonic amplitudes $h_{rr'}$ are replaced by their Born values, the integrands in Eq. (5) coincide with the integrands of the LO DGLAP expressions in which the most singular in $\omega$ terms are retained. Further expansions of $h_{rr'}$ and substituting them in Eq. (8) lead to the NLO (as well as to NNLO DGLAP, etc), where the most singular terms only are accounted for in each order in $\alpha _s$.

2.2 Extending the small-x Eqs. (5, 8) to region A

Expressions in Eqs. (5, 8) are defined in the region B. Now we are going to obtain an interpolation formulae for amplitudes $T^{(col)}_{q,g}$, which would reproduce the DGLAP expressions at large x and at the same time would coincide with Eqs. (5, 8) at small x. Such extension can be obtained with the four steps:

Step 1::

Subtract the most singular in $\omega$ terms (i.e. the terms $\sim \alpha _s/\omega$ in the case of LO DGLAP; $\alpha ^2_s/\omega ^3$ in the case of NLO DGLAP, etc.) from the DGLAP anomalous dimensions $\gamma _{(\pm )}^{(DGLAP)} (\omega , \alpha _s)$. We denote $\widetilde{\gamma }^{DGLAP}_{(\pm )}$ the result of such amputation.

Step 2::

Add $\widetilde{\gamma }^{DGLAP}_{(\pm )}$ to $\Omega _{(\pm )}$. The new anomalous dimensions

$$\begin{aligned} \widetilde{\Omega }_{(\pm )} = \Omega _{(\pm )} + \widetilde{\gamma }^{DGLAP}_{(\pm )} \end{aligned}$$

(12)

contain the total resummations of the double-logarithmic contributions. They are essential at small x and unimportant at large x. At the same time, (12) contains less singular in $1/\omega ^n$ DGLAP contributions which are dominant at large x.

Step 3::

Subtract the LO DGLAP term $=1$ and the most singular in $\omega$ terms (i.e. the term 1 $\sim \alpha _s/\omega ^2$ in the case of NLO DGLAP, $\alpha ^2_s/\omega ^4$ in the case of NNLO DGLAP, etc.) from the DGLAP expressions for the coefficient functions. We denote $\Delta \hat{C}^{(\pm )}_{q,g}$ the result of such amputation.

Step 4::

Add the results obtained in Step 3 to the DL expressions $C^{(\pm )}_{q,g}$, arriving thereby at new coefficient functions $\widetilde{C}^{(\pm )}_{q,g}$:

$$\begin{aligned} \widetilde{C}^{(\pm )}_{q,g} = C^{(\pm )}_{q,g} + \Delta \hat{C}^{(\pm )}_{q,g}. \end{aligned}$$

(13)

The coefficient functions $\widetilde{C}^{(\pm )}_{q,g}$ include both DL contributions and the less singular DGLAP terms. The subtractions in Steps 1,3 are necessary to avoid the double counting.

Replacing $\Omega _{(\pm )}$ and $C^{(\pm )}_{q,g}$ in Eq. (5) by $\widetilde{\Omega }_{(\pm )}$ and $\widetilde{C}^{(\pm )}_{q,g}$, we obtain the interpolation expressions $\widetilde{T}^{(col)}_{q,g}$ for the Compton amplitudes :

$$\begin{aligned} \widetilde{T}^{(col)}_q (x/\beta , Q^2/\mu ^2)= & {} \int _{-\imath \infty }^{\imath \infty } \frac{d \omega }{2 \imath \pi } \left( x/\beta \right) ^{-\omega } \xi ^{(+)} (\omega )\nonumber \\&\left[ \widetilde{C}_q^{(+)} e^{\widetilde{\Omega }_{(+)} y} + \widetilde{C}_q^{(-)} e^{\widetilde{\Omega }_{(-)} y}\right] , \nonumber \\ T^{(col)}_g (x/\beta , Q^2/\mu ^2)= & {} \int _{-\imath \infty }^{\imath \infty } \frac{d \omega }{2 \imath \pi } \left( x/\beta \right) ^{-\omega } \xi ^{(+)} (\omega )\nonumber \\&\left[ \widetilde{C}_g^{(+)} e^{\widetilde{\Omega }_{(+)} y} + \widetilde{C}_g^{(-)} e^{\widetilde{\Omega }_{(-)} y} \right] . \end{aligned}$$

(14)

Equation (14) combines the small-x evolution in DLA with the DGLAP results for the coefficient functions and anomalous dimensions, which are important at large x. These expressions can universally be used as the interpolation formulae for $T^{(col)}_{q,g}$ in the region $\mathbf{A} \oplus \mathbf{B}$.

2.3 Extending Eq. (14) to the small-$Q^2$ region $\mathbf{C} \oplus \mathbf{D}$

Extension of the expressions (14) to describe the amplitudes $\widetilde{T}^{(col)}_{q,g}$ to the region $\mathbf{C} \oplus \mathbf{D}$ is also not rigorous. The standard approach suggested in Ref. [28] and used since that in many papers (see e.g. Refs. [29,30,31]) to describe DIS at low $Q^2$ is to make a shift of $Q^2$:

$$\begin{aligned} Q^2 \rightarrow Q^2 + m^2, \end{aligned}$$

(15)

where the mass scale m was fixed on basis of certain physical considerations, depending on specific situation. In contrast to preceding papers, we proved in Ref. [27] (see also the overview [26]) that the scale m with DL accuracy can be unambiguously specified: the IR cut-off $\mu$ plays the role of the scale m. Our proof was based on the well-known fact that DL contributions arise from integrations $\sim d k^2_{i \perp }/k^2_{i \perp }$ over the transverse momenta $k_{i \perp }$ of virtual partons, which requires introducing an IR cut-off $\mu$. It can be introduced through the shift $k^2_{i \perp } \rightarrow k^2_{i \perp } + \mu ^2$, which eventually leads to the shift (15), with

$$\begin{aligned} m = \mu . \end{aligned}$$

(16)

The proof of (16) in Refs. [26, 27] was done in the context of the spin-dependent structure function $g_1$ but it holds for amplitudes $\widetilde{T}^{(col)}_{q,g}$ either. Applying the Principle of Minimal Sensitivity[32,33,34,35], we estimated in Refs. [24, 25] the value of $\mu$ of Eq. (16):

$$\begin{aligned} \mu = 2.3 \Lambda _{QCD} \approx 1 {\text {GeV}}. \end{aligned}$$

(17)

So, the universal expression for the Compton amplitudes $\widetilde{T}^{(col)}_{q,g}$ valid in the region $\mathbf{A} \oplus \mathbf{B} \oplus \mathbf{C} \oplus \mathbf{D}$ (i.e. at arbitrary values of x and $Q^2$) in the framework of Collinear factorization is

$$\begin{aligned} \widetilde{T}^{(col)}_q (x/\beta , Q^2/\mu ^2)= & {} \int _{-\imath \infty }^{\imath \infty } \frac{d \omega }{2 \imath \pi } \left( \widetilde{x}/\beta \right) ^{-\omega } \xi ^{(+)} (\omega ) \nonumber \\&\left[ \widetilde{C}_q^{(+)} e^{\widetilde{\Omega }_{(+)} \widetilde{y}} + \widetilde{C}_q^{(-)} e^{\widetilde{\Omega }_{(-)} \widetilde{y}}\right] , \nonumber \\ \widetilde{T}^{(col)}_g (x/\beta , Q^2/\mu ^2)= & {} \int _{-\imath \infty }^{\imath \infty } \frac{d \omega }{2 \imath \pi } \left( \widetilde{x}/\beta \right) ^{-\omega } \xi ^{(+)} (\omega )\nonumber \\&\left[ \widetilde{C}_g^{(+)} e^{\widetilde{\Omega }_{(+)} \widetilde{y}} + \widetilde{C}_g^{(-)} e^{\widetilde{\Omega }_{(-)} \widetilde{y}} \right] , \end{aligned}$$

(18)

where we have denoted

$$\begin{aligned} \widetilde{x} = x + \mu ^2/w \equiv x + x_0, \quad \widetilde{y} = \ln \left( (Q^2 + \mu ^2)/\mu ^2\right) . \end{aligned}$$

(19)

2.4 Small-x asymptotics of the Compton amplitudes and comparison with the DGLAP asymptotics

Asymptotics of $T^{(col)}_{q,g}$ at $x \rightarrow 0$ and $Q^2 > \mu ^2$ were considered in detail in Refs. [24, 25]. In the present paper we briefly remind results of Refs. [24, 25] and compare these asymptotics with the asymptotics of the same amplitudes obtained in the DGLAP approach. The standard mathematical tool to calculate the small-x asymptotics of $T^{(col)}_{q,g}$ is Saddle Point method. Applying this method to $T^{(col)}_{q,g}$, we obtain that the small-x asymptotics of amplitudes $T^{(col)}_{q,g}$ are of the Regge type. They both have the same intercepts $\omega _0$:

$$\begin{aligned}&T^{(col)}_q \sim \frac{\Pi _q(\omega _0)}{(\ln (1/x))^{3/2}} x^{- \omega _0} (Q^2/\mu ^2)^{\omega _0/2},\nonumber \\&\quad T^{(col)}_g \sim \frac{\Pi _g(\omega _0)}{(\ln (1/x))^{3/2}} x^{- \omega _0} (Q^2/\mu ^2)^{\omega _0/2}. \end{aligned}$$

(20)

The factors $\Pi _{q,g}(\omega _0)$ in Eq. (20) are called the impact factors.³ They are the only difference between the asymptotics of $T^{(col)}_q$ and $T^{(col)}_g$. The value of the intercept $\omega _0$ in Eq. (20) proved to be dependent on accuracy of the calculations. The maximal intercept $\omega ^{DL}_H$ corresponded to the roughest approximation where the quark contributions were neglected and $\alpha _s$ was fixed while the minimal intercept $\omega ^{DL}_S$ corresponded to the most accurate calculation where both gluon and quark contributions were accounted for and $\alpha _s$ was running:

$$\begin{aligned} \omega ^{DL}_H = 1.35,~~\omega ^{DL}_S = 1.07. \end{aligned}$$

(21)

As the both intercepts $> 1$, the Reggeons of Eq. (20) with the intercepts (21) are the DL contributions to Pomeron, or DL Pomerons. In accordance with the conventional Pomeron terminology we call them hard (with the subscript H) and soft (with the subscript S) DL Pomerons respectively. It is interesting fact that $\omega ^{DL}_H$ is close to the LO BFLK Pomeron intercept and $\omega ^{DL}_S$ almost coincides with the NLO BFLK Pomeron intercept despite that BFKL have nothing in common with resummation of DL contributions. The asymptotics in Eq. (20) are given by much simpler expressions than the parent amplitudes in Eq. (18). However, the asymptotics should not be used outside their applicability region. It was shown in Refs. [24, 25] that the asymptotics should be used at $x < x_{max}$ and estimates of $x_{max}$ at various values of $Q^2$ were obtained. In particular, at $Q^2 = 10$ GeV$^2$

$$\begin{aligned} x_{max} = 10^{-6}. \end{aligned}$$

(22)

It was shown in Refs. [24, 25] that the greater is $Q^2$, the less is $x_{max}$. When $x \ge x_{max}$ the parent amplitudes $T_{q,g}$ should be used instead of the asymptotics.

2.5 Remark on asymptotic scaling

Equation (20) can be written in such a way:

$$\begin{aligned}&T^{(col)}_q \sim \frac{\Pi _q(\omega _0)}{\ln ^{3/2} (1/x)} \left( \zeta /\mu ^2\right) ^{\omega _0/2},\nonumber \\&\quad T^{(col)}_g \sim \frac{\Pi _g(\omega _0)}{\ln ^{3/2} (1/x)} \left( \zeta /\mu ^2\right) ^{\omega _0/2}, \end{aligned}$$

(23)

with

$$\begin{aligned} \zeta = Q^2/x^2. \end{aligned}$$

(24)

Although both $T^{(col)}_q$ and $T^{(col)}_g$ by definition depend on two independent variables x and $Q^2$, Eq. (23) manifests that $T^{(col)}_{q,g} \ln ^{3/2} (1/x)$ asymptotically depend on the single variable $\zeta$ only. We name this remarkable property the Asymptotic Scaling. This property is absent in the DGLAP approach. Indeed, DGLAP predicts that the x- and $Q^2$- dependence of $T^{(col)}_{q,g}$ at $x \rightarrow 0$ are unrelated:

$$\begin{aligned} T^{(DGLAP)}_{q,g} \sim x^{-a} (Q^2/\mu ^2)^{\gamma _{DGLAP}/b}, \end{aligned}$$

(25)

where $\gamma _{DGLAP}$ is the anomalous dimension and b is the first coefficient of the $\beta$-function. The intercept a has the phenomenological origin: it is generated by the terms $x^{-a}$ in the fits for the initial parton densities.

2.6 Perturbative power $Q^2$-contributions

We begin studying the power $Q^2$-corrections with considering $T^{(col)}_q$ at the large-$Q^2$ region, where $Q^2 \gg \mu ^2$ and where the logarithmic variable $\widetilde{y}$ defined in (19) can be expanded in the series as follows:

$$\begin{aligned} \widetilde{y} = y + \sum _{n=1}^{\infty } c_n \left( \frac{\mu ^2}{Q^2}\right) ^n. \end{aligned}$$

(26)

Being substituted in Eq. (18), it allows us to write $T^{(col)}_q$ as

$$\begin{aligned} \widetilde{T}^{(col)}_q (x/\beta , \widetilde{Q}^2)= & {} \widetilde{T}^{(col)}_q (x/\beta ,Q^2) \nonumber \\&+ \left( \frac{\mu ^2}{Q^2}\right) C_1 + \left( \frac{\mu ^2}{Q^2}\right) ^2 C_2 + \ldots \end{aligned}$$

(27)

The first term in the r.h.s. of Eq. (27) describes the Compton amplitude in the region $\mathbf{A} \otimes \mathbf{B}$. At large x it is given by the DGLAP formulae whereas the second and third terms can wrongly be interpreted as contributions of the higher twists, probably of the non-perturbative origin though actually they are altogether perturbative:

$$\begin{aligned} C_1 = \frac{\partial \widetilde{T}^{(col)}_q (x/\beta ,y)}{\partial y},~~ C_2 = \frac{1}{2} \frac{\partial ^2 \widetilde{T}^{(col)}_q (x/\beta ,y)}{\partial y^2}. \end{aligned}$$

(28)

This example demonstrates that ignoring the shift (15) and interpretating all terms inversely proportional to $Q^2$ as an impact of higher twist could be misleading. On the other, at $Q^2 < \mu ^2$ the expansion (26) is replaced by another one:

$$\begin{aligned} \widetilde{y} = \sum _{n=1}^{\infty } c'_n \left( \frac{Q^2}{\mu ^2}\right) ^n. \end{aligned}$$

(29)

It leads to the small-$Q^2$ expression for $\widetilde{T}^{(col)}_q$:

$$\begin{aligned} \widetilde{T}^{(col)}_q (x/\beta , \widetilde{Q}^2)= \sum _{n-1}^{\infty } \left( \frac{Q^2}{\mu ^2}\right) ^n C'_n \end{aligned}$$

(30)

which decreases down to zero when $Q^2 \rightarrow 0$. It explains very well why the terms $\sim 1/(Q^2)^n$ are never seen at small $Q^2$ where, naively, their impact could be great. We remind that our estimate of $\mu$ is $\mu \approx 1$ GeV (see Eq. (17)). Disappearing of the terms $\sim 1/(Q^2)^n$ at $Q^2 \lesssim 1$ GeV obtained from analysis of experimental data could confirm correctness of our reasoning.

3 Calculating perturbative Compton amplitudes in $K_T$ factorization

Originally, $K_T$ factorization was introduced in Refs. [15,16,17] to make possible applying BFKL for description of hadronic reactions. It implied the kinematic region of very high, or asymptotic, energies, i.e. at $x \ll 1$. However, in the cases when BFKL is not involved one can use $K_T$ factorization at $x \sim 1$ as well. In the present Sect. we generalize DL expressions for $T^{(col)}_{q,g}$ to $K_T$ factorization. In the framework of $K_T$ factorization Eq. (1) takes the following form:

$$\begin{aligned}&T^{(KT)} = \int _x^1 \frac{d \beta }{\beta }\int _{\mu ^2}^w \frac{d k^2_{\perp }}{k^2_{\perp }}\nonumber \\&\qquad \times \left[ T^{(KT)}_q(x/\beta ,Q^2,k^2_{\perp },\mu ^2) \Phi ^{(KT)}_q (\beta ,k^2_{\perp },\mu ^2) \right. \nonumber \\&\qquad \left. + T^{(KT)}_g(x/\beta ,Q^2,k^2_{\perp },\mu ^2) \Phi ^{(KT)}_g (\beta ,k^2_{\perp },\mu ^2)\right] , \end{aligned}$$

(31)

where the superscript “KT” refers to $K_T$ factorization, $\mu$ is the factorization scale, $\beta$ is the longitudinal fraction of the external partons (see Fig. 1) and $k^2_{\perp }$ stands for their transverse momentum. $\Phi ^{(KT)}_{q,g}$ denote initial parton distributions and amplitudes $T^{(KT)}_{q,g}$ are perturbative. The subscripts $``q,g''$ refer to quarks and gluons in the same way as in Sect. 2. We are going to calculate $T^{(KT)}_{q,g}$ in DLA. DL contributions to them arrive from the kinematic region

$$\begin{aligned} w \gg Q^2, k^2_{\perp } \gg \mu ^2. \end{aligned}$$

(32)

However, amplitudes $T^{(KT)}_{q,g}$ in DLA cannot be described by a single universal expression at different virtualities $k^2_{\perp }$ in (32). There are two regions, where they are given by different expressions:

Region E: Moderate-virtual $k^2_{\perp }$, where

$$\begin{aligned} k^2_{\perp } \ll \mu ^2/x. \end{aligned}$$

(33)

Region F: Deeply-virtual $k^2_{\perp }$, where

$$\begin{aligned} k^2_{\perp } \gg \mu ^2/x. \end{aligned}$$

(34)

In order to avoid confusions, we will denote $T^{(\mathbf{E} )}_{q,g}$ and $T^{(\mathbf{F} )}_{q,g}$ the amplitudes $T^{(KT)}_{q,g}$ in the regions E and F respectively.

We will use the Mellin transform for $T^{(\mathbf{E},F) }_{q,g}$ in the following form:

$$\begin{aligned} T^{(\mathbf{E} )}_{q,g} = \int _{-\imath \infty }^{\imath \infty } \frac{d \omega }{2 \imath \pi } \left( w/\mu ^2\right) ^{\omega } \xi ^{(+)} (\omega ) \varphi ^{(\mathbf{E} )}_{q,g}(\omega , y, z), \nonumber \\ T^{(\mathbf{F} )}_{q,g} = \int _{-\imath \infty }^{\imath \infty } \frac{d \omega }{2 \imath \pi } \left( w/\mu ^2\right) ^{\omega } \xi ^{(+)} (\omega ) \varphi ^{(\mathbf{F} )}_{q,g}(\omega , y, z), \end{aligned}$$

(35)

where y is given by Eq. (6) and the new variable

$$\begin{aligned} z = \ln (k^2_{\perp }/\mu ^2) \end{aligned}$$

(36)

describes dependence of $T^{(KT)}_{q,g}$ on $k_{\perp }$ in the kinematics (32). This dependence differs $T^{(KT)}_{q,g}$ from amplitudes $T^{(col)}_{q,g}$ considered in Sect. 2 in Collinear factorization. In addition to y and z, it is convenient to introduce one more logarithmic variable:

$$\begin{aligned} \rho = \ln (w/\mu ^2). \end{aligned}$$

(37)

In terms of the logarithmic variables regions E and F defined in Eqs. (33, 34) look as follows:

• Region E: $\rho > y + z$,

• Region F: $\rho < y + z$.

3.1 Calculating the off-shell Compton amplitudes in region E

IREEs for $\varphi ^{(\mathbf{E} )}_{q,g}$ have the following form:

$$\begin{aligned}&\frac{\partial \varphi ^{(\mathbf{E} )}_q }{\partial y} + \frac{\partial \varphi ^{(\mathbf{E} )}_q }{\partial z} + \omega \varphi ^{(\mathbf{E} )}_q = F^{(col)}_q (\omega ,y) H_{qq} (\omega ,z) \nonumber \\&\quad + F^{(col)}_g (\omega ,y) H_{gq} (\omega ,z), \nonumber \\&\frac{\partial \varphi ^{(\mathbf{E} )}_g}{\partial y} +\frac{\partial \varphi ^{(\mathbf{E} )}_g}{\partial z} + \omega \varphi ^{(\mathbf{E} )}_g = F^{(col)}_q (\omega , y) H_{qg} (\omega ,z)\nonumber \\&\quad + F^{(col)}_g (\omega ,y) H_{gg} (\omega ,z). \end{aligned}$$

(38)

The l.h.s. of IREEs in (38) are obtained with applying the differential operator

$$\begin{aligned} -\mu ^2 d/d \mu ^2 = \partial /\partial \rho + \partial /\partial y + \partial /\partial z \end{aligned}$$

(39)

to Eq. (35). As a result, the l.h.s.of Eq. (38) contain explicitly the derivatives over y and z while the factor $\omega$ corresponds to differentiation of the Mellin factor $(w/\mu ^2)^{\omega }$. The convolutions in r.h.s. of (38) are similar in structure to the convolutions in the DGLAP evolution equations. They involve amplitudes $F^{(col)}_q$ which were considered in Sect. 2 and amplitudes $H_{rr'}$ which are still unknown. We will calculate amplitudes $H_{rr'}$ in the next Sect. In order to specify general solutions to Eq. (38), we will use the matching

$$\begin{aligned}&T^{(\mathbf{E} )}_q (w,y,z)|_{z = 0} = T^{(col)}_q (\omega , y),\nonumber \\&T^{(\mathbf{E} )}_g(w,y,z)|_{z = 0} = T^{(col)}_g (\omega , y), \end{aligned}$$

(40)

with $T^{(col)}_{q,g}$ defined in Eq. (5). The matching (40) implies the following hierarchy between y and z:

$$\begin{aligned} y > z. \end{aligned}$$

(41)

The requirement (41) is temporary. The final expressions for $T^{(\mathbf{E} )}_{q,g}$ will be written in the form free of this hierarchy. Solving Eq. (38) goes easier when y and z are replaced by new variables $\xi , \eta$:

$$\begin{aligned} \xi = \frac{1}{2} (y + z), \quad \eta = \frac{1}{2} (y - z). \end{aligned}$$

(42)

Obviously, the inverse transform is

$$\begin{aligned} y = \xi + \eta , \quad z = \xi - \eta . \end{aligned}$$

(43)

In terms of $\xi ,\eta$ Eq. (38) looks simpler:

$$\begin{aligned}&\frac{\partial \varphi ^{(\mathbf{E} )}_q }{\partial \xi } + \omega \varphi ^{(\mathbf{E} )}_q = F^{(col)}_q (\omega ,y) H_{qq} (\omega ,z) \nonumber \\&\qquad + F^{(col)}_g (\omega ,y) H_{gq} (\omega ,z), \nonumber \\&\quad \frac{\partial \varphi ^{(\mathbf{E} )}_g}{\partial \xi } + \omega \varphi ^{(\mathbf{E} )}_g = F^{(col)}_q (\omega , y) H_{qg} (\omega ,z)\nonumber \\&\qquad + F^{(col)}_g (\omega ,y) H_{gg} (\omega ,z). \end{aligned}$$

(44)

Solution to Eq. (44) is:

$$\begin{aligned}&\varphi ^{(\mathbf{E} )}_q = e^{-\omega \xi } \left[ T^{(col)}_q (\omega , \eta ) \right. \nonumber \\&\quad \left. + \int _{\eta }^{\xi } d v e^{\omega v}\left( F^{(col)}_q (\omega ,y') H_{qq} (\omega ,z') \right. \right. \nonumber \\&\quad \left. \left. + F^{(col)}_g (\omega ,y') H_{gq} (\omega ,z')\right) \right] , \nonumber \\&\varphi ^{(\mathbf{E} )}_g = e^{-\omega \xi } \left[ T^{(col)}_g (\omega , \eta )\right. \nonumber \\&\quad \left. + \int _{\eta }^{\xi } d v e^{\omega v}\left( F^{(col)}_q (\omega ,y') H_{qg} (\omega ,z')\right. \right. \nonumber \\&\quad \left. \left. + F^{(col)}_g (\omega ,y') H_{gg} (\omega ,z')\right) \right] , \end{aligned}$$

(45)

with the variables $y',z'$ defined as follows:

$$\begin{aligned} y' = v + \eta ,~~z' = v - \eta . \end{aligned}$$

(46)

In order to lift the relation between y and z of Eq. (41) we replace $\eta$ with $|\eta |$ everywhere save Eq. (46). Doing so and substituting Eq. (45) in (35), we arrive at expressions for amplitudes $T^{(\mathbf{E} )}_{q,g}$ in region E:

$$\begin{aligned}&T^{(\mathbf{E} )}_q = \int _{-\imath \infty }^{\imath \infty } \frac{d \omega }{2 \imath \pi } \xi ^{(+)} (\omega ) \left( \frac{s}{\sqrt{Q^2 k^2_{\perp }}}\right) ^{\omega } \nonumber \\&\quad \left[ T^{(col)}_q (\omega , |\eta |) +\int _{|\eta |}^{\xi } d v e^{\omega v}\left( F^{(col)}_q (\omega ,y') H_{qq} (\omega ,z')\right. \right. \nonumber \\&\qquad \left. \left. + F^{(col)}_g (\omega ,y') H_{gq} (\omega ,z')\right) \right] , \nonumber \\&T^{(\mathbf{E} )}_g = \int _{-\imath \infty }^{\imath \infty } \frac{d \omega }{2 \imath \pi } \xi ^{(+)} (\omega ) \left( \frac{s}{\sqrt{Q^2 k^2_{\perp }}}\right) ^{\omega } \nonumber \\&\quad \times \left[ T^{(col)}_g (\omega , |\eta |) + \int _{|\eta |}^{\xi } d v e^{\omega v}\left( F^{(col)}_g (\omega ,y') H_{qg} (\omega ,z') \right. \right. \nonumber \\&\qquad \left. \left. + F^{(col)}_g (\omega ,y') H_{gg} (\omega ,z')\right) \right] . \end{aligned}$$

(47)

3.2 Calculating the off-shell Compton amplitudes in region F

IREEs for $T^{(\mathbf{F} )}_{q,g}$ are very simple:

$$\begin{aligned}&\frac{\partial T^{(\mathbf{F} )}_q}{\partial \rho } + \frac{\partial T^{(\mathbf{F} )}_q}{\partial y} + \frac{\partial T^{(\mathbf{F} )}_q}{\partial z} = 0, \nonumber \\&\quad \frac{\partial T^{(\mathbf{F} )}_g}{\partial \rho } + \frac{\partial T^{(\mathbf{F} )}_g}{\partial y} + \frac{\partial T^{(\mathbf{F} )}_g}{\partial z} = 0. \end{aligned}$$

(48)

We do not use the Mellin transform for $T^{(\mathbf{F} )}_{q,g}$ and because of it the l.h.s. of (48) contain derivatives over $\rho$, y and z. Integration over momenta of all virtual partons in the deeply-virtual region F do not bring any dependence⁴ of $T^{(\mathbf{F} )}_{q,g}$on $\mu$. As a result, the r.h.s. of Eq. (48) are zeros. A general solution to Eq. (48) is

$$\begin{aligned}&T^{(\mathbf{F} )}_q = \Psi _q \left( (\rho - y),(\rho - z)\right) ,\nonumber \\&T^{(\mathbf{F} )}_g = \Psi _g \left( (\rho - y),(\rho - z)\right) , \end{aligned}$$

(49)

with $\Psi _q$ and $\Psi _g$ being arbitrary functions. In order to specify them we use the following matching: Amplitudes $T^{(\mathbf{F} )}_{q,g}$ coincide with amplitudes $T^{(\mathbf{E} )}_{q,g}$ on the border surface between regions E and F, where $\rho = y + z$:

$$\begin{aligned} T^{(\mathbf{F} )}_q (y,z) = \bar{T}^{(\mathbf{E} )}_q (y,z), ~~T^{(\mathbf{F} )}_g (y,z) = \bar{T}^{(\mathbf{E} )}_g (y,z), \end{aligned}$$

(50)

with the new amplitudes $\bar{T}^{(\mathbf{E} )}_{q,g}$ defined as follows:

$$\begin{aligned}&\bar{T}^{(\mathbf{E} )}_q (y,z) = T^{(\mathbf{E} )}_q (\rho ,y,z)|_{\rho = y + z},\nonumber \\&\bar{T}^{(\mathbf{E} )}_g (y,z) = T^{(\mathbf{E} )}_g (\rho ,y,z)|_{\rho = y + z}. \end{aligned}$$

(51)

According to Eq. (49) the expression for $T^{(\mathbf{F} )}_q, T^{(\mathbf{F} )}_g$ in the whole region F can be obtained from amplitudes $\bar{T}^{(\mathbf{E} )}_{q,g}$ by the simple change of their arguments:

$$\begin{aligned}&T^{(\mathbf{F} )}_q (\rho , y, z) = \bar{T}^{(\mathbf{E} )}_q (\rho -y, \rho - z),\nonumber \\&T^{(\mathbf{F} )}_g (\rho , y, z) = \bar{T}^{(\mathbf{E} )}_g (\rho -y, \rho - z). \end{aligned}$$

(52)

Both $\rho - y$ and $\rho - z$ do not depend on the IR cut-off $\mu$, so amplitudes $T^{(\mathbf{F} )}_{q,g}$ are IR stable.

3.3 Extension of amplitudes $T^{(\mathbf{E},F )}_{q,g}$ to the region of small $Q^2$

Extension of $T^{(\mathbf{E} )}_{q,g}$ to the small-$Q^2$ region can be done with the shift of $Q^2$ like it was done in Collinear factorization. As a result, amplitudes $T^{(\mathbf{E} )}_{q,g}$ can be extended to the small-$Q^2$ region with replacement of x, y in Eq. (47) by $\widetilde{x},\widetilde{y}$ defined in Eq. (19). A similar extension of $T^{(\mathbf{F} )}_{q,g}$ is impossible because it would involve partons with virtualities $k^2_{\perp } > w$ which contradicts to Eq. (32).

3.4 Extension of amplitudes $T^{(\mathbf{E},F )}_{q,g}$ to basic factorization

It follows from Refs. [18, 19] that extension of Compton amplitudes $T^{(\mathbf{E} )}_{q,g}$ and $T^{(\mathbf{F} )}_{q,p}$ defined in Eqs. (47, 52) to basic factorization can be done with the very simple replacement: it is necessary and sufficient to replace $k^2_{\perp }$ by $|k^2|$ in Eqs. (47, 52).

3.5 Off-shell parton–parton amplitudes $H_{rr'}$

Expressions for Compton amplitudes $T^{(KT)}_{q,g}$ in Eqs. (47, 52) include off-shell Mellin amplitudes $H_{rr'}$. Below we calculate them in DLA. They stem from the Mellin transform for off-shell parton–parton amplitudes $\widetilde{A}_{rr'}$:

$$\begin{aligned} \widetilde{A}_{rr'} (w,z) = \int _{- \imath \infty }^{\imath \infty } \frac{d \omega }{2 \pi \imath } e^{\omega \rho } \xi ^{(\omega )} \widetilde{f}_{rr'} (\omega ,z) \end{aligned}$$

(53)

and the following definition (cf. (10)):

$$\begin{aligned} H_{rr'} (\omega ,z) = \frac{1}{8 \pi ^2} \widetilde{f}_{rr'} (\omega ,z). \end{aligned}$$

(54)

Amplitudes $H_{rr'} (\omega ,z)$ can also be found with constructing and solving appropriate IREEs. The IREEs for the off-shell $H_{rr'}$ are quite similar to Eq. (38):

$$\begin{aligned} \frac{\partial }{\partial z} H_{qq} + \omega H_{qq}= & {} h_{qq} H_{qq} + h_{qg} H_{gq}, \nonumber \\ \frac{\partial }{\partial z} H_{gq} + \omega H_{gq}= & {} h_{gq} H_{qq} + h_{gg} H_{gq}, \nonumber \\ \frac{\partial }{\partial z} H_{qg} + \omega H_{qg}= & {} h_{qq} H_{qg} + h_{qg} H_{gg}, \nonumber \\ \frac{\partial }{\partial z} H_{gg} + \omega H_{gg}= & {} h_{gq} H_{qg} + h_{gg} H_{gg}, \end{aligned}$$

(55)

where l.h.s. of each equation corresponds to applying operator $-\mu ^2 d/d \mu ^2$ to Eq. (53) while each r.h.s involves convolutions of $H_{rr'}$ and $h_{rr'}$. Specifying the general solution to Eq. (55) should be done with using the matching:

$$\begin{aligned} H_{rr'}|_{z = 0} = h_{rr'}. \end{aligned}$$

(56)

Solving (55) and using the matching (56), we obtain the following expressions for $H_{rr'}$:

$$\begin{aligned} H_{qq}= & {} e^{- \omega z} \left[ C_1 e^{\Omega _{(+)} z} + C_2 e^{\Omega _{(-)} z}\right] , \nonumber \\ H_{gq}= & {} e^{- \omega z} \left[ \frac{h_{qq} - \Omega _{(+)}}{h_{qg}}~ C_1 e^{\Omega _{(+)} z} + \frac{h_{qq} - \Omega _{(-)}}{h_{qg}}~C_2 e^{\Omega _{(-)} z}\right] , \nonumber \\ H_{gg}= & {} e^{- \omega z} \left[ C'_1 e^{\Omega _{(+)} z} + C'_2 e^{\Omega _{(-)} z}\right] , \nonumber \\ H_{qg}= & {} e^{- \omega z} \left[ \frac{h_{gg} - \Omega _{(+)}}{h_{gq}}~ C'_1 e^{\Omega _{(+)} z} + \frac{h_{gg} - \Omega _{(-)}}{h_{gq}}~C'_2 e^{\Omega _{(-)} z}\right] .\nonumber \\ \end{aligned}$$

(57)

Explicit expressions for the terms $\Omega _{(\pm )}$ are presented in Eq. (B1) while $C_{1,2}$ and $C'_{1,2}$ are defined in Eq. (C1). The overall factor $e^{- \omega z}$ in Eq. (57) converts the IR-dependent Mellin factor $(w/\mu ^2)^{\omega }$ of Eq. (53) in the IR-stable factor $\left( w/k^2_{\perp }\right) ^{\omega }$.

4 Photoproduction amplitudes

It follows from Eqs. (1, 3) that the perturbative components $A_{\gamma q}, A_{\gamma g}$ of the photoproduction are related to the perturbative Compton amplitudes $T_{q,g}$ in a simple manner:

$$\begin{aligned} A_{\gamma q} = T_q|_{q^2 = 0}, \quad A_{\gamma g} = T_g|_{q^2 = 0}. \end{aligned}$$

(58)

Equation (58) holds in any form of QCD factorization but expressions for the photoproduction amplitudes are different in different forms of factorizations. We start with obtaining them in Collinear factorization.

4.1 Photoproduction amplitudes in Collinear kinematics

According to Eq. (58), putting $q^2 = 0$ in Eqs. (5, 8) should yield $A^{(col)}_{\gamma q}$ and $A^{(col)}_{\gamma q}$ in DLA. However, such procedure cannot be done in the straightforward way because the Mellin amplitudes $F^{(col)}_{q,g}$ in (8) were obtained in Refs. [24, 25] for $Q^2 \gg \mu ^2$ only and they cannot be used at $Q^2 < \mu ^2$. In order to describe $A^{(col)}_{q,g}$ at low $Q^2$, including $Q^2 = 0$, we use the prescription in the Sect. 2 and replace x, y in Eqs. (5, 8) by $\widetilde{x},\widetilde{y}$ defined in Eq. (19). Then, putting $Q^2 = 0$ in $\widetilde{x},\widetilde{y}$, we obtain

$$\begin{aligned} \widetilde{x}|_{q^2 = 0} \equiv x_0 = \mu ^2/w,~~~\widetilde{y}|_{q^2 = 0} \equiv y_0 = 0. \end{aligned}$$

(59)

Replacement of $\widetilde{x},\widetilde{y}$ by $x_0, y_0$ in Eqs. (5, 8) allows us to obtain photoproduction amplitudes in DLA in Collinear factorization: combining Eqs.  (5, 8) and (59), we obtain:

$$\begin{aligned} A^{(col)}_{\gamma q}= & {} a_{\gamma q} \int _{-\imath \infty }^{\imath \infty } \frac{d \omega }{2 \imath \pi } \left( x_0/ \beta \right) ^{-\omega } \xi ^{(+)} (\omega ) f^{(col)}_{\gamma q} (\omega ), \nonumber \\ A^{(col)}_{\gamma g}= & {} a_{\gamma q} \int _{-\imath \infty }^{\imath \infty } \frac{d \omega }{2 \imath \pi } \left( x_0/ \beta \right) ^{\omega } \xi ^{(+)} (\omega ) f^{(col)}_{\gamma g} (\omega ), \end{aligned}$$

(60)

with

$$\begin{aligned} f^{(col)}_{\gamma q}= & {} a_{\gamma q} \frac{ (\omega - h_{gg})}{G(\omega )}, \nonumber \\ f^{(col)}_{\gamma g}= & {} a_{\gamma q} \frac{ h_{qg}}{G(\omega )}, \end{aligned}$$

(61)

where $a_{\gamma q}$ is the averaged photon–quark coupling $a_{\gamma q} = \bar{e_q^2}$, $x_0 = \mu ^2/w$ and

$$\begin{aligned} G = (\omega - h_{qq})(\omega - h_{gg})- h_{gg}h_{qg}. \end{aligned}$$

(62)

Accounting for non-DL radiative correction in $A^{(col)}_{\gamma q}, A^{(col)}_{\gamma g}$ can be done by the same way as it was done in Sect. 2.2 for the Compton amplitudes.

4.2 Photoproduction amplitudes in $K_T$-factorization

DL contributions to the perturbative photoproduction amplitudes $A^{(KT)}_{\gamma q}(s, k^2_{\perp })$ and $A^{(KT)}_{\gamma g}(s, k^2_{\perp })$ come from the region

$$\begin{aligned} w \gg k^2_{\perp }. \end{aligned}$$

(63)

We will use the Mellin transform for $A^{(KT)}_{\gamma q}$ and $A^{(KT)}_{\gamma g}$ in the following form:

$$\begin{aligned} A^{(KT)}_{\gamma q}= & {} \int _{-\imath \infty }^{\imath \infty } \frac{d \omega }{2 \imath \pi } \left( w/\mu ^2\right) ^{\omega } \xi ^{(+)} (\omega ) F^{(KT)}_{\gamma q} (\omega , z), \nonumber \\ A^{(KT)}_{\gamma g}= & {} \int _{-\imath \infty }^{\imath \infty } \frac{d \omega }{2 \imath \pi } \left( w/\mu ^2\right) ^{\omega } \xi ^{(+)} (\omega ) F^{(KT)}_{\gamma g} (\omega , z). \end{aligned}$$

(64)

IREE for the Mellin amplitudes $F_{\gamma q} (\omega , z),F_{\gamma g} (\omega , z)$ are similar to Eq. (55):

$$\begin{aligned}&\frac{\partial }{\partial z} F^{(KT)}_{\gamma q} (\omega ,z) + \omega F^{(KT)}_{\gamma q} (\omega ,z) = f^{(col)}_{\gamma q} (\omega ) H_{qq} (\omega ,z) \nonumber \\&\qquad + f^{(col)}_{\gamma g} (\omega ) H_{gq} (\omega ,z), \nonumber \\&\quad \frac{\partial }{\partial z} F^{(KT)}_{\gamma g} (\omega ,z) + \omega F^{(KT)}_{\gamma g} (\omega ,z) = f^{(col)}_{\gamma q} (\omega ) H_{qg} (\omega ,z) \nonumber \\&\qquad + f^{(col)}_{\gamma g} (\omega ) H_{gg} (\omega ,z). \end{aligned}$$

(65)

Expressions for on-shell amplitudes $f^{(col)}_{\gamma q}$ and $f^{(col)}_{\gamma g}$ in the r.h.s. of Eq. (65) are given by Eq. (61) while new off-shell parton–parton amplitudes $H_{rr'} (\omega ,z)$ are unknown and should be specified. The general solution to Eq. (65) should be specified by the matching:

$$\begin{aligned} A^{(KT)}_{\gamma q}(w,z) |_{z = 0} = A^{(col)}_{\gamma q} (w). \end{aligned}$$

(66)

Solving Eq. (65) and using the matching of Eq. (64) yields expressions for $A^{(KT)}_{\gamma q}$ and $A^{(KT)}_{\gamma g}$:

$$\begin{aligned} A^{(KT)}_{\gamma q}= & {} \int _{-\imath \infty }^{\imath \infty } \frac{d \omega }{2 \imath \pi } \left( w/k^2_{\perp }\right) ^{\omega } \xi ^{(+)} (\omega ) \nonumber \\&\left[ f^{(col)}_{\gamma q}\left( 1 + \int _0^z d u e^{ \omega u} H_{qq} (\omega ,z')\right) \right. \nonumber \\&\left. + f^{(col)}_{\gamma g} \int _0^z d u e^{ \omega u} H_{gq} (\omega ,z') \right] , \nonumber \\ A^{(KT)}_{\gamma g}= & {} \int _{-\imath \infty }^{\imath \infty } \frac{d \omega }{2 \imath \pi } \left( w/k^2_{\perp }\right) ^{\omega } \xi ^{(+)} (\omega ) \nonumber \\&\left[ f^{(col)}_{\gamma q} \int _0^z d u e^{ \omega u} H_{qg} (\omega ,z') \right. \nonumber \\&\left. + f^{(col)}_{\gamma g}\left( 1 + \int _0^z d u e^{ \omega u} H_{gg} (\omega ,z')\right) \right] . \end{aligned}$$

(67)

We remind that expressions for amplitudes $f^{(col)}_{\gamma q}$ and $f^{(col)}_{\gamma g}$ can are obtained in Eq. (61) while $H_{rr'}$ are defined in Eq. (57). To conclude this Sect. we notice that non-DL corrections can be incorporated in Eqs. (60, 67) absolutely similarly to the prescription of Sect. 2.2. Transition from $K_T$ factorization to Basic one is done with replacement of $k^2_{\perp }$ by $|k^2|$.

5 Conclusion

In this paper we have studied first the perturbative amplitudes $T_{q,g}$ of elastic Compton scattering off quarks and gluons and then perturbative components $A_{\gamma q},A_{\gamma g}$ of the photoproduction amplitudes. $T_{q,g}$ were calculated in Refs. [24, 25] in DLA at small x and large photon virtualities $Q^2$ (i.e. in kinematic region B) in the framework of Collinear factorization . We converted these results in expressions which can be used at arbitrary x and $Q^2$ in Collinear, $K_T$ and basic factorizations. Extension to Region A was done with combining the total resummation of DL contributions and DGLAP description of $T_{q,g}$. By doing so we obtained in Eq. (14) the interpolation expressions reproducing $T_{q,g}$ in DLA at small x and coinciding with the DGLAP description of $T_{q,g}$ when x are not small. Using the shift of Eq. (15), we extended description $T_{q,g}$ to small $Q^2$. As a result, we arrived at Eq. (18) to the expressions for $T_{q,g}$ in Collinear factorization, which can be used at arbitrary x and $Q^2$.

In contrast to Collinear factorization, $T_{q,g}$ are the essentially off-shell in $K_T$ factorization and they cannot be described in DLA by a single expression valid at arbitrary values of virtualities $k^2_{\perp }$ of the external partons. It made us consider separately regions of moderate (Eq. (33)) and deep (Eq. 34) virtualities and obtain expressions Eqs. (47) and (52) for $T_{q,g}$ in those regions. We obtained them by constructing appropriate IREEs and solving them.

After transition from Region B to the to low $Q^2$ Region C has been studied, we became able to obtain explicit expressions (60) and (67) for the photoproduction amplitudes $A_{\gamma q}, A_{\gamma g}$ in Collinear and $K_T$ factorizations respectively.

Small-x asymptotics of amplitudes $T_{q,g}$ are of the Regge type with the same intercept in any form of QCD factorization. Because of it we considered such asymptotics in Collinear factorization (see Eq. (20)) and discussed dependence of its intercept on accuracy of the calculations: the higher is the accuracy, the lesser is the intercept. In other words, the hard Pomeron becomes the soft one, when the accuracy grows. We think that further increasing the accuracy can lead to vanishing supercritical Pomeron(s) and restoration of the Unitarity.

The next interesting point is that when $T_{q,g}$ are calculated in DLA, their asymptotics depends on the single variable $\zeta = Q^2/x^2$ as shown in Eq. (23). Neither DGLAP nor BFKL cause such dependence.

It is important to use the Regge asymptotics within their applicability region, i.e. at $x < x_{max}$, with $x_{max}$ given by Eq. (22). When $x > x_{max}$ the asymptotic is considerably less than the parent amplitudes, so such amplitudes should be used instead of the asymptotics. Ignoring this point leads to various misconceptions: for instance, appearance of artificial/model (hard) Pomerons and spin-dependent Pomerons.

To conclude, let us notice that DL Pomeron can play an important role for description of various hadronic reactions where Pomerons are used and the diffractive DIS in the first place, see e.g. [37].

Appendices

Appendix A: Expressions for the parton–parton amplitudes

$$\begin{aligned}&h_{qq} = \frac{1}{2} \Big [ \omega - Z - \frac{b_{gg} - b_{qq}}{Z}\Big ],\qquad h_{qg} = \frac{b_{qg}}{Z}~, \nonumber \\&h_{gg} = \frac{1}{2} \Big [ \omega - Z + \frac{b_{gg} - b_{qq}}{Z}\Big ],\qquad h_{gq} =\frac{b_{gq}}{Z}~, \end{aligned}$$

(A1)

where

$$\begin{aligned} Z = \frac{1}{\sqrt{2}}\sqrt{ Y + W }~, \end{aligned}$$

(A2)

with

$$\begin{aligned} Y = \omega ^2 - 2(b_{qq} + b_{gg}) \end{aligned}$$

(A3)

and

$$\begin{aligned} W = \sqrt{(\omega ^2 - 2(b_{qq} + b_{gg}))^2 - 4 (b_{qq} - b_{gg})^2 - 16b_{gq} b_{qg} }. \end{aligned}$$

(A4)

Equations (A1, A3, A4) express $h_{rr'}$ through terms $b_{rr'}$. The terms $b_{rr'}$ include the Born factors $a_{rr'}$ and contributions of non-ladder graphs $V_{rr'}$:

$$\begin{aligned} b_{rr'} = a_{rr'} + V_{rr'}. \end{aligned}$$

(A5)

The Born factors are (see Ref. [26] for detail):

$$\begin{aligned}&a_{qq} = \frac{A(\omega )C_F}{2\pi },~a_{qg} = \frac{A'(\omega )C_F}{\pi },~a_{gq} \nonumber \\&\quad = -\frac{A'(\omega )n_f}{2 \pi }. ~a_{gg} = \frac{2N A(\omega )}{\pi }, \end{aligned}$$

(A6)

where A and $A'$ stand for the running QCD couplings:

$$\begin{aligned}&A = \frac{1}{b} \left[ \frac{\eta }{\eta ^2 + \pi ^2} - \int _0^{\infty } \frac{d z e^{- \omega z}}{(z + \eta )^2 + \pi ^2}\right] , \nonumber \\&A' = \frac{1}{b} \left[ \frac{1}{\eta } - \int _0^{\infty } \frac{d z e^{- \omega z}}{(z + \eta )^2}\right] , \end{aligned}$$

(A7)

with $\eta = \ln \left( \mu ^2/\Lambda ^2_{QCD}\right)$ and b being the first coefficient of the Gell–Mann–Low function. When the running effects for the QCD coupling are neglected, $A(\omega )$ and $A'(\omega )$ are replaced by $\alpha _s$. The terms $V_{rr'}$ are represented in a similar albeit more involved way (see Ref. [26] for detail):

$$\begin{aligned} V_{rr'} = \frac{m_{rr'}}{\pi ^2} D(\omega )~, \end{aligned}$$

(A8)

with

$$\begin{aligned}&m_{qq} = \frac{C_F}{2 N}~,\quad m_{gg} = - 2N^2~,\quad m_{gq} = n_f \frac{N}{2}~,\nonumber \\&m_{qg} = - N C_F~, \end{aligned}$$

(A9)

and

$$\begin{aligned}&D(\omega ) = \frac{1}{2 b^2} \int _{0}^{\infty } d z e^{- \omega z} \ln \big ( (z + \eta )/\eta \big ) \nonumber \\&\quad \Big [ \frac{z + \eta }{(z + \eta )^2 + \pi ^2} - \frac{1}{z + \eta }\Big ]~. \end{aligned}$$

(A10)

Appendix B: Explicit expressions for ingredients of Eq. (8)

The factors $C^{(\pm )}_{q,g}$ and $\Omega _{(\pm )}$ of Eq. (5 were obtained in Refs. [24, 25]. We list them below. All of them are expressed though the parton–parton amplitudes $h_{rr'}$ of Appendix A. The factors $\Omega _{(\pm )}$ are:

$$\begin{aligned} \Omega _{(\pm )} = \frac{1}{2} \left[ h_{gg} + h_{qq} \pm \sqrt{R}\right] \end{aligned}$$

(B1)

and

$$\begin{aligned} R&= (h_{gg} + h_{qq})^2 - 4(h_{qq}h_{gg} - h_{qg}h_{gq}) \nonumber \\&= (h_{gg} - h_{qq})^2 + 4 h_{qg}h_{gq} . \end{aligned}$$

(B2)

The factors $C_{(\pm )}$ are also expressed through the parton–parton amplitudes:

$$\begin{aligned} C_q^{(+)}= & {} a_{\gamma q}\frac{h_{qg}h_{gq} - (\omega - h_{gg})\left( h_{gg} - h_{qq} - \sqrt{R}\right) }{2 G \sqrt{R}}, \nonumber \\ C_q^{(-)}= & {} a_{\gamma q}\frac{ -h_{qg}h_{gq} + (\omega - h_{gg})\left( h_{gg} - h_{qq} + \sqrt{R}\right) }{2 G \sqrt{R}}. \nonumber \\ \end{aligned}$$

(B3)

$$\begin{aligned} C_g^{(+)}= & {} C_q^{(+)} \frac{h_{gg} - h_{qq} + \sqrt{R}}{2h_{qg}}, \nonumber \\ C_g^{(-)}= & {} C_q^{(-)} \frac{h_{gg} - h_{qq} - \sqrt{R}}{2h_{qg}}. \end{aligned}$$

(B4)

APPENDIX C: Expressions for the factors $C_{1,2}$ and $C'_{1,2}$ of Eq. (57)

The terms

$$\begin{aligned} C_1 = \frac{2 h_{qg}h_{gq} - h^2_{qq} + h_{qq}h_{gg} + h_{qq}\sqrt{R}}{2 \sqrt{R}}, \nonumber \\ C_2 = \frac{h^2_{qq} - h_{qq}h_{gg} - 2 h_{qg}h_{gq} + h_{qq}\sqrt{R}}{2 \sqrt{R}}, \nonumber \\ C'_1 = \frac{2 h_{qg}h_{gq} - h^2_{gg} + h_{qq}h_{gg} + h_{gg}\sqrt{R}}{2 \sqrt{R}}, \nonumber \\ C'_2 = \frac{h^2_{gg} - h_{qq}h_{gg} - 2 h_{qg}h_{gq} + h_{gg}\sqrt{R}}{2 \sqrt{R}}, \end{aligned}$$

(C1)

where R is given by Eq. (B2).