1 Introduction

Precision cosmology is imperfect without the precise measurements in physical observations of the universe at different scales and epochs. The extent of precision in observations decides the extent of our knowledge of the physical system. Unfortunately, the major portion of our observable universe is not completely known to us in Einstein’s General Relativity (GR) framework. Also, Einstein’s gravity theory with a positive cosmological constant (\(\Lambda \)) based on GR supported by observations still cannot be regarded as a completely satisfactory gravity theory because of the recent stronger-than-before Planck’s observation of an accelerating universe (having the shifted w from -1) and its inability to reconcile with the quantum theory completely and also, more importantly, the fundamental properties of the dark sector (dark energy and cold dark matter) are largely unknown besides its distribution. Thus, the observational evidences at different redshifts nurture the concept of modified gravity theory instead of the Einstein’s physical gravity theory of GR with \(\Lambda \) (positive) and cold dark matter (CDM) [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. The investigation of deviation in Einstein’s GR theory has become an active area of research under the study of precision concordance cosmology with sufficient motivation to search for an alternative theory of gravity.

Brans and Dicke first explored the scalar-tensor approach of gravity theory as an alternative to the Einstein–Hilbert (E–H) gravity theory [17] and thereafter Buchdahl, Starobinsky and others carried out the study of higher order Lagrangian or non-linear Lagrangian for exploring the cosmic evolution and also for the phenomenological explanation of the major observational issues at different cosmological redshifts of the universe [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46]. The main implicit strength of the modified gravity theory can be understood in two ways. On one hand, it can address the dark sector (dark matter and dark energy) with the different degrees of freedom, [32] and on the other, it can precisely address the deviation from the existing gravity theory i.e. Einstein’s GR theory with some new dynamical features, which at present is very exciting issue in literature [47,48,49,50,51,52,53]. Such alternate gravity theory may also pave a possible approach to study the unified theory of dark matter and dark energy [54].

Along this direction, as motivated by the dynamical modelling of massive test masses in f(R) gravity model by B\(\ddot{o}\)hmer et al. [55] and also by our recently investigated power-law f(R) model at low redshifts [49,50,51] and by others [56,57,58,59] for the clustered dark matter explanation, we further analyze here the strict phenomenological constraints on the model parameter \(\delta \) in \(R\rightarrow R^{1+\delta }\). We investigate the constraints corresponding to different geodesics (null and non-null) along with their conformal analogue at the galactic and planetary scales under an idealistic consideration with the f(R) modified potential explored in [57,58,59]. Moreover, our recent combined analysis of light deflection profiles via rotation curves for typical spiral massive galaxies may, in principle, also distinguish the present f(R) model from other profiles in standard dark matter model of galaxy (say Pseudo-isothermal model) in terms of lensing angle [51]. With such motivation along with work of several authors such as [55], we look for \(\delta \) as a distinguishing parameter for the phenomenological investigation of constraints through a study of different geodesics with the conformal analogue. Such power-law f(R) modification was initially carried out for study of the cosmic evolution at very early epochs, late-time epochs and for the explanation of galactic dynamics and [55,56,57,58,59] and [60,61,62].

From the phenomenological point of view, it seems that, using the baryonic matter content, the f(R) formulation has scope for explanation of the most abundant dark sector of the energy budget of our universe. From the mathematical point of view motivated by the earlier Jordan–Brans–Dicke Lagrangian [17], the f(R) action formulation can be recast into the scalar-tensor form so that one can clearly see the appearance of an extra scalar degree of freedom (scalar field) which replaces the dark sector, unlike some gravity theories in which we have an ad hoc scalar fields [63]. Such an extra f(R) scalar degree of freedom has non-minimal coupling with the spacetime geometry. Thus, in alternate gravity theories, gravitational interaction can also be mediated via the scalar degrees of freedom (scalaron) together with the spacetime metric tensor (\(g_{\mu \nu }\)). Further, f(R) formulation also has two characteristic length scales, of which one is the Schwarzschild length scale and the other is the f(R) characteristic length scale which has the advantage of providing a screening mechanism [47, 48] corresponding to the extra force in high-density environments.

For investigating the physical observable effects of such extra f(R) scalar degrees of freedom alone (scalaron as scalar field particle), it is preferred in the literature that the extra scalar degree of freedom should be coupled minimally with the Einstein–Hilbert spacetime geometry (R) in the action integral so that we can trace its dynamical influence via solving the second-order field equations instead of fourth-order field equations. This can be possible through the conformal analysis of spacetime metric tensor [63]. Thus, we have two f(R) gravity actions before and after the conformal transformation i.e., Jordan frame (because the dynamical equations resembles the Jordan–Brans–Dicke gravity theory) and conformal Einstein frame (because the dynamical equations resembles with the Einstein–Hilbert gravity theory). Also, pertaining to the physical observations at different scales, which frame one should prefer is still under debate and several research works have been reported from the early investigations [64,65,66,67,68,69], till recent analyses [70,71,72,73,74,75,76]. Hence, the well-known issue in the literature regarding the choice of a true physical frame is long-standing i.e. which spacetime metric tensor among the conformally related (\(g_{\mu \nu }\) or \({\tilde{g}}_{\mu \nu }\) ) should one may choose for representing the geometry of spacetime pertaining to the physical observations. Some scientists claim that both frames are equivalent whereas others claim opposite [73,74,75,76]. The issue can only be settled down at the classical level through the phenomenological investigations of the different physical systems.

Several authors had explored this issue before without any firm discussions regarding the most profound physical observations confronted with different geodesics (null and non-null) along with its conformal analog under the shifted (\(R\rightarrow R^{1+\delta }\)) Einstein–Hilbert theory at local scales. Therefore, together with discussions on different conformally related geodesics, we also explore the nature of an additional force in terms of f(R) model parameter \(\delta \). We further envisage this shifted parameter (\(\delta \)) as a distinguishing tool for the study of motion at different geodesics to impose the strict constraints on the f(R) model through observations.

We also acquired the motivation to explore the bare effects of f(R) modification at different scales from some pre-existing resources. These include the analysis about the limit to GR in f(R) theory of gravity by Olmo [77], study of f(R) model constraints at different scale by Hu and Sawicki [40], the early and recent investigation of the Yukawa-like potential in f(R) theory [78, 79], study of power-law f(R) gravity theory [56,57,58,59], recent investigation of an uncertainty in the GR prediction for the Mercury orbit under the current (MESSENGER) and planned (the European-Japanese BepiColombo) missions [80,81,82,83,84], the analysis of Yukawa type potential in the Schwarzschild-like background for perihelion precession of planets to address the gauge bosons as a possible candidate of fuzzy dark matter [85] and the relativistic effects and dark matter in the Solar system through the observations of planets and spacecraft [86].

In the present work, we study the deviations in GR in the form \(R^{1+\delta }\) (\(\delta \) being the dimensionless physical observable quantity). Instead of investigating the Yukawa-like correction potential as done by other authors [78, 79], we explore the bare f(R) effects in the form of \(\delta \) for various observations without including any versions of the dark sector. Such form can be modelled in the f(R) gravity framework. Also, since physical observations of the system are confronted with different geodesics, we obtain its conformal analogue and investigate the deviations at different scales. For instance, we study the geodesics (null and non-null) along with their conformal analogue at local scales under ideal considerations and obtain the strict constraints on \(\delta \) at galactic and planetary scales. Such constraints are strict in the sense that for orbital motions at local scales, \(\delta \) can be physically represented as \(v_{orbital}^2/c^2\) with known \(v_{orbital}\) [55]. Further, we explore the extent and nature of an additional force on the test mass due to the shifted f(R) modification parameterized by \(\delta \). The present paper is organized in different sections as follows. In Sect. 2, we discuss dynamical f(R) field equations with reference to the Jordan and Einstein frames. In Sect. 3, we discuss the parametrization for geodesics and investigate the null geodesics for the conformally consistent light deflection angles with \(\delta \ll 1\) due to massive spiral galaxies as a lens. In Sect. 4, we discuss the non-null geodesics and investigate its Newtonian limit for the explanation of additional force in f(R) theory. Further, we explore it for the conformally related orbital precession of planet (Mercury) at the solar system scale and analyse and diagnose the tight constraint via specifying \(\delta \) as \(v^2_{orbital}/c^2\). We end with the discussion and concluding remarks on results about the constraints in Sect. 5.

Throughout the paper, we follow the signature of the spacetime metric as (−, +, +, +) and indices \(\mu \) (or \(\nu \)) = (0, 1, 2, 3).

2 f(R) gravity and conformally related field equations

Lovelock’s theorem suggests a possible modification to the gravity theory. Accordingly, Einstein’s gravity theory of GR is unique theory of gravity, if we demand [87]: (i) the metric tensor (\(g_{\mu \nu }\)) is the only field, (ii) invariance under diffeomorphism, (iii) the equation of motion is second order, and (iv) to work with four dimensions.

Any violation of one of these assumptions will provide an alternative or modified gravity theory. f(R) gravity theory focuses on the metric tensor and equations of motion. The metric tensor (\(g_{\mu \nu }\)) is not the only field (but also scalar field) and also the equations of motions are not second order (but becomes forth-order) in f(R) gravity theory [36, 37].

We consider the 4-dimensional action integral having the gravity Lagrangian density of some general function f(R) of the Ricci scalar with the usual standard matter action in units of \(c=\hbar =1\) as

$$\begin{aligned} {\mathcal {A}}= \frac{1}{2}\int \sqrt{-g} \left[ \frac{1}{8\pi G_N}f(R)\right] d^{4}x+ {\mathcal {A}}_m(g_{\mu \nu }, \Psi _m) , \end{aligned}$$
(1)

where g is the determinant of the metric tensor \(g_{\mu \nu }\), \(8\pi G_N\) is the Einstein’s gravitational constant with \(G_N\) the Newtonian gravitational constant, and \({\mathcal {A}}_m\) is the action of the standard matter part with matter field \(\Psi _m\).

Varying the action (1) with respect to \(g_{\mu \nu }\), we obtain the generalized Einstein field equations given by

$$\begin{aligned}&{F(R)R_{\mu \nu }-\frac{1}{2}f(R)g_{\mu \nu }-\nabla _{\mu } \nabla _{\nu } F(R)} \nonumber \\&+{g_{\mu \nu }\Box F(R)=\kappa ^2 T_{\mu \nu }}, \end{aligned}$$
(2)

where \(F(R)\equiv f_{R}=\frac{\partial f}{\partial R}\), \(T_{\mu \nu }\) is the energy-momentum tensor for the standard matter and \(\kappa ^2=8\pi G=M_{pl}^{-2}\) with \(M_{pl}\) as the Planck mass.

We can also write the gravity Lagrangian density of Eq. (1) similar to the Jordan–Brans–Dicke gravity theory [17] whose action is given as

$$\begin{aligned} {\mathcal {A}}_{J}= \int \sqrt{-g} \left[ \frac{1}{2\kappa ^2}R F(R)- U\right] d^{4}x , \end{aligned}$$
(3)

where \(U=\frac{RF(R)-f(R)}{2\kappa ^2}\).

From the action written in the form of Eq. (3), we can see that the extra scalar degrees of freedom in the form of F(R) are non-minimally coupled with the geometry (R) and have the similar form as observed in the Jordan–Brans–Dicke gravity action [17]. One can also explore Eq. (1) in Helmholtz-Jordan frame and obtain the same f(R) action which have non-vanishing second derivative of f(R) w.r.t. R [19, 20]. We can perform conformal re-scaling of the spacetime metric tensor to explore further the dynamics contained in the extra scalar degrees of freedom.

Therefore, following the well established procedure of conformal transformation of the scalar-tensor theory [63], the conformal map from the 4-dimensional spacetime manifold \({\mathcal {M}}_J\) with Jordan frame metric \(g_{\mu \nu }\) to the 4-dimensional spacetime manifold \({\mathcal {M}}_E\) but with Einstein frame metric \({\tilde{g}}_{\mu \nu }\),

$$\begin{aligned} {\tilde{g}}_{\mu \nu }=\Omega ^2 g_{\mu \nu }=F(R) g_{\mu \nu }, \end{aligned}$$
(4)

along with

$$\begin{aligned} R=\Omega ^2[{\tilde{R}} + 6 {\tilde{\Box }} \omega - 6 {\tilde{g}}^{\mu \nu } \partial _{\mu } \omega \partial _{\nu } \omega ] , \end{aligned}$$
(5)

whose second term (within square bracket) vanishes when Eq. (5) is used in the action (3) by following the Gauss’ theorem of total derivative which transforms the action (3) in Einstein frame as

$$\begin{aligned} {\mathcal {A}}_{E}= \int d^{4}x \sqrt{-{\tilde{g}}} \left[ \frac{1}{2\kappa ^2}{\tilde{R}}-6{\tilde{g}}^{\mu \nu }\partial _{\mu } \omega \partial _{\nu } \omega - V(\omega )\right] , \end{aligned}$$
(6)

where

$$\begin{aligned} V(\omega )=\frac{U}{2F^2}=\frac{RF-f}{2\kappa ^2 F^2} \end{aligned}$$
(7)

is the scalar potential term written in parametric form for general f(R) model which has non-vanishing second derivative and \(\omega \equiv \ln \Omega \), \(\Omega \) being the conformal factor.

Here, in this section, instead of considering a new parametric scalar fieldFootnote 1 (\(\phi \)), we work out with the action (6) in its simplest form and explore its field equations.

The field equations in this frame are obtained by varying Eq. (6) w.r.t the metric tensor (\({\tilde{g}}^{\mu \nu }\)) and the scalar field (\(\omega \)) which are given as [88]

$$\begin{aligned} {\tilde{G}}_{\mu \nu }= 6\left[ {\tilde{\nabla }}_\mu \omega {\tilde{\nabla }}_\nu \omega - \frac{1}{2} {\tilde{g}}_{\mu \nu } ({\tilde{\nabla }} \omega )^2 \right] - {\tilde{g}}_{\mu \nu } V(\omega ) , \end{aligned}$$
(8)

and

$$\begin{aligned} {\tilde{\Box }} \omega =\frac{1}{6} V^\prime (\omega ). \end{aligned}$$
(9)

Now, one can obtain the field equations by transforming Eqs. (8) and (9) back to notation (without tilde) in the Jordan frame as [88]

$$\begin{aligned} {G}_{\mu \nu }= \left[ -2{\nabla }_\mu {\nabla }_\nu \omega +4 {\nabla }_\mu \omega {\nabla }_\nu \omega \right] - {g}_{\mu \nu } W(\omega ) , \end{aligned}$$
(10)

where

$$\begin{aligned} W( \omega )=\frac{f+RF}{6F} V^\prime (\omega ). \end{aligned}$$
(11)

and

$$\begin{aligned} {\Box } \omega =\frac{e^{2\omega }}{6} V^\prime (\omega )+2(\nabla \omega )^2 . \end{aligned}$$
(12)

Hence, we obtain the conformally related equations.

Thus, one can mathematically transform set of equations between the two versions of frame with \(g_{\mu \nu }\) or \({\tilde{g}}_{\mu \nu }\). But their physical equivalence is still under debate [65,66,67, 70,71,72,73,74,75,76] and can be settled down through the phenomenological investigations. We wish to obtain the precise constraints through conformal analysis of the f(R) theory with the physical observations corresponding to different geodesics.

Therefore, we investigate the null and non-null geodesic equations at the local scales. We then explore the light deflection angle due to typical massive galaxies and also the perihelion advance of the planet like Mercury’s orbit in the shifted f(R) model with parameter \(\delta \).

3 f(R) conformal investigation of geodesics and phenomenology for null geodesics

The conformal transformation generalizes the spacetime metric according to the form of f(R) (see Eq. 4). Here, we investigate the geodesic equations in different ways i.e., under the re-parametrization and under the conformal analysis for addressing the null and non null dynamics. We express its conformally shifted parameter with new parameter (\(\rho \)) instead of using tilde notations. The statement can be understood as the action is re-parametrization invariant, so it is possible to express the geodesics (which is a geometrical entity) with different parameter, say \(\uplambda \). For instance, the geodesics equations in terms of proper time can be written for the material particle following the curve (\(x^\gamma (\tau )\)) as,

$$\begin{aligned} \frac{d^2{x^\gamma }}{d\tau ^2}+ \Gamma ^{\gamma }_{\mu \nu }\frac{d{x^\mu }}{d\tau }\frac{d{x^\nu }}{d\tau }=0, \end{aligned}$$
(13)

In terms of new parameter \(\uplambda \), we can express (13) as,

$$\begin{aligned} \frac{d^2{x^\gamma }}{d\uplambda ^2}+\Gamma ^{\gamma }_{\mu \nu }\frac{d{x^\mu }}{d\uplambda }\frac{d{x^\nu }}{d\uplambda }+\frac{d{x^\gamma }}{d\uplambda } \frac{d^2{\uplambda }}{d\tau ^2}\frac{d{\tau }}{d\uplambda }=0, \end{aligned}$$
(14)

Thus, we obtain the generalized equation for geodesics (\(x^\gamma (\uplambda )\)).

The affine or non-affine nature of the newly assigned parameter can be traced if it is expressible in terms of the old parameter (\(\tau \)) as \(\tau \rightarrow \tau (\uplambda )\) (or possibly vice-versa). So, on switching from \(x^\gamma (\tau )\) to \(x^\gamma (\uplambda )\), if \(\tau \) and \(\uplambda \) has a linear relation, then only we can recover the original geodesics equations (13). Such parameters in GR literature can be assigned as affine parameters.

Now, if \(x^\gamma (\uplambda )\) represents the curves in \(g_{\mu \nu }\), then under Eq. (4), the Levi-Civita connections in \({\tilde{g}}_{\mu \nu }\) have the following relation with the Levi-Civita connections in \({g}_{\mu \nu }\) as,

$$\begin{aligned} \begin{aligned} {\Gamma }^{\gamma }_{\mu \nu } ({\tilde{g}}_{\mu {\nu }})&={\Gamma }^{\gamma }_{\mu {\nu }} ({g}_{\mu {\nu }})+ {\delta }^{\gamma }_{\nu }{\partial _{\mu }}(\ln \Omega )+{\delta }^{\gamma _{\mu }}{\partial _{\nu }}(\ln \Omega )\\&\quad -g_{\mu {\nu }} {{\partial }^{\gamma }}(\ln \Omega ). \end{aligned} \end{aligned}$$
(15)

Thus, the geodesic equation now gets conformally transformed under Eq. (4) and is given as,

$$\begin{aligned} \begin{aligned}&\frac{d^2{x^\gamma }}{d\uplambda ^2}+\Gamma ^{\gamma }_{\mu \nu }\frac{d{x^\mu }}{d\uplambda }\frac{d{x^\nu }}{d\uplambda }+ 2 \frac{d}{d\uplambda }(\ln \Omega ) \frac{d{x^\gamma }}{d\uplambda }\\&\quad -\partial ^\gamma (\ln \Omega ) g_{\mu \nu }\frac{d{x^\mu }}{d\uplambda }\frac{d{x^\nu }}{d\uplambda }=0 . \end{aligned} \end{aligned}$$
(16)

From this equation, it becomes clear that if \(x^\gamma (\uplambda )\) represents the geodesics in \(g_{\mu \nu }\), then it may not be a geodesic in \({\tilde{g}}_{\mu \nu }\). Therefore, for the curve \(x^\gamma (\uplambda )\) in \({\tilde{g}}_{\mu \nu }\), the parameter \(\uplambda \) must also be conformally shifted.

It is interesting that Eq. (16) resembles the generalized geodesic equation (14) but under the f(R) conformal transformation and hence it represents conformally modified geodesics in f(R) theory. The nature of its parameter \(\uplambda \) in terms of conformal shifting or affine (non-affine) as argued for Eq. (14) can be traced for the null and non-null cases. For the null case, the last term of conformally modified geodesic equation (16) vanishes because \(g_{\mu \nu } u^\mu u^\nu =0\). So, Eq. (16) gets reduced to

$$\begin{aligned} \frac{d^2{x^\gamma }}{d\uplambda ^2}+\Gamma ^{\gamma }_{\mu \nu }\frac{d{x^\mu }}{d\uplambda }\frac{d{x^\nu }}{d\uplambda }+2 \frac{d}{d\uplambda }(\ln \Omega ) \frac{d{x^\gamma }}{d\uplambda }=0 . \end{aligned}$$
(17)

Further, to trace the conformal shift (or affine nature) of parameter \(\uplambda \), we reduce the Eq. (17) as argued for Eq. (14).

Therefore, we re-parameterize the Eq. (17) under \(\uplambda \rightarrow \rho \), with \(\rho \) as a new parameter (conformally shifted), and then it is given as,

$$\begin{aligned} \begin{aligned}&\frac{d}{d\rho }\left( \frac{dx^\gamma }{d\rho }\frac{d\rho }{d\uplambda }\right) \frac{d\rho }{d\uplambda }+ \Gamma ^{\gamma }_{\mu \nu }\frac{d{x^\mu }}{d\rho }\frac{d{x^\nu }}{d\rho } \left( \frac{d\rho }{d\uplambda } \right) ^2\\&\quad + 2\frac{d{x^\gamma }}{d\rho }\frac{d\rho }{d\uplambda }\frac{d}{d\rho }(\ln \Omega ) \frac{d\rho }{d\uplambda }=0 . \end{aligned} \end{aligned}$$
(18)

We find that, if the parameter \(\rho \) has a conformal relation with \(\uplambda \) as,

$$\begin{aligned} \frac{d\rho }{d\uplambda }=\Omega ^{-2}, \end{aligned}$$
(19)

then under such conformal relation, Eq. (18) becomes,

$$\begin{aligned} \frac{d^2{x^\gamma }}{d\rho ^2}+ \Gamma ^{\gamma }_{\mu \nu }\frac{d{x^\mu }}{d\rho }\frac{d{x^\nu }}{d\rho }=0. \end{aligned}$$
(20)

Thus, the geodesics of particles having zero rest mass remain unaffected for the conformally related spacetime equation (4) in f(R) theory. Hence, \(\rho \) can be regarded as a conformally shifted (or an affine) parameter. Therefore, the conformally transformed spacetime metric exhibits the same causal structure.

Now, for the phenomenological study of null geodesics, we explore the light deflection angle due to a typical spiral massive galaxies. Following [57,58,59], let us consider a static Schwarzschild-like metric element outside the source under the 4-dimensional spacetime with \(c=1\) as

$$\begin{aligned} ds^{2}= -A(r)dt^{2}+B(r)dr^2+r^2( d\theta ^{2}+\sin ^{2}\theta d\varphi ^{2}), \end{aligned}$$
(21)

where the quantities A(r) and B(r) act like the functions of weak gravitational potential (\(\Phi \)). The actual form of potentials can be determined via solving the vacuum f(R) field equations (2) for the specific function of Ricci scalar, f(R) entering in the generalized Einstein–Hilbert gravity action integral (1).

Under the conformal transformation (4), Eq. (21) becomes

$$\begin{aligned} {d{\tilde{s}}}^{2}= -{\tilde{A}}dt^{2} + {\tilde{B}}{d{\tilde{r}}}^2 + {\tilde{r}}^2( d\theta ^{2}+\sin ^{2}\theta d\varphi ^{2}). \end{aligned}$$
(22)

Now, to calculate the deflection angle in f(R) gravity theory, we must know the complete form of metric elements (Eqs. (21) or (22)) or the form of the effective potential. For the investigation of light deflection angle, we closely follow the references [57, 58]. It becomes clear from the discussions of [57] that the formal expression for the total deflection angle of light ray (following null geodesics) in f(R) gravity theory must remain the same under the weak field limit of Schwarzschild-like metric. The components of such metric critically depend upon the expression chosen for f(R).

Thus, for the physically motivated metric element like Eq. (21) with f(R) obeying the power-law in Ricci curvature scalar (\(f(R)\propto R^{(1+\delta )}, with \delta \) as the dimensionless constant), we can conventionally write an explicit relation among the metric components in the weak field limit as \(A=\frac{1}{B}=1+2\Phi _{effective}(r)\) and look for a solution of f(R) field equations.

For a point-like baryonic mass M in f(R) background, we look for a solution of vacuum f(R) field equations (2) with the effective gravitational potential (\(\Phi _{effective}\)) that may be written as [58]

$$\begin{aligned} {\Phi _{effective}(r)}\approx -\frac{GM}{2r}\left[ 1+ \left( \frac{r}{r_c}\right) ^{\beta }\right] , \end{aligned}$$
(23)

where \(\beta \) and \(r_c\) are the free parameters.

The main motivation to look for such solution of f(R) field equations (2) in vacuum arises from the fact that the fourth-order f(R) theories induce modifications to the gravitational potential by altering the Newtonian 1/r scaling [58, 89]. Moreover, in metric formalism, the gravity theory of order 2N possesses N characteristic length scales [47, 48, 90]. For instance, Einstein’s GR is a second-order metric theory of gravity, and so it has one characteristic length scale which is the Schwarzschild length scale. f(R) formulation is built on a fourth-order theory and it must have two characteristic length scales, of which one is the Schwarzschild length scale and the other is the f(R) characteristic length scale appearing generally because of the extent of power-law modification (\(f(R)\propto R^{(1+\delta )}\)) in the gravity action integral.

In order to check whether the assumed Eq. (23) is indeed a viable solution of vacuum f(R) field equations (2), or in order to find the unknown components of the metric element (21), i.e., functions A(r) and B(r), we first obtain and combine the 00-vacuum component with the trace of the f(R) field equations (2) in the absence of matter (\(T_{\mu \nu }=0\)) that is \(3\Box F(R) +R F(R) -2 f(R)=0\), to obtain a single equation given as

$$\begin{aligned} {g_{00}\left[ \frac{F(R)R_{00}}{g_{00}}- \frac{F(R)R}{3}-\frac{F(R)_{;00}}{g_{00}}+\frac{f(R)}{6}\right] =0. } \end{aligned}$$
(24)

Since \(g_{00}\ne 0\), so for \(f(R)\propto R^{(1+\delta )}\), the above equation becomes

$$\begin{aligned} {R_{00}(r)=\frac{2\delta +1}{6(1+\delta )} A(r) R(r)- \frac{\delta }{2 B(r)}\frac{dA(r)}{dr}\frac{d}{dr}\ln R(r), }\nonumber \\ \end{aligned}$$
(25)

while the trace equation becomes

$$\begin{aligned} {\Box R^{\delta }=\frac{1-\delta }{3(1+\delta )}R^{1+\delta }.} \end{aligned}$$
(26)

Clearly, we can recover the Schwarzschild-like solution with \(\delta =0\).

Now, we have two non-linear coupled differential equations (25) and (26) for the two functions A(r) and B(r) which are both solved for Eq. (23) if [58]

$$\begin{aligned} {\delta (\beta -3)[-\beta (1+\beta )V_1 \eta ^{\beta -3}]^{\delta }{\times } \left( 1+\frac{\beta V_1 {\mathcal {P}}_0}{{\mathcal {P}}_1\eta }\right) {\mathcal {P}}_1\eta =0,} \nonumber \\ \end{aligned}$$
(27)

with \(\eta \equiv r/r_c\), \(V_1\equiv GM/c^2r_c\) and

$$\begin{aligned}&{{\mathcal {P}}_0\equiv 3(\beta -3)^2({\bar{\delta }})^3} {-(5\beta ^2-31\beta +48)({\bar{\delta }})^2}\nonumber \\&\qquad \quad -{(3\beta ^2-16\beta +17){\bar{\delta }}} { -(\beta ^2-4\beta -5),} \end{aligned}$$
(28)
$$\begin{aligned}&{{\mathcal {P}}_1\equiv 3(\beta -3)^2(1-\beta )({\bar{\delta }})^3 } {+(5\beta -7)(\beta -3)^2({\bar{\delta }})^2}\nonumber \\&\qquad \quad -{(3\beta ^3-17\beta ^2+34\beta -36){\bar{\delta }}} {+(\beta ^2-3\beta -4)\beta ,}\nonumber \\ \end{aligned}$$
(29)

where \({\bar{\delta }}\equiv 1+\delta \).

Equation (27) is identically satisfied for particular values of \(\delta \) and \(\beta \). However, there are some simple considerations that allow us to exclude such values. As a consequence, we can look for a factored solution of Eq. (27) by solving

$$\begin{aligned} {{\mathcal {P}}_1({\bar{\delta }},\beta )\eta +\beta V_1{\mathcal {P}}_0({\bar{\delta }},\beta )=0}. \end{aligned}$$
(30)

In the limit to local scales as we are considering, \(V_1(\equiv GM/c^2r_c) \ll 1\). Therefore, Eq. (30) gets reduced to

$$\begin{aligned} {{\mathcal {P}}_1({\bar{\delta }},\beta )\eta =0.} \end{aligned}$$
(31)

It is clear that Eq. (31) is an algebraic equation for \(\beta \) as a function of \({\bar{\delta }}\) with the following three solutions:

$$\begin{aligned} {\beta }={\left\{ \begin{array}{ll} \frac{3{\bar{\delta }}-4}{{\bar{\delta }}-1}, &{}\\ \frac{12{\bar{\delta }}^2-7{\bar{\delta }}-1-\sqrt{p({\bar{\delta }})}}{q({\bar{\delta }})}, &{}\\ \frac{12{\bar{\delta }}^2-7{\bar{\delta }}-1+\sqrt{p({\bar{\delta }})}}{q({\bar{\delta }})}, \end{array}\right. } \end{aligned}$$
(32)

where

\(p({\bar{\delta }})\equiv 36 {\bar{\delta }}^4 + 12 {\bar{\delta }}^3- 83 {\bar{\delta }}^2+ 50 {\bar{\delta }}+1\), and

\(q({\bar{\delta }})\equiv 6{\bar{\delta }}^2- 4{\bar{\delta }}+2.\)

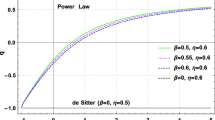
It is easy to check that, for \(\delta =0\), the second expression above gives \(\beta =0\), that is, the approximate solution reduces to the Newtonian one as expected. Therefore, we work with the second solution, i.e., with \(\beta \) given as

(33)

for investigating the local dynamics of effective potential given by Eq. (23).

Furthermore, we have also recently investigated the constraint on the model parameter \(\delta \) to be \({\mathcal {O}}(10^{-6})\) from the combined study of flatness profile of rotation curves and the corresponding deflection angle profile in the halo of scalaron cloud (instead of dark matter) surrounding the typical massive galaxies [35, 37]. B\(\ddot{o}\)ehmer et al., investigated the small value of the power-law f(R) model [55] valid for the discussion at local scale. Therefore, it is possible to rewrite Eq. (23) in the narrowest range of \(\delta \) and \(\beta \) for the study of local scale dynamics. In the extremely narrow range, the orders of \(\delta \) and \(\beta \) are equal (Fig. 1).

Fig. 1
figure 1

The plot shows the mutual behaviour of small values of \(\delta \) and \(\beta \). It is clear that in the very narrow range, we can consider \({\mathcal {O}}\)(\(\delta \))\(\approx \) \({\mathcal {O}}\)(\(\beta \))

Full size image

Thus, we can express Eq. (23) in terms of f(R) model parameter \(\delta \) for small values as

$$\begin{aligned} {\Phi _{effective}(r)}\approx -\frac{GM}{2r}\left[ 1+ \left( \frac{r}{r_c}\right) ^{\delta }\right] . \end{aligned}$$
(34)

Clearly, for \(\delta =0\), we recover the GR Lagrangian along with its relevant Newtonian potential.

The profile of \(\delta \) concerning \(\Phi _{effective}\) can be understood from Fig. 2.

Fig. 2
figure 2

The behaviour of \(\Phi _{eff}\) diverges for \(\delta >1\) (it has an unstable profile), whereas \(\delta <1\) has a suitable profile for the interpretation of galactic dynamics with \(\frac{r}{r_c}>1\)

Full size image

Thus, we prefer to work with the small values of model parameter \(\delta \). Based on our recent investigation of constraints on \(\delta \) [35, 37], we have \(\beta \ll 1\) for \(\delta \ll 1\), (from Fig. 1), that is, \({\mathcal {O}}\)(\(\delta \))\(\approx \) \({\mathcal {O}}\)(\(\beta \)). Also, since we are interested in the significant effect of f(R) theory in removing the requirement for the presence of dark matter and not in the accurate modeling of the lens system, we assume that the lens is spherically symmetric, point-like system and study the geodesic, i.e., null geodesics (for lensing angle investigation) in contrast to the extended mass profile explored by Capozziello et al. This is the main reason for distinction of the investigated constraints on \(\delta \) (or \(\beta \)) from the other references as in [58, 59].

Under the conformal transformation \({\tilde{r}}= \Omega r \) (obtained through Eqs. (21) and (22)), the effective potential (Eq. (34)) can be conformally shifted on making use of Eq. (4) in the weak field limit and is written as,

$$\begin{aligned} {\Phi _{effective}({\tilde{r}})}\approx -\frac{GM}{2{\tilde{r}}} \left( 1+{\frac{\phi ({\tilde{r}})}{\sqrt{6} M_{Pl.}}} \right) \left[ 1+ \left( \frac{{\tilde{r}}}{{\tilde{r}}_c}\right) ^{\delta }\right] ,\nonumber \\ \end{aligned}$$
(35)

where \(\phi ({\tilde{r}})\) is the scalar field in the Einstein frame. Further, with Eq. (4) under the footnote (1) for \(f(R)=\frac{R^{1+\delta }}{R_{(c)} ^{\delta }}\) with \(R_{(c)}\) as a weight constant having dimension of Ricci Scalar (R), we have

$$\begin{aligned} R= R_{(c)}\left[ \frac{e^{\kappa \phi \sqrt{\frac{2}{3}}}}{1+\delta }\right] ^{\frac{1}{\delta }}. \end{aligned}$$
(36)

In the weak field limit, \(\kappa \phi \ll 1\) with \(\frac{R}{R_{(c)}}\) normalized to unity, we have

$$\begin{aligned} \delta = {\frac{2\phi ({\tilde{r}})}{\sqrt{6} M_{pl.}}}. \end{aligned}$$
(37)

Thus, Eq. (35) can be rewritten on using Eq. (37) as,

$$\begin{aligned} {\Phi _{effective}({\tilde{r}})}\approx -\frac{GM}{2{\tilde{r}}} \left( 1+\frac{\delta }{2}\right) \left[ 1+ \left( \frac{{\tilde{r}}}{{\tilde{r}}_c}\right) ^{\delta }\right] . \end{aligned}$$
(38)

The light deflection angle for a spherically symmetric lens (a typical massive spiral galaxy) with the effective potential (Eq. (34)), in f(R) background is given as [57]

$$\begin{aligned} {\alpha }= \frac{2GM}{c^2 r_c}\left( \frac{\xi }{r_c}\right) ^{-1}\left[ 1+\left( \frac{\xi }{r_c}\right) ^{\delta } \frac{\sqrt{\pi }(1-\delta )\Gamma (1-\frac{\delta }{2})}{2\Gamma (\frac{3}{2}-\frac{\delta }{2})}\right] ,\nonumber \\ \end{aligned}$$
(39)

where, \(\xi \) is a two-dimensional impact parameter, G is the Newtonian gravitational constant (\(= 4.3\times 10^{-6}\) kpc km\(^{2}\) sec\(^{-2}\) M \(_{\odot }^{-1}\)), \(r_c\) is fundamental scaling parameter in f(R) theory apart from the Schwarzschild length scale [47, 48] and M is galaxy mass in solar mass unit. The famous classical result of light deflection angle is recovered for \(\delta =0\).

For the conformally transformed effective lens potential (Eq. (38)), the light deflection angle will be

$$\begin{aligned} {{\tilde{\alpha }}}= & {} \frac{2GM (1+\frac{\delta }{2})}{c^2 {\tilde{r}}_c}\left( \frac{{\tilde{\xi }}}{{\tilde{r}}_c}\right) ^{-1}\nonumber \\&\times \left[ 1+\left( \frac{{\tilde{\xi }}}{{\tilde{r}}_c}\right) ^{\delta } \frac{\sqrt{\pi }(1-\delta )\Gamma (1-\frac{\delta }{2})}{2\Gamma (\frac{3}{2}-\frac{\delta }{2})}\right] . \end{aligned}$$
(40)

The profile of net deflection angles according to the Eqs. (39) and (40) is plotted in Figs. 3 and 4.

Fig. 3
figure 3

The plot shows the behavior of the two conformally related deflection angle profiles w.r.t \(\delta <1\) when \(\frac{2GM}{c^2 r_c}\) is normalized to unity for the scaled impact parameter, \(\frac{{\xi }}{{r}_c}(>1)\). The solid (Black) curve corresponds to \(\alpha \), whereas the dashed curve corresponds to \({\tilde{\alpha }}\). Here, the left wing of both deflection angle curves (\(\alpha \) and \({\tilde{\alpha }}\)) seems to be conformally consistent for \(\delta \ll 1\)

Full size image

Thus, it becomes clear by the profile of net light deflection angles from different figures (Figs. 3, 4) to choose the narrow values of \(\delta \)(\( \ll 1\)) for conformal equivalence. The small (about \(10^{-6}\)) value of \({\delta }\) is also recently confirmed from our study of galactic dynamics [50, 51].

Fig. 4
figure 4

The curve is plotted for smaller values of \(\delta ( \ll 1)\) under the convention used in Fig. 3. It is interpreted from the curve that the profile of deflection angle seems to be observationally as well as conformally consistent, i.e., the profile of the two deflection angles (\(\alpha \) and \({\tilde{\alpha }}\)) are conformally equivalent

Full size image

Therefore, to provide a the physical interpretation, we explore the small values of \(\delta \) for the light deflection angles due to the typical massive spiral galaxy system acting as a point-like lens and trace it with the known data of physical observations of lensing for a few galaxies culled from [91] and references therein.

For instance, the quantitative analysis of the net modified deflection angle can be explored by considering the case of an object having a solar mass unit (like a typical massive spiral galaxy) in the galactic halo (halo of scalaron cloud due to the f(R) background) acting as a weak lens for the light rays coming from the source star positioned in the external galaxy, like the Magellanic Clouds.

Fig. 5
figure 5

The variation of the light deflection angles (Eqs. (39) and (40)) as a function of the scaled impact parameter has been plotted together with the data from [91] with \(\delta \approx {\mathcal {O}} (10^{-6})\). The dashed and solid horizontal lines correspond to the minimum and maximum values of the deflection angles observed for the considered data sample of typical massive galaxies [91]. The plots that a galaxy with larger mass has a bigger deflection angle. For smaller value of \(\delta \), the f(R) contribution is more concentrated in the vicinity of baryonic mass with \(\xi /r_c<1\), and thus we have a decreasing profile of deflection angle in the galactic halo of scalaron cloud background with \(\xi /r_c>1\)

Full size image

Figure 5 shows the profile of deflection angles plotted with smaller value of \(\delta ( \ll 1)\) for different typical massive galaxies acting as a point lens. The diagram for the light deflection angle consistently indicates that a galaxy with larger mass has a larger deflection angle. The light deflection angle decreases in the halo of scalaron cloud background (or f(R) background) surrounding the galaxies with increasing value of the scaled impact parameter, i.e., \(\xi /r_c>1\). Indeed, this is due to the fact that for small value of \(\delta \)(\( \ll 1\)), the f(R) contribution is more concentrated in the close vicinity of baryonic mass with \(\xi /r_c<1\). The observed profile of deflection angle for the galaxies [91] is in agreement with the f(R) model for \(\delta \approx {\mathcal {O}} (10^{-6})\) explored here. Thus, the conformally related deflection angles seem to be physically equivalent for small values of \(\delta \) [51, 91].

We have also plotted in Fig. 6 the deflection angle for typical massive galaxies of mass M, as taken in Fig. 5 in GR (with \(\delta =0\)). Of course, here, we do not intend to compute M from the deflection angle, rather, on the other hand, for the known typical galaxy masses (in solar mass units) with different impact parameters, we have plotted the deflection angle in Fig. 6. It is clear from the plot that as the impact parameter increases, the deflection angle decreases for a known galaxy mass.

Fig. 6
figure 6

The plot shows the deflection angle (in arcsec) as a function of lens mass M in the GR theory with \(\delta =0\) in Eq. (39). The horizontal (dashed) gray lines correspond to the minimum and maximum values of the deflection angles observed for the considered different typical massive galaxies of mass M as in Fig. 5 [91]. We plot the curves for two typical impact parameter values 6 kpc and 12 kpc, respectively. It is seen that as the impact parameter increases, the deflection angle decreases for a particular galactic mass

Full size image

An important point to draw attention here is that the extent of \(\delta \) can also be probed directly with the study of orbital motion of neutral hydrogen clouds (as a test particle) in stable orbits far from the visible extent of typical spiral galaxies with \(\delta =v_{orbital}^2/c^2\) taking \(\mid v_{orbital} \mid \approx 220-300\) km/s [55].

4 f(R) conformal non-null geodesics analysis and phenomenology for perihelion shift

The uncertainty in the GR predicted results of Mercury’s orbit [80,81,82,83] as well as the prospects of the upcoming probes [84] motivate us to study the Mercury’s orbit in f(R) theory in order to investigate the bare effect of deviation (\(\delta \)) at the planetary scale, i.e., \(R\rightarrow R^{1+\delta }\).

Earlier investigation for the present case was done with Yukawa-like potential in f(R) theory [78, 79]. Unlike deflection of light, here the case is that an object (test mass) never gets out to infinity where the spacetime metric is asymptotically Minkowskian. Hence, for the study of f(R) conformal non-null geodesics, we start from Eq. (16). Under this case, the last term of Eq. (16) does not vanish for the non-relativistic material particles having non-zero rest mass and so it is not further possible to reduce the Eq. (16) to the original one (13) by using different conformal relations like Eq. (19). Thus, Eq. (16) suggests that under the conformally related f(R) spacetime (Eq. (4)), the non-null trajectories experience an extra force for a unit test mass. This extra force can be associated with a new carrier particle. In f(R) gravity theory, this new particle will be identified as the scalar field particle called scalaron [36, 92].

Let us investigate the non-relativistic case of Eq. (16) for the material particle (non-zero rest mass) tracing the curve \(x^\gamma (\tau )\). For mathematical convenience, we normalize its last term, \(g_{\mu \nu }\frac{d{x^\mu }}{d\tau }\frac{d{x^\nu }}{d\tau }=-1\) [93]. Thus, Eq. (16) can be re-written as,

$$\begin{aligned} \begin{aligned}&\frac{d^2{x^\gamma }}{d\tau ^2}+\Gamma ^{\gamma }_{\mu \nu }\frac{d{x^\mu }}{d\tau }\frac{d{x^\nu }}{d\tau }+ 2\frac{d}{d\tau }(\ln \Omega ) \frac{d{x^\gamma }}{d\tau }\\&\quad +\partial ^\gamma (\ln \Omega )=0 , \end{aligned} \end{aligned}$$
(41)

In the non-relativistic limit with \(\gamma =i\) (space coordinates) one should get the Newtonian equation with the conventional gravitational force [93]. Therefore, Eq. (41) has the following form,

$$\begin{aligned} \begin{aligned}&\frac{d^2{x^i}}{d\tau ^2}+\Gamma ^{i}_{\mu \nu }\frac{d{x^\mu }}{d\tau }\frac{d{x^\nu }}{d\tau }+ 2\frac{d}{d\tau }(\ln \Omega ) \frac{d{x^i}}{d\tau }\\&\quad +\partial ^i (\ln \Omega )=0 , \end{aligned} \end{aligned}$$
(42)

Therefore, under the non-relativistic Newtonian limit, Eq. (42) becomes,

$$\begin{aligned} \frac{d^2{x^i}}{d\tau ^2}=-[\partial ^i \Phi + \partial ^i (\ln \Omega )]= -[\vec {\nabla }_{3D}\Phi + \vec {\nabla }_{3D} (\ln \Omega ) ].\nonumber \\ \end{aligned}$$
(43)

Now, if \(-\vec {\nabla }_{3D}\Phi \) is the conventional (or standard) force of gravity, then under the conformal transformation of spacetime metric (Eq. (4)), we have an additional force on the unit test mass,

$$\begin{aligned} {\vec {F}_{\Omega }}=-\vec {\nabla }_{3D} (\ln \Omega ), \end{aligned}$$
(44)

where \(\Omega =\left( \frac{\partial f(R)}{\partial R}\right) ^{\frac{1}{2}}\) is the general conformal factor of the f(R) theory.

Clearly, the strength of such extra force will depend upon the extent of f(R) model parameter (\(\delta \)) and vanishes for \(\delta =0\). Also, in contrast to the Newtonian gravitational force, it dies off in strength slowly as,

$$\begin{aligned} {\vec {F}_{\Omega }}=-\frac{f_{RR}}{2f_R} R_r=\frac{\delta (3-\delta )}{2r}{\hat{r}}, \end{aligned}$$
(45)

where, \(f_{RR}=\frac{\partial F}{\partial R}\), \(R_r=\frac{\partial R}{\partial r}\) and R is the Ricci scalar curvature corresponding to the metric equations (21) with (34). It becomes clear from Eq. (45) that the suppression of such extra force depends on the constrained values of \(\delta \) which, from the observations in high-density regions, must be very small.

It is concluded from the non-vanishing value of R given as,

$$\begin{aligned} R=\delta (3-\delta ) \frac{GM}{r^3}, \end{aligned}$$
(46)

that outside the source, the value of Ricci curvature scalar R depends on the model parameter \(\delta \) and vanishes for \(\delta =0\) in GR theory, and hence the corresponding force also vanishes. As it is well known that a deviation from the \(\frac{1}{r^2}\) Newtonian force is responsible for a perihelion advancement of Mercury’s orbit (explained observationally by Einstein’s gravity theory), therefore, any modification in Einstein’s GR theory must be much smaller for a viable phenomenological interpretation of the present case.

Now, for the study of f(R) conformal non-null geodesics under an idealized consideration of system, we explore the time-like orbit of Mercury at the Solar system scale.

We simplify the problem in f(R) theory by using the corresponding symmetries and write the modified gravity Lagrangian following Eq. (21) as,

$$\begin{aligned} 2L= & {} -(1+2\Phi _{effective}) {\dot{t}}^{2} \nonumber \\&+ (1+2\Phi _{effective})^{-1} {\dot{r}}^{2} + r^2 {\dot{\varphi }}^{2}, \end{aligned}$$
(47)

where \(\Phi _{effective}\) is given by Eq. (23) and the dot denotes differentiation w.r.t the proper time (\(\tau \)).

The \((\varphi )\) and (t) equations following from this Lagrangian are given by using Euler’s Lagrangian formalism as,

$$\begin{aligned} r^2 {\dot{\varphi }}=l, \end{aligned}$$
(48)

and

$$\begin{aligned} (1+2\Phi _{effective}) {\dot{t}}=k, \end{aligned}$$
(49)

where, l and k are constants. The (r) equation can be simplified for material particle, with \(c=1\) as,

$$\begin{aligned} 1{=} -(1+2\Phi _{effective}) {\dot{t}}^{2} + (1+2\Phi _{effective})^{-1} {\dot{r}}^{2} {+} r^2 {\dot{\varphi }}^{2}.\nonumber \\ \end{aligned}$$
(50)

Dividing throughout by \({\dot{\varphi }}^{2}\), and using Eqs. (48) and (49), we obtain,

$$\begin{aligned} \left( \frac{dr}{d\varphi }\right) ^2= & {} {-r}^2 (1+2\Phi _{effective}) + \frac{r^4}{l^{2}} \nonumber \\&\times \left( k^{2}+1+ 2\Phi _{effective}\right) . \end{aligned}$$
(51)

Now, defining a new variable as,

$$\begin{aligned} u\equiv \frac{1}{r}, \end{aligned}$$
(52)

and

$$\begin{aligned} \left( \frac{dr}{d\varphi }\right) = -\frac{1}{u^2} \frac{du}{d\varphi }. \end{aligned}$$
(53)

Thus, Eq. (51) can be written as,

$$\begin{aligned} \left( \frac{du}{d\varphi }\right) ^2= & {} \frac{1}{l^2}\left[ (k^2 + 1)-2GMu\left( \frac{1}{2}+\frac{1}{2} \frac{u^{-\delta }}{r_c^{\delta }}\right) \right] \nonumber \\&\quad - u^2\left[ 1-2 GMu\left( \frac{1}{2}+\frac{1}{2} \frac{u^{-\delta }}{r_c^{\delta }}\right) \right] , \end{aligned}$$
(54)

where M is the mass of the Sun.

In contrast to the Newtonian classical equation of motion [93], we have

$$\begin{aligned} \left( \frac{du}{d\varphi }\right) ^2= \frac{2E}{l^2}+ \frac{2GM}{l^2}u-u^2, \end{aligned}$$
(55)

we can rewrite the modified relativistic equation (54) as,

$$\begin{aligned} \left( \frac{du}{d\varphi }\right) ^2= & {} \frac{2E}{l^2}+ \left( \frac{-2GM}{l^2}\right) u \left( \frac{1}{2}+\frac{1}{2} \frac{u^{-\delta }}{r_c^{\delta }}\right) -u^2 \nonumber \\&\quad + 2GMu^3\left( \frac{1}{2}+\frac{1}{2} \frac{u^{-\delta }}{r_c^{\delta }}\right) , \end{aligned}$$
(56)

where, \(2E\equiv k^2 +1\) with E as total energy of the system. We observe that the relativistic correction factor (the last term which is responsible for the advancement of perihelion motion of a planet) is also enhanced by modification. Therefore, the \(\delta \) inspired (i.e., \(R \rightarrow R^{1+\delta }\)) f(R) modification must be small enough not to violate the GR result, but must still be large enough to probe the uncertainty, if any, in various current or future projects to have an agreement or disagreement with observations. Thus, such modification may be compatible for explaining an uncertainty in the GR prediction under the (MESSENGER) [83] and planned (the European-Japanese BepiColombo) [84] missions.

If we denote 2GM by \(\epsilon \) as a Schwarzschild length in units of \(c=1\) and \(\bar{{\epsilon }} =\epsilon \left( \frac{1}{2}+\frac{1}{2}\frac{u^{-\delta }}{r_c^{\delta }}\right) \) as a modified Schwarzschild length, then (56) can be written as,

$$\begin{aligned} \left( \frac{du}{d\varphi }\right) ^2= \bar{{\epsilon }} u^3-u^2-\bar{{\epsilon }} \frac{u}{l^2} + \frac{2E}{l^2}. \end{aligned}$$
(57)

Clearly, for \(\delta =0\), we recover the GR differential equation of motion and hence, the shift in perihelion can be obtained through the standard perturbation approach to the Newtonian solution [93].

Now, to determine the shift in perihelion, we solve Eq. (57) by equating it to zero, since for perihelion and aphelion \(\varphi \) is fixed. Actually, this suggests different positions. Since Eq. (57) is a cubic equation, so it has \(u_1, u_2\) and \(u_3\) as three different solutions or roots. But the semi-classical observed problem has bounded solution between perihelion \((u_1)\) and aphelion \((u_2)\). This means that among the three solutions, one solution must be an non-physical. Therefore, if we assume that \(u_3\) as an non-physical solution, then we must eliminate it from Eq. (57) for the study of bounded motion.

From Eq. (57), it is possible to replace the right hand side with the three roots, viz., \(u_1\), \(u_2\) and \(u_3\) as,

$$\begin{aligned} \left( \frac{du}{d\varphi }\right) = [\bar{{\epsilon }}(u-u_1)(u-u_2)(u-u_3)]^{\frac{1}{2}}. \end{aligned}$$
(58)

Under the assumption of bounded motion, \(u_1\le u \le u_2\), Eq. (58) can be rewritten as,

$$\begin{aligned} \left( \frac{du}{d\varphi }\right) = [\bar{{\epsilon }}(u-u_1)(u_2-u)(u_3 -u)]^{\frac{1}{2}}, \end{aligned}$$
(59)

To eliminate the assumed non-physical solution \(u_3\) from Eq. (59), we must impose a boundary condition on the three solutions.

Since u has the dimension of inverse of length, \({\bar{\epsilon }}\) has the dimension of length. Because \(u_1\) and \(u_2\) are basically considered as two roots of Eq. (55), so \(u_1+u_2\) represents the inverse length of major axis [93] and if \(u_3\) is positive then \(u_1+u_2+u_3\) must be a large in contrast to modified Schwarzschild length \(\bar{{\epsilon }}\). So, the plausible boundary condition can be constructed as,

$$\begin{aligned} u_1 + u_2 + u_3 =\frac{1}{\bar{{\epsilon }}}. \end{aligned}$$
(60)

From Eqs. (59) and (60), for the bounded motion, the change in the angle between \(u_1\) and \(u_2\) is,

$$\begin{aligned} \begin{aligned} \mid \triangle \varphi \mid&\approx \int _{u_1}^{u_2} \left( \frac{1}{(u-u_1)(u_2-u)}\right) ^{\frac{1}{2}}\\&\quad \times \left( 1+\frac{{\bar{\epsilon }}}{2}(u+u_1+u_2)\right) \ du \end{aligned} \end{aligned}$$
(61)

Let us now simplify Eq. (61) by defining two parameters as,

$$\begin{aligned} \alpha \equiv \frac{1}{2}[u_1+u_2], \end{aligned}$$
(62)

and

$$\begin{aligned} \beta \equiv \frac{1}{2}[u_2-u_1], \end{aligned}$$
(63)

Thus, following Eqs. (62) and (63), we have \(u_1=\alpha -\beta \), \(u_2=\alpha +\beta \) and \((u-u_1)(u_2-u)=[\beta ^2-(u-\alpha )^2]\).

Now, Eq. (61) become,

$$\begin{aligned} \mid \triangle \varphi \mid \approx \int _{u_1}^{u_2} {\left( \frac{1+\frac{{\bar{\epsilon }}}{2}u + {\bar{\epsilon }} \alpha }{[\beta ^2-(u-\alpha )^2]^\frac{1}{2}}\right) \ du} . \end{aligned}$$
(64)

Further, Eq. (64) can be solved to give,

$$\begin{aligned} \mid \triangle \varphi \mid \approx \left[ -\frac{1}{2}{\bar{\epsilon }}(\beta ^2-(u-\alpha )^2)^{\frac{1}{2}}+ \left( 1+ \frac{3{\bar{\epsilon }}}{2}\alpha \right) {\sin }^{-1}\frac{u-\alpha }{\beta }\right] _{u_1}^{u_2} .\nonumber \\ \end{aligned}$$
(65)

By using Eqs. (62) and (63), we get from Eq. (65),

$$\begin{aligned} \mid \triangle \varphi \mid \approx \pi \left( 1+ \frac{3}{2}{\bar{\epsilon }}\alpha \right) . \end{aligned}$$
(66)

The twice of the left hand side of the Eq. (66) suggests the angle between successive perihelion. The perihelion shift can be computed as,

$$\begin{aligned} \Delta \varphi =2\mid \triangle \varphi \mid -2\pi . \end{aligned}$$
(67)

Thus, the required perihelion shift in f(R) gravity theory is,

$$\begin{aligned} \Delta \varphi= & {} 3 \pi {\bar{\epsilon }}\alpha =3\pi (2GM)\left( \frac{1}{2}+\frac{1}{2}{\left( \frac{r}{r_c}\right) }^{\delta } \right) \nonumber \\&\quad \times \left( \frac{1}{2}(u_1+u_2)\right) . \end{aligned}$$
(68)

The last factor of above equation can be classically given from the values of perihelion and aphelion in terms of semi-major axis and eccentricity [93]. So, we can rewrite Eq. (68) under the observed bounded motion as,

$$\begin{aligned} \Delta \varphi =\frac{6\pi G M \left( \frac{1}{2}+\frac{1}{2}{\left( \frac{r}{r_c}\right) }^{\delta }\right) }{c^2 a(1-e^2)} , \end{aligned}$$
(69)

where a is the semi-major axis, e is the eccentricity of the orbit which for a planet like Mercury are available from the observations and c is the speed of light. The last term in the numerator of Eq. (69) indicates that deviation \(\delta \) arising due to modification in Einstein gravity under \(R \rightarrow R^{1+\delta }\), contributes to the perihelion shift within the permissible limit and therefore, must be much small. Thus, the effect of such modification must be able to probe the uncertainty in GR result as suggested through various missions [80,81,82,83,84].

We investigate Eq. (69) for \(\delta =0\) with the values of \(a \approx 58\times 10^9\) m and \(e \approx 0.2056\) for Mercury precession about the massive Sun, \(M \approx 1.989\times 10^{30}\) kg and \(G = 6.672\times 10^{-11}\) m\(^{3}\)/(kg-sec\(^{-2}\)). The data is culled from NASA’s Solar System Bodies [94, 95]. With these values we get, \(\Delta \varphi \approx 0.5 \times 10^{-6}\) radian per revolution or \(\approx 0.10312^{\prime \prime }\) per revolution. As, the periodic time of Mercury around the Sun is 88 Earth-days it makes \(\frac{365}{88} \approx 4.148\) revolution per year, or 415 revolutions in one century. Therefore, the advance of the perihelion of Mercury in 1 century is \(0.10312\times 415 \approx 42.79\) seconds of arc. Thus, the GR result is fully recovered.

The relativistic conformal shift of the perihelion of Mercury orbit can be written (following Eqs. (36) and (37)) as,

$$\begin{aligned} \Delta {\tilde{\varphi }}=\left( 1+\frac{\delta }{2}\right) \frac{6\pi G M \left( \frac{1}{2}+ \frac{1}{2}(\frac{{\tilde{r}}}{{\tilde{r}}_c})^{\delta }\right) }{c^2 a(1-e^2)} . \end{aligned}$$
(70)

The profile of perihelion shift according to the Eqs. (69) and (70) is plotted in Figs. 7 and 8 for different values of f(R) model parameter \(\delta \).

Fig. 7
figure 7

The plot shows the behaviour of perihelion shifts for \(\delta <1\) with \(\frac{r}{{r}_c}>1\). The solid (Black) curve shows that \(\Delta {\varphi }\) increases with increasing values of \(\delta \), whereas \(\Delta {\tilde{\varphi }}\) (the dashed curve) increases more rapidly in contrast to the solid (Black) curve w.r.t. smaller \(\delta \). The narrow vertical strip corresponds to the allowed smaller values of \(\delta \) required for conformal equivalence, whereas the horizontal narrow strip corresponds to the observed values [80,81,82,83, 94, 95]

Full size image

It becomes clear from Fig. 7 that the perihelion shifts (\(\Delta {\varphi }\) and \(\Delta {\tilde{\varphi }}\)) vary largely w.r.t. the small deviation in the f(R) model parameter and also not observationally consistent with \(\delta <1\) . But, from Fig. 8, it is clear that for \(\delta \ll 1\) the perihelion shift approximately attains an observable constant value for \(\Delta {\varphi }\) and \(\Delta {\tilde{\varphi }}\).

Fig. 8
figure 8

Plot for the perihelion shift with extremely small values of \(\delta \). It becomes clear that for \(\delta \ll 1\), the perihelion shift of Mercury orbit seems to explain the observed result (\(42.98^{\prime \prime }\) per century)

Full size image

As a further interesting curiosity, we look for the number of revolutions corresponding to the age of our Solar System. For instance, for the 1 degree shift of the orbit, the time taken will be \(\frac{3600}{42.98}\approx 84\) centuries. Now, for 360 degrees, the required time is \(\approx 3.028\) millions of years (or 3, 028, 037 years). Of course, this is not too much at the cosmological time scale. In about 5 billion years (during which Sun, Earth, and other planets formed and evolved) before the present epoch, the number of revolutions the axis of Mercury has gone through is \(\frac{5\times 10^9}{3.028\times 10^6}\approx 1651\).

According to Fig. 8, the perihelion shift can be successfully explained for \(\delta \approx {\mathcal {O}} (10^{-7})\). Such constraint can be directly probed via specifying the model parameter \(\delta \) with the orbital velocity of Mercury (48 km/s) as \(\delta =v_{orbital}^2/c^2\). Contrasting with the constraints explored by Zakharov et al., ( \(\delta \approx 10^{-13}\)) and Clifton ( \(\delta \approx 10^{-19}\)) [56, 96], our constraint is at variance and corresponds to the extra force which drops off as \(r^{-1}\). Such relativistic effects are likely to be detected by different probes as discussed in [84]. It is also in close approximation to the parameterized post-Newtonian (PPN) estimates.

Thus, with such profile of \(\delta \) (with extremely small value) (Fig. 8), the additional fifth force given by Eq. (44) can be approximated as a small, screened-off force at the Solar system scales [40, 97].

5 Summary and discussions

To summarise the paper, we have studied an approach to model the deviations in Einstein–Hilbert GR action. Deviations from Einstein’s GR theory are indeed predicted mostly in various extra-dimensional theories. Contrasting alternatives to Einstein GR is useful to understand precisely which features of the theory have been tested in a particular experiment, and also to suggest new experiments probing different features. Such a study can be modeled in the f(R) gravity framework. Therefore, we study the deviations in GR in the form \(R^{1+\delta }\) with \(\delta \) being the dimensionless physical observable quantity. We focus on null and non-null geodesics at local scales and explore them in conformal f(R) theory. Our discussion shows that f(R) conformal transformation of spacetime metric (\(g_{\mu \nu }\)) leaves the null geodesic unchanged (Sect. 3). On the other hand, the effect of such transformation for non-null geodesics produces an additional force on the unit test mass which can be traced under the Newtonian limit (see Eq. (43) or (44)). We discuss the extent of this additional force in the f(R) Schwarzschild background and investigate its relativistic effect on the perihelion advance of Mercury’s orbit by obtaining the expressions for the f(R) conformally related orbital precession of Mercury. We also explore some features of the f(R) model for small deviations in Figs. 1, 2, and 3, whereas in Figs. 4, 5, and 8 we investigate the physical observations of the system confronted with different geodesics along with its conformal analog and explore the deviation. The main motivation to study the deviation \(\delta \) in the extremely narrow value comes from the recent unified investigation of galactic dynamics for the power-law f(R) model [50, 51, 55] as well as from [40, 56].

The extra force can be screened off in the high density environment as it directly depends on \(\delta \) with \(\delta \ll 1\) (Eq. (45)) and the observational results can be matched with small \(\delta \) (Fig. 8). Such deviation can be envisaged as a distinguishing factor since \(\delta \) can be specified as \(v_{orbital}^2/c^2\).

The phenomenological study of different geodesics, light deflection angle for null geodesics, and perihelion advance of mercury orbit for non-null geodesics (under an ideal considerationFootnote 2) along with its conformal analog at local scales imposes the strict constraints on \(\delta \) to be \({\mathcal {O}}(10^{-6})\) with a difference of unity in order at galactic and planetary scales (Figs. 4, 5 and 8). Such constraints are strict in the sense that for orbital motions at local scales, \(\delta \) can be physically represented as \(v_{orbital}^2/c^2\) with \(v_{orbital}\) known through observations. Our recent analysis of the light deflection angle through rotational curves may also, in principle, diagnose the explored constraint for the null geodesic [51]. Also, for the lensing in the halo of scalaron clouds background, we do not consider any specific kind of scalaron halo mass profile (singular or flat-core). This is due to the fact that the rotation curve data might lack sufficient spatial resolution near the center of the galaxy to distinguish unambiguously between a density profile with a flat-density core and one with a singular profile. We will attempt to address it in our future studies with the data coming from the advanced probes [9, 103].

Our analysis of perihelion advance of mercury orbit in contrast to the work by other authors [56, 94,95,96] shows the new constraints within bare f(R) framework to be about \({\mathcal {O}}(10^{-7})\) . Here, we do not consider the frame-dragging effect on the metric. Since, different missions (surveys) have reported an uncertainty in the GR result for the Mercury orbit [80,81,82,83,84, 94, 95], so f(R) gravity theory may be a potential candidate in this regard. Thus, the present model preserves the same form for the explanation of local-scale dynamics including the planetary scales, and hence proposes a unique f(R) at the local scale. Our analysis provides a powerful tool to obtain the precise constraints on the shifted parameter modeled in f(R) gravity.

It is interesting to note that such small values for \(\delta \) are also consistent with cosmological constraints coming from primordial nucleosynthesis [40, 89, 98].

In future studies, we will investigate the constraint on the deviation parameter \(\delta \) to provide a null test of dark energy corresponding to the different observations and also for testing whether the \(H_0\) tension can be solved within the f(R) theory [101, 102].

In addition to it, since all present or future projects aimed at the detection of gravitational waves, including LIGO, Virgo, and LISA are based on geodesic deviation equation, so we will also extend our present work in future for the study of binary systems and gravitational wave (GW) analysis.

The present status of the clustered (DM) and unclustered (DE) dark sectors hypothesis and the modified gravity alternatives, deduce that there is a lack of definitive convincing arguments in favor of any of the two concepts or particular theories. All gravity models have some successful predictions but also problematic comparisons with some observations and experiments. Therefore, it seems that new observations are necessary, especially on the scale of stars and planetary systems.

The investigation of precise modification in the f(R) model at early epochs has been attempted by several authors [99, 100]. The investigated f(R) model seems to be consistent with the explanation of clustered dark matter-like dynamics at local scales and therefore would bridge the gap among the gravitational anomalies ranging from stellar to galactic scales. Thus, our present findings are also in close agreement with the recent analysis carried out by us at galactic scales and provide a new phenomenological constraint for the study of the perihelion advance of Mercury orbit.

Hence, we conclude that for \(\delta \approx {\mathcal {O}}(10^{-6})\) with a difference of unity in order, we have a unified f(R) gravity at local scales.