Abstract
We present an extension of the GM2Calc software to calculate the muon anomalous magnetic moment (\({a_\mu ^{{\text {BSM}}}}\)) in the Two-Higgs Doublet Model. The Two-Higgs Doublet Model is one of the simplest and most popular extensions of the Standard Model. It is one of the few single field extensions that can give large contributions to \({a_\mu ^{{\text {BSM}}}}\). It is essential to include two-loop corrections to explain the long standing discrepancy between the Standard Model prediction and the experimental measurement in the Two-Higgs Doublet Model. The new version GM2Calc 2 implements the state of the art two-loop calculation for the general, flavour violating Two-Higgs Doublet Model as well as for the flavour aligned Two-Higgs Doublet Model and the type I, II, X and Y flavour conserving variants. Input parameters can be provided in either the gauge basis or the mass basis, and we provide an easy to use SLHA-like command-line interface to specify these. Using this interface users may also select between Two-Higgs Doublet Model types and choose which contributions to apply. In addition, GM2Calc 2 also provides interfaces in C++, C, Python and Mathematica, to make it easy to interface with other codes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The anomalous magnetic moment of the muon, \(a_\mu \), is one of the most important observables in particle physics. Its importance stems from the fact that it is one of the most precisely measured physical quantities and that it is very sensitive to new physics as well as the strong, weak and electromagnetic interactions of the Standard Model (SM). The significance of \({a_\mu }\) has increased further in the wake of the recent release of the first results from the Fermilab Muon \(g-2\) experiment [1]. This collaboration found, in combination with the results from the Brookhaven National Laboratory [2], an experimental value of
The SM prediction from the Muon \(g-2\) Theory Initiative White Paper [3] is
which combines quantum electrodynamic contributions [4, 5], electroweak contributions [6, 7], hadronic vacuum- polarization [8,9,10,11,12,13,14] and light-by-light contributions [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29].Footnote 1 The experimental measurement differs from the SM prediction by \(4.2\sigma \) which suggests a beyond the Standard Model (BSM) contribution of
The high precision in both the experimental measurement and the SM theoretical prediction requires BSM contributions to be known with a similar level of accuracy.
The Two-Higgs Doublet Model (2HDM) is one of the simplest and most widely studied extensions of the SM (see e.g. Ref. [42] for a review or the relevant chapters of Ref. [43]). Although the 2HDM has been studied for many decades and the only Higgs boson discovered is closely SM-like [44, 45], interest in this model has not waned, and recent progress has been achieved e.g. on LHC interpretations [46,47,48,49,50], B-physics [51,52,53,54,55], theoretical constraints [56,57,58,59,60], electroweak phase transitions in the early universe [61,62,63,64,65], precision calculations of Higgs decays [66,67,68,69,70,71,72,73,74]. Remarkably, the 2HDM is one of the very few single field extensions of the Standard Model that can explain the deviation between \({a_\mu ^\text {Exp}}\) and \({a_\mu ^{{\text {SM}}}}\) [75] while satisfying existing constraints from collider physics searches and other observables.
A second Higgs doublet that can couple to SM fermions generically induces large tree-level flavour changing neutral currents at odds with experiment. Due to this 2HDM s are often classified according to the discrete symmetries imposed to conserve flavour, giving four types [76]: type I [77], type II [78], type X (often called the lepton specific 2HDM) [79, 80] and type Y (sometimes refereed to as the flipped 2HDM) [81, 82]. Large flavour changing neutral currents can also be avoided by assuming an alignment in flavour space between the Yukawa matrices of the two doublets, giving the so-called flavour-aligned 2HDM (FA2HDM) [83, 84]. After the first results of the LHC, Ref. [85] systematically investigated the phenomenology of all 2HDM versions with discrete symmetries and showed that among them, only the type X variant is able to provide significant contributions to \({a_\mu }\). The type X explanation of the deviation between \({a_\mu ^\text {Exp}}\) and \({a_\mu ^{{\text {SM}}}}\) has been further explored in Refs. [86,87,88,89,90,91,92,93,94,95,96,97,98,99]. The more general flavour-aligned 2HDM and its contributions to \({a_\mu }\) were studied in Refs. [75, 100,101,102,103,104]. Other variants, including more general realisations that allow for Higgs-mediated flavour violation were investigated in Refs. [105,106,107,108,109,110,111,112].
Phenomenological investigations of BSM physics are greatly enhanced by the use of precise software tools. These tools can automate the calculation of precision corrections, or provide numerical methods to quickly and reliably solve related problems. For example in the 2HDM one is often concerned that a particular benchmark point respects measured limits of electroweak oblique parameters, or that the new couplings and bosons do not provide contributions to Higgs decays which violate collider constraints. For the 2HDM a widely used software package is 2HDMC [113], which provides calculations of the spectrum, decays, oblique S, T and U parameters as well as a calculation of the 2HDM new physics contributions to \({a_\mu }\). There also exists the tool ScannerS [114] which can place theoretical, experimental, dark matter, and electroweak phase transition constraints on extended scalar sectors, including the 2HDM. A more precise calculation of the decays is available from the 2HDM decay dedicated code 2HDECAY [115], while PROPHECY4F [116] provides a package which focuses on calculating \(h\rightarrow WW/ZZ\rightarrow 4f\) decays. Additionally, the tools HiggsBounds [117,118,119,120,121] and  [122,123,124] allow one to place constraints on the Higgs sectors of BSM physics through the measured behaviour of Higgs bosons from collider search experiments.
[122,123,124] allow one to place constraints on the Higgs sectors of BSM physics through the measured behaviour of Higgs bosons from collider search experiments.
Higher precision calculations for the spectrum, decays and other observables in the 2HDM are also available for arbitrary user-defined extensions of the SM through codes such as SARAH/SPheno [125,126,127,128,129,130] and FlexibleSUSY [131,132,133,134] (with decays recently added in FlexibleDecay [134]) where model files for the 2HDM are already distributed. Additionally, both packages provide one-loop contributions to \({a_\mu ^{{\text {BSM}}}}\). For two-loop contributions to \({a_\mu ^{{\text {BSM}}}}\) in the MSSM, FlexibleSUSY links to the dedicated tool GM2Calc [135]. For the 2HDM there was no such option until now. Here we extend GM2Calc with the 2HDM to provide a program which includes state of the art two-loop level contributions of Ref. [102] to the anomalous magnetic moment of the muon.
The 2HDM contributions implemented in GM2Calc version 2 include the one-loop contributions, the two-loop fermionic corrections (including the well-known Barr-Zee diagrams), and the complete set of bosonic two-loop corrections. The one-loop contributions are of the order \(\mathcal {O}(m_\mu ^4)\) and therefore usually subdominant. The two-loop contributions arise at \(\mathcal {O}(m_\mu ^2)\) and are implemented at this order. Ref. [102] has assumed the flavour-aligned 2HDM with vanishing couplings \(\lambda _{6,7}\), but here we relax this assumption and allow the more general case. The 2HDM version of GM2Calc 2 allows the user to input deviations from the aligned limit, as well as select any one of the 2HDM types I, II, X or Y. Just like version 1, GM2Calc 2 allows the user to input parameter information using an SLHA-like [136, 137] input file. We also provide interfaces in C, C++, Python and Mathematica to make it easy to link to other public codes. Furthermore, GM2Calc 2 (hereafter GM2Calc) can be used as a standalone tool for studies of \(a_\mu \) in the 2HDM, or to explore the 2HDM phenomenology more broadly it can be used in combination with other codes via the SLHA interface. For example, GM2Calc can be called alongside FlexibleSUSY, or in combination with other standalone tools like 2HDECAY or alongside the 2HDMC package, replacing its native calculation of the anomalous magnetic moment of the muon. The MSSM calculation is already available in GAMBIT [138, 139] and it should be straightforward to extend this to also use the 2HDM calculation in future versions.
The rest of this paper is divided into the following sections. Section 2 provides a pedagogical introduction to the 2HDM, giving the Lagrangian both before and after electroweak symmetry breaking, and defining the Yukawa couplings in the various types of the 2HDM. There we give the one- and two-loop contributions to \({a_\mu ^{{\text {BSM}}}}\), and the uncertainty estimate for the calculation. Section 3 describes various ways to use the 2HDM in GM2Calc. It also shows how to interface GM2Calc using C++, C, Python and Mathematica. Finally, Sect. 4 demonstrates various possible ways GM2Calc can be applied to calculate the BSM contributions to the anomalous magnetic moment of the muon in the 2HDM.
2 Review of 2HDM and implemented contributions to \({a_\mu }\)
2.1 The Model
The Two-Higgs Doublet Model (2HDM) extends the Standard Model (SM) with an additional scalar \({\text {SU}(2)}\) doublet. We denote the two complex Higgs \({\text {SU}(2)}\) doublets in the 2HDM as \(\Phi _i\) (\(i=1,2\)),
where \(b_i\) and \(c_i\) are real scalar fields and \(a_i^+\) are complex scalar fields. Each Higgs doublet acquires a real non-zero vacuum expectation value (VEV), \(v_i\), which satisfy
with \(0 \le \beta \le \pi /2\) and \({v \approx 246\,\text {GeV}}\), which implies \(v_1 = v\cos \beta \) and \(v_2 = v\sin \beta \). The extended Lagrangian includes the Higgs potential \(\mathcal {L}_{\text {Scalar}}\) and the Yukawa interaction part \(\mathcal {L}_{\text {Yuk}}\),
The most general form of Higgs potential is
where \(\lambda _5\), \(\lambda _6\), \(\lambda _7\) and \(m_{12} ^2\) are real for the CP-conserving Higgs potential. The mass eigenstates of Higgs and Goldstone bosons h, H, A, \(H^+\), \(G^0\) and \(G^+\) are obtained as
with
from Eq. (7). The orthogonal matrices \(Z_{\mathcal {H}^0}\), \(Z_{\mathcal {A}}\) and \(Z_{\mathcal {H}^\pm }\) for Eq. (8) are given as
The corresponding mass square matrices \(M_{\mathcal {H}^0} ^2\), \(M_{\mathcal {A}} ^2\) and \(M_{\mathcal {H}^+} ^2\) for \(\mathcal {H}^0\), \(\mathcal {A}\) and \(\mathcal {H}^+\) in Eq. (9), respectively, are diagonalized as
The Higgs boson mass eigenvalues are denoted as
where in Feynman gauge \(m_{G^+}=m_W\) and \(m_{G^0}=m_Z\). We chose the CP-even Higgs boson mixing angle \(\alpha \) such that \(-\pi /2 \le \beta - \alpha \le \pi /2\) [113].
The general form of the Yukawa interaction Lagrangian is given as
where \(\Phi _i^{c} \equiv \text {i}\sigma ^2 \Phi _i^*\), and \(q_L ^0\), \(l_L ^0\), \(u_R ^0\), \(d_R ^0\), and \(e_R ^0\) are fermion gauge eigenstates.Footnote 2 In general the Yukawa coupling matrices, \(\Gamma _f ^0\) and \(\Pi ^0_f\) (\(f=u,d,l\)) are complex and non-diagonal \(3\times 3\) matrices which can not be simultaneously diagonalized, which produces flavour changing neutral currents (FCNC).
From the Yukawa interaction Lagrangian in Eq. (13) the \(3\times 3\) fermion mass matrices \(M_f\) (\(f=u,d,l\)) are obtained as
The fermion mass matrices are diagonalized using singular value decomposition. The diagonal fermion mass matrices \(M_f^D\) (\(f=u,d,l\)) are given by
where \(V_f\) and \(U_f\) are unitary matrices, and the corresponding fermion mass eigenstates \(f=u,d,l\) are obtained as
By combining Eq. (5) and Eqs. (14)–(16), \(\Gamma _u ^0\), \(\Gamma _d ^0\) and \(\Gamma _l ^0\) can be expressed in terms of \(M_f\) and \({\Pi ^0_f}\) as
The Yukawa interaction Lagrangian Eq. (13) can be also written in the so-called Higgs basis, where only one Higgs doublet has non-zero VEV. This can be obtained by rotating \(\Phi _{1,2}\) and the Yukawa matrices as
such that only \(\Phi _v\) has the VEV v and \(\Sigma ^0_f\) are its Yukawa couplings. It contains the SM-like Goldstone bosons, whereas the second field \(\Phi _\perp \) contains non-SM Higgs bosons \(H^\pm \) and A, and its Yukawa couplings \(\rho ^0_f\) are important parameters in the 2HDM.Footnote 3 With this transformation the Yukawa interaction Lagrangian becomes
In this way, the fermion masses are purely generated from the Higgs doublet \(\Phi _v\), and the fermion mass matrices in Eqs. (14)–(16) become
which implies \(V_f \Sigma _f^0 U_f^\dagger = \sqrt{2}M_f^D/v\). In parallel to Eqs. (17)–(19) we may define Yukawa matrices in the basis of mass eigenstates as (\(f=u,d,l\))
Importantly, in the Higgs basis the \(\Sigma _f ^0\) are diagonalized by the singular value decomposition involving \(V_f\) and \(U_f\), but in general the \({\rho ^0_f}\) are not. This implies that Higgs-mediated FCNCs are induced by the coupling with the zero-VEV Higgs doublet \(\Phi _\perp \).
From Eqs. (17)–(19), (23), and (25) we obtain
where \(\Pi _f \equiv V _f \Pi ^0_f U _f ^\dagger \) and \({\rho _f \equiv V _f \rho ^0_f U _f ^\dagger }\). The \(\rho _f\) matrices contain non-zero off-diagonal components, which reflects that in general the two types of Yukawa coupling matrices \(\Gamma _f ^0\) and \(\Pi ^0_f\) can not be simultaneously diagonalized in the 2HDM. The \(\rho _f\) term in Eq. (27) can induce Higgs-mediated flavour-changing neutral currents (FCNC) at the tree-level. GM2Calc implements several variants of the 2HDM with or without Higgs-mediated FCNC:
-
The four well-known types with \(Z_2\) symmetry: type I, type II, type X, type Y,
-
the flavour-aligned 2HDM (FA2HDM) [83, 84], which also avoids tree-level Higgs-mediated FCNC and contains the four previous types as special cases,
-
the 2HDM with general Yukawa structures.
We will now describe these variants of the 2HDM. The most common way to avoid FCNC is to impose a \(Z_2\) symmetry, which leads to four different types of Yukawa interactions in which specific subsets of Yukawa couplings vanish. In the type I model all quarks and charged leptons couple to \(\Phi _2\), so we set
In the type II model all up-type quarks couple to \(\Phi _2\), while the down-type quarks and charged leptons couple to \(\Phi _1\), so we set
In the type X model all quarks couple to \(\Phi _2\), while the charged leptons couple to \(\Phi _1\), so we set
In the type Y model the up-type quarks and charged leptons couple to \(\Phi _2\), while the down-type quarks couple to \(\Phi _1\), so we set
In all these cases, trivially \(\Gamma _f ^0\) and \({\Pi ^0_f}\) can be diagonalized simultaneously, and Higgs-mediated FCNC is avoided.
In the flavour-aligned Two-Higgs Doublet Model (FA2HDM) [83, 84] it is assumed that the \(\Pi ^0_f\) matrices are proportional to the \(\Gamma _f ^0\) matrices, and we set
where \(\zeta _f\) are the alignment parameters which are constrained by experimental results and used in phenomenological studies. Note that the aligned model contains the type I, II, X and Y models as special cases when the alignment parameters \(\zeta _f\) take the values given in Table 1.
We can summarize the fundamental Yukawa coupling matrices \(\rho _f\) (\(f=u,d,l\)) for the different 2HDM variants and in different parametrizations as follows:
Here the \(\zeta _f\) are the parameters introduced in Eq. (32) and Table 1, and the \((*)\) notation indicates the conjugate is present for the case \(f=u\) and not present for \(f=d,l\). GM2Calc offers two parametrizations for the general 2HDM. The “FA2HDM parametrization” starts from the FA2HDM and allows to directly modify the \(\rho _f\) by additional matrices \(\Delta _f\), which represents the deviation from the flavour-aligned (or type I, II, X, Y) limit. The second “\(\Pi \) parametrization” starts from Eq. (27) and allows to directly specify the fundamental Yukawa matrices \(\Pi _f\).
After suitable unitary transformations, the Yukawa interaction in the Lagrangian of Eq. (13) takes the following form:
with the CKM matrix \({V_{\text {CKM}}= V_u V_d^{\dagger }}\) and the fermion mass eigenstates \(f=f_L + f_R\), \((f=u,d,l)\), defined in Eq. (20). The coupling matrices \(y_f^S\) are defined as [102]:
and the coupling between the charged Higgs and each of the fermions is:
where \(\rho _f\) is given in Eq. (33).
2.2 Implemented contributions to \({a_\mu }\)
Relevant 2HDM contributions to \({a_\mu }\) arise at the one-loop and the two-loop level. The one-loop contributions are suppressed by two additional powers of the muon Yukawa coupling and thus of \({\mathcal {O}(m_\mu ^4)}\); they are typically subleading unless some of the non-SM-like Higgs bosons have very small mass around a few GeV. The two-loop contributions can be classified into fermionic and bosonic contributions. They arise at the \({\mathcal {O}(m_\mu ^2)}\) and are typically dominant. An important subclass of two-loop contributions are the so-called Barr–Zee diagrams, which contain a \(\gamma \gamma \)-Higgs one-loop subdiagram. These diagrams have been studied extensively [140,141,142,143,144] and fully calculated in Ref. [100]. The full set of two-loop bosonic and fermionic diagrams (at \({\mathcal {O}(m_\mu ^2)}\)) has been computed in Ref. [102] (see also Ref. [103] for further phenomenological discussions of the individual contributions). GM2Calc implements the full set of one-loop BSM contributions \(a_\mu ^{1\ell }\) of \({\mathcal {O}(m_\mu ^4)}\) and the two-loop BSM contributions \(a_\mu ^{2\ell }\) of \({\mathcal {O}(m_\mu ^2)}\) in the 2HDM from Ref. [102]. The full BSM contribution in the 2HDM (i.e. the difference between the 2HDM and the SM contributions) calculated by GM2Calc is therefore the sum
In the following subsections we provide the explicit analytic results implemented in GM2Calc.
2.2.1 One-loop contributions
The one-loop BSM contributions to \({a_\mu ^{1\ell }}\) in the 2HDM is of \({\mathcal {O}(m_\mu ^4)}\) and are given by
with \(m_l = (m_e, m_\mu , m_\tau )\), \(m_\nu = (m_{\nu _e}, m_{\nu _\mu }, m_{\nu _\tau })\) and
Note, that the one-loop contribution from the SM Higgs boson \({{h_{{\text {SM}}}}}\) is subtracted in Eq. (40) and is therefore not included in \({a_\mu ^{1\ell }}\). The loop functions \(F_1^C\), \(F_2^C\) and \(F_1^N\) are given by
2.2.2 Two-loop contributions
The two-loop contributions of \({\mathcal {O}(m_\mu ^2)}\) are divided into fermionic and bosonic loop contributions according to Ref. [102] as
where the very small contribution from the shift of the Fermi constant, \({a_\mu ^{\Delta r\text {-shift}}}\), is neglected. We generalize the fermionic two-loop contributions from Ref. [102] in the general 2HDM to the case of CKM mixing as follows:
Note, that the two-loop contribution from the SM Higgs boson \({{h_{{\text {SM}}}}}\) is subtracted in Eq. (51) and is therefore not included in \({a_\mu ^{2\ell }}\). The loop functions \(f_f^S\) (\({S=h,H,A,{h_{{\text {SM}}}}}\)) are defined as:
where \(N^c_f = (1,3,3)\), \(g^f_v = T^3_f/2 - s_W^2 q_f\), \(T^3_f = (-1/2,-1/2,1/2)\) and \(q_f=(-1,-1/3,2/3)\) for \(f=(l,d,u)\). The loop function \(f_f^{H^\pm }\) is defined as:
where \(f'_j\) is the \(\text {SU}(2)_L\) partner of generation j of the fermion \(f_i\) from generation i, and
and
The loop function \(\Phi (m_1^2,m_2^2,m_3^2)\) [145] is defined as:
The bosonic two-loop contributions to the general 2HDM are composed of three parts as follows:
The two terms \({a_\mu ^{\text {B,EW add}}}\) and \({a_\mu ^{\text {B,nonYuk}}}\) correspond to diagrams with the SM-like Higgs boson and diagrams without the new Yukawa couplings, respectively. They are typically subdominant, and full details on their definition and phenomenological impact are given in Refs. [102, 103]. The Yukawa contribution is given by
where the equations for \(a_{\lambda ,t}^{\eta }\) (with the common prefactor put in the front of the above Eq. (67)) are given in the appendix of Ref. [102]. Compared to this reference, the expression has been generalized to include \(\lambda _6\) and \(\lambda _7\).Footnote 4 These bosonic contributions are implemented in the realistic approximation of small \(\cos (\beta -\alpha )\), and only terms up to linear order in \(\cos (\beta -\alpha )\) are taken into account. In this scenario the boson h has the tree-level couplings of the SM Higgs boson [146]. Furthermore, the bosonic contributions are derived only for the flavour-aligned 2HDM. Referring to the different cases of Yukawa couplings in Eq. (33), the bosonic corrections apply for the cases of the discrete symmetries, for the FA2HDM, and also for the general 2HDM in FA2HDM parametrization (assuming the \(\Delta _f\) matrices are small). In contrast, we set \(\zeta _l=0\) in Eq. (67) in the case of the general 2HDM in \(\Pi \) parametrization since in this case the bosonic corrections are not applicable in this form.
The bosonic two-loop contributions are also available in the GM2Calc source code and in the form of a Mathematica file.
2.2.3 Running couplings
Among the fermionic two-loop contributions, the diagrams with an internal top quark, bottom quark or tau lepton loop give the dominant contribution to \({a_\mu ^{{\text {BSM}}}}\). These diagrams are proportional to the values of the fermion masses in the loop. So long as there is no three-loop calculation available in the 2HDM, it is formally irrelevant which renormalization scheme to use for the fermion masses in the loop. In GM2Calc two possible definitions of these fermion masses are implemented:
In the “input masses” scheme, the top quark pole mass \(m_t\), the \({{\overline{\text {MS}}}}\) bottom quark mass in the SM with five active quark flavours, \({m_b^{\overline{\text {MS}}}}\), at the renormalization scale \({Q=m_b^{\overline{\text {MS}}}}\), and the tau lepton pole mass \(m_\tau \) are used in the loops. These masses are typically used as input for spectrum generators [136, 137]. In the “running masses” scheme, the running \({{\overline{\text {MS}}}}\) top quark mass \({m_t^{\overline{\text {MS}}}(Q)}\), the \({{\overline{\text {MS}}}}\) bottom quark mass \({m_b^{\overline{\text {MS}}}(Q)}\) and the \({{\overline{\text {MS}}}}\) tau lepton mass \({m_\tau ^{\overline{\text {MS}}}(Q)}\) are used in the loops. The renormalization scale Q is set to the mass of the Higgs boson in the Feynman diagram. The “running masses” scheme is also used in 2HDMC [113]. The difference between these two schemes is shown in Sect. 4.
2.2.4 Uncertainty estimate
We provide an uncertainty estimate for \({a_\mu ^{{2\ell }}}\) as follows:
where
and
The term \({\delta a_\mu ^{{2\ell },\Delta r}}\) accounts for the fact that the two-loop contribution \({a_\mu ^{\Delta r\text {-shift}}}\) has been neglected in Eq. (49). In Refs. [102, 147] it was shown that in the relevant parameter space \({|a_\mu ^{\Delta r\text {-shift}}| \le 2\times 10^{-12}}\), which we use as an upper bound in the uncertainty estimate. The term \({\delta a_\mu ^{{2\ell },m_\mu ^4}}\) estimates missing two-loop terms of \({\mathcal {O}(m_\mu ^4)}\) using the known universal two-loop QED logarithmic contributions [148]. The term \({a_\mu ^{{3\ell }}}\) is an estimate for the expected three-loop contributions. From experience the QED contributions are among the largest contributions at each loop level. For this reason we use again the known universal logarithmic QED contributions from Ref. [148] to provide an estimate for the unknown three-loop contributions.
3 Program details and usage
3.1 Quick start
GM2Calc can be downloaded from https://gm2calc.hepforge.org/ or https://github.com/GM2Calc/GM2Calc, for example asFootnote 5

To build GM2Calc run the following commands:

To calculate \({a_\mu ^{{\text {BSM}}}}\) in the 2HDM with GM2Calc from the command line, run

Here,  is the name of the file that contains the input parameters.Footnote 6
is the name of the file that contains the input parameters.Footnote 6
3.2 Requirements
To build GM2Calc the following programs and libraries are required:
-
C++14 and C11 compatible compilers
-
Eigen library, version 3.1 or higher [149] [http://eigen.tuxfamily.org]
-
Boost library, version 1.37.0 or higher [150] [http://www.boost.org]
-
(optional)
 Mathematica or
Mathematica or  [151]
[151] -
(optional) Python 2 or Python 3 [152], using the package
 [153] [https://pypi.org/project/cppyy/]
[153] [https://pypi.org/project/cppyy/]
3.3 Running GM2Calc from the command line
GM2Calc can be run from the command line with an SLHA-like [136, 137] input file as

where  is the name of the SLHA-like input file. Alternatively, the input parameters can be piped in an SLHA-like format into GM2Calc as
is the name of the SLHA-like input file. Alternatively, the input parameters can be piped in an SLHA-like format into GM2Calc as

The calculated value for \({a_\mu ^{{\text {BSM}}}}\) and \({\delta a_\mu }\) is written to the standard output. Depending on the input options and parameters, the output may contain the following block with \({a_\mu ^{{\text {BSM}}}}\) and \({\delta a_\mu }\):

The SLHA-like format for the input parameters is defined in the following subsections.
3.3.1 General options
In the SLHA-like input the selection of the configuration flags for GM2Calc can be given in the  block as defined in Ref. [135]. An example
block as defined in Ref. [135]. An example  block reads as follows:
block reads as follows:

The entry  defines the output format. If
defines the output format. If  , a single number is printed to the
, a single number is printed to the  . This number is the value of \({a_\mu ^{{\text {BSM}}}}\) or the uncertainty \({\delta a_\mu }\), depending on the value of
. This number is the value of \({a_\mu ^{{\text {BSM}}}}\) or the uncertainty \({\delta a_\mu }\), depending on the value of  : If
: If  , the value of \({a_\mu ^{{\text {BSM}}}}\) is printed. If
, the value of \({a_\mu ^{{\text {BSM}}}}\) is printed. If  , the value of \({\delta a_\mu }\) is printed. If
, the value of \({\delta a_\mu }\) is printed. If  , a detailed output, suitable for debugging, is printed. If
, a detailed output, suitable for debugging, is printed. If  , the value of \({a_\mu ^{{\text {BSM}}}}\) is written to the output block entry
, the value of \({a_\mu ^{{\text {BSM}}}}\) is written to the output block entry  . If
. If  , the value of \({a_\mu ^{{\text {BSM}}}}\) is written to the output block entry
, the value of \({a_\mu ^{{\text {BSM}}}}\) is written to the output block entry  . If
. If  (default), the value of \({a_\mu ^{{\text {BSM}}}}\) is written to the output block entry
(default), the value of \({a_\mu ^{{\text {BSM}}}}\) is written to the output block entry  .
.
The entry  defines the loop order of the calculation, which can be set to
defines the loop order of the calculation, which can be set to  or
or  . The default value is
. The default value is  (recommended), which corresponds to the two-loop calculation of \({a_\mu ^{{\text {BSM}}}}\).
(recommended), which corresponds to the two-loop calculation of \({a_\mu ^{{\text {BSM}}}}\).
The entry  disables/enables the resummation of \(\tan \beta \) in the MSSM. By default \(\tan \beta \) resummation is enabled, which corresponds to
disables/enables the resummation of \(\tan \beta \) in the MSSM. By default \(\tan \beta \) resummation is enabled, which corresponds to  . To disable \(\tan \beta \) resummation, set
. To disable \(\tan \beta \) resummation, set  . When the calculation is performed in the 2HDM, the value of
. When the calculation is performed in the 2HDM, the value of  is ignored.
is ignored.
The next two options are useful for debugging. By setting the entry  (default:
(default:  ), the output of GM2Calc can be forced, even if a physical problem (e.g. a tachyon) has occurred. Warning: If a physical problem has occurred, the output cannot be trusted. Forcing the output should only be used for debugging. By setting the entry
), the output of GM2Calc can be forced, even if a physical problem (e.g. a tachyon) has occurred. Warning: If a physical problem has occurred, the output cannot be trusted. Forcing the output should only be used for debugging. By setting the entry  (default:
(default:  ), additional information about the model parameters and the calculation is printed.
), additional information about the model parameters and the calculation is printed.
With the entry  the calculation of the uncertainty \({\delta a_\mu }\), c.f. Eq. (74), can be disabled/enabled (
the calculation of the uncertainty \({\delta a_\mu }\), c.f. Eq. (74), can be disabled/enabled ( or
or  ).
).
The entry  (default:
(default:  ) is new in GM2Calc 2.0.0 and controls the definition of the fermion masses that are inserted into the fermionic two-loop contribution \({a_\mu ^{\text {F}}}\), see Sect. 2.2.3. If
) is new in GM2Calc 2.0.0 and controls the definition of the fermion masses that are inserted into the fermionic two-loop contribution \({a_\mu ^{\text {F}}}\), see Sect. 2.2.3. If  , the input masses (72) are used. If
, the input masses (72) are used. If  , the running masses (73) are used. The difference between these two schemes is shown in Sect. 4.
, the running masses (73) are used. The difference between these two schemes is shown in Sect. 4.
3.3.2 Standard Model input parameters
The Standard Model input parameters are read from the  ,
,  and
and  blocks. Example blocks that define the Standard Model input parameters may read:
blocks. Example blocks that define the Standard Model input parameters may read:

The entries of the  and
and  are defined in Refs. [136, 137]. In the block entry
are defined in Refs. [136, 137]. In the block entry  the mass of the Standard Model Higgs boson can be given. Unset parameters in the
the mass of the Standard Model Higgs boson can be given. Unset parameters in the  and
and  blocks are assigned default values. Unset parameters in the
blocks are assigned default values. Unset parameters in the  block are assumed to be zero.
block are assumed to be zero.
3.3.3 Two-Higgs Doublet Model input parameters
We allow the specification of the 2HDM input parameters in two different “bases”, see Table 2. The basis parameters are defined as in [113]. In the “gauge basis” the Lagrangian parameters, \(\lambda _{1, \ldots , 7}\) are used as input. In the “mass basis” the Higgs boson masses and the mixing parameter \(\sin (\beta -\alpha )\) are used as input, instead of the Lagrangian parameters \(\lambda _{1, \ldots , 5}\), but \(\lambda _6\) and \(\lambda _7\) can still be used. All available input parameters are listed in Table 3.
Mass basis input parameters The “mass basis” input parameters are read from the  and
and  blocks for compatibility with 2HDMC [113]. The following shows an example input in the “mass basis” for the type II 2HDM:
blocks for compatibility with 2HDMC [113]. The following shows an example input in the “mass basis” for the type II 2HDM:

Unset parameters in the  and
and  blocks are assumed to be zero, except for \(\tan \beta \) which will raise an error. Entry 24 of the
blocks are assumed to be zero, except for \(\tan \beta \) which will raise an error. Entry 24 of the  is used to select the type of 2HDM. Specifically the integer values \(1, \ldots , 6\) for the Yukawa type correspond to: 1 = type I, 2 = type II, 3 = type X, 4 = type Y, 5 = Flavour-Aligned, 6 = general 2HDM. The input entries 21, 22, and 23 in the
is used to select the type of 2HDM. Specifically the integer values \(1, \ldots , 6\) for the Yukawa type correspond to: 1 = type I, 2 = type II, 3 = type X, 4 = type Y, 5 = Flavour-Aligned, 6 = general 2HDM. The input entries 21, 22, and 23 in the  block can be used to set the values of \(\zeta _u\), \(\zeta _d\) and \(\zeta _l\) in the Flavour-Aligned 2HDM, and are ignored for all other types. Additional blocks for the general case are described below.
block can be used to set the values of \(\zeta _u\), \(\zeta _d\) and \(\zeta _l\) in the Flavour-Aligned 2HDM, and are ignored for all other types. Additional blocks for the general case are described below.
Gauge basis input parameters Alternatively, the input can be given in the “gauge basis” in a format compatible with 2HDMC [113]. In the “gauge basis” the 2HDM parameters must be given in the  block. The available “gauge basis” input parameters are listed in Table 3. The following shows an example input in the “gauge basis”:
block. The available “gauge basis” input parameters are listed in Table 3. The following shows an example input in the “gauge basis”:

Two parametrizations for the general 2HDM are implemented, see Eq. (33). The first option is a deviation from the FA2HDM (or types I, II, X, Y), parametrized by the additional matrices \(\Delta _f\). Thus, after choosing Yukawa type = 1, ..., 5, i.e. type I, II, X, Y and FA2HDM, the matrices \(\Delta _u\), \(\Delta _d\) and \(\Delta _l\) can be optionally given in the following dedicated blocks:

The other option for the general 2HDM corresponds to the \(\Pi \) parametrization, implemented when setting Yukawa type = 6. In this case, the input parameters \(\Delta _u\), \(\Delta _d\) and \(\Delta _l\) are ignored and the real parts of the matrices \(\Pi _u\), \(\Pi _d\) and \(\Pi _l\) can be given in the following dedicated blocks:

The input parameters \(\Pi _u\), \(\Pi _d\) and \(\Pi _l\) are ignored when choosing Yukawa type = 1, ..., 5, i.e. type I, II, X, Y and FA2HDM.
The SLHA-like interface described so far is very convenient and intuitive to use and it does not require any prior knowledge of programming languages to run GM2Calc this way. The execution time for this is also very short, around \(5\,\text {ms}\) per point on current laptops.Footnote 7 Nevertheless even faster execution times and easy interfacing with other existing calculators and sampling algorithms are enabled through our C++ (\(0.05\,\text {ms}\)), C (\(0.05\,\text {ms}\)), Mathematica (\(0.5\,\text {ms}\)) and Python (\(0.08\,\text {ms}\)) interfaces. In the following subsections we describe how to use each of these interfaces.
3.4 Running GM2Calc from within C++
GM2Calc provides a C++ programming interface, which allows for calculating of \({a_\mu ^{{\text {BSM}}}}\) in the 2HDM up to the two-loop level. The following C++ source code snippet shows a two-loop example calculation in the 2HDM of type II with input parameters defined in the “mass basis”, see Table 2.  This example source code can be compiled as follows (assuming GM2Calc has been compiled to a shared library
This example source code can be compiled as follows (assuming GM2Calc has been compiled to a shared library  on a UNIX-like operating system with
on a UNIX-like operating system with  installed):
installed):

Here  is the file that contains the above listed source code. The variable
is the file that contains the above listed source code. The variable  contains the path to the GM2Calc root directory and
contains the path to the GM2Calc root directory and  contains the path to the Eigen library header files. Running the created executable
contains the path to the Eigen library header files. Running the created executable  yields
yields

In line 12 of the example source code an object of type  is created, which contains the input parameters in the mass basis, see Table 2. The mass basis input parameters are set in lines 13–31. Note that the Yukawa type is set to type II in line 13, which implies that given values of \(\zeta _f\) are ignored and internally fixed to the values given in Table 1. Additionally the inputs \(\Pi _f\) and \(\Delta _f\) are unused for this type, and ignored. In line 34 an object of type
is created, which contains the input parameters in the mass basis, see Table 2. The mass basis input parameters are set in lines 13–31. Note that the Yukawa type is set to type II in line 13, which implies that given values of \(\zeta _f\) are ignored and internally fixed to the values given in Table 1. Additionally the inputs \(\Pi _f\) and \(\Delta _f\) are unused for this type, and ignored. In line 34 an object of type  is created that contains all SM input parameters. The SM input parameters are set to reasonable default values from the PDG [154]. In lines 35–39 the values for \({\alpha _{\text {em}}(m_Z)}\), \(m_t\), \({m_c^{\overline{\text {MS}}}(2\,\text {GeV})}\), \({m_b^{\overline{\text {MS}}}(m_b^{\overline{\text {MS}}})}\) and \(m_\tau \) are set to specific values. In line 42 an object of type
is created that contains all SM input parameters. The SM input parameters are set to reasonable default values from the PDG [154]. In lines 35–39 the values for \({\alpha _{\text {em}}(m_Z)}\), \(m_t\), \({m_c^{\overline{\text {MS}}}(2\,\text {GeV})}\), \({m_b^{\overline{\text {MS}}}(m_b^{\overline{\text {MS}}})}\) and \(m_\tau \) are set to specific values. In line 42 an object of type  is created, which contains the options to customize the calculation of \({a_\mu ^{{\text {BSM}}}}\) and \({\delta a_\mu }\). In line 43 the “running masses” scheme is chosen, see Sect. 2.2.3. In line 47 the 2HDM model is created, given the 2HDM and SM input parameters and the configuration options defined above. The value of \({a_\mu ^{{\text {BSM}}}= a_\mu ^{1\ell }+ a_\mu ^{2\ell }}\) is calculated in lines 50–51. The corresponding uncertainty \({\delta a_\mu }\) is calculated in line 54–55. The values \({a_\mu ^{{\text {BSM}}}}\) and \(\delta a_\mu \) are printed in line 57. Note that the 2HDM model should be created within a
is created, which contains the options to customize the calculation of \({a_\mu ^{{\text {BSM}}}}\) and \({\delta a_\mu }\). In line 43 the “running masses” scheme is chosen, see Sect. 2.2.3. In line 47 the 2HDM model is created, given the 2HDM and SM input parameters and the configuration options defined above. The value of \({a_\mu ^{{\text {BSM}}}= a_\mu ^{1\ell }+ a_\mu ^{2\ell }}\) is calculated in lines 50–51. The corresponding uncertainty \({\delta a_\mu }\) is calculated in line 54–55. The values \({a_\mu ^{{\text {BSM}}}}\) and \(\delta a_\mu \) are printed in line 57. Note that the 2HDM model should be created within a  block, because the constructor of the 2HDM class throws an exception if a physical problem occurs (e.g. a tachyon) or an input parameter has been set to an invalid value, see Table 3.
block, because the constructor of the 2HDM class throws an exception if a physical problem occurs (e.g. a tachyon) or an input parameter has been set to an invalid value, see Table 3.
Alternatively, the 2HDM input parameters can be given in the “gauge basis”, i.e. in terms of the Lagrangian parameters, see Table 2. The following C++ source code snippet shows a corresponding example two-loop calculation in the 2HDM of type II, where the input parameters are defined in the “gauge basis”.  In line 12 an object of type
In line 12 an object of type  is created, which is filled with the gauge basis input parameters in lines 13–25. With the defined gauge basis input parameters the calculation of \({a_\mu ^{{\text {BSM}}}}\) and \({\delta a_\mu }\) continues as in the mass basis example above.
is created, which is filled with the gauge basis input parameters in lines 13–25. With the defined gauge basis input parameters the calculation of \({a_\mu ^{{\text {BSM}}}}\) and \({\delta a_\mu }\) continues as in the mass basis example above.
3.5 Running GM2Calc from within C
Alternatively to the C++ programming interface detailed in Sect. 3.4, GM2Calc also provides a C programming interface. The following C source code snippet shows a two-loop example calculation in the 2HDM of type II with input parameters defined in the “mass basis”, see Table 2.  This example source code can be compiled as follows (assuming GM2Calc has been compiled to a shared library
This example source code can be compiled as follows (assuming GM2Calc has been compiled to a shared library  on a UNIX-like operating system with
on a UNIX-like operating system with  installed):
installed):

Here  is the file that contains the above listed source code.
is the file that contains the above listed source code.
The C example source code is very similar to the mass basis C++ example. In line 12 an object of type  is created and filled with the mass basis input parameters in lines 13–32. The Yukawa type of the model is defined in line 13 to be type II. In line 35 an object of type
is created and filled with the mass basis input parameters in lines 13–32. The Yukawa type of the model is defined in line 13 to be type II. In line 35 an object of type  is created, which contains the SM input parameters. The SM input parameters are set to their default values in line 36. In lines 37–41 the values of \({\alpha _{\text {em}}(m_Z)}\), \(m_t\), \({m_c^{\overline{\text {MS}}}(2\,\text {GeV})}\), \({m_b^{\overline{\text {MS}}}(m_b^{\overline{\text {MS}}})}\) and \(m_\tau \) are set to specific values. In line 44 a config object of type
is created, which contains the SM input parameters. The SM input parameters are set to their default values in line 36. In lines 37–41 the values of \({\alpha _{\text {em}}(m_Z)}\), \(m_t\), \({m_c^{\overline{\text {MS}}}(2\,\text {GeV})}\), \({m_b^{\overline{\text {MS}}}(m_b^{\overline{\text {MS}}})}\) and \(m_\tau \) are set to specific values. In line 44 a config object of type  is created which contains options to customize the calculation. These options are set to default values in line 45. In line 48 a null-pointer to a 2HDM model of type
is created which contains options to customize the calculation. These options are set to default values in line 45. In line 48 a null-pointer to a 2HDM model of type  is created. In line 49 the 2HDM model is created and the pointer is set to point to the model. If an error occurrs, the pointer is set to 0 and the returned
is created. In line 49 the 2HDM model is created and the pointer is set to point to the model. If an error occurrs, the pointer is set to 0 and the returned  variable is set to a value that is not
variable is set to a value that is not  . If no error has occurred, the example continues to calculate \({a_\mu ^{{\text {BSM}}}}\) and \({\delta a_\mu }\) in lines 53–58, respectively. The result is printed in line 60. In line 65 the memory reserved for the 2HDM model is freed.
. If no error has occurred, the example continues to calculate \({a_\mu ^{{\text {BSM}}}}\) and \({\delta a_\mu }\) in lines 53–58, respectively. The result is printed in line 60. In line 65 the memory reserved for the 2HDM model is freed.
Alternatively, the 2HDM input parameters can be given in the “gauge basis”, similarly to the gauge basis C++ example. The following C source code snippet shows a corresponding example two-loop calculation in the 2HDM of type II, where the input parameters are defined in the “gauge basis”.  In line 12 an object of type
In line 12 an object of type  is created, which is filled with the gauge basis input parameters in lines 13–26. In line 43 the 2HDM model is created, using the gauge basis input parameters. The calculation of \({a_\mu ^{{\text {BSM}}}}\) and \({\delta a_\mu }\) is performed in lines 47–52, as in the “mass basis” example above.
is created, which is filled with the gauge basis input parameters in lines 13–26. In line 43 the 2HDM model is created, using the gauge basis input parameters. The calculation of \({a_\mu ^{{\text {BSM}}}}\) and \({\delta a_\mu }\) is performed in lines 47–52, as in the “mass basis” example above.
3.6 Running GM2Calc from within Mathematica
GM2Calc can be run from within Mathematica using the  interface. The following source code snippet shows an example calculation of \({a_\mu ^{{\text {BSM}}}}\) and its uncertainty at the two-loop level using input parameters given in the “gauge basis”.
interface. The following source code snippet shows an example calculation of \({a_\mu ^{{\text {BSM}}}}\) and its uncertainty at the two-loop level using input parameters given in the “gauge basis”.  In line 1 GM2Calc’s
In line 1 GM2Calc’s  executable
executable  , which is created when building GM2Calc, is loaded into the Mathematica session. In lines 4–6 two configuration options to customize the calculation are set: The calculation shall be performed at the two-loop level using the “running masses” scheme defined in Sect. 2.2.3. In lines 9–29 the SM input parameters are defined. Unset parameters are set to reasonable default values, see
, which is created when building GM2Calc, is loaded into the Mathematica session. In lines 4–6 two configuration options to customize the calculation are set: The calculation shall be performed at the two-loop level using the “running masses” scheme defined in Sect. 2.2.3. In lines 9–29 the SM input parameters are defined. Unset parameters are set to reasonable default values, see  . In lines 32–46 the values of \({a_\mu ^{{\text {BSM}}}}\) and \({\delta a_\mu }\) are calculated using the function
. In lines 32–46 the values of \({a_\mu ^{{\text {BSM}}}}\) and \({\delta a_\mu }\) are calculated using the function  , which takes the gauge basis input parameters as arguments, see Table 3. The result is printed in line 48.
, which takes the gauge basis input parameters as arguments, see Table 3. The result is printed in line 48.
Alternatively, the calculation can be performed using input parameters given in the “mass basis”. The following source code snippet shows an example calculation of \({a_\mu ^{{\text {BSM}}}}\) and its uncertainty at the two-loop level using input parameters given in the “mass basis”.  The calculation of \({a_\mu ^{{\text {BSM}}}}\) and \({\delta a_\mu }\) is performed in lines 32–51 with the function
The calculation of \({a_\mu ^{{\text {BSM}}}}\) and \({\delta a_\mu }\) is performed in lines 32–51 with the function  , which takes the mass basis input parameters as arguments, see Table 3. The result is printed in line 53.
, which takes the mass basis input parameters as arguments, see Table 3. The result is printed in line 53.
3.7 Running GM2Calc from within Python
Newly implemented in GM2Calc 2.0.0 is the ability to interface with Python using the package  . An example calculation using the interface is shown in the code snippet below, working in the “mass basis”.
. An example calculation using the interface is shown in the code snippet below, working in the “mass basis”.  Note similarity between the above code and the C++ and C interfaces. Line 3 is to make sure that this example which is written using Python 3-style
Note similarity between the above code and the C++ and C interfaces. Line 3 is to make sure that this example which is written using Python 3-style  functions can still work in Python 2. Line 4 imports the interface script
functions can still work in Python 2. Line 4 imports the interface script  which loads the
which loads the  and
and  packages, as well as the header and library locations. This interface file is originally in the
packages, as well as the header and library locations. This interface file is originally in the  subdirectory. After performing
subdirectory. After performing

the interface script will be copied into the subdirectory  , and it will be filled with the path information for the GM2Calc headers, library, and the
, and it will be filled with the path information for the GM2Calc headers, library, and the  path. The interface can be imported from there by other Python scripts, or moved to an appropriate location where the user has their own Python scripts. Lines 6–11 load the relevant header files, and line 13 loads the GM2Calc shared library. In lines 16–20 the necessary namespaces from C++ are loaded into Python. In line 23 the 2HDM
path. The interface can be imported from there by other Python scripts, or moved to an appropriate location where the user has their own Python scripts. Lines 6–11 load the relevant header files, and line 13 loads the GM2Calc shared library. In lines 16–20 the necessary namespaces from C++ are loaded into Python. In line 23 the 2HDM  object is initialized, while on line 24 the 2HDM is specified to be type II. Lines 25–36 involve setting the values for simple attributes in the basis. Lines 36–42 assign values to the
object is initialized, while on line 24 the 2HDM is specified to be type II. Lines 25–36 involve setting the values for simple attributes in the basis. Lines 36–42 assign values to the  attributes, however since these are meant to be ignored, they are just set to 0. Lines 44–49 initialize an
attributes, however since these are meant to be ignored, they are just set to 0. Lines 44–49 initialize an  object and ensures it has the appropriate parameters. Line 51 initializes the
object and ensures it has the appropriate parameters. Line 51 initializes the  object, which is used to flag the use of running coupling in the next line. Line 56 initializes a
object, which is used to flag the use of running coupling in the next line. Line 56 initializes a  object using the
object using the  ,
,  , and
, and  information. Lines 58–63 prints out the values of \({a_\mu ^{{\text {BSM}}}}\) and \({\delta a_\mu }\) which are calculated using the interface functions
information. Lines 58–63 prints out the values of \({a_\mu ^{{\text {BSM}}}}\) and \({\delta a_\mu }\) which are calculated using the interface functions  ,
,  , and
, and  . Alternatively an error message will be printed out on line 63 should a problem arise.
. Alternatively an error message will be printed out on line 63 should a problem arise.
Another example of the Python interface is shown below, this time using the “gauge basis”:  In line 23 we instead initialize a
In line 23 we instead initialize a  object. To define the attribute
object. To define the attribute  , we need to circumvent Python’s reserved keywords. This is done by defining a \(7\times 1\)
, we need to circumvent Python’s reserved keywords. This is done by defining a \(7\times 1\)
 in line 26. This
in line 26. This  is initialized to 0 before assigned the appropriate entires elementwise on lines 28–34. Then the method
is initialized to 0 before assigned the appropriate entires elementwise on lines 28–34. Then the method  can be used to interface the values to the C++ code. Then the other values can be defined on lines 36–53, and finally the result for \({a_\mu ^{{\text {BSM}}}}\) is printed on line 65.
can be used to interface the values to the C++ code. Then the other values can be defined on lines 36–53, and finally the result for \({a_\mu ^{{\text {BSM}}}}\) is printed on line 65.
4 Applications
4.1 Parameter scan in the type II and X models
As an application we perform a 2-dimensional parameter scan over \(m_A\) and \(\tan \beta \) for the type II and type X 2HDM models, similarly to Ref. [85]. However, in contrast to Ref. [85] we include the two-loop bosonic contributions and use the updated value of \({a_\mu ^{{\text {BSM}}}= (25.1 \pm 5.9)\times 10^{-10}}\) from Eq. (3). The following C++ source code shows the program to perform the scan.  The function
The function  calculates \({a_\mu ^{{\text {BSM}}}}\) in the 2HDM at the two-loop level for a given value of \(m_A\) and \(\tan \beta \) and a specified Yukawa type. The remaining 2HDM input parameters in the mass basis are set to \(m_h=126\,\text {GeV}\), \(m_H=m_{H^\pm }=200\,\text {GeV}\), \(\sin (\beta -\alpha )=1\), \(\lambda _6=\lambda _7=0\), \(m_{12}^2=m_H^2/\tan \beta + (m_h^2 - \lambda _1 v^2)/\tan ^3\beta \) and \(\lambda _1=\sqrt{4\pi }\). In the
calculates \({a_\mu ^{{\text {BSM}}}}\) in the 2HDM at the two-loop level for a given value of \(m_A\) and \(\tan \beta \) and a specified Yukawa type. The remaining 2HDM input parameters in the mass basis are set to \(m_h=126\,\text {GeV}\), \(m_H=m_{H^\pm }=200\,\text {GeV}\), \(\sin (\beta -\alpha )=1\), \(\lambda _6=\lambda _7=0\), \(m_{12}^2=m_H^2/\tan \beta + (m_h^2 - \lambda _1 v^2)/\tan ^3\beta \) and \(\lambda _1=\sqrt{4\pi }\). In the  function the loop over \(m_A\) and \(\tan \beta \) is performed and \({a_\mu ^{{\text {BSM}}}}\) is calculated for the type II and type X 2HDM and the result is written to the standard output. The 2-dimensional output is shown in Fig. 1 for the two types of the 2HDM.
function the loop over \(m_A\) and \(\tan \beta \) is performed and \({a_\mu ^{{\text {BSM}}}}\) is calculated for the type II and type X 2HDM and the result is written to the standard output. The 2-dimensional output is shown in Fig. 1 for the two types of the 2HDM.
Two-loop prediction of \({a_\mu ^{{\text {BSM}}}}\) in the 2HDM of type II (left) and type X (right) as a function of \(\tan \beta \) and \(m_A\) with \(m_h=126\,\text {GeV}\), \(m_H=m_{H^\pm }=200\,\text {GeV}\), \(\sin (\beta -\alpha )=1\), \(\lambda _6=\lambda _7=0\), \(m_{12}^2=m_H^2/\tan \beta + (m_h^2 - \lambda _1 v^2)/\tan ^3\beta \) and \(\lambda _1=\sqrt{4\pi }\). In the green, yellow and gray regions the 2HDM predicts the correct value of \({a_\mu ^{{\text {BSM}}}= (25.1 \pm 5.9)\times 10^{-10}}\) from Eq. (3) within one, two and three standard deviations, respectively
4.2 Size of fermionic and bosonic contributions
In the following we illustrate the calculation of the two-loop fermionic and bosonic contributions, \({a_\mu ^{\text {F}}}\) and \({a_\mu ^{\text {B}}}\), separately. For the illustration we perform a scan over \(m_A\) for the demo parameter scenario from 2HDMC [113], which is a type II 2HDM scenario where \(m_H= 400\,\text {GeV}\), \(m_{H^\pm }=440\,\text {GeV}\), \(\tan \beta =3\), \(\sin (\beta -\alpha )=0.999\), \(\lambda _6=\lambda _7=0\) and \(m_{12}^2=(200\,\text {GeV})^2\). The following C source code shows the program to perform the scan.  The SM input parameters and the configuration options are set to their default values by passing 0 as the last two arguments to the function
The SM input parameters and the configuration options are set to their default values by passing 0 as the last two arguments to the function  that creates the 2HDM model in line 39. The individual bosonic and fermionic contributions are calculated in lines 42–43 and written to the standard output in line 45.
that creates the 2HDM model in line 39. The individual bosonic and fermionic contributions are calculated in lines 42–43 and written to the standard output in line 45.
Different contributions to \({a_\mu ^{{\text {BSM}}}}\) in the 2HDM. In the left panels we show scenarios from the type II 2HDM as a function of \(m_A\) with \(m_H= 400\,\text {GeV}, m_{H^\pm }=440\,\text {GeV}\), \(\tan \beta =3\), \(\sin (\beta -\alpha )=0.999\), \(\lambda _6=\lambda _7=0\) and \(m_{12}^2=(200\,\text {GeV})^2\). In the right panels we show FA2HDM scenarios with \(m_h = 125\,\text {GeV}\), \(m_H=150\,\text {GeV}\), \(m_{H^\pm }=150\,\text {GeV}\), \(\sin (\beta -\alpha )=0.999\), \(\lambda _6=0\), \(\lambda _7=0\), \(\tan \beta = 2\), \(m_{12}^2\) is fixed to avoid \(h\rightarrow AA\) decays using a polynomial equation shown in the related source code, \(\zeta _u=\zeta _d = -0.1\), \(\zeta _l = 50\) based on scenarios found for Fig. 10 of Ref. [103]. In the top panels we show fermionic (red solid line) and bosonic (blue dashed-dotted line) two-loop contributions separately. The top right panel also shows a purple region over the values of \(m_A\) where it is possible to explain Eq. (3). In the bottom panels we compare the fermionic two-loop contributions, when the running 3rd generation fermion masses shown in (73) are used (red solid line) and when the 3rd generation input masses from (72) are used (green dashed line). The red and green bands show the corresponding uncertainties. The bottom left panel also shows two-loop fermionic contributions calculated from 2HDMC as a black dotted line. *This is not a vanilla 2HDMC calculation, the SM-Higgs-like two-loop contributions have been removed, and the two-loop charged Higgs Barr–Zee contributions have been added as explained in the text
In the top left panel of Fig. 2 we show the results for the fermionic (red solid line) and bosonic (blue dashed-dotted line) contributions as a function of \(m_A\) for this demo scenario from 2HDMC. For the shown parameter space the fermionic contributions decrease, while the bosonic contributions increase for increasing \(m_A\). Furthermore, the bosonic contributions are negative, while the fermionic contributions are positive, which leads to a partial cancellation of the two contributions. However, as is generally the case for the type II 2HDM scenarios that are not already excluded by other constraints, the scenarios we plot here cannot explain the large deviation between the Standard Model prediction and experiment given in Eq. (3).
If instead we consider the FA2HDM scenarios, as in the top right panel of Fig. 2 it is now possible to explain large deviations. Here we fix the following parameters \(m_h = 125\,\text {GeV}\), \(m_H=150\,\text {GeV}\), \(m_{H^\pm }=150\,\text {GeV}\), \(\sin (\beta -\alpha )=0.999\), \(\lambda _6=0\), \(\lambda _7=0\), \(\tan \beta = 2\), \(\zeta _u=\zeta _d=-0.1\), \(\zeta _l = 50\) based on results used for Fig. 10 of Ref. [103]. It should be noticed that, once the masses for the charged and CP-even scalar are close together and below around 300 GeV, electroweak as well as unitarity and perturbativity constraints can be evaded for arbitrarily low values of \(m_A\) [85]. The input parameters here are chosen accordingly. Since \({m_A < m_{h_{\text {SM}}}/2}\), it is possible for \(h \rightarrow A A\) decays to occur unless we enforce the coupling \(C_{hAA}=0\).Footnote 8 This fixes the value of \(\lambda _1\) according to Eq. (12) in Ref. [103], which can be set in the mass basis using \(m_{12}^2\) and applying the relations in Eqs. (2.12)–(2.13) in Ref. [102]. This leads to the fitted 2nd-order polynomial relation with a dependence on \(m_A\) seen in the source code below.
These scenarios have a very light pseudoscalar mass, but LHC limits are much weaker compared to the type II case and can be evaded for these scenarios. The two-loop fermion contributions rise rapidly as the pseudoscalar mass decreases, dominating over the two-loop bosonic contributions, though the latter are just large enough to have an impact on constraints from \({a_\mu }\). Note that for higher values of \(m_A\) it is possible to get larger bosonic contributions as can be seen in Fig. 10 of Ref. [103]. In the scenarios we plot here the one-loop contributions, which are not shown in Fig. 2, have a negative effect on the contributions, with a size of approximately one-third of the two-loop fermionic contributions. Thus it can be seen that \({a_\mu ^{{\text {BSM}}}}\) can be explained with a very low \(m_A\) for the values of \(m_A\) in the purple region. The scan for this scenario can be performed with the following C source code: 
4.3 Running fermion masses
In this subsection we study the effect of using the input vs. running fermion masses in the two-loop fermionic contributions as described in Sect. 2.2.3, and compare the results with 2HDMC. The following Mathematica source code shows a program to perform a scan over \(m_A\) using the same type II 2HDM parameter region as in Sect. 4.2.  The function
The function  calculates the two-loop fermionic contribution \(a_\mu ^{\text {F}}\) and the uncertainty \(\delta a_\mu \) for a given value of \(m_A\) and the mass basis input parameters defined above. In line 20 the usage of running fermion masses is disabled and the calculation is performed in the subsequent line. Similarly, in line 24 the usage of running fermion masses is enabled and the calculation is performed in the subsequent line. The results are collected in the variable
calculates the two-loop fermionic contribution \(a_\mu ^{\text {F}}\) and the uncertainty \(\delta a_\mu \) for a given value of \(m_A\) and the mass basis input parameters defined above. In line 20 the usage of running fermion masses is disabled and the calculation is performed in the subsequent line. Similarly, in line 24 the usage of running fermion masses is enabled and the calculation is performed in the subsequent line. The results are collected in the variable  and are exported to a file in line 31. We also used a very similar script to do the same calculations for the FA2HDM scenarios discussed in Sect. 4.2.
and are exported to a file in line 31. We also used a very similar script to do the same calculations for the FA2HDM scenarios discussed in Sect. 4.2.
The effect of using running fermion masses in the two-loop fermionic contributions is shown in Fig. 2 for the type II (bottom left panel) and flavour aligned (bottom right panel) scenarios matching those described in the previous section. The red solid line shows the value of \({a_\mu ^{\text {F}}}\) when the running masses (73) are used, i.e. the 3rd generation fermion masses are run to the scale of the Higgs boson in the two-loop fermionic Barr-Zee Feynman diagrams. Note that although the vertical axes are slightly different, the red lines shown in the bottom panels are identical to the red lines from the corresponding panels immediately above them, which were discussed in the previous section. The green dashed lines show the value of \({a_\mu ^{\text {F}}}\) when input fermion masses listed in (72) are used. In both scenarios that we look at the value of \({a_\mu ^{\text {F}}}\) is smaller when running masses are used, though the difference is only distinguishable for the type II case where the size of the contributions is much smaller. The reason for this is that due to the negative fermion mass \(\beta \) functions the running masses are numerically smaller than the corresponding input masses in the shown scenarios, which leads to a systematic reduction of the fermionic two-loop contributions.
In addition to the red solid and green dashed lines from GM2Calc, as the scenario in question is a benchmark point for 2HDMC [113], we show in the bottom left panel of Fig. 2 the corresponding result obtained with 2HDMC 1.8.0 as black dotted line. Note that at the two-loop level 2HDMC includes only fermionic contributions to \({a_\mu ^{{\text {BSM}}}}\). Furthermore, 2HDMC does not subtract the contributions from the SM Higgs boson and does not include the two-loop contributions from the charged Higgs boson. Therefore to obtain this black dotted line we have thus subtracted the two-loop SM Higgs contributions from the 2HDMC result and added the two-loop contributions from the charged Higgs boson. Since 2HDMC inserts running fermion masses into the fermionic contributions, the black dotted line can be compared to the red solid line in the figure. There is a small deviation between these two lines, which originates from the inclusion of fermionic Barr-Zee diagrams with an internal Z boson in GM2Calc, which are not included in 2HDMC.
In the bottom panels of Fig. 2 we also show the uncertainties calculated with (74) as lighter shaded regions of the corresponding color about the red and green lines. In the bottom left panel the red and green lines both lie within the uncertainty estimate for the alternative prediction (shaded green and shaded red regions respectively) for all values of \(m_A\) plotted. This is also true in the bottom right panel though there is no visible distinction between the red and green lines or their uncertainties here. Since the difference between the lines is of higher order, this indicates that our uncertainty estimate is working as expected and accounts for the expected higher order corrections.
5 Summary
We have presented version 2 of GM2Calc, with its new capability to calculate the BSM contributions to the anomalous magnetic moment of the muon in the 2HDM. The contributions include all the one-loop diagrams, two-loop fermionic Bar-Zee diagrams, as well as the bosonic two-loop contributions. The new version of GM2Calc provides the calculation of the 2HDM contributions with a precision of up to \(\mathcal {O}(m_\mu ^4)\) at one-loop and \(\mathcal {O}(m_\mu ^2)\) at two-loop level along with an estimate of uncertainty of the evaluation. GM2Calc performs this state of the art precision calculation at high speed, with execution times that can be as short as \(\mathcal {O}(0.05\,\text {ms})\) per point, allowing for rapid sampling of the parameter space. GM2Calc is easy to configure and run. The user can select well-known types of the 2HDM, specifically type I, II, X, Y as well as the flavour-aligned version (FA2HDM), or the fully general 2HDM. For the latter the user can specify the inputs as deviations away from the flavour alignment of the FA2HDM (or from type I, II, X, and Y) or by directly specifying the more fundamental Yukawa matrices, \(\Pi _f\) defined in Eq. (27). The user can also decide whether they will give inputs in the gauge basis using \(\lambda _{1,\ldots ,7}\) or the mass basis using \(m_{h,H,A,H^\pm }\), \(\lambda _{6,7}\), and \(\sin (\beta -\alpha )\). The input parameters and settings can be specified in an SLHA-like input file, mirroring the original MSSM version. Additionally, GM2Calc can be interfaced to other programs using C++, C, Mathematica, or Python, the latter being a new interface developed for GM2Calc 2.
For each of these interfaces we presented simple and easy to follow usage examples in Sect. 3, that are straightforward to adapt. In Sect. 4 we have also presented some applications and results, demonstrating different features of the code. In each of these we show the source code in the manual and also provide them as supplementary files. GM2Calc is actively developed on GitHub and users with any questions may contact the authors through our GitHub page or directly by email.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Author’s comment: The data used to create Figures 1 and 2 can be reproduced with GM2Calc 2.0.0 using the source code examples in the paper.]
Notes
As discussed extensively in the Theory Initiative White Paper [3], the proposed SM prediction does not use lattice gauge theory evaluations of the hadronic vacuum polarization. The lattice world average evaluated in Ref. [3], based on [30,31,32,33,34,35,36,37,38], is compatible with the data-based result [8,9,10,11,12,13,14], has a higher central value and larger uncertainty. However more recent lattice results are obtained in Refs. [39, 40], and in particular Ref. [39] obtains a result with smaller uncertainty, which would shift the SM prediction for \({a_\mu }\) closer to the experimental value. Scrutiny of these results is ongoing (see e.g. Ref. [41]) and further progress can be expected.
The \(\Gamma ^0\) and \(\Pi ^0\) matrices correspond to \(\eta _{1}\) and \(\eta _{2}\) in Ref. [42], see their Eq. (92).
The \(\Sigma ^0\) and \({\rho ^0}\) matrices correspond to \(\eta \) and \(\hat{\xi }\) in Ref. [42], see their Eq. (30).
These two Higgs potential parameters only enter via triple Higgs couplings, and they enter only via the combination \(\Lambda _{567}\) defined in Eq. (69). The suitable generalizations of Eqs. (3.25)–(3.26) of Ref. [102] for the required triple Higgs couplings can be obtained e.g. from formulas in the Appendix of Ref. [146] and can simply be written as
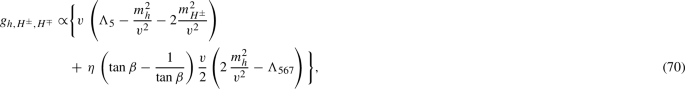

This structure clarifies the appearance of \(\Lambda _{567}\) in Eq. (67).
To track changes made to GM2Calc and get automatic updates one may alternatively clone the
 repository https://github.com/GM2Calc/GM2Calc
repository https://github.com/GM2Calc/GM2CalcFor instructions and examples of running the MSSM evaluation see Ref. [135].
Based a machine with an Intel(R) Core(TM) i7-5600U CPU @ 2.60 GHz processor.
The coupling \(C_{hAA}\) has been discussed in detail in Ref. [103]. Setting \(C_{hAA}=0\) directly corresponds to the choice \(\Lambda _6=0\), where \(\Lambda _6\) is a potential parameter in the so-called Higgs basis, and to a specific relation between all potential parameters in the general basis. It has been checked that although non-null values for \(C_{hAA}\) can be allowed, they are experimentally strongly constrained. Thus, for simplicity, we have adopted \(C_{hAA}=0\) in our analysis, which automatically guarantees that \(\lambda _1\) (or equivalently \(m_{12}^2\)) will not be chosen in a region excluded by experimental constraints or by unitarity or perturbativity.
References
Muon \(g-2\) Collaboration collaboration, B. Abi et al., Measurement of the positive muon anomalous magnetic moment to 0.46 ppm. Phys. Rev. Lett. 126, 141801 (2021). https://doi.org/10.1103/PhysRevLett.126.141801
Particle Data Group collaboration, M. Tanabashi et al., Review of particle physics. Phys. Rev. D 98, 030001 (2018). https://doi.org/10.1103/PhysRevD.98.030001
T. Aoyama et al., The anomalous magnetic moment of the muon in the standard model. Phys. Rep. 887, 1–166 (2020). arXiv:2006.04822
T. Aoyama, M. Hayakawa, T. Kinoshita, M. Nio, Complete tenth-order QED contribution to the Muon \(g-2\). Phys. Rev. Lett. 109, 111808 (2012). https://doi.org/10.1103/PhysRevLett.109.111808arXiv:1205.5370
T. Aoyama, T. Kinoshita, M. Nio, Theory of the anomalous magnetic moment of the electron. Atoms 7, 28 (2019). https://doi.org/10.3390/atoms7010028
A. Czarnecki, W.J. Marciano, A. Vainshtein, Refinements in electroweak contributions to the muon anomalous magnetic moment. Phys. Rev. D 67, 073006 (2003). https://doi.org/10.1103/PhysRevD.67.073006arXiv:hep-ph/0212229
C. Gnendiger, D. Stöckinger, H. Stöckinger-Kim, The electroweak contributions to \((g-2)_\mu \) after the Higgs boson mass measurement. Phys. Rev. D 88, 053005 (2013). https://doi.org/10.1103/PhysRevD.88.053005arXiv:1306.5546
M. Davier, A. Hoecker, B. Malaescu, Z. Zhang, Reevaluation of the hadronic vacuum polarisation contributions to the Standard Model predictions of the muon \(g-2\) and \({\alpha (m_Z^2)}\) using newest hadronic cross-section data. Eur. Phys. J. C 77, 827 (2017). https://doi.org/10.1140/epjc/s10052-017-5161-6arXiv:1706.09436
A. Keshavarzi, D. Nomura, T. Teubner, Muon \(g-2\) and \(\alpha (M_Z^2)\): a new data-based analysis. Phys. Rev. D 97, 114025 (2018). https://doi.org/10.1103/PhysRevD.97.114025arXiv:1802.02995
G. Colangelo, M. Hoferichter, P. Stoffer, Two-pion contribution to hadronic vacuum polarization. JHEP 02, 006 (2019). https://doi.org/10.1007/JHEP02(2019)006arXiv:1810.00007
M. Hoferichter, B.-L. Hoid, B. Kubis, Three-pion contribution to hadronic vacuum polarization. JHEP 08, 137 (2019). https://doi.org/10.1007/JHEP08(2019)137arXiv:1907.01556
M. Davier, A. Hoecker, B. Malaescu, Z. Zhang, A new evaluation of the hadronic vacuum polarisation contributions to the muon anomalous magnetic moment and to \(\varvec {\alpha }({\bf m}_{\bf Z}^2)\). Eur. Phys. J. C 80, 241 (2020). https://doi.org/10.1140/epjc/s10052-020-7792-2arXiv:1908.00921
A. Keshavarzi, D. Nomura, T. Teubner, The \(g-2\) of charged leptons, \(\alpha (M_Z^2)\) and the hyperfine splitting of muonium. Phys. Rev. D 101, 014029 (2020). https://doi.org/10.1103/PhysRevD.101.014029arXiv:1911.00367
A. Kurz, T. Liu, P. Marquard, M. Steinhauser, Hadronic contribution to the muon anomalous magnetic moment to next-to-next-to-leading order. Phys. Lett. B 734, 144–147 (2014). https://doi.org/10.1016/j.physletb.2014.05.043arXiv:1403.6400
K. Melnikov, A. Vainshtein, Hadronic light-by-light scattering contribution to the muon anomalous magnetic moment revisited. Phys. Rev. D 70, 113006 (2004). https://doi.org/10.1103/PhysRevD.70.113006arXiv:hep-ph/0312226
P. Masjuan, P. Sánchez-Puertas, Pseudoscalar-pole contribution to the \((g_{\mu }-2)\): a rational approach. Phys. Rev. D 95, 054026 (2017). https://doi.org/10.1103/PhysRevD.95.054026arXiv:1701.05829
G. Colangelo, M. Hoferichter, M. Procura, P. Stoffer, Dispersion relation for hadronic light-by-light scattering: two-pion contributions. JHEP 04, 161 (2017). https://doi.org/10.1007/JHEP04(2017)161arXiv:1702.07347
M. Hoferichter, B.-L. Hoid, B. Kubis, S. Leupold, S.P. Schneider, Dispersion relation for hadronic light-by-light scattering: pion pole. JHEP 10, 141 (2018). https://doi.org/10.1007/JHEP10(2018)141arXiv:1808.04823
A. Gérardin, H.B. Meyer, A. Nyffeler, Lattice calculation of the pion transition form factor with \(N_f=2+1\) Wilson quarks. Phys. Rev. D 100, 034520 (2019). https://doi.org/10.1103/PhysRevD.100.034520arXiv:1903.09471
J. Bijnens, N. Hermansson-Truedsson, A. Rodríguez-Sánchez, Short-distance constraints for the HLbL contribution to the muon anomalous magnetic moment. Phys. Lett. B 798, 134994 (2019). https://doi.org/10.1016/j.physletb.2019.134994arXiv:1908.03331
G. Colangelo, F. Hagelstein, M. Hoferichter, L. Laub, P. Stoffer, Longitudinal short-distance constraints for the hadronic light-by-light contribution to \((g-2)_\mu \) with large-\(N_c\) Regge models. JHEP 03, 101 (2020). https://doi.org/10.1007/JHEP03(2020)101arXiv:1910.13432
V. Pauk, M. Vanderhaeghen, Single meson contributions to the muon‘s anomalous magnetic moment. Eur. Phys. J. C 74, 3008 (2014). https://doi.org/10.1140/epjc/s10052-014-3008-yarXiv:1401.0832
I. Danilkin, M. Vanderhaeghen, Light-by-light scattering sum rules in light of new data. Phys. Rev. D 95, 014019 (2017). https://doi.org/10.1103/PhysRevD.95.014019arXiv:1611.04646
F. Jegerlehner, The anomalous magnetic moment of the muon. Springer Tracts Mod. Phys. 274, 1–693 (2017). https://doi.org/10.1007/978-3-319-63577-4
M. Knecht, S. Narison, A. Rabemananjara, D. Rabetiarivony, Scalar meson contributions to \(a_\mu \) from hadronic light-by-light scattering. Phys. Lett. B 787, 111–123 (2018). https://doi.org/10.1016/j.physletb.2018.10.048arXiv:1808.03848
G. Eichmann, C.S. Fischer, R. Williams, Kaon-box contribution to the anomalous magnetic moment of the muon. Phys. Rev. D 101, 054015 (2020). https://doi.org/10.1103/PhysRevD.101.054015arXiv:1910.06795
P. Roig, P. Sánchez-Puertas, Axial-vector exchange contribution to the hadronic light-by-light piece of the muon anomalous magnetic moment. Phys. Rev. D 101, 074019 (2020). https://doi.org/10.1103/PhysRevD.101.074019arXiv:1910.02881
T. Blum, N. Christ, M. Hayakawa, T. Izubuchi, L. Jin, C. Jung et al., The hadronic light-by-light scattering contribution to the muon anomalous magnetic moment from lattice QCD. Phys. Rev. Lett. 124, 132002 (2020). https://doi.org/10.1103/PhysRevLett.124.132002arXiv:1911.08123
G. Colangelo, M. Hoferichter, A. Nyffeler, M. Passera, P. Stoffer, Remarks on higher-order hadronic corrections to the muon \(g-2\). Phys. Lett. B 735, 90–91 (2014). https://doi.org/10.1016/j.physletb.2014.06.012arXiv:1403.7512
Fermilab Lattice, LATTICE-HPQCD, MILC collaboration, B. Chakraborty et al., Strong-isospin-breaking correction to the muon anomalous magnetic moment from lattice QCD at the physical point. Phys. Rev. Lett. 120, 152001 (2018). https://doi.org/10.1103/PhysRevLett.120.152001. arXiv:1710.11212
Budapest-Marseille-Wuppertal collaboration, S. Borsanyi et al., Hadronic vacuum polarization contribution to the anomalous magnetic moments of leptons from first principles. Phys. Rev. Lett. 121, 022002 (2018). https://doi.org/10.1103/PhysRevLett.121.022002. arXiv:1711.04980
RBC, UKQCD collaboration, T. Blum, P. A. Boyle, V. Gülpers, T. Izubuchi, L. Jin, C. Jung et al., Calculation of the hadronic vacuum polarization contribution to the muon anomalous magnetic moment. Phys. Rev. Lett. 121, 022003 (2018). https://doi.org/10.1103/PhysRevLett.121.022003. arXiv:1801.07224
D. Giusti, V. Lubicz, G. Martinelli, F. Sanfilippo, S. Simula, Electromagnetic and strong isospin-breaking corrections to the muon \(g - 2\) from Lattice QCD + QED. Phys. Rev. D 99, 114502 (2019). https://doi.org/10.1103/PhysRevD.99.114502arXiv:1901.10462
PACS collaboration, E. Shintani, Y. Kuramashi, Hadronic vacuum polarization contribution to the muon \(g-2\) with 2+1 flavor lattice QCD on a larger than (10 fm)\(^4\) lattice at the physical point. Phys. Rev. D 100, 034517 (2019). https://doi.org/10.1103/PhysRevD.100.034517. arXiv:1902.00885
Fermilab Lattice, LATTICE-HPQCD, MILC collaboration, C.T.H. Davies et al., Hadronic-vacuum-polarization contribution to the muon’s anomalous magnetic moment from four-flavor lattice QCD. Phys. Rev. D 101, 034512 (2020). https://doi.org/10.1103/PhysRevD.101.034512. arXiv:1902.04223
A. Gérardin, M. Cè, G. von Hippel, B. Hörz, H.B. Meyer, D. Mohler et al., The leading hadronic contribution to \((g-2)_\mu \) from lattice QCD with \(N_{\rm f}=2+1\) flavours of O(\(a\)) improved Wilson quarks. Phys. Rev. D 100, 014510 (2019). https://doi.org/10.1103/PhysRevD.100.014510arXiv:1904.03120
C. Aubin, T. Blum, C. Tu, M. Golterman, C. Jung, S. Peris, Light quark vacuum polarization at the physical point and contribution to the muon \(g-2\). Phys. Rev. D 101, 014503 (2020). https://doi.org/10.1103/PhysRevD.101.014503arXiv:1905.09307
D. Giusti, S. Simula, Lepton anomalous magnetic moments in Lattice QCD+QED. PoS LATTICE2019, 104 (2019). https://doi.org/10.22323/1.363.0104arXiv:1910.03874
S. Borsanyi et al., Leading hadronic contribution to the muon 2 magnetic moment from lattice QCD. arXiv:2002.12347
C. Lehner, A.S. Meyer, Consistency of hadronic vacuum polarization between lattice QCD and the R-ratio. Phys. Rev. D 101, 074515 (2020). https://doi.org/10.1103/PhysRevD.101.074515arXiv:2003.04177
G. Colangelo, M. Hoferichter, P. Stoffer, Constraints on the two-pion contribution to hadronic vacuum polarization. Phys. Lett. B 814, 136073 (2021). https://doi.org/10.1016/j.physletb.2021.136073arXiv:2010.07943
G.C. Branco, P.M. Ferreira, L. Lavoura, M.N. Rebelo, M. Sher, J.P. Silva, Theory and phenomenology of two-Higgs-doublet models. Phys. Rep. 516, 1–102 (2012). https://doi.org/10.1016/j.physrep.2012.02.002arXiv:1106.0034
J.F. Gunion, H.E. Haber, G.L. Kane, S. Dawson, The Higgs Hunter’s Guide, vol. 80 (2000)
ATLAS collaboration, G. Aad et al., Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 716, 1–29 (2012). https://doi.org/10.1016/j.physletb.2012.08.020. arXiv:1207.7214
CMS collaboration, S. Chatrchyan et al., Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 716, 30–61 (2012). https://doi.org/10.1016/j.physletb.2012.08.021. arXiv:1207.7235
H.E. Haber, O. Stål, New LHC benchmarks for the \(mathcal CP \)-conserving two-Higgs-doublet model. Eur. Phys. J. C 75, 491 (2015). https://doi.org/10.1140/epjc/s10052-015-3697-xarXiv:1507.04281
J. Baglio, O. Eberhardt, U. Nierste, M. Wiebusch, Benchmarks for Higgs pair production and heavy Higgs boson searches in the Two-Higgs-Doublet Model of Type II. Phys. Rev. D 90, 015008 (2014). https://doi.org/10.1103/PhysRevD.90.015008arXiv:1403.1264
O. Eberhardt, U. Nierste, M. Wiebusch, Status of the two-Higgs-doublet model of type II. JHEP 07, 118 (2013). https://doi.org/10.1007/JHEP07(2013)118arXiv:1305.1649
D. Chowdhury, O. Eberhardt, Global fits of the two-loop renormalized Two-Higgs-Doublet model with soft Z\(_{2}\) breaking. JHEP 11, 052 (2015). https://doi.org/10.1007/JHEP11(2015)052arXiv:1503.08216
D. Chowdhury, O. Eberhardt, Update of global two-Higgs-doublet model fits. JHEP 05, 161 (2018). https://doi.org/10.1007/JHEP05(2018)161arXiv:1711.02095
M. Misiak, M. Steinhauser, Weak radiative decays of the B meson and bounds on \(M_{H^\pm }\) in the Two-Higgs-Doublet Model. Eur. Phys. J. C 77, 201 (2017). https://doi.org/10.1140/epjc/s10052-017-4776-yarXiv:1702.04571
Q.-Y. Hu, X.-Q. Li, Y.-D. Yang, \(B^0\rightarrow K^{\ast 0}\mu ^+\mu ^-\) decay in the aligned two-Higgs-doublet model. Eur. Phys. J. C 77, 190 (2017). https://doi.org/10.1140/epjc/s10052-017-4748-2arXiv:1612.08867
X.-Q. Li, J. Lu, A. Pich, \(B_{s, d}^0 \rightarrow \ell ^+\ell ^-\) decays in the aligned two-Higgs-doublet model. JHEP 06, 022 (2014). https://doi.org/10.1007/JHEP06(2014)022arXiv:1404.5865
T. Enomoto, R. Watanabe, Flavor constraints on the Two Higgs Doublet Models of Z\(_{2}\) symmetric and aligned types. JHEP 05, 002 (2016). https://doi.org/10.1007/JHEP05(2016)002arXiv:1511.05066
P. Arnan, D. Bečirević, F. Mescia, O. Sumensari, Two Higgs doublet models and \(b\rightarrow s\) exclusive decays. Eur. Phys. J. C 77, 796 (2017). https://doi.org/10.1140/epjc/s10052-017-5370-zarXiv:1703.03426
A. Barroso, P.M. Ferreira, I.P. Ivanov, R. Santos, Metastability bounds on the two Higgs doublet model. JHEP 06, 045 (2013). https://doi.org/10.1007/JHEP06(2013)045arXiv:1303.5098
P.S. Bhupal Dev, A. Pilaftsis, Maximally symmetric two Higgs doublet model with natural standard model alignment. JHEP 12, 024 (2014). https://doi.org/10.1007/JHEP12(2014)024arXiv:1408.3405
S. Kanemura, K. Yagyu, Unitarity bound in the most general two Higgs doublet model. Phys. Lett. B 751, 289–296 (2015). https://doi.org/10.1016/j.physletb.2015.10.047arXiv:1509.06060
P. Draper, A. Ekstedt, H.E. Haber, A natural mechanism for approximate Higgs alignment in the 2HDM. JHEP 05, 235 (2021). https://doi.org/10.1007/JHEP05(2021)235arXiv:2011.13159
S. Gori, H.E. Haber, E. Santos, High scale flavor alignment in two-Higgs doublet models and its phenomenology. JHEP 06, 110 (2017). https://doi.org/10.1007/JHEP06(2017)110arXiv:1703.05873
P. Basler, M. Krause, M. Muhlleitner, J. Wittbrodt, A. Wlotzka, Strong first order electroweak phase transition in the CP-conserving 2HDM revisited. JHEP 02, 121 (2017). https://doi.org/10.1007/JHEP02(2017)121arXiv:1612.04086
P. Basler, M. Mühlleitner, J. Wittbrodt, The CP-violating 2HDM in light of a strong first order electroweak phase transition and implications for Higgs pair production. JHEP 03, 061 (2018). https://doi.org/10.1007/JHEP03(2018)061arXiv:1711.04097
P. Basler, M. Mühlleitner, J. Müller, Electroweak phase transition in non-minimal Higgs sectors. JHEP 05, 016 (2020). https://doi.org/10.1007/JHEP05(2020)016arXiv:1912.10477
K. Kainulainen, V. Keus, L. Niemi, K. Rummukainen, T.V.I. Tenkanen, V. Vaskonen, On the validity of perturbative studies of the electroweak phase transition in the Two Higgs Doublet model. JHEP 06, 075 (2019). https://doi.org/10.1007/JHEP06(2019)075arXiv:1904.01329
P. Basler, M. Mühlleitner, J. Müller, Electroweak baryogenesis in the CP-violating two-Higgs doublet model. arXiv:2108.03580
M. Krause, R. Lorenz, M. Muhlleitner, R. Santos, H. Ziesche, Gauge-independent renormalization of the 2-Higgs-doublet model. JHEP 09, 143 (2016). https://doi.org/10.1007/JHEP09(2016)143arXiv:1605.04853
M. Krause, M. Muhlleitner, R. Santos, H. Ziesche, Higgs-to-Higgs boson decays in a 2HDM at next-to-leading order. Phys. Rev. D 95, 075019 (2017). https://doi.org/10.1103/PhysRevD.95.075019arXiv:1609.04185
L. Altenkamp, S. Dittmaier, H. Rzehak, Precision calculations for \(h \rightarrow WW/ZZ \rightarrow 4\) fermions in the two-Higgs-Doublet Model with Prophecy4f. JHEP 03, 110 (2018). https://doi.org/10.1007/JHEP03(2018)110arXiv:1710.07598
L. Altenkamp, S. Dittmaier, H. Rzehak, Renormalization schemes for the Two-Higgs-Doublet Model and applications to h \(\rightarrow \) WW/ZZ \(\rightarrow \) 4 fermions. JHEP 09, 134 (2017). https://doi.org/10.1007/JHEP09(2017)134arXiv:1704.02645
L. Altenkamp, M. Boggia, S. Dittmaier, H. Rzehak, Electroweak corrections in the two-Higgs-doublet model and singlet extension of the standard model. PoS LL2018, 011 (2018). https://doi.org/10.22323/1.303.0011arXiv:1807.05876
A. Denner, S. Dittmaier, J.-N. Lang, Renormalization of mixing angles. JHEP 11, 104 (2018). https://doi.org/10.1007/JHEP11(2018)104arXiv:1808.03466
S. Kanemura, M. Kikuchi, K. Mawatari, K. Sakurai, K. Yagyu, Loop effects on the Higgs decay widths in extended Higgs models. Phys. Lett. B 783, 140–149 (2018). https://doi.org/10.1016/j.physletb.2018.06.035arXiv:1803.01456
M. Krause, M. Mühlleitner, Impact of electroweak corrections on neutral Higgs boson decays in extended Higgs sectors. JHEP 04, 083 (2020). https://doi.org/10.1007/JHEP04(2020)083arXiv:1912.03948
M. Aiko, S. Kanemura, K. Sakurai, Radiative corrections to decays of charged Higgs bosons in two Higgs doublet models. arXiv:2108.11868
P. Athron, C. Balázs, D.H.J. Jacob, W. Kotlarski, D. Stöckinger, H. Stöckinger-Kim, New physics explanations of \(\text{ a}_{{{\mu }}}\) in light of the FNAL muon g-2 measurement. J. High Energy Phys. 2021, 80 (2021). https://doi.org/10.1007/JHEP09(2021)080arXiv:2104.03691
V.D. Barger, J.L. Hewett, R.J.N. Phillips, New constraints on the charged Higgs sector in two Higgs doublet models. Phys. Rev. D 41, 3421–3441 (1990). https://doi.org/10.1103/PhysRevD.41.3421
H.E. Haber, G.L. Kane, T. Sterling, The Fermion mass scale and possible effects of Higgs bosons on experimental observables. Nucl. Phys. B 161, 493–532 (1979). https://doi.org/10.1016/0550-3213(79)90225-6
L.J. Hall, M.B. Wise, Flavor changing Higgs-boson couplings. Nucl. Phys. B 187, 397–408 (1981). https://doi.org/10.1016/0550-3213(81)90469-7
R.M. Barnett, G. Senjanovic, L. Wolfenstein, D. Wyler, Implications of a light Higgs scalar. Phys. Lett. B 136, 191–195 (1984). https://doi.org/10.1016/0370-2693(84)91179-1
R.M. Barnett, G. Senjanovic, D. Wyler, Tracking down Higgs scalars with enhanced couplings. Phys. Rev. D 30, 1529 (1984). https://doi.org/10.1016/0370-2693(84)91179-1
V. Barger, H.E. Logan, G. Shaughnessy, Identifying extended Higgs models at the LHC. Phys. Rev. D 79, 115018 (2009). https://doi.org/10.1103/PhysRevD.79.115018arXiv:0902.0170
H.E. Logan, D. MacLennan, Charged Higgs phenomenology in the flipped two Higgs doublet model. Phys. Rev. D 81, 075016 (2010). https://doi.org/10.1103/PhysRevD.81.075016arXiv:1002.4916
A. Pich, P. Tuzon, Yukawa alignment in the two-Higgs-doublet model. Phys. Rev. D 80, 091702 (2009). https://doi.org/10.1103/PhysRevD.80.091702arXiv:0908.1554
P. Tuzon, A. Pich, The aligned two-Higgs doublet model. Acta Phys. Polon. Supp. 3, 215–220 (2010). arXiv:1001.0293
A. Broggio, E.J. Chun, M. Passera, K.M. Patel, S.K. Vempati, Limiting two-Higgs-doublet models. JHEP 11, 058 (2014). https://doi.org/10.1007/JHEP11(2014)058arXiv:1409.3199
L. Wang, X.-F. Han, A light pseudoscalar of 2HDM confronted with muon g-2 and experimental constraints. JHEP 05, 039 (2015). https://doi.org/10.1007/JHEP05(2015)039arXiv:1412.4874
T. Abe, R. Sato, K. Yagyu, Lepton-specific two Higgs doublet model as a solution of muon g - 2 anomaly. JHEP 07, 064 (2015). https://doi.org/10.1007/JHEP07(2015)064arXiv:1504.07059
E.J. Chun, The muon g\(-\)2 in two-Higgs-doublet models. EPJ Web Conf. 118, 01006 (2016). https://doi.org/10.1051/epjconf/201611801006arXiv:1511.05225
E.J. Chun, Z. Kang, M. Takeuchi, Y.-L.S. Tsai, LHC \({\tau }\)-rich tests of lepton-specific 2HDM for (g - 2)\({_{\mu }}\). JHEP 11, 099 (2015). https://doi.org/10.1007/JHEP11(2015)099 [arxiv:1507.08067]
E.J. Chun, J. Kim, Leptonic precision test of leptophilic two-Higgs-doublet model. JHEP 07, 110 (2016). https://doi.org/10.1007/JHEP07(2016)110arXiv:1605.06298
L. Wang, J.M. Yang, M. Zhang, Y. Zhang, Revisiting lepton-specific 2HDM in light of muon \(g-2\) anomaly. Phys. Lett. B 788, 519–529 (2019). https://doi.org/10.1016/j.physletb.2018.11.045arXiv:1809.05857
E.J. Chun, J. Kim, T. Mondal, Electron EDM and Muon anomalous magnetic moment in Two-Higgs-Doublet Models. JHEP 12, 068 (2019). https://doi.org/10.1007/JHEP12(2019)068arXiv:1906.00612
E.J. Chun, T. Mondal, Searching for a light Higgs boson via the Yukawa process at lepton colliders. Phys. Lett. B 802, 135190 (2020). https://doi.org/10.1016/j.physletb.2019.135190arXiv:1909.09515
W.-Y. Keung, D. Marfatia, P.-Y. Tseng, Axion-like particles, two-Higgs-doublet models, leptoquarks, and the electron and Muon g-2. LHEP 2021, 209 (2021). https://doi.org/10.31526/lhep.2021.209arXiv:2104.03341
P.M. Ferreira, B.L. Gonçalves, F.R. Joaquim, M. Sher, (g-2)\({\mu }\) in the 2HDM and slightly beyond: an updated view. Phys. Rev. D 104, 053008 (2021). https://doi.org/10.1103/PhysRevD.104.053008arXiv:2104.03367
X.-F. Han, T. Li, H.-X. Wang, L. Wang, Y. Zhang, Lepton-specific inert two-Higgs-doublet model confronted with the new results for muon and electron g-2 anomalies and multi-lepton searches at the LHC. arXiv:2104.03227
J.C. Eung, T. Mondal, Leptophilic bosons and muon g-2 at lepton colliders. JHEP 07, 044 (2021). https://doi.org/10.1007/JHEP07(2021)044arXiv:2104.03701
A. Jueid, J. Kim, S. Lee, J. Song, Type-X two Higgs doublet model in light of the muon \(\mathbf{g-2}\): confronting Higgs and collider data. arXiv:2104.10175
A. Dey, J. Lahiri, B. Mukhopadhyaya, Muon g-2 and a type-X two Higgs doublet scenario: some studies in high-scale validity. arXiv:2106.01449
V. Ilisie, New Barr-Zee contributions to \(({ g}-{ 2})_\mu \) in two-Higgs-doublet models. JHEP 04, 077 (2015). https://doi.org/10.1007/JHEP04(2015)077arXiv:1502.04199
T. Han, S.K. Kang, J. Sayre, Muon \(g-2\) in the aligned two Higgs doublet model. JHEP 02, 097 (2016). https://doi.org/10.1007/JHEP02(2016)097arXiv:1511.05162
A. Cherchiglia, P. Kneschke, D. Stöckinger, H. Stöckinger-Kim, The muon magnetic moment in the 2HDM: complete two-loop result. JHEP 01, 007 (2017). https://doi.org/10.1007/JHEP01(2017)007arXiv:1607.06292
A. Cherchiglia, D. Stöckinger, H. Stöckinger-Kim, Muon g-2 in the 2HDM: maximum results and detailed phenomenology. Phys. Rev. D 98, 035001 (2018). https://doi.org/10.1103/PhysRevD.98.035001arXiv:1711.11567
S.-P. Li, X.-Q. Li, Y.-Y. Li, Y.-D. Yang, X. Zhang, Power-aligned 2HDM: a correlative perspective on \((g-2)_{e,\mu }\). JHEP 01, 034 (2021). https://doi.org/10.1007/JHEP01(2021)034arXiv:2010.02799
A. Crivellin, J. Heeck, P. Stoffer, A perturbed lepton-specific two-Higgs-doublet model facing experimental hints for physics beyond the Standard Model. Phys. Rev. Lett. 116, 081801 (2016). https://doi.org/10.1103/PhysRevLett.116.081801arXiv:1507.07567
Y. Omura, E. Senaha, K. Tobe, Lepton-flavor-violating Higgs decay \(h \rightarrow \mu \tau \) and muon anomalous magnetic moment in a general two Higgs doublet model. JHEP 05, 028 (2015). https://doi.org/10.1007/JHEP05(2015)028arXiv:1502.07824
S. Iguro, Y. Omura, M. Takeuchi, Testing the 2HDM explanation of the muon g - 2 anomaly at the LHC. JHEP 11, 130 (2019). https://doi.org/10.1007/JHEP11(2019)130arXiv:1907.09845
S. Jana, V.P. K., S. Saad, Resolving electron and muon \(g-2\) within the 2HDM. arXiv:2003.03386
W.-S. Hou, R. Jain, C. Kao, G. Kumar, T. Modak, Collider prospects for Muon \(g-2\) in general two Higgs doublet model. arXiv:2105.11315
W.-S. Hou, G. Kumar, Charged lepton flavor violation in light of Muon \(g-2\). arXiv:2107.14114
W.-S. Hou, Decadal mission for the new physics Higgs/flavor era. arXiv:2109.02557
O. Atkinson, M. Black, A. Lenz, A. Rusov, J. Wynne, Cornering the two Higgs doublet model type II. arXiv:2107.05650
D. Eriksson, J. Rathsman, O. Stal, 2HDMC: two-Higgs-doublet model calculator physics and manual. Comput. Phys. Commun. 181, 189–205 (2010). https://doi.org/10.1016/j.cpc.2009.09.011arXiv:0902.0851
M. Mühlleitner, M.O.P. Sampaio, R. Santos, J. Wittbrodt, ScannerS: parameter scans in extended scalar sectors. arXiv:2007.02985
M. Krause, M. Mühlleitner, M. Spira, 2HDECAY—a program for the calculation of electroweak one-loop corrections to Higgs decays in the Two-Higgs-Doublet Model including state-of-the-art QCD corrections. Comput. Phys. Commun. 246, 106852 (2020). https://doi.org/10.1016/j.cpc.2019.08.003arXiv:1810.00768
A. Denner, S. Dittmaier, A. Mück, PROPHECY4F 3.0: a Monte Carlo program for Higgs-boson decays into four-fermion final states in and beyond the Standard Model. Comput. Phys. Commun. 254, 107336 (2020). https://doi.org/10.1016/j.cpc.2020.107336arXiv:1912.02010
P. Bechtle, O. Brein, S. Heinemeyer, G. Weiglein, K.E. Williams, HiggsBounds: confronting arbitrary Higgs sectors with exclusion bounds from LEP and the tevatron. Comput. Phys. Commun. 181, 138–167 (2010). https://doi.org/10.1016/j.cpc.2009.09.003arXiv:0811.4169
P. Bechtle, O. Brein, S. Heinemeyer, G. Weiglein, K.E. Williams, HiggsBounds 2.0.0: confronting neutral and charged Higgs sector predictions with exclusion bounds from LEP and the tevatron. Comput. Phys. Commun. 182, 2605–2631 (2011). https://doi.org/10.1016/j.cpc.2011.07.015arXiv:1102.1898
P. Bechtle, O. Brein, S. Heinemeyer, O. Stal, T. Stefaniak, G. Weiglein et al., Recent developments in HiggsBounds and a preview of HiggsSignals. PoS CHARGED2012, 024 (2012). https://doi.org/10.22323/1.156.0024arXiv:1301.2345
P. Bechtle, O. Brein, S. Heinemeyer, O. Stål, T. Stefaniak, G. Weiglein et al., \( HiggsBounds -4\): improved tests of extended Higgs sectors against exclusion bounds from LEP, the tevatron and the LHC. Eur. Phys. J. C 74, 2693 (2014). https://doi.org/10.1140/epjc/s10052-013-2693-2arXiv:1311.0055
P. Bechtle, S. Heinemeyer, O. Stal, T. Stefaniak, G. Weiglein, Applying exclusion likelihoods from LHC searches to extended Higgs sectors. Eur. Phys. J. C 75, 421 (2015). https://doi.org/10.1140/epjc/s10052-015-3650-zarXiv:1507.06706
O. Stål, T. Stefaniak, Constraining extended Higgs sectors with HiggsSignals. PoS EPS–HEP2013, 314 (2013). https://doi.org/10.22323/1.180.0314arXiv:1310.4039
P. Bechtle, S. Heinemeyer, O. Stål, T. Stefaniak, G. Weiglein, \(HiggsSignals\): confronting arbitrary Higgs sectors with measurements at the Tevatron and the LHC. Eur. Phys. J. C 74, 2711 (2014). https://doi.org/10.1140/epjc/s10052-013-2711-4arXiv:1305.1933
P. Bechtle, S. Heinemeyer, O. Stål, T. Stefaniak, G. Weiglein, Probing the Standard Model with Higgs signal rates from the Tevatron, the LHC and a future ILC. JHEP 11, 039 (2014). https://doi.org/10.1007/JHEP11(2014)039arXiv:1403.1582
F. Staub, From superpotential to model files for FeynArts and CalcHep/CompHep. Comput. Phys. Commun. 181, 1077–1086 (2010). https://doi.org/10.1016/j.cpc.2010.01.011arXiv:0909.2863
F. Staub, Automatic calculation of supersymmetric renormalization group equations and self energies. Comput. Phys. Commun. 182, 808–833 (2011). https://doi.org/10.1016/j.cpc.2010.11.030arXiv:1002.0840
F. Staub, SARAH 3.2: Dirac Gauginos, UFO output, and more. Comput. Phys. Commun. 184, 1792–1809 (2013). https://doi.org/10.1016/j.cpc.2013.02.019arXiv:1207.0906
F. Staub, SARAH 4: a tool for (not only SUSY) model builders. Comput. Phys. Commun. 185, 1773–1790 (2014). https://doi.org/10.1016/j.cpc.2014.02.018arXiv:1309.7223
W. Porod, SPheno, a program for calculating supersymmetric spectra, SUSY particle decays and SUSY particle production at e+ e- colliders. Comput. Phys. Commun. 153, 275–315 (2003). https://doi.org/10.1016/S0010-4655(03)00222-4arXiv:hep-ph/0301101
W. Porod, F. Staub, SPheno 3.1: extensions including flavour, CP-phases and models beyond the MSSM. Comput. Phys. Commun. 183, 2458–2469 (2012). https://doi.org/10.1016/j.cpc.2012.05.021arXiv:1104.1573
P. Athron, J.-H. Park, D. Stöckinger, A. Voigt, FlexibleSUSY—a spectrum generator generator for supersymmetric models. Comput. Phys. Commun. 190, 139–172 (2015). https://doi.org/10.1016/j.cpc.2014.12.020arXiv:1406.2319
P. Athron, J.-H. Park, T. Steudtner, D. Stöckinger, A. Voigt, Precise Higgs mass calculations in (non-)minimal supersymmetry at both high and low scales. JHEP 01, 079 (2017). https://doi.org/10.1007/JHEP01(2017)079arXiv:1609.00371
P. Athron, M. Bach, D. Harries, T. Kwasnitza, J.-H. Park, D. Stöckinger et al., FlexibleSUSY 2.0: extensions to investigate the phenomenology of SUSY and non-SUSY models. Comput. Phys. Commun. 230, 145–217 (2018). https://doi.org/10.1016/j.cpc.2018.04.016arXiv:1710.03760
P. Athron, A. Büchner, D. Harries, W. Kotlarski, D. Stöckinger, A. Voigt, FlexibleDecay: an automated calculator of scalar decay widths. arXiv:2106.05038
P. Athron, M. Bach, H.G. Fargnoli, C. Gnendiger, R. Greifenhagen, J.-H. Park et al., GM2Calc: precise MSSM prediction for \((g - 2)\) of the muon. Eur. Phys. J. C 76, 62 (2016). https://doi.org/10.1140/epjc/s10052-015-3870-2arXiv:1510.08071
P.Z. Skands et al., SUSY Les Houches accord: interfacing SUSY spectrum calculators, decay packages, and event generators. JHEP 07, 036 (2004). https://doi.org/10.1088/1126-6708/2004/07/036arXiv:hep-ph/0311123
B.C. Allanach et al., SUSY Les Houches Accord 2. Comput. Phys. Commun. 180, 8–25 (2009). https://doi.org/10.1016/j.cpc.2008.08.004arXiv:0801.0045
GAMBIT collaboration, P. Athron et al., GAMBIT: the global and modular beyond-the-standard-model inference tool. Eur. Phys. J. C 77, 784 (2017). https://doi.org/10.1140/epjc/s10052-017-5321-8. arXiv:1705.07908
GAMBIT Models Workgroup collaboration, P. Athron et al., SpecBit, DecayBit and PrecisionBit: GAMBIT modules for computing mass spectra, particle decay rates and precision observables. Eur. Phys. J. C 78, 22 (2018). https://doi.org/10.1140/epjc/s10052-017-5390-8. arXiv:1705.07936
S.M. Barr, A. Zee, Electric dipole moment of the electron and of the neutron. Phys. Rev. Lett. 65, 21–24 (1990). https://doi.org/10.1103/PhysRevLett.65.21
D. Chang, W.-F. Chang, C.-H. Chou, W.-Y. Keung, Large two loop contributions to g-2 from a generic pseudoscalar boson. Phys. Rev. D 63, 091301 (2001). https://doi.org/10.1103/PhysRevD.63.091301arXiv:hep-ph/0009292
K.-M. Cheung, C.-H. Chou, O.C.W. Kong, Muon anomalous magnetic moment, two Higgs doublet model, and supersymmetry. Phys. Rev. D 64, 111301 (2001). https://doi.org/10.1103/PhysRevD.64.111301arXiv:hep-ph/0103183
Y.-L. Wu, Y.-F. Zhou, Muon anomalous magnetic moment in the standard model with two Higgs doublets. Phys. Rev. D 64, 115018 (2001). https://doi.org/10.1103/PhysRevD.64.115018arXiv:hep-ph/0104056
M. Krawczyk, Precision muon g-2 results and light Higgs bosons in the 2HDM(II). Acta Phys. Polon. B 33, 2621–2634 (2002). arXiv:hep-ph/0208076
A. Davydychev, J. Tausk, Two-loop self-energy diagrams with different masses and the momentum expansion. Nucl. Phys. B 397, 123–142 (1993). https://doi.org/10.1016/0550-3213(93)90338-P
J.F. Gunion, H.E. Haber, The CP conserving two Higgs doublet model: the approach to the decoupling limit. Phys. Rev. D 67, 075019 (2003). https://doi.org/10.1103/PhysRevD.67.075019arXiv:hep-ph/0207010
D. Lopez-Val, J. Sola, Delta r in the two-Higgs-doublet model at full one loop level- and beyond. Eur. Phys. J. C 73, 2393 (2013). https://doi.org/10.1140/epjc/s10052-013-2393-yarXiv:1211.0311
G. Degrassi, G.F. Giudice, QED logarithms in the electroweak corrections to the muon anomalous magnetic moment. Phys. Rev. D 58, 053007 (1998). https://doi.org/10.1103/PhysRevD.58.053007arXiv:hep-ph/9803384
G. Guennebaud, B. Jacob et al., Eigen v3 (2010). http://eigen.tuxfamily.org
Boost, Boost C++ Libraries (2021). http://www.boost.org/
W. R. Inc., Mathematica
G. van Rossum, Python. http://www.python.org
W.T. Lavrijsen, A. Dutta, High-performance Python–C++ bindings with PyPy and Cling (2018). http://cern.ch/wlav/Cppyy_LavrijsenDutta_PyHPC16.pdf
Particle Data Group collaboration, P. Zyla et al., Review of particle physics. PTEP 2020, 083C01 (2020). https://doi.org/10.1093/ptep/ptaa104
Acknowledgements
We would like to thank the other authors of version 1 of GM2Calc, M. Bach, H. G. Fargnoli, C. Gnendiger, R. Greifenhagen, J. Park, and S. Paßehr. We also thank T Gonzalo and C. S. Fonseca for their assistance with work dealing with two-loop contributions to the anomalous magnetic moment of the muon. The research placement of D.J. for this work was supported by the Australian Government Research Training Program (RTP) Scholarship and the Deutscher Akademischer Austauschdienst (DAAD) One-Year Research Grant. The work of P.A. was supported by the Australian Research Council Future Fellowship grant FT160100274. The work of P.A. and C.B. was also supported with the Australian Research Council Discovery Project grant DP180102209. This project was undertaken with the assistance of resources and services from the National Computational Infrastructure, which is supported by the Australian Government. We thank Astronomy Australia Limited for financial support of computing resources.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Athron, P., Balazs, C., Cherchiglia, A. et al. Two-loop prediction of the anomalous magnetic moment of the muon in the Two-Higgs Doublet Model with GM2Calc 2. Eur. Phys. J. C 82, 229 (2022). https://doi.org/10.1140/epjc/s10052-022-10148-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-022-10148-9



 [
[ [
[

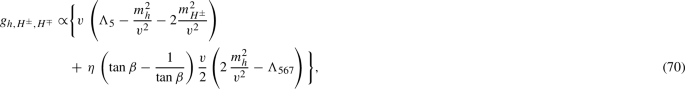

 repository
repository