The pumping action of the space-time curvature is the primary source of relic gravitons [1, 2] but when a conventional stage of inflationary expansion is replaced by a radiation-dominated epoch, the spectral energy density in critical units at the present conformal time \(\tau _{0}\) (denoted hereunder by \(\Omega _{gw}(\nu ,\tau _{0})\)) is quasi-flat for comoving frequencies \(\nu \) larger than 100 aHz [3]. The transition across the epoch of matter-radiation equality leads to an infrared branch where \(\Omega _{gw}(\nu ,\tau _{0}) \propto \nu ^{-2}\) between the aHz and 100 aHz [4]. The conventional inflationary evolution seems to exclude the possibility of a drastic deviation from scale-invariance in the direction of blue spectral indices for typical frequencies larger than fHz where, in a conservative perspective, \(h_{0}^2 \Omega _{gw}(\nu ,\tau _{0}) = {\mathscr {O}}(10^{-16.5})\). On the contrary the corrections typically go into the direction of a decreasing spectral slope as it happens, for instance, in the single-field case where, thanks to the consistency relations, the tensor spectral index \(n_{T}\) is notoriously related to the tensor to scalar ratio \(r_{T}\) as \(n_{T} \simeq - r_{T}/8\). Since \(r_{T}\) is currently assessed from the analysis of the temperature and polarization anisotropies of the Cosmic Microwave Background (CMB) it is difficult to argue that \(n_{T}\) could be positive. For typical frequencies larger than the mHz the spectral energy density increases provided the post-inflationary evolution is stiffer than radiation. For frequencies between the fHz and the mHz the spectral index can be blue in generalized gravity theories and when the dominant energy condition is violated (see, for instance, [5] for a recent review focussed on these issues).

Gravitational waves also acquire an effective index of refraction when they travel in curved space-times [6, 7]. In this context the blue spectral slopes arise from a more mundane effect associated with the variation of the refractive index even if the background geometry evolves according to a conventional stage of expansion possibly supplemented by a standard decelerated epoch [8]. The general idea behind this suggestion is that the effective action of single-field inflationary models involves all the different terms that include four derivatives and are suppressed by the negative powers of a large mass scale [9]. If parity breaking terms are included in the effective action [10, 11], the relic graviton background may be polarized but this possibility has been already discussed elsewhere [12]. There are however non-generic models of inflation where the higher-order corrections assume a particular form since the inflaton has some particular symmetry (like a shift symmetry \(\varphi \rightarrow \varphi + c\)) or because the rate of inflaton roll remains constant (and possibly larger than 1), as it happens in certain fast-roll scenarios [13] (see also, for instance, [14, 15]). Other examples include the situation where the higher-order curvature corrections are given in terms of the Gauss-Bonnet combination weighted by some inflaton dependent-coupling [16,17,18]. In [8] (see also [19, 20]) it has been argued that in all these situations the effective action of the relic gravitons is be modified and ultimately assumes the following general form:

$$\begin{aligned} S_{g} = \frac{1}{8 \ell _{P}^2} \int d^{4} x \biggl [ A(\tau )\, \,\partial _{\tau } h_{i j} \, \partial _{\tau } h^{i j} - B(\tau )\, \partial _{k} h_{i j} \partial ^{k} h^{i j} \biggr ], \nonumber \\ \end{aligned}$$
(1)

where we assume that the background is conformally flat and \(\partial _{i} h_{j}^{\,\,\,\, i}= h_{i}^{\,\,\,\,i} =0\). While both terms \(A(\tau )\) and \(B(\tau )\) depend on the conformal time coordinate \(\tau \) we can always factor \(A(\tau )\) and introduce an effective refractive index \(n(\tau )\) associated with the interactions with the background geometry, as originally argued in Ref. [6,7,8]:

$$\begin{aligned} S_{g} = \frac{1}{8 \ell _{P}^2} \int d^{4} x \,\,a^2(\tau ) \,\,\biggl [ \partial _{\tau } h_{i j} \, \partial _{\tau } h^{i j} - \frac{\partial _{k} h_{i j} \partial ^{k} h^{i j}}{n^2(\tau )} \biggr ], \end{aligned}$$
(2)

where \(a(\tau )\) is the scale factor in the conformal time coordinate; we are assuming here a conformally flat background metric \(\overline{g}_{\mu \nu } = a^2(\tau ) \, \eta _{\mu \nu }\). After Eq. (2) has been proposed in Ref. [8] apparently different parametrizations have been later introduced (see [19, 20] and discussion therein). The difference between these strategies consists in modifying the first term (rather than the second) inside the squared bracket of Eq. (2). This choice is immaterial since the two parametrizations of the effect are related by a rescaling of the four-dimensional metric through a conformal factor that involves the refractive index itself. Equation (2) simplifies by introducing a new time coordinate conventionally referred to as the \(\eta \)-time:

$$\begin{aligned} S_{g}= & {} \frac{1}{8 \ell _{P}^2} \int \,\,d^{4} x \,\,b^2(\eta )\,\, \biggl [ \partial _{\eta } h_{i j} \,\, \partial _{\eta } h^{i j} - \partial _{k} h_{i j} \,\,\partial ^{k} h^{i j} \biggr ], \nonumber \\ b(\eta )= & {} \frac{a(\eta )}{\sqrt{n(\eta )}}, \qquad \ell _{P} = \sqrt{8 \pi G}. \end{aligned}$$
(3)

Since the \(\eta \)-time is defined by \(n(\eta ) \, d\eta \,=\,d\tau \) and the scale factor is everywhere continuous with its first derivative,Footnote 1 the evolution of the refractive index is specified unambiguously by assigning n(a). Equation (3) generalizes the standard Ford-Parker action [21] to the case of a dynamical refractive index. Even if the phase velocity of the relic gravitons is not required to be sub-luminal we shall consider the situation where \(n(a) \ge 1\). In what follows for the sake of illustration we shall be assuming that n(a) changes appreciably during inflation and it goes to 1 during the standard decelerated stage of expansion:

$$\begin{aligned} n(a)= & {} n_{*} \frac{ (a/a_{*})^{\alpha } \,\,e^{- \xi (a/a_{1})}}{(a/a_{*})^{\alpha } + 1} + 1, \nonumber \\ n_{*}= & {} n_{i} (a_{*}/a_{i})^{\alpha } = n_{i} e^{\alpha \, N_{*}}, \end{aligned}$$
(4)

where \(a_{i}\) and \(a_{1}\) mark, respectively, the beginning and the end of the inflationary epoch; \(a_{*}\) defines the boundary of the refractive stage. What matters is not the specific analytical form (that only affects the transition regions) but the three successive physical regimes described by Eq. (4). In particular we have that \(n(a) \rightarrow 1\) when \(a\gg a_{1}\) and the sharpness of this transition is controlled by \(\xi \ge 1\). When \(a_{*}< a < a_{1}\) n(a) is constant (but still larger than 1), i.e. \(n(a)\simeq n_{*} > 1\). Finally for \(a< a_{*}\) we have the truly refractive stage where \(n (a) \simeq n_{*} (a/a_{*})^{\alpha }\). Even if in Ref. [8] more general possibilities have been examined (including a post-inflationary evolution of n(a)), for the present ends it is enough to consider the minimal case illustrated by Eq. (4).

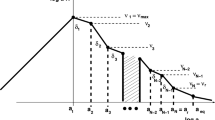
The different dynamical stages of the model are illustrated in the cartoon of Fig. 1 where the common logarithm of the effective horizon \(\dot{b}/b\) is reported. In contrast with the standard notations, the overdot denotes here a derivation with respect to the \(\eta \) coordinate (and not a derivation with respect to the cosmic time as usually implied). From the shape of Fig. 1 we can deduce that the spectral energy density will have three different branches. The modes \( k < k_{eq}\) correspond to wavelengths leaving the Hubble radius for \(b< b_{*}\) and reentering during the matter-dominated stage. We remind that, as usual, \(k_{eq} = 0.0732\, h_{0}^2 \Omega _{M0}\, \mathrm {Mpc}^{-1}\) where \(\Omega _{M0}\) is the present fraction in dusty matter.Footnote 2

Fig. 1
figure 1

The common logarithm effective horizon is approximately illustrated in terms of the scale factor. The different wavenumbers hit twice the effective horizon and the two crossings determine the slope of the spectrum in a given dynamical stage

Full size image

The modes \(k_{eq}< k < k_{*}\) (where \(k_{*} = 1/\eta _{*}\)) correspond to the wavelengths leaving the Hubble radius during the refractive stage and reentering when the background is dominated by radiation. In this range of wavenumbers the spectral energy density is either blue or violet, depending on the value of \(\alpha \) which is always positive as long as the refractive index is larger than 1. Finally in the region \( k_{*}< k < k_{1}\) the spectrum is quasi-flat since the corresponding wavelengths cross the Hubble radius during the inflationary phase (when the refractive index is not dynamical anymore) and reenter in the radiation stage of expansion. The comoving frequencies \(\nu _{max}= k_{max}/(2\,\pi )\) and \(\nu _{*}= k_{*}/(2\,\pi )\) cannot be assigned at wish depending on the convenience of the potential signal but they are determined from the various stages of the model. In particular the maximal frequency is typically \({\mathscr {O}}(200)\) MHz:

$$\begin{aligned} \nu _{max}&= 0.26 \, \biggl (\frac{\epsilon }{0.003}\biggr )^{1/4} \biggl (\frac{{\mathscr {A}}_{\mathscr {R}}}{2.41 \times 10^{-9}} \biggr )^{1/4} \, \nonumber \\&\quad \times \biggl (\frac{h_{0}^2 \Omega _{R0}}{4.15 \times 10^{-5}} \biggr )^{1/4}\, \mathrm {GHz}, \end{aligned}$$
(5)

where \(\epsilon \) denotes the slow-roll parameter and \({\mathscr {A}}_{{\mathscr {R}}}\) is the amplitude of the scalar power spectrum; according to the current determinations we have that the tensor to scalar ratio should be smaller than 0.064 [24, 25]; in a conservative perspective we shall be requiring \(\epsilon \le 0.06/16 \simeq 0.003\) as assumed in Eq. (5). We remind that the typical value of the pivot scale used in this discussion is \(k_{p} = 0.002\, \mathrm {Mpc}^{-1}\) corresponding to a typical comoving frequency \(\nu _{p} = 3.092\,\,\mathrm {aHz}\). Given \(\nu _{max}\) the value of \(\nu _{*}\) defines the knee of the spectrum:

$$\begin{aligned} \nu _{*} = \biggl (1 + \frac{\alpha }{1 - \epsilon }\biggr ) e^{N_{*} (\alpha +1) - N_{t}} \, \, \nu _{max}, \end{aligned}$$
(6)

where \(N_{t}\) denotes the total number of e-folds while, as in Eq. (4), \(N_{*} = \ln {(a_{*}/a_{i})}\). In Eq. (6) as well as in the forthcoming discussion we shall always be assuming that \(n_{i} \rightarrow 1\); different choices are possible (provided \(n_{i} \ge 1\)) but their effect does not modify the conclusions since the value of \(n_{i}\) can always be traded for a shorter refractive phase. The relevant point to appreciate is that \(\nu _{*}\) will control the typical frequency of the knee of the spectrum and it does depend on \(N_{*}\), \(N_{t}\) and \(\alpha \).

The Hamiltonian associated with Eq. (3) is directly expressible in the \(\eta \)-time and it is:

$$\begin{aligned}&H_{g}(\eta ) = \int d^{3} x \biggl [ \frac{8 \ell _{P}^2}{b^2} \pi _{i\,j} \, \pi ^{\,i \, j} + \frac{b^2}{8 \ell _{P}^2} \partial _{k} h_{i\,j} \, \partial ^{k} h^{\, i \, j} \biggr ], \nonumber \\&\pi _{i\, j}= \frac{b^2}{8 \ell _{P}^2} \partial _{\eta } h_{i\,j}. \end{aligned}$$
(7)

After promoting the field operators and their conjugate momenta to the status of quantum operators, from Eq. (7) the governing equations for \(\widehat{h}_{i\,j}\) and \(\widehat{\pi }_{i\,j}\) are:

$$\begin{aligned} \partial _{\eta } \widehat{h}_{i\, j} = \frac{ 8 \ell _{P}^2}{b^2}\, \widehat{\pi }_{i\, j}, \qquad \qquad \partial _{\eta } \widehat{\pi }_{i\, j} = \frac{b^2}{ 8 \ell _{P}^2}\, \nabla ^2 \widehat{h}_{i\, j}. \end{aligned}$$
(8)

In Fourier space Eq. (8) implies a specific solution of the corresponding mode functions \(F_{k}(\eta )\) and \(G_{k}(\eta )\); more specifically we have

$$\begin{aligned} \widehat{h}_{ij}(\vec {x}, \eta )= & {} \frac{\sqrt{2}\, \ell _{P}}{(2\pi )^{3/2}}\sum _{\lambda } \int \, d^{3} k \,\,e^{(\lambda )}_{ij}(\vec {k})\, \biggl [ F_{k,\lambda }(\eta )\, \widehat{a}_{\vec {k},\,\lambda } e^{- i \vec {k} \cdot \vec {x}}\nonumber \\&+ F^{*}_{k,\lambda }(\eta ) \,\widehat{a}_{\vec {k},\,\lambda }^{\dagger } e^{ i \vec {k} \cdot \vec {x}}\biggr ], \end{aligned}$$
(9)
$$\begin{aligned} \widehat{\pi }_{ij}(\vec {x}, \eta )= & {} \frac{1}{4 \, \sqrt{2} \,\ell _{P} \, (2\pi )^{3/2}}\sum _{\lambda } \int \, d^{3} k \,\,e^{(\lambda )}_{ij}(\vec {k})\, \biggl [ G_{k,\lambda }(\eta ) \nonumber \\&\times \widehat{a}_{\vec {k},\,\lambda } \,e^{- i \vec {k} \cdot \vec {x}} + G^{*}_{k,\lambda }(\eta ) \,\widehat{a}_{\vec {k},\,\lambda }^{\dagger } \, e^{ i \vec {k} \cdot \vec {x}}\biggr ]. \end{aligned}$$
(10)

In Eqs. (9)–(10) \(\lambda = \oplus ,\, \otimes \) runs over the tensor polarizations but, as in the conventional situation, the evolution of the mode functions is the same for each of the two values of \(\lambda \):

$$\begin{aligned} \dot{G}_{k,\,\lambda } = - k^2 \,b^2 \, F_{k,\,\lambda }, \qquad \dot{F}_{k, \, \lambda } = \frac{G_{k,\, \lambda }}{b^2}, \end{aligned}$$
(11)

where we recall, as already mentioned in connection with Fig. 1 that the overdot now denotes a derivation with respect to \(\eta \) (i.e. \(\dot{F}_{k, \, \lambda } = \partial _{\eta } \,F_{k, \, \lambda }\)). From Eqs. (9)–(10) the canonical commutation relations at equal \(\eta \)-times become

$$\begin{aligned}{}[ \widehat{h}_{i\,j}(\vec {x}, \eta ), \, \widehat{\pi }_{m\,n}(\vec {y}, \eta )] = i \, {\mathscr {S}}_{i\,j\,m\,n}(\hat{k}) \, \delta ^{(3)}(\vec {x}- \vec {y}), \end{aligned}$$
(12)

In Eq. (12) \({\mathscr {S}}_{i\,j\,m\,n}(\hat{k})\) follows from the sum over the tensor polarizations and the Wronskian of the mode functions is fixed:

$$\begin{aligned}&{\mathscr {S}}_{i\,j\,m\,n}(\hat{k}) = \frac{1}{4} \biggl [ p_{i\,m}(\hat{k})\, p_{j\,n}(\hat{k}) + p_{j\,m}(\hat{k})\, p_{i\,n}(\hat{k})\nonumber \\&\qquad \qquad \qquad \qquad - p_{i\,j}(\hat{k})\, p_{m\,n}(\hat{k})\biggr ], \end{aligned}$$
(13)
$$\begin{aligned}&F_{k,\, \lambda }(\eta )\, G_{k,\, \lambda }^{*}(\eta ) - F_{k,\, \lambda }^{*}(\eta )\, G_{k,\, \lambda }(\eta ) \, = \, i, \end{aligned}$$
(14)

where \(p_{i \, j}(\hat{k}) = (\delta _{i\, j} - \hat{k}_{i}\, \hat{k}_{j})\) denotes the standard projector and \(\hat{k}^{i} = k^{i}/|\vec {k}|\). Note that if the normalization of the Wronskian differs from Eq. (14) the commutation relation of Eq. (12) is not canonical anymore.

The mode functions are normalized during the refractive phase where, according to Eq. (4), the \(\eta \)-time and the conformal time are related as \((- \eta /\eta _{*}) = (- \tau /\tau _{*})^{\alpha /(1- \epsilon ) +1}\) and \(\eta _{*} = \tau _{*} (1 - \epsilon )/[n_{*} (1 + \alpha -\epsilon )]\); both relations follow from the definition of the \(\eta \)-time (i.e. \(n(\eta ) d\eta =d\tau \)) and also from \(n(a) = n_{*} (a/a_{*})^{\alpha }\), as implied by Eq. (4) when \(a< a_{*}\). In the \(\eta \)-time the explicit expression of \(b(\eta )\) is:

$$\begin{aligned} b(\eta ) = b_{*} \biggl (-\frac{\eta }{\eta _{*}}\biggr )^{-\sigma },\sigma =\frac{2- \alpha }{2( 1 + \alpha - \epsilon )}, \mathrm {for}\;\eta < - \eta _{*},\nonumber \\ \end{aligned}$$
(15)

where \(b_{*} = a_{*}/\sqrt{n_{*}}\). In the refractive regime the solution of Eq. (11) is therefore given by:

$$\begin{aligned} F_{k}(\eta )= & {} \frac{{\mathscr {N}}}{\sqrt{ 2 k} \, b(\eta )} \, \sqrt{- k \eta } \, H_{\mu }^{(1)}(- k\, \eta ),\nonumber \\ G_{k}(\eta )= & {} - {\mathscr {N}} \,b(\eta ) \,\sqrt{\frac{k}{2}} \,\sqrt{- k\eta } \, H_{\mu -1}^{(1)}(- k \eta ), \end{aligned}$$
(16)

where \(\mu = \sigma +1/2\) and \(H_{\mu }^{(1)}(-k\eta )\) is the Hankel function of first kind [26]; note that \(|{\mathscr {N}}| = \sqrt{\pi /2}\) and, with this choice, the Wronskian normalization condition of Eq. (14) is satisfied. Thanks to Eq. (16) we can compute the tensor power spectrum that eventually determines the low-frequency normalization of the spectral energy density:

$$\begin{aligned}&{\mathscr {P}}_{T}(k, \eta ) \nonumber \\&\quad =\frac{4 \ell _{P}^2 \, k^{3}}{\pi ^2} \bigl | F_{k}(\eta ) \bigr |^2 \rightarrow \biggl (\frac{H_{1}}{M_{P}}\biggr )^2\,\,{\mathscr {C}}(n_{T}, N_{*}, N_{t}, \epsilon ) \,\, \biggl (\frac{k}{a_{1} H_{1}}\biggr )^{n_{T}}, \nonumber \\\end{aligned}$$
(17)
$$\begin{aligned}&{\mathscr {C}}(n_{T}, N_{*}, N_{t}, \epsilon ) \nonumber \\&\quad = \frac{ 2^{6 - n_{T}}}{\pi ^2} \biggl | 1 + \frac{\alpha }{1 -\epsilon }\biggr |^{2 - n_{T}}\, \Gamma ^2\biggl (\frac{3 -n_{T}}{2}\biggr )e^{\alpha \, N_{*}( 3 - n_{T}) - n_{T} (N_{*} - N_{t})}, \nonumber \\ \end{aligned}$$
(18)

The second expression at the right hand side of Eq. (17) corresponds to the limit \(| k \eta | \ll 1\) where \({\mathscr {P}}_{T}(k, \eta )\) becomes constant in time and the tensor to scalar ratio is:

$$\begin{aligned}&r_{T}(\nu ) = \frac{\epsilon }{\pi } \, {\mathscr {C}}(n_{T}, N_{*}, N_{t}, \epsilon ) \biggl (\frac{\nu }{\nu _{max}}\biggr )^{n_{T}}, \nonumber \\&\lim _{\alpha \rightarrow 0} {\mathscr {C}}(n_{T}, N_{*}, N_{t}, \epsilon ) = 16\pi . \end{aligned}$$
(19)

For \(\alpha \rightarrow 0\) we have that \(r_{T}\rightarrow 16 \epsilon \) and the standard consistency relation is recovered. In the same limit the tensor spectral index goes to \( - 2\epsilon \):

$$\begin{aligned} n_{T} = \frac{3 \alpha - 2 \epsilon }{1+ \alpha - \epsilon } = \frac{3 \alpha }{1 + \alpha } + \frac{\epsilon (\alpha - 2)}{(1 + \alpha )^2} + {\mathscr {O}}(\epsilon ^2). \end{aligned}$$
(20)

Equation (20) defines the tensor spectral index in the intermediate frequency range where \(\alpha \) is larger than \(\epsilon \) and this is why the exact result can always be expanded in the limit \(\epsilon \ll 1\). The slope of the tensor power spectrum evaluated for the wavelengths larger than the Hubble radius coincides, after reentry, with the slope of spectral energy density before the knee:

$$\begin{aligned} h_{0}^2 \,\,\Omega _{\mathrm {gw}}(\nu ,\tau _{0}) = {\mathscr {T}}^2(\nu , \nu _{eq}) \,\,r_{\mathrm {T}}(\nu _{p}) \,\,\biggl (\frac{\nu }{\nu _{p}}\biggr )^{n_{\mathrm {T}}}, \qquad \nu < \nu _{*}, \nonumber \\ \end{aligned}$$
(21)

where \(\nu _{p} = 3.092\,\,\mathrm {aHz}\) and \({\mathscr {T}}(\nu , \nu _{eq}) \) is:

$$\begin{aligned}&{\mathscr {T}}(\nu , \nu _{eq})\nonumber \\= & {} 6.453\times 10^{-8} \sqrt{1 + c_{2}\biggl (\frac{\nu _{eq}}{\nu }\biggr )+b_{2}\biggl (\frac{\nu _{eq}}{\nu }\biggr )^2},\nonumber \\ c_{2}= & {} 0.5238, b_{2}=0.3537, \end{aligned}$$
(22)

where the constants \(c_{2}\) and \(b_{2}\) follow from the transfer function for the spectral energy density [22, 23] and are obtained by integrating the mode functions across the radiation-matter transition and by computing \(\Omega _{\mathrm {gw}}(\nu ,\tau )\) for different frequencies. Above \(\nu _{*}\) the spectral energy density is instead quasi-flat, as anticipated in Fig. 1 and it is approximately given by:

$$\begin{aligned}&h_{0}^2 \Omega _{\mathrm {gw}}(\nu ,\tau _{0}) = {\mathscr {T}}^2(\nu , \nu _{eq})\,\,r_{\mathrm {T}}(\nu _{p}) \,\,\biggl (\frac{\nu _{*}}{\nu _{p}}\biggr )^{n_{\mathrm {T}}}\,\,\biggl (\frac{\nu }{\nu _{*}}\biggr )^{- 2 \epsilon }, \nonumber \\&\nu _{*}< \nu < \nu _{max}, \end{aligned}$$
(23)

where the contribution of \({\mathscr {T}}^2(\nu , \nu _{eq})\) is, in practice, frequency-independent for \(\nu > \nu _{*}\) and it can be approximated as \(4.165\times 10^{-15}\). The results of Eqs. (21,22) and (23) agree with the previous results of Ref. [8] and are a natural candidate for exploring a potential signal in the nHz range: the blue spectrum in the intermediate range and the flat slope at high-frequencies have a clear dynamical rationale which is encoded in Fig. 1. It is however clear that the spectral energy density obtained in this concrete scenario does not support the viewpoint that \(n_{T}\), \(r_{T}\) and \(\nu _{*}\) could be independently assigned without worrying about their mutual interplay.

There are two classes of recent constraints that are relevant for the present discussions. The 12.5 yrs data set of the NANOGrav pulsar timing array (PTA) experiment reported evidence of a stochastic signal in the nHz range. The features of this purported signal would imply, in the present notations, thatFootnote 3 [27]:

$$\begin{aligned}&10^{-8.6}< \, h_{0}^2 \Omega _{gw}(\nu ,\tau _{0})< \, 10^{-9.8}, \nonumber \\&3\,\mathrm {nHz}< \nu < 100 \, \mathrm {nHz}. \end{aligned}$$
(24)

The Kagra, LIGO and Virgo collaborations, in their attempt to constrain the stochastic backgrounds of relic gravitons also reported a limit [30] implying, in the case of a flat spectral energy density,

$$\begin{aligned} \Omega _{gw}(\nu , \tau _{0})< 5.8 \times 10^{-9},\quad \;20 \,\, \mathrm {Hz}< \nu _{KLV} < 76.6 \,\, \mathrm {Hz}, \nonumber \\ \end{aligned}$$
(25)

where \(\nu _{KLV}\) denotes the Kagra-LIGO-Virgo frequency. This limit improves on a series of bounds previously deduced by the wide-band interferometers (see [5] for a recent review). In particular in Ref. [31] the analog of Eq. (25) implied \( \Omega _{gw}(\nu , \tau _{0}) < 6 \times 10^{-8}\) for a comparable frequency interval and always in the case of a flat spectral energy density. While the bound of Eq. (25) could be immediately used also in our case since at high-frequency the spectral energy density is nearly scale-invariant, it is useful to elaborate on the result of Ref. [30]. The collaboration actually reports a threefold bound which could be parametrized as

$$\begin{aligned} \Omega _{gw}(\nu , \tau _{0}) = \overline{\Omega }(\delta ) \biggl (\frac{\nu }{\nu _{ref}}\biggr )^{\delta }, \qquad \qquad \nu _{ref} = 25 \,\, \mathrm {Hz}. \end{aligned}$$
(26)

In terms of Eq. (26) the results of Ref. [30] read \(\overline{\Omega }(0) < 5.8 \times 10^{-9}\) (valid in the case \(\delta =0\)), \(\overline{\Omega }(2/3) < 3.4 \times 10^{-9}\) (when \(\delta = 2/3\)) and \(\overline{\Omega }(3) < 3.9 \times 10^{-10}\) (when \(\delta = 3\)). When the value of \(\delta \) increases the bound becomes more restrictive once the reference frequency has been kept fixed. The three results are unified in the following interpolating formula

$$\begin{aligned} \log {\overline{\Omega }}(\delta ) < -\,8.236 -\, 0.335\, \delta - 0.018\, \delta ^2. \end{aligned}$$
(27)

While the quadratic fit is slightly more accurate the linear one, the essence of the arguments does not change in the two cases since the different points fall approximately on the same straight line (i.e. \( - 8.223 - 0.393\, \delta \)). Since in the present case the bound (27) should be applied at high-frequencies we will have \( \delta =- 2 \epsilon / (1- \epsilon )\) with \(\epsilon < 0.01\). We can immediately see from Eq. (27) that, to leading order in \(\epsilon \), Eq. (27) implies that \(\log {\overline{\Omega }}(\epsilon ) < -\,8.236 -\, 0.335\, \epsilon -0.393 \epsilon ^2\) giving, at most, a negligible correction in the exponent. The pivotal parameters that determine the spectrum are \(\alpha \), \(N_{*}\) and \(N_{t}\). If \(N_{*}\) is of the order of \(N_{t}\) the transition to normalcy occurs at the end of inflationFootnote 4 When \(N_{*} <N_{t}\) the transition to normalcy takes place well before the onset of the radiation-dominated epoch (i.e. when the background is still inflating deep inside the quasi-de Sitter stage of expansion). The scale-dependent constraint on the tensor to scalar ratio is conventionally applied at the pivot scale \(k_{p}\) (see the discussion after Eq. (5)) corresponding to the comoving frequency \(\nu _{p} = {\mathscr {O}}(3)\) aHz. In a conservative perspective we therefore require the limit [24, 25] \(r_{T}(\nu _{p}) \le 0.06\). The bounds coming from big-bang nucleosynthesis [32,33,34] imply instead a constraint on the integral of the spectral energy density of the gravitons:

$$\begin{aligned}&h_{0}^2 \int _{\nu _{bbn}}^{\nu _{max}} \Omega _{\mathrm {gw}}(\nu ,\tau _{0}) d\ln {\nu }\nonumber \\&= 5.61 \times 10^{-6} \Delta N_{\nu } \biggl (\frac{h_{0}^2 \Omega _{\gamma 0}}{2.47 \times 10^{-5}}\biggr ), \end{aligned}$$
(28)

where \(\Omega _{\gamma 0}\) is the (present) critical fraction of CMB photons. The lower limit of integration in Eq. (28) is given by the frequency corresponding to the Hubble rate at the nucleosynthesis epoch:

$$\begin{aligned}&\nu _{bbn} = 2.252\times 10^{-11} \biggl (\frac{N_{eff}}{10.75}\biggr )^{1/4} \biggl (\frac{T_{\mathrm {bbn}}}{\,\,\mathrm {MeV}}\biggr )\nonumber \\&\quad \qquad \qquad \times \biggl (\frac{h_{0}^2 \Omega _{\mathrm {R}0}}{4.15 \times 10^{-5}}\biggr )^{1/4}\,\,\mathrm {Hz} \simeq 0.01\, \mathrm {nHz}, \end{aligned}$$
(29)

where \(N_{eff}\) denotes the effective number of relativistic degrees of freedom entering the total energy density of the plasma and \(T_{\mathrm {bbn}}\) is the temperature of big-bang nucleosynthesis. The limit of Eq. (28) sets an indirect constraint on the extra-relativistic species (and, among others, on the relic gravitons). Since Eq. (28) is relevant in the context of neutrino physics (when applied to massless fermionic species), the limit is often expressed for practical reasons in terms of \(\Delta N_{\nu }\) representing the contribution of supplementary neutrino species. The actual bounds on \(\Delta N_{\nu }\) range from \(\Delta N_{\nu } \le 0.2\) to \(\Delta N_{\nu } \le 1\); the integrated spectral density in Eq. (28) is thus between \(10^{-6}\) and \(10^{-5}\).

Fig. 2
figure 2

The allowed region of the parameter space is illustrated together with the explicit form of the spectral energy density when the corresponding parameters are selected within the shaded region where all the relevant are satisfied. The different contours appearing in the plot at the left correspond to the values of \(h_{0}^2 \, \Omega _{gw}(\nu _{KLV}, \tau _{0})\) where \(\nu _{KLV}\) approximately denotes most sensitive frequency domain of the wide-band interferometers (i.e. Kagra-LIGO-Virgo) that recently provided interesting results that can be interpreted as upper limits on the spectral energy density of the relic gravitons. The shaded box highlights the region suggested by the PTA. We finally recall that \(\log {}\) denotes the common logarithm (as opposed to the natural logarithm) employed, for instance, in the definition of the number of e-folds (see Eq. (6) and comments thereafter)

Full size image

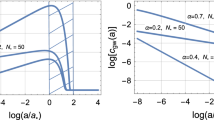
The limits stemming from CMB analyses (i.e. \(r_{T}(\nu _{p}) < 0.06\)), the requirement of Eq. (24), the Kagra-LIGO-Virgo limit (KLV) of Eq. (25) (see also Eqs. (26)–(27)) and the BBN constraints of Eq. (28) have all been enforced in Fig. 2. The shaded area (appearing in the plot at the left of Fig. 2 and resembling a circular segment) illustrates the region where are all the various constraints are concurrently satisfied when \(N_{t}\) is fixed to a fiducial value. On top of the mentioned bounds, for consistency it is preferable to require, in a model-independent perspective, that \(\nu _{*} > \nu _{bbn}\): if this condition is not included the allowed region in Fig. 2 gets even larger. The shaded box appearing in Fig. 2 illustrates the region defined by Eq. (24) where the tentative signal of the PTA should be approximately located. In the right plot of Fig. 2 the spectral energy density is reported for different values of \(\alpha \) and \(N_{*}\) all falling within the shaded region that appears in the left plot. When the parameters are selected within the circular segment the corresponding spectral energy density falls within the PTA box while the limits coming from wide-band interferometers are satisfied. The results of Fig. 2 suggest that a large signal in the nHz range is obtained when the variation of the refractive index occurs sufficiently early during the inflationary stage and anyway not beyond the first 20 e-folds. In units of the inflationary Hubble rate, the rate of variation of the refractive index must fall in the range \(0.25< \alpha < 0.55\). For this portion of the parameter space the frequency of the knee is in the nHz range.

It is now interesting to fix \(\alpha \) to some fiducial value and to deduce the constraints in the plane \((N_{*}, \, N_{t})\): this strategy is illustrated in Fig. 3. It is clear that for \(\alpha \simeq 2/7\) the allowed region and the maximal signal of the model (see the right plot of Fig. 3) occur for \(N_{t} = {\mathscr {O}}(60)\) and \(N_{*} = {\mathscr {O}}(20)\). Furthermore for \( \alpha = 2/7 \simeq {\mathscr {O}}(0.28)\), \(N_{t}= {\mathscr {O}}(60)\) and \(N_{*} = {\mathscr {O}}(20)\) the spectral energy density passes through the PTA box and undershoots the KLV bound. The rationale for the apparently peculiar choice of \(\alpha \) appearing in Fig. 3 stems, in short, from the following consideration. The PTA results are often reported in terms of a chirp amplitude scaling as \(\nu ^{-2/3}\) for a typical reference frequency \({\mathscr {O}}(\mathrm {yr}^{-1})\). If, at the present time, \(h_{c}(\nu ,\tau _{0})\) scales as \(\nu ^{\beta }\) the spectral energy density has the following dependence on the comoving frequencyFootnote 5:

$$\begin{aligned} h_{c}(\nu ,\tau _{0})= & {} Q \biggl (\frac{\nu }{\nu _{ref}}\biggr )^{\beta }, \Rightarrow \Omega _{gw}(\nu ,\tau _{0})\nonumber \\= & {} \frac{2\, \pi ^2 \, \nu ^2}{3 H_{0}^2} Q^2 \biggl (\frac{\nu }{\nu _{ref}}\biggr )^{2\beta } \propto \biggl (\frac{\nu }{\nu _{ref}}\biggr )^{2+ 2\beta }, \end{aligned}$$
(30)

where, as already mentioned, \(\nu _{ref} = {\mathscr {O}}(\mathrm {yr}^{-1})\) and Q just denotes a constant amplitude. If \(\beta = -2/3\) we have that \(\Omega _{gw} \propto \nu ^{2/3}\). The value of \(\alpha \) corresponding to \(\beta = -2/3\) is obtained by setting \(n_{T} \simeq 2/3\) in Eq. (20). Consequently we have that \(\alpha = (2 + 4 \epsilon )/7\) which can be approximated as \(\alpha = 2/7 + {\mathscr {O}}(\epsilon )\) since \(\epsilon < 10^{-3}\). In this case the spectral energy density is illustrated in the right plot of Fig. 3 for a set of values selected within the allowed region of the parameter space. If we would really pretend that the PTA measures a real signal with chirp amplitude proportional to \(\nu ^{-2/3}\) the region of the parameter space illustrated in Fig. 3 should be the most promising one.

Fig. 3
figure 3

In the plot at the left we compute the allowed region in the parameter space when \(\alpha \) is fixed to 2/7. This choice implies that the chirp amplitude scales as \(\nu ^{-2/3}\) while the spectral energy density goes as \(\nu ^{2/3}\). In the plot at the right we illustrate the spectral energy density for a set of parameters selected within the shaded region appearing in the exclusion plot at the right. As in Fig. 2 common logarithms are employed on both axes of the right plot

Full size image

If the results of the PTA are interpreted as an upper limit, the allowed region of the parameter space gets wider as we can argue by comparing the left plot of Fig. 4 with the corresponding result reported in Fig. 2, always in the plot at the left. The logic of the upper limit has been encouraged by the observational collaborations themselves in the 11-yr release [28] where the PTA data implied, within our notations, that \(h_{0}^2 \Omega _{gw}(\nu _{ref}, \tau _{0}) < 3.4(1) \times 10^{-10}\). If we apply this viewpoint to the present case (and consequently avoid the requirements associated with Eq. (24)) we obtain the exclusion plot reported at the left of Fig. 4 where the shaded area corresponds, as usual, to the allowed region. From Fig. 4 the area where \(\alpha < 0.25\) is now viable and it corresponds to a value of \(N_{*}\) that is comparatively larger than in Fig. 2. It is however clear that, in this region, the purported “signal” attributed to relic gravitons cannot be reproduced. Indeed in the right plot of Fig. 4 the spectral energy density of the relic gravitons always undershoots the PTA box and the upper limits of wide-band detectors.

All in all the evolution of refractive index of the gravitons during the early stages of the inflationary evolution leads to a blue (i.e. slightly increasing) slope of the spectral energy density at intermediate frequencies above the fHz. While the specific values of the slopes are determined by the competition of the slow-roll parameter and of the rate of variation of the refractive index, the general idea suggests that increasing frequency spectra can also be obtained in the framework of conventional inflationary scenarios. Some time ago [5] (see also [19, 20]) it was suggested that the allowed regions of the parameter space could only be probed by some of the planned detectors operating in the audio band or in the mHz region. Broadly speaking the previous results assumed \(h_{0}^2 \Omega _{gw}(\nu _{pulsar}, \tau _{0}) < 10^{-8}\) for \(\nu _{pulsar}= {\mathscr {O}}(10)\) nHz. The generous bounds previously applied (and motivated by the early stage of the PTA) are now being improved. In this investigation, following some recent claims, we focussed the attention on the nHz domain and demonstrated that the recent findings, if confirmed, are compatible with the variation of the refractive index of the relic gravitons during the early stages of the inflationary evolution. The results reported here have been purposely derived in the minimal framework where the high-frequency plateau ranges between the nHz and the MHz region. If the slow-roll condition is violated towards the end of inflation the spectral energy density is not constant at high-frequencies and the flat plateau is replaced by a decreasing branch. In this case the spectral energy density may even develop a maximum between the nHz and the kHz. To address a large signal in the nHz domain the present analysis suggests that the realistic spectra should have at least three branches: the low-frequency branch in the aHz region originally discussed in [4], an intermediate region where the spectral index increases and the high-frequency domain (extending up to the MHz) where the spectrum is nearly scale-invariant. We could easily have spectra with four different branches [35]. This behaviour arises since the post-inflationary evolution is not dominated by radiation but it contains either a stiff epoch or a delayed reheating.

Fig. 4
figure 4

The shaded area is obtained by imposing all the previous constraints except for Eq. (24) which is instead replaced by the limit \(h_{0}^2 \Omega _{gw}(\nu _{ref}, \tau _{0}) < 3.4(1) \times 10^{-10}\) for \(\nu _{ref} = {\mathscr {O}}(10^{-8})\) Hz. In the plot at the right a specific choice of the parameters. This result shows that if the PTA results are interpreted as upper limits (as originally done when introducing the variation of the refractive index [5]) the range of variation of \(N_{*}\) and \(\alpha \) gets larger even in the minimal model examined here.

Full size image

The inflationary evolution of the refractive has been discussed in a minimal scenario where the spectral energy density of cosmic gravitons is blue at intermediate frequencies and then flattens out at high-frequency. The obtained spectra satisfy all the constraints associated with the stochastic backgrounds of relic gravitons and may also explain the recent findings of the PTA that however need a convincing confirmation. While the EPTA (European Pulsar Timing Array) [36, 37] and the PPTA (Parkes Pulsar Timing Array) [38, 39] should eventually offer an independent (and convincing) evidence for the claim, it would also be quite interesting to see if the present bounds coming from wide-band interferometers could be improved by, at least, a couple of orders of magnitude. The improved limits would allow to decide if the spectral energy-density at high-frequencies is really flat or should instead decrease. The theoretical perspective conveyed here suggests that the blue spectral index, the tensor to scalar ratio and the knee of the spectra cannot be independently assigned but their mutual relations are essential to determine the allowed regions of the parameter space. For this reason we expect that the potential signatures of the refractive index will be distinguishable from other potential sources of power at intermediate frequencies. If the forthcoming measurements will not support the evidences currently claimed by the PTA measurements we will have to conclude that the variation of the refractive index may be even longer and potentially lead to a large signal in the MHz domain. In this case, however, also other spikes are potentially expected and the improved bounds of the PTA arrays (together with the upper limits of the wide-band detectors) will clarify the origin of the signals in the high-frequency and ultra-high-frequency domains.

Note added After this paper was completed I became aware of three papers [40,41,42] where the evidence suggested by the NANOGrav findings has been further scrutinized. The Parkes Pulsar Timing Array [40], the European Pulsar Timing Array [41] and the International Pulsar Timing Array [42] reach in fact a rather similar conclusion. While the determinations of the three collaborations are broadly compatible with the NANOGrav results, Refs. [40,41,42] correctly suggest that a definitive detection of the gravitational wave background is the presence of specific spatial correlations in the arrival times of the signals. This correlation has not been observed so far. It is therefore fair to conclude that the present results do not confirm or rule out that the current evidence should be undoubtedly attributed to a stochastic gravitational-wave signal. I thank an anonymous Referee for prompting my comment on these results.