The propagating speed of relic gravitational waves and their refractive index during inflation

Abstract

If the refractive index of the tensor modes increases during a conventional inflationary stage of expansion the relic graviton spectrum is tilted towards high frequencies. Two apparently diverse parametrizations of this effect are shown to be related by a rescaling of the four-dimensional metric through a conformal factor that involves the refractive index itself. Non-monotonic spectra with a maximum in the MHz region correspond to a limited variation of the refractive index terminating well before the end of inflation. After exploring a general approach encompassing the ones proposed so far, we estimate the required sensitivity for the direct detection of the predicted gravitational radiation and demonstrate that the allowed regions of the parameter space are within reach for some of the planned detectors operating either in the audio band (like Ligo/Virgo and Kagra) or in the mHz band (like Lisa, Bbo and Decigo).

1 Introduction

The tensor modes of the geometry are known to be parametrically amplified in the early Universe thanks to the pumping action of the gravitational field, as suggested by Grishchuk well before the formulation of the conventional inflationary paradigm [1,2,3]. According to the quantum theory of parametric amplification (originally developed in the case of optical photons [4, 5]), relic gravitons are produced from the vacuum or from a specific initial state with opposite momenta [6]. Squeezed states of relic gravitons are characteristic of many scenarios and, in particular, of conventional inflationary models [7, 9]. The degree of quantum coherence of the large-scale correlations could be used to disambiguate their origin, at least in principle [10].

Gravitational waves might acquire an effective index of refraction when they travel in curved space-times [11, 12] and this possibility has been recently revisited by studying the parametric amplification of the tensor modes of the geometry during a quasi-de Sitter stage of expansion [13]: when the refractive index mildly increases during inflation the corresponding speed of propagation of the waves diminishes and the power spectra of the relic gravitons are then blue, i.e. tilted towards high frequencies. After the analysis of [13] the same idea has been pursued in two similar papers [14, 15]. The first goal of the present analysis is a specific discussion of the relation between the approaches of Refs. [13,14,15] which ultimately coincide since they are related by a conformal rescaling involving the refractive index. We shall then explore a more general approach encompassing the ones discussed previously and analyze the actual phenomenological constraints together with the associated detectability prospects.

A refractive index varying in the early Universe is implicitly contained in the work of Szekeres [11, 12] aiming at the general formulation of a macroscopic theory of gravitation. An effective index of refraction may also arise in modified theories of gravity violating the equivalence principle [13,14,15]. In the model-independent perspective pursued in Ref. [13] and subsequently followed in [14, 15] (see, in particular, the second paper) the pivotal parameter of the discussion will therefore be the rate of variation of the refractive index in units of the Hubble rate, conventionally denoted by $\alpha$ and defined by:

$$\begin{aligned} \alpha = \frac{n \, H}{{\dot{n}}}, \qquad \epsilon = - \frac{{\dot{H}}}{H^2}\ll 1,\qquad c_{gw}(t) = \frac{c}{n(t)}. \end{aligned}$$

(1.1)

In Eq. (1.1) the overdot denotes a derivation¹ with respect to the cosmic time coordinate t; $\epsilon$ and $c_{gw}(t)$ are, respectively, the standard slow-roll parameter $\epsilon$ and the phase velocity of the relic gravitons in units of the speed of light. The phase velocity coincides, in the present case, with the group velocity and if the refractive index increases during inflation neither the phase velocity nor the group velocity will be superluminal. Note finally that the conventional slow-roll dynamics does not necessarily imply the validity of the so-called consistency relations which are instead broken by the presence of the refractive index so that the tensor spectral index and the tensor-to-scalar ratio are not solely determined by $\epsilon$, as it happens when the consistency relations are not violated.

During the last year the Ligo/Virgo collaboration published the three-detector observations of gravitational waves from black-hole coalescence [16], the evidence of gravitational waves from neutron star inspiral [17], and the observation of a 50-solar-mass binary black hole coalescence for a redshift $z =0.2$ [18]. As gravitational wave astronomy is opening a new window for the observation of the present Universe, the theory is beginning to consider more concretely the potential implications of the current developments for the early Universe. In the course of inflation, the evolution of the space-time curvature induces a stochastic background of relic gravitons [11, 12] with a spectral energy density extending today from frequencies ${{\mathcal {O}}}(\mathrm {aHz})$ (i.e. $1 \,\mathrm {aHz} = 10^{-18}\, \mathrm {Hz}$) up to frequencies ${{\mathcal {O}}}(\mathrm {GHz})$ (i.e. $1\, \mathrm {GHz} = 10^{9} \mathrm {Hz}$). In the conventional scenario the absolute normalization of the tensor power spectrum solely depends on the tensor to scalar ratio Here we shall be assuming the limit $r_{T}<0.07$ for the tensor spectral index from a joint analysis of Planck and BICEP2/Keck array data [19] (see also [20]). The typical energy density of inflationary gravitational waves between the mHz (i.e. $1 \,\mathrm {mHz} = 10^{-3}$ Hz) and the kHz is, optimistically, ${{\mathcal {O}}}(10^{-16.5})$ in terms of $\Omega _{\mathrm {gw}}(\nu ,\tau _{0})$ which will denote throughout the spectral energy density in critical units at the present (conformal) time $\tau _{0}$. The corresponding chirp amplitude $h_{c}(\nu ,\tau _{0})$ will therefore be ${{\mathcal {O}}}(10^{-29})$ for a typical comoving frequency of 0.1 kHz as it follows from the general relation:

$$\begin{aligned} h_{c}(\nu ,\tau _{0}) = 1.263 \times 10^{-20} \biggl (\frac{100 \,\, \mathrm {Hz}}{\nu }\biggr ) \, \sqrt{h_{0}^2 \,\Omega _{\mathrm {gw}}(\nu ,\tau _{0})}, \end{aligned}$$

(1.2)

connecting the chirp amplitude to the spectral energy density in critical units. While the $h_{c}$ corresponding to the astronomical signals detected by the Ligo/Virgo collaboration is ${{\mathcal {O}}}(10^{-21})$ [16,17,18], various improvements are expected at least in the so-called audio band between few Hz and 10 kHz. In this perspective it is useful to discuss potential deviations from the conventional inflationary signal hoping for larger spectral amplitudes over intermediate and high frequencies.

The plan of this paper is the following. In Sect. 2 we shall demonstrate that the apparently different actions proposed so far to account for the same effects are indeed equivalent up to conformal rescaling of the four-dimensional metric. A general approach to the analysis of the power spectrum is proposed in Sect. 3 where the tensor to scalar ratio and the relevant power spectra are explicitly derived. In Sect. 4 the phenomenological constraints relevant to the present scenario will be studied by charting the corresponding parameter space; the potential signals will be confronted with the hoped sensitivities of the wide-band interferometers on the ground and in space. The concluding remarks are collected in Sect. 5 and some useful details are relegated to the Appendix A for the interested readers.

2 Actions and their parametrization

Let us start with an obvious remark and recall that, in the Einstein frame, the metric can be separated into a background value supplemented by the inhomogeneous contribution:

$$\begin{aligned} g_{\mu \nu }^{(E)} = \overline{g}_{\mu \nu }^{(E)} + \delta _{\mathrm {t}} g_{\mu \nu }^{(E)}, \end{aligned}$$

(2.1)

where $\delta _{t} g_{\mu \nu }^{(E)}$ denotes the tensor fluctuations of the geometry; in the present context the vector modes are anyway suppressed and shall be completely disregarded while the scalar fluctuations are described in terms of the gauge-invariant curvature inhomogeneities (see e.g. Eqs. (A.7) and (A.8) and discussion therein) but will not play a direct role in the forthcoming considerations since the refractive index is fully homogeneous.

Even if the analysis of the present section does not demand the absence of the intrinsic curvature, we shall now restrict the attention to the case where $\overline{g}_{\mu \nu }^{(E)}$ is conformally flat i.e.

$$\begin{aligned} \overline{g}_{\mu \nu }^{(E)}= a^2_{E}(\tau ) \eta _{\mu \nu }, \qquad \delta _{\mathrm {t}} g_{ij} = - a^2_{E}(\tau ) h_{ij}^{(E)}, \end{aligned}$$

(2.2)

where $\eta _{\mu \nu }=\mathrm {diag}(+\,1, \, -\,1,\, -\,1,\, -\,1)$ is the Minkowski metric with signature mostly minus and the three-dimensional rank-two tensor $h_{ij}^{(E)}$ is both divergenceless and traceless. In Eq. (2.2) and throughout the rest of the paper $\tau$ denotes the conformal time coordinate. In the frame defined by Eq. (2.1) the action for the tensor modes of the geometry has been derived long ago by Ford and Parker in Refs. [21,22,23]:

$$\begin{aligned} S^{(E)}= & {} \frac{1}{8 \ell _{P}^2} \int d^{4} x \, \sqrt{ - \overline{g}_{(E)}} \, \overline{g}^{\,\mu \nu }_{(E)} \partial _{\mu } h^{(E)}_{ij} \partial _{\nu } h^{(E)}_{ij}, \nonumber \\ \ell _{P}= & {} \sqrt{8 \pi G} = \frac{1}{\overline{M}_{P}}. \end{aligned}$$

(2.3)

Equation (2.3) can be supplemented by a second term containing the dependence on the refractive index $n(\tau )$ which is the inverse of the phase velocity² in natural units $\hbar = c =1$, i.e. $c_{gw}(\tau ) = 1/n(\tau )$:

$$\begin{aligned} S^{(E)}= & {} \frac{1}{8 \ell _{P}^2} \int d^{4} x \sqrt{-\overline{g}_{(E)}} \left\{ \overline{g}^{\mu \nu }_{(E)} \partial _{\mu } h^{(E)}_{ij} \partial _{\nu } h^{(E)}_{ij}\right. \nonumber \\&\left. +\, [c_{gw}^2(\tau ) -1 ]\overline{P}^{\mu \nu }_{(E)} \partial _{\mu } h^{(E)}_{ij} \partial _{\nu } h^{(E)}_{ij} \right\} , \end{aligned}$$

(2.4)

where $\overline{P}^{\mu \nu }_{(E)}$ is the conventional spatial projector tensor orthogonal to $\overline{u}^{(E)}_{\mu }$:

$$\begin{aligned} \overline{P}^{\mu \nu }_{(E)} = \overline{g}^{\mu \nu }_{(E)} - \overline{u}^{\mu }_{(E)} \overline{u}^{\nu }_{(E)}, \qquad \overline{g}^{\mu \nu }_{(E)} \overline{u}^{(E)}_{\mu } \overline{u}^{(E)}_{\nu } =1. \end{aligned}$$

(2.5)

Since in comoving coordinates $\overline{u}^{(E)}_{\mu } = \overline{g}^{(E)}_{\mu 0}/\sqrt{\overline{g}^{(E)}_{00}}$ and $\overline{u}^{\mu }_{(E)}= \delta ^{\mu }_{0}/\sqrt{\overline{g}^{(E)}_{00}}$ the action of Eq. (2.4) after straightforward modifications assumes the following form [13]:

$$\begin{aligned} S^{(E)}= & {} \frac{1}{8 \ell _{P}^2} \int d^{3} x \int d\tau \,\,a^2_{E} \,\,\left[ \partial _{\tau } h^{(E)}_{ij} \partial _{\tau } h^{(E)}_{ij}\right. \nonumber \\&\left. -\,c_{gw}^2(\tau ) \partial _{k} h^{(E)}_{ij} \partial ^{k} h^{(E)}_{ij} \right] . \end{aligned}$$

(2.6)

When the refractive index grows in time [13] $c_{gw}(\tau )=1/n(\tau )$ decreases but what matters is that thanks either to a conformal rescaling or to a field redefinition the action (2.6) can be brought into the following generalized form:

$$\begin{aligned} S= & {} \frac{1}{8 \ell _{P}^2} \int d^{3} x \int d\tau \left[ A(\tau ) \partial _{\tau } h_{ij} \partial _{\tau } h_{ij} \right. \nonumber \\&\left. -\,B(\tau ) \partial _{k} h_{ij} \partial ^{k} h_{ij} + C(\tau ) h_{ij} h_{ij} \right] , \end{aligned}$$

(2.7)

where $A(\tau )$, $B(\tau )$ and $C(\tau )$ depend on the conformal time coordinate $\tau$ and are themselves functionals of either the scale factor, or of the refractive index or even of both [13]. A term like $C(\tau )$ may appear by a banal field redefinition of the type $a_{E} h^{(E)}_{ij} = h_{ij}$ so we shall not dwell about this issue and focus hereunder on $A(\tau )$ and $B(\tau )$. After the results of Ref. [13], the authors of Refs. [14, 15] suggested the following form of the action:

$$\begin{aligned} S = \frac{1}{8 \ell _{P}^2} \int d^{3} x \int d\tau a^2 \left[ n^2(\tau ) \partial _{\tau } h_{ij} \partial _{\tau } h_{ij} - \partial _{k} h_{ij} \partial _{k} h_{ij} \right] , \end{aligned}$$

(2.8)

and argued that it leads to a blue spectrum of tensor modes.³ It is relevant to point out that Eq. (2.6) has been used in Ref. [13] to argue that the spectra of relic gravitons may indeed increase in the presence of an inflating background. The authors of Refs. [14, 15] did consider instead Eq. (2.8), reached a similar conclusion, but did not realize (or acknowledge) that Eq. (2.8) is conformally related to Eq. (2.6). As a consequence Refs. [14, 15] analyzed the case where the background is inflating but in the frame defined by Eq. (2.8). The choice of Refs. [14, 15] is not particularly consistent and it is even confusing in the light of the previous analyses of Ref. citetwo. We shall propose a generalized parametrization which may hopefully address and clarify the potentially confusing statements present in the current literature (see, in particular, Eq. (3.1) and discussion therein).

To show the conformal equivalence of Eqs. (2.6) and (2.8) let us now define a frame conformally related to Eq. (2.1) by positing

$$\begin{aligned} g_{\mu \nu }^{(E)} = \Omega ^2(\tau ) G_{\mu \nu }, \qquad \sqrt{- g_{(E)}} = \Omega ^4(\tau ) \, \sqrt{-G}. \end{aligned}$$

(2.9)

Exactly as in the case of Eq. (2.1), the $G_{\mu \nu }$ can be decomposed into a homogeneous part supplemented by its own tensor inhomogeneities:

$$\begin{aligned} G_{\mu \nu } = \overline{G}_{\mu \nu }+ \delta _{t} G_{\mu \nu },\qquad \overline{G}_{\mu \nu }= a^2(\tau ) \eta _{\mu \nu }. \end{aligned}$$

(2.10)

In the frame defined by Eqs. (2.9) and (2.10) the tensor modes of the geometry obey:

$$\begin{aligned} \delta _{\mathrm {t}} G_{ij} = - a^2(\tau ) h_{ij}, \qquad \partial _{i} h^{i}_{j} = h_{i}^{i}. \end{aligned}$$

(2.11)

The tensor modes of Eq. (2.11) coincide with $h_{ij}^{(E)}$, i.e. $h_{ij}^{(E)} = h_{ij}$: this means that the tensor fluctuations are not only invariant under infinitesimal coordinate transformations but they are equally invariant under conformal rescaling. To appreciate this well known aspect we can take the tensor fluctuations of both sides of Eq. (2.10) and obtain:

$$\begin{aligned} \delta _{\mathrm {t}} g_{\mu \nu }^{(E)} = \Omega ^2 \delta _{t} G_{\mu \nu }, \qquad \overline{g}^{(E)}_{\mu \nu } = \Omega ^2(\tau ) \overline{G}_{\mu \nu }. \end{aligned}$$

(2.12)

Inserting Eqs. (2.2) and (2.10) into Eq. (2.12) we simply have, as anticipated, that

$$\begin{aligned} h_{ij}^{(E)} = h_{ij}, \qquad a_{E}(\tau ) = \Omega (\tau ) a(\tau ). \end{aligned}$$

(2.13)

Equation (2.13) implies that if the two backgrounds are conformally related the gauge-invariant tensor amplitudes are also the same in the two frames. A similar property holds for the curvature perturbations on comoving orthogonal hypersurfaces.⁴ Bearing in mind the results of Eqs. (2.12) and (2.13) we can perform the conformal rescaling of the projector and of the four-velocities:

$$\begin{aligned}&\overline{P}^{\mu \nu }_{(E)} = \frac{1}{\Omega ^2} \overline{P}^{\mu \nu }, \qquad \overline{P}^{\mu \nu } = \overline{G}^{\mu \nu } - \overline{U}^{\mu } \overline{U}^{\nu },\nonumber \\&\overline{G}_{\mu \nu } \overline{U}^{\mu } \overline{U}^{\nu } =1,\qquad \overline{U}^{\mu } = \frac{ \overline{u}^{\mu }_{(E)}}{\Omega }, \end{aligned}$$

(2.14)

so that, thanks to Eqs. (2.12)–(2.14) the action (2.1) in the conformally related frame becomes:

$$\begin{aligned} S^{(E)} \rightarrow S= & {} \frac{1}{8 \ell _{P}^2} \int d^{4} x \left\{ \sqrt{-\overline{G}} \left[ \overline{G}^{\mu \nu } \Omega ^2 \partial _{\mu } h_{ij} \partial _{\nu } h_{ij} \right. \right. \nonumber \\&\left. \left. + [c_{gw}^2(\tau ) -1] \Omega ^2 \overline{P}^{\mu \nu }\partial _{\mu } h_{ij} \partial _{\nu } h_{ij} \right] \right\} . \end{aligned}$$

(2.15)

If we now identify the conformal factor with the refractive index itself

$$\begin{aligned} \Omega (\tau ) = \frac{1}{c_{gw}(\tau )} = n(\tau ), \end{aligned}$$

(2.16)

the action of Eq. (2.15) becomes

$$\begin{aligned} S = \frac{1}{8 \ell _{P}^2} \int d^{3} x \int d\tau a^2 \left[ n^2(\tau ) \partial _{\tau } h_{ij} \partial _{\tau } h_{ij} - \partial _{k} h_{ij} \partial _{k} h_{ij} \right] , \end{aligned}$$

(2.17)

which is exactly the action anticipated in Eq. (2.8) and discussed in Refs. [14, 15]. All in all the action of Eqs. (2.4) and (2.6) (originally discussed in [13]) and the action (2.17) (subsequently used in Refs. [14, 15]) are one and the same action since they are simply related by a conformal rescaling.

To make even more transparent the equivalence of the two descriptions it is useful to write down explicitly the evolution of the tensor modes in the two frames. From Eq. (2.8) it follows that the evolution of $h_{ij}^{(E)}$ is given by:

$$\begin{aligned} h_{ij}^{(E)\, \prime \prime } + 2 \frac{a_{E}^{\prime }}{a_{E}} h_{ij}^{(E)\, \prime } - \frac{\nabla ^2 h_{ij}^{(E)}}{n^2(\tau )} =0. \end{aligned}$$

(2.18)

Similarly, the equation for $h_{ij}$ can be deduced from Eq. (2.17) and the result will be:

$$\begin{aligned} h_{ij}^{\prime \prime } + 2 \biggl (\frac{a^{\prime }}{a} + \frac{n^{\prime }}{n} \biggr ) h_{ij}^{ \prime } - \frac{\nabla ^2 h_{ij}}{n^2(\tau )} =0. \end{aligned}$$

(2.19)

By virtue of Eq. (2.13) we see that Eqs. (2.18) and (2.19) are two ways of writing the same equation since

$$\begin{aligned} \frac{a_{E}^{\prime }}{a_{E}} = \frac{a^{\prime }}{a} + \frac{n^{\prime }}{n}, \qquad h_{ij}^{(E)} = h_{ij}. \end{aligned}$$

(2.20)

We must finally remark that $n(\tau )$ and $c_{gw}(\tau )$ are completely homogeneous. While this is the simplest situation, if the spectral index is not fully homogeneous there will be additional scalar fluctuations mixing with the scalar adiabatic mode. At the end of Appendix A it is demonstrated that the curvature perturbations share the same property of the tensor amplitudes since they are gauge-invariant and also invariant under conformal rescaling.

3 Generalized form of the tensor to scalar ratio

3.1 Diagonal form of the action

If we conventionally define the pivotal frame as the one where the background experiences a phase a quasi-de Sitter expansion, we should conclude that the choice of the pivotal frame is to some extent ambiguous, as already suggested. This ambiguity is not of a fundamental nature but simply stems from the current literature. Indeed, as already mentioned, in Ref. [13] the action (2.6) has been used to argue that the dynamics of the refractive index during an inflationary stage induces a growing spectrum of the tensor modes. After Ref. [13] the authors of Refs. [14, 15] suggested instead the action (2.8) and considered (in their own framework) an inflating background. The authors of Refs. [14, 15] did not acknowledge the results of Ref. [13] and did not notice or appreciate that the actions (2.6) and (2.8) are one and the same action, up to a conformal rescaling: this is the main reason of the frame ambiguity mentioned above. It is not a surprise that if we impose that the background in inflating in both frames defined by Eqs. (2.6) and (2.8), growing spectra of the tensor modes will be obtained in both frames. In what follows the aim will be first to quantize the problem in general terms and then to deduce the spectral energy density in various cases that have not been addressed so far. For this purpose and to account of the perspectives of Refs. [13,14,15] it is convenient to analyze simultaneously the two situations by considering the following diagonal form of the action for the tensor modes⁵:

$$\begin{aligned} S= \frac{1}{8 \ell _{P}^2} \int d^{4} x\, a^2 n^{2 \gamma } \left[ \partial _{\tau } h_{ij} \partial _{\tau } h_{ij} - \frac{1}{n^2} \partial _{k} h_{ij} \partial _{k} h_{ij}\right] , \end{aligned}$$

(3.1)

where $\gamma$ is a further parameter varying between 0 and 1. If $\gamma =0$ the action (3.1) reproduces exactly Eq. (2.6) with $c_{gw}(\tau ) = 1/n(\tau )$. Conversely when $\gamma = 1$ Eq. (3.1) reproduces Eq. (2.17) (or Eq. (2.8)). According to a purely heuristic logic the values of $\gamma$ may also lie outside the interval $0\le \gamma \le 1$: in this perspective $\gamma$ can be considered as a further parameter that simply rescales the tensor spectral index from its value for $\gamma =0$. However, if $\gamma \ne 0$ the sign of the tensor spectral index does not change, as we shall see. The presence of the refractive index in the second term inside the squared bracket suggests that the action can be diagonalized in terms of a new time coordinate, namely $d\tau = n(\eta ) d\eta$. In the $\eta$-parametrization the action of Eq. (3.1) becomes:

$$\begin{aligned}&S = \frac{1}{8 \ell _{P}^2} \int d^{3}x \, d\eta \,\, b^2(\eta ) \left[ \partial _{\eta } h_{ij} \partial _{\eta } h_{ij} - \partial _{k} h_{ij} \partial _{k} h_{ij}\right] , \nonumber \\&b(\eta ) = a(\eta ) \, n^{\gamma -1/2}(\eta ). \end{aligned}$$

(3.2)

While the relation of $b(\eta )$ to $a(\eta )$ and $n(\eta )$ may change, what matters is the overall dependence of the power spectrum on the background fields. The parametrization of Eq. (3.2) will be used to demonstrate, in a unified approach to the problem, that both Eqs. (2.8) and (2.17) lead to a growing power spectrum for typical wavelengths larger than the Hubble radius.

3.2 Quantization and power spectrum

For a correct normalization of the power spectrum the quantization of the system is essential and for this purpose the $\eta$-parametization is more convenient, as already emphasized in Ref. [13] without specific details. This gap will now be bridged by only using the action of Eq. (3.2) for the explicit derivation of the power spectrum, of the tensor to scalar ratio and of all the other relevant quantities. We start by noticing that from the explicit form of the tensor polarizations given in Eq. (A.1) it is convenient to introduce $h_{\lambda }(\vec {x},\eta )$

$$\begin{aligned} h_{ij}(\vec {x},\eta ) = \sqrt{2} \,\ell _{P}\sum _{\lambda = \oplus , \, \otimes } h_{\lambda }(\vec {x},\eta ) \, e^{(\lambda )}_{ij}. \end{aligned}$$

(3.3)

Inserting Eq. (3.3) into Eq. (3.2) the action becomes

$$\begin{aligned} S = \frac{1}{2} \sum _{\lambda } \int d^{3}x\, d\eta \,\, b^2(\eta )\,\,\left[ \dot{h}_{\lambda }^2 - \partial _{k} h_{\lambda } \partial ^{k} h_{\lambda } \right] , \end{aligned}$$

(3.4)

where the overdot denotes a derivation with respect to $\eta$, i.e. $\dot{h}_{\lambda } = \partial _{\eta } h_{\lambda }$. From the definition of the canonical momenta, the Hamiltonian in the $\eta$-parametrization becomes⁶:

$$\begin{aligned} H(\eta )= & {} \frac{1}{2} \sum _{\lambda } \int d^{3}x \, \biggl [ \frac{\pi _{\lambda }^2}{b^2(\eta )} + b^2(\eta ) \partial _{k} h_{\lambda } \partial ^{k} h_{\lambda } \biggr ], \nonumber \\ \pi _{\lambda }= & {} b^2(\eta ) \dot{h}_{\lambda }. \end{aligned}$$

(3.5)

The canonical form of the commutation relations at equal $\eta$-times

$$\begin{aligned} {[}\hat{h}_{\lambda }(\vec {x}, \eta ), \, \hat{\pi }_{\lambda ^{\prime }}(\vec {y}, \eta ) ] = i\, \delta ^{(3)}(\vec {x} - \vec {y}) \, \delta _{\lambda \, \lambda ^{\prime }}, \end{aligned}$$

(3.6)

and the explicit form of the Hamiltonian (3.5) lead directly to the evolution equations for $\hat{h}_{\lambda }$ and $\hat{\pi }_{\lambda }$:

$$\begin{aligned} \partial _{\eta } \hat{h} = i [\hat{H}, \hat{h}_{\lambda }] = \frac{\hat{\pi }_{\lambda }}{b^2}, \qquad \partial _{\eta } \hat{\pi } = i [\hat{H}, \hat{\pi }_{\lambda }] = b^2 \nabla ^2 \hat{h}_{\lambda }. \end{aligned}$$

(3.7)

Using Eq. (3.7) the Fourier representations of the operators $\hat{h}_{\lambda }$ and $\hat{\pi }_{\lambda }$ is:

$$\begin{aligned} \hat{h}_{\lambda }(\vec {x},\eta )= & {} \frac{1}{(2\pi )^{3/2}} \int d^{3} k \left[ \hat{a}_{\vec {k},\, \lambda } \, F_{k,\, \lambda } e^{- i \vec {k} \cdot \vec {x}} \right. \nonumber \\&\left. +\,\hat{a}^{\dagger }_{\vec {k},\, \lambda } \, F^{*}_{k,\, \lambda } e^{- i \vec {k} \cdot \vec {x}} \right] , \end{aligned}$$

(3.8)

$$\begin{aligned} \hat{\pi }_{\lambda }(\vec {x},\eta )= & {} \frac{1}{(2\pi )^{3/2}} \int d^{3} k \left[ \hat{a}_{\vec {k},\, \lambda } \, G_{k,\, \lambda } e^{- i \vec {k} \cdot \vec {x}} \right. \nonumber \\&\left. +\, \hat{a}^{\dagger }_{\vec {k},\, \lambda } \, G^{*}_{k,\, \lambda } e^{- i \vec {k} \cdot \vec {x}} \right] , \end{aligned}$$

(3.9)

where $[ a_{{\vec {k}, \, \lambda }}, \, \hat{a}^{\dagger }_{{\vec {p}, \, \lambda }}] = \delta ^{(3)}(\vec {k}-\vec {p}) \, \delta _{\lambda ,\, \lambda ^{\prime }}$; the evolution of the mode functions $F_{k,\lambda }$ and $G_{k,\lambda }$ and the normalization of their Wronskian immediately follows from Eqs. (3.6)–(3.7) and (3.8)–(3.9):

$$\begin{aligned}&\dot{F}_{k,\,\lambda } = \frac{G_{k,\,\lambda }}{b^2}, \qquad \dot{G}_{k,\,\lambda } = - k^2 b^2 F_{k,\,\lambda } \end{aligned}$$

(3.10)

$$\begin{aligned}&F_{k,\, \lambda }(\eta ) G^{*}_{k,\, \lambda }(\eta ) - F_{k,\, \lambda }^{*}(\eta ) G_{k,\, \lambda }(\eta ) = i. \end{aligned}$$

(3.11)

The evolution equations of the mode functions can be decoupled as:

$$\begin{aligned} \ddot{F_{k}} + 2 \frac{\dot{b}}{b} \dot{F}_{k} + k^2 F_{k} =0, \qquad G_{k}= b^2 \dot{F}_{k}, \end{aligned}$$

(3.12)

where the polarization index has been omitted since the result of Eq. (3.12) holds both for $\oplus$ and for $\otimes$. The quantum mechanical initial conditions correspond to

$$\begin{aligned} \lim _{\eta \rightarrow - \infty } F_{k}(\eta ) \rightarrow \frac{1}{\sqrt{2 k } b(\eta )} e^{- i k \eta }. \end{aligned}$$

(3.13)

In the limit $n(\eta ) \rightarrow 1$ the $\eta$-time turns into the conformal time while $b(\eta ) \rightarrow a(\tau )$: therefore the initial data of Eq. (3.13) generalize the standard quantum mechanical initial condition to the case where the refractive index is dynamical. Note that since $b(\eta )$ has a power-law dependence for $\eta < - \eta _{*}$ (see below Eqs. (3.23) and (3.24)), Eq. (3.12) can be exactly solved in the $\eta$-time (see Eq. (3.25)) with the initial conditions dictated by Eq. (3.13).

Fig. 1

In the left plot the common logarithm of the refractive index as a function of the scale factor is illustrated for two profiles characterized by different values of $\alpha$ and of $N_{*}$. In the right plot we report instead the common logarithm of the propagating speed (coinciding, in our case, with the phase velocity) in natural units. On the horizontal axes of both plots the common logarithm of the scale factor is reported

In conclusion we have that the full mode expansion of the tensor amplitude $\hat{h}_{ij}(\vec {x},\eta )$ in the $\eta$-time parametrization easily follows from the combination of Eqs. (3.3) and (3.8) and it is given by:

$$\begin{aligned} \hat{h}_{ij}(\vec {x},\eta )= & {} \frac{\sqrt{2} \ell _{P}}{(2\pi )^{3/2}}\sum _{\lambda } \int \, d^{3} k \,\,e^{(\lambda )}_{ij}(\vec {k})\, \left[ F_{k,\lambda }(\eta ) \hat{a}_{\vec {k}\,\lambda } e^{- i \vec {k} \cdot \vec {x}}\right. \nonumber \\&\left. +\,F^{*}_{k,\lambda }(\eta ) \hat{a}_{\vec {k}\,\lambda }^{\dagger } e^{ i \vec {k} \cdot \vec {x}}\right] , \end{aligned}$$

(3.14)

The two-point function computed from Eqs. (3.14) is simply⁷

$$\begin{aligned} \left\langle \hat{h}_{ij}(\vec {x}, \eta ) \, \hat{h}_{ij}(\vec {x}+ \vec {r},\eta ) \right\rangle = \int d\ln {k} \, {{\mathcal {P}}}_{T}(k,\eta ) j_{0}(k r), \end{aligned}$$

(3.15)

where $j_{0}(kr)$ is the spherical Bessel function of zeroth order [28, 29]. The tensor power spectrum of Eq. (3.15) is then given by

$$\begin{aligned} {{\mathcal {P}}}_{T}(k,\eta ) = \frac{4 \ell _{P}^2}{\pi ^2} k^3 |F_{k}(\eta )|^2. \end{aligned}$$

(3.16)

3.3 Explicit evolution of the mode functions and related matters

As already mentioned in Eq. (1.1) the variation of the refractive index is measured in units of the Hubble rate and for the sake of concreteness we shall consider the general situation where

$$\begin{aligned} n(a) = n_{i} \biggl (\frac{a}{a_{i}}\biggr )^{\alpha }, \qquad a< a_{*}, \end{aligned}$$

(3.17)

while $n(a) = 1$ for $a> a_{*}$. It is not difficult to imagine various continuous interpolation between the two regimes but what matters is the continuity of n(a), not the specific form of the profile across the normalcy transition. One of the simplest possibilities is given by⁸ $n(a,\xi ) = n_{i} (a/a_{i})^{\alpha } e^{- \xi a/a_{*}} +1$, going as $a^{\alpha }$ for $a < a_{*}$ and approaching 1 quite rapidly when $a > a_{*}$ and $\xi >1$. These profiles are illustrated in Fig. 1 for $\xi = 2$ and for various values of $\alpha _{*}$ and $N_{*}$. Different values of $\xi$ lead to a transition which is more or less delayed; in any case, the explicit form of the profile only affects the power spectrum in a limited range of wavenumbers. The intermediate shaded area in Fig. 1 will therefore be immaterial for the accuracy of the present analysis.

The typical scale $a_{*}$ (roughly corresponding to the maximum of n(a)) may coincide with the end of the inflationary phase. The value of $a_{*}$ corresponds with a critical number of efolds $N_{*}$ which is of the order of $N_{t}$ (i.e. the total number of efolds) if $a_{*}$ marks the end of the inflationary phase. This identification is however not mandatory and it will also be interesting to consider the case $N_{*} < N_{t}$ or even $N_{*} \ll N_{t}$.

It is finally useful to bear in mind that the scale factor during the different stages of the evolution are continuous and differentiable. An explicitly continuous parametrization of the scale factors is given by:

$$\begin{aligned} a_{inf}(\tau )= & {} \biggl (- \frac{\tau _{1}}{\tau }\biggr )^{\beta }, \qquad \tau \le - \tau _{1}, \end{aligned}$$

(3.18)

$$\begin{aligned} a_{r}(\tau )= & {} \frac{\beta \tau + (\beta +1) \tau _{1}}{\tau _{1}}, \qquad -\tau _{1} < \tau \le \tau _{2}, \end{aligned}$$

(3.19)

$$\begin{aligned} a_{m}(\tau )= & {} \frac{[ \beta \tau + \beta \tau _{2} + 2 (\beta +1) \tau _{1}]^2}{4 \tau _{1} [ \beta \tau _{2} + (\beta + 1)\tau _{1}]}, \qquad \tau > \tau _{2}, \end{aligned}$$

(3.20)

where $\tau _{1}$ coincides with the end of the inflationary phase and $\tau _{2}$ coincides with the time of matter-radiation equality; note that $\beta \rightarrow 1$ in the case of a pure de Sitter phase and $\beta = 1 - {{\mathcal {O}}}(\epsilon )$ in the quasi-de Sitter case. The transition to the domination of the dark energy does not affect the slope and it has a mild effect on the amplitude of the spectrum [24,25,26,27]; this effect will be included in the actual estimates of Sect. 4 by following the approach already pursued in [26, 27]. A similar comment holds for other effects which are customarily associated with potential suppression of the amplitude of the power in the intermediate frequency branch such as the neutrino free streaming [30, 31] or the effective evolution of number of relativistic species. Equations (3.18)–(3.20) are all continuous with their first derivatives at the transition points.⁹ If the scale factor is continuous at the transition points and if n(a) is continuous and differentiable as a function of the scale factor, then the relation between $\eta$ and $\tau$ is also continuous and differentiable. All in all we can say that whenever n(a) is a well behaved function interpolating between the two regimes illustrated in Fig. 1 it will always be possible to consider the evolution as piecewise continuous without worrying about the evolution in the transition regime.

By then recalling Eq. (3.2) and the explicit relation between $\eta$ and $\tau$, we have that for $a< a_{*}$ the $\eta$-time and the conformal time are related as:

$$\begin{aligned} \eta = \int \frac{d\tau }{n_{*} a^{\alpha }(\tau )} = \frac{1}{n_{*}} \int d \tau \biggl (- \frac{\tau }{\tau _{*}}\biggr )^{\alpha \beta }. \end{aligned}$$

(3.21)

When $\tau _{*} = \tau _{1}$ (i.e. $N_{*} = N_{t}$) Eq. (3.21) is explicitly given by

$$\begin{aligned} \biggl ( - \frac{\eta }{\eta _{*}} \biggr ) = \biggl ( - \frac{\tau }{\tau _{*}}\biggr )^{\alpha \beta +1}, \qquad \frac{1}{\eta _{*}} = \frac{n_{*} (\alpha \beta +1)}{\tau _{*}}, \end{aligned}$$

(3.22)

so that, in the conformal time parametrization, $b(\tau )$ turns out to be:

$$\begin{aligned} b(\tau ) = a(\tau ) n^{\gamma -1/2}(\tau ) = n_{*}^{\gamma -1/2} \biggl (- \frac{\tau }{\tau _{*}}\biggr )^{ - \beta [ 1 + \alpha (\gamma -1/2)]}. \nonumber \\ \end{aligned}$$

(3.23)

Using Eq. (3.22) into Eq. (3.23) the expression of $b(\eta )$ is easily derived:

$$\begin{aligned} b(\eta ) = n_{*}^{\gamma -1/2} \biggl (- \frac{\eta }{\eta _{*}}\biggr )^{-\sigma }, \qquad \sigma = \frac{\beta [2 + \alpha ( 2 \gamma -1)]}{2 ( 1 + \alpha \beta )}. \nonumber \\ \end{aligned}$$

(3.24)

In the regime of Eq. (3.24) we can easily solve Eq. (3.12) by defining the auxiliary mode function $F_{k}(\eta ) b(\eta ) = f_{k}(\eta )$. The resulting equation can be solved in terms of Hankel functions and $F_{k}(\eta )$ is then given by¹⁰:

$$\begin{aligned} F_{k}(\eta )= & {} \frac{{{\mathcal {N}}}}{\sqrt{2 k} \,\,b(\eta )} \sqrt{- k \eta } \, \,H^{(1)}_{\mu }(- k \eta ), \nonumber \\ {{\mathcal {N}}}= & {} \sqrt{\frac{\pi }{2}} e^{i \, \pi (\sigma + 1/2)/2}, \nonumber \\ \mu= & {} \sigma + \frac{1}{2}= \frac{1 + \beta [ ( 2 + \alpha ) + \alpha ( 2 \gamma -1)]}{2 ( 1 +\alpha \beta )}, \end{aligned}$$

(3.25)

where $H^{(1)}_{\mu }(k \eta )$ is the Hankel function¹¹ of the first kind [28, 29]. Note that with the characteristic choice of the phase appearing in ${{\mathcal {N}}}$ the limit of Eq. (3.25) for $\eta \rightarrow - \infty$ is exactly the one already mentioned in Eq. (3.13).

3.4 Power spectra and tensor to scalar ratio

Inserting Eqs. (3.24) and (3.25) into Eq. (3.16) the explicit form of the tensor power spectrum becomes:

$$\begin{aligned} {{\mathcal {P}}}_{T}(k,\eta ) = \frac{k^2}{\pi \overline{M}_{P}^2} (- k \eta ) \biggl (- \frac{\eta }{\eta _{*}}\biggr )^{2\sigma } n_{*}^{1 - 2 \gamma } \biggl |H_{\mu }^{(1)}(- k \eta )\biggr |^2. \end{aligned}$$

(3.26)

In the simplest situation $\eta _{*} = \eta _{1}$ (i.e. $N_{*} = N_{t}$) and when the relevant modes are larger than the Hubble radius Eq. (3.26) can be modified by recalling Eq. (3.22); in this limit we obtain [28, 29]:

$$\begin{aligned} \lim _{k\ll a H} {{\mathcal {P}}}_{T}(k,\eta )= & {} \frac{k^3\,\eta _{1}}{\pi ^3\, \overline{M}_{P}^2} \biggl (- \frac{\eta }{\eta _{1}}\biggr )^{2\sigma +1} n_{1}^{1 - 2 \gamma } \Gamma ^2(\mu )\nonumber \\&\times \biggl (- \frac{k\eta }{2} \biggr )^{ - 2 \mu }. \end{aligned}$$

(3.27)

Since the limits $k\ll a H$ and $k \eta \ll 1$ describe the same physical regime, after some algebra Eq. (3.27) becomes¹²:

$$\begin{aligned} {{\mathcal {P}}}_{T}(k,\eta _{1})= & {} \biggl (\frac{H_{1}}{M_{P}}\biggr )^2 \frac{2^{ 2 \mu + 3}}{\pi ^2} \Gamma ^2(\mu ) n_{1}^{3 - 2 \gamma } \, \bigl |1 + \alpha \beta \bigr |^2 \, |k\eta _{1}|^{3 - 2 \mu }. \nonumber \\ \end{aligned}$$

(3.28)

From Eq. (3.28) the tensor spectral index is defined as $n_{T} = 3 - 2 \mu$; using then Eq. (3.25) the explicit expression of $n_{T}$ depends on $\alpha$, $\beta$ and $\gamma$ in the following manner:

$$\begin{aligned} n_{T}(\alpha ,\beta ,\gamma ) = \frac{2 ( 1 -\beta ) + \alpha \beta ( 3 - 2 \gamma )}{(1 + \alpha \beta )}. \end{aligned}$$

(3.29)

The result of Eq. (3.28) can be further modified by including the slow-roll corrections¹³ and by recalling, from Eq. (3.22), that $\eta _{1}$ and $\tau _{1}$ are related as $\eta _{1}= \tau _{1}/[n_{1} ( 1 + \alpha \beta )]$. Equation (3.28) becomes:

$$\begin{aligned} {{\mathcal {P}}}_{T}(k,\tau _{1})= & {} \biggl (\frac{H_{1}}{M_{P}}\biggr )^2\,\, \frac{2^{6 - n_{T}}}{\pi ^2} \,\Gamma ^2\biggl (\frac{3 - n_{T}}{2}\biggr ) \, n_{1}^{ 3 - n_{T} - 2\gamma }\, \biggl | 1 \nonumber \\&+ \frac{\alpha }{1 - \epsilon }\biggr |^{2 -n_{T}} \,\,\biggl ( \frac{k}{k_{\mathrm {max}}}\biggr )^{n_{T}}. \end{aligned}$$

(3.30)

Denoting with $\Omega _{{R}0}$ the present value of the critical fraction of radiative species (in the concordance paradigm photons and neutrinos) and with ${{\mathcal {A}}}_{R}$ the amplitude of the scalar power spectrum at the pivot scale (see Eq. (A.8)) the value of $k_{\mathrm {max}}$ in $\mathrm {Mpc}^{-1}$ units is:

$$\begin{aligned}&\left( \frac{k_{\mathrm {max}}}{\mathrm {Mpc^{-1}}} \right) = 2.247 \times 10^{23}\, \left( \frac{H_{r}}{H_{1}}\right) ^{\delta -1/2} \left( \frac{\epsilon }{0.01}\right) ^{1/4}\nonumber \\&\quad \times \left( \frac{{{\mathcal {A}}}_{{{\mathcal {R}}}}}{2.41 \times 10^{-9}} \right) ^{1/4} \left( \frac{h_{0}^2 \Omega _{R0}}{4.15 \times 10^{-5}}\right) ^{1/4}. \end{aligned}$$

(3.31)

In Eq. (3.31) the $\delta$ accounts for the possibility of a delayed reheating terminating at an Hubble scale $H_{r}$ smaller than the Hubble rate during inflation. In what follows, as already mentioned in Sect. 1, we shall rather stick to the conventional case where the reheating is sudden and $\delta = 1/2$ (or $H_{1} = H_{r}$ since the end of the inflationary phase coincides with the beginning of the radiation epoch¹⁴).

As suggested in Ref. [13], whenever $\alpha > 0$ the spectral index gets blue since it is always greater than the slow-roll correction. Using Eq. (3.29) this statement can be made more precise by expanding $n_{T}(\alpha ,\beta , \gamma )$ in the limit $\epsilon <1$:

$$\begin{aligned}&n_{T}(\alpha , \frac{1}{1-\epsilon }, \gamma ) = \frac{ \alpha ( 3 - 2 \gamma ) - 2 \epsilon }{1 + \alpha - \epsilon } \end{aligned}$$

(3.32)

$$\begin{aligned}&\rightarrow \frac{\alpha ( 3 - 2 \gamma )}{1 + \alpha } + \frac{[ -2 + \alpha ( 1 - 2\gamma )]\epsilon }{(1 + \alpha )^2} + {{\mathcal {O}}}(\epsilon ^2). \end{aligned}$$

(3.33)

When $\gamma =0$ we are in the situation of Ref. [13] and Eqs. (3.32) and (3.33) imply that the tensor spectral index is:

$$\begin{aligned} n_{T} = \frac{3 \alpha }{1 + \alpha } + \frac{[ -2 + \alpha ]\epsilon }{(1 + \alpha )^2} + {{\mathcal {O}}}(\epsilon ^2). \end{aligned}$$

(3.34)

When $\gamma =1$ we are in the situation of Refs. [14, 15] and Eqs. (3.32) and (3.33) implies instead:

$$\begin{aligned} n_{T} = \frac{\alpha }{1 + \alpha } - \frac{(2 + \alpha )\epsilon }{(1 + \alpha )^2} + {{\mathcal {O}}}(\epsilon ^2). \end{aligned}$$

(3.35)

Finally when $\alpha = \gamma =0$ the standard result is recovered, i.e. $n_{T} = - 2 \epsilon + {{\mathcal {O}}}(\epsilon ^2)$. Concerning the results of Eqs. (3.32)–(3.33) and of Eqs. (3.34)–(3.35) few comments are in order. From Eq. (3.32) it is immediate to appreciate that the spectrum is blue and $n_{T}>0$ provided:

$$\begin{aligned} \epsilon< 1 + \alpha , \qquad \epsilon < \frac{\alpha ( 3 - 2\gamma )}{2}; \end{aligned}$$

(3.36)

these two conditions are always verified in practice by definition of slow-roll parameter (implying $\epsilon \ll 1$). All in all we can then say that within the physical range of the parameters the presence of $\gamma$ just shifts the value of the tensor spectral index (see Eqs. (3.34) and (3.35)) but does not change qualitatively the whole picture.¹⁵

If the transition to normalcy is sufficiently sudden, the details of the transition will be immaterial for the large-scale spectrum. We then have that the tensor to scalar ratio is given by¹⁶:

$$\begin{aligned} r_{T}(k_{p})= & {} \epsilon \frac{2^{6 - n_{T}}}{\pi } \Gamma ^2\biggl (\frac{3 - n_{T}}{2} \biggr ) n_{i}^{3 - n_{T} - 2 \gamma } \nonumber \\&\times e^{N_{*} \alpha ( 3 - n_{T} - 2 \gamma )}\ \biggl | 1 + \frac{\alpha }{ 1 - \epsilon }\biggr |^{ 2 - n_{T}} \biggl (\frac{k_{p}}{k_{\mathrm {max}}}\biggr )^{n_{T}}. \nonumber \\ \end{aligned}$$

(3.37)

Equations (3.32) and (3.37) demonstrate that the consistency relations do not hold in the case where the gravitons have a refractive index. A similar phenomenon has been suggested in [32] as a consequence of the opposite physical situation where the initial thermal bath of primordial phonons (i.e. large-scale quanta of curvature perturbations) is characterized by a sound speed different from the speed of light.

The large-scale power spectra are not modified in the large-scale limit as long as the evolution of $b(\eta )$ is continuous. For this purpose, without indulging in the explicit analytic expression in the transition region, we can consider the situation where before $-\eta _{*}$ the large-scale power spectrum is given by the solution (3.25). The resulting power spectrum at a later time is therefore directly computable since, in the large-scale limit, Eq. (3.12) becomes¹⁷ $\partial _{\eta }[ b^2(\eta ) \partial _{\eta } F_{k}(\eta )]= 0$. This equation can then be explicitly integrated from $-\eta _{2}$ onwards, namely:

$$\begin{aligned}&F_{k}(\eta ) = F_{k}(-\eta _{2}) + G_{k}(-\eta _{2}) \int _{- \eta _{2}}^{\eta } \frac{d\eta ^{\prime }}{b^2(\eta ^{\prime })}, \nonumber \\&G_{k}(-\eta _{2}) = b^2(- \eta _{2}) \dot{F}_{k}(-\eta _{2}), \end{aligned}$$

(3.38)

where the time $-\eta _{2}$ is a generic reference time before $-\eta _{*}$ and very close to it. With this observation we have that the power spectrum after $- \eta _{*}$ can be written as

$$\begin{aligned} {{\mathcal {P}}}_{T}(k, \eta )= & {} \frac{4 \ell _{P}^2 k^3}{\pi ^2} \bigl | F_{k}(-\eta _{*})\bigr |^2 \biggl [ 1 + \biggl (\frac{1}{2} - \mu \biggr ) b_{*}^2\nonumber \\&\times \int _{-\eta _{*}}^{\eta } \frac{ d (\eta ^{\prime }/\eta _{*})}{b^2(\eta ^{\prime })} \biggr ]^2. \end{aligned}$$

(3.39)

Equation (3.39) shows that the only thing that counts is the continuity of $b(\eta )$ across the transition. Well after $-\eta _{*}$ we also have that $b(\eta )\rightarrow a(\eta ) = a(\tau )$ and the background still evolves like quasi-de Sitter with slow-roll parameter given by $\epsilon$. It is then clear that the second term inside the square bracket is subleading and this shows, as expected, that the large-scale power spectrum at large-scale is not affected by this kind of continuous transitions.

3.5 The spectral energy density

The independent variation of the tensor spectral index $n_{T}$ and of the tensor to scalar ratio $r_{T}(k_{p})$ can be investigated from the absolute normalization of the spectral energy density [26, 27]. When the relevant modes are today inside the Hubble radius¹⁸ the relation between the spectral energy density and the power spectrum at the corresponding time is given by:

$$\begin{aligned} \Omega _{\mathrm {gw}}(k,\tau )= & {} \frac{k^2}{12 H^2 a^2} {{\mathcal {P}}}_{\mathrm {T}}(k,\tau )\biggl [ 1 + {{\mathcal {O}}}\biggl (\frac{{{\mathcal {H}}}^2}{k^2}\biggr )\biggr ],\nonumber \\ {{\mathcal {H}}}= & {} \frac{a^{\prime }}{a}. \end{aligned}$$

(3.40)

There are two possibilities for an accurate assessment of the absolute normalization appearing in Eq. (3.40). In the first approach we can compute the transfer function for the amplitude as [20, 26, 27, 33,34,35]

$$\begin{aligned} T_{h}(k/k_{\mathrm {eq}})= & {} \sqrt{1 + c_{1} \biggl (\frac{k}{k_{\mathrm {eq}}}\biggr ) + b_{1} \biggl (\frac{k}{k_{\mathrm {eq}}}\biggr )^2},\nonumber \\ c_{1}= & {} 1.260, \qquad b_{1}= 2.683, \end{aligned}$$

(3.41)

$$\begin{aligned} k_{\mathrm {eq}}= & {} 0.0732\,\, h_{0}^2 \Omega _{\mathrm {M}0} \, \,\mathrm {Mpc}^{-1} \end{aligned}$$

(3.42)

where $\Omega _{\mathrm {M}0}$ denotes the present critical fraction of dusty matter in the concordance paradigm. By using the transfer function for the tensor amplitude, the spectral energy density for frequencies $\nu \gg \nu _{\mathrm {eq}}$ can be simply given by:

$$\begin{aligned}&h_{0}^2 \Omega _{\mathrm {gw}}(\nu ,\tau _{0}) = {{\mathcal {N}}}_{h} \,\, r_{\mathrm {T}} \,\, \left( \frac{\nu }{\nu _{\mathrm {p}}}\right) ^{n_{\mathrm {T}}} e^{- 2\beta \frac{\nu }{\nu _{\mathrm {max}}}}, \end{aligned}$$

(3.43)

$$\begin{aligned}&{{\mathcal {N}}}_{h} = 7.992 \times 10^{-15} \biggl (\frac{h_{0}^2 \Omega _{\mathrm {M}0}}{0.1326}\biggr )^{-2} \biggl (\frac{h_{0}^2 \Omega _{\mathrm {R}0}}{4.15\times 10^{-5}}\biggr )\nonumber \\&\quad \times \,\left( \frac{d_{\mathrm {A}}}{1.4115 \times 10^{4}\, \mathrm {Mpc}}\right) ^{-4}, \end{aligned}$$

(3.44)

where $d_{\mathrm {A}}$ is the (comoving) angular diameter distance to decoupling and $\Omega _{\mathrm {R}0}$ is the fraction of critical energy density attributed to massless particles (photons and neutrinos in the concordance paradigm). The second strategy is to use the direct integration of the mode functions and discuss the transfer function directly in terms of the spectral energy density [26, 27, 35]:

$$\begin{aligned} h_{0}^2 \Omega _{\mathrm {gw}}(\nu ,\tau _{0})= & {} {{\mathcal {N}}}_{\rho } T^2_{\rho }(\nu /\nu _{\mathrm {eq}}) r_{\mathrm {T}}(k_{p}) \biggl (\frac{\nu }{\nu _{\mathrm {p}}}\biggr )^{n_{\mathrm {T}}} e^{- 2 \beta \frac{\nu }{\nu _{\mathrm {max}}}} \nonumber \\\end{aligned}$$

(3.45)

$$\begin{aligned} {{\mathcal {N}}}_{\rho }= & {} 4.165 \times 10^{-15} \biggl (\frac{h_{0}^2 \Omega _{\mathrm {R}0}}{4.15\times 10^{-5}}\biggr ). \end{aligned}$$

(3.46)

where $\nu _{\mathrm {eq}}$ denotes the equality frequency:

$$\begin{aligned} \nu _{\mathrm {eq}} = \frac{k_{\mathrm {eq}}}{2 \pi } = 1.597\times 10^{-17} \biggl (\frac{h_{0}^2 \Omega _{\mathrm {M}0}}{0.1411}\biggr ) \biggl (\frac{h_{0}^2 \Omega _{\mathrm {R}0}}{4.15 \times 10^{-5}}\biggr )^{-1/2}\,\, \mathrm {Hz}, \nonumber \\ \end{aligned}$$

(3.47)

where $T_{\rho }(\nu /\nu _{\mathrm {eq}})$ is the transfer function of the spectral energy density:

$$\begin{aligned} T_{\rho }(\nu /\nu _{\mathrm {eq}})= & {} \sqrt{1 + c_{2}\biggl (\frac{\nu _{\mathrm {eq}}}{\nu }\biggr ) + b_{2}\biggl (\frac{\nu _{\mathrm {eq}}}{\nu }\biggr )^2},\nonumber \\ c_{2}= & {} 0.5238,\qquad b_{2}=0.3537. \end{aligned}$$

(3.48)

Equation (3.48) is obtained by integrating the mode functions across the radiation-matter transition and by computing $\Omega _{\mathrm {gw}}(\nu ,\tau )$ for different frequencies. By comparing Eqs. (3.45)–(3.46) to Eqs. (3.43)–(3.44), the amplitude for $\nu \gg \nu _{\mathrm {eq}}$ differs, roughly, by a factor 2. This coincidence is not surprising since Eqs. (3.43)–(3.44) have been obtained by averaging over the oscillations (i.e. by replacing cosine squared with 1 / 2). These manipulations are less accurate than the procedure used to derive the transfer function for the spectral energy density, as stressed in the past [26, 27].

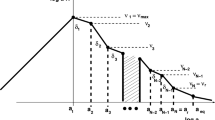
Recalling Fig. 1 and the related discussion, when the critical number of efolds equals the total number of efolds (i.e. $N_{*} = N_{t}$) the form of the spectral energy density is the same as in the standard case with the difference that the tensor to scalar ratio and the spectral index dapend on the parameters of the model and are given, respectively, by Eqs. (3.29) and (3.37). If $N_{*} < N_{t}$ the spectral energy density is characterized by two branches. More specifically the full expression of the spectral energy density can be written as:

$$\begin{aligned} h_{0}^2 \Omega _{\mathrm {gw}}(\nu ,\tau _{0})= & {} {{\mathcal {N}}}_{\rho } T^2_{\rho }(\nu /\nu _{\mathrm {eq}}) r_{\mathrm {T}}(\nu _{p})\biggl (\frac{\nu }{\nu _{\mathrm {p}}}\biggr )^{n_{\mathrm {T}}}, \qquad \nu < \nu _{*} \nonumber \\ \end{aligned}$$

(3.49)

$$\begin{aligned}= & {} {{\mathcal {N}}}_{\rho } r_{\mathrm {T}}(\nu _{p}) \biggl (\frac{\nu _{*}}{\nu _{\mathrm {p}}}\biggr )^{n_{\mathrm {T}}}\, \nonumber \\&\times \biggl (\frac{\nu }{\nu _{*}}\biggr )^{- 2 \epsilon }\, e^{- 2 \beta \frac{\nu }{\nu _{\mathrm {max}}}}, \qquad \nu > \nu _{*}, \end{aligned}$$

(3.50)

where $\nu _{*}$ and $\nu _{\mathrm {max}}$ are given, respectively, by:

$$\begin{aligned} \nu _{\mathrm {max}}= & {} 0.3 \,\left( \frac{r_{T}}{0.1}\right) ^{1/4} \biggl (\frac{{{\mathcal {A}}}_{{\mathcal {R}}}}{2.41 \times 10^{-9}}\biggr )^{1/4}\nonumber \\&\times \left( \frac{h_{0}^2 \Omega _{\mathrm {R}0}}{4.15 \times 10^{-5}}\right) ^{1/4} \,\mathrm {GHz}, \end{aligned}$$

(3.51)

$$\begin{aligned} \nu _{*}= & {} \left( 1 + \frac{\alpha }{1 - \epsilon }\right) e^{N_{*}(\alpha + 1) - N_{t}}\nu _{\mathrm {max}}. \end{aligned}$$

(3.52)

In general terms, as we shall see, $\nu _{*}$ will always be larger than ${{\mathcal {O}}}(10^{-11})$ Hz but, depending on the values of $\alpha$ and $N_{*}$ it can be either larger or smaller than the Hz.

4 Phenomenological implications

The rate of variation of the refractive index $\alpha$ and the critical number of efolds $N_{*}$ are the two pivotal parameters for the analysis reported in the present section. If $N_{*}$ is of the order of $N_{t}$ the transition to normalcy occurs at the end of inflation; conversely when $N_{*} <N_{t}$ (as in the case of Fig. 1) the transition to normalcy takes place well before the onset of the radiation-dominated epoch (i.e. when the background is still inflating deep inside the quasi-de Sitter stage of expansion). These two different situations will now be separately examined by assuming, for illustrative purposes, a fiducial number of inflationary efolds $N_{t} = {{\mathcal {O}}}(70)$. Larger values of $N_{t}$ do not affect the main conclusions inferred below.

4.1 Basic constraints

The scale-dependent constraint on the tensor to scalar ratio is conventionally applied at the pivot scale $k_{p}= 0.002\,\, \mathrm {Mpc}^{-1}$ corresponding to the comoving frequency $\nu _{p} = k_{p}/(2 \pi )$. While the Planck data alone would suggest an upper limit $r_{T}(k_{p}) < 0.11$, the joint analysis of Planck and BICEP2/Keck array data [19] already demands $r_{T}(k_{p})<0.07$. In a conservative perspective we shall therefore require the limit:

$$\begin{aligned}&r_{T}(\nu _{p}) \le 0.06,\nonumber \\&\qquad \nu _{p} = \frac{k_{p}}{2 \pi } = 3.092\times 10^{-18} \,\, \mathrm {Hz}= 3.092\,\,\mathrm {aHz} \end{aligned}$$

(4.1)

on the tensor to scalar ratio computed in Eq. (3.37).

Fig. 2

In both plots the various curves and the corresponding labels illustrate different values of the common logarithm of $h_{0}^2 \Omega _{\mathrm {gw}}$. The two plots refer to two different frequencies within the audio band

Fig. 3

As in Fig. 2 the curves illustrate the different values of the common logarithm of $h_{0}^2 \Omega _{\mathrm {gw}}$ reported in the corresponding labels. The frequencies of the two plots fall within the mHz band

The bounds coming from big-bang nucleosynthesis [36,37,38] imply instead a constraint on the integral of the spectral energy density of the gravitons:

$$\begin{aligned}&h_{0}^2 \int _{\nu _{\mathrm {bbn}}}^{\nu _{\mathrm {max}}} \Omega _{\mathrm {gw}}(\nu ,\tau _{0}) d\ln {\nu }\nonumber \\&\quad = 5.61 \times 10^{-6} \Delta N_{\nu } \biggl (\frac{h_{0}^2 \Omega _{\gamma 0}}{2.47 \times 10^{-5}}\biggr ). \end{aligned}$$

(4.2)

The lower limit of integration in Eq. (4.2) is given by the frequency corresponding to the Hubble rate at the nucleosynthesis epoch:

$$\begin{aligned} \nu _{\mathrm {bbn}}= & {} 2.252\times 10^{-11} \biggl (\frac{g_{\rho }}{10.75}\biggr )^{1/4} \biggl (\frac{T_{\mathrm {bbn}}}{\,\,\mathrm {MeV}}\biggr )\nonumber \\&\times \left( \frac{h_{0}^2 \Omega _{\mathrm {R}0}}{4.15 \times 10^{-5}}\right) ^{1/4}\,\,\mathrm {Hz}\nonumber \\\simeq & {} 0.01\, \mathrm {nHz}, \end{aligned}$$

(4.3)

where $g_{\rho }$ denotes the effective number of relativistic degrees of freedom entering the total energy density of the plasma and $T_{\mathrm {bbn}}$ is the temperature of big-bang nucleosynthesis. The limit of Eq. (4.2) sets an indirect constraint on the extra-relativistic species (and, among others, on the relic gravitons). Since Eq. (4.2) is relevant in the context of neutrino physics (when applied to massless fermionic species), the limit is often expressed for practical reasons in terms of $\Delta N_{\nu }$ representing the contribution of supplementary neutrino species. The actual bounds on $\Delta N_{\nu }$ range from $\Delta N_{\nu } \le 0.2$ to $\Delta N_{\nu } \le 1$; the integrated spectral density in Eq. (4.2) is thus between $10^{-6}$ and $10^{-5}$. Finally the pulsar timing measurements determine a local bound on the spectral energy density [39, 40]

$$\begin{aligned} \Omega _{\mathrm {gw}}(\nu _{pul},\tau _{0}) < 1.9 \times 10^{-8}, \qquad \nu _{pul} \simeq \,10^{-8}\,\mathrm {Hz}, \end{aligned}$$

(4.4)

which is an upper limit at a typical frequency, roughly corresponding to the inverse of the observation time along which the timing has been monitored. Various applications and refinements of the pulsar timing constraint have been discussed through the years and also recently (see e.g. Refs. [41,42,43,44]).

4.2 Target sensitivities and speculations

Generally speaking the phenomenological constraints of Eqs. (4.1), (4.2) and (4.4) are satisfied in a certain corner of the parameter space of a given model. The game will then be to see to what extent these regions overlap with the areas where the signal is sufficiently large to be detected in the future. For instance in Figs. 1 and 2 the constraints of Eqs. (4.1), (4.2) and (4.4) are satisfied in the shaded area which has been obtained by assuming (incorrectly, as we shall see in a moment) that the spectral index and the tensor to scalar ratio change independently. The labels appearing on the curves of the plots of Figs. 2 and 3 denote the common logarithm of $h_{0}^2 \Omega _{\mathrm {gw}}$ at the four frequencies indicated above each of the plots.

The two frequencies discussed in Fig. 2 correspond, respectively, to 10 and 100 Hz: they illustrate the spectral energy density in the so-called audio band ranging between few Hz and 10 kHz. Terrestrial wide-band interferometers, depending on their respective physical dimensions, operate within this band. The two frequencies illustrated in Fig. 3 fall instead within the mHz band ranging between a fraction of the mHz and few Hz. Space-borne detectors operate within this band. We can finally define a MHz band, extending between 100 kHz and few GHz; this band is irrelevant for the signal coming from conventional inflationary models but could play a relevant role in the present context since, in this case, most of the signal is concentrated exactly in this region.

Fig. 4

The constraints on $r_{T}$ and $n_{T}$ are translated in the $(\alpha ,\,\gamma )$ plane for the values of $n_{T}$ compatible with an observable signal in the audio band (i.e. $\mathrm {Hz} \le \nu \le 10^{4} \mathrm {Hz}$) and in the generic case of an instrument able to probe spectral energy densities ${{\mathcal {O}}}(10^{-10})$

While the current upper limits on stochastic backgrounds of relic gravitons are still far from the final targets [45, 46], the advanced Ligo/Virgo projects are described in [47, 48]. We shall then suppose, according to Refs. [47, 48] that the terrestrial interferometers (in their advanced version) will be one day able to probe chirp amplitudes ${{\mathcal {O}}}(10^{-25})$ corresponding to spectral amplitudes $h_{0}^2 \Omega _{\mathrm {gw}} = {{\mathcal {O}}}(10^{-11})$. In the foreseeable future there should be two further interferometers (with different designs) operational in the audio band namely the Japanese Kagra¹⁹ (Kamioka Gravitational Wave Detector) [56, 57] and the Einstein telescope [58] both with improved sensitivities in comparison with the advanced Ligo/Virgo interferometers.

The target sensitivity to detect the stochastic background of inflationary origin should be $h_{c}={{\mathcal {O}}}(10^{-29})$ (or smaller) in the chirp amplitude and $h_{0}^2 \Omega _{\mathrm {gw}} = {{\mathcal {O}}}(10^{-16})$ (or smaller) in the spectral energy density. These figures directly come from the amplitude of the quasi-flat plateau produced in the context of single-field inflationary scenarios; in this case the plateau encompasses the mHz and the audio bands with basically the same amplitude. Even though these sensitivities are beyond reach for the current interferometers, a number of ambitious projects will be hopefully operational in the future.

The space-borne interferometers, such as (e)Lisa (Laser Interferometer Space Antenna) [49], Bbo (Big Bang Observer) [50], and Decigo (Deci-hertz Interferometer Gravitational Wave Observatory) [51, 52], might operate between few mHz and the Hz hopefully within the following score year. While the sensitivities of these instruments are still at the level of targets, we can say that they should probably range between $h_{0}^2 \Omega _{\mathrm {gw}} = {{\mathcal {O}}}(10^{-12})$ and $h_{0}^2 \Omega _{\mathrm {gw}} = {{\mathcal {O}}}(10^{-15})$.

In spite of the minute signals related to conventional inflationary scenarios, if the spectrum increases in frequency (i.e. $n_{T} >0$) Figs. 2 and 3 seem to suggest potentially large signals both for terrestrial interferometers (in their advanced version) and for space-borne detectors. However, this way of reasoning is misleading, at least partially. Indeed, while it is true that in the present situation the consistency relations are violated, it is equally true that $r_{T}$ and $n_{T}$ depend on $\epsilon$, $N_{*}$, $\alpha$ and $\gamma$ in a specific way (see e.g. Eqs. (3.32) and (3.37)).

4.3 Charting the parameter space in the $N_{*} = {{\mathcal {O}}}(N_{t})$ case

When $N_{*} = {{\mathcal {O}}}(N_{t})$ the spectrum consists of only two branches: the standard infrared branch in the aHz region and an increasing branch extending up to the GHz. Since in this subsection we are discussing the case $N_{*} = {{\mathcal {O}}}(N_{t})$ the only two parameters are, in practice, $\alpha$ and $\gamma$. The problem is therefore to pin down the regions in the $(\alpha ,\,\gamma )$ plane where the spectrum is blue, the signal is large and the constraints are not violated. The result of this analysis is illustrated in Figs. 4 and 5 where the parameters $N_{t}$ and $\epsilon$ have been selected as²⁰ respectively, 70 and $10^{-3}$. The conclusion suggested by Figs. 4 and 5 is that the regions where the constraints are satisfied and the spectrum is sufficiently blue to guarantee a signal in the audio band do not overlap.

Consider first the regions $r_{T} <0.06$ (from Eq. (3.37)) and $n_{T} >0.4$ (see Eq. (3.32)): Fig. 4 shows that these two corners of the parameter space are mutually exclusive. If we relax a bit the requirement on the spectral index and impose $n_{T} >0.3$ the two regions get a bit closer (see right plot in Fig. 4). Whenever $N_{t} = {{\mathcal {O}}}(N_{*})$ the potential signals due to relic gravitons in the audio band are excluded and this result holds on spite of the value of $\gamma$.

Fig. 5

The constraints on $r_{T}$ and $n_{T}$ are translated in the $(\alpha ,\,\gamma )$ plane for the values of $n_{T}$ compatible with an observable signal in the mHz band typical of space-borne interferometers

By looking at Fig. 5 we see that the only appreciable overlap between the areas $n_{T} >0.07$ and $r_{T}<0.06$ is a tiny slice representing the allowed region of the parameter space. By going back to Fig. 3 we see that the spectral energy density corresponding to the allowed region of Fig. 5 is $h_{0}^2 \Omega _{\mathrm {gw}} = {{\mathcal {O}}}(10^{-15})$. These values of the spectral energy density will be hopefully probed by Bbo/Decigo interferometer. We therefore conclude that in the case $N_{t}= N_{*}$ the variation of the refractive index does lead to a blue spectrum which is however only relevant in the mHz band (but not in the audio band). In particular in the mHz band this signal can be larger (by a couple of orders of magnitude) than the spectral energy density coming from the conventional inflationary models.

4.4 Charting the parameter space in the $N_{*} \ll N_{t}$ case

When $N_{*} < N_{t}$ (or even $N_{*}\ll N_{t}$) the spectral energy density consist of three branches: the usual infrared branch is supplemented by an intermediate regime (where the spectral slope is blue) terminating with a quasi-flat plateau at high frequencies. In the high-frequency region the spectrum is quasi-flat with a red slope determined by the value of $\epsilon$.

Fig. 6

The regions $\nu _{\mathrm {bbn}}< \nu _{*} < \mathrm {Hz}$ and $\nu _{*}> \mathrm {Hz}$ are illustrated in the $(\alpha ,\, N_{*})$ plane. The shaded area is determined by the overlap between the regions where the corresponding inequalities are satisfied

The frequency $\nu _{*}$ divides the intermediate branch of the spectrum from the high-frequency tail and it only depends on $N_{*}$, $N_{t}$ and $\alpha$. There are two complementary physical possibilities. If $\nu _{\mathrm {bbn}}< \nu _{*} < \mathrm {Hz}$ the transition regime takes place between the frequency of the big-bang nucleosynthesis and the mHz band where space-borne interferometers will be operating; this region correspond to the shaded area appearing in the left plot of Fig. 6. In the complementary regime we have instead that $\nu _{*} > \mathrm {Hz}$ and the break of the spectrum is in the audio range. This region corresponds to the shaded area appearing in the right plot of Fig. 6. As long as $25< N_{*} < 50$ and $0<\alpha < 2$, the results of Fig. 6 confirm that $\nu _{\mathrm {bbn}}< \nu _{*} < \mathrm {Hz}$, as expected from qualitative arguments. For the same range of $\alpha$ the condition $\nu _{*}> \mathrm {Hz}$ will be verified for a comparatively larger $N_{*}$.

We are now in conditions of charting the parameter space in the $(\alpha , \, N_{*})$ plane by requiring that the constraints of Eqs. (4.1), (4.2) and (4.4) are simultaneously satisfied. In Fig. 7 we enforced all the relevant bounds and also required²¹

$$\begin{aligned} h_{0}^2 \Omega _{\mathrm {gw}}(\nu _{LV},\tau _{0}) > 10^{-11},\qquad \nu _{LV} =0.1 \, \mathrm { kHz}, \end{aligned}$$

(4.5)

where $\nu _{LV}$ denotes the Ligo/Virgo frequency falling within the audio band. While the variation of $\gamma$ can also be considered continuous in the purely heuristic perspective invoked after Eq. (3.1), we shall just illustrate the cases $\gamma = 0$ and $\gamma =1$ corresponding to the two equivalent parametrizations of the action discussed in Sects. 2 and 3. In this connection we can remark that in the case $\gamma =0$ (left plot in Fig. 7) the allowed region is larger than in the case $\gamma =1$ (right plot in Fig. 7). Note that in Fig. 7 the frequency $\nu _{a}=0.1 \mathrm {kHz}$ has been chosen as representative of the typical signal in the audio-band where the sensitivity of wide-band detectors is approximatively larger. A different choice in the range $\mathrm {Hz}< \nu _{a} < \mathrm {kHz}$ will lead to similar conclusions.²²

Fig. 7

We illustrate the regions where the relevant phenomenological bounds are satisfied and the spectral energy density (in critical units) exceeds $10^{-11}$ at the centre of the audio band in the cases $\gamma =0$ (left plot) and $\gamma =1$ (right plot). The dashed areas denote the regions where the constraints are simultaneously satisfied and $h_{0}^2 \Omega _{\mathrm {gw}}(\nu _{LV},\tau _{0}) > 10^{-11}$

Fig. 8

We illustrate the regions where the relevant phenomenological bounds are satisfied and the spectral energy density (in critical units) exceeds $10^{-12}$ at the centre of the mHz band in the cases $\gamma =0$ (left plot) and $\gamma =1$ (right plot). The dashed areas denote the regions of the parameter space where the three constraints are simultaneously satisfied. Figures 7 and 8 pin down the two complementary portions of the parameter space: by comparison we can see that the dashed areas of Figs. 7 and 8 do overlap

In Fig. 8 the same analysis of Fig. 7 is extended to mHz band. The dashed areas in Fig. 8 have the same meaning of those depicted in Fig. 7 with the difference that we are now imposing a more stringent requirement on the spectral energy density namely:

$$\begin{aligned} h_{0}^{2} \Omega _{\mathrm {gw}}(\nu _{m}, \tau _{0}) > 10^{-12}, \qquad \nu _{m}= 10^{-3}\, \mathrm {Hz}. \end{aligned}$$

(4.6)

The comparison of Figs. 7 and 8 demonstrates that there exist a tiny overlap between the shaded areas appearing in the two figures. The overlap between the dashed areas of Figs. 7 and 8 defines, for each value of $\gamma$, a sweet spot in the $(\alpha , \, N_{*})$ plane where the signal is be potentially visible both in the audio band and in the mHz band.

If we would require a larger sensitivity in the mHz band (such as the the ones often quoted for the Bbo or Decigo projects) we would be led to demand, for instance,

$$\begin{aligned} h_{0}^{2} \Omega _{\mathrm {gw}}(\nu _{m}, \tau _{0}) > 10^{-16}, \qquad \nu _{m}= 10^{-3}\, \mathrm {Hz}. \end{aligned}$$

(4.7)

In Fig. 9 the Bbo/Decigo target sensitivities are illustrated in the $(\alpha ,\,N_{*})$ plane. As it is clearly visible from the direct comparison of Figs. 8 and 9 the dashed areas get larger. Still the allowed region in the $\gamma = 1$ case is always larger than for $\gamma =0$. By comparing Figs. 7, 8 and 9 in a unified perspective, the sweet spots now get larger if we demand that space-borne interferometers will be able to probe values of the spectral energy density as low as the ones of Eq. (4.7). In particular the dashed area of Fig. 7 is now all contained within the dashed area of Fig. 9: this means that by remaining in the dashed slice of Fig. 7 the resulting signal will be, a fortiori, visible both in the audio band and in the mHz band.

Fig. 9

We illustrate the regions where the relevant phenomenological bounds are satisfied and the spectral energy density is critical units exceeds $10^{-16}$ at the centre of the mHz band in the cases $\gamma =0$ (left plot) and $\gamma =1$ (right plot). The dashed areas denote, as usual, the regions of the parameter space where the three constraints are simultaneously satisfied

Even if the target sensitivities of Eq. (4.7) look by definition quite optimistic they might not be totally insane if we bluntly assume that the minimal detectable chirp (or strain) amplitudes are the same in the mHz and in the audio band. The argument goes in short as follows. A given chirp (or strain amplitude) of the signal in the audio band (say for $\nu =\nu _{LV} = {{\mathcal {O}}}(0.1) \mathrm {kHz}$) probes a spectral energy density which is comparatively larger than the one achievable, with the same sensitivity, in the mHz band. To appreciate this we can consider, for instance, Eq. (1.1) and suppose that the spectral energy density of the signal will be, in critical units, $h_{0}^2 \Omega _{\mathrm {gw}}(\nu _{a}, \tau _{0}) = {{\mathcal {O}}}(10^{-10})$. The required sensitivity in terms of $h_{c}$ will therefore be of the order of $10^{-25}$. Let us now pretend that the achievable sensitivity (in terms of the chirp amplitude and in the mHz band) is the same as in the audio band, i.e. $h_{c}= {{\mathcal {O}}}(10^{-25})$. Since the frequency in the mHz band is ${{\mathcal {O}}}(10^{-3})$ Hz, Eq. (1.1) can be inverted in order to obtain the minimal spectral amplitude detectable in the mHz band; the result will be $h_{0}^2 \Omega _{\mathrm {gw}}(\nu _{a}, \tau _{0}) = {{\mathcal {O}}}(10^{-15})$.

We shall now select the values of $\alpha$ and $N_{*}$ within the dashed areas of Figs. 7, 8 and 9 and present some interesting example.

Fig. 10

The spectral energy density is illustrated for various choices of $N_{*}$ with $N_{*} < N_{t}$. The other values have been selected within the allowed regions of the parameter space and they are $\alpha = 0.14$ and $\gamma =0$

In Fig. 10 we illustrate the spectral energy density by fixing $\alpha = 0.14$ (for $\gamma =0$); similarly in Fig. 11 we demand $\alpha =0.42$ (for $\gamma =1$). Both in Figs. 10 and 11 we choose different values of $N_{*}$ (i.e. $N_{*}= 40,\, 50,\, 60$). As $N_{*} \rightarrow N_{t}$ the results discussed at the beginning of this section are recovered: the high-frequency plateau gets narrower and asymptotically disappears. Conversely, when the value of $N_{*}$ decreases, $\nu _{*}$ also diminishes and the quasi-flat branch of the spectrum gets wider, as it can be seen from Figs. 10 and 11.

Let us now consider more closely the values of $\alpha$ and $\gamma$. In the left plot of Fig. 9 (i.e. $\gamma =0$) the value of $\alpha =0.14$ is within the shaded region and the same is true for $\alpha =0.42$ in the right plot (i.e. $\gamma = 1$) of the same figure. The value of $\alpha$ in Fig. 10 is three times smaller than the one of Fig. 11 and this occurrence has a simple explanation²³ which is directly related to Eqs. (3.34) and (3.35). By looking at Figs. 10 and 11 we see that for a value of $\alpha$ leading to the same $n_{T}$ in the cases $\gamma =0$ and $\gamma =1$, the spectral energy density in the case $\gamma =1$ is smaller than in the case $\gamma =0$ for the same choice of $N_{*}$.

Fig. 11

The spectral energy density is illustrated for $N_{*} < N_{t}$; to compare this plot with the one of Fig. 10 we stress that $\alpha = 0.42$ and $\gamma = 1$

Fig. 12

The spectral energy density in critical units for a peculiar choice of the parameters selected within the shaded regions in Fig. 9 (plot at the left)

All in all, when $N_{*} < N_{t}$ the spectral energy density develops two branches for $\nu > \nu _{\mathrm {eq}}$. The intermediate branch corresponds to those modes leaving the Hubble radius during inflation when the refractive index is still dynamical. These modes will then lead to an increasing spectral slope for $\nu _{\mathrm {eq}}< \nu < \nu _{*}$. The second branch of the spectrum corresponds to those modes that left the Hubble radius when the refractive index already ceased to be dynamical: in this branch the spectrum decreases as $\nu ^{- 2 \epsilon }$ for $\nu _{*}< \nu < \nu _{\mathrm {max}}$. In Fig. 10 the audio branch of the spectrum and the mHz branch have been illustrated, respectively, with trapeziodal and triangular shapes encompassing the respective frequency ranges. The heights of the two triangles roughly matches the hoped sensitivities of (e)Lisa and Bbbo/Decigo. Similarly the height of the trapezoid in the audio branch approximately correspond to the sensitivities of terrestrial wide-band detectors (in their advanced version). Not all the curves of Figs. 10 and 11 match the required sensitivities of future detectors.

In the $(\alpha ,\,N_{*})$ plane there exist regions that are potentially visible both in the audio band and in the mHz bands. These regions lie within the shaded areas of Figs. 7 and 9 and are illustrated in Fig. 12 in the case $\gamma =0$.

The trapezoidal shape of Fig. 12 generously encompasses the best sensitivities in the spectral energy density for terrestrial and space-borne detectors in the audio and mHz bands. The parameters illustrated in Fig. 12 belong to the same fine-tuning line: if the parameters lie along that line in the $(\alpha , \, N_{*})$ plane we can be reasonably sure that the corresponding spectral energy density in critical units will be potentially visible both by terrestrial and by space-borne detectors. The parameters leading to a comparatively large spectral energy density in the case $\gamma =0$ correspond to a much smaller value of $h_{0}^2 \Omega _{\mathrm {gw}}$ in the case $\gamma =1$. This conclusion is clear by comparing the two plots of Fig. 12: the two plots share exactly the same parameters but correspond to different values of $\gamma$. As explained above in connection with Figs. 10 and 11 this feature has a simple explanation since different values of $\gamma \ne 0$ simply shift the tensor spectral index of the intermediate branch in comparison with the case $\gamma =0$.

5 Concluding remarks

We showed that a rather generic scenario for the evolution of the refractive index during the early stages of a conventional inflationary phase leads to power spectrum of relic gravitons naturally tilted towards frequencies. The spectral slope is determined, in this context, by the competition between the rate of variation of the refractive index and the expansion rate of the quasi-de Sitter stage. We argued that it is always possible to redefine the time coordinate and to compute the evolution of the field operators in terms of an effective horizon incorporating the dynamical effects due to the variation of the refractive index.

The slope of the tensor spectrum differs for the modes crossing the effective horizon in the subsequent phase where the gravitons propagate again at the speed of light and the refractive index goes back to 1. In this branch the spectral slope is quasi-flat but it decreases at a rate that depends on the slow-roll parameter. If the evolution of the refractive index stops at the end of inflation, the spectral energy density consists of the usual low-frequency branch (between few aHz and 0.1 fHz) supplemented by a growing branch extending up to the MHz or even GHz regions. Conversely if the evolution of the refractive index terminates before the end of inflation the previous branches are supplemented by a quasi-flat plateau at high frequencies. The frequency range of the plateau depends on the rate of variation of the refractive index (in units of the expansion rate) and on the critical number of efolds during which the refractive index evolves. After imposing the usual phenomenological constraints, it turns out that the plateau may extend from the mHz band to the GHz band. In a sweet spot of the parameter space all the known bounds are satisfied and the resulting signal could be detectable, in principle, either by terrestrial interferometers (in their advanced and enhanced configuration) or by space-borne detectors.

A Tensor, scalars and their frame-invariance

The two polarizations of the gravitational wave are defined as:

$$\begin{aligned} e_{ij}^{(\oplus )}(\hat{k}) = (\hat{m}_{i} \hat{m}_{j} - \hat{q}_{i} \hat{q}_{j}), \quad e_{ij}^{(\otimes )}(\hat{k}) = (\hat{m}_{i} \hat{q}_{j} + \hat{q}_{i} \hat{m}_{j}), \nonumber \\ \end{aligned}$$

(A.1)

where $\hat{k}_{i} = k_{i}/|\vec {k}|$, $\hat{m}_{i} = m_{i}/|\vec {m}|$ and $\hat{q} =q_{i}/|\vec {q}|$ are three mutually orthogonal directions and $\hat{k}$. It follows directly from Eq. (A.1) that $e_{ij}^{(\lambda )}\,e_{ij}^{(\lambda ')} = 2 \delta _{\lambda \lambda '}$ while the sum over the polarizations gives:

$$\begin{aligned}&\sum _{\lambda } e_{ij}^{(\lambda )}(\hat{k}) \, e_{m n}^{(\lambda )}(\hat{k})\nonumber \\&= \biggl [p_{m i}(\hat{k}) p_{n j}(\hat{k}) + p_{m j}(\hat{k}) p_{n i}(\hat{k}) - p_{i j}(\hat{k}) p_{m n}(\hat{k}) \biggr ]; \nonumber \\ \end{aligned}$$

(A.2)

where $p_{ij}(\hat{k}) = (\delta _{i j} - \hat{k}_{i} \hat{k}_{j})$. Defining the Fourier transform of $\hat{h}_{ij}(\vec {x},\eta )$ as

$$\begin{aligned} \hat{h}_{ij}(\vec {x},\eta ) = \frac{1}{(2\pi )^{3/2}}\, \sum _{\lambda } \, \int d^{3} k \, \hat{h}_{ij}(\vec {k},\eta )\,\, e^{- i \vec {k}\cdot \vec {x}}, \end{aligned}$$

(A.3)

we also have that:

$$\begin{aligned}&\hat{h}_{ij}(\vec {p}, \eta )\nonumber \\&= \sum _{\lambda } \left[ e_{ij}^{(\lambda )}(\hat{p}) F_{k,\, \lambda }(\eta ) \hat{a}_{\vec {p}\, \lambda } + e_{ij}^{(\lambda )}(-\hat{p}) F_{k,\, \lambda }^{*}(\eta ) \hat{a}_{-\vec {p}\, \lambda }^{\dagger } \right] , \nonumber \\ \end{aligned}$$

(A.4)

The tensor power spectra ${{\mathcal {P}}}_{T}(k,\eta )$ and ${{\mathcal {Q}}}_{T}(k,\eta )$ determine the two-point function at equal times:

$$\begin{aligned} \langle \hat{h}_{ij}(\vec {k},\eta ) \, \hat{h}_{mn}(\vec {p},\eta ) \rangle = \frac{2\pi ^2}{k^3} {{\mathcal {P}}}_{T}(k,\eta ) \, {{\mathcal {S}}}_{ijmn}(\hat{k}) \delta ^{(3)}(\vec {k} +\vec {p}), \end{aligned}$$

(A.5)

where ${{\mathcal {P}}}_{T}(k,\eta )$ is the power spectrum in the $\eta$ parametrization while:

$$\begin{aligned} {{\mathcal {S}}}_{ijmn}(\hat{k})= & {} \sum _{\lambda } e_{ij}^{(\lambda )}(\hat{k}) \, e_{m n}^{(\lambda )}(\hat{k})/4 \nonumber \\= & {} \frac{1}{4} \left[ p_{mi}(\hat{k}) p_{nj}(\hat{k}) + p_{mj}(\hat{k}) p_{ni}(\hat{k}) - p_{ij}(\hat{k}) p_{m n}(\hat{k}) \right] . \nonumber \\ \end{aligned}$$

(A.6)

Equation (A.5) follows the same conventions used when deriving the spectrum of curvature perturbations on comoving orthogonal hypersurfaces (customarily denoted by ${{\mathcal {R}}}(\vec {x},\tau )$)

$$\begin{aligned} \langle {{\mathcal {R}}}(\vec {k},\tau ) \, {{\mathcal {R}}}(\vec {p},\tau ) \rangle = \frac{2\pi ^2}{k^3} {{\mathcal {P}}}_{{{\mathcal {R}}}}(k,\tau ) \delta ^{(3)}(\vec {k} +\vec {p}), \end{aligned}$$

(A.7)

which is the quantity employed to set the initial conditions for the evolution of the temperature and polarization anisotropies of the Cosmic Microwave Background. According to the standard convention, the scalar power spectrum is assigned as:

$$\begin{aligned} {{\mathcal {P}}}_{{{\mathcal {R}}}}(k)= {{\mathcal {A}}}_{{{\mathcal {R}}}} \biggl (\frac{k}{k_{p}}\biggr )^{n_{s} -1}, \qquad k_{p} = 0.002\, \mathrm {Mpc}^{-1}, \end{aligned}$$

(A.8)

where $k_{p}$ is called the pivot scale, $n_{s}$ is the scalar spectral index and ${{\mathcal {A}}}_{R}$ is the amplitude of the scalar power spectrum at the pivot scale.

The conformal rescaling of Eq. (2.1) assumes that the refractive index is homogeneous. If this is not the case the results for the tensor modes will be exactly the same while the scalar modes will be modified since the fluctuations of the conformal factor contribute to the scalar and not to the tensor problem. More specifically, the scalar modes of the geometry in the Einstein frame:

$$\begin{aligned} \delta _{s} g^{(E)}_{00}= & {} 2 a_{E}^2 \phi _{E},\qquad \delta _{s} g^{(E)}_{i j} = 2 a_{E}^2( \psi _{E} \delta _{ij} - \partial _{i}\partial _{j } C_{E}),\nonumber \\ \delta _{s} g^{(E)}_{0i}= & {} - a_{E}^2 \partial _{i} B_{E}, \end{aligned}$$

(A.9)

will be related to the scalar modes in the conformally related frame via the scalar fluctuation of Eq. (2.9), i.e.

$$\begin{aligned} \delta _{s} g_{\mu \nu }^{(E)} = \delta _{s} n \, \overline{G}_{\mu \nu }^{(s)} + n\, \delta _{s} G_{\mu \nu }. \end{aligned}$$

(A.10)

Now the scalar fluctuations in the new frame can always be parametrized as in Eq. (A.9) but with different arbitrary functions:

$$\begin{aligned} \delta _{s} G_{00}= & {} 2 a^2 \phi ,\qquad \delta _{s} G_{i j} = 2 a^2 ( \psi \delta _{ij} - \partial _{i}\partial _{j } C),\nonumber \\ \delta _{s} G_{0i}= & {} - a^2 \partial _{i} B. \end{aligned}$$

(A.11)

Equation (A.10) implies a specific relation between the perturbed components in the two frames, i.e.

$$\begin{aligned} \phi= & {} \phi _{E} - \frac{1}{2} \biggl (\frac{\delta _{s} n}{n}\biggr ),\qquad \psi = \psi _{E} + \frac{1}{2} \biggl (\frac{\delta _{s} n}{n} \biggr ), \nonumber \\ C= & {} C_{E}, \qquad B = B_{E}. \end{aligned}$$

(A.12)

Note, however, that the curvature perturbations on comoving orthogonal hypersurfaces are frame-invariant. Indeed in the two frames they are simply given by

$$\begin{aligned} {{\mathcal {R}}}_{E} = - \psi _{E} - \frac{{{\mathcal {H}}}_{E}}{n^{\prime }} \, \delta _{s} n ,\qquad {{\mathcal {R}}} = - \psi - \frac{{{\mathcal {H}}}}{n'}\,\delta _{s} n. \end{aligned}$$

(A.13)

Equation (A.13) does not imply that ${{\mathcal {R}}}_{E} \ne {{\mathcal {R}}}$, as it could be superficially concluded: since $\psi _{E} \ne \psi$ (see Eq. (A.12)) Eqs. (2.13) and (2.16) imply ${{\mathcal {H}}}_{E} \ne {{\mathcal {H}}}$. However, the mismatch between $\psi _{E}$ and $\psi$ is exactly compensated by the mismatch between ${{\mathcal {H}}}_{E}$ and ${{\mathcal {H}}}$. In fact, from Eq. (2.13) we have $2 ({{\mathcal {H}}}_{E} - {{\mathcal {H}}})= n^{\prime }/n$ so that Eq. (A.13) implies ${{\mathcal {R}}}= {{\mathcal {R}}}_{E}$. We therefore have, as anticipated, that the tensor modes of the geometry discussed in the bulk of the paper and the curvature perturbations on comoving orthogonal hypersurfaces are both frame-invariant and gauge-invariant.