Epicyclic oscillations in spinning particle motion around Kerr black hole applied in models fitting the quasi-periodic oscillations observed in microquasars and AGNs

Abstract

The study of the quasi-periodic oscillations (QPOs) of X-ray flux observed in the stellar-mass black hole (BH) binaries or quasars can provide a powerful tool for testing the phenomena occurring in strong gravity regime. We thus fit the data of QPOs observed in the well known microquasars as well as active galactic nuclei (AGNs) in the framework of the model of geodesic oscillations of Keplerian disks modified for the epicyclic oscillations of spinning test particles orbiting Kerr BHs. We show that the modified geodesic models of QPOs can explain the observational fixed data from the microquasars and AGNs but not for all sources. We perform a successful fitting of the high frequency QPOs models of epicyclic resonance and its variants, relativistic precession and its variants, tidal disruption, as well as warped disc models, and discuss the corresponding constraints of parameters of the model, which are the spin of the test particle, mass and rotation of the BH.

1 Introduction

The motion of a spinning test-body in a fixed gravitational background is a long-standing problem in general relativity [25]. The rotation of a system plays a very important role in astrophysics. The spin or angular momentum can completely alter the evolution of the system. In a dynamical system, the spin or rotation is quite important as it may cause the chaotic behavior. It is known that the spin-orbit interaction produces the chaos in Newtonian gravity. It might be true in some relativistic system such as the evolution of a binary system. The motion of coalescing binary systems of neutron stars and BHs is quite interesting to explore because they are promising sources of gravitational waves.

The Quasi-periodic oscillations in X-ray flux light curves have long been observed in stellar-mass BH binaries and considered as one of the most efficient tests of strong gravity models. These variations appear very close to the BH, and present the frequencies that scale inversely with the mass of the BH. The current technical possibilities to measure the frequencies of QPOs with high precision allow us to get useful knowledge about the central object and its background. According to the observed frequencies of QPOs, which cover the range from few mHz up to 0.5 kHz, different types of QPOs were distinguished. Mainly, these are the high frequency (HF) and low frequency (LF) QPOs with frequencies up to 500 Hz and up to 30 Hz, respectively. The oscillations of HF QPOs in BH microquasars are usually stable and detected with the twin peaks which have frequency ratio close to 3:2 [26]. However, this phenomenon is not universal, the HF QPOs have been observed in only 11 out of 7000 observations of 22 stellar mass BHs [2]. The oscillations usually occur only in specific states of hardness and luminosity, moreover, in X-ray binaries, HF QPOs occur in “anomalous” high-soft state or steep power law state, both corresponding to a luminous state with a soft X-ray spectrum.

Microquasars are binary systems composed of a BH and a companion (donor) star; matter floating from the companion star onto the BH forms an accretion disk and relativistic jets – bipolar outflow of matter along the BH – accretion disk rotation axis. Due to friction, the matter of the accretion disk becomes hot and emits electromagnetic radiation, a phenomenon observed in X-rays and in the vicinity of BH horizon.

Applying the methods of spectroscopy (frequency distribution of photons) and timing (photon number time dependence) for particular microquasars, one can extract useful information regarding the range of parameters of the system [26]. In this connection, the binary systems containing BHs, being compared to neutron star systems, seem to be promising due to the reason that any astrophysical BH is thought to be a Kerr BH (corresponding to the unique solution of general relativity in 4D for uncharged BHs which does not violate the no hair theorem and the weak cosmic censorship conjecture) that is determined by only two parameters: the BH mass M and the BH spin parameter $|a/M|\le ~1$.

After the first detection of QPOs, there were various attempts to fit the observed QPOs, and different models have been proposed, such as the disko-seismic models, hot-spot models, warped disk model and many versions of resonance models. The most extended are thus the so called geodesic oscillatory models where the observed frequencies are related to the frequencies of the geodesic orbital and epicyclic motion – for review see [36]. It is particularly interesting that the characteristic frequencies of HF QPOs are close to the values of the frequencies of test particle, geodesic epicyclic oscillations in the regions near the innermost stable circular orbit (ISCO) which makes it reasonable to construct the model involving the frequencies of oscillations associated with the orbital motion around Kerr BHs [36]. However, until now, the exact physical mechanism of the generation of HF QPOs is not known, since none of the models can fit the observational data from different sources [3]. Even more serious situation has been exposed in the case of HF QPOs related to accretion disks orbiting supermassive BHs in active galactic nuclei [19, 31]. One possible way to overcome this issue is related to the electromagnetic interactions of slightly charged matter orbiting a magnetized BH [15, 16, 38]. Here, we concentrate on different possibilities related to the internal rotation of accreating matter.

In the present paper, we consider the orbital and epicyclic motion of neutral spinning test particles orbiting a Kerr BH. We look especially for the existence and properties of QPOs as well as harmonic oscillations of neutral spinning test particles in the background of Kerr BH. The quasi-harmonic oscillations around a stable equilibrium location and the frequencies of these oscillations are then compared with the frequencies of the HF and LF QPOs observed in microquasars GRS 1915+105, GRO 1655-40, XTE 1550-564, and XTE J1650-500 [22, 40] as well as AGNs TON S 180, ESO 113-G010, 1H0419-577, RXJ 0437.4-4711, 1H0707-495, RE J1034+396, Mrk 766, ASASSN-14li, MCG-06-30-15, XMMU J134736.6+173403, Sw J164449.3+573451, MS 2254.9-3712 [31].

Throughout the present paper, we use the spacelike signature $(-,+,+,+)$. Greek indices are taken to run from 0 to 3. However, for expressions having astrophysical relevance we use the physical constants explicitly.

2 Spinning particle dynamics

The motion of a spinning test particle with mass $\mu$, and spin S can be characterized by the Mathisson–Papapetrou (MP) equations and their formulation reads [6, 7, 25],

$$\begin{aligned} \frac{dx^\alpha }{d\tau }= & {} v^\alpha , \end{aligned}$$

(1)

$$\begin{aligned} \frac{D p^\alpha }{D\tau }= & {} -\frac{1}{2} R^{\alpha }_{\mu \nu \rho } S^{\nu \rho }v^\mu , \end{aligned}$$

(2)

$$\begin{aligned} \frac{D S^{\alpha \beta }}{D\tau }= & {} p^\alpha v^\beta - v^\beta p^\alpha , \end{aligned}$$

(3)

where $\tau$ is the proper time, $D/D\tau$ is the covariant derivative along the particle trajectory, $R^{\alpha }_{\mu \nu \rho }$ defines the Riemann curvature tensor, $S^{\alpha \beta }$ is the antisymmetric spin tensor, $v^\alpha$ (tangent to the particle’s worldline), and $p^\alpha$ represents the four-velocity and four-momentum of a test particle, respectively.

The right-hand side of Eq. (2) indicates the spin-orbit coupling through a strong gravitational field. The spinning particle does not follow the geodesic path. In this situation, the four-momentum deviates from the geodesic trajectory (non-spinning case) because of the spin-curvature force which produces due to the coupling of spin tensor with the Riemann tensor. In the case of vanishing spin ($S^{\alpha \beta }=0$) or flat spacetime ($R^{\alpha }_{\mu \nu \rho }=0$), we recover the geodesic equation $D p^\alpha / D\tau = 0$.

The MP equations are the first order non-linear ordinary differential equations but not a closed set, i.e., in order to evolve the system, there are less equations than necessary. Thus one needs further conditions to specify a reference point about which the spin and momentum of the particle can be calculated. This reference point can be taken as a centre of mass of the body. Different spin supplementary conditions (SSCs) have been proposed to close the set of MP equations [20, 28]. Since the SSC fixes the center of the mass, and different SSCs define different centers, for each SSC we have a different world line, hence, each SSC specifies a different evolution of the MP equations. Thus the equations of motion of a spinning particle are not unique. In order to evolve the MP equations, we use the Tulczyjew–Dixon (TD) SSC defined by [6, 7]

$$\begin{aligned} p_{\sigma } S^{\sigma \rho } =0. \end{aligned}$$

(4)

Using the above condition, one can write the explicit relation between $v^\mu$ and $p^\mu$ as [8]

$$\begin{aligned} v^\mu = N \left( p^{\mu } + \frac{2 S^{\mu \nu } p^{\lambda } R_{\nu \lambda \rho \sigma } S^{\rho \sigma }}{4 \mu ^{2} + S^{\alpha \beta } R_{\alpha \beta \gamma \delta } S^{\gamma \delta } }\right) , \end{aligned}$$

(5)

where the normalization constant N can be fixed using the constraint $v_{\alpha }v^{\alpha }=-1$. The tensor and vector formulations of the spin for TD SSC are related by

$$\begin{aligned} S^{\alpha \beta }= -\eta ^{\alpha \beta \gamma \delta } S_{\gamma } u_{\delta }, \end{aligned}$$

(6)

and

$$\begin{aligned} S_\alpha = -\frac{1}{2}\eta _{\alpha \beta \mu \nu } u^{\beta } S^{\mu \nu }, \end{aligned}$$

(7)

where $\eta _{\alpha \beta \mu \nu } = \sqrt{-g} ~ \epsilon _{\alpha \beta \mu \nu }$ is the Levi-Civita tensor, $\epsilon _{\alpha \beta \mu \nu }$ denotes the Levi-Civita symbol, $u^{\alpha }=p^{\alpha }/\mu$ ($=p^{\alpha }$ in normalized units) represents a unit vector parallel to the momentum. One can prove that the mass $\mu$ and spin magnitude S of the particle defined by

$$\begin{aligned} \mu= & {} \sqrt{- p^\alpha p_{\alpha }}, \end{aligned}$$

(8)

$$\begin{aligned} S^2= & {} S^\alpha S_\alpha = \frac{1}{2} S^{\alpha \beta } S_{\alpha \beta }, \end{aligned}$$

(9)

are the constant of motion independent from the symmetry of the background spacetime. However, the constant of motion dependent on the symmetry of the background spacetime can be constructed using the Killing vector $\xi$ as [43]

$$\begin{aligned} C({\xi }) = p^{\alpha } \xi _{\alpha } -\frac{1}{2} S^{\alpha \beta } \xi _{\alpha ; \beta }. \end{aligned}$$

(10)

The numerical study of MP equations entails a bunch of interesting numerical challenges. The efficient integration of equations of motion over a long time interval needs the structure preserving algorithms [9], i.e., symplectic schemes, which have been successfully applied for simulations in different fields of general relativity. Furthermore, the MP equations have no Hamiltonian structure, therefore one would expect usual symplectic integration schemes to lose their theoretical advantage over ordinary, not so efficient ones.

2.1 Astrophysical relevance of test particle spin

The system we are considering in this paper is a compact spinning body of mass $\mu$ orbiting a large body of mass M, which is assumed to be a solarmass or supermassive Kerr BH, satisfying the condition $\mu \ll M$. The spin parameter is measured in $\mu M$, hence $S/(\mu M)$ is a dimensionless quantity. As for the spin of a particle with mass $\mu$, we usually expect the condition $S \le O(\mu ^{2})$, therefore for the present case, we have

$$\begin{aligned} \tilde{S} = \frac{S}{\mu M} = \frac{S}{\mu ^2} \frac{\mu }{M} \le O \left( \frac{\mu }{M} \right) \ll 1. \end{aligned}$$

(11)

Thus the physically realistic values of the spin parameter must satisfy $\tilde{S} \ll 1$ for the compact objects (neutron stars, BHs, and white dwarfs). Most models of neutron stars have the spin bound $\tilde{S} \le 0.6 ~ \mu /M$. The realistic values of spin parameter $\tilde{S}$ for LISA sources fall in the range $10^{-4}{-}10^{-7}$. For a central BH having mass $M = 10^{6} M_{\odot }$, the spin parameter bound is $S \le 9 \times 10^{-6}$ (corresponding to a white dwarf with $\mu = 0.5 M_{\odot }$) [10]. Furthermore, it is worthwhile to mention that for $\tilde{S} > 1$, the Papapetrou equations are not physically realistic, since they are derived in the limit of spinning test particles, which must satisfy $\mu \ll M$. Thus one cannot draw reliable results about the behavior of astrophysical systems for $\tilde{S} > 1$.

2.2 Rotating Kerr black hole

The geometry of the Kerr BH can be described by the line element

$$\begin{aligned} \mathrm {d}s^2 = g_{tt}\mathrm {d}{t}^2 + g_{rr}\mathrm {d}{r}^2 + g_{\theta \theta }\mathrm {d}\theta ^2 + g_{\phi \phi }\mathrm {d}\phi ^2 +2g_{t\phi }\mathrm {d}{t}\mathrm {d}\phi , \nonumber \\ \end{aligned}$$

(12)

with the nonzero components of the metric tensor $g_{\mu \nu }$ taking in the standard Boyer–Lindquist coordinates the form

$$\begin{aligned} g_{tt}= & {} -\left( \frac{\varDelta -a^{2}\sin ^{2}\theta }{\varSigma }\right) , \quad g_{rr} = \frac{\varSigma }{\varDelta }, \quad g_{\theta \theta } = \varSigma ,\nonumber \\ g_{\phi \phi }= & {} \frac{\sin ^{2}\theta }{\varSigma }\left[ (r^{2}+a^{2})^{2}-\varDelta a^{2}\sin ^{2}\theta \right] , \nonumber \\ g_{t\phi }= & {} \frac{a\sin ^{2}\theta }{\varSigma }\left[ \varDelta -(r^{2}+a^{2})\right] , \end{aligned}$$

(13)

where

$$\begin{aligned} \varDelta= & {} r^2 - 2GMr + a^2, \nonumber \\ \varSigma= & {} r^2 + a^2 \cos ^2\theta . \end{aligned}$$

(14)

The outer horizon is situated at

$$\begin{aligned} r_{+} = M + \sqrt{ M^2 -a^2 }. \end{aligned}$$

(15)

For our convenience, we introduce the dimensionless quantities as

$$\begin{aligned} \tilde{a} = \frac{a}{M}, \quad \tilde{S}=\frac{S}{\mu M}, \quad \tilde{J_{z}}=\frac{J_z}{\mu M}, \quad \tilde{E}=\frac{E}{\mu }. \end{aligned}$$

(16)

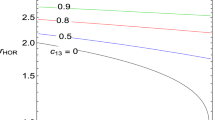
The geometrical structure of horizon of Kerr BH for different values of $\tilde{a}$ is shown in Fig. 1. We see that the horizon is only dependent on the rotation parameter $\tilde{a}$. It is observed that radius of horizon decreases when BH rotates rapidly.

Fig. 1

The position of horizon and ISCO of a spinning neutral test particle orbiting Kerr BH. The first row is plotted for different values of spin parameter $\tilde{S}$ while second row is plotted for different values of rotation parameter $\tilde{a}$

Fig. 2

Radial profiles of frequencies of small harmonic oscillations $\nu _{r}$, $\nu _{\theta }$ and $\nu _{\phi }$ of neutral spinning test particles in the background of Kerr BH having mass $M=10 M_{\odot }$ measured by a static distant observer. The dotted lines represent the ISCO position

The circular orbits are very important from the astrophysical point of view as they govern the thin (Keplerian) accretion disks, and even the toroidal fluid configurations. The position of the smallest stable circular orbit so called ISCO is illustrated in Fig. 1. The Value $|\tilde{S}|$ shows the magnitude of the spin and $\tilde{S}$ itself is its projection on the z-axis. It is more evident to consider the spin in terms of the particle spin angular momentum which is parallel to the BH spin angular momentum, when $\tilde{S} > 0$, and antiparallel, when $\tilde{S} < 0$. It means that the spin $\tilde{S} > 0$ corresponds to the spin vector parallel to the rotation of BH (co-rotation with BH), while spin $\tilde{S} < 0$ is antiparallel to it.

The co-rotating particles of ISCO shift towards the BH horizon with increase of the BH rotation $\tilde{a}$, while counter-rotating particles shift away from the BH horizon. However, when spin of particle is parallel to that of the BH, then for increasing values of spin parameter $\tilde{S}$, both counter-rotating as well as co-rotating particles of ISCO shift towards the BH horizon, while for antiparallel case, both counter and co-rotating particles shift away from the BH. It is noted that the non-spinning particle has greater (smaller) ISCO as compared to spinning case when spin of particle is parallel to that of the BH (antiparallel case).

Fig. 3

Perturbed circular orbit for spinning particles around Schwarzschild BH; numerical frequencies (from trajectory Fourier spectra) and analytical frequencies (Eqs. 18–20) are given. Numerical and analytical frequencies are identical for exactly circular orbit only, but as we can see they are quite similar even for large deviation for circular orbit. The initial conditions used for components of spin-tensor $S^{\alpha \beta }_0$ for each trajectory are given in the middle plot

2.3 Spinning particle fundamental frequencies

In order to study the oscillatory motion of neutral particle one can use the perturbation of equations of motion around the stable circular orbits. The first discussion on perturbation of circular orbits in Kerr background has been given in [4]. If a test particle is slightly displaced from the equilibrium state corresponding to a stable circular orbit situated in an equatorial plane, the particle will start to oscillate around the stable orbit realizing thus epicyclic motion governed by linear harmonic oscillations. If the frequencies of small harmonic oscillations measured by distant observer are expressed in physical units, one need to extend the corresponding dimensionless form by the factor $c^3/GM$. Thus the frequencies of neutral spinning particle orbiting Kerr BH measured by distant observer are given by

$$\begin{aligned} \nu _{j}=\frac{1}{2\pi }\frac{c^{3}}{GM} \, \varOmega _{j}[\mathrm{Hz}], \end{aligned}$$

(17)

where $j\in \{r,\theta ,\phi \}$. The dimensionless radial $(\varOmega _{r})$, latitudinal ($\varOmega _{\theta }$) and axial ($\varOmega _{\phi }$) angular frequencies measured by a distant observer for a neutral spinning test particle around a Kerr BH are given by [11]

$$\begin{aligned} \varOmega _{r}^{2}= & {} \frac{r^{3/2}(\alpha - 3 \tilde{a}^2\pm 8 \tilde{a} \sqrt{r}) + \beta \delta }{r^{7/2} \left( \tilde{a}+r^{3/2}\right) ^2} + O(\tilde{S}^2), \end{aligned}$$

(18)

$$\begin{aligned} \varOmega _{\theta }^{2}= & {} \frac{r \left( \left( 3 \tilde{a}^2\mp 4 \tilde{a} \sqrt{r}\right) +r^2\right) ^3}{\left( \tilde{a} + r^{3/2}\right) ^2 + (X + Y)^2 } + O(\tilde{S}^2), \end{aligned}$$

(19)

$$\begin{aligned} \varOmega _{\phi }^{2}= & {} \frac{1}{\left( \tilde{a} + r^{\frac{3}{2}}\right) ^2}, \end{aligned}$$

(20)

$$\begin{aligned} \alpha= & {} r (r-6), \quad \beta = (r-3) \sqrt{r}\pm 2 \tilde{a}, \end{aligned}$$

(21)

$$\begin{aligned} \ \delta= & {} 6 \tilde{S} \left( \pm \sqrt{r} - \tilde{a} \right) , \quad X = r^{7/2}+9 \tilde{a} \sqrt{r} \tilde{S}, \end{aligned}$$

(22)

$$\begin{aligned} \ Y= & {} r^{3/2} \left( 3 \tilde{a}^2\mp 4 \tilde{a} \sqrt{r}\right) \mp 6 \tilde{a}^2 \tilde{S} -3 \tilde{a} r^{3/2} \tilde{S}, \end{aligned}$$

(23)

where the upper and lower signs correspond to the co-rotating and counter rotating orbits, respectively. It is worth to mention that the orbital frequency for spinning test particle $\varOmega _\phi$ has been also derived in [14, 21, 24, 39, 43] in different form from the expression we are using here [11]. A different approach to the spinning test particles, with results on epicyclic frequencies of spinning test particles around Schwarzschild BH has been discussed in [5].

The radial profiles of the frequencies $\nu _{j}$ of small harmonic oscillations of neutral particle measured by a distant static observer are shown in Fig. 2, for different values of spin $\tilde{S}$ and rotation parameter $\tilde{a}$. In the case of non-rotating BHs (Schwarzschild), radial ($\nu _{r}$) and latitudinal ($\nu _{\theta }$) frequencies coincide, but for rotating BHs (Kerr), $\nu _{r}$ and $\nu _{\theta }$ can be observed with different profiles. The profiles of frequencies lowering down or up depending on the direction of the spin S. The presence of spin $\tilde{S}$ contributes to lowering down the peaks of all the frequencies $\nu _{r}$, $\nu _{\theta }$ and $\nu _{\phi }$ when particle has antiparallel spin to that of the BH, while the peaks rises up when spin of the particle is parallel to that of the BH. It is also noted that radial profiles of frequencies shift towards the BH with the increase of the rotation parameter $\tilde{a}$ of the BH. In the case of non-spinning particle, the peaks of the radial profiles of frequencies are lower (high) as compared to the case of the spinning particle when spin rotation is parallel to that of BH (antiparallel to that of BH).

The newly introduced particle spin parameter $\tilde{S}$ allow the greatest diversity in radial profiles of fundamental frequencies as shown in Fig. 2. The spin effect on particle frequencies is very relevant in the region close ($\nu _r=0$) or below the ISCO ($r<r_\mathrm{ISCO}$) position as well as for high spin values $\tilde{S}, \tilde{a} \rightarrow ~1$. For $r<r_\mathrm{ISCO}$, where the oscillations are unstable against the radial perturbations, one can assume the behavior fundamentally different from the non-spinning case ($\tilde{S}$ = 0) especially when nonlinear terms in spin parameter $\tilde{S}$ will be included. In this study we are interested in stable particle oscillations above ISCO, where the fundamental frequencies are similar to non-spinning case but slightly shifted.

The behavior of the particle fundamental frequencies lowering down or increasing up depends on the direction of the BH rotation $\tilde{a}$ and test particle spin $\tilde{S}$. Both parameters $\tilde{a}$ and $\tilde{S}$ contribute to increase the fundamental frequencies, however, higher frequencies can be observed when the spin is aligned to the z-axis ($\tilde{S} > 0$) while lower frequencies in the opposite case ($\tilde{S} <$). It is also noticed that co-rotating particles ($\tilde{a} > 0$) have higher frequencies as compared to contra-rotating particles ($\tilde{a}<0$).

2.4 Numerical analysis

We numerically integrate the equations of motion of a neutral spinning test body in the background of rotating Kerr BH using the Gauss Runge Kutta method of order four and investigate the fundamental frequencies numerically with the help of the Fourier transformation. We plotted perturbation of circular orbit and calculate the corresponding fundamental frequencies, see Fig. 3. In order to find out appropriate initial conditions, we use spin-1 form instead of spin tensor. We can not choose the initial conditions randomly to evolve the system, instead, our initial data should satisfy the following constraint equations

$$\begin{aligned} \tilde{E}= & {} -p_t - \frac{1}{2} g_{t\alpha , \beta } \eta ^{\alpha \beta \rho \delta } S_{\rho } p_{\delta }, \end{aligned}$$

(24)

$$\begin{aligned} \tilde{J_z}= & {} p_\phi + \frac{1}{2} g_{\phi \alpha , \beta } \eta ^{\alpha \beta \rho \delta } S_{\rho } p_{\delta }, \end{aligned}$$

(25)

$$\begin{aligned} 0= & {} g^{\alpha \beta } S_\alpha p_\beta . \end{aligned}$$

(26)

$$\begin{aligned} \mu ^2= & {} -g^{\alpha \beta } p_\alpha p_{\beta }, \end{aligned}$$

(27)

$$\begin{aligned} \tilde{S}^2= & {} g^{\alpha \beta } S_\alpha S_\beta . \end{aligned}$$

(28)

Initially we consider the motion of a spinning test particle on an equatorial plane, and assume that the spin-vector of the particle is aligned with the orbital angular momentum, i.e., the direction of spin is parallel to the rotational axis. Thus we have

$$\begin{aligned} \theta = \frac{\pi }{2}, \quad p^{\theta } = 0, \quad S^{\alpha } = S^{\theta }\delta ^{\alpha }_{\theta }. \end{aligned}$$

(29)

Under these assumptions, using the Eq. (28), the spin-vector can be expressed in terms of spin magnitude $\tilde{S}$ as

$$\begin{aligned} S_{\theta } = -\sqrt{g_{\theta \theta }} ~ \tilde{S}, \end{aligned}$$

(30)

with $\tilde{S} {>} 0 ~ (\tilde{S} {<} 0)$ corresponding to a spin-vector (anti-) aligned with the orbital angular momentum, which by convention is always pointing along the positive z-direction.

For the existence of circular orbits, we set $p^{r} = 0$, the energy $\tilde{E}$ and angular momentum $\tilde{J_{z}}$ can be written as [11]

$$\begin{aligned} \tilde{E}= & {} \frac{\sqrt{\varDelta }}{r} p^{t} + \frac{1}{r} \left( \tilde{a} + \tilde{S} \right) p^{\phi }, \end{aligned}$$

(31)

$$\begin{aligned} \tilde{J_{z}}= & {} \frac{\sqrt{\varDelta }}{r} \left( \tilde{a} + \tilde{S} \right) p^{t} + \frac{1}{r} \left( \tilde{a}^{2} + r^{2} + \tilde{a} \tilde{S} \left( 1 + \frac{1}{r} \right) \right) p^{\phi }.\nonumber \\ \end{aligned}$$

(32)

In the present situation, we have only two non-zero components of spin-tensor given by

$$\begin{aligned} S^{tr} = - S^{\theta }p_{\phi } = \frac{p_{\phi }}{r} \tilde{S}, \quad S^{r\phi } = -S^{\theta } p_{t} = \frac{p_{t}}{r} \tilde{S}. \end{aligned}$$

(33)

The spinning particle fundamental frequencies calculated as perturbation of circular orbit can also be used for oscillations with relatively large amplitudes, see Fig. 3. It is shown that the numerically calculated frequencies using Eqs. (1)–(3) are approximately the same as calculated analytically with Eqs. (18)–(20).

Fig. 4

The position of Quasars, and AGNs depending on the product of mass and frequencies as well as the spin parameter a/M. The shaded regions represent the objects with mass estimates, often with large errors, but no spin estimates in the literature. The colored blocks specify those objects for which the spin is estimated, while the black regions indicate those objects for which only lower limit of spin is known

Fig. 5

Radial profiles of lower $\nu _{\mathrm{L}}(r)$ and upper $\nu _{\mathrm{U}}(r)$ frequencies for various HF QPOs models, see Sect. 3.1. We compare the frequencies for neutral non-spinning particles ($\tilde{S}=0$, gray curves) with the neutral spinning particles ($\tilde{S} = -1$, black curves) orbiting Kerr BH. The position of $\nu _{\mathrm{U}}{:}\nu _{\mathrm{L}}=3{:}2$ resonance radii $r_{3:2}$ is also plotted. Black hole spin is taken to be $\tilde{a}=0.7$ in all cases

Table 1 Observational data for QPOs around stellarmass and supermassive BHs [31]. In objects where multiple HF QPOs are reported in small integer ratios, only the lowest frequency is given. Superscripts on the spin ranges indicate the measurement methods: Fe K$\alpha$ reflection spectroscopy (r) or continuum fitting (c). Restrictions on mass and spin of the BHs located in them, based on measurements independent of the HF QPO measurements given by the optical measurement for mass estimates and by the spectral continuum fitting for spin estimates [26, 29]

3 Quasi-periodic oscillations models

Spinning particle oscillations around circular orbits, studied in the previous section, suggest interesting astrophysical application, related to HF QPOs observed in selected AGNs and microquasars. In the following subsection, we discuss the general constraint methods of BH parameters from QPOs on the predictions of the rotation and mass parameters of BHs. In the later subsections we describe the general technique useful for the QPO fittings and consider different QPO models, namely: epicyclic resonance (ER) model and its variants (ER1, ER2, ER3, ER4, ER5), relativistic precession (RP) model and its variants (RP1, RP2), tidal disruption (TD) model and warped disc (WD) model.

The twin peaks of the HF QPOs with upper $f_{\mathrm {U}}$ and lower $f_{\mathrm {L}}$ frequencies are sometimes observed in the Fourier power spectra. In the microquasars and AGNs, the twin HF QPOs appear at the fixed frequencies that usually have nearly exact 3:2 ratio [22, 31]. The observed high frequencies are close to the orbital frequency of the marginally stable circular orbit representing the inner edge of the accretion disks orbiting BHs; therefore, the strong gravity effects are believed to be relevant for the explanation of HF QPOs [40]. The models of twin HF QPOs involving the orbital motion of matter around BH can be generally separated into four classes: the hot spot models (the relativistic precession model and its variations [32, 36], the tidal precession model [18]), resonance models [37, 40] and disk oscillation (disko-seismic) models [23, 27]. These models were applied to match the twin HF QPOs and the LF QPO for the microquasar GRO J1655-40 in [35]. Of course, the models can be applied also for intermediate massive BHs [34]. Unfortunately, none of the models recently discussed in literature, based on the frequencies of the harmonic geodesic epicyclic motion, is able to explain the HF QPOs in AGNs and all four microquasars simultaneously, assuming that their central attractor is a BH [31, 41]. One of the most promising ways of explaining these QPO phenomena in AGNs and microquasars could be charged particle oscillations around magnetized BHs [15,16,17, 42].

3.1 Tested HF QPOs models

The original resonance models invoked nonlinear coupling between the radial and orbital epicyclic frequency, or between the radial and vertical epicyclic frequencies in the accretion disk. In the latter case, a coupling was assumed when the frequencies were in 3:2 ratio, in agreement with the peaks seen in a handful of X-ray power spectra known at that time. To understand this coupling, Horák [12] analyzed weak nonlinear interactions between the epicyclic modes in slender tori and found the strongest resonance between the axisymmetric modes when their frequencies were in a 3:2 ratio.

There are two AGN in which LF QPOs candidate have been claimed: 2XMM J123+1106, and KIC 9650712. The LF QPO identification was based on mass scaling of frequency assuming a linear relationship between the BH mass and LF QPO periods, yielding consistent masses with other independent estimates, as well as low coherence and high fractional variability consistent with XRB LF QPOs. Since LF QPOs are not likely to be caused by the same mechanism as HF QPOs, thus, we do not include them in this analysis.

The identification of these oscillations as HF rather than LF QPOs is achieved by several factors. Some HF QPOs have been detected in sources where there is no mass or spin determination. The first AGN QPO detection in RE J1034+396 has a high coherence and a measured BH mass consistent with the known mass-frequency scaling relation for HF QPOs in XRBs. As in several of the other cases, assuming the detected QPO frequency was an LF QPO results in mass upper limits that are inconsistent with the BH mass measurements from independent sources, and are often unfeasible low for AGN $(\sim 10^{5} M_{\odot })$.

The hot spot models assume radiating spots in thin accretion discs following nearly circular geodesic trajectories. In the standard RP model [33], the upper of the twin frequencies is identified with the orbital (azimuthal) frequency, $\nu _{\mathrm{U}}=\nu _\mathrm{\mathrm {\phi }}$, while the lower one is identified with the periastron precession frequency, $\nu _{\mathrm{L}}=\nu _\mathrm{\mathrm {\phi }} - \nu _\mathrm {r}$. The radial profile of the frequencies $\nu _U$ and $\nu _L$ of the RP model is presented in Fig. 5. The epicyclic resonance models [1, 40] consider a resonance of axisymmetric oscillation modes of accretion discs. Frequencies of the disc oscillations are related to the orbital and epicyclic frequencies of the circular geodesic motion. The radial profile of the frequencies $\nu _U$ and $\nu _L$ of the ER model is presented in Fig. 5. The tidal disruption TD model, where $\nu _{\mathrm{U}}=\nu _\mathrm{\mathrm {\phi }} + \nu _\mathrm {r}$ and $\nu _{\mathrm{L}}=\nu _\mathrm{\mathrm {\phi }}$, could resemble to some degree the hot spot models as numerical simulations of disruption of inhomogeneities (e.g. asteroids for microquasars or stars for quasars) by the BH tidal forces demonstrate existence of an orbiting radiating core in the created ring-like structure [18]. The warped disc WD oscillation model of twin HF QPOs assumes non-axisymmetric oscillatory modes of a thin disc [13].

3.2 Resonant radii and the fitting technique

The HF QPOs come in pair of two peaks with upper $f_{\mathrm {U}}$ and lower $f_{\mathrm {L}}$ frequencies in the timing spectra. The frequency ratios $f_{\mathrm {U}}{:}f_{\mathrm {L}}$ are very close to the fraction 3:2 indicating the existence of the resonances between two modes of oscillations. In case of geodesic QPO models, the observed frequencies are associated with linear combinations of the particle fundamental frequencies $\nu _{r}, \nu _{\theta }$ and $\nu _{\phi }$. In the case of spinning neutral particle orbiting Kerr BH, the upper and lower frequencies of HF QPOs are the functions of spin parameter $\tilde{S}$, rotation $\tilde{a}$, BH mass M, and the resonance position r,

$$\begin{aligned} \nu _{\mathrm {U}} = \nu _{\mathrm {U}}(r,M,\tilde{a},\tilde{S}), \quad \nu _{\mathrm {L}} = \nu _{\mathrm {L}}(r,M,\tilde{a},\tilde{S}). \end{aligned}$$

(34)

It is worth to note that the frequencies $\nu _{\mathrm {U}}$ and $\nu _{\mathrm {L}}$ are inversely proportional to the mass M of a BH, while the dependence of frequencies on the BH spin $\tilde{a}$ and orbiting particle spin $\tilde{S}$ is more complicated and hidden inside $\varOmega _{r},\varOmega _{\theta },\varOmega _{\phi }$ functions, as given by Eq. (17). In order to fit the frequencies observed in HF QPOs with the BH parameters, one needs first to calculate the so called resonant radii $r_{3:2}$

$$\begin{aligned} \nu _{\mathrm {U}}(r_{3:2}){:}\nu _{\mathrm {L}}(r_{3:2})=3{:}2 . \end{aligned}$$

(35)

Resonant radii $r_{3:2}$ in general case are given as the numerical solution of higher order polynomial in r, for given values of spin $\tilde{a}$. Since the Eq. (35) is independent of the BH mass explicitly, the resonant radius solution also has no explicit dependence on the BH mass and techniques introduced in [36] can be used.

The position of resonant radii $r_{3:2}$ for various HF QPOs models, i.e., RP, RP1, ER0, ER1, ER2, ER3, ER4, ER5, TD, and WD, has been depicted in Fig. 5, and the comparison of spinning particle frequencies with the non-spinning particle is also shown. The resonant radii of spinning particles with spin parameter $\tilde{S} = -1$ are located at larger distance as compared to the spinless particle ($\tilde{S} = 0$). It is quite interesting to note that ER0 model has the largest, while ER4 model has the smallest resonant radius among all the models.

Fig. 6

Fitting of quasars and AGNs with different spinning particle HF QPOs models. On the horizontal axis the BH spin a/M is given, while on the vertical axis we give BH mass M multiplied by observed upper HF QPOs frequency $\mu _{\mathrm{U}}$. Boxes represent the observed mass-frequency $M \cdot f$ and spin $\tilde{a}$ values for various microquasar and AGNs (microquasars have dashed boundary), see Table 1, and Fig. 4. The curves represent the test particle frequencies at $r_{3:2}$ resonant radii $f_{\mathrm{U}} = \nu _{r}(r_{3:2},\tilde{a},\tilde{S})$ as function of BH spin $\tilde{a}$ for different values of spin parameter $\tilde{S}$. The solid curves are plotted for co-rotating spinning particles while dot-dashed curves for contra-rotating particles and the thick curves (solid and dashed) show the non-spinning fit ($\tilde{S}=0$). The numbers on the curves represent the value of spin parameter $\tilde{S}$

Substituting the resonance radius into the Eq. (34), we get the frequency $\nu _{\mathrm {U}}$ in terms of the BH mass, rotation $\tilde{a}$ and particle spin $\tilde{S}$. Now we can compare calculated frequency $\nu _{\mathrm {U}}$ with observed HF QPOs frequency $f_{\mathrm {U}}$, see Table 1. Calculated upper frequency at resonant radii $r_{3:2}$ as function of BH spin $\nu _{\mathrm {U}}(\tilde{a})$ has been used to fit observed BH spin and mass data in Fig. 6 for various QPO models.

We have shown the behavior for both co-rotating and contra-rotating spinning particles, and the particle spin values $(-1,-0.5,0,0.5,1)$ for the rotation parameter $\tilde{a}$ has been used. It can be seen that spinning particle QPOs models can fit the data for all four microquasars and also some of AGN sources. However, there is no spinning particle QPOs model which can fit all AGN sources.

The oscillating test particle with spin could represent whirl or spinning hot spot in plasma moving around central BH. It could also represent spinning asteroid for microquasars or rotating star, neutron star in the case of AGNs. Obviously the maximal spin $\tilde{S}=\pm 1$ used in QPOs fits Fig. 6 is upper bound for any realistic situation and the spin of any astrophysically relevant object must be lower.

4 Discussion and conclusions

In this article we have studied classical spinning test particle motion around rotating Kerr BH and applied spinning particle fundamental frequencies to observe the QPOs in microquasars as well as AGNs.

There are four possible situations of spinning test particle motion depending on the direction of the BH rotation $\tilde{a}$ and particle spin $\tilde{S}$. The co-rotating particles of ISCO shift towards the BH horizon with increase of the BH rotation $\tilde{a}$, while counter-rotating particles shift away from the BH horizon. Furthermore, the position of ISCO is situated close to the horizon when the particle spin is aligned to the z-axis as compared to the case when the spin is anti-aligned.

The radius of ISCO decreases with the increase of rotation $\tilde{a}$ as well as of spin parameter $\tilde{S}$. The non-spinning particle has greater (smaller) ISCO as compared to spinning case when spin of particle is parallel (antiparallel) to that of the BH. This result can be understood noting that, when the particle has some positive value of spin, it adds an intrinsic contribution to the total angular momentum, allowing it to get closer to the compact object. Thus, the spin-orbital coupling plays the role of an attractive force when the total angular momentum $\tilde{J_z}$ and spin of either BH or a test body are parallel and repulsive when they are antiparallel.

We have explored the particle fundamental frequencies of small harmonic oscillations around circular orbits. The behavior of frequencies lowering down or increasing up depends on the direction of the BH rotation and test particle spin. Both parameters $\tilde{a}$ and $\tilde{S}$ contribute to increase the fundamental frequencies, however, higher frequencies can be observed when the spin is perpendicular to the equatorial plane while lower frequencies in the opposite case. It is also noticed that co-rotating particles have higher frequencies in comparison with the contra-rotating particles.

For the case of non-spinning particle, the peaks of the radial profiles of frequencies are lower (higher) as compared to the spinning particle case when spin is parallel to the rotation of BH (anti-parallel). However, when the spin of the particle is directed along the z-axis, the radial profiles of spinning particle are closer to the BH horizon as compared to the non-spinning case, however, when spin is anti-aligned, we have opposite behavior. Thus, we can conclude that spin-orbit coupling has an attractive character for $\tilde{S} > 0$, and repulsive for $\tilde{S} < 0$

The newly introduced particle spin parameter $\tilde{S}$ allows larger diversity in radial profiles of fundamental frequencies. The effect of particle spin on frequencies is very relevant in a region close or below the ISCO position, as well as for high spin values. For a region below the ISCO, where the oscillations are unstable against the radial perturbations, one can assume the behavior fundamentally different from the non-spinning case especially when nonlinear terms in spin parameter $\tilde{S}$ will be included.

We numerically integrate the equations of motion of a neutral spinning test body orbiting the Kerr BH using the Gauss Runge Kutta scheme and explore the fundamental frequencies numerically with the help of the Fourier transformation. These numerically calculated spinning particle fundamental frequencies as perturbations of circular orbits can also be used for oscillations with relatively large amplitudes. We compare the numerically calculated frequencies with the analytical expressions and observe that they are quite similar even for large deviation of the circular orbit.

We have examined the radial profiles of upper $\nu _{\mathrm{U}}(r)$ and lower $\nu _{\mathrm{L}}(r)$ frequencies for various HF QPOs models (RP, RP1, ER0, ER1, ER2, ER3, ER4, ER5, TD, and WD) and explored the position $\nu _{\mathrm{U}} {:} \nu _{\mathrm{L}} = 3{:}2$ of resonant radii $r_{3:2}$. It is observed that for all models, the resonant radii for spinning particles $(\tilde{S} < 0 )$ are at larger distance as compared to the non-spinning case. We notice that the resonance radius for the ER0 model is located at the largest radial distance from BH horizon, while the ER4 model has the smallest resonance radius among all the models. The same situation can be observed for the case of parameter $\alpha$ of Kerr-MOG BH [17].

We have fitted the QPOs data observed in microquasars GRS 1915+105, GRO 1655-40, XTE 1550-564, and XTE J1650-500 as well as various AGNs TON S 180, ESO 113-G010, 1H0419-577, RXJ 0437.4-4711, 1H0707-495, RE J1034+396, Mrk 766, ASASSN-14li, MCG-06-30-15, XMMU J134736.6+173403, Sw J164449.3+573451, MS 2254.9-3712 by spinning both co-rotating and contra-rotating particle fundamental frequencies, for many different HF QPOs models, i.e., RP, RP1, ER0, ER1, ER2, ER3, ER4, ER5, TD and WD, as introduced in [18, 23, 27, 32, 40]. The co-rotating spinning particle QPOs models ER0, ER2, ER5 can fit the data for all four microquasars (GRS 1915+105, GRO 1655-40, XTE 1550-564, XTE J1650-500), while ER1, RP0, RP1, and RP2 partially fit, however, TD, WD, ER3, and ER4 models don’t fit any microquasar data. Different situation can be observed for counter-rotating particles, in this case the models ER3, ER4, RP1, TD, and WD fit all four microquasars, and ER1, RP0, and RP2 partially fit, while ER0, ER2, and ER5 don’t fit any microquasar. Thus we can conclude that spinning particle QPOs models can fit the data for all four microquasars and also some of AGN sources. Unfortunately, there is no spinning particle QPOs model which can fit all AGN sources: the sources (Sw J164449.3+573451, ASASSN-14li) with too high frequency mass scale ($f~\times ~M>100$) and the sources (TON S 180, XMMU J134736.6+173403) with too low frequency mass scale ($f~\times ~M<5$) can not be fitted. Additionally, for the vanishing spin $\tilde{S} =0$, our results reduced to the spinless particle [31].

All test particle spin effects are relevant for high spins $|\tilde{S}|\sim ~1$ only. Test particle spin for astrophysically realistic object is low $\tilde{S}\le 1$, only in the case of BH-BH mergers where large spins are relevant only can assume significant shifts in spinning particle frequencies [30].