1 Introduction

The mysteries of the Universe have always been a source of great attractions for physicists. We are living in the Universe undergoing an accelerating expansion which is considered due to the presence of a mysterious form of repulsive gravity named as dark energy. The matter which can only be observed by its gravitational effects on the visible matter rather than seeing it directly is called dark matter (DM).

Zwicky [54] deduced that there is an inconsistency between the luminous mass and the dynamical mass for the Coma cluster. He proposed that there must exist DM at the scale of clusters of galaxies. The observations of the rotation curves of spiral galaxies by Robin and Ford [33] also shows that the galaxies need missing mass in the context of Newtonian gravity. The main paradigm to explain the missing mass in the universe is the theory of DM, supposing that the unseen matter accounts for more than 20% of the Universe matter content. This hypothetical matter is made up of weakly interacting particles (i.e.,WIMPs) that may only interact with ordinary matter due to gravity. Experiments have been performed to directly detect DM particles by sensitive particle physics detectors, but no positive signal has been obtained until now [1].

An alternative approach to resolve the problem of DM is to modify the law of gravity. One of the first phenomenological efforts to modify the Newtonian gravity was Modified Newtonian Dynamics (MOND) proposed by Milgrom [22]. This model is based on a non-linear Poisson equation for the gravitational potential with a characteristic acceleration \(a_0\); Newtonian gravity is modified for particles with acceleration \(a < a_0\). The model can successfully explain the rotation curves of galaxies but it fails to be consistent with the temperature and gas density profiles of clusters of galaxies without invoking DM [5].

The extension of MOND in the so-called Tensor-vector-scalar (TeVeS) gravity developed by Bekenstein [8] is the covariant and relativistic gravitational theory which can be considered as an alternative to General Relativity (GR) without DM. It produces the MOND in the non-relativistic weak acceleration limit while its non-relativistic strong acceleration regime is Newtonian. It consists of two metric tensors (the physical metric \(\tilde{g}_{\sigma \nu }\) on which all matter fields propagate, and the Einstein metric \(g_{\sigma \nu }\) which interacts with the additional fields in the theory), a time-like vector field, and a non-dynamical auxiliary scalar field. The theory is also associated with a free function \(\mathrm {F}\), two dimensionless constants, and a length scale l. TeVeS passes the Solar system tests of GR, predicts gravitational lensing in agreement with the observations (without DM), does not exhibit superluminal propagation, and provides a specific formalism for constructing cosmological models.

Moffat [23] formulated the modified theory of gravity (MOG) also known as scalar-tensor-vector gravity (STVG) which can be considered as another alternative to GR without DM in the present Universe. This MOG is based on an action which consists of the usual Einstein–Hilbert term associated with the metric \(g_{\mu \nu }\), massive vector field \(\phi _\mu \), and three scalar fields representing running values of the gravitational constant G, the vector field mass \(\mu \), and its coupling strength \(\omega \). The vector field is related with the fifth force charge which is proportional to mass-energy. This fifth force is repulsive; for a large source mass, at large distances, gravity is stronger than that predicted by Einstein or Newton, but at short range, this stronger gravitational attraction is cancelled by the fifth force field, leaving only Newtonian gravity. This theory fit the cluster dynamics, galaxy dynamics and early universe cosmology data without detectable DM in the present universe. In contrast, the MOND is unable to fit the cluster observations (without DM) or cosmology observations.

Both TeVeS and STVG seem to be good candidates for a new gravity theory. They both propose vectorial manifestations of the gravitational field and have many differences. In contrast with the TeVeS bimetric theory, MOG has only one metric \(g_{\mu \nu }\). In the case of MOG, both gravitons and photons move along the same null geodesic paths, as in GR, and will arrive at the destination at the same time. Since this theory is based on an action principle, the field equations are generally covariant and the MOG vector field \(\phi _\mu \) is not a classical time-like vector as in TeVeS type theories [14].

Moffat [24] derived the non-rotating and rotating BHs in this gravity named as Schwarzschild-MOG and Kerr-MOG BHs, respectively. Particle dynamics, thermodynamics epicyclic frequencies an energy extraction as well as the shadow for these MOG BHs has been discussed in [25, 28, 29, 38, 39].

The optical phenomena around MOG Kerr BHs can be to some extend related to those of the Kerr–Newman BHs [34,35,36]. The test particle motion could be also related to the motion around Kerr–Newmann or magnetized BHs [6, 16, 17, 46, 47]. Of special interests are phenomena that could be directly tested due to observations of microquasars, namely those corresponding profiled lines and QPOs, observed in the X-ray spectra that could be related to oscillations in some regions of accretion disks. The profiled spectral lines or QPOs observed in the X-ray spectra are considered as one of the most efficient tests of strong gravity models.

Microquasars are binary systems composed of a BH and a companion (donor) star; matter floating from the companion star onto the BH forms an accretion disk and relativistic jets - bipolar outflow of matter along the BH - accretion disk rotation axis. Due to friction, matter of the accretion disk becomes to be hot and emits electromagnetic radiation, also in X-rays in vicinity of the BH horizon.

Applying the methods of spectroscopy (frequency distribution of photons) and timing (photon number time dependence) for particular microquasars, one can extract a useful information regarding the range of parameters of the system [31]. In this connection, the binary systems containing BHs, being compared to neutron star systems, seem to be promising due to the reason that any astrophysical BH is thought to be a Kerr BH (corresponding to the unique solution of general relativity in 4D for uncharged BHs which does not violate the no hair theorem and the weak cosmic censorship conjecture) that is determined by only two parameters: the BH mass M and the dimensionless spin \(|a| \le 1\).

However, alternative gravity theories predicts small deviations of the Kerr metric that can be tested due to observations of physical phenomena arising in strong gravity near the BH. For various ways of explaining the observed HF QPOs see [31].

One of the promising tools to probe the phenomena occurring in the field of the BH candidates is the study of the QPOs of the X-ray power density observed in microquasars. The current technical possibilities to measure the frequencies of QPOs with high precision allow us to get useful knowledge about the central object and its background. According to the observed frequencies of QPOs, which cover the range from few mHz up to 0.5 kHz, different types of QPOs were distinguished. Mainly, these are the HF and low frequency (LF) QPOs with frequencies up to 500 Hz and up to 30 Hz, respectively. The HF QPOs in BH microquasars are usually detected with the twin peaks which have frequency ratio close to 3:2. This is the case of the Galactic BH microquasars GRS 1915+105, XTE 1550-564 and GRO J1655-40 that we consider here.

After the first detection of QPOs, there were various attempts to fit the observed QPOs, and different models have been proposed, such as the disko-seismic models, hot-spot models, warped disk model and many versions of resonance models, developed in the framework of general relativity or alternative theories of gravity. The most extended are thus the so called geodesic oscillatory models where the observed frequencies are related to the frequencies of the geodesic orbital and epicyclic motion. It is particularly interesting that the characteristic frequencies of HF QPOs are close to the values of the frequencies of test particle, geodesic epicyclic oscillations in the regions near the innermost stable circular orbit (ISCO) which makes it reasonable to construct the model involving the frequencies of oscillations associated with the orbital motion around Kerr BHs [49]. However, until now, the exact physical mechanism of the generation of HF QPOs is not known, since none of the models can fit the observational data from different sources [12].

In the present paper, we consider the orbital and epicyclic motion of neutral test particles around a Kerr-MOG BH. We look especially for the existence and properties of the harmonic or quasi-harmonic oscillations of neutral particle in the background of Kerr-MOG BH. The quasi-harmonic oscillations around a stable equilibrium location and the frequencies of these oscillations are then compared with the frequencies of the HF and LF QPOs observed in the three particular microquasars GRS 1915+105, XTE 1550-564, and GRO 1655-40 [21, 51].

Throughout the present paper, we use the spacelike signature \((-,+,+,+)\). Greek indices are taken to run from 0 to 3. However, for expressions having astrophysical relevance we use the physical constants explicitly.

2 Kerr-MOG black hole

The Kerr-MOG BH is a stationary, axially symmetric and asymptotically flat solution of MOG field equations. The geometry of Kerr-MOG BH can be described by the line element [24]

$$\begin{aligned} \mathrm {d}s^2 = g_{tt}\mathrm {d}{t}^2 + g_{rr}\mathrm {d}{r}^2 + g_{\theta \theta }\mathrm {d}\theta ^2 + g_{\phi \phi }\mathrm {d}\phi ^2 +2g_{t\phi }\mathrm {d}{t}\mathrm {d}\phi , \nonumber \\ \end{aligned}$$
(1)

with the nonzero components of the metric tensor \(g_{\mu \nu }\) taking in the standard Boyer–Lindquist coordinates the form

$$\begin{aligned} g_{tt}= & {} -\left( \frac{\varDelta -a^{2}\sin ^{2}\theta }{\varSigma }\right) , \quad g_{rr} = \frac{\varSigma }{\varDelta }, \quad g_{\theta \theta } = \varSigma ,\nonumber \\ g_{\phi \phi }= & {} \frac{\sin ^{2}\theta }{\varSigma }\left[ (r^{2}+a^{2})^{2}-\varDelta a^{2}\sin ^{2}\theta \right] , \nonumber \\ g_{t\phi }= & {} \frac{a\sin ^{2}\theta }{\varSigma }\left[ \varDelta -(r^{2}+a^{2})\right] , \end{aligned}$$
(2)

where

$$\begin{aligned} \varDelta= & {} r^2 - 2GMr + a^2 + \alpha G_\mathrm{N}G M^2 , \nonumber \\ \varSigma= & {} r^2 + a^2 \cos ^2\theta . \end{aligned}$$
(3)

where \(G=G_\mathrm{N}(1+\alpha )\) is the enhanced gravitational constant. The source mass M form MOG modified Newtonian acceleration law [25, 26] must be distinguished from the so-called Arnowitt–Deser–Misner (ADM) mass \(\mathcal {M}=M(1+\alpha )\), see [40].

The dimensionless parameter \(\alpha \) determines the gravitational field strength. For \(\alpha =0\) and \(a=0\), the Kerr-MOG BH reduces to the Kerr and Schwarzschild-MOG BH, respectively. Moreover, \(\alpha =a=0\), leads to the Schwarzschild BH. It is worthy to mention that the gravitational source charge \(\mathcal {Q}\) of the MOG vector field is related with the mass M of the source by the relation

$$\begin{aligned} \mathcal {Q} = \sqrt{\alpha G_\mathrm{N}} M. \end{aligned}$$
(4)

The metric for Kerr-MOG BH is identical to the Kerr–Newman metric with the replacement of \(\alpha \) by \(q^2\), where q is the electric charge of Kerr–Newman BH. Using the value of G, the expression for \(\varDelta \) can be written as

$$\begin{aligned} \varDelta = r^2 - 2G_{N}(1+\alpha ) M r + a^2 + \alpha G_\mathrm{N}^2 (1+\alpha )M^2. \end{aligned}$$
(5)

In the following calculations we will chose gravitational constant in such a way \(G_{N}=1\). We can also express all coordinates and parameters using dimensions quantities \(r~\rightarrow ~r/M, a~\rightarrow ~a/M\), such setup is equivalent to the setting \(M=1\) in all following equations, for example the expression for \(\varDelta \) can be rewritten as

$$\begin{aligned} \varDelta = r^2 - 2(1+\alpha )r +a^2 +\alpha (1+\alpha ). \end{aligned}$$
(6)

The outer horizon is situated at

$$\begin{aligned} r_{+} = M(1+\alpha ) + \sqrt{ M^2(1+\alpha ) -a^2 }. \end{aligned}$$
(7)

The event horizon exists provided that \(M^2(1+\alpha )>a^2\)

$$\begin{aligned} \frac{\mathcal {M}^2}{(1+\alpha )} > a^2. \end{aligned}$$
(8)

It is worthwhile to note that for the positiveness of radicand of Eqs. (4) and (7), the physical bounds of parameter \(\alpha \) should be

$$\begin{aligned} 0 \le \alpha \le \frac{M^2}{a^2}-1. \end{aligned}$$
(9)

The constraint on the parameter \(\alpha \) from the Solar system observation is [20, 23]

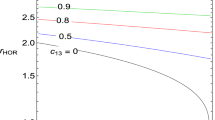
$$\begin{aligned} \alpha _\odot < 1.5 \cdot 10^5 \, \mathrm{cm} \cdot \frac{c^2}{G_N} \frac{1}{M_\odot } \sim 1. \end{aligned}$$
(10)

The geometrical structure of horizon of Kerr-MOG BH for different values of a and \(\alpha \) is shown in Fig. 1. It is observed that radius of horizon increases as parameter \(\alpha \) increases but when BH rotates rapidly, its horizon decreases. The Kerr-MOG BH has greater horizon in comparison with the Kerr BH.

Fig. 1
figure 1

Position of ISCO and horizon in Ker-MOG BH. The first row is plotted for different values of \(\alpha \) while second row is plotted for different values of rotation parameter a

Full size image

3 Circular obits around Kerr-MOG BH

The Hamiltonian for the neutral particle motion can be written as

$$\begin{aligned} H=\frac{1}{2}g^{\mu \nu } p_{\mu } p_{\nu } + \frac{1}{2}m^2, \end{aligned}$$
(11)

where \(u^{\mu }=\frac{d x^{\mu }}{d\tau }\) denotes the four-velocity, \( \tau \) is the proper time, and \( p^{\mu }=m u^{\mu } \) is the four-momentum of the particle with mass m. The Hamilton equations of motion can be written as

$$\begin{aligned} \frac{dx^{\nu }}{d\zeta }\equiv m u^{\nu }=\frac{\partial H}{\partial p_{\nu }}, \quad \frac{d p_{\nu }}{d\zeta } = -\frac{\partial H}{\partial x^{\nu }}, \end{aligned}$$
(12)

where \( \zeta =\tau /m\) is the affine parameter. Using the Hamiltonian formalism, one can find the equations of motion. Due to the symmetries of the BH geometry, components of the four-velocity remain conserved and can be expressed as

$$\begin{aligned} -\mathcal {E}= & {} \frac{p_{t}}{m}=g_{tt}u^{t}+g_{t\phi }u^{\phi }, \end{aligned}$$
(13)
$$\begin{aligned} \mathcal {L}= & {} \frac{p_{\phi }}{m}=g_{\phi \phi }u^{\phi }+g_{t\phi }u^{t}, \end{aligned}$$
(14)

where \(\mathcal {E}=E/m\) and \(\mathcal {L}=L/m\) are interpreted as the specific energy and specific angular momentum of the particle, respectively. The quasi-periodic oscillations are allowed only around the stable circular orbits. Due to the hidden symmetries of the Kerr-MOG spaceimes, the equations of motion in \(r-\theta \) plane can be separated and integrated to the form [13, 47]

$$\begin{aligned} \frac{\mathrm {d} \theta }{\mathrm {d} \lambda }= & {} 0, \end{aligned}$$
(15)
$$\begin{aligned} r^2\frac{\mathrm {d} r}{\mathrm {d} \lambda }= & {} \pm \sqrt{R(r)},\end{aligned}$$
(16)
$$\begin{aligned} r^2\frac{\mathrm {d} \phi }{\mathrm {d} \lambda }= & {} -\left( a E-L\right) + \frac{a P(r)}{\varDelta },\end{aligned}$$
(17)
$$\begin{aligned} r^2\frac{\mathrm {d} t}{\mathrm {d} \lambda }= & {} -a\left( a E-L\right) +\frac{\left( r^2+a^2\right) P(r)}{\varDelta }, \end{aligned}$$
(18)

where

$$\begin{aligned} P(r)= & {} E\left( r^2+a^2\right) -L a ,\end{aligned}$$
(19)
$$\begin{aligned} R(r)= & {} P(r)^2-\varDelta \left[ m^2 r^2 + (aE-L)^2\right] . \end{aligned}$$
(20)

The circular orbits are given by simultaneous conditions

$$\begin{aligned} R(r)=0, \quad \mathrm {d}R / \mathrm {d}r =0, \end{aligned}$$
(21)

their specific energy and specific angular momentum are given by relations [47]

$$\begin{aligned} \mathcal {E}= & {} \frac{r^2-2 \mathcal {M} r+ \chi \pm a\sqrt{\mathcal {M} r - \chi }}{r(r^2 - 3 \mathcal {M} r + 2\chi \pm 2a\sqrt{\mathcal {M} r-\chi })^{1/2}}, \end{aligned}$$
(22)
$$\begin{aligned} \mathcal {L}= & {} \pm \frac{\sqrt{\mathcal {M} r-\chi }\left( r^2+a^2\mp 2a\sqrt{\mathcal {M} r-\chi } \right) \mp a \chi }{r\left( r^2-3 \mathcal {M} r+2\chi \pm 2a\sqrt{\mathcal {M} r-\chi }\right) ^{1/2}}, \end{aligned}$$
(23)

where \(\mathcal {M}=M(1+\alpha )\) and \( \chi = M \alpha \). The innermost stable circular orbit (ISCO) has \(\mathrm {d}^2 R / \mathrm {d}r^2 = 0\) and the position of ISCO is illustrated in Fig. 1. Counter-rotating particles of ISCO shift away from the BH horizon with increasing values of BH spin a, while the co-rotating particles shift towards the BH horizon. While for increasing values of parameter \(\alpha \), both counter-rotating as well as co-rotating particles of ISCO shift away from the BH horizon. In the case of Kerr-MOG BH, the radius of ISCO is greater in comparison with the Kerr BH.

Fig. 2
figure 2

Estimation of BH rotation parameter a for different values of Kerr-MOG parameter \(\alpha \). Spectral continuum fitting for three microquasars restrict allowed regions (gray) of BH spin a and \(\alpha \) parameter by energy condition (22), dashed line separate BH and naked singularity spacetime

Full size image
Table 1 Observed twin HF QPO data for three microquasars and the restrictions on mass and spin of the BHs located in them, based on measurements independent of the HF QPO measurements given by the optical measerument for mass estimates and by the spectral continuum fitting for spin estimates [31, 37]. For Kerr-MOG BH we modified spin estimation with dependence on parameter \(\alpha \) (second part of the table). Note that in the GRS 1915+105 microquasar more HF QPOs are observed [9]. Here we concentrate attention to the pair of HF QPOs demonstrating the frequency ratio 3:2, common with those observed in other two microquasars
Full size table

The neutral particle dynamics around Kerr-MOG BH can be tested on Galactic Low Mass X-Ray Binaries (LMXB) containing neutron stars [7] or BHs [10, 30]. We have selected three microquasars, GRO 1655-40, XTE 1550-564 and GRS 1915+105, where the central object is a BH candidate and for which the masses M and spins a can be estimated by the observation of companion star dynamic and by the spectral continuum fitting [31, 37]. Crucial for spectral continuum fitting method is the location of accretion disk inner edge - how deep can disk go into BH gravitational potential, or more specifically the particle energy on the ISCO. For Kerr-MOG BH we must modify BHs spin estimations since energy at ISCO is depending on Kerr-MOG \(\alpha \) parameter, see Fig. 2. Allowed regions of BH spin a and \(\alpha \) parameter are given by energy condition (22) for every three microquasars. The restrictions on Kerr-MOG BH spin a for given specific values of \(\alpha \in \{0,0.2,0.5,1\}\) parameter are summarized in Table 1; for Kerr-MOG BH we can have spin parameter \(a>1\), see condition (9). As it can be seen from Fig. 2 there exist maximal value of Kerr-MOG parameter given by energetic restriction from spectral continuum fitting method, see Table 1.

4 Harmonic oscillations as perturbation of circular orbits

In order to study the oscillatory motion of neutral particle we use the perturbation of equations of motion around the stable circular orbits. If a test particle is slightly displaced from the equilibrium state corresponding to a stable circular orbit situated in an equatorial plane, the particle will start to oscillate around the stable orbit realizing thus epicyclic motion governed by linear harmonic oscillations. The stability of the circular orbits against vertical (latitudinal) perturbation can be inferred from [11]. Locally measured radial \((\omega _{r})\), latitudinal (\(\omega _{\theta }\)) and orbital or axial (\(\omega _{\phi }\)) frequencies of the harmonic oscillations of neutral particle are given by (for details see [47])

$$\begin{aligned} \omega _{r}^{2}= & {} \frac{8a\rho ^{\frac{1}{2}} \delta ^{\frac{3}{2}} - 4\alpha ^2\mathcal {M}^4 + \beta \rho ^2 + \gamma \rho }{2 \alpha \mathcal {M}^2 r^4 \rho + r^5 (r-3 \mathcal {M}) \rho ^{2} + 2 a r^4 \rho ^{\frac{3}{2}}\delta ^{\frac{1}{2}}}, \end{aligned}$$
(24)
$$\begin{aligned} \omega _{\theta }^{2}= & {} \frac{r^2\delta + a^2 \mathcal {M} \sigma + 2 a \mathcal {M} (\mathcal {M} \alpha - 2 r \rho )\delta ^{\frac{1}{2}} \rho ^{-\frac{1}{2}} }{r^{4}(2 \alpha \mathcal {M}^2 + r(r-3 \mathcal {M}) \rho +2 a \rho ^{\frac{1}{2}}\delta ^{\frac{1}{2}})}, \end{aligned}$$
(25)
$$\begin{aligned} \omega _{\phi }^{2}= & {} \frac{\mathcal {M} (-\alpha \mathcal {M}+\alpha r + r)}{r^{2}(2 \alpha \mathcal {M}^2 + r(r-3 \mathcal {M}) \rho +2 a \rho ^{\frac{1}{2}}\delta ^{\frac{1}{2}})}, \end{aligned}$$
(26)

where the introduced coefficients read

$$\begin{aligned} \beta= & {} \mathcal {M} r \left( r (r-6 \mathcal {M}) - 3 a^2\right) ,\nonumber \\ \gamma= & {} \alpha \mathcal {M}^2 \left( 4 a^2 + 9 \mathcal {M} r\right) , \nonumber \\ \rho= & {} (1+\alpha ), \nonumber \\ \delta= & {} \mathcal {M} (-\alpha \mathcal {M} + r \rho ), \nonumber \\ \sigma= & {} (3 \rho r-2 \alpha M). \end{aligned}$$
(27)

The locally measured angular frequencies are related with the angular frequencies measured by static distant observer (\(\varOmega \)), by the gravitational redshift transformation. If the frequencies of small harmonic oscillations measured by distant observer are expressed in physical units, one need to extend the corresponding dimensionless form by the factor \(c^3/GM\). Thus the frequencies of neutral particle measured by distant observer are given by

$$\begin{aligned} \nu _{j}=\frac{1}{2\pi }\frac{c^{3}}{GM} \, \varOmega _{j} \; (\mathrm{Hz}), \end{aligned}$$
(28)
Fig. 3
figure 3

Radial profiles of frequencies of small harmonic oscillations \(\nu _{r}\), \(\nu _{\theta }\) and \(\nu _{\phi }\) of neutral particle around Kerr-MOG black hole having mass \(M=10 M_{\odot }\) measured by static distant observer

Full size image

where \(j\in \{r,\theta ,\phi \}\). The dimensionless radial \((\varOmega _{r})\), latitudinal (\(\varOmega _{\theta }\)) and axial (\(\varOmega _{\phi }\)) angular frequencies measured by a distant observer for a neutral particle harmonic oscillations around a Kerr-MOG BH are given by (see also similar results of [19, 47])

$$\begin{aligned} \varOmega _{r}^{2}= & {} \frac{8a\rho ^{\frac{1}{2}} \delta ^{\frac{3}{2}} - 4\alpha ^2\mathcal {M}^4 + \beta \rho ^2 + \gamma \rho }{r^2 \rho (r^2 \rho ^{\frac{1}{2}} + a \delta ^{\frac{1}{2}})^{2}}, \end{aligned}$$
(29)
$$\begin{aligned} \varOmega _{\theta }^{2}= & {} \frac{r^2\delta + a^2 \mathcal {M} \sigma + 2 a \mathcal {M} (\mathcal {M} \alpha - 2 r \rho )\delta ^{\frac{1}{2}} \rho ^{-\frac{1}{2}} }{(r^3 \rho ^{\frac{1}{2}} +a r \delta ^{\frac{1}{2}})^{2}}, \end{aligned}$$
(30)
$$\begin{aligned} \varOmega _{\phi }^{2}= & {} \frac{\mathcal {M} (-\alpha \mathcal {M}+\alpha r + r)}{(r^2 \rho ^{\frac{1}{2}} + a \delta ^{\frac{1}{2}})^{2}}, \end{aligned}$$
(31)

The radial profiles of the frequencies \(\nu _{j}\) of small harmonic oscillations of neutral particle measured by a distant static observer are shown in Fig. 3, for different values of spin a and dimensionless parameter \(\alpha \). In the case of non-rotating BHs (Schwarzschild and Schwarzschild-MOG), radial (\(\nu _{r}\)) and latitudinal (\(\nu _{\theta }\)) frequencies coincide, but for rotating BHs (Kerr and Kerr-MOG), \(\nu _{r}\) and \(\nu _{\theta }\) can be observed with different profiles. The presence of \(\alpha \) contributes to lowering down the peaks of all the frequencies \(\nu _{r}\), \(\nu _{\theta }\) and \(\nu _{\phi }\). The greatest change can be observed for large value of \(\alpha \). It is also noted that radial profiles of frequencies shift towards the BH with the increase of the rotation parameter a of the BH but for increasing values of \(\alpha \), radial profiles moves away from the BH. In the case of Kerr-MOG BH, the peaks of the radial profiles of frequencies are lower as compared to the case of the Kerr BH. The profiles can be observed at small radial distance r for Kerr BH in comparison with the Kerr-MOG BH.

5 Quasi-periodic oscillations models

The neutral particle oscillations around circular orbits, studied in the previous section, suggest interesting astrophysical application, related to HF QPOs observed in selected three microquasars, GRO 1655-40, XTE 1550-564 and GRS 1915+105. In the following subsection, we discuss the general constraint methods of BH parameters from QPOs on the predictions of the rotation and mass parameters of BHs. In the later subsections we describe the general technique useful for the QPO fittings and consider different QPO models, namely: epicyclic resonance (ER) model and its variants (ER1, ER2, ER3, ER4, ER5), relativistic precession (RP) model and its variants (RP1, RP2), tidal disruption (TD) model and warped disc (WD) model.

Fig. 4
figure 4

Radial profiles of lower \(\nu _\mathrm{L}(r)\) and upper \(\nu _\mathrm{U}(r)\) frequencies for various HF QPOs models, see Sect. 5.2. The frequencies are plotted for classical Kerr BH (\(\alpha =0\)) as gray curves, while as black curves for Kerr-MOG BH with \(\alpha =1\) parameter. Black hole spin is taken to be \(a=0.7\) in all cases. The position of \(\nu _\mathrm{U}:\nu _\mathrm{L}=3:2\) resonance radii \(r_{3:2}\) is also plotted

Full size image

5.1 General properties of QPOs and constraints of black hole parameters

The twin peaks of the HF QPOs with upper \(f_{\mathrm {U}}\) and lower \(f_{\mathrm {L}}\) frequencies are sometimes observed in the Fourier power spectra. In the microquasars, i.e., LMXB systems containing a BH, the twin HF QPOs appear at the fixed frequencies that usually have nearly exact 3:2 ratio [21]. The observed high frequencies are close to the orbital frequency of the marginally stable circular orbit representing the inner edge of the accretion disks orbiting BHs; therefore, the strong gravity effects are believed to be relevant for the explanation of HF QPOs [51].

The models of twin HF QPOs involving the orbital motion of matter around BH can be generally separated into four classes: the hot spot models (the relativistic precession model and its variations [41, 49], the tidal precession model [18]), resonance models [48, 50, 51] and disk oscillation (diskoseismic) models [27, 32]. These models were applied to match the twin HF QPOs and the LF QPO for the microquasar GRO J1655-40 in [45]. Of course, the models can be applied also for intermediate massive BHs [43].

Unfortunately, none of the models recently discussed in literature, based on the frequencies of the harmonic geodesic epicyclic motion, is able to explain the HF QPOs in all three microquasars simultaneously, assuming that their central attractor is a BH [52].

One way of explaining these QPO phenomena in the microquasars is formation of the oscillatory particle motion around magnetized BHs [16, 17, 53] or around tidally charged BHs [4, 19, 47]. Here we discuss the other modification of the strong gravity due to the MOG BHs.

5.2 Tested HF QPOs models

The hot spot models assume radiating spots in thin accretion discs following nearly circular geodesic trajectories. In the standard RP model [42], the upper of the twin frequencies is identified with the orbital (azimuthal) frequency, \(\nu _\mathrm{U}=\nu _\mathrm{\mathrm {\phi }}\), while the lower one is identified with the periastron precession frequency, \(\nu _\mathrm{L}=\nu _\mathrm{\mathrm {\phi }} - \nu _\mathrm {r}\). The radial profile of the frequencies \(\nu _U\) and \(\nu _L\) of the RP model is presented in Fig. 4. From the variants of the RP model [49], we select the RP1 model introduced in [12], where \(\nu _\mathrm{U}=\nu _\mathrm{\mathrm {\theta }}\) and \(\nu _\mathrm{L}=\nu _\mathrm{\mathrm {\phi }} - \nu _\mathrm {r}\), and the “total precession model” RP2 introduced in [49], where \(\nu _\mathrm{U}=\nu _\mathrm{\mathrm {\phi }}\) and \(\nu _\mathrm{L}=\nu _\mathrm{\mathrm {\theta }} - \nu _\mathrm {r}\) (see Table 2). Both the RP1 and RP2 models predict frequencies \(\nu _{U}\) and \(\nu _{L}\) close to those of the RP model.

Table 2 Restrictions on the Kerr-MOG BH \(\alpha \) parameter given by observed HF QPOs frequencies and BH spin a for all the three microquasars GRO 1655-40, XTE 1550-564 and GRS 1915+105. Restriction on Kerr-MOG BH spin a are changing according to Kerr-MOG BH \(\alpha \) parameter. The symbol \(\not \exists \) is when the fitting with the QPO model is not possible, or maximal \(\alpha \) parameter for given source has been reach, see Table 1
Full size table

The epicyclic resonance (ER) models [2, 51] consider a resonance of axisymmetric oscillation modes of accretion discs. Frequencies of the disc oscillations are related to the orbital and epicyclic frequencies of the circular geodesic motion. The radial profile of the frequencies \(\nu _U\) and \(\nu _L\) of the ER model is presented in Fig. 4. In the ER model that has axisymmetric oscillatory modes with frequencies \(\nu _{\theta }\) and \(\nu _{r}\), the oscillating torus (or circle) is assumed to be radiating uniformly. A sufficiently large inhomogeneity on the radiating torus, which orbits with the frequency \(\nu _{\phi }\), enables the introduction of the nodal frequency related to this inhomogeneity [44, 45].

The tidal disruption TD model, where \(\nu _\mathrm{U}=\nu _\mathrm{\mathrm {\phi }} + \nu _\mathrm {r}\) and \(\nu _\mathrm{L}=\nu _\mathrm{\mathrm {\phi }}\), could resemble to some degree the hot spot models as numerical simulations of disruption of inhomogeneities (e.g., asteroids) by the BH tidal forces demonstrate existence of an orbiting radiating core in the created ring-like structure [18]. The warped disc WD oscillation model of twin HF QPOs assumes non-axisymmetric oscillatory modes of a thin disc [15], for the WD model with frequencies presented in Table 2, we have to introduce the vertical oscillatory frequency \(\nu _{\theta }\) by assumption of vertical axisymmetric oscillations of the thin disc.

Fig. 5
figure 5

Fitting of three microquasar sources with different HF QPOs models. On the horizontal axis the BH spin a/M is given, while on the vertical axis we give BH mass M divided by observed upper HF QPOs frequency \(\mu _\mathrm{U}\). Gray boxes are the values of BH mass M and spin a estimated from the observations, see Table 1. Black lines are upper test particle frequency at \(r_{3:2}\) resonresonat radii \(f_\mathrm{U} = \nu _{r}(r_{3:2},a,\alpha )\) as function of BH spin a for different values of Kerr-MOG parameter \(\alpha \)

Full size image

5.3 Resonant radii and the fitting technique

The HF QPOs come in pair of two peaks with upper \(f_{\mathrm {U}}\) and lower \(f_{\mathrm {L}}\) frequencies in the timing spectra. For the QPOs from BH microquasars given in Table 1, the frequency ratios \(f_{\mathrm {U}}:f_{\mathrm {L}}\) are very close to the fraction 3:2. Observation of this effect in different non-linear systems indicates the existence of the resonances between two modes of oscillations. In case of geodesic QPO models, the observed frequencies are associated with linear combinations of the particle fundamental frequencies \(\nu _{r}, \nu _{\theta }\) and \(\nu _{\phi }\). In the case of Kerr-MOG BH, the upper and lower frequencies of HF QPOs for a neutral particle are the functions of dimensionless parameter \(\alpha \), spin a, BH mass M, and the resonance position r,

$$\begin{aligned} \nu _{\mathrm {U}} = \nu _{\mathrm {U}}(r,M,a,\alpha ), \quad \nu _{\mathrm {L}} = \nu _{\mathrm {L}}(r,M,a,\alpha ). \end{aligned}$$
(32)

It is worth to note that the frequencies \(\nu _{\mathrm {U}}\) and \(\nu _{\mathrm {L}}\) are inversely proportional to the mass M of a BH, while the dependence of frequencies on the spin a and parameter \(\alpha \) is more complicated and hidden inside \(\varOmega _{r},\varOmega _{\theta },\varOmega _{\phi }\) functions, as given by Eq. (28). The resonant models of the twin HF QPOs assume a particular parametric or non-linear forced resonance of the oscillatory modes of the accretion disk [3]. In order to fit the frequencies observed in HF QPOs with the BH parameters, one needs first to calculate the so called resonant radii \(r_{3:2}\)

$$\begin{aligned} \nu _{\mathrm {U}}(r_{3:2}):\nu _{\mathrm {L}}(r_{3:2})=3:2 \end{aligned}$$
(33)

Resonant radii \(r_{3:2}\) in general case are given as the numerical solution of higher order polynomial in r, for given values of spin a. Since the Eq. (33) is independent of the BH mass explicitly, the resonant radius solution also has no explicit dependence on the BH mass and techniques introduced in [49] can be used. Substituting the resonance radius into the Eq. (32), we get the frequencies \(\nu _{\mathrm {U}}\) and \(\nu _{\mathrm {L}}\) in terms of the BH mass, spin and parameter \(\alpha \).

Now we can compare calculated frequencies \(\nu _{\mathrm {U}}\) and \(\nu _{\mathrm {L}}\) with observed HF QPOs frequenies \(f_{\mathrm {U}}\) and \(f_{\mathrm {L}}\), see Table 1. If one assume that observed frequencies are exactly in 3:2 ratio, \(f_{\mathrm {U}}:f_{\mathrm {L}} = 3:2 \), then the following equations

$$\begin{aligned} f_{\mathrm {U}} = \nu _{\mathrm {U}}(r,M,a,\alpha ), \quad f_{\mathrm {L}} = \nu _{\mathrm {L}}(r,M,a,\alpha ), \end{aligned}$$
(34)

are equivalent with

$$\begin{aligned} f_{\mathrm {U}} = \nu _{\mathrm {U}}(r_{3:2},M,a,\alpha ), \end{aligned}$$
(35)

where in the second case we have only one equation due to use of resonant radii \(r_{3:2}\). Solving the Eq. (34) using BH spin and mass data from Table 1 for each of the three microquasar, one can get restriction on the free Kerr-MOG parameter \(\alpha \). Observed frequency fits for various QPO models has been done in Fig. 5 for \(\alpha \) values (0, 0.5, 1, 2), and the exact estimations of \(\alpha \) parameter is given in Table 2 for every one of the three microquasar sources.

6 Discussion and conclusions

We have explored the QPOs of neutral particle orbiting Kerr-MOG BH and examined the influence of the MOG \(\alpha \) parameter. The position of ISCO and horizon for Kerr-MOG BH has been discussed. It is noted that the parameter \(\alpha \) has great influence of the characteristics of Kerr-MOG BH. The horizon radius of the BH increases as the parameter \(\alpha \) increases. The particles revolving in the ISCO shift away from the BH for increasing \(\alpha \). Particle energy at ISCO obtained by spectral continuum fitting method can restrict maximal value of parameter \(\alpha \).

We have obtained the expressions for fundamental frequencies of small harmonic oscillations. It is observed that radial profiles of frequencies shift towards the BH as the rotation of BH increases, but the maxima of the radial profiles shift away from the BH as parameter \(\alpha \) increases. It is worthy to mention that for Kerr-MOG BH, the peaks of radial profiles of frequencies are lower as compared to the Kerr BH.

We have explored the radial profiles of lower \(\nu _\mathrm{L}(r)\) and upper \(\nu _\mathrm{U}(r)\) frequencies for various HF QPOs models (RP, RP1, ER0, ER1, ER2, ER3, ER4, ER5, TD and WD) and examined the position of \(\nu _\mathrm{U}:\nu _\mathrm{L}=3:2\) resonance radii \(r_{3:2}\). It is interesting to note that for all models, in the case of Kerr-MOG BH, the resonance radii are larger as compared to the classical Kerr BH and the position of resonance radii is shifted away from the BH as parameter \(\alpha \) increases. We observe that the resonance radius for the ER0 model can be observed at the largest radial distance from BH horizon, while the ER4 model has the smallest resonance radius among all the models. Using the geodesic fundamental frequencies, we have investigated the range of parameter \(\alpha \) fitting different models for all the three microquasars GRO 1655-40, XTE 1550-564 and GRS 1915+105. We observed that ER3, ER4, TD and WD models fit all three microquasars while ER0, ER2 and ER5 models does not fit GRO 1655-40, XTE 1550-564 . Moreover, RP and RP2 models completely fit XTE 1550-564 and GRS 1915+105 microquasars but partially fit GRO 1655-40. Also, RP2 model fit GRS 1915+105 microquasar but partially fit GRO 1655-40, XTE 1550-564 microquasars.