1 Introduction

From the outset, the cancellation of quadratic divergences has been and continues to be important in assisting our understanding of fundamental particle physics. The first accurate study of the subject in the Standard Model (SM) was initially hypothesized by Decker and Pestieau [1] before being elaborated by Veltman [2], in which they demonstrated that the contributions to the quadratic divergence of the Higgs mass arising from both fermionic and bosonic sectors could be canceled, thus providing bounds on the free parameters of the model. And now that the Higgs boson is well established by Large Hadron Collider (LHC) experiments [3, 4] with more precise measurements [5], as well as the fact that no other new particles have yet materialized at the LHC, any extension beyond the SM (BSM) that is addressed must take this criterion into account to continue the search for new physics. Indeed, utilizing this cancellation as an additional constraint reveals the value of including a specific multiplet in the SM sector that matches the existing restrictions.

In this regard, the so-called Veltman condition (VC), though not unique, remains one of the options to deal with the naturalness problem. In this context, many approaches have been adopted for deriving it, either (i) using regularization by dimensional reduction [6,7,8], (ii) using conventional dimensional regularization [9], or (iii) through a cutoff regularization scheme [10]; however, the first two approaches remain the most appreciated regarding the gauge and Lorentz invariance, respectively.

Basically, the Veltman study [2], which is a conjecture about the quadratic divergences and poles in less than four dimensions, goes to the very heart of our subject, wondering whether their famous mass relation holds. Therefore, taking as an example \(d=4\), such relation will reflect the significant quantum correction that the SM Higgs boson mass receives at one loop independently from the regularization procedure. Such an approach leads to

$$\begin{aligned} \delta \,m_{H}^2 \propto 3m_H^2+3m_Z^2+6m_W^2-12m_t^2, \end{aligned}$$
(1)

and this correction should be tuned to \(\simeq 0\) for the Higgs mass to be natural.Footnote 1

The other approach looks very appealing, given that (i) there might be heavy degrees of freedom that couple to the Higgs and appear in the low-energy scale, and (ii) also considering the possibility of distinguishing quadratic from logarithmic radiative corrections, by widening the formalism of dimensional regularization. Thus the fine-tuning could be explained by investigating the gauge-independent poles that occur in the L-loop corrections to the bare Lagrangian when the space-time dimension approaches \(d_L=4-2/L\). In this way, the \(d_1\) pole of the one-loop correction to the Higgs mass has been evaluated such that \(\delta \,m_{H}^2\) is slightly modified as [11]

$$\begin{aligned} \delta \,m_{H}^2 \propto 3m_H^2+2m_W^2+m_Z^2-3\,\text {Tr}(I_n)m_t^2, \end{aligned}$$
(2)

where \(\text {Tr}(I_n)\) is the Dirac trace associated with the fermion loops. Nevertheless, the corresponding Higgs mass that we would obtain will be \(\approx \,314\) GeV, which is in stark contradiction to experimental data, so then new physics is required to scale up the SM contribution.

In fact, debates over naturalness have long been an open question for physicists [12], and many extensions BSM have already touched upon this in either the SM extended with a real singlet [13, 14], two-Higgs-doublet model [15] and beyond [16], or the SM+triplet [17, 18], thus attempting to resolve the fine-tuning problem by applying the VC criterion. And to us, we underline an extension where two real scalar singlets are added to the SM sector, TRSM. In fact, this has been examined extensively BSM, notably to provide a basis for reopening the dark matter argument [19, 20] and a wide phenomenological context [21, 22]. However, it remains to be seen whether the VC constraint implementation could be used and be compatible with theoretical requirements and experimental data.

This work is organized as follows: In Sect. 2, we briefly review the main features of the TRSM and present the full set of constraints on the parameters of the Higgs potential. Section 3 is devoted to the derivation of the VC in the TRSM, the analysis, and discussion of the results performed, with emphasis on the effects of the VC on the model parameters. Conclusions, with a summary of our results, will be drawn in Sect. 4.

2 The Two-Real-Singlet-Model (TRSM)

2.1 Scalar potential and Higgs masses

In order to look for a wide variety of phenomenological processes, the TRSM postulates extending the SM Higgs sector by two real scalar fields \(S_1\) and \(S_2\), which transform under the discrete symmetry \({\mathbb {Z}}_{2}^{0}\otimes {\mathbb {Z}}_{2}^{1}\) as

$$\begin{aligned} \begin{aligned} {\mathbb {Z}}_{2}^{(0)} :\quad (S_{1},S_{2}) \rightarrow (-S_{1},S_{2}) \\ {\mathbb {Z}}_{2}^{(1)} :\quad (S_{1},S_{2}) \rightarrow (S_{1},-S_{2}). \end{aligned} \end{aligned}$$
(3)

Neither singlet contributes to gauge interactions, which would explain its partial derivative in the most general, renormalizable, and symmetric Lagrangian density, which is expressed as

$$\begin{aligned} {\mathcal {L}} = (D_{\mu }H)^{\dagger }(D^{\mu }H) + \frac{1}{2} \sum _{i=1}^{2} \partial _{\mu }S_{i}\partial ^{\mu }S_{i} - V(H,S_1,S_2) \end{aligned}$$
(4)

where

$$\begin{aligned} V(H,S_i)&= \mu _{H}^{2}H^{\dagger }H + \lambda _H \big ( H^{\dagger }H \big )^{2} + \sum _{i=1}^{2} \left( \mu _{S_i}^{2}S_{i}^{2} + \frac{\lambda _i}{2}S_{i}^{4} \right) \nonumber \\&\quad + \lambda _{3} \big (S_{1} S_{2} \big )^{2} + H^{\dagger }H\,\big (\lambda _{4}S_{1}^{2} + \lambda _{5}S_{2}^{2} \big ) \end{aligned}$$
(5)

is the scalar potential, and \(H^T=\big (\Phi ^+, \Phi ^0\big )\) stands for the SM Higgs doublet. It is worth mentioning here that the charged (\(\Phi ^+\)) and imaginary part (\(\mathfrak {I}[\Phi ^0]\)) are the Goldstone bosons eaten by the longitudinal components of the W and Z bosons, respectively.

After electroweak symmetry breaking (EWSB), the \(\Phi ^0\), \(S_1\), and \(S_2\) neutral components become non-vanishing VEV, given by \(\upsilon _{EW}\) (=246 GeV), \(\upsilon _{1}\), and \(\upsilon _{2}\), respectively.

$$\begin{aligned} \langle H \rangle = \begin{pmatrix} 0 \\ \frac{\upsilon _{EW}}{\sqrt{2}} \end{pmatrix}, \quad \langle S_1 \rangle = \frac{\upsilon _{1}}{\sqrt{2}} \quad \mathrm{and} \quad \langle S_2 \rangle = \frac{\upsilon _{2}}{\sqrt{2}} \end{aligned}$$
(6)

and then three minimization equations are expressed as

$$\begin{aligned} \begin{aligned} -2\,\mu _{H}^{2}&= 2 \lambda _H \upsilon _{EW}^{2} + \lambda _4 \upsilon _{1}^{2} + \lambda _5 \upsilon _{2}^{2} \\ -2\,\mu _{S_1}^{2}&= \lambda _4 \upsilon _{EW}^{2} + \lambda _1 \upsilon _{1}^{2} + \lambda _3 \upsilon _{2}^{2} \\ -2\,\mu _{S_2}^{2}&= \lambda _5 \upsilon _{EW}^{2} + \lambda _3 \upsilon _{1}^{2} + \lambda _2 \upsilon _{2}^{2} \end{aligned} \end{aligned}$$
(7)

while the three non-physical fields involving the same electric charges (\(Q=0\)) mix with each other, leading to three massive physical CP-even Higgs bosons as

$$\begin{aligned} \begin{pmatrix} h_1 \\ h_2 \\ h_3 \end{pmatrix} = R\, \begin{pmatrix} \phi _H \\ \phi _1 \\ \phi _2 \end{pmatrix}. \end{aligned}$$
(8)

Here, \(\phi _H\), \(\phi _1\), and \(\phi _2\) stand for the real part of the neutral components \(\Phi ^0\), \(S_1\), and \(S_2\), respectively, and the \(R_{\alpha _i}\) is a 3 by 3 unitary matrix given by

$$\begin{aligned} R = \begin{pmatrix} c_{1} c_{2} &{} s_{1} c_{2} &{} s_{2}\\ -(c_{1} s_{2} s_{3} + s_{1} c_{3}) &{} c_{1} c_{3} - s_{1} s_{2} s_{3} &{} c_{2} s_{3} \\ - c_{1} s_{2} c_{3} + s_{1} s_{3} &{} -(c_{1} s_{3} + s_{1} s_{2} c_{3}) &{} c_{2} c_{3} \end{pmatrix}. \end{aligned}$$
(9)

The short notations \(c_i\) and \(s_i\) stand for \(\cos \alpha _i\) and \(\sin \alpha _i\), respectively, where the mixing \(\alpha _i\) \((i=1,2,3),\) all lie in the interval \(\big [-\pi /2, \pi /2\big ]\).

At the breaking scale, the dimensionless quartic couplings (\(\lambda _H\), \(\lambda _1\), \(\lambda _2\), \(\lambda _3\), \(\lambda _4\), and \(\lambda _5\)) can be expressed completely in terms of the doublet-singlets’ VEVs, as well as the Higgs masses taken on the following sequencing: \(m_{h_1}< m_{h_2} < m_{h_3}\). Indeed, by drawing on the diagonalization property

$$\begin{aligned} \text {diag}(m^2_{h_1},m^2_{h_2},m^2_{h_3}) = R M^2_{S} {R^{\text{ T }}}, \end{aligned}$$

where \(M^2_{S}\) is a \(3\times 3\) mass matrix for the CP-even Higgs sector, one gets

$$\begin{aligned} \lambda _H&= \frac{1}{2\upsilon _{EW}^2} \sum _{i=1}^{3} R_{i1}^2 m_{h_i}^2,&\lambda _1&= \frac{1}{\upsilon _{1}^2} \sum _{i=1}^{3} R_{i2}^2 m_{h_i}^2, \nonumber \\ \lambda _2&= \frac{1}{\upsilon _{2}^2} \sum _{i=1}^{3} R_{i3}^2 m_{h_i}^2,&\lambda _3&= \frac{1}{\upsilon _{1}\upsilon _{2}} \sum _{i=1}^{3} R_{i2} R_{i3} m_{h_i}^2, \nonumber \\ \lambda _4&= \frac{1}{\upsilon _{1}\upsilon _{EW}} \sum _{i=1}^{3} R_{i1} R_{i2} m_{h_i}^2,&\lambda _5&= \frac{1}{\upsilon _{2}\upsilon _{EW}} \sum _{i=1}^{3} R_{i1} R_{i3} m_{h_i}^2. \end{aligned}$$
(10)

In the first stage, and to assess the TRSM space parameter, a random scan over the Higgs masses and the singlets’ VEVs up to 1.2 TeV has been performed in our study, while requiring the light Higgs boson \(h_{1}\) to behave as the SM Higgs boson observed at 125 GeV. Later, the concept will be extended to include two benchmark points where \(h_2\) or \(h_3\) mimics the observed boson. It is in this vein that the above dimensionless couplings can be determining factors, since they are subject to theoretical and experimental scrutiny, as we shall see in the following.

2.2 Theoretical and experimental constraints

Theoretical requirements are often justified as being necessary to uncover the regularities hidden in the experimental data, by identifying new directions for high-energy physics in as simple and precise a way as possible. In this context, the TRSM Higgs potential parameters are not free, but have to obey several constraints arising from such requirements, and their range is set based on the following constraints:

Vacuum stability

It is a necessary condition for the potential to be bounded from below (BFB) when the doublet and singlet fields become large in any direction in the space. The TRSM constraints ensuring that issue are expressed [22] as

$$\begin{aligned}&\lambda _H, \lambda _{1}, \lambda _{2}> 0 \nonumber \\&a_{1} \equiv \lambda _{4} + \sqrt{\lambda _H\lambda _{1}}> 0 \nonumber \\&a_{2} \equiv \lambda _{5} + \sqrt{\lambda _H\lambda _{2}}> 0 \nonumber \\&a_{3} \equiv \lambda _{3} + \sqrt{\lambda _{1}\lambda _{2}}> 0 \nonumber \\&a_{4} \equiv \sqrt{\lambda _H\lambda _{1}\lambda _{2}} + \lambda _{4}\sqrt{\lambda _{2}} + \lambda _{5}\sqrt{\lambda _{1}} + \lambda _{3}\sqrt{\lambda _H} \nonumber \\&\qquad + 2\sqrt{a_{1}a_{2}a_{3}} > 0, \end{aligned}$$
(11)

but although this provides a highly efficient and reliable means of evaluation, BFB remains an insufficient condition for constraining the space parameter.

Unitarity

In addition, the above BFB constraints need to be supplemented by unitarity, which holds that the probability of all possible quantum interactions must add up to 1. Nevertheless, at the large \(\sqrt{s}\) limit, i.e., in the limit where any mass scale in the TRSM is below the energies of the scattering processes, only the two-body ones of the latter arising from the quartic terms of the scalar potential have been considered. The results from [22] for the TRSM are summarized as

$$\begin{aligned}&|\lambda _H |< 4\pi , \end{aligned}$$
(12)
$$\begin{aligned}&|\lambda _{3} |, |\lambda _{4} |, |\lambda _{5} |< 8\pi , \end{aligned}$$
(13)
$$\begin{aligned}&|x_{1,2,3} |< 16\,\pi \end{aligned}$$
(14)

where \(x_{1,2,3}\) are the three real roots of the cubic polynomial

$$\begin{aligned}&x^3 - 3x^{2}\,\Big [4\lambda _H + (\lambda _{1} + \lambda _{2})\Big ] + x\,\Big [36 \lambda _H \big (\lambda _{1} + \lambda _{2} \big ) \nonumber \\&\quad -4 \big (\lambda _{4}^{2} + \lambda _{5}^{2}\big ) - \lambda _{3}^{2} + 9\lambda _{1}\lambda _{2}\Big ] + \lambda _H\,\big (12\lambda _{3}^{2} - 108\lambda _{1}\lambda _{2}\big ) \nonumber \\&\quad -8\lambda _{3}\lambda _{4}\lambda _{5} + 12\,\big (\lambda _{2}\lambda _{4}^{2} + \lambda _{1}\lambda _{5}^{2}\big ) = 0. \end{aligned}$$
(15)

It may be recalled that the quartic couplings involving \(S_i^2\) and \(S_i^4\) are of particular interest, which is why the above constraints are closely correlated with the perturbativity, where the absolute values of all dimensionless quartic couplings must be \(\le 4\pi \).

Oblique parameters

It should be pointed out that, as the singlet fields do not contribute to gauge boson masses, there is no deviation of the \(\rho \) parameter prediction within the TRSM and the SM. Thus, assuming the \(U_{\mathrm{TRSM}}\approx 0\), the only radiative corrections of the electroweak parameters within this model are coming from the oblique parameters S and T, where the major contribution comes from the loops involving the new singlet-like scalars. In our study, the general definition in Ref. [23] is adopted, and in keeping with the transformation scheme given by Eq. (9), the corresponding expressions are stated as

$$\begin{aligned} S_{\mathrm{TRSM}}&= \bigg \{ \big (R_{11}^2+R_{21}^2-1\big ) \ln (m_{h_1}^2)+\big (R_{12}^2+R_{22}^2\big ) \ln (m_{h_2}^2) \nonumber \\&\quad + \big (R_{13}^2+R_{23}^2\big ) \ln (m_{h_3}^2) + \big ( c_1^2c_2^2 -1\big ) G(m_{h_1}^2,m_{Z}^2) \nonumber \\&\quad + s_1^2c_2^2 G(m_{h_2}^2,m_{Z}^2)+s_2^2 G(m_{h_3}^2,m_{Z}^2) \bigg \}\Big /(24\pi ) \end{aligned}$$
(16)
$$\begin{aligned} T_{\mathrm{TRSM}}&= 3 \bigg \{ \big (1-c_1^2c_2^2\big )\Big [F(m_Z^2,m_{h_1}^2)-F(m_W^2,m_{h_1}^2)\Big ] \nonumber \\&\quad + s_1^2c_2^2\Big [F(m_Z^2,m_{h_2}^2)-F(m_W^2,m_{h_2}^2)\Big ] \nonumber \\&\quad + s_2^2\Big [F(m_Z^2,m_{h_3}^2)-F(m_W^2,m_{h_3}^2)\Big ] \bigg \}\Big /(16\pi s_w^2m_W^2) \end{aligned}$$
(17)

where \(R_{ij}\) are the matrix entries in Eq. (9), and \(G\left( I,J \right) \) and \(F\left( I,J \right) \) are two mathematical functions given by [24]

$$\begin{aligned} G\left( I, J \right)&= -\frac{79}{3}+9\frac{I}{J}-2\frac{I^2}{J^2}\nonumber \\ {}&\quad +\Big (-10+18\frac{I}{J}-6\frac{I^2}{J^2}+\frac{I^3}{J^3} -9\frac{I+J}{I-J}\Big )\ln (J)\nonumber \\&\quad +\Big (12-4\frac{I}{J}+\frac{I^2}{J^2}\Big )\frac{f(I,I^2-4IJ)}{J} \nonumber \\ F\left( I, J \right)&= \left\{ \begin{array}{lcl} \displaystyle { \frac{I + J}{2} - \frac{I J}{I - J}\, \ln {\frac{I}{J}} } &{} \Leftarrow &{} I \ne J,\\ 0 &{} \Leftarrow &{} I = J, \end{array} \right. \end{aligned}$$
(18)

with

$$\begin{aligned} f \left( t,r\right) \equiv \left\{ \begin{array}{lcl} {\displaystyle \sqrt{r}\, \ln {\left| \frac{t - \sqrt{r}}{t + \sqrt{r}} \right| } } &{} \Leftarrow &{} r > 0, \\ 0 &{} \Leftarrow &{} r = 0, \\ {\displaystyle 2\, \sqrt{-r}\, \arctan {\frac{\sqrt{-r}}{t}} } &{} \Leftarrow &{} r < 0. \end{array} \right. \end{aligned}$$
(19)

Experimentally, the global fit yields [25]

$$\begin{aligned} T=0.07\pm 0.06,\quad S=0.02\pm 0.07 \end{aligned}$$
(20)

and the TRSM falls safely within the \(2\sigma \) allowed region of these oblique parameters.

3 Naturalness criteria and phenomenology

3.1 Modified VC

Even if the parameters introduced by the scalar potential could be determined from the requirements given above, and from its appearance in the couplings of the doublet and singlet fields, some strong constraints on those parameters related to the fine-tuning problem originating from the radiative corrections to the Higgs mass can be derived using a new argument such as the Veltman quadratic cancellation conditions. In this regard, the conventional dimensional regularization approach would be much more consistent and particularly suitable for preserving the local gauge symmetry of the underlying Lagrangian.

Fig. 1
figure 1

Feynman diagrams contributing to the tadpole residue to one-loop order. The straight (a), wiggly (b), short-dashed (c), and long-dashed lines stand for fermion, vector boson, scalar, and ghost contributions, respectively

Full size image

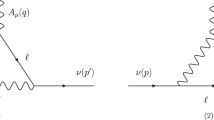
Therefore, by working at the one-loop level within the TRSM, in a complex dimensional regularization, \(d_L=4-2/L=2\), such that the overall quadratic divergences are picked out exclusively. The relevant contributions can be illustrated by the diagrams in Fig. 1, where the straight, wiggly, short-dashed, and long-dashed lines stand for fermion, vector boson, scalar, and Faddeev–Popov ghost contributions, respectively. Consequently, the corresponding one-loop residue is given by

$$\begin{aligned} \Delta _1 = \sum _{i}\,V_i\,A(m_i^2) \end{aligned}$$
(21)

where the sum runs over all the previous contributions, \(V_i\) includes all the vertices, Dirac traces, and the symmetry factors, and the \(A(m_i^2)\), which unfolds as a simple form in terms of the Passarino–Veltman function [26], is a pure UV-divergent term that can be factorized to provide reliable results.

Although we do not provide a wide calculation, for further details, we refer the reader to more advanced discussions in previous works [17, 18]. Also, we would like to clarify a very important point, that, relying on the renormalizability of spontaneously broken theories [27], where the quadratic divergences in the tadpole are equivalent to those in the scalar self-energy, such cancellation does not depend upon symmetry breaking, and so our results could be obtained in the symmetry unbroken phase. Further, it turns out that combinations between the three possible tadpoles \(T_{h_i}\) (i=1,2,3) and the \(R_{\alpha _i}\) matrix elements induce simplification, and one ends up with short expressions that have no mixing angle dependence. For the sake of brevity, we refer the reader to the calculations put forward in our previous study [17].

3.2 Phenomenological analysis

By keeping only the dominant top quark contribution and neglecting leptons, the modified VC in the framework of TRSM for the three CP-even states \(h_1\), \(h_2\), and \(h_3\) that should be canceled, or at least be kept at a manageable level, is expressed as

$$\begin{aligned} \begin{aligned} \delta m_{h_1}^2\,\sim ~&2m_{W}^2+m_{Z}^2-3\,\text {Tr}(I_n)\,m_t^2+ \Big (6\lambda _H+\lambda _4+\lambda _5\Big )\upsilon _{EW}^2, \\ \delta m_{h_2}^2\,\sim ~&\Big ( 3\lambda _1+\lambda _3+2\,\lambda _4 \Big )\upsilon _{1}^2, \\ \delta m_{h_3}^2\,\sim ~&\Big ( 3\lambda _2+\lambda _3+2\,\lambda _5 \Big )\upsilon _{2}^2 \end{aligned} \end{aligned}$$
(22)

where we choose \(\text {Tr}(I_n)=2^{n/2}\).

It might initially seem that the absence of the \(\lambda _H\) coupling in the last two equations in (22) is obvious, since such a parameter is purely a doublet quartic interaction, and, by the same token, the lack of \(\lambda _1\), \(\lambda _2\) and \(\lambda _3\) is natural in \(\delta m_{h_1}^2\), since these three couplings only concern the singlet fields. In this sense, if we consider no mixing between the SM doublet H and the singlet fields \(S_{1,2}\), which is achieved by simultaneously taking \(\lambda _4,\lambda _5 \rightarrow 0\), two remarks may be reported:

  1. (i)

    The correction \(\delta m_{h_1}^2\) matches well that of Refs. [2, 11, 28], and is expressed as

    $$\begin{aligned} 3\,h-3\,\text {Tr}(I_n)\,t+2\,c^2+1=0, \end{aligned}$$

    with \(h \equiv m_{h_1}^2/m_Z^2\), \(t \equiv m_{t}^2/m_Z^2\) and \(c^2 \equiv \cos ^2\theta _w\).

  2. (ii)

    Similarly, the quadratic divergences for \(h_2\) and \(h_3\) Higgs bosons reduce to \( (3\lambda _1+2\lambda _4)\upsilon _{1}^2\) and \((3\lambda _2+2\lambda _5)\upsilon _{2}^2\), which agree with the results in [14, 29,30,31,32].

Even so, for the restricting of the allowed TRSM parameter space, the approximate expression of \(\lambda _4+\lambda _5\) from the upper part of (22) could be used,

$$\begin{aligned} \lambda _4+\lambda _5 = (6\,m_t^2-2\,m_W^2-m_Z^2-3\,m_{h_1}^2)/\upsilon _{EW}^2 \sim 1.82, \end{aligned}$$
(23)

in order to cancel the quadratic divergences.

Hereafter, we will examine what effect the above VC will have on the parameter space of the TRSM. To do so, we assume that the deviations \(\delta m_{h_i}^2\,(i=1,2,3)\) should not exceed the Higgs mass scale, and for such purpose, we have allowed each \(\delta m_{h_i}^2/m_{h_i}^2\) to vary within a certain range \(\epsilon ^2\) in all our analysis. In addition, it is important to mention that further investigation is performed by interfacing the model with HiggsBounds-5.2.0beta [33] and HiggsSignals-2.2.0beta [34] packages, thus testing the existing exclusion limits at the 95\(\%\) confidence level from Higgs searches at LEP, LHC, and Tevatron; checking the Higgs signal rate constraints from various searches and taking into account the recent LHC 13 TeV results in the framework of the TRSM.

As outlined above, we mainly consider the case where \(h_1\) mimics the observed Higgs boson at 125 GeV, i.e., \(h_{125}=h_1\). The one-loop quadratically divergent correction to \(m_{h_1}^2\), given by the upper part in Eq. (22), sets a lower (upper) possible value for \(\lambda _4,\lambda _5\) in order to cancel the divergences. As illustrated in Fig. 2, the lowest possible value for \(\lambda _4\) is \(\approx -1.4\), which corresponds to an upper limit for \(\lambda _5\) of the order of \(\approx 3.3\), and thereafter increases almost inversely with \(\lambda _5\), ending at \(\approx 2.45\) for \(\lambda _5\approx -0.68\). Furthermore, it is noteworthy that all remaining couplings, i.e., \(\lambda \), \(\lambda _1\), and \(\lambda _2\), are not impacted by the VC constraint, except \(\lambda _3\), whose allowed range is narrowed; we found it nowhere outside the \([-0.57, 1.18]\) interval.

Fig. 2
figure 2

Correction \(\delta m_{h_1}^2/m_{h_1}^2\) in the TRSM shown as a scatter plot in the \((\lambda _4,\lambda _5)\) plan. We set \(m_{h_1}=125.09\) GeV, \(130~\text {GeV} \le m_{h_2} +2.5~\text {GeV} \le m_{h_3} \le 1.2~\text {TeV}\), and \(10~\text {GeV} \le v_1,v_2 \le 1.2~\text {TeV}\)

Full size image

Secondly, as for Higgs masses, one can observe that cancellation of the quadratic divergences appears possible over the entire \(m_{h_2}\) range, which renders it unaffected by the VC, as can be seen in Fig. 3, while for \(m_{h_3}\) it may occur only over a minimal value. This is, in fact, a remarkable feature of the effects of the VC on the scalar mass spectrum, notably the NP mass dependence on \(\lambda _4+\lambda _5\), which is stronger for \(m_{h_3}\) than for \(m_{h_2}\); if the VC is to be fulfilled, the lower bound on \(m_{h_3}\) must stretch out 500 GeV. Nevertheless, these overall resulting ranges are compatible with the LHC exclusion limits for heavy resonances decaying into a pair of Z/W gauge boson final states [35, 36].

Fig. 3
figure 3

Radiative correction \(\delta m_{h_1}^2/m_{h_1}^2\) as a function of the Higgs boson masses, \(m_{h_2,h_3}\), in the TRSM. Inputs as in Fig. 2

Full size image

As with other parameters, assuming the gluon–gluon fusion production process is dominant, we point out that realization of the VC can involve extensive scrutiny for the mixing angle \(\alpha _i\) \((i=1,2,3),\) which should afford theoretical insights for the best-fit signal strength of the \(h_1\) for ggF production. The latter is directly related to \(\alpha _1\) and \(\alpha _2\) in the TRSM, and is expressed as

$$\begin{aligned} \mu _{ggF}=\frac{\sigma _{ggF}}{\sigma _{ggF}^{SM}}=\kappa _1=\cos ^2\alpha _1\cos ^2\alpha _2 \end{aligned}$$
(24)

while its updated experimental value is

$$\begin{aligned} \mu _{ggF}= {\left\{ \begin{array}{ll} 1.04^{+0.09}_{-0.09},&{}\text {ATLAS 37}\\ \\ 1.22^{+0.14}_{-0.12}, &{} \text {CMS 38}. \end{array}\right. } \end{aligned}$$
(25)

In this regard, the upper panel in Fig. 4 shows that our theoretical predictions deviate significantly from the CMS experimental measurements, whereas for ATLAS, they are in line at \(1\sigma \). On the other hand, regarding the gluonic decay, \(h_1 \rightarrow gg\), all the amplitudes \(A_{\frac{1}{2}}\) at the lowest order for fermionic contributions are shifted by the same reduced couplings, \(\cos \alpha _1\cos \alpha _2\). This is what justifies the fact that \(\kappa _1\) would remain under unity over the entire TRSM space parameter. Also, we note here that the allowed range for mixing angles would be \(-\pi /9 \le \alpha _1,\alpha _2 \le +\pi /9\) at \(1\sigma \).

Fig. 4
figure 4

\(\mu _{ggF}\) signal strength (upper panel) and \(\delta m_{h_1}^2/m_{h_1}^2\) radiative correction (lower panel) shown as a scatter plot in the \((\alpha _1,\alpha _2)\) plan within the TRSM. Inputs as in Fig. 2

Full size image

However, the naturalness criteria could drastically influence the situation. To further clarify this point, we exhibit in the lower panel of Fig. 4 the prevalence of \(\delta m_{h_1}^2/m_{h_1}^2\) in the \([\alpha _1,\alpha _2]\) plane. At first sight, contrary to the best-fit \(\kappa \), which regains its standard value for \(\alpha _1=\alpha _2=0\), no exact cancellation of the quadratic divergences can be achieved in such alignment limit (the pure doublet compound \(h_1\) remains unstable to ultraviolet corrections), even more so when both mixing angles are simultaneously varied within a negative interval. On the other hand, the quadratic divergences become less noticeable once both \(\alpha _{1}\) and \(\alpha _{2}\) become positive, and their cancellation restricts \(\alpha _{1}\) and \(\alpha _{2}\) to lie within more reduced intervals \(0 \le \alpha _1 \le \pi /12\) and \(0 \le \alpha _2 \le \pi /13\). Ultimately, it might be worthwhile to investigate the other sub-dominant Higgs production processes, since they are all sensitive to the same combination of mixing angles. However, we leave the detailed exploration of the prospects for various production modes to future studies.

Fig. 5
figure 5

\(g_{3}/g_{3}^{SM}\) versus \(g_{4}/g_{4}^{SM}\) in the TRSM. The palette color shows the radiative correction, \(\delta m_{h_1}^2/m_{h_1}^2\). Inputs as in Fig. 2

Full size image

Furthermore, the fact that the trilinear \(g_3\) and quartic \(g_4\) Higgs couplings are the most important that NP should nail down regarding their crucial role in ascertaining any extension BSM, the TRSM has provided a useful framework for addressing this [39]. We, on our part, have investigated the impact of VC on these couplings that are expected to deviate from the SM. Figure 5 below illustrates these couplings normalized to their SM value. A quick peek just before imposing VC shows that the \(g_3\), which is positive, may not exceed \(20\%\) below its SM value, whereas \(g_4\) goes much further, reaching \(\approx 11\,g_4^{SM}\).

However, once the VC conditions are turned on, the coupling \(g_3\) decreases slightly (\(0.84 \le g_{3}/g_{3}^{SM} \le 0.98\)), yielding a significant reduction for the quartic coupling, e.g., \(2 \le g_{4}/g_{4}^{SM} \le 6.1\). Nevertheless, this expected constraint on the latter is quite weak, and it would therefore be appropriate to restrict it depending on the specific values for \(g_3\). For example, taking \(g_3 \approx 0.96 g_{3}^{SM}\) required the \(g_{4}/g_{4}^{SM} \in [2, 2.5]\), which, while it might not be a wide enough range, is compatible within the \(1\sigma \) level with recent indirect bounds on the quartic Higgs self-couplings [40, 41]. For the Higgs boson masses, the VC seems to favor \(m_{h_2}\) to lie roughly between the electroweak scale and 1 TeV, as mentioned above, while for the heavy Higgs, \(h_3\), must have a mass sufficiently high, e.g., \(0.85\,\mathrm{TeV}\le m_{h_3}\le 1.15\, \mathrm{TeV}\), to impart the absence of fine tuning in the Higgs mass parameter.

Table 1 Input parameter values for two benchmark scenarios
Full size table
Fig. 6
figure 6

The mass spectra of the \(h_{1,2}\) Higgs bosons for BP1. The color code shows \(BR(h_2 \rightarrow h_1 h_1)\) (upper panel) and the \(\sigma (pp \rightarrow h_2 \rightarrow h_1 h_1)\) (lower panel). We set \(\epsilon =7\)

Full size image
Fig. 7
figure 7

The mass spectra of the \(h_{1,3}\) Higgs bosons for BP2. The color code shows \(BR(h_3 \rightarrow h_1 h_1)\) (upper panel) and the \(\sigma (pp \rightarrow h_3 \rightarrow h_1 h_1)\) (lower panel). We set \(\epsilon =7\)

Full size image

Finally, it is worth noting that VC, although it could not be exactly as it sounds, may have a significant impact on some experimental searches where \(h_2=h_{125}\) or \(h_3=h_{125}\). To maintain this point, we study two benchmark points, BP1 and BP2, that were already addressed and referred to as BP4 and BP5 in Ref. [22], and show how the situation will change when the VC is met. The chosen parameter inputs are displayed in Table 1, and for both BPs we set \(\delta m_{h_i}^2/m_{h_i}^2 < \epsilon ^2\).

The phenomenology of BP1 is shown in Fig. 6. At first sight, it could be concluded that there is a drastic reduction in the allowed range for the \(h_1\) and \(h_2\) Higgs boson masses, such that the lower bounds are very sensitive to the VC and shrink to 47.5 and 96 GeV, respectively, compared to BP4 in Ref. [22]. Consequently, repercussions on the branching ratio \(BR(h_2 \rightarrow h_1 h_1)\) and the signal rate \(\sigma (pp \rightarrow h_2 \rightarrow h_1 h_1)\) are evident enough. Indeed, for the first one, \(h_2\) decays dominantly into the \(h_1h_1\) pair with a branching ratio of more than \(95\%\), as shown in Fig. 6(upper). Furthermore, when the VC enters into the game, the signal rates may not exceed \({\mathcal {O}}\)(3.5pb), as reflected in the lower panel of Fig. 6, given that the LEP search for \(e^+e^-\rightarrow Zh_2 \rightarrow Z({\bar{b}}b)\) [42] is not subject to review under the high-mass region of \(m_{h_2}\).

Similar analysis is seen for the BP2. Here, the VC effect is somewhat remarkable. In fact, while the \(BR(h_3 \rightarrow h_1h_1)\), illustrated in the upper side in Fig. 7, rises above \(97.5\%\) for low values of \(m_{h_3}<150\) GeV, the corresponding signal rate \(\sigma (pp \rightarrow h_3 \rightarrow h_1 h_1)\) shows a reduction from 3 pb to 2.7 pb when the conditions of the modified VC are considered.

4 Concluding remarks

In summary, we have investigated how Veltman conditions of cancellation of quadratic divergent corrections to the scalar masses could put additional constraints on the parameter space of the TRSM, an extension of the SM with two extra real singlet scalar fields, \(S_{1,2}\), giving rise to a wide phenomenology in seeking new physics. We have shown that at one loop, and depending on the mixing angles, these quadratic divergences are softened and go to zero within the allowed space parameter for the observed 125 GeV, but on the whole, the issue remains in its infancy as long as there is no allowed parameter space where the quadratic divergences are simultaneously canceled out for both the SM-like Higgs boson and the new scalar mass squares, which is an increasingly pressing issue in light of recent LHC data. The tadpole equations for the new physics, as already derived, are not yet sufficient to make a critical test for quadratic divergence cancellation, especially if the scale of new physics is too large. With a view to maintaining the corrections to the new Higgs states within acceptable limits, the scale of singlet VEVs also needed be too low and has meaningful deviations from the electroweak scale.