Charged anisotropic compact star core-envelope model with polytropic core and linear envelope

Abstract

This manuscript is related to the construction of relativistic core-envelope model for spherically symmetric charged anisotropic compact objects. The polytropic equation of state is considered for core, while it is linear in the case of envelope. We present that core, envelope and the Reissner Nordstr$\ddot{o}$m exterior regions of stars match smoothly. It has been verified that all physical parameters are well behaved in the core and envelope region for the compact stars SAX J1808.4-3658 and 4U1608-52. Various physical parameters inside star are discussed herein, non-singularity and continuity at the junction has been catered as well. Impact of charged compact object together with core-envelope model on the mass, radius and compactification factor is described by graphical representation in both core and envelop regions. The stability of the model is worked out with the help of Tolman–Oppenheimer–Volkoff equations and radial sound speed.

1 Introduction

The phenomenon of gravitational collapse depicts gravitational interaction within gravitating sources termed as compact objects. This phenomenon takes place as a consequence of unbalance in internal gravitational pull and outward drawn pressure stresses. The collapse of massive stars results in the formation of gravitating objects such as neutron stars, white dwarfs and black holes. These stellar residues are extremely dense in nature depicting strong gravitational interaction. Schwarzschild [1] described gravitational field of spherically symmetric compact objects and presented the solutions of field equations for internal and external spacetime geometry of star. Chandrasekhar and Milne [2] explained the phenomenon of gravitational collapse responsible for creation of compact stars. Oppenheimer and Volkoff [3] studied gravitational analysis of compact stars and discussed role of pressure stresses within gravitating sources.

Einstein’s general theory of relativity is based on the study of spacetime curvature. Symmetries in spacetime describe it’s geometrical properties. In general relativity (GR), spherical symmetry is mostly considered as one can discuss the characteristics and properties of gravitating objects more conveniently. Spherical symmetry may also be considered due to weak magnetic field in compact stars [4]. Moreover, it is believed that consideration of spherical symmetry is essential for many solutions of Einstein’s field equations. Hillebrandt and Steinmetz [5] discussed the stability of spherically symmetric compact objects. Das et al. [6] constructed model of spherically symmetric gravitational equations by solving partial differential equations with initial value problem. Herrera et al. [7] presented an algorithm for spherically symmetric solutions of Einstein’s field equations. Spherically symmetric relativistic compact star models were constructed in to analyze the phenomenon of gravitational collapse of stars [8, 9].

Takisa et al. [10] described that in spherically symmetric compact stars the physical parameters like density, pressure, temperature and redshift are positive throughout the region. In the study of compact object the discussion of inner fluid is of primary importance. Different types of fluid configurations can used to explore various aspects of compact stars such as perfect fluid, isotropic fluid, anisotropic fluid etc. In isotropic fluid, radial and tangential pressures of compact object are same. The property which makes anisotropic fluid different from perfect fluid is that in anisotropic fluid, radial and tangential pressures are not equal. In compact objects anisotropy in fluid pressure may also exist because of the presence of solid core and occurrence of various physical processes in star. Dynamics and structural features of gravitating systems in anisotropic environment are explored in detail in [11,12,13,14]. Maharaj and Chaisi [15] presented the construction of anisotropic models by using solutions calculated from isotropic models. The study of Ivanov [16] is based on the characteristics of anisotropy and how anisotropy is assists in study of compact star models. Lakshmi [17] presented model of Einstein’s field equation of anisotropic compact star by using line element with spherically symmetric coordinates and discussed density distribution in anisotropic fluid sphere. Sah and Prakas [18] discussed anisotropic fluid distribution in spherically symmetric compact star.

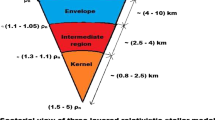
The core and envelope are two different but adjacent layers of a star. They hold different matter distributions and have different macroscopic physical features comprising of mass of inertia, a measure of density, evaluation of mass, or radius. The core envelope models for enormous relativistic stars have been studied in the past several years. Durgarpal and Gehlot [19] provided exact interior solutions with different energy densities for the core and envelope regions. Das and Narlikar [20] determined gravitational redshifts from the core-envelope boundary to an object’s surface under various conditions and their effect on the equation of state (EoS). Negi et al. [21] discussed the construction of core-envelope models for varying physical parameters, in particular distinct EoS for core and envelope region. Sharma and Mukherjee [22] demonstrated the Vaidya−Tikekar model for a star with a quark phase in its inner core, surrounded by less compact baryonic envelope. Ramesh and Thomas [23] described the core region of the star for anisotropic matter configuration. Paul and Tikekar [24] remarked in their work that interior of compact star based on core region and envelope region. Ward and Whitworth [25] described the role of core region of star in last stage during evolution of compact star, the occurrence of fusion process in the core region binds lighter elements into heavier. Also, it preserve equilibrium between gravity and pressure of the star. The occupation of heavier elements in core region gets enlarged and size of star also increases. When surrounding pressure of envelope is reduces, the temperature of core region cools down resulting in dense compact objects. Core region of the star is surrounded by envelope region. Hansraj et al. [26] found solutions of nonlinear Riccati equations by constructing core-envelope models. Takisa et al. [27] discussed the envelope matter and construct anisotropic compact star model. Gedela et al. established core-envelope models for superdense compact stars [28].

In compact star core region is of quark matter and envelope region is baryonic matter. Weber et al. [29] discussed the properties of quark matter in detail. Annala et al. [30] discussed that on the bases of the behavior of compact matter the quark matter is composed of three states (i) up, (ii) down and (iii) strange quark. The densities of all these three states of quark matter is equal. Pure quark matter possess more stability then other nuclear matter. Quark masses have strong internal coupling which vary with the environment. The baryonic matter is made up of baryons which itself is made up of subatomic particles such as electron, proton and neutron. Its supposed that at finite baryon number the baryonic matter is quark matter. Naoz et al. [31] showed the formation of early structure of baryon. It is believed that about 68% of universe is made up of dark energy, 27% is dark matter and remaining 5% is of other matters. Baryonic matter is a form of dark matter. Thats why baryonic matter is helpful while dealing with cold and dense stars.

Inclusion of charge with matter anisotropy unfolds many intersecting features in the study of gravitational interaction within compact objects. Bonnor [32] presented the model of anisotropic sphere, in his study electrical repulsion affects self-gravitating charged matter. The gravitational field in compact stars is not exerted by the electrical energy of the charge of that star. In fact, energy of the electric field of charge object is used to balance the gravitational field. Bhatia et al. [33] described the creation of electric field of charge as a consequence of movement of electrons from the core of the compact star. Rao et al. [34] have studied effects of charge on the pressure of fluid, mass and redshift of compact objects. Ray et al. [35] discussed the high value of radius of charged supermassive compact objects effected by repulsive force and limiting value of amount of charge that a star can bear.

In comparison to the heavy ion particles, the lighter weight electron particles arise and move to the top of surface of star. So, to stop the rise and escape of electrons from the surface of star, the electric field is generated by charge. After the lose of some electrons from the surface, the star become stable because of the electric field generated by charge and net charge of star become positive. In charged stars, mass increases as an effect of presence of electric repulsive forces. Their exist relation between mass and central density, so central density increase with the increase in mass of charged star. The reason of increase in the value of redshift of charged compact star, is due to the emitted light rays from the surface of star that are shifted towards the red [10].

Sun et al. [36] described that gravitational collapse occur when inside pressure is not enough to balance gravity in stars. The existence of charge counterbalance the pressure gradient and avoid collapse. Pant et al. [37] described that charge present in fluid can keep singularity away from system. The validity and reliability of charged anisotropic compact stars is verified by evaluating its physical conditions such as stability, mass, radius and adiabatic index. Kiess [38] explained the relation between mass density, charge density, radius and central density of compact object. The study of Takisa et al. [39] showed that charge present in the compact star can change its whole appearance and structure. Panahi et al. [40] presented a comparison of charge anisotropy with isotropy. Tamta and Fuloria [41] obtained solutions for Einstein Maxwell’s field equations for charged anisotropic fluid. Ratanpal and Bhar [42] constructed models on anisotropic compact stars in the presence of charge. Malaver and Manuel [43] constructed charged anisotropic model without singularities in matter which fulfil the physical properties required by realistic star.

Maurya [44] presented family of solutions for relativistic charged compact stars with anisotropic sphere. He discussed that at the center of compact star the electric charge is zero. Hence charge increases while moving away from center and attain maximum value at the surface of star. As a result of this type of distribution of charge at the center and surface, the core become less stable as compare to the surface of a charged object. The solution for charged anisotropy by taking conformal symmetry in spherically symmetric spacetime was discussed in [10]. Prasad and Kumar [45] explained solutions of Einstein’s–Maxwell field equations with uniform charge distribution in compact stars by Pseudo-spheroidal spacetime. The same authors gave three energy conditions for charged fluid sphere are null energy conditions, weak and strong energy conditions.

An EoS is an equation which explains the state of matter under various physical conditions. The EoS provides information about fluid type, solid matter, interior structure and variables as density and pressure of compact stars. To understand the structure and properties of compact object establishment of EoS is very significant. It relates physical parameters of the system in a single relation. It explains the dependence of pressure on density in a star. Zeldovich [46] presented the EoS with physical parameters like density and pressure. Barreto and Rojas [47] explained anisotropic fluid distribution of compact star by EoS. Chan and Ryong [48] explained the state of matter of self gravitating stars by using EoS. Compact star models with different state equations have been studied in [49,50,51,52,53,54].

All the properties and conditions of a strong gravitational system as compact star can’t be explained just by a single EoS so we use various EoS’s. It can be of the form of linear, polytropic, quadratic or of other dependence. Sometimes when solutions are known EoS’s are selected without physical motivational reasons just to clarify differential equations of models. Tooper [55] explained that how polytropic EoS deals with equilibrium of system and also relate pressure and density in the sphere. Nilsson and Uggla [56] constructed model with polytropic EoS for compact stars. In polytropic equation, the density and pressure of compact stars are linked together by a power law. Negi and Durgapal [57] examined many EoS’s and their physical parameters. Sharma and Maharaj [58] applied a linear EoS for compact stars with quark matter. Seveso et al. [59] defined the results of relativistic EoS extended by polytropic equation for compact stars.

In astrophysics, static gravitational equilibrium is defined by Tolman–Oppenheimer–Volkoff (TOV) equation. The TOV equation determines the properties and structure of spherically symmetric objects in equilibrium state. In 1939, it was first time when the issue of obtaining exact solutions for spherically symmetric fluid body was discussed. That discussion was started with the research of Tolman [60] and Oppenheimer and Volkoff [3]. We have discussed the viability of our developed model with the help of TOV equations.

The manuscript is arranged as follows: in Sect. 2, Einstein Maxwell field equations are constructed followed by Line elements for ore, envelope and Boundary region. Viability conditions for construction of core-envelope model are explained in Sect. 3, constituting subsections related to details of constructed model. Physical analysis for core-envelope model and graphical representation of physical parameters is given in Sect. 4. In last section the results are summarized, followed by the list of references.

2 Einstein Maxwell field equations

Spherically symmetric spacetime for charged anisotropic fluid in Schwarzschild coordinates defined as $(x^{i}) = (x^{0}, x^{1}, x^{2}, x^{3}) = (t, r, \theta , \phi )$ is employed in this work, written as

$$\begin{aligned} ds^2=e^{\nu (r)}dt^{2}-e^{\lambda (r)}dr^{2}-r^2(d\theta ^2+sin^2\theta d\phi ^2), \end{aligned}$$

(1)

where $\nu (r)$ and $\lambda (r)$ are the metric potentials. The Einstein’s field equations are of the form

$$\begin{aligned} -8\pi (T_{ij}+E_{ij})=R_{ij}-\frac{1}{2}Rg_{ij}. \end{aligned}$$

(2)

In above equation, we have used gravitational units i.e., $8 \pi G = c = 1$. Ricci tensor is defined by $R_{ij}$ and R represents the scalar curvature. The energy-momentum tensor for charged anisotropic matter distribution is of the form

$$\begin{aligned} T_{ij}=[(p_{t}+\rho )v_{i}v_{j}-p_{t}g_{ij}+(p_{r}-p_{t})\chi _{i}\chi _{j}]. \end{aligned}$$

(3)

In Eq. (3), $v^{i}$ and $\chi ^{i}$ stands for 4-velocity and radial 4-vector respectively and are given as

$$\begin{aligned} v^{i}=\sqrt{\frac{1}{g_{ii}}} \delta _{0}^{i}, ~~~~~~~~~~ \chi ^{i}=\sqrt{\frac{-1}{g_{ii}}} \delta _{1}^i, \end{aligned}$$

(4)

where $g_{j}^{i}v_{i}v^{i} = 1$ and $g_{j}^{i}\chi ^{i}\chi _{j} = -1$. The electromagnetic energy momentum tensor in Eq. (2) is given by

$$\begin{aligned} E_{ij}=\frac{1}{4\pi }(F_{i}^{\gamma }F_{j\gamma }-\frac{1}{4}F^{\gamma \delta } F_{\gamma \delta }g_{ij}), \end{aligned}$$

(5)

where, $F_{ij}$ denotes the electromagnetic field tensor, which satisfies following relations

$$\begin{aligned} F_{ij}= & {} \phi _{j,i}-\phi _{i,j}, \end{aligned}$$

(6)

$$\begin{aligned} F^{ij}_{;j}= & {} 4\pi J^{i}, \end{aligned}$$

(7)

where $\phi _{i}$ and $J^{i}$ are the 4-potential and 4-current density respectively, and can be defined by the following relations

$$\begin{aligned} \phi _{i}=\Phi \delta _{i}^{0},~~~~~~~~~~~J^{i}=\varsigma V^{i}, \end{aligned}$$

(8)

where, $\Phi = \Phi (r)$, and $\varsigma$ is the charge density. Now, let us assume the total charge contained inside a sphere of radius r is denoted by S(r), and defined as

$$\begin{aligned} S(r)=4\pi \int _{0}^{r}\varsigma r^{2}e^{\frac{\lambda }{2}}dr. \end{aligned}$$

(9)

Now, by simplifying Maxwell Eqs. (6) and (7), we obtain following differential equation

$$\begin{aligned} \Phi ^{''}-\bigg ( \frac{\lambda ^{'}}{2}+\frac{\nu ^{'}}{2}-\frac{2}{r}\bigg ) \Phi ^{'}=4\pi \varsigma e^{\frac{\nu }{2}}e^{\lambda }, \end{aligned}$$

(10)

where ‘prime’ denotes the derivative with respect to radial coordinate r. Integrating Eq. (10) w.r.t ‘r’, we have

$$\begin{aligned} \Phi ^{'}=\frac{S(r)e^{\frac{\nu }{2}}e^{\frac{\lambda }{2}}}{r^{2}}. \end{aligned}$$

(11)

Onset of Einstein–Maxwell field equations is

$$\begin{aligned}&8\pi \rho =\frac{(1-e^{-\lambda })}{r^{2}}+\frac{{\lambda }^{'}e^{-\lambda }}{r}+\frac{S^{2}}{r^{4}}, \end{aligned}$$

(12)

$$\begin{aligned}&8\pi p_{r}=\frac{{\nu }^{'}e^{-\lambda }}{r}-\frac{(1-e^{-\lambda })}{r^{2}}-\frac{S^{2}}{r^{4}}, \end{aligned}$$

(13)

$$\begin{aligned}&8\pi p_{t}=\frac{e^{-\lambda }}{4}\bigg (2{\nu }^{''}+{\nu ^{'2}} -{\nu }^{'}{\lambda }^{'}+\frac{2{\nu }^{'}}{r}-\frac{2{\lambda }^{'}}{r}\bigg )+\frac{S^{2}}{r^{4}}, \end{aligned}$$

(14)

$$\begin{aligned}&\varsigma =\frac{1}{4\pi r^2}(r^2S)'. \end{aligned}$$

(15)

From Eqs. (13) and (14), we can obtain the following equation.

$$\begin{aligned} 8\pi \Delta= & {} 8\pi (p_{t}-p_{r})=e^{-\lambda }\bigg (\frac{{\nu }^{''}}{2}-\frac{{\lambda }^{'}{\nu }^{'}}{4}+\frac{{\nu }^{'2}}{4}+\frac{({\lambda }^{'}-{\nu }^{'})}{2r} \nonumber \\&+\frac{(e^{\lambda }-1)}{r^{2}}+\frac{2S^{2}}{r^{4}}\bigg ), \end{aligned}$$

(16)

where $\Delta = p_{t}-p_{r}$ is anisotropy factor, it vanishes at the origin $(r = 0)$ and in the scenarios where $p_{t} = p_{r}$. The force due to anisotropic pressure of fluid is attractive if $p_{t} < p_{r}$, and repulsive if $p_{t} > p_{r}$ [44]. Implementation of the transformation $x = r^{2}$, $z(x) = e^{-\lambda (r)}$ and $y(x) = e^{\nu (r)}$, to the system of Eqs. (12)–(15) implies

$$\begin{aligned}&8\pi \rho =\frac{(1-z)}{x}-\frac{z_{x}}{\sqrt{x}}+\frac{S^{2}}{x}, \end{aligned}$$

(17)

$$\begin{aligned}&8\pi p_{r}=\frac{zy_{x}}{\sqrt{x}y}-\frac{(1-z)}{x}-\frac{S^{2}}{x^{2}}, \end{aligned}$$

(18)

$$\begin{aligned}&8\pi p_{t}=\bigg (\frac{z}{4}\bigg (\frac{2y_{xx}}{y}-\frac{(y_{x})^{2}}{y^{2}}+\frac{2y_{x}}{\sqrt{x}y}\bigg ) \nonumber \\&\quad +\frac{z_{x}}{4}\bigg (\frac{y_{x}}{y}+\frac{2}{\sqrt{x}}\bigg )+\frac{S^{2}}{x^{2}}\bigg ), \end{aligned}$$

(19)

$$\begin{aligned}&8\pi \Delta =\bigg (\frac{z}{4}\bigg (\frac{2y_{xx}}{y}-\frac{y_{x}^{2}}{y^{2}}-\frac{2y_{x}}{\sqrt{x}y}\bigg ) +\frac{z_{x}}{4}\bigg (\frac{y_{x}}{y}+\frac{2}{\sqrt{x}}\bigg ) \nonumber \\&\quad +\frac{(1-z)}{x}+\frac{2S^{2}}{x^{2}}\bigg ), \end{aligned}$$

(20)

$$\begin{aligned}&\varsigma =\frac{1}{2\pi x}\Big (x\sqrt{x}S_x+\sqrt{x}S\Big ). \end{aligned}$$

(21)

Here, ‘$z_{x}$, $y_{x}$’ and ‘$y_{xx}$’ denotes first and second derivative with respect to x, respectively.

In order to construct a core-envelope model for spherically symmetric spacetime, the matching of interior spacetime to exterior spacetime is required. Further, the interior of compact objects is of two regions, the inner layer is known as core and outer layer is known as envelope. The spacetime for core region $(R_{C})$ and envelope region $(R_{E})$ are taken as

$$\begin{aligned} ds^2|_{C}= & {} e^{\nu _{C}(r)}dt^{2}-e^{\lambda _{C}(r)}dr^{2}-r^2(d\theta ^2+sin^2\theta d\phi ^2), \nonumber \\ \end{aligned}$$

(22)

$$\begin{aligned} ds^2|_{E}= & {} e^{\nu _{E}(r)}dt^{2}-e^{\lambda _{E}(r)}dr^{2}-r^2(d\theta ^2+sin^2\theta d\phi ^2),\nonumber \\ \end{aligned}$$

(23)

where, we match interior spacetime from Eqs. (22) and (23) to the exterior Reissner–Nordström spacetime $(R_{B})$ (we consider $r=R$ at boundary, where R is radius of star). The exterior metric is given by

$$\begin{aligned} ds^{2}= & {} \bigg (1-\frac{2M}{R_{E}}+\frac{Q^{2}}{R_{E}^{2}}\bigg )dt^{2} -\frac{dr^{2}}{\big (1-\frac{2M}{R_{E}}+\frac{Q^{2}}{R_{E}^{2}}\big )} \nonumber \\&-r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$

(24)

where M and Q denotes the total mass and total charge of anisotropic charged star, respectively.

3 Viability conditions for core-envelope model

Physical viability demands that the model should meet the following requirements in core, envelope and exterior region (developed by [27] are discussed below)

• Geometrical constancy: All physical parameters should be well behaved throughout within the star, in its center, in core and envelope [27].

• Viable trends in density and pressure: Matter density $(\rho )$ and pressure stresses (radial and transverse pressure) shall be continuous at the matching, shall have positive values at the core and envelope of the compact object. Moreover, the pressure to density ratio should be continuous at the matching and this ratio shall be positive everywhere within the star [46].

• Compactification factor u(r), gravitational red shift z(r) and mass–radius relation m(r) shall be continuous in core and envelope region. Further, these parameters shall either be increasing or decreasing along radial coordinate.

• Anisotropy factor $(\Delta )$: The radial pressure $(p_{r})$ should match with the tangential pressure $(p_{t})$ within the star leading to vanishing anisotropy factor $(\Delta =0)$.

• Causality conditions: For a compact star model the radial sound speed shall meet the causality conditions at the center. It should be continuous at the junction and decreasing outward.

• Both core and envelope region shall satisfy the energy conditions and should be continuous at the point of matching.

• TOV equations: The TOV equations should be fulfilled inside the star and all three forces $(F_{g}, F_{h}, F_{a})$ should be continuous at the matching which leads to the static equilibrium.

• At the boundary of compact object $p_{r}(R_{E})=0$ [27].

• The metric functions of the core region should match with the gravitational potential of the envelope region [27].

3.1 The core-envelope model

For core region, we assume an anisotropic type of well-known Tolman VII [61] for metric potential $e^{-\lambda _{C}}$ with polytropic EoS given by

$$\begin{aligned}&z=e^{-\lambda _{C}}=1-ax+bx^{2}, \end{aligned}$$

(25)

$$\begin{aligned}&p_{r_{C}}=\alpha \rho ^{1+\frac{1}{n}}, \end{aligned}$$

(26)

where n denotes polytropic index, a, b and $\alpha$ are constants. Herein, we assume polytropic index $n = 1$ in Eq. (26).

The fundamental assumption of theory of polytropes is that the pressure stresses of gravitating sources are density dependent. Chandrasekhar [62, 63] worked on polytropic gaseous sphere to account density and mass of white dwarfs. The same author provided the detailed framework on thermodynamical properties of compact objects via polytropic EoS [64]. Tooper [65] discussed relativistic polytropes and constructed the general framework for the derivation of LEe. Kaplan and Lupanov [66] worked structure of polytropic spheres and discussed its stability. Kaufmann [67] constricted relationship in mass and radius for spherical polytropes by taking different values of polytropic index. Occhionero [68] and Kovetz [69] worked on the structure of rotating polytropes to ascertain refinements in the theory of polytropes presented by Chandrasekhar [64]. Eriguchi [70, 71] explored hydrostatic equilibrium of polytropes by using numerical computations extended his method for larger values of polytropic index i.e., $n=4,~4.9$. Sharma [72] approximated the solution to field equations for spherical polytropes by making use of $Pad\acute{e}$ approximation. Moreover, theory of relativistic polytropes and impact of polytopic EoS in different physical situations is discussed in [73, 74].

By substituting value of $S^{2}$ and using Eqs. (17), and (25) in Eq. (26), we get following equations as follows

$$\begin{aligned} \frac{y_x}{y}= & {} \frac{d_{1}+d_{2}x+d_{3}x^{2}}{(1-ax+bx^{2})}, \end{aligned}$$

(27)

$$\begin{aligned} y= & {} e^{\nu _{C}} =e^{\int \frac{d_{1}+d_{2}x+d_{3}x^{2}}{(1-ax+bx^{2})}dx}, \end{aligned}$$

(28)

where

$$\begin{aligned}&d_{1}=\bigg (\frac{\alpha P_{1}^{2}r}{8\pi }+ar+\frac{P_{2}S^{2}r}{4\pi }\bigg ),\quad \\&\qquad d_{2}=\bigg (\frac{\alpha P_{1}P_{2}r}{4\pi }-br+\frac{\alpha P_{1}S^{2}}{4\pi r^{3}}\bigg ),\\&\qquad d_{3}=\bigg (\frac{\alpha P_{2}r}{8\pi }+\frac{\alpha (S^{2})^{2}}{8\pi r^{7}}+\frac{S^{2}}{r^{7}}\bigg ),\quad \\&\qquad S^{2}=r^{4}\bigg (\frac{(-a+2br^{2})^{2}}{(1-ar^{2}+br^{4})^{4}}\bigg ). \end{aligned}$$

Here $P_{1} = a\big (1+\frac{1}{r}\big )$ and $P_{2} = -b\big (1+\frac{2}{r}\big )$ are integrating constants.

Substitution of $x = r^{2}$ and use of Eqs. (25), (27) and (25) in the Eqs. (17)–(20) leads to the following equations:

$$\begin{aligned} \rho _{C}= & {} \frac{P_{1}+P_{2}r^{2}+\frac{S^{2}}{r^{2}}}{8\pi }, \end{aligned}$$

(29)

$$\begin{aligned} p_{r_{C}}= & {} \frac{\alpha }{8\pi }\bigg (P_{1}+P_{2}r^{2}+\frac{S^{2}}{r^{2}}\bigg ), \end{aligned}$$

(30)

$$\begin{aligned} p_{t_{C}}= & {} \frac{1}{8\pi }\bigg (f_{1}+\frac{f_{2}+f_{3}r^{2}+f_{4}r^{4}}{4(1-ar^{2}+br^{4})}\bigg ), \end{aligned}$$

(31)

$$\begin{aligned} \Delta _{C}= & {} p_{t_{C}}-p_{r_{C}}, \end{aligned}$$

(32)

where

$$\begin{aligned} d_{4}= & {} \bigg (\frac{-\alpha P_{1}b}{4\pi }-\frac{\alpha aP_{2}}{8\pi }\bigg ),\\ d_{5}= & {} \bigg (\frac{-\alpha aP_{1}}{8\pi }-\frac{\alpha bP_{1}r^{3}}{4\pi }+\frac{\alpha P_{1}S^{2'}r}{4\pi }-\frac{\alpha P_{1}S^{2}}{4\pi r} \\&-\frac{\alpha bP_{2}r^{5}}{4\pi }-\frac{\alpha bP_{2}r^{4}}{4\pi }\\&+\frac{\alpha P_{2}S^{2'}r^{3}}{4\pi }-\frac{\alpha P_{2}S^{2}r}{4\pi }-\frac{\alpha S^{2}br}{4\pi }\\&-\frac{\alpha S^{2}b}{4\pi }+\frac{\alpha S^{2}S^{2'}}{4\pi r}-br^{3}+\frac{S^{2'}}{r}\bigg ),\\ d_{6}= & {} \bigg (\frac{-\alpha aS^{2}}{8\pi }-\frac{\alpha (S^{2})^{2}}{4\pi r}-\frac{2S^{2}}{r}\bigg ),\\ f_{1}= & {} \bigg (\frac{d_{4}}{2}+\frac{d_{5}}{2r^{2}}+\frac{d_{6}}{2r^{4}}-\frac{a}{2r}+br+\frac{S^{2}}{r^{4}}\bigg ), \\ f_{2}= & {} \bigg ((d_{1}^{2}+d_{2})+(2d_{2}d_{3}+2bd_{2}r)r^{6}\bigg ),\\ f_{3}= & {} \bigg (2d_{1}d_{2}+\frac{d_{1}}{r^{4}}+d_{3}+\frac{2d_{1}}{r^{3}}+\frac{2d_{2}}{r}+2d_{3}r \\&-\frac{2ad_{1}}{r}-2ad_{2}r\bigg ),\\ f_{4}= & {} \bigg ((2d_{1}d_{3}+d_{2}^{2}-2ad_{3}r+2bd_{1}r)+(d_{3}^{2}+2bd_{3}r)r^{4}\bigg ). \end{aligned}$$

For realistic modeling a single EoS may not be appropriate, since we are studying the structure of star in two layers. That is why two different EoS are employed for the discussion of the stellar model. We have chosen an EoS which linearly relates the energy density and radial pressure in the envelope. Linear EoS is consistent in the modeling of compact objects, one can achieve modeling of anisotropic spherical objects with quark matter distributions [74, 75]. It is suitable in retrieving the mass–radius relationship and values of surface redshifts corresponding to realistic stars [76, 77]. For envelope region, we assume the same anisotropic Tolman VII [61] with linear EoS

$$\begin{aligned}&z=e^{-\lambda _{E}}=1-ax+bx^{2}, \end{aligned}$$

(33)

$$\begin{aligned}&p_{r_{E}}=\alpha \rho -\beta , \end{aligned}$$

(34)

where a, b, $\alpha$ and $\beta$ are constants. Substituting values from Eqs. (33) and (17) in Eq. (34), we have

$$\begin{aligned} \frac{y_x}{y}= & {} \frac{d_{7}+d_{8}x}{(1-ax+bx^{2})}, \end{aligned}$$

(35)

$$\begin{aligned} y= & {} e^{\int \frac{d_{7}+d_{8}x}{(1-ax+bx^{2})}}dx. \end{aligned}$$

(36)

Here

$$\begin{aligned} d_{7}= & {} \bigg (\alpha P_{1}+\alpha S^{2}-8\pi \beta +a+\frac{S^{2}}{x^{2}}\bigg )\sqrt{x}, \quad \\ d_{8}= & {} (\alpha P_{2}-b)\sqrt{x}, \end{aligned}$$

making use of Eqs. (33), (34) and $x = r^{2}$ in system of Eqs. (17)–(4), we get following equations

$$\begin{aligned} \ \rho _{E}= & {} \frac{1}{8\pi }\bigg (P_{1}+P_{2}r^{2}+\frac{S^{2}}{r^{2}}\bigg ), \end{aligned}$$

(37)

$$\begin{aligned} p_{r_{E}}= & {} \frac{\alpha }{8\pi }\bigg (P_{1}+P_{2}r^{2}+\frac{S^{2}}{r^{2}}\bigg )-\beta , \end{aligned}$$

(38)

$$\begin{aligned} p_{t_{E}}= & {} \frac{1}{8\pi }\bigg (f_{5}+\frac{f_{6}+f_{7}r^{2}+f_{8}r^{4}}{4(1-ar^{2}+br^{4})}\bigg ), \end{aligned}$$

(39)

$$\begin{aligned} \Delta _{E}= & {} p_{t_{E}}-p_{r_{E}}, \end{aligned}$$

(40)

where

$$\begin{aligned} P_{3}= & {} \bigg (\frac{-br^{2}}{2}-\frac{\alpha a}{2}-2br^{3}+S^{2'}r\bigg ), \quad \\ P_{4}= & {} \bigg (S^{2'}-S^{2}-\frac{2S^{2}}{r^{2}}\bigg ),\\ d_{9}= & {} \frac{1}{(1-ar^{2}+br^{4})}\bigg (\frac{P_{3}}{r^{2}}+\frac{P_{4}}{r^{3}}\bigg ),\quad \\ f_{5}= & {} \bigg (\frac{d_{9}(1-ar^{2}+br^{4})}{2}+\frac{-a+2br^{2}}{2r}+\frac{S^{2}}{r^{4}}\bigg ),\\ f_{6}= & {} \bigg (d_{7}^{2}+d_{8}-2ad_{7}-2ad_{8}\big ), \\ \quad f_{8}= & {} \big (d_{8}^{2}+bd_{8}+4brd_{8}\bigg ), \\ f_{7}= & {} \bigg (2d_{7}d_{8}+\frac{d_{7}}{r^{4}}+d_{7}b+\frac{2d_{7}}{r^{3}}+\frac{2d_{8}}{r} -\frac{2ad_{7}}{r} \\&-2ard_{8}+4brd_{7}\bigg ). \end{aligned}$$

3.2 Matching at the core-envelope and boundary

The line elements given in Eqs. (22) and (23) of core and envelope region must match at boundary $r = R_C$. Metric potential and radial pressure must also be continuous at boundary.

3.2.1 Matching conditions of interface metrics

The structure of numerous compact stars is made up of core and envelope layers with different pressures. To build such star model, following matching conditions are important.

$$\begin{aligned} e^{\lambda _{C}}(R_{C})= & {} e^{\lambda _{E}}(R_{C}), \end{aligned}$$

(41)

$$\begin{aligned} e^{\nu _{C}}(R_{C})= & {} e^{\nu _{E}}(R_{C}), \end{aligned}$$

(42)

$$\begin{aligned} p_{r_{C}}(R_{C})= & {} p_{r_{E}}(R_{C}). \end{aligned}$$

(43)

Fig. 1

Variation of density with radial coordinate

Fig. 2

Variation of radial pressure with radial coordinate

3.2.2 Matching conditions of envelope and exterior

The line elements Eqs. (23) and (24) of envelope and exterior region must match at boundary $r = R_{E}$ (where $R_{E}$ is the radius of star).

$$\begin{aligned} e^{\lambda _{E}}(R_{E})= & {} \bigg (1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}\bigg )^{-1}, \end{aligned}$$

(44)

$$\begin{aligned} e^{\nu _{E}}(R_{E})= & {} \bigg (1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}\bigg ), \end{aligned}$$

(45)

$$\begin{aligned} p_{r_{E}}(R_{E})= & {} 0. \end{aligned}$$

(46)

In matching conditions (41)–(46) constants are M, $R_{E}$, C, $\beta$ and $\sigma$, defined as

$$\begin{aligned} M= & {} \frac{1}{2}R^{2}_{E}(a-bR^{2}_{E}), \end{aligned}$$

(47)

$$\begin{aligned} R_{E}= & {} \sqrt{\frac{3aAb+4\pi (\sqrt{b^{2}(4AC+B^{2})}+bB)}{5Ab^{2}}}. \end{aligned}$$

(48)

Here, M and $R_{E}$ is mass and radius of star, respectively.

$$\begin{aligned} C= & {} \frac{(3a-5bR_{E}^{2})(3aA-5AbR_{E}^{2}+8 \pi B)}{64 \pi ^{2}}, \end{aligned}$$

(49)

$$\begin{aligned} \beta= & {} \frac{(3a-5bR_{C}^{2})(8\pi \alpha +5Ab(R_{C}^{2}-R_{E}^{2}))}{64\pi ^{2}}+ \sigma , \end{aligned}$$

(50)

where

$$\begin{aligned} \sigma =\frac{5bC(R_{C}^{2}-R_{E}^{2})}{3a-5bR_{E}^{2}}. \end{aligned}$$

(51)

The constants a, b, $\alpha$, A and B are free parameters. The values of these constants are taken in such a way that all physical properties of assumed compact objects are well-behaved.

4 Physical analysis for core-envelope model

The viability conditions for well behaved core-envelope model are explained in following subsections. The realistic stars SAX J1808.4-3658 and 4U1608-52 are considered to show physical acceptability of developed model. Following table provides values of parameters that are calculated to arrive at masses and radii of core and envelope for 4U1608-52.

4.1 Geometrical nonsingularity

The metric potentials are stated as $e^{\nu }=positive constant$ and $e^{-\lambda }=1$ at the center of star. According to this $e^{\nu }$ and $e^{-\lambda }$ are invariable and non-singular at the center of star. Additionally, $e^{\nu }$ and $e^{-\lambda }$ are continuous at the matching and increase or decrease about radial coordinate r.

4.2 Viable direction of physical parameters

4.2.1 Density and pressure trends

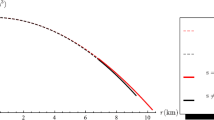
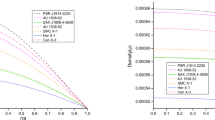
The fluid density $(\rho )$ and pressures $(p_{r}, p_{t})$ for core-envelope star model are continuous at the matching, having positive values throughout the region [78] (Figs. 1, 18, 3). Additionally, the Zeldovich’s condition [46] that the ratios of pressure and density are positive and smaller then 1 in the star and continuous at matching (Fig. 20).

Fig. 3

Variation of tangential pressure with radial coordinate

Fig. 4

variation of pressure and density ratio with radial coordinate

4.2.2 Mass–radius relation, red-shift and compactification factor

Earman [79] described the objectives of studying red-shift of compact stars in GR. The mass (m(r)) and red-shift (z(r)) are continuous at the matching and increases or decreases respectively with radial coordinate r for the compact stars SAX $J1808.4-3658$ and $4U1608-52$ (Figs. 21, 6). Additionally, compactification factor (u(r)) is continuous at the matching and increase w.r.t r (Fig. 7) and be within Buchdahl limit [80].

Fig. 5

variation of mass with radial coordinate

Fig. 6

Variation of red-shift with radial coordinate

Fig. 7

Variation of compactification factor with radial coordinate

4.2.3 Anisotropic constant

The plot of anisotropy factor is continuous as shown in (Fig. 8).

Fig. 8

Variation of anisotropy with radial coordinate

4.2.4 Causality conditions of radial sound speed

The radial sound speed fulfill the causal conditions of compact star and decrease monotonically at the exterior and continuous at matching. The $v_{r}^{2}$ of core-envelope model of star is in Fig. 9.

Fig. 9

Variation of radial velocity with radial coordinate

4.2.5 Adiabatic index

In relativistic anisotropic sphere the adiabatic index $\Gamma _{r}$ and the proportion of two specific heats take account of stability of stars, defined by [81],

$$\begin{aligned} \ \Gamma _{r}=\frac{\rho +p_{r}}{p_{r}}\frac{\partial p_{r}}{\partial \rho }. \end{aligned}$$

(52)

For a stable Newtonian sphere $\Gamma >\frac{4}{3}$ [62,63,64]. For core-envelope model of stars adiabatic indexes are plotted in Fig. 10. The Fig. 10 presents the continuity of adiabatic index at matching.

Fig. 10

Variation of adiabatic index with radial coordinate

4.2.6 Energy conditions

For a physically stable arrangement, the core and envelope of stars fulfill some inequalities called as energy conditions [82] are following: (i) Null energy condition

$$\begin{aligned} \ NEC : \rho + p_{r} \ge 0, \end{aligned}$$

(53)

(ii) Weak energy conditions for radial and tangential pressures

$$\begin{aligned} \ WEC_{r} : \rho + p_{r} \ge 0, \rho\ge & {} 0, \end{aligned}$$

(54)

$$\begin{aligned} WEC_{t} : \rho + p_{t} + \frac{E^{2}}{4\pi } \ge 0, \rho\ge & {} 0, \end{aligned}$$

(55)

(iii) Strong energy condition

$$\begin{aligned} \ SEC : \rho + p_{r} + 2p_{t} + \frac{E^{2}}{4\pi } \ge 0, \end{aligned}$$

(56)

where, $E = \frac{S}{r^{2}}$. The change in energy conditions w.r.t r is continuous at matching and fulfill realistic conditions for core and envelope of star (Fig. 11).

Fig. 11

Variation of energy conditions with radial coordinate

4.2.7 TOV equation of core-envelope model

For static equilibrium in compact stars we assume the three force components of TOV equation. The three resulting forces of equilibrium state are; gravitational force $(F_{g})$, hydrostatic force $(F_{h})$ and anisotropic force $(F_{a})$ should be zero everywhere inside star and continuous at matching. The TOV equation [83] is defined as

$$\begin{aligned} \underbrace{-\frac{M_{g}(r)(\rho +p_{r})}{r^{2}}e^{\frac{\nu -\lambda }{2}}}_{F_{g}}-\underbrace{\frac{d p_{r}}{dr}}_{F_{h}}+\underbrace{\frac{2\Delta (r)}{r}}_{F_{a}}=0, \end{aligned}$$

(57)

Here, gravitational mass is function or r is denoted by $M_{g}(r)$ and defined as

$$\begin{aligned} \ M_{g}(r)=\frac{1}{2}r^{2}\nu ^{'}e^{\frac{\nu -\lambda }{2}}, \end{aligned}$$

(58)

through the formula Tolman-Whittaker and Einstein’s field equations.

Following is the equilibrium force equation which is equivalent to Eq. (57)

$$\begin{aligned} \ F_{g}+F_{h}+F_{a}=0, \end{aligned}$$

(59)

Here, elements of Eq. (57) are $F_{g}$, $F_{h}$ and $F_{a}$.

The TOV equation is fulfilled inside the star and forces ($F_{g}$, $F_{h}$ and $F_{a}$) are continuous at matching and system is in equilibrium (Fig. 12).

Fig. 12

Variation of balancing forces with radial coordinate

Table 1 Calculated values of parameters that give core radii $(R_{C}$, mass and envelope radii $R_{E})$ for SAX J1808.4-3658

Table 2 Calculated values of constants that give core radii $(R_{C}$, masses and envelope radii $R_{E})$ for $4U1608-52$

5 Summary and conclusion

In this paper we have constructed a core-envelope model by taking a spherically symmetric compact object with anisotropic charged matter configuration. Polytropic EoS is chosen for inner layer termed as core region while a linear EoS is employed to discuss envelope region of compact stars. It is worth mentioning here that, the spacetime geometry of core, envelope and exterior region of star match smoothly. In order to develop a physically viable core-envelop model, we have accounted the values of masses, radii and compactification factors for two stars namely SAX $J1808.4-3658$ and $J1808.4-3658$ by incorporating electromagnetic effects. The viability conditions for core-envelop model are discussed in section III. For SAX $J1808.4-3658$ the mass of star is $M = 0.7 M_{\bigodot }$, radius of core to be $R_{C} = 3.393$ and radius of envelope as $R_{E} = 6.2$ km. The mass of star $4U1608-52$ is $M = 1.85 M_{\bigodot }$, radius of core is $R_{C} = 2.459$ and envelope has radius $R_{E} = 8.2$ km. The values of b, A, B, $\alpha$ and $\beta$ for star SAX $J1808.4-3658$ and $4U1608-52$ are given below in Tables 1 and 2. Herein, we shall summarize the results determined from graphical representation of physical parameters and required conditions as follows:

Table 3 Behavior of physical parameters for star SAX $J1808.4-3658$ with $M = 0.7M_{\bigodot }$, $M_{\bigodot } = 2\times 10^{30}$ kg, $G = 6.67\times 10^{-11}$ $\mathrm{m}^{3}\mathrm{kg}^{-1}\mathrm{s}^{-2}$, radius $R_{E} = 6.2$ km, $C = 3\times 10^{8}$ $\mathrm{ms}^{-1}$ and $R_{C} = 3.393$ km

Table 4 Values of physical parameters for star $4U1608-52$ with $C = 3\times 10^{8}$ $\mathrm{ms}^{-1}$, $M = 1.85M_{\bigodot }$, $R_{C} = 2.459$ km, radius $R_{E} = 8.2$ km, $G = 6.67\times 10^{-11}$ $\mathrm{m}^{3}\mathrm{kg}^{-1}\mathrm{s}^{-2}$ and $M_{\bigodot } = 2\times 10^{30}$ kg

• The density profile and pressure components of both stars under consideration are displayed in Figs. 1, 2 and 19. It can be clear that these physical parameters are continuous at the junction and positively defined.

• Graphical representation of pressure to density ratios given in Fig. 4 shows continuity at the matching and this ratio is positive everywhere within the stars.

• The mass function is displayed in Fig. 5, that shows increasing trend in mass from center to the exterior boundary.

• Variation of gravitational red-shift with radial coordinate is expressed in Fig. 6 for both stars that shows positive and monotonically increasing behavior from center to exterior boundary.

• The compactification factor, i.e. the mass-to-radius ratio of a compact star is calculated by using the formula, $u=\frac{M}{R}$. The compactification factor can be used to classify the compact objects in various categories, when $u=\frac{1}{2}$, it represents a black hole. From Fig. 7, it can bee seen that compactification factor increases with the radial coordinate r.

• The anisotropy factor has been plotted in Fig. 8, it is evident from the graph that anisotropy factor has minimum value near the center and it increases gradually as we move from the center towards boundary.

• The radial sound speed $v_r^{2}$ satisfies the casuality condition, i.e., continuous at the junction and decreases with r as shown in Fig. 9.

• The adiabatic index defined as $\Gamma _{r}=({\rho +p_{r}})/{p_{r}}{\partial p_{r}}/{\partial \rho }$, depicts variation in anisotropic pressure density with a given change in density. The adiabatic shall have value in range $\Gamma >\frac{4}{3}$ for stable stellar configuration, that is achieved in Fig. 10.

• For a physically stable model, the star’s core and envelope must satisfy the energy conditions. It is evident that at the junction, the variation in energy conditions with r of the core and envelope is satisfied as given in Fig. 11.

• In general relativity, the TOV equation constrains the structure of a spherically symmetric body in static gravitational equilibrium. From Fig. 12, the TOV condition is satisfied and the three balancing forces are continuous at the junction. This concludes that the system is in static equilibrium state.

From the Tables 3 and 4, we can see that by increasing the mass of star its central density also increase. In this paper, we verify all physical properties of stars by equilibrium forces of TOV equations.

Viability of above mentioned conditions represent a physically acceptable core envelope model.