1 Introduction

Black holes are relativistic objects which are massive and curious in the universe. Aspects of black hole physics have been studied extensively for a long time. Stability is one of the interesting problems in black hole physics. Superradiance is an important factor which affects the stability of the charged or rotating black holes [1]. When a (charged) bosonic wave is scattering off a black hole, the bosonic wave can be amplified under certain conditions through extracting energy from the black hole. This is called a superradiance process. For a charged rotating black hole, the superradiance condition is

$$\begin{aligned} \omega <m \Omega _{H}+q \Phi _{H}, \end{aligned}$$
(1.1)

where m and q are azimuthal quantum number and the charge of the incoming bosonic wave, \(\Omega _{H}\) is the angular velocity of the black hole horizon and \(\Phi _{H}\) is the electromagnetic potential of the black hole horizon [2,3,4,5,6,7,8]. If there is a mirror between the black hole horizon and spatial infinity, the amplified superradiant modes may be reflected back and forth and grows exponentially, which is the so-called black hole bomb mechanism proposed by Press and Teukolsky [9].

Various kinds of black holes have been studied extensively about their superradiant (in)stability in the literature. Regge and Wheeler proved that the spherically symmetric Schwarzschild black hole is stable under perturbations [10]. In the asymptotically flat background, the charged Reissner–Nordstrom (RN) black hole proved superradiantly stable against charged massive perturbation  [11,12,13,14,15,16,17,18]. The reason is that if the parameters of RN black holes and perturbations satisfy superradiant conditions, there is no effective trapping potential well (mirror) outside the black hole horizon, which reflects the superradiant modes back and forth. A similar case exists for charged RN black holes in string theory. The stringy RN black hole is shown to be superradiantly stable against charged massive scalar perturbation [19].

When a mirror or a cavity is placed around a charged RN black hole, it is proved that this black hole is superradiantly unstable under charged massive scalar perturbation in certain parameter spaces  [20,21,22,23,24]. If the charged RN black holes are in asymptotically curved backgrounds, such as anti-de Sitter/de Sitter(AdS/dS) space, these curved backgrounds may provide natural mirror-like boundary conditions which lead to superradiant instability of the black hole and perturbation systems  [25,26,27,28,29]. A similar case exists for charged RN black holes in string theory. When a mirror is introduced, superradiant modes are supported and the stringy RN black hole becomes superradiantly unstable under charged massive scalar perturbation  [30,31,32]. It is also found that extra coupling between the scalar field and the gravity can result in superradiant instability of RN/RN-AdS black holes  [33, 34].

In addition, previous studies imply that magnetic field surrounding a black hole can also provide a confining mechanism. In the weak magnetic field approximation, Refs. [35, 36] showed that when a scalar field is propagating on the Ernst background [37], the magnetic field can induce an effective mass \(\mu _{\text {eff}}\varpropto B\) (B is the magnetic field strength) for the scalar field. A first fully-consistent linear analysis of the superradiant instability of the Ernst spacetime and scalar perturbations is given in [38]. By studying scalar perturbation of a magnetized Kerr–Newman black hole, the authors confirm the details of the superradiant instability and find a constraint on the black-hole spin and the surrounding magnetic field.

The influence of magnetic fields on black hole superradiance is an interesting topic and may have astrophysical application. The Ernst black hole is not asymptotically flat and describes a black hole immersed in an asymptotically uniform magnetic field. In this paper we will discuss the superradiant stability of a class of asymptotically flat magnetically charged black holes-dyonic RN black holes [39]. The spacetime metric of this kind of black holes are very similar with RN black holes, however, there is an additional magnetic field. By comparing the superradiant stability properties of the dyonic RN black holes with that of the RN black holes, we can clearly see the effect of the magnetic field on black hole superradiance.

The paper is organized as follows. In Sect.  2, we describe the dyonic RN black hole and scalar perturbation system and analyze the angular part and radial part of the equation of motion of the scalar perturbation. In Sect. 3, we derive the effective potential experienced by the scalar perturbation and analyze the asymptotical behaviors of the effective potential. In Sect. 4, we carefully analyze the shape of the effective potential and get the superradiantly stable parameter region for the system. Section 5 is devoted to the summary.

2 Equations of motion of the scalar perturbation

The dyonic RN black hole is a stationary and spherically symmetric spacetime geometry, which is a solution of the Einstein–Maxwell theory [39]. Using the spherical coordinates (\(t,r,\theta ,\phi \)), the line element can be expressed in the form (we use natural unit in which \(G=c=\hbar \)=1)

$$\begin{aligned} ds^{2}=-\frac{\Box }{r^2}\text {dt}^2+\frac{ r^2}{\Box }\text {dr}^2+ r^2\text {d}\theta ^2+ r^2 \sin ^2\theta \text {d}\phi ^2, \end{aligned}$$
(2.1)

where

$$\begin{aligned} \Box =-2 M r+r^{2}+Q_e^2+Q_m^2, \end{aligned}$$
(2.2)

M is the mass of the black hole, \(Q_{e}\) and \(Q_{m}\) are electric and magnetic charges of the black hole respectively. The dyonic RN black hole has an outer horizon at \(r_{+}\) and an inner horizon at \(r_{-}\),

$$\begin{aligned} r_{+}=M +\sqrt{M^2-Q_e^2-Q_m^2},\quad r_{-}=M -\sqrt{M^2-Q_e^2-Q_m^2}. \end{aligned}$$
(2.3)

Obviously, they satisfy the following relations

$$\begin{aligned} \Box =\left( r-r_{+}\right) \left( r-r_{-}\right) ,\quad r_{+}r_{-}=Q_e^2+Q_m^2,\quad r_{+}+r_{-}=2M. \end{aligned}$$
(2.4)

The equation of motion for an electrically charged massive scalar perturbation \(\Phi \) in the dyonic RN black hole background is descried by the covariant Klein–Gordon (KG) equation

$$\begin{aligned} \left( D^{\nu }D_{\nu }-\mu ^{2}\right) \Phi =0, \end{aligned}$$
(2.5)

where \(D^{\nu }=\bigtriangledown ^{\nu }-i q A^{\nu }\) and \(D_{\nu }\)=\(\bigtriangledown _{\nu }-i q A_{\nu }\) are the covariant derivatives, q and \(\mu \) are the charge and mass of the scalar field respectively. The electromagnetic field of the dyonic black hole is described by the following vector potential

$$\begin{aligned} A_{\nu }=\left( -\frac{Q_{e}}{r},0,0, Q_{m}\left( \cos \theta \mp 1\right) \right) , \end{aligned}$$
(2.6)

where the upper minus sign applies to the north half-sphere of the black hole and the lower plus sign applies to the south half-sphere [39].

The solution of the KG equation can be decomposed as following form

$$\begin{aligned} \Phi (t,r,\theta ,\phi )=R( r ) Y( \theta ) e^{im\phi }e^{-i\omega t}, \end{aligned}$$
(2.7)

where \(\omega \) is the angular frequency of the scalar perturbation and m is azimuthal harmonic index. \(Y( \theta )\) is the angular part and R(r) is the radial part of the solution. Plugging the above solution into the KG equation, we can get the radial and angular parts of the equation of motion. Considering the electromagnetic potentials of the northern and southern hemispheres are different, we will discuss the angular equation of motion in two cases in the following.

2.1 The north half-sphere of the black hole (\(0\leqslant \theta \leqslant \frac{\pi }{2}\))

In this half-sphere, the angular part of the KG equation is

$$\begin{aligned}&\!\!\!\frac{1}{\sin \theta }\partial _{\theta }\left( \sin \theta \partial _{\theta }Y_{1}(\theta )\right) \nonumber \\&\!\!\!\quad +\left( \lambda _{1}-\frac{m^{2}+2\left( m q Q_{m}+q^{2}Q_{m}^{2}\right) (1-\cos \theta )}{\sin ^{2}\theta }\right) Y_{1}(\theta )=0.\nonumber \!\!\!\!\!\\ \end{aligned}$$
(2.8)

Defining \(\chi =\cos \theta \) and plugging it into the above angular equation, we can obtain the following differential equation

$$\begin{aligned}&\frac{d^2 Y_{1}}{d\chi ^2}+\left( \frac{1}{\chi -1}+\frac{1}{\chi +1}\right) \frac{dY_{1}}{d\chi }+\left[ -\frac{m^{2} }{2(\chi -1)}\right. \nonumber \\&\left. +\frac{(2 q Q_{m}+m)^{2}}{2(\chi +1)}-\lambda _{1}\right] \frac{Y_{1}}{(\chi -1)(\chi +1)}=0. \end{aligned}$$
(2.9)

The above is a Fuchs-type equation with three singularities \((-1,1,\infty )\). The general solutions of it can be expressed by hypergeometric functions as

$$\begin{aligned} \begin{aligned} Y_{1}(\chi )&= C_{1} (1-\chi )^{\frac{-m}{2}}(1+\chi )^{\frac{ m +2 q Q_{m}}{2}} {}_2F_{1}\left( \alpha _{1},\beta _{1};\gamma _{1};z_{1}\right) \\&\quad +C_{2}(1\!-\!\chi )^{\frac{m}{2}}(1\!+\!\chi )^{\frac{ -m -2 q Q_{m}}{2}} {}_2F_{1}\left( \alpha _{2},\beta _{2};\gamma _{2};z_{2}\right) , \end{aligned} \end{aligned}$$
(2.10)

where \(C_{1},C_{2}\) are constants. The parameters in the hypergeometric functions are given by

$$\begin{aligned} \begin{aligned} \alpha _{1}&=\frac{1}{2}\left( 1+2 q Q_{m}+\sqrt{1+4\lambda _{1}}\right) , \\ \alpha _{2}&=\frac{1}{2}\left( 1-2 q Q_{m}+\sqrt{1+4\lambda _{1}}\right) ;\\ \beta _{1}&=\frac{1}{2}\left( 1+2 q Q_{m}-\sqrt{1+4\lambda _{1}}\right) , \\ \beta _{2}&=\frac{1}{2}\left( 1-2 q Q_{m}-\sqrt{1+4\lambda _{1}}\right) ; \\ \gamma _{1}&=1-m,\quad \quad \quad \quad \quad \quad \quad \quad \qquad \gamma _{2}=1+m;\\ z_{1}&=\frac{1}{2} (1-\chi ), \quad \quad \quad \quad \quad \quad \quad \quad \quad z_{2}=\frac{1}{2} (1-\chi ). \end{aligned} \end{aligned}$$
(2.11)

In this case, the radial part of the KG equation is

$$\begin{aligned} \Box \frac{d}{dr}\left( \Box \frac{dR}{dr}\right) +U_{1}R=0, \end{aligned}$$
(2.12)

where

$$\begin{aligned} U_{1}=\left( \omega r^2-q Q_e r\right) ^2+\Box \left( q^2 Q^2_m-\mu ^{2}r^{2}-\lambda _{1}\right) . \end{aligned}$$
(2.13)

2.2 The south half-sphere of the black hole (\(\frac{\pi }{2}\leqslant \theta \leqslant \pi \))

In this half-sphere, the angular part of the KG equation is

$$\begin{aligned}&\!\!\!\frac{1}{\sin \theta }\partial _{\theta }\left( \sin \theta \partial _{\theta }Y_{2}(\theta )\right) \nonumber \\&+\left( \lambda _{2}-\frac{m^{2}-2\left( m q Q_{m}-q^{2}Q_{m}^{2}\right) (1+\cos \theta )}{\sin ^{2}\theta }\right) Y_{2}(\theta )\nonumber \\&=0. \end{aligned}$$
(2.14)

Similarly, we define \(\eta =\cos \theta \) and the above equation can be rewritten as

$$\begin{aligned}&\!\!\!\frac{d^2 Y_{2}}{d\eta ^2}+\left( \frac{1}{\eta -1}+\frac{1}{\eta +1}\right) \frac{dY_{2}}{d\eta }\nonumber \\&\quad +\left[ \frac{m^{2} }{2(\eta +1)} -\frac{\left( 2 q Q_{m}-m\right) ^{2}}{2(\eta -1)}-\lambda _{2}\right] \frac{Y_{2}}{(\eta -1)(\eta +1)}=0. \nonumber \\ \end{aligned}$$
(2.15)

The above is also a Fuchs-type equation with three singularities \((-1,1,\infty )\). The general solutions of it can be expressed by hypergeometric functions as

$$\begin{aligned} \begin{aligned} Y_{2}(\eta )&=C_{3} (1-\eta )^{\frac{-m+2 q Q_{m}}{2}}(1+\eta )^{\frac{ m}{2}} {}_2F_{1}\left( \alpha _{3},\beta _{3};\gamma _{3};z_{3}\right) \\&\quad -C_{4}(1-\eta )^{\frac{m-2 q Q_{m}}{2}}(1+\eta )^{\frac{-m}{2}} {}_2F_{1}\left( \alpha _{4},\beta _{4};\gamma _{4};z_{4}\right) , \end{aligned} \end{aligned}$$
(2.16)

where \(C_{3},C_{4}\) are constants. The parameters in the hypergeometric functions are given by

$$\begin{aligned} \begin{aligned} \alpha _{3}&=\frac{1}{2}\left( 1+2 q Q_{m}+\sqrt{1+4\lambda _{2}}\right) , \\ \alpha _{4}&=\frac{1}{2}\left( 1-2 q Q_{m}+\sqrt{1+4\lambda _{2}}\right) ;\\ \beta _{3}&=\frac{1}{2}\left( 1+2 q Q_{m}-\sqrt{1+4\lambda _{2}}\right) ,\\ \beta _{4}&=\frac{1}{2}\left( 1-2 q Q_{m}-\sqrt{1+4\lambda _{2}}\right) ; \\ \gamma _{3}&=1-m+2 q Q_{m},\quad \quad \quad \quad \quad \quad \gamma _{4}=1+m-2 q Q_{m};\\ z_{3}&=\frac{1}{2} (1-\eta ), \quad \quad \quad \quad \quad \quad \quad \quad \quad z_{4}=\frac{1}{2} (1-\eta ). \end{aligned} \end{aligned}$$
(2.17)

In this case, the radial part of the KG equation is given by

$$\begin{aligned} \Box \frac{d}{dr}\left( \Box \frac{dR}{dr}\right) +U_{2}R=0, \end{aligned}$$
(2.18)

where

$$\begin{aligned} U_{2}=\left( \omega r^2-q Q_e r\right) ^2+\Box \left( q^2 Q^2_m-\mu ^{2}r^{2}-\lambda _{2}\right) . \end{aligned}$$
(2.19)

2.3 Analysis of the angular functions

In order to ensure that the angular functions \(Y_{i}(\theta )\) \((Y_{1}(\chi ), Y_{2}(\eta ))\) are finite at the north and south poles, the general solutions in equations (2.10) and (2.16) are chosen as follows,

$$\begin{aligned} Y_{1}(\chi )= & {} C_{2}(1-\chi )^{\frac{m}{2}}(1+\chi )^{\frac{ -m -2 q Q_{m}}{2}} {}_2F_{1}\left( \alpha _{2},\beta _{2};\gamma _{2};z_{2}x\right) ,\nonumber \!\!\!\!\!\!\\ \end{aligned}$$
(2.20)
$$\begin{aligned} Y_{2}(\eta )= & {} C_{3} (1-\eta )^{\frac{-m+2 q Q_{m}}{2}}(1+\eta )^{\frac{ m}{2}} {}_2F_{1}\left( \alpha _{3},\beta _{3};\gamma _{3};z_{3}\right) .\nonumber \!\!\!\!\!\\ \end{aligned}$$
(2.21)

We also have the following remarks on the parameters in the angular functions,

  1. I:

    Finiteness of the factors \((1-\chi )^{\frac{m}{2}}\) and \((1+\eta )^{\frac{ m}{2}}\) implies

    $$\begin{aligned} m\geqslant 0. \end{aligned}$$
    (2.22)
  2. II:

    In order for the convergence of the functions \(_2F_1(\alpha _{2}\), \(\beta _{2};\gamma _{2};z_{2})\), \(_2F_1(\alpha _{3}\), \(\beta _{3};\gamma _{3};z_{3})\) when \(|z_2|,|z_{3}|\leqslant 1\), we obtain the charge quantization condition and constraints on \(\lambda _{1},\lambda _{2}\)

    $$\begin{aligned} qQ_m= \text {integer}, \lambda _{1}=\lambda _{2}=l(l+1) ,\quad l>q Q_m .\quad \end{aligned}$$
    (2.23)

2.4 The radial equation of motion

Now, we study the radial part of the equation of motion of the scalar perturbation. Based on the discussion of the angular part of the equation of motion, radial equations (2.13) and (2.19) can be rewritten as

$$\begin{aligned} \Box \frac{d}{dr}\left( \Box \frac{dR}{dr}\right) +UR=0, \end{aligned}$$
(2.24)

where

$$\begin{aligned} U=\left( \omega r^2-q Q_e r\right) ^2+\Box \left( q^2 Q^2_m-\mu ^{2}r^{2}-\lambda \right) . \end{aligned}$$
(2.25)

In order to discuss the asymptotic solutions of the radial function near the outer horizon of the black hole, it is convenient to use the tortoise coordinate. Define the tortoise coordinate \(r_{\star }\) by the equation

$$\begin{aligned} \frac{dr_{\star }}{dr}=\frac{r^{2}}{\Box }, \end{aligned}$$
(2.26)

and define a new radial function as \(\xi =rR\), the radial equation (2.24) can be rewritten as

$$\begin{aligned} \frac{d^{2}\xi }{dr^{2}_{\star }}+U_{1}\xi =0, \end{aligned}$$
(2.27)

where

$$\begin{aligned} U_{1}=\frac{U}{r^{4}}-\frac{ \Box }{r^{3}}\frac{d}{dr}\left( \frac{\Box }{r^{2}}\right) . \end{aligned}$$
(2.28)

Here the suitable boundary conditions we need are ingoing wave near the outer horizon (\(r_{\star } \rightarrow -\infty \), i.e. \(r\rightarrow r_{+}\)) and exponentially decaying wave at spatial infinity(\(r_{\star }\rightarrow +\infty \), i.e. \(r\rightarrow +\infty \)). Hence, the radial equation of motion has the following asymptotic solutions

$$\begin{aligned} \xi \thicksim \left\{ \begin{array}{l} {e^{-i\left( \omega -\omega _{c}\right) r_{\star }}},\quad \,\,r_{\star }\rightarrow -\infty ,\\ \\ {e^{-\sqrt{\mu ^2-\omega ^2}r_{\star }}},\quad \,\,r_{\star }\rightarrow +\infty .\\ \end{array} \right. \end{aligned}$$
(2.29)

In the above equation, the critical angular frequency \(\omega _c\) is defined as

$$\begin{aligned} \omega _{c}=q \Psi , \end{aligned}$$
(2.30)

where \(\Psi \) is the electromagnetic potential of the outer horizon of the dyonic RN black hole, \(\Psi =Q_e/r_+\). The superradiant condition for an electrically charged massive scalar perturbation on the dyonic RN black hole background is

$$\begin{aligned} \omega <\omega _{c}=\frac{q Q_{e}}{r_{+}}. \end{aligned}$$
(2.31)

The bound state condition at spatial infinity for the scalar perturbation is

$$\begin{aligned} \omega ^2<\mu ^2. \end{aligned}$$
(2.32)

3 Effective potential and its asymptotic analysis

In this section, we will derive the effective potential from the radial equation of motion and analyze its asymptotic behaviours at the horizons and spatial infinity when the parameters of the scalar field and the black hole satisfy the bound state condition \(\omega ^2<\mu ^2\) and the superradiance condition \(0<\omega <qQ_e/r_+\).

Define a new radial function \(\psi \) by \(\psi =\Box ^\frac{1}{2}R\), then the radial equation of motion (2.24) can be transformed into a Schrodinger-like equation

$$\begin{aligned} \frac{d^2 \psi }{dr^2}+\left( \omega ^2-V\right) \psi =0, \end{aligned}$$
(3.1)

where

$$\begin{aligned} V=\omega ^2-\frac{U+\left( r_{+}-M\right) ^{2}}{\Box ^2} \end{aligned}$$
(3.2)

is the effective potential experienced by the scalar perturbation field. If there is no potential well outside the outer horizon of the dyonic RN black hole, the system composing of the charged massive scalar perturbation field and the dyonic RN black hole is superradiantly stable.

The asymptotic behaviors of the effective potential V at the two horizons and spatial infinity are respectively

$$\begin{aligned}&V\left( r\rightarrow r_-\right) \rightarrow -\infty , ~ V\left( r\rightarrow r_+\right) \rightarrow -\infty ; \end{aligned}$$
(3.3)
$$\begin{aligned}&V(r\rightarrow +\infty )\rightarrow \mu ^2+\frac{2}{r} f(\omega )+O\left( \frac{1}{r^2}\right) . \end{aligned}$$
(3.4)

The asymptotic behavior of the derivative of V at spatial infinity is

$$\begin{aligned} V^{'}(r\rightarrow +\infty )\rightarrow -\frac{ 2}{r^2} f(\omega )+O\left( \frac{1}{r^3}\right) , \end{aligned}$$
(3.5)

where the function \(f(\omega )\) is

$$\begin{aligned} f(\omega )=-2 M \omega ^2+ q Q_e \omega + M \mu ^2. \end{aligned}$$
(3.6)

Now, let’s prove that \(f(\omega )\) is positive with the conditions (2.31) and (2.32). Obviously, there are one negative and one positive real roots for \(f(\omega )=0\) and the positive one is

$$\begin{aligned} \omega _{+}=\frac{q Q_{e}+\sqrt{q^{2} Q_{e}^2+8M^2 \mu ^2}}{4M}. \end{aligned}$$
(3.7)

In order to ensure \(f(\omega )\) is positive, we just need to prove \(0<\omega <\omega _{+}\). We will discuss this in two cases.

  • Case I: \(\omega<\mu <\frac{q Q_{e}}{r_{+}}\)

    $$\begin{aligned} \omega _{+}=\frac{q Q_{e}+\sqrt{q^{2} Q_{e}^2+8M^2 \mu ^2}}{4M}=\frac{q Q_{e}}{4 M}+\sqrt{\frac{q^{2} Q_{e}^{2}}{16 M^{2}}+\frac{\mu ^{2}}{2}}. \end{aligned}$$
    (3.8)

    Since \(r_{+}=M+\sqrt{M^{2}-Q_{e}^{2}-Q_{m}^{2}}>M\), we get an inequality as follows

    $$\begin{aligned} \omega _{+}=\frac{q Q_{e}}{4 M}+\sqrt{\frac{q^{2} Q_{e}^{2}}{16 M^{2}}+\frac{\mu ^{2}}{2}}> \frac{\mu }{4}+\sqrt{\frac{\mu ^{2}}{16}+\frac{\mu ^{2}}{2}}=\mu > \omega . \end{aligned}$$
    (3.9)

  • Case II: \(\omega<\frac{q Q_{e}}{r_{+}}<\mu \)

    We can also easily get

    $$\begin{aligned} \omega _{+}>\frac{q Q_{e}}{4 r_{+}}+\sqrt{\frac{q^2 Q_{e}^2}{16 r_{+}^2}+\frac{q^2 Q_{e}^2}{2 r_{+}^2}}= & {} \frac{q Q_{e}}{4 r_{+}}+\sqrt{\frac{ 9q^2 Q_{e}^2}{16 r_{+}^2}}\nonumber \\= & {} \frac{q Q_{e}}{r_{+}}>\omega . \end{aligned}$$
    (3.10)

From the three equations of (3.33.4)–(3.5), we know that there is at least one extreme between the inner horizon and the outer horizon (\(r_{-}<r<r_{+}\)) and there exists at least one maximum outside the outer horizon (\(r>r_{+}\)) since \(f(\omega )>0\). There is no potential well near the spatial infinity and the system may be superradiantly stable. In next section, we will go a step further and find the regime, satisfied by the parameters of the system, where there is only one maximum outside the outer horizon for the effective potential and no potential well exists, which means the system is superradiantly stable.

4 Analysis of superradiant stability

In this section, we will find the regions in the parameter space where the system of dyonic RN black hole and massive scalar perturbation is superradiantly stable. We determine the parameter regions by considering the extremes of the effective potential in the range \(r_{-}<r<+\infty \).

4.1 Explicit expression of derivative of V

Now, we define a new variable y, \(y=r-r_{-}\). The expression of the derivative of the effective potential V is

$$\begin{aligned} V'(r)= & {} \frac{-2\left( Ar^4+Br^3+Cr^2+Dr+E\right) }{\bigtriangleup ^{3}}\nonumber \\= & {} V'(y)=\frac{-2 \left( A_{1}y^4+B_{1}y^3+C_{1}y^2+D_{1}y+E_{1}\right) }{\bigtriangleup ^{3}},\nonumber \\ \end{aligned}$$
(4.1)

where

$$\begin{aligned} A_{1}= & {} A;\quad B_{1}=\left( 4r_{-}\right) A_{1}+B, \end{aligned}$$
(4.2)
$$\begin{aligned} C_{1}= & {} \left( 6r_{-}^{2}\right) A_{1}+\left( 3r_{-}\right) B_{1}+C, \end{aligned}$$
(4.3)
$$\begin{aligned} D_{1}= & {} \left( 4 r_{-}^{3}\right) A_{1}+\left( 3 r_{-}^{2}\right) B_{1}+\left( 2r_{-}\right) C_{1}, \end{aligned}$$
(4.4)
$$\begin{aligned} E_{1}= & {} \left( r_{-}^{2}\right) A_{1}+\left( r_{-}^{3}\right) B_{1} +\left( r_{-}^{2}\right) C_{1}+\left( r_{-}\right) D_{1}+E.\nonumber \\ \end{aligned}$$
(4.5)

Explicitly,

$$\begin{aligned} A_{1}&= - 2 M \omega ^2 + q Q_e \omega +M \mu ^2, \end{aligned}$$
(4.6)
$$\begin{aligned} B_{1}=&-2\left( 8 M^2-6 M r_++r_+^2\right) \omega ^2+2 q Q_e \left( 5 M-2 r_+\right) \omega \nonumber \\&\quad +\mu ^2 \left( 6 M^2-6 M r_++r_+^2\right) -q^2 \left( Q_e^2+Q_m^2\right) +\lambda , \end{aligned}$$
(4.7)
$$\begin{aligned} C_{1}=&-6 \left( 2 M-r_+\right) {}^3 \omega ^2+9 q Q_e\left( 2 M-r_+\right) {}^2 \omega \nonumber \\&\quad +3\left( \left( M-r_{+}\right) \left( \mu ^{2}\left( 2M-r_{+}\right) ^{2}\right. \right. \nonumber \\&\quad \left. \left. -q^{2}Q_{e}^{2}-q^{2}Q_{m}^{2}+\lambda \right) -Mq^{2}Q_{e}^{2}\right) , \end{aligned}$$
(4.8)
$$\begin{aligned} D_{1}=&-2 \left( 4 M-3 r_+\right) \left( 2 M-r_+\right) {}^3 \omega ^2\nonumber \\&\quad +2 q Q_e \left( 7 M-5 r_+\right) \left( 2 M-r_+\right) {}^2 \omega \nonumber \\&\quad +2 q^2 \left( -Q_m^2 \left( M^2-5 Q_e^2\right) +4 Q_e^4+Q_m^4\right) \nonumber \\&\quad -2 q^2 Q_e^2 \left( 3 M \left( r_+-2 M\right) \right. \nonumber \\&\quad +2 \mu ^2 \left( 2 M^2-3 M r_++r_+^2\right) {}^2\nonumber \\&\quad \left. +2 \left( Q_e^2+Q_m^2\right) \right) -12 M q^2 Q_e^2 r_-\nonumber \\&\quad +2\left( M-r_+\right) {}^2(\lambda -1), \end{aligned}$$
(4.9)
$$\begin{aligned} E_{1}&=\left( r_+-r_-\right) \left( q Q_e-\omega r_- \right) {}^2r_-^2 +\frac{1}{4} \left( r_+-r_-\right) ^3. \end{aligned}$$
(4.10)

Because we are interested in the extremes of effective potential V, i.e. the roots of \(V'\), in the next we mainly analyze the numerator of \(V'\), which is

$$\begin{aligned} g(y)=A_{1}y^4+B_{1}y^3+C_{1}y^2+D_{1}y+E_{1}. \end{aligned}$$
(4.11)

4.2 Analysis of roots of \(V'=0\)

From the asymptotic behaviors of the effective potential at the inner and outer horizons and spatial infinity, we know that there are at least two positive roots for \(g(y)=0\). These two positive real roots are denoted by \(y_{1}\), \(y_{2}\), namely

$$\begin{aligned} y_{1}>0,\quad y_{2}>0. \end{aligned}$$
(4.12)

The numerator of the derivative of the effective potential g(y) is a quartic polynomial in y. The equation \(g(y)=0\) has four roots, which are denoted by \(y_{1},y_{2},y_{3}\) and \(y_{4}\). By the Vieta theorem, we have

$$\begin{aligned} y_{1}+y_{2}+y_{3}+y_{4}&=-\frac{B_{1}}{A_{1}}, \end{aligned}$$
(4.13)
$$\begin{aligned} y_{1}y_{2}+y_{1}y_{3}+y_{1}y_{4}+y_{2}y_{3}+y_{2}y_{4}+y_{3}y_{4}&=\frac{C_{1}}{A_{1}}, \end{aligned}$$
(4.14)
$$\begin{aligned} y_{1}y_{2}y_{3}+y_{1}y_{2}y_{4}+y_{1}y_{3}y_{4}+y_{2}y_{3}y_{4}&=-\frac{D_{1}}{A_{1}}, \end{aligned}$$
(4.15)
$$\begin{aligned} y_{1}y_{2}y_{3}y_{4}&=\frac{E_{1}}{A_{1}}. \end{aligned}$$
(4.16)

It is worth an immediate remark here. The four roots are not necessary all real. \(y_3, y_4\) may be complex roots and \(y_3=y^*_4\). We suppose the four roots are all real. This is the most worse case and we just want to find a sufficient condition for the system to be superradiantly stable.

In the following, we would like to analyze the three coefficients \(A_{1}, C_{1}\) and \(E_{1}\). The coefficient \(A_{1}\) has already proved to be positive in previous section. For coefficient \(E_{1}\), it is easy to see that

$$\begin{aligned} r_{+}>r_{-},\quad E_{1}= & {} \left( r_+-r_-\right) \left( q Q_e-\omega r_- \right) {}^2r_-^2 \nonumber \\&+\frac{1}{4} \left( r_+-r_-\right) ^3>0. \end{aligned}$$
(4.17)

Thus, according to the Eq. (4.16) of Vieta theorem, there are two cases for the four roots of the equation \(g(y)=0\): two positive roots and two negative roots or all four positive roots. If \(C_{1}\) is less than 0, these four roots are two positive and two negative roots, there is no potential well outside the outer horizon and the system is superradiantly stable.

In the following, we will find the regime where \(C_{1}<0\). \(C_{1}\) can be treated as a quadratic polynomial in \(\omega \),

$$\begin{aligned} \begin{aligned} C_1(\omega )&=-6 \left( 2 M-r_+\right) {}^3 \omega ^2+9 q Q_e\left( 2 M-r_+\right) {}^2 \omega \\&\quad +3\left( \left( M-r_{+}\right) \left( \mu ^{2}\left( 2M-r_{+}\right) ^{2}-q^{2}Q_{e}^{2}\right. \right. \\&\quad \left. \left. -q^{2}Q_{m}^{2}+\lambda \right) -Mq^{2}Q_{e}^{2}\right) . \end{aligned} \end{aligned}$$
(4.18)

Given the condition \((M-r_{+})<0\) and the inequality (2.23), \(-q^{2}Q_{m}^{2}+\lambda >0\), we have

$$\begin{aligned}&C_1(\omega )<-6 r_-^3 \omega ^2+9 q Q_e r_-^2 \omega \nonumber \\&\quad +3\left( M-r_{+}\right) \left( \mu ^{2}r_{-}^{2}-q^{2}Q_{e}^{2}\right) -3Mq^{2}Q_{e}^{2}. \end{aligned}$$
(4.19)

Using the equation \(M-r_+=r_--M\), the above inequality can be rewritten as

$$\begin{aligned} C_1(\omega )< & {} -6 r_-^3 \omega ^2+9 q Q_e r_-^2 \omega \nonumber \\&+\frac{3}{2}\mu ^{2} r_-^{3}-\frac{3}{2}\mu ^{2}r_{+}r_{-}^{2}-3 q^{2}Q_{e}^{2}r_{-}. \end{aligned}$$
(4.20)

Considering the bound state condition (2.32) and the above inequality, we have

$$\begin{aligned} C_1(\omega )< & {} -6 r_-^3 \omega ^2+9 q Q_e r_-^2 \omega \nonumber \\&+\frac{3}{2}\omega ^{2} r_-^{3}-\frac{3}{2}\omega ^{2}r_{+}r_{-}^{2}-3 q^{2}Q_{e}^{2}r_{-}\equiv 3r_- h(\omega ),\nonumber \\ \end{aligned}$$
(4.21)

where

$$\begin{aligned} h(\omega )=-\frac{1}{2} \left( 3 r_-^2+r_+ r_-\right) \omega ^2 +3 q Q_e r_- \omega -q^2 Q_e^2.\nonumber \\ \end{aligned}$$
(4.22)

When \(h(\omega )<0\), we have \(C_1<0\). Regarding \(h(\omega )\) as a quadratic function of \(\omega \), the discriminant of h, \(\Delta _{h}\), is

$$\begin{aligned} \Delta _{h}=q^2 Q_e^2 r_{-}\left( 3r_- -2r_+\right) . \end{aligned}$$
(4.23)

It is obvious that when

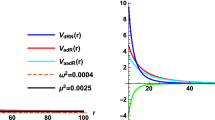
$$\begin{aligned} \frac{r_{-}}{r_{+}}<\frac{2}{3}, \end{aligned}$$
(4.24)

\(\Delta _{h}<0\), \(h(\omega )<0\) and \(C_1(\omega )<0\). Two examples of the superradiantly stable effective potential are illustrated in Fig. 1

Fig. 1
figure 1

Superradiantly stable effective potentials. The black hole mass is chosen as \(M=1\). The charges are chosen as \(Q_{e}=0.4, Q_{m}=0.4\) and \(Q_{e}=0.7,Q_{m}=0.3\) for the solid curve and dashed curve respectively. The other parameters are chosen as \(l=2,\omega =0.02, \mu =0.05, q=0.1 \)

Full size image

5 Summary

We have investigated the superradiant stability property of a system consisting of a dyonic RN black hole and an electrically charged massive scalar perturbation. The dyonic RN black hole is an electrically and magnetically charged black hole which is also spherical and asymptotically flat. The equation of motion of the scalar perturbation in the dyonic RN black hole background is separated into angular and radial parts. We discuss the angular equations in two cases and obtain the charge quantization condition

$$\begin{aligned} qQ_m=\text {integer}, \end{aligned}$$
(5.1)

and a bound on the magnetic charge of the black hole

$$\begin{aligned} l(l+1)>q^{2}Q^{2}_{m}. \end{aligned}$$
(5.2)

The radial equation of motion is transformed into a Schrodinger-like equation and the effective potential V experienced by the scalar perturbation is derived. Through the analysis of the effective potential, we find the following simple regime

$$\begin{aligned} \frac{r_{-}}{r_{+}}<\frac{2}{3}, ~~\text {or}~~ \frac{Q_e^2+Q_m^2}{M^2}<\frac{24}{25} \end{aligned}$$
(5.3)

where there exists no trapping potential outside the black hole horizon and the system is superradiantly stable.

By taking \(Q_m=0\) limit in (5.3), we obtain that the electrically charged RN black hole is superradiantly stable when \(\frac{Q_e^2}{M^2}<\frac{24}{25}\), which is consistent with the previous result that all electrically charged RN black holes with \(\frac{Q_e^2}{M^2}\leqslant 1\) are superradiantly stable under charged massive scalar perturbation  [11,12,13,14]. It is obvious that the limit is not the same as the previous result. This is because we take some approximations in the proof here and the result in (5.3) is a sufficient condition for the dyonic RN black hole to be superradiantly stable. It will be interesting to further study the complementary parameter regime of our result here and get full understand of the superradiance (in)stability for the system with a dyonic RN black hole and scalar perturbation.