1 Introduction

Superradiance is an interesting phenomenon in black hole physics. For a charged rotating black hole, an impinging charged bosonic wave will be amplified by the black hole when the wave frequency \(\omega \) satisfies

$$\begin{aligned} 0<\omega < m\varOmega _H+q\varPhi _H, \end{aligned}$$
(1)

where q and m are the charge and azimuthal quantum number of the incoming wave, \(\varOmega _H\) is the angular velocity of black hole horizon and \(\varPhi _H\) is the electromagnetic potential of the black hole horizon. This superradiance mechanism can be used to extract electromagnetic or rotational energy from black holes by scattering off the black holes with bosonic matter fields. For a comprehensive review on black hole superradiance and its application in various physics areas, one can see [1] and references therein.

Superradiance is important in analyzing the (in)stability property of black holes. If there is a mirror between the black hole horizon and space infinity, the amplified superradiant modes may be scattered back and forth and grows exponentially. This is called a black hole bomb mechanism, which was first suggested by Press and Teukolsky in 1972 [2] and may lead to the superradiant instability of the background black hole geometry [3,4,5].

Superradiant (in)stability of various kinds of black holes have been studied extensively in the literature. Charged Reissner–Nordstrom (RN) black holes were proved superradiantly stable against charged massive scalar perturbation [6,7,8,9,10]. The argument is as follows: when superradiant modes exist for a charged massive scalar perturbation in a RN black hole background, there is no effective trapping potential/mirror outside the black hole horizon, which reflects the superradiant modes back and forth [11,12,13,14,15]. Rotating Kerr black holes may also be superradiantly unstable under massive scalar perturbation, where the mass of the scalar provides a natural mirror [16,17,18,19,20,21,22,23,24,25]. If a mirror-like boundary condition is imposed outside the black hole horizon or if the RN/Kerr black hole is asymptotically non-flat, the black hole is superradiantly unstable in certain parameter spaces [26,27,28,29,30,31]. Besides scalar perturbations, a massive vector perturbation on a rotating Kerr black hole has also been discussed [32, 33].

The superradiant instability properties of charged and rotating Kerr–Newman (KN) black holes under charged massive scalar perturbation were also discussed in literature [34,35,36,37,38]. In [34], the growth rate of unstable modes of the massive scalar field was obtained for \(\mu M\le 1\), where \(\mu \) is the proper mass of the scalar field and M is the mass of the KN black hole. Maximal growth rates were also found for some chosen parameters. In [35], complex resonance spectrum of a charged massive scalar field in a near extremal KN black hole spacetime was studied. It was shown that the superradiant instability growth rates of the scalar fields are characterized by the dimensionless charge-to-mass ratio \(q/\mu \), where q is the charge of the scalar field. Due to the electromagnetic interaction between the scalar field and the KN black hole, it was shown that the growth rate of the instability of KN black hole can be larger than that of a scalar field in Kerr spacetime of the same rotation parameter [37]. For asymptotically non-flat KN-anti-de Sitter black holes, its superradiant instability under charged massive scalar perturbation was studied in [38] and the result indicates that the small KN-anti-de Sitter black hole is unstable against the massive scalar perturbation with small charge.

Although there are some results on superradiant instability of the KN black hole and charged massive scalar perturbation system, there are a few studies of superradiantly stable property of the system. As a complementary study, it will be interesting to investigate the superradiantly stable regions in the parameter space of the system. This investigation will help us to get a further and more comprehensive understanding of the superradiant property of the system in the full parameter space.

As a purely theoretical study, in this paper we will use analytic method to find the superradiantly stable parameter regions for a KN black hole against charged massive scalar perturbation. The radial equation of motion and effective potential for the scalar perturbation are the main objects in our analysis. We will find a region in the parameter space where the superradiance condition and bound state condition hold but there is no potential well outside the black hole outer horizon in the effective potential [21, 25]. It is noteworthy that unexpected simplicity is found in our analysis of some seemingly complicated coefficients in the effective potential.

The paper is organized as follows. In Sect. 2, we provide a simple introduction of the KN-black-hole-massive-scalar system and the angular part of the equation of motion. In Sect. 3, the Schrodinger-like radial equation and the effective potential for the scalar perturbation in KN background are reviewed. Several important asymptotic behaviors of the effective potential and derivative of the effective potential are discussed. In Sect. 4, detailed analysis of the effective potential is given and the superradiantly stable parameter space regions are obtained. Section 5 is devoted to a summary.

2 Kerr–Newman black hole and a charged massive scalar perturbation

In this section, a description of our model and the equation of motion for the scalar perturbation will be given. The physical system consists of a rotating charged Kerr–Newman black hole and a minimally coupled charged massive scalar perturbation. The metric of the 4-dimensional Kerr–Newman black hole in Boyer–Lindquist coordinates \((t,r,\theta ,\phi )\) is (we use natural unit, \(G=\hbar =c=1\))

$$\begin{aligned} ds^2= & {} -\frac{\varDelta }{\rho ^2}\left( dt-\text {a} \sin ^2\theta d\phi \right) ^2+\frac{\rho ^2}{\varDelta }dr^2\nonumber \\&+\rho ^2d\theta ^2+\frac{\sin ^2\theta }{\rho ^2}\left[ \left( r^2+a^2 \right) d\phi -adt \right] ^2, \end{aligned}$$
(2)

where

$$\begin{aligned} \rho ^2\equiv r^2+a^2\cos ^2\theta ,\varDelta \equiv r^2-2Mr+a^2+Q^2, \end{aligned}$$
(3)

Q,  M are the charge and mass of the KN black hole and a is the black hole angular momentum per unit mass. The inner and outer horizons of the Kerr–Newman black hole are

$$\begin{aligned} {{r}_{\pm }}=M\pm \sqrt{{{M}^{2}}-{{a}^{2}}-{{Q}^{2}}}, \end{aligned}$$
(4)

and they satisfy the following obvious relations

$$\begin{aligned} {{r}_{+}}+{{r}_{-}}=2M,\quad {{r}_{+}}{{r}_{-}}={{a}^{2}}+{{Q}^{2}}. \end{aligned}$$
(5)

The background electromagnetic potential is

$$\begin{aligned} A_{\nu }=\left( -\frac{Qr}{\rho ^2},0,0,\frac{aQr\sin ^2\theta }{\rho ^2} \right) . \end{aligned}$$
(6)

The equation of motion for a minimally coupled charged massive scalar perturbation field \(\Phi \) is governed by the following covariant Klein–Gordon equation

$$\begin{aligned} ( \nabla ^{\nu }-iqA^{\nu })( \nabla _{\nu }-iqA_{\nu }) \Phi =\mu ^2\Phi , \end{aligned}$$
(7)

where \(\nabla ^{\nu }\) is the covariant derivative in the KN background. The above equation is separable and the solution of the above equation with definite frequency can be decomposed as

$$\begin{aligned} \Phi ( t,r,\theta ,\phi ) =\sum _{lm}R_{lm}( r ) S_{lm}( \theta ) e^{im\phi }e^{-i\omega t}. \end{aligned}$$
(8)

The radial function \(R_{lm}\) satisfy the radial part of the equation of motion (see Eq. (11) below), which is the main equation studied in the paper. The angular function \(S_{lm}\) are scalar spheroidal harmonics satisfying the angular part of the equation of motion (see Eq. (9) below). \(l(=0,1,2,\ldots )\) and m are integers, \(-l\le m\le l\) and \(\omega \) is the angular frequency of the scalar perturbation.

The angular part of the equation of motion is an ordinary differential equation which is written as follows [39,40,41],

$$\begin{aligned}&\frac{1}{\sin \theta }\frac{d}{d\theta }\left( \sin \theta \frac{dS_{lm}}{d\theta }\right) \nonumber \\&+\left[ \lambda _{lm}+( \mu ^2-\omega ^2) a^2\sin ^2\theta -\frac{m^2}{\sin ^2\theta } \right] S_{lm}=0, \end{aligned}$$
(9)

where \(\lambda _{lm}\) are angular eigenvalues. This equation is the standard spheroidal differential equation which is important in many physical problems and has been studied for a long time. The spheroidal functions \(S_{lm}\) are called prolate (oblate) for \(( \mu ^2-\omega ^2) a^2>0( <0)\). In this paper, we will consider only the prolate case. There is no explicitly analytic expression for angular eigenvalues \(\lambda _{lm}\). Here we choose the following lower bound for this separation constant [23],

$$\begin{aligned} \lambda _{lm}>m^2 -a^2( \mu ^2-\omega ^2). \end{aligned}$$
(10)

The radial part of the Klein–Gordon equation satisfied by \(R_{lm}\) is given by

$$\begin{aligned} \varDelta \frac{d}{dr}\left( \varDelta \frac{dR_{lm}}{dr}\right) +UR_{lm}=0, \end{aligned}$$
(11)

where

$$\begin{aligned} U= & {} \left[ \omega ( a^2+r^2)-am-qQr\right] ^2\nonumber \\&+\varDelta \left[ 2am\omega -\lambda _{lm}-\mu ^2( r^2+a^2)\right] . \end{aligned}$$
(12)

2.1 Boundary conditions

In order to study the superradiant modes of KN black hole under the charged massive scalar perturbation, appropriate boundary conditions should be considered for asymptotic solutions of the radial equation near the horizon and at spatial infinity. Here we use tortoise coordinate to analyse the boundary conditions for the radial function. Define the tortoise coordinate \(r_*\) by following equation

$$\begin{aligned} \frac{dr_*}{dr}=\frac{r^2+a^2}{\varDelta }. \end{aligned}$$
(13)

The boundary conditions we are interested are purely ingoing wave near the outer horizon and exponentially decaying wave at spatial infinity. Therefore, the asymptotic solutions of the radial wave function at these two boundaries are chosen as follows

$$\begin{aligned} R_{lm}( r) \sim {\left\{ \begin{array}{ll} e^{-i( \omega -\omega _c) r_*}, &{}r^*\rightarrow -\infty \text {(}r\rightarrow r_+ \text {)}\\ \frac{e^{-\sqrt{\mu ^2-\omega ^2}r}}{r}, &{}r^*\rightarrow +\infty \text {(}r\rightarrow +\infty \text {)}.\\ \end{array}\right. } \end{aligned}$$

It is easy to see that in order to get decaying modes at spatial infinity we need following bound state condition

$$\begin{aligned} \omega ^2<\mu ^2. \end{aligned}$$
(14)

Here the critical frequency \(\omega _c\) is defined as

$$\begin{aligned} \omega _c=m\varOmega _H+q\varPhi _H, \end{aligned}$$
(15)

where \(\varOmega _H=\frac{a}{r_{+}^{2}+a^2}\) is angular velocity of the outer horizon and \(\varPhi _H=\frac{Qr_+}{r_{+}^{2}+a^2}\) is the electric potential of outer horizon.

3 The radial equation of motion and effective potential

By defining a new radial wave function

$$\begin{aligned} \psi _{lm}\equiv \varDelta ^{\frac{1}{2}}R_{lm}. \end{aligned}$$
(16)

We can transform the radial equation of motion (11) into a Schrodinger-like wave equation

$$\begin{aligned} \frac{d^2\Psi _{lm}}{dr^2}+( \omega ^2-V) \Psi _{lm}=0, \end{aligned}$$
(17)

where

$$\begin{aligned} \omega ^2-V=\frac{U+M^2-a^2-Q^2}{\varDelta ^2}, \end{aligned}$$
(18)

and V is the effective potential, whose explicit expression is

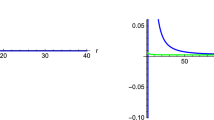
$$\begin{aligned}&V(r)=\omega ^2-\frac{1}{\varDelta ^2}\left[ \left( \omega ( a^2+r^2)-am-qQr\right) ^2\right. \nonumber \\&\left. +\varDelta \left( 2am\omega -\lambda _{lm}-\mu ^2( r^2+a^2)\right) +M^2-a^2-Q^2\right] .\nonumber \\ \end{aligned}$$
(19)

Given the superradiant condition (1), i.e. \(\omega <\omega _c\), and bound state condition (14), if there is no trapping potential well outside the outer horizon of the KN black hole, the KN black hole and charged massive scalar perturbation system will be superradiantly stable. In the following, we will analyze the shape of the effective potential V and discuss the nonexistence of a trapping well. Two typical shapes of this effective potential outside the black hole horizon are shown in Fig. 1.

The asymptotic behaviors of the effective potential V near the inner and outer horizons and at spatial infinity are

$$\begin{aligned}&V( r\rightarrow +\infty ) \rightarrow \mu ^2\nonumber \\&\quad -\frac{2( 2M\omega ^2-qQ\omega -M\mu ^2)}{r}+\mathcal{O}\left( \frac{1}{r^2}\right) , \end{aligned}$$
(20)
$$\begin{aligned}&V( r\rightarrow r_+ ) \rightarrow -\infty ,~~ V( r\rightarrow r_-) \rightarrow -\infty . \end{aligned}$$
(21)

From the above equations, we know the effective potential approaches to a constant at spatial infinity and there is at least one extreme between inner and outer horizons.

Fig. 1
figure 1

Two typical kinds of effective potential V. a is a superradiantly stable potential. The parameters of the scalar field are chosen as \(\omega =0.02, q=0.1,\mu =0.05\). The parameters of the KN black hole are \(M=1, Q=0.6, a=0.3\). The eigenvalue of the angular equation and the azimuthal quantum number are taken as \(\lambda _{lm}=12, m=1\). b is a superradiantly unstable potential. The parameters of the KN black hole and scalar field are taken as \(M=1, Q=0.2, a=0.1, \omega =0.3,q=0.1,\mu =0.1\). The eigenvalue of the angular equation and the azimuthal quantum number are taken as \(\lambda _{lm}=2, m=1\)

Full size image

3.1 Derivative of the effective potential near spatial infinity

The asymptotic behaviour of the derivative of the effective potential V at spatial infinity is

$$\begin{aligned}&V'( r\rightarrow +\infty ) \rightarrow \nonumber \\&\quad -\frac{-4M\omega ^2+2qQ\omega +2M\mu ^2}{r^2}+\mathcal{O}\left( \frac{1}{r^3}\right) . \end{aligned}$$
(22)

The no trapping well condition requires that the derivative of the effective potential is negative. This means the following quadratic function f for \(\omega \)

$$\begin{aligned} f(\omega )=-4M\omega ^2+2Qq\omega +2M\mu ^2, \end{aligned}$$
(23)

should be positive. There are two real roots for equation \(f(\omega )=0\). One is positive and the other one is negative. The positive real root is

$$\begin{aligned} \omega _+=\frac{Qq+\sqrt{Q^2q^2+8M^2\mu ^2}}{4M}. \end{aligned}$$
(24)

Given the bound state condition (14), in order to obtain \(f(\omega )>0\), we just need \(\omega _+>\mu \). Consider the following difference

$$\begin{aligned} \omega _+-\mu= & {} \frac{Qq+\sqrt{Q^2q^2+8M^2\mu ^2}}{4M}-\mu \nonumber \\= & {} \frac{Qq-4M\mu +\sqrt{Q^2q^2+8M^2\mu ^2}}{4M}, \end{aligned}$$
(25)

if

$$\begin{aligned} \left[ \sqrt{Q^2q^2+8M^2\mu ^2}\right] ^2-(Qq-4M\mu )^2 > 0, \end{aligned}$$
(26)

i.e.

$$\begin{aligned} \frac{q}{\mu }\frac{Q}{ M}>1, \end{aligned}$$
(27)

we will get \(\omega _+-\mu >0\) and \(f(\omega )>0\). This is one simple and key result of this paper.

Given the condition (27), there is no trapping well near the spatial infinity and the black hole may be superradiantly stable. In the next section, we will go a step further and find the superradiant stable regions of the parameter space where there is only one extreme outside the outer horizon \(r_+\) and there is no trapping well from the horizon to spatial infinity.

4 The superradiant stability analysis

In this section, the superradiant stable parameter space regions will be determined for the KN black hole and charged massive scalar perturbation system. We will determine these regions by requiring that there is no potential well for the effective potential between the outer horizon and spatial infinity.

4.1 The derivative of the effective potential

Based on the aymptotic analysis of the effective potential V(r) at the inner and outer horizons and spatial infinity, we know that there is at least one real root for \(V'(r)=0\) in each interval of \(r_-< r < r_+\) and \(r>r_+\), given \(A_1>0\). In order to use this root information and exclude irrelevant intervals, we define a new radial coordinate z, \(z=r-{r_-}\). Then the explicit expression of the derivative of the effective potential V in radial coordinates z and r can be written as follows,

$$\begin{aligned} V'( r)= & {} \frac{Ar^4+Br^3+Cr^2+Dr+E}{-\varDelta ^3}\nonumber \\= & {} V'( z)=\frac{A_1z^4+B_1z^3+C_1z^2+D_1z+E_1}{-\varDelta ^3}. \end{aligned}$$
(28)

The relations between the two sets of coefficients are

$$\begin{aligned} A_1= & {} A, \end{aligned}$$
(29)
$$\begin{aligned} {B_1}= & {} B+4r_-A_1, \end{aligned}$$
(30)
$$\begin{aligned} {C_1}= & {} C+3r_-B_1-6r_{-}^{2}A_1, \end{aligned}$$
(31)
$$\begin{aligned} {D_1}= & {} D+4r_{-}^{2}A_1-3r_{-}^{2}B_1+2r_-C_1, \end{aligned}$$
(32)
$$\begin{aligned} {E_1}= & {} E-r_{-}^{4}A_1+r_{-}^{3}B_1-r_{-}^{2}C_1+r_-D_1. \end{aligned}$$
(33)

We use \(f_1 (z)\) to denote the numerator of the derivative of the effective potential \(V'(z)\), which is a quartic polynomial of z. We can study whether there is an trapping well outside the horizon by analyzing the property of the roots of the equation \(f_1(z) = 0\). The four roots of \(f_1(z) = 0\) are denoted by \(z_1\), \(z_2\), \(z_3\) and \(z_4\). According to Vieta theorem, we have the following relations,

$$\begin{aligned} z_1z_2z_3z_4= & {} \frac{E_1}{A_1}, \end{aligned}$$
(34)
$$\begin{aligned} z_1z_2z_3+z_1z_2z_4+z_1z_3z_4+z_2z_3z_4= & {} \frac{-D_1}{A_1}, \end{aligned}$$
(35)
$$\begin{aligned} z_1z_2+z_1z_3+z_1z_4+z_2z_3+z_2z_4+z_3z_4= & {} \frac{C_1}{A_1}, \end{aligned}$$
(36)
$$\begin{aligned} z_1+z_2+z_3+z_4= & {} \frac{-B_1}{A_1}. \end{aligned}$$
(37)

From the asymptotic analysis of V, we know that \(f_1(z)=0\) has at least two positive real roots when \(z> 0\). We denote these two positive real roots by \(z_1, z_2\). Then by requiring the other two roots (\(z_3,z_4\)) are both negative, we can obtain that there is no potential well for V in \(r>r_+\). Given \(A_1>0\), \(E_1>0\) is a necessary condition for \(z_3,z_4 <0\). In principle, \(D_1>0\), or \(C_1<0\), or \(B_1>0\) are all sufficient conditions for \(z_3,z_4 <0\). Here we choose \(C_1<0\), which is easier to be analyzed and leads to a simple constraint on the parameters of the system. The three coefficients, which are relevant with our analysis, are listed as follows

$$\begin{aligned} A_1= & {} 2qQ\omega +2M\mu ^2-4M\omega ^2,\end{aligned}$$
(38)
$$\begin{aligned} C_1= & {} -3(r_+-r_-)\lambda _{lm}+12r_-(Q^2-r_-^2-r_+r_-)\omega ^2\nonumber \\&+6\left[ am(r_-+r_+)-(Q^2-3r_-^2-r_-r_+)qQ\right] \omega \nonumber \\&-3\left( Q^2r_--Q^2r_+-r_-^3+r_+^2 r_-\right) \mu ^2\nonumber \\&-6amqQ-6q^2Q^2r_-,\end{aligned}$$
(39)
$$\begin{aligned} E_1= & {} -4a^2M+4a^2m^2M+4M^3-4MQ^2\nonumber \\&+2amqQ( a^2+Q^2) +4a^2M( -a^2-Q^2) \mu ^2\nonumber \\&+2a^2M( a^2+Q^2) \mu ^2+4M( -a^2-Q^2) \lambda _{lm}\nonumber \\&+2M( a^2+Q^2) \lambda _{lm}+4a^2r_--4a^2m^2r_-\nonumber \\&+4amMqQr_-+2a^2q^2Q^2r_-+4a^2M^2\mu ^2r_-\nonumber \\&-2a^2Q^2\mu ^2r_-+4M^2( -1+\lambda _{lm}) r_-\nonumber \\&+2a^2\lambda _{lm}r_-+2Q^2\Bigg [ 2+Q^2( q-\mu )( q+\mu ) \nonumber \\&+\lambda _{lm}] r_--6amqQr_{-}^{2}-6M( -Q^2\mu ^2\nonumber \\&+\lambda _{lm}) r_{-}^{2}-4M^2\mu ^2r_{-}^{3}-2Q^2( q^2+\mu ^2) r_{-}^{3}\nonumber \\&+2\lambda _{lm}r_{-}^{3}+2M\mu ^2r_{-}^{4}+\omega ^2( 4a^4M+4a^2Q^2r_-\nonumber \\&+4Q^2r_{-}^{3}-4Mr_{-}^{4}) +\omega [ -8a^3mM\nonumber \\&-8amM( -a^2-Q^2) -4amM( a^2+Q^2) \nonumber \\&-2a^2qQ( a^2+Q^2)-4a^2MqQr_-\nonumber \\&-8am( M^2+Q^2) r_-+12amMr_{-}^{2}-6qQ^3r_{-}^{2}\nonumber \\&+4MqQr_{-}^{3}+2qQr_{-}^{4}\Bigg ]. \end{aligned}$$
(40)

In the following, we will discuss the parameter regions of the system arising from the following requirement

$$\begin{aligned} E_1>0, \quad C_1<0, \end{aligned}$$
(41)

under the condition (27). In these regions, there is no trapping potential well acting as a mirror outside the outer horizon of the Kerr–Newman black hole and the black hole and scalar perturbation system is superradiantly stable.

4.2 Analysis of the coefficient \(E_1\)

The coefficient \(E_1\) is lengthy and involves a separation constant \(\lambda _{lm}\) without exact analytic expression, so it seems that it is not easy to get a general analytic proof for its sign. However, we find that this is not the case. An expectedly simple proof for the sign of \(E_1\) will be provided in the following of this section.

Take \(E_1\) as a quadratic function of \(\omega \), which is written as follows,

$$\begin{aligned} E_1\left( \omega \right) =a_{E_1}\omega ^2+b_{E_1}\omega +c_{E_1}, \end{aligned}$$
(42)

where

$$\begin{aligned} a_{E_1}&=4( a^2+r_{-}^{2})\left[ a^2M+r_-Q^2-Mr_{-}^{2}\right] , \nonumber \\ b_{E_1}&=-2a\left( aqQ^3-2mMQ^2+a^3qQ+2a^2mM\right) \nonumber \\&\quad -2r_-\left[ 2a\left( 2mQ^2+aMqQ+2mM^2\right) \right. \nonumber \\&\quad \left. -r_-\left( qQr_{-}^{2}+2qQMr_-+6amM-3qQ^3\right) \right] , \nonumber \\ c_{E_1}&=4M^3+2a^3mqQ+2amqQ^3-2a^4M\mu ^2\nonumber \\&\quad -2MQ^2( 2+\lambda _{lm} ) -2a^2M( 2-2m^2+Q^2\mu ^2\nonumber \\&\quad +\lambda _{lm} ) +4amMqQr_--2a^2r_-\left[ -2+2m^2\right. \nonumber \\&\quad \left. -q^2Q^2+( -2M^2+Q^2) \mu ^2-\lambda _{lm} \right] \nonumber \\&\quad +4M^2r_-( -1+\lambda _{lm}) +2Q^2r_-\left[ 2\right. \nonumber \\&\quad \left. +Q^2( q+\mu )( q-\mu ) +\lambda _{lm}\right] -2r_{-}^{2}\left\{ 3\left[ amqQ\right. \right. \nonumber \\&\quad \left. \left. +M( -Q^2\mu ^2+\lambda _{lm})\right] +r_-\left[ 2M^2\mu ^2\right. \right. \nonumber \\&\quad \left. \left. +Q^2( q^2+\mu ^2) -\lambda _{lm}-M\mu ^2r_-\right] \right\} . \end{aligned}$$
(43)

Firstly, the coefficient \(a_{E_1}\) can be simplified by the relationship between M, a, Q and \(r_-\), \(r_+\) as follows,

$$\begin{aligned} a_{E_1}=2\left( a^2+r_{-}^{2} \right) ^2\left( r_+-r_- \right) , \end{aligned}$$
(44)

which is obviously positive, i.e.,\(a_{E_1}>0\). This means \(E_1\) will be larger than 0 for all \(\omega \) if \(\varDelta _{E_1}<0\). The discriminant of \(E_1\) can be calculated directly as follows,

$$\begin{aligned} \varDelta _{E_1}&=64(a^2 - M^2 + Q^2)^2\left( 4a^2M^2 - 8M^4\right. \nonumber \\&\quad \left. + 8M^2Q^2- Q^4 + 8M^3 \sqrt{-a^2 + M^2 - Q^2}\right. \nonumber \\&\quad \left. - 4MQ^2 \sqrt{-a^2 + M^2 - Q^2}\right) \nonumber \\&\quad =-64(a^2 - M^2 + Q^2)^2( a^2+r_{-}^{2}) ^2<0. \end{aligned}$$
(45)

So we conclude that for any \(\omega \)

$$\begin{aligned} E_1>0. \end{aligned}$$
(46)

This is an interesting result. It is noteworthy to point out that the separation constant \(\lambda _{lm}\) disappears in the discriminant \(\varDelta _{E_1}\).

Then according to the analysis above, we have

$$\begin{aligned} z_1 z_2 z_3 z_4>0. \end{aligned}$$
(47)

As we mentioned before, \(z_1\) and \(z_2\) are two positive roots of the derivative of the effective potential. From the above equation, we find that \(z_3\) and \(z_4\) can only be both positive or both negative when they are real roots.

4.3 Analysis of the coefficient \(C_1\)

In this section, we want to identify a parameter region where \(C_1<0\), then the roots \(z_3, z_4\) are both negative under the condition (27). The expression of \(C_1\) is

$$\begin{aligned} C_1= & {} -3(r_+-r_-)\lambda _{lm}+12r_-(Q^2-r_-^2-r_+r_-)\omega ^2\nonumber \\&+6\left[ am(r_-+r_+)-(Q^2-3r_-^2-r_-r_+)qQ\right] \omega \nonumber \\&-3\left( Q^2r_--Q^2r_+-r_-^3+r_+^2 r_-\right) \mu ^2\nonumber \\&-6amqQ-6q^2Q^2r_-. \end{aligned}$$
(48)

Here, for the eigenvalue of the spheroidal angular equation \(\lambda _{lm}\), we choose the following lower bound [23],

$$\begin{aligned} \lambda _{lm}>m^2 -a^2( \mu ^2-\omega ^2). \end{aligned}$$
(49)

Due to the negative coefficient of \(\lambda _{lm}\) in (48), we can obtain following inequality,

$$\begin{aligned} C_1&<-3(r_+-r_-)[m^2 -a^2( \mu ^2-\omega ^2)]\nonumber \\&\quad +12r_-(Q^2-r_-^2-r_+r_-)\omega ^2\nonumber \\&\quad +6\left[ am(r_-+r_+)-(Q^2-3r_-^2-r_-r_+)qQ\right] \omega \nonumber \\&\quad -3(Q^2r_--Q^2r_+-r_-^3+r_+^2 r_-)\mu ^2\nonumber \\&\quad -6amqQ-6q^2Q^2r_-=-3r_-^2(r_+-r_-)\mu ^2\nonumber \\&\quad +3\left[ 2(a^2+2Q^2)r_--(a^2+4r_-^2)(r_-+r_+)\right] \omega ^2\nonumber \\&\quad +6\left[ -qQ^3+qr_-(3r_-+r_+)Q+am(r_-+r_+)\right] \omega \nonumber \\&\quad -6q^2r_-Q^2-6amqQ+3m^2(r_--r_+). \end{aligned}$$
(50)

Considering the inequality (14) and the negative coefficient of \(\mu \), the above inequality can be further written as

$$\begin{aligned} C_1< & {} -3(3r_-+r_+)(a^2+r_-^2)\omega ^2\nonumber \\&+6[-qQ^3+qr_-(3r_-+r_+)Q+am(r_-+r_+)]\omega \nonumber \\&-6q^2r_-Q^2-6amqQ+3m^2(r_--r_+). \end{aligned}$$
(51)

Now we treat the right side of the above inequality as a quadratic function of \(\omega \),

$$\begin{aligned} g(\omega )= & {} -3(3r_-+r_+)(a^2+r_-^2)\omega ^2\nonumber \\&+6\left[ -qQ^3+qr_-(3r_-+r_+)Q+am(r_-+r_+)\right] \omega \nonumber \\&-6q^2r_-Q^2-6amqQ+3m^2(r_--r_+). \end{aligned}$$
(52)

Identifying a parameter region where \(g(\omega )<0\) will be a sufficient condition for \(C_1<0\) in the same region. We will do this in the following.

It is easy to see that the quadratic coefficient of \(g(\omega )\) is negative. So if the determinant of \(g(\omega )\), \(\Delta _{g(\omega )}\), is negative, then \(g(\omega )<0\). Here we take \(\Delta _{g(\omega )}\) as a quadratic function of the azimuthal quantum number m, which is expressed as

$$\begin{aligned} \Delta _{g(\omega )}\equiv K(m)=36\left[ a_{K(m)}m ^2+b_{K(m)}m +c_{K(m)}\right] , \end{aligned}$$
(53)

where

$$\begin{aligned} a_{K(m)}= & {} r_{-}^{2}\left( 3r_{-}^{2}+2r_+r_--r_{+}^{2}-4Q^2\right) ,\nonumber \\ b_{K(m)}= & {} 4aqQ^3r_- ,\nonumber \\ c_{K(m)}= & {} q^2Q^2\left( 3r_{-}^{4}-2r_+r_{-}^{3}-r_{+}^{2}r_{-}^{2}+Q^4\right) . \end{aligned}$$
(54)

First, let’s consider the quadratic coefficient of K(m), \(a_{K(m)}\). Because \(Q^2>0\), \(a_{K(m)}\) will be negative if the following inequality holds,

$$\begin{aligned} 3r_{-}^{2}+2r_+r_--r_{+}^{2}\leqslant 0, \end{aligned}$$
(55)

i.e.

$$\begin{aligned} \frac{r_-}{r_+}\leqslant \frac{1}{3}. \end{aligned}$$
(56)

This is another important result in this paper.

Next, we consider the discriminant of K(m), \(\Delta _{K(m)}\). The expression of \(\Delta _{K(m)}\) is

$$\begin{aligned} \begin{aligned} \Delta _{K(m)}&=4q^2Q^2r_{-}^{2}(r_{-}^{2}+a^2)\left[ r_-(3r_{+}-r_-)+Q^2\right] \\&\quad \times \left( 3r_{-}^{2}-2r_+r_--r_{+}^{2}\right) . \end{aligned} \end{aligned}$$
(57)

On the right side of the above equation, factors are all obviously positive except the last factor. With the relation \(\frac{r_-}{r_+}\leqslant \frac{1}{3}\) in (56), we can easily prove the sign of the last factor is negative.

$$\begin{aligned}&3r_{-}^{2}-2r_+r_--r_{+}^{2}=r_{+}^{2}\left[ 3\left( \frac{r_-}{r_+}\right) ^2-2\left( \frac{r_-}{r_+}\right) -1\right] <0.\nonumber \\ \end{aligned}$$
(58)

Then,

$$\begin{aligned} \Delta _{K(m)}<0. \end{aligned}$$
(59)

So under the condition \(\frac{r_-}{r_+}\leqslant \frac{1}{3}\),

$$\begin{aligned} \Delta _{g(\omega )}=K(m)<0. \end{aligned}$$
(60)

Then we finally have

$$\begin{aligned} g(\omega )<0,\quad C_1<g(\omega )<0. \end{aligned}$$
(61)

The two real roots \(z_3,z_4\) should be both negative. Then there is only a maximum outside the outer horizon for the effective potential. No trapping potential well exists from outer horizon to spatial infinity.

5 Summary

In this work, the superradiant stability property is analytically studied for a system consisting of a background Kerr–Newman black hole and a charged massive scalar perturbation. The equation of motion of the minimally coupled scalar perturbation in the KN black hole background is separated into angular and radial parts. In our study, the spheroidal angular equation is prolate. The radial equation of motion of the incoming scalar field is written as a Schrodinger-like equation and the superradiant stable parameter space region of the system is determined by analyzing the effective potential V(r).

Under the conditions that the superradiant modes exist in the KN black hole and scalar perturbation system, if there is no trapping potential well outside the KN black hole outer horizon \(r_+\), the system is superradiantly stable. By analysing the derivative of the effective potential V(r), it is found that when the ratio of inner and outer horizons of the KN black hole satisfies

$$\begin{aligned} \frac{r_-}{r_+}\leqslant \frac{1}{3}, \end{aligned}$$
(62)

and the charge-to-mass ratios of the KN black hole and scalar perturbation satisfy

$$\begin{aligned} \frac{q}{\mu }\frac{Q}{M}>1, \end{aligned}$$
(63)

the KN black hole is superradiantly stable against charged massive scalar perturbation.