Abstract
In this paper, we present two new families of spatially homogeneous black hole solution for \(z=4\) Hořava–Lifshitz Gravity equations in \((4+1)\) dimensions with general coupling constant \(\lambda \) and the especial case \(\lambda =1\), considering \(\beta =-1/3\). The three-dimensional horizons are considered to have Bianchi types II and III symmetries, and hence the horizons are modeled on two types of Thurston 3-geometries, namely the Nil geometry and \(H^2\times R\). Being foliated by compact 3-manifolds, the horizons are neither spherical, hyperbolic, nor toroidal, and therefore are not of the previously studied topological black hole solutions in Hořava–Lifshitz gravity. Using the Hamiltonian formalism, we establish the conventional thermodynamics of the solutions defining the mass and entropy of the black hole solutions for several classes of solutions. It turned out that for both horizon geometries the area term in the entropy receives two non-logarithmic negative corrections proportional to Hořava–Lifshitz parameters. Also, we show that choosing some proper set of parameters the solutions can exhibit locally stable or unstable behavior.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 General considerations
The non-relativistic power counting renormalizable theory of Hořava–Lifshitz gravity was proposed by Hořava at the Lifshitz point aimed at resolving the problems concerning the ultraviolet behavior of Einstein gravity [1,2,3]. Hořava–Lifshitz gravity explicitly breaks the Lorentz invariance and restores Einstein’s general relativity at low-energy limits [4]. This modified theory of gravity, which preserves spatial general covariance and time reparametrization invariance, can be regarded as a good candidate for presenting a quantum field theory of gravity [5].
Hořava–Lifshitz gravity has received growing interest and a large number of studies have explored the implications of this proposal in detail. For instance, the cosmological solutions of Hořava–Lifshitz gravity have been studied in [6,7,8,9,10], cosmological perturbation and the related properties have been discussed in [11,12,13,14,15,16,17,18], and some other properties of Hořava–Lifshitz gravity have been investigated in [19,20,21,22]. Particularly, much attention has been paid to black hole solutions and their thermodynamics behavior in the framework of Hořava–Lifshitz gravity [23,24,25,26,27,28,29,30,31,32]. In this context, for instance, the quantum gravity effects by using Hořava–Lifshitz black hole have been investigated in [33], phase transition and the quasinormal modes of a massive scalar field in the background of a rotating Hořava AdS black hole was analyzed in [34, 35], and properties of the black hole solutions were researched in [29, 36,37,38,39,40].
The Hořava–Lifshitz solutions are usually classified by the anisotropy degree between space and time, indicated by the so-called z parameter. Particularly, the \(z = 3\) case has attracted much attention for which the theory is a non-relativistic renormalizable gravity model at short distance, providing a candidate quantum field theory of gravity in the UV [27]. Many works have been done in \(z = 3\) Hořava–Lifshitz gravity, such as black hole solutions [23, 26, 28], Hawking radiation [38], thermodynamical properties [36, 41], perturbation [15], and observational effects [42]. Soon after intruding the original Hořava–Lifshitz gravity, the z = 4 Hořava–Lifshitz gravity was proposed in [27], studied on \((4+1)\) and \((3+1)\) dimensions for instance in [3, 23, 27, 39, 43]. Despite its importance, the \(z= 4\) case has been studied much less extensively than \(z=3\). One of the main motivations to consider this case is its importance in \((3+1)\) dimensions, where from the viewpoint of spectral dimension, the \(z=4\) is favorable because of its consistency with the results of lattice quantum gravity numerical simulations [3, 44]. On the other hand, in \((4 + 1)\) dimensions, power counting super renormalizability in UV region requires \(z = 4\) [2]. Further discussions supporting \(z=4\) case have also been presented [2, 27, 45].
In this work, we are going to consider \( z=4 \) Hořava–Lifshitz gravity in \((4+1)\) dimensions, searching for new topological black hole solutions. The topological black hole solutions in Hořava–Lifshitz gravity were first found in [28]. So far, the horizon geometries of topological black hole solutions in Hořava–Lifshitz theory in \((4+1)\) and \((3+1)\) dimensions have been considered to be spherical, hyperbolic, or flat, indicated by the constant scalar curvature of the horizon, namely \(k=1,-1\), and 0. However, in \((4+1)\) dimensions the situation can be more extensive, where the event horizon of a stationary black hole can be orientable compact 3-dimensional Riemann manifolds, which are required to be endowed with a metric. Based on Thurston geometrization conjecture [46], proved later by Perelman [47], the geometry of such 3-manifolds is locally isometric to one of the eight Thurston type geometries, including three isotropic constant scalar curvature cases of spherical \(S^3\), Hyperbolic \(H^3\), and Euclidean \(E^3\), product constant curvature types \(S^2 \times R\), \(H^2 \times R\), and twisted product types of \(\widetilde{{SL_2R}}\), Solve geometry, and Nil geometry [46]. Except for \(S^3\) and \(E^3\), the other Thurston type geometries are negatively curved spaces. All of these model geometries admit homogeneous metrics and show a close correspondence with the Bianchi types and Kantowski–Sachs homogeneous models [48, 49]. The homogeneous spacetimes, possessing a symmetry called the spatial homogeneity [50], have been widely used in finding cosmological solution in the context of Einstein gravity [51], string theory [52,53,54,55,56], and Hořava–Lifshitz gravity theory [9, 10].
Particularly interesting families of \((4+1)\) dimensional black hole solutions of some gravity theories have been presented in the framework of Bianchi type spacetimes, where the horizons are modeled by some of the Thurston 3-geometries [57,58,59,60,61,62,63,64,65]. These types of black holes are especially of interest in the context of AdS/CFT and holography approaches, where the generators of the translational symmetry are generalized to Bianchi symmetries to avoid some complications for theories in \((3+1)\) dimensions [57, 64]. So far, no black hole solution with Thurston horizon geometries has been obtained for the Hořava–Lifshitz gravity theory. Thus, considering Hořava–Lifshitz gravity as a candidate quantum gravity theory and the importance of investigating AdS/CFT correspondence in the framework of this theory [66, 67], it is interesting to find black hole solutions with special Thurston type horizon geometries for \((4+1)\) dimensional Hořava–Lifshitz gravity, for which the power counting super renormalizability requires \(z=4\).
In this paper, we are interested in spatially homogeneous black hole solutions for \(z=4\) Hořava–Lifshitz gravity on \((4+1)\) dimensional spacetimes, where the three-dimensional horizons are particularly assumed to be homogeneous spaces corresponding to Bianchi types II and III with closed geometries of Nil and \(H^2\times R\), respectively. These negatively curved homogeneous geometries are non-trivial in the sense that they are not constant scalar curvature type geometries that have been extensively studied in previous topological black hole solutions in Hořava–Lifshitz gravity.
The paper is organized as follows: In Sect. 2, a review on Hořava–Lifshitz gravity and its action for \(z=4\) case in \((4+1)\) dimensions is presented. In Sect. 3, we obtain topological black hole solution for the equations of motion of \(z=4\) Hořava–Lifshitz gravity on \((4+1)\) dimensional spacetimes, whose horizons corresponding to the Bianchi types II and III homogeneous spaces, have Nil geometry and \(H^2\times R\) geometry, respectively. Then, the thermodynamic behavior of the solutions is investigated in Sect. 4. Finally, some concluding remarks are presented in Sect. 5.
2 Brief review on Hořava–Lifshitz gravity
In this section, we present some introductory remarks on \(z = 4\) Hořava–Lifshitz gravity [1, 2, 27]. On \((D+1)\) dimensional spacetime, the ADM metric decomposition can be considered as follows
where N, \(N^i\), and \(g_{ij}\) are, respectively, the lapse function, shift function, and spatial metric. The Hořava gravity models exhibit an anisotropic time and space scaling invariance, given by
where the dynamical critical exponent z indicates the degree of anisotropy between space and time. Under this transformation \(g_{ij}\) and N are invariant, but \(N^i\) is scaled as \(N^i\rightarrow l^{1-z} N^i\). In the inverse spatial length units, the dimensions of time and space in the Hořava–Lifshitz gravity are \([t] = -z,\) \( [x] = -1,\) \( [c] = z-1\), at the fixed point with Lifshitz index z. The Hořava–Lifshitz gravity in \(z=1\) case yields the familiar general relativity in the IR limit. In the UV region, renormalizability of Hořava–Lifshitz theory requires different values of z, where the theory becomes power-counting renormalizable with \(z_{UV} = D\), and super-renormalizable with \(z_{UV} > D\).
The simplest kinetic for Hořava–Lifshitz gravity is given by [1, 2, 27]
where g is determinant of the D-dimensional metric \( g_{ij} \), and
is the extrinsic curvature associated with the spatial metric, \( K=g^{ij}K_{ij} \) is its trace, \( \kappa \) is a coupling constant with the scaling dimension at the fixed point \( [\kappa ]=\frac{z-D}{2} \) that is dimensionless in \(D= z=4 \) case, and \( \lambda \) is a dimensionless parameter. Particularly, the \( \lambda =1 \) restores the kinetic term of Einstein’s theory.
The potential term, which satisfies the so-called “detailed balance condition”, is given by [1, 2]
where
is the inverse of DeWitt supermetric, defined by \( {{{\mathcal {G}}}}^{ijkl} =\frac{1}{2}(g^{ik}g^{jl} + g^{il}g^{jk}) - {\lambda } g^{ik}g^{jl} \) where \({{{\mathcal {G}}}}_{ijmn}{{{\mathcal {G}}}}^{mnkl}=\frac{1}{2}(\delta _i^k\delta _j^l+\delta _i^l\delta _j^k)\). Also, \(E^{ij}\) coming from the D-dimensional relativistic action [1, 2]
is the detailed balance condition, which establishes the connection between D-dimensional system described by the action \(W_D\) to a \((D +1)\) dimensional system described by the action \(S_K -S_V\). A theory with spatial isotropy would require \(W _{D}\) to be the action of relativistic theory in Euclidean signature.
2.1 Action for \(z=4\) Hořava–Lifshitz gravity in \((4+1)\) dimensions
In this paper, our focus will be on \(z=4\) Hořava–Lifshitz gravity in \((4+1)\) dimensional spacetimes, where the theory is power-counting renormalizable. In this case, 4-dimensional relativistic Lagrangian is given in the following general form [2, 27]
in which \( k_w \), \( \varLambda _W \), M, and \( \beta \) are coupling constants and \( R_{ij} \) and R are the Ricci tensor and Ricci scalar, respectively. Noting that the Gauss-Bonnet combination is a topological invariant in four dimensions, the second term in (8) includes the most general form of curvature square contribution. Now, according to (7), \(E^{ij}\) is given by
where
Then, combining the kinetic and potential terms, the \(z=4\) Hořava–Lifshitz gravity in \((4+1)\) dimensions is given by the following Lagrangian [27, 68]
in which
In order to restore general relativity in the IR region, the relations between the effective couplings and the speed of light c, Newton coupling G, and the effective cosmological constant \(\varLambda \) are emerged as
Then, in IR region, the \(\lambda =1\) case gives rise to general relativity, provided that the \(\varLambda _w\) takes negative value to have a well-defined c. Then, with negative \(\varLambda _W\), reality of physical parameters in (16) needs \(\lambda >\frac{1}{4}\).
3 Topological \((4+1)\) dimensional black hole solutions for \(z = 4\) Hořava–Lifshitz gravity
We are looking for black hole solutions of \(z=4\) Hořava–Lifshitz gravity equations of motion on \((4+1)\) dimensional spacetime, where the r and t constant hypersurfaces will be assumed to be given by homogeneous spaces corresponding to Bianchi types II and III. There is a correspondence between geometries of Bianchi type II and III symmetric spaces and the Thurston type Nil and \(H^2\times R\) geometries [46], respectively, where \(H^2\) denotes two-dimensional hyperbolic space. The former space is a twisted product manifold while the latter one is a product of constant curvature manifolds.
Setting \(N^i=0\) in (1), we start with the following metric ansatz
where \(\alpha =1, 2, 3\), and the \(\sigma ^{\alpha }\) are left invariant 1-form basis of Bianchi types, given by [52, 69]
As long as the metric coefficients are independent of \(x^i\), the metric will be automatically invariant under the Bianchi type isometrics [57, 69]. The horizons for these topological black holes are negatively curved spaces that can not be described by Einstein spaces metric, i.e. \(R_{\alpha \beta }=k g_{\alpha \beta }\).
It is difficult to obtain solutions for the general value of \(\beta \) in (12). We will restrict our attention to special value \(\beta =-\frac{1}{3}\). Following the method of [26, 28], we will obtain the solutions by substituting the metric ansatz into the Hořava–Lifshitz action with the Lagrangian (12).
3.1 Solution in Bianchi type II
In this Bianchi type, noting (17) and (18), the metric ansatz can be considered as follows
where n, m, a and b are constants. The a and b constants introduce eventual additional scales. The components of \(R_{ij}\), R, \(K_{ij}\), and \(L_{ij}\) for this case are presented in Appendix A, considering \(\beta =-\frac{1}{3}\). It is quite difficult to find the exact solution for general values of n and m. Interestingly, setting \(m=n\) leaves only the two derivative terms in the Hořava–Lifshitz actionFootnote 1
where prim, here and hereafter, stands for derivative with respect to r. Variation of this action with respect to f(r) gives the following equation of motion
Also, the equation of motion of N(r) function can be read easily from the action (21).
In order to guarantee the existence of black hole solutions which are not necessarily extremal, we impose the boundary conditions at the event horizon with \(f(r_H)=0\), \(f'(r_H)\ne 0\), and finite lapse function \(N(r_H)\), where the subscript H, here and in what follows, denotes quantities evaluated at the horizon. Then, the equations of motions yield the following conditions on the horizon
It is worth mentioning that the negative Ricci scalar of the horizon in this Bianchi type is \(R^{(3)}=-\frac{a}{2b^2r_H^{n}}\). Accordingly, we define the following parameter for further uses
Now, solving the equations of motion, we find the following three classes of solutions:
-
For special case \(\lambda =1\) we obtain the following solutions
$$\begin{aligned} N(r)= & {} N_0r^{\frac{n}{2}-1}, \end{aligned}$$(26)$$\begin{aligned} f(r)= & {} - \frac{4}{3} {\frac{{r}^{2} \varLambda }{{{ n}}^{2}}}- \frac{2}{3} {\frac{{r}^{2-n}{\alpha }}{{{ n}}^{2 }}}+\frac{16}{9}{\frac{ {{\alpha }}^{2} k_w^2 {r}^{2(1-n)}}{ M{{ n}}^{ 2}}} \nonumber \\&-\frac{1}{9}{\frac{{r}^{2- n}}{Mb^8{{ n}}^{2}}}\bigg ( 9 {n} {b}^{8}{M}^{2} \left( 9 {C_1} {{n}}^{3}{b}^{8 }+16 {a}^{4}\ln \left( r \right) \right) \nonumber \\&+256 \left( 3 {b}^{4}M- 2 {a}^{2} k_w^2{r}^{-{n}} \right) {a}^{6} k_w^2{ r}^{-{n}} \bigg )^{\frac{1}{2}}, \end{aligned}$$(27)in which the \(N_0\) and \(C_1\) are integrating constants. This set of solutions satisfies the boundary conditions (23) and (24), using \(f(r_H)=0\).
When the conditions (16) hold, general relativity in the IR region can be recovered in the \(\lambda =1\) case, at \(M\rightarrow \infty \) limit, noting (8) and (9). Black hole solutions in the presence of a negative cosmological constant with Nil geometry horizon have been obtained for general relativity in [57, 60, 64], however with different values for the m and n constants in the metric (20), as a consequence of applying generalized Lifshitz scaling invariance on the metric. Here, the obtained solution for f(r) function with considering only the Bianchi symmetry and setting \(m=n\) in metric (20), recasts the following form when \(M\rightarrow \infty \)
which compared to the solutions of [57, 60] contains an extra logarithmic term, even with \(n=2\). However, it is worth mentioning that (28) may remind the Nil geometry solutions with intermediate scaling obtained in [64], which contains logarithmic function at the boundary.
-
When \(\lambda \) is allowed to have any value, in the special case of \(n=2\) we obtain
$$\begin{aligned}&N(r)= N_0, \end{aligned}$$(29)$$\begin{aligned} \&f(r)=-\frac{\alpha }{6}+C_2r^2+\frac{C_1}{r^2}, \end{aligned}$$(30)where \(C_1\) and \(C_2\) are integrating constants. \(C_2\) is actually the cosmological constant redefined up to a factor. These two functions satisfy the boundary conditions on the horizon, given by (23) and (24).
-
Also, another class of solution can be obtained for general values of n and \(\lambda \) as follows
$$\begin{aligned}&N(r)= N_0, \end{aligned}$$(31)$$\begin{aligned}&\begin{aligned} f(r)=- \frac{4}{3} {\frac{{r}^{2} \varLambda }{{{ n}}^{2}}}- \frac{2}{3} {\frac{{r}^{2-n}{\alpha }}{{{ n}}^{2 }}}+&\frac{16}{9}{\frac{ {{\alpha }}^{2} k_w^2 {r}^{2(1-n)}}{ M{{ n}}^{ 2}}}\\&- C_1 r^{s_1}+C_2 r^{s_2}, \end{aligned} \end{aligned}$$(32)in which
$$\begin{aligned} s_1=-\frac{3 }{4}(n-2)-{\sqrt{\mu }},\quad s_2=-\frac{3 }{4}(n-2)+{\sqrt{\mu }},\nonumber \\ \end{aligned}$$(33)and
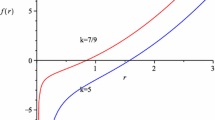
$$\begin{aligned} \mu ={\frac{ \left( 3 n+2 \right) ^{2}\lambda -21 {n}^{2}+12 n-4}{16 (\lambda -1)}}. \end{aligned}$$(34)The solutions (31) and (32) are consistent with the boundary conditions on the horizon. Reminding the \(\lambda >\frac{1}{4}\) condition required by reality of the speed of light in (16), we will also exclude the values of \(\lambda \) in the range of \(1<\lambda <{\frac{21 {n}^{2}-12 n+4}{ \left( 3 n+2 \right) ^{2}}}\), for which \(\mu \) is negative. Here, similar to the solutions presented in [29], there are two branches in (32). It is easy to find that \(s_1\) is negative for any values of n and \(\lambda \), but \(s_2\) can have different signs. Practically, with \(n>2\), for \(\lambda >{\frac{21 {n}^{2}-12 n+4}{ \left( 3 n+2 \right) ^{2}}}\) the power of r in \(C_1\)-dependent term is negative and in the range of \((\frac{3}{2}(2-n),-\frac{3}{2}n+1)\), while for \(C_2\)-dependent term the power of r is in the range of \((\frac{3}{2}(2-n),2)\), which can be either positive or negative, but still less than 2. Also, with \(n>2\), for \(\frac{1}{4}<\lambda <1\) the power of \(C_1\)-dependent term is again negative, while for \(C_2\)-dependent term the power is larger than 2. On the other hand, for \(n<2\), \(s_1\) is again negative for any values of \(\lambda \) but \(s_2\), being positive, is less then 2 as \(\frac{1}{4}<\lambda <1\) and larger than 2 in \(\lambda >{\frac{21 {n}^{2}-12 n+4}{ \left( 3 n+2 \right) ^{2}}}\) range. Dominance of \(\varLambda r^2\) term in (32) at large distance suggests that the solution can have asymptotic behavior of AdS spacetime . But, in the cases that the \(C_2\)-dependent term, having the power of r larger than 2, is dominant at the large distances, the solutions may not have clear physical meaning [29]. Considering this point, to investigate the thermodynamic behavior of this family of solutions we consider the following two cases:
-
(i)
When n and \(\lambda \) are primarily independent and arbitrary parameters, from the asymptotic behavior point of view, similar to the solutions presented in [29] that only the negative branch solutions were selected, we will focus only on the \(C_1\)-dependent term which has negative power of r for any values of \(\lambda \) and n.Footnote 2
-
(ii)
Another special case appears if, keeping the \(\lambda \) parameter general, the following relation between \(\lambda \) and n holds
$$\begin{aligned} \lambda =\frac{3}{4}{\frac{{ n} \left( { n}-2 \right) }{3 { n}-2}}+1. \end{aligned}$$(35)It leads to \(s_2=0\) for \(n\ge 2\), where f(r) function recasts the following formFootnote 3
$$\begin{aligned} \begin{aligned} f(r)&=- \frac{4}{3} {\frac{{r}^{2} \varLambda }{{{ n}}^{2}}}- \frac{2}{3} {\frac{{r}^{2-n}{\alpha }}{{{ n}}^{2 }}}+{\frac{16 {r}^{2(1-n)}{{\alpha }}^{2} k_w^2}{9 M{{ n}}^{ 2}}} \\&\quad +{ C_2}-{r}^{-\frac{3}{2}n+3}{ C_1}, \end{aligned}\nonumber \\ \end{aligned}$$(36)where the \(\varLambda \) term is dominant at large r because the exponents of the other terms are negative. With \(n=2\), which according to (35) is accompanied with \(\lambda =1\), the f(r) function turns into that of \((4+1)\) dimensional black hole solution in \(z=4\) Hořava–Lifshitz gravity with spherical, flat and hyperbolic horizons for \(\lambda =1\) case, presented in [43], where the thermodynamic behavior of solutions has been also discussed. Hence, we will restrict our attention in this case on \(n>2\).
-
(i)
It is worth adding a remark on the asymptotic isometries of the considered classes of solutions with Nil geometry horizon for \(\lambda =1\) and general \(\lambda \). In general, the obtained metrics at \(r\rightarrow \infty \) contain a generalized dilatation generator whose action on the coordinates is given as following
with constant \(\rho \), using a scaling in the constant a of metric. Note that for \(n=2\), there is only one anisotropic direction \(x^2\), similar to the Nil horizon black hole solution for general relativity obtained in [60], while for general values of n, or equivalently the general values of \(\lambda \), the anisotropy appears in all \(x^i\) directions.
3.2 Solutions in Bianchi type III
In this Bianchi type, noting (17) and (19), we can have the following metric ansatz
where n, m, a and b are constants. The components of \(R_{ij}\), R, \(K_{ij}\), and \(L_{ij}\) for this case are presented in Appendix A. Particularly, setting \(m=n\) and substituting the metric into the action gives
Variation of this action with respect to f(r) gives the equation of motion as follows
where the equation of motion of N(r) can be easily read of the action. Also, on the horizon, with the conditions \(f(r_H)=0\) and \(f'(r_H)\ne 0\) and finite lapse function \(N(r_H)\), we should have
The horizon geometry of the black hole solutions with Bianchi type III with metric (38) is equivalent to \(H^2\times R\), and the negative Ricci scalar of the horizon is \(R^{(3)}=-\frac{2}{ar_H^n}\). For further uses, we define the parameter \(\alpha \) in this Bianchi type by
Now, solving the equations of motion we obtain the following classes of solutions:
-
For the special case \(\lambda =1\), we obtain
$$\begin{aligned} N(r)= & {} N_0r^{\frac{n}{2}-1}, \end{aligned}$$(44)$$\begin{aligned} f(r)= & {} -\frac{4}{3}{\frac{{r}^{2}\varLambda }{{n} ^{2}}}-\frac{2}{3}{\frac{{r}^{2-n}{ \alpha }}{{n}^{2}}}+\frac{1}{9}{\frac{{r}^{2(1-n)}{ { k_w}}^{2}{{ \alpha }}^{2}}{M{n}^{2}}}\nonumber \\&-\frac{1}{9}\frac{r^{-n+2}}{n^2 M} \bigg (9{M}^{2}n \left( 9{ C_1}{n}^{3}+4\ln \left( r \right) {\alpha }^{2} \right) \nonumber \\&+2{\alpha }^{3}{{ k_w}}^{2}{r}^{-n} \left( 12M - k_w^2{r}^{-n} \alpha \right) \bigg )^{\frac{1}{2}}, \end{aligned}$$(45)which are consistent with the boundary conditions (41) and (42), without any extra condition on the constants. Similar to the solutions with Nil geometry horizon (27), even at \(M\rightarrow \infty \), the obtained f(r) function for metric (38) with \(m=n\), contains logarithmic function that has not appeared in the other solutions with \(H^2\times R\) geometry horizon, where apart from the 3-isometries of Bianchi type III, the metric was required to be invariant Lifshitz generalized transformations imposing \(n=0\) [58].
-
When \(\lambda \) is allowed to have general values, with \(n=2\) we find the solutions
$$\begin{aligned} N(r)= & {} N_0, \end{aligned}$$(46)$$\begin{aligned} f(r)= & {} -\frac{\alpha }{6}+C_2r^2-\frac{C_1}{r^2}. \end{aligned}$$(47) -
Also, for the general value of \(\lambda \) and n we obtain the solutions
$$\begin{aligned} N(r)= & {} N_0, \end{aligned}$$(48)$$\begin{aligned} f(r)= & {} -\frac{4}{3}{\frac{{r}^{2}\varLambda }{{n} ^{2}}}-\frac{2}{3}{\frac{{r}^{2-n}{ \alpha }}{{n}^{2}}}+\frac{1}{9}{\frac{{r}^{2(1-n)}{ { k_w}}^{2}{{ \alpha }}^{2}}{M{n}^{2}}}\nonumber \\&- C_1 r^{s_1}+C_2 r^{s_2}, \end{aligned}$$(49)where the \(s_1\) and \(s_2\) constants are again given by (33). Here, similar to what we had in the Bianchi type II solutions given by (31) and (32), we will highlight two cases. First, when the n and \(\lambda \) are independent, we will focus on the \(C_1\)-dependent term. In the second case, imposing the special relation (35) between \(\lambda \) and n, we obtain the f(r) function in the following form
$$\begin{aligned} \begin{aligned} f(r)&=-\frac{4}{3}{\frac{{r}^{2}\varLambda }{{n} ^{2}}}-\frac{2}{3}{\frac{{r}^{2-n}{ \alpha }}{{n}^{2}}}+\frac{1}{9}{\frac{{r}^{2(1-n)}{ { k_w}}^{2}{{ \alpha }}^{2}}{M{n}^{2}}}\\&\quad +{ C_2}-{r}^{-\frac{3}{2}n+3}{ C_1}, \end{aligned} \end{aligned}$$(50)in which no inconsistency arises in presence of \(C_2\)-term.
The obtained solutions in all three classes of \(\lambda =1\), \(n=2\) and general \(\lambda \) for Bianchi types II and III are seemed to resemble each other closely. The thermodynamic behavior of the solutions will be studied in the following, where we can compare the physical behaviors. It is worth mentioning that, the solutions in these two Bianchi type classes are not of the constant curvature type with \(R_{\alpha \beta }=kg_{\alpha \beta }\), and the Ricci scalar of the horizon is a function of the radius of the horizon. However, the \(\alpha \) parameters, defined by \(\alpha =-R^{(3)}r_H^{n}\), appeared in the solutions somehow similar to the k parameter of the topological black hole solutions with constant curvature horizons [26,27,28,29,30].
All group of solutions obtained for \(H^2\times R\) horizon geometry with general \(\lambda \) and \(\lambda =1\) are asymptotically invariant under the following Lifshitz generalized transformations
with constant \(\rho \), if one uses the scaling of a. Accordingly, for \(n=2\) the solutions are asymptotically isotropic, while for general values of n, or equivalently general values of \(\lambda \), the anisotropy appears in \(x^2\) direction.
4 Thermodynamic properties of the black hole solutions
In this section we are going to establish the thermodynamic of the obtained solutions, using the canonical Hamilton formulation, where noting the metric (17), the Euclidean continuation of the action is given by [29]
in which B denotes the boundary term. In our cases \(N^i=0\) and we have
where \(\beta \) is the period of Euclidean time, \(\varOmega =\int \sigma ^1\times \sigma ^2\times \sigma ^3\) denotes the volume of 3-dimensional closed space, and \(r_+\) is the radius of the black hole outer horizon defined by the largest root of \(f(r)=0\). For static black holes, the constraint \({{{\mathcal {H}}}}=0\) is required to be satisfied and then the Euclidean action reduces to the boundary term B. Namely, for the on-shell solutions we have
In fact, supplementing the action with boundary term ensures obtaining a well-defined variational principle on these non-asymptotically flat space-times.
Regularity of Euclidean black hole solution requires the time period \(\beta \) to follow the following relation [27, 29]
which yields the temperature of the black hole by
Also, the relation between Euclidean action and free energy \(F_e\)
can be used to obtain the mass m and entropy S of the black hole solutions.
4.1 Thermodynamics of Bianchi type II black hole solutions with Nil geometry horizon
There is a correspondence between the geometry of Bianchi type II spaces and Thurston’s Nil geometry and Heisenberg group, whose isotropy groups are SO(2) and e, respectively [49]. We have found the black hole solutions in this Bianchi type in Sect. 3.1, represented in terms of the Hořava–Lifshitz constants \(\kappa , k_w, M\), \(\lambda \), and the horizon curvature constant related parameter \(\alpha =\frac{a}{2b^2}\). The area of the horizon for this Bianchi type solutions is
We would like to investigate thermodynamic of the solutions using a redefinition of the f(r) function in terms of a new function F(r), similar to the procedure employed in [29]. For instance, with the obtained solutions for \(\lambda =1\) (27) and general \(\lambda \) (32) in mind, defining
the Euclidean action takes the following considerably simplified form
To have a well-defined variation principle the variation of the boundary term B should have the following form
To evaluate this variation on the boundary at the horizon, we will use the following identity for the variation of F [70]
where
leads to
4.1.1 The \(\lambda =1\) case
In this case, the equations of motion of (60) gives N(r) and F(r) in agreement with (26) and (27), and we have
The constant \(N_0\) in the lapse function (26) can be removed by a time redefinition and hence it is not a physical parameter. Also, the mass m and \(N_0\) are a conjugate pair, where \(N_0\) should be kept fixed while m is being varied [29]. The only solution parameter that will be varied here is the \(C_1\) constant, which is related to the physical parameter mass. Using (65), at the boundary at infinity we have
and on the horizon, using (64), the variation of the boundary term is given by
Also, using (55) and (56), temperature in this class of solutions is given by
Here, we can calculate the entropy either by using the \(\delta B_+\) and free energy or by using the first law of thermodynamics (assuming its validity) \(S=\int T^{-1}\frac{d m}{dr_+}dr_++S_0\), where \(S_0\) is an integrating constant.Footnote 4 Either way, we get
The first term is proportional to the area of the horizon. The entropy does not contain logarithmic correction term that is common in \((3+1)\) dimensional Hořava–Lifshitz black hole solutions, but still diverges at \(r_+\rightarrow 0\). The first two terms in the entropy resemble the entropy of \((4+1)\) dimensional black hole solutions with spherical and hyperbolic horizon [27, 43]. Here, for non-constant scalar curvature horizon with Nil geometry, the entropy included also the Hořava–Lifshitz parameter \(k_w\) dependent term which is actually proportional to \(A_H^{-\frac{1}{3}}\).
Also, using (16), the mass recasts the following form in terms of the radius of horizon \(r_+\)
where \(m_0\) is an integrating constant. To investigate the local stability of the solutions we can consider the heat capacity, which using the mass and temperature is given by
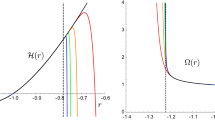
It is not straightforward to use the heat capacity (71) in its general form to determine whether this black hole solution is thermodynamic stable or not. We would like, though, to provide some examples choosing particular set of values for the constants. For instance, with \(\{n = 3, \varLambda = - 1/4, k_w = M=\alpha =b = 1\}\) the positive definiteness of temperature demands \(r_+\gtrsim 1.55\), where the heat capacity is always positive. On the other hand, for example with \(\{n = 3, M = 1/3, k_w = {1}/{2},\varLambda = -0.1, \alpha =b = 1\}\), temperature is positive definite between \(1.54\lesssim r_+\lesssim 1.68\), where the heat capacity starting from zero, is positive until a divergent point at \(r_+\approx 1.6\) and then negatively approaches zero at the upper bound of \(r_+\). Hence, similar to the other black hole solutions of Hořava–Lifshitz gravity [29], depending on the values of parameters, this class of solutions can exhibit locally stable or non-stable behaviors.
As it has been mentioned before, in the \(\lambda =1\) case Hořava–Lifshitz gravity can reduce to general relativity. Black hole solutions for vacuum Einstein field equations with Nil geometry horizon have been obtained in [57, 60], where suitable parameters have been selected to provide a horizon metric admitting additional isometry corresponding to Lifshitz scale invariance and hyperscaling violation. Although we have considered only the 3-isometries of Bianchi types to obtain the solutions, the horizon metric in (20) can be rewritten in the form of the Lifshitz scale invariant metric given in [57], by setting \(a={r_+^{-\frac{n}{2}}}\), or equivalently \(\alpha =\frac{2}{3}r_+^{{ n}}\varLambda \, \left( 4p-3 \right) \) in which for further simplicity we set \(b=\frac{3}{2\sqrt{-3\varLambda (3-4p)}}\), where p is a constant. In this case, as \(M\rightarrow \infty \) the obtained thermodynamic quantities for \(\lambda =1\) solutions behave similar to the general relativity solutions with
where \(A_h=\frac{3}{2\sqrt{-3\varLambda (3-4p)}}r_+^{2n}\) and \(N_0\) has been eliminated by a rescaling in time. The entropy in this limit, being propositional to the area of horizon, is in the form of Bekenstein–Hawking entropy. However, despite the Nil geometry solutions with hyperscaling violation [60], the entropy is positive with positive T.
4.1.2 A non-Einstein case: general \(\lambda \) and \(n=2\)
To investigate the thermodynamic behavior of this class of solutions, given by (29) and (30), noting that the \(C_2\) constant in (30) can be removed by a rescaling of r, we define the new function F(r) by
which yields the action
whose equation of motion gives
From the variation of (74), we find that the variation of the boundary term B should be given by
On the horizon using \(f(r_{+})=0\) and (64) we obtain
and at infinity we have
Removing the variations from this kind of equations to obtain the mass and entropy needs boundary conditions to be imposed [72, 73].Footnote 5 In particular, it requires \(C_2\) to be functionally related to \(C_1\). We will take advantageous of the first law of thermodynamics to determine this functional relation.
The temperature of the black hole can be computed using Euclidean regularity, which gives
The first law of thermodynamics
is then satisfied if the \(C_2\) constant takes one of the following forms
which also gives the relation between \(C_1\) and \(C_2\) using \(f(r_+)=0\). The first expression, being denoted by the “ex” symbol that here and hereafter stands for the extremal case, coincides with the determined \(C_2\) by the condition of degenerate horizon \(f(r)=f'(r)=0\) . Generally, the \(C_2\) parameters in (81) are accompanied by the following \(C_1\) expression, respectively,
Considering these points, the extremal radius of horizon is given by
Now, performing the integrals, the mass and entropy are obtained as follows
Also, the heat capacity is given by
Evidently, the thermodynamic behavior is independent of the value of \(\lambda \). Generally, the heat capacity vanishes when \(r_+\) equals to one of the following radii
and diverges when
Temperature is positive definite for \(r_+\geqslant r_1\) and \(r_1\) is actually the extremal point indicated by (83). Obviously, the heat capacity divergent point \(r_4\) is in the positive temperature range of \(r_+\). But for the zero points \(r_2\) and \(r_3\), depending on the values of parameters, we can have different situations:
-
(i)
If a set of parameters is selected for which \({192 \varLambda M k_w^2+9 {M}^{2}}<0\), there are no real \(r_2\) and \(r_3\) and the solutions at \(r_+\geqslant r_1\) range are stable until \(r_+=r_4\) and then become unstable.Footnote 6
On the other hand, if \({192 \varLambda M k_w^2+9 {M}^{2}}>0\), the \(r_2\) and \(r_3\) are both real. Then,
-
(ii)
If one selects a set of parameters for which \(r_2<r_1<r_4<r_3\), then the solutions are unstable in \(r_1<r_+<r_4\), stable after the divergent point \(r_4\) in \(r_4<r_+<r_3\) range, and then become unstable.Footnote 7
-
(iii)
If a set of parameters is selected to have \(r_2<r_1<r_3<r_4\), the solutions with \(T>0\) are unstable as \(r_1<r_+<r_3\), stable as \(r_3<r_+<r_4\), and then become unstable.Footnote 8
4.1.3 Non-Einstein case: general \(\lambda \)
When the Hořava–Lifshitz coupling constant \(\lambda \) is allowed to have any value, the black hole solutions with Nil geometry horizon have been obtained as given by (31) and (32). As we have mentioned earlier, we intend to consider two cases in this class of solutions. First, in the most general case when n and \(\lambda \) have general and primarily independent values, noting the asymptotic behavior of metric, similar to the solutions obtained in [29], our emphasis is on the negative power of r branch in (32), indicated by \(C_1\) term. The second case is when there is a special relation of type (35) between \(\lambda \) and n, which leaded to f(r) function of the form (36).
In the first category, for which only the \(C_1\) term in the f(r) function (36) is present, to investigate the thermodynamics in Hamiltonian formalism we consider the F(r) function defined by (59), where the Euclidean action takes the form of (60), and the solution for its equations of motion gives
where \(\mu \) is given by (34). Noting the variation of the boundary term of Euclidean action, given by (61), it is easy to find that a definite and non-vanishing \(\delta B_{\infty }\) demands
which, practically, relates the n constant in metric to the \(\lambda \) parameter by
This is, on the other hand, equivalent to \(\mu =0\), which practically leaves no difference between \(C_1\) and \(C_2\) dependent terms in (60). Applying this condition we get
Also, temperature of this black hole solution is given by
These thermodynamic quantities satisfy the first law of thermodynamics. Also, the \(C_1\) constant can be written in terms of radius of horizon as follows
Noting this, we can perform the integrating to obtain the mass and entropy as follows
The first term in entropy is proportional to the area of horizon \(A_H\), given by (58), and there is a divergent in mass and entropy at \(r_+\rightarrow 0\) limit. The heat capacity for this class of solution is given by
which vanishes when \(r_+\) equals to either of the following radii
and diverges when \(r_+\) equals to the following radii
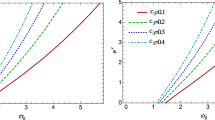
Noting \(\varLambda <0\), \(r_3\) is not real, even for odd valued n. As \(r_+=r_4\), this category of black hole solutions becomes extremal with vanishing temperature. The reality of these radii and local stability depend on the values of parameters. For example, choosing the set of parameters \(\{n = 4, \varLambda = -0.02, k_w=M= \alpha = 1\}\) that keeps only the \(r_1<r_4<r_2\) real, the temperature is positive as \(r_+>r_4\) and in this region the heat capacity is negative until \(r_+=r_2\), and then becomes positive without any divergent. As an another example, if one sets \(\{n=4,M=2,\varLambda =-0.01,k_w=0.1,\alpha =1\}\), the real radii are in the order of \(r_1<r_4<r_6<r_5<r_2\). Here, the positive definiteness of temperature demands, again, \(r_+>r_4\). In this region, the solutions are unstable as \(r_4<r_+<r_5\), then become stable between two divergent points \(r_5\) and \(r_6\), and then the unstable phase in \(r_5<r_+<r_2\) range is followed by another stable phase where \(r_+>r_2\).
In the second case of this class of solutions we consider the category of parameters for the solutions (32) in which \(\lambda \) and n are related to each other by the relation (35), and consequently the f(r) function reduces to (36), in which no asymptotic problem occurs in presence of the \(C_2\) constant. As we have mentioned before, the \(\lambda =1\) case in this class of solutions, which corresponds to \(n=2\), is similar to the solutions for \(\lambda =1\) presented in [43], however with different horizon geometries of flat, spherical, and hyperbolic. Our focus here is on \(n>2\) case. The solution contains two integrating constant \(C_1\) and \(C_2\), while the only physical parameter characterizing this black hole is mass. In topological black hole solutions, whose horizons are constant curvature Einstein spaces, the requirement of asymptotic AdS behavior of the spacetime relates the integrating constant of type \(C_2\) to the curvature constant k of the horizon [74]. However, the Bianchi type II space does not admit Einstein space metric and the horizon curvature depends on \(r_H\). Hence, we consider \(C_2\) as a yet undetermined constant. Then, rewriting the action in terms of the new function F(r) defined by
we obtain the Euclidean action
whose equations of motion gives
The variation of the boundary term for (102) should be given by
Then, using (103), at infinity and on the horizon we obtain
Similar to (78), removing the variations from these equations to obtain the mass and entropy needs boundary conditions to be imposed as a functional relation between \(C_2\) and \(C_1\), or equivalently \(r_+\). To obtain the explicit form of this functional relation we establish the first law of thermodynamics. Noting that, based on Euclidean regularity, the temperature is given by
the first law of thermodynamics revels that the obtained thermodynamic quantities satisfy the first law if we have
which also fixes the relation between \(C_1\) and \(C_2\) using \(f(r_+)=0\). Substituting the expression of \(C_2\) with positive sign in (108) into \(f(r_+)=0\) leads to \(C_1r_+^{\frac{3}{2}(n-2)}=0\), which is not an interesting case. On the other hand, the negative sign in (108) gives an expression for \(C_2\) coincided with the \(C_2\) obtained in extremal case from the conditions \(f(r_+)=f'(r_+)=0\), which is accompanied by the following form of \(C_1\) constant
Hence, the consistent solutions in this class is the extremal case. Temperature vanishes for this solutions and entropy is given by
The near horizon geometry for this extremal solutions can be obtained by using the following change of the variables
and then sending \(\epsilon \rightarrow 0\), which yields the near horizon metric as follows
where
By a scaling of time, the above solution can be rewritten as a product space of \(AdS_2 \times Nil\) with different radii
4.2 Thermodynamics of Bianchi type III solutions with \(H^2\times R\) horizon geometry
Thurston closed geometries of product constant curvature type \(H^2\times R\) and twisted product type \( \widetilde{ {SL_2R}}\) can locally possess Bianchi type III symmetry with SO(2) isotropy [49]. In our considered case, for the Bianchi type III symmetric spacetime metric (38) the geometry of horizon is equivalent to \(H^2\times R\). Families of black hole solutions for this Bianchi type have been obtained in (44)-(49) for \(\lambda =1\) and general \(\lambda \), given in terms of horizon curvature related parameter \(\alpha =\frac{2}{a}\). The area of horizon for these solutions is given by
Having found the solutions for f(r) function beforehand, to investigate the thermodynamics of the solutions (45) and (49) we can rewrite the action in terms of new F(r) function
which gives the Euclidean action
Here, the variation of boundary term B must have the following form
The solutions for this Bianchi type have similar structure to those of Bianchi type II, and to study the thermodynamic properties we will follow the same procedures here.
4.2.1 The \(\lambda =1\) case
With \(\lambda =1\), the solution of equations of motion of action (117), being in agreement with (44) and (45), gives
Using \(f(r_+)=0\), temperature in this class of solutions is given by
Also, using (118) and (119) we have
The first law of thermodynamics is satisfied and the mass and entropy can be calculated up to additive constants as follows
Also, the heat capacity is given by
Depending on the values of parameters we can have stable and unstable solutions here. For example with \(\{\varLambda = -1/3, k_w = 2, n = 3,\alpha = M = 1\}\), temperature is positive definite at \(r_+\gtrsim 1.02\), where the heat capacity is always positive. Also, as an another example, with \(\{\varLambda = -1/30, k_w = 2, n = 4,\alpha = M = 1\}\), respecting the positive definiteness of temperature, the solutions are stable at \(0.645\lesssim r_+\lesssim 0.68\) and \(r_+>2.12\), but unstable in \(0.9\lesssim r_+\lesssim 1.95\) range.
For this class of solutions, to have Lifshitz rescaling invariant horizon metric, similar to that of \(H^2\times R\) horizon geometry solutions for Einstein field equations with negative \(\varLambda \) presented in [58], one can set \(a=-\frac{3}{2\varLambda }r_+^{-n}\) or equivalently \(\alpha =-\frac{4\varLambda }{3}r_+^n\). Then, at \(M\rightarrow \infty \) limit, when the Hořava–Lifshitz theory tends to general relativity, the thermodynamic quantities are obtained as
where \(A_H=\frac{3\varOmega }{2\mid \varLambda \mid }\sqrt{br_+^{n}}\) and we have eliminated \(N_0\) by rescaling of time. The entropy is explicitly in the form of Bekenestein–Hawking entropy form obtained in the solutions of general relativity.
4.2.2 A non-Einstein case: general \(\lambda \) and \(n=2\)
Noting the original form of solutions obtained for general \(\lambda \) and \(n=2\), given by (46) and (47), here we consider a different F(r) from that is given by (116), as
which leads to
whose equations of motion gives
The variation of the Euclidean action requires the variation of the boundary term in the following form
where, using (129), we get
Also, the temperature based on Euclidean regularity is given by
Satisfaction of the first law of thermodynamics by these thermodynamic quantities restricts the \(C_2\) constant to have one of the following forms
where the first expression is identical to the extremal case. Using \(f(r_+)=0\), these two \(C_2\) are accompanied by the following \(C_1\) constant
It is worth mentioning that, in this case the extremal radius of horizon is given in terms of Hořava–Lifshitz parameters as follows
Now, using the second expressions in (134) and (135), and performing the integrals we obtain
Also, the heat capacity is given by
which vanishes when the \(r_+\) equals to the following radiuses
and diverges when
Behavior of heat capacity of this family of solutions is similar to that of the Bianchi type II solutions, given by (86). Temperature is positive definite for \(r_+\geqslant r_1\) and \(r_1\) is actually the extremal radius of horizon introduced by (136). Depending on the values of parameters, we can have different behaviors:
-
(i)
If a set of parameters is chosen that makes \({12 \varLambda M k_w^2+9 {M}^{2}}<0\), there are no real \(r_2\) and \(r_3\) and the solutions at \(r_+ \geqslant r_1\) are stable until \(r_+=r_4\) and then become unstable.Footnote 9
-
(ii)
If a set of parameters is chosen that holds \({12 \varLambda M k_w^2+9 {M}^{2}}>0\), giving \(r_2<r_1<r_4<r_3\), the solutions are unstable at \(r_1<r_+<r_4\) region, and then, after the divergent point \(r_4\), showing stable behavior at \(r_4<r_+<r_3\) range, becomes unstable at \(r_+>r_3\) region.Footnote 10
-
(iii)
If a set of parameters is chosen that yields \({12 \varLambda M k_w^2{+}9 {M}^{2}}>0\), giving the real radii in the order of \(r_2<r_1<r_3<r_4\), the solutions with \(T>0\) are unstable when \(r_1<r_+<r_3\), stable when \(r_3<r_+<r_4\) and after divergent point \(r_4\) become unstable.Footnote 11
4.2.3 Non-Einstein case: general \(\lambda \)
When \(\lambda \) and n constants are arbitrary, the solutions for Bianchi type Bianchi type III spacetime are given by (48) and (49). There is a resemblance between these solutions and those of Bianchi type II spacetime, given by (31) and (32), whose thermodynamic behavior has been studied in Sect. 4.1.3. Similarly, we would like to study the thermodynamic behavior of this family of solutions in two cases.
First, we consider the case that n and \(\lambda \) are essentially arbitrary and independent, where concerning the asymptotic behavior for \(C_1\) and \(C_2\) dependent terms in f(r) function (49), similar to the solutions of [29], we keep only the \(C_1\)-dependent terms which has negative power of r for all values of n and \(\lambda \). Using the Euclidean action (117), written in terms of the F(r) function defined by (116), where the variation of boundary term is given by (118), the solution for the equation of motion of (117) gives the F(r) by
where \(\mu \) is given by (34). It can be checked that in order to have non-vanishing and definite \(\delta B_{\infty }\), the constraint of type (90) and (91) is again required for this Bianchi type solutions. Applying this condition we get
Also, temperature of this black hole solution is given by
These thermodynamic quantities satisfy the first law of thermodynamics. Noting that, the \(C_1\) constant is given in terms of radius of horizon by
the mass and entropy are obtained as follows
Also, the heat capacity for this class of solutions is
which vanishes when \(r_+\) equals to either of following radii
and diverges when \(r_+\) equals to
Similar to what we had in (99), the \(r_3\) is not real with \(\varLambda <0\). In addition, positive definite temperature requires \(r_+\geqslant r_4\), where \(r_4\) is the extremal radius of horizon.
To explore the thermodynamic behavior of heat capacity we choose some values for the appeared parameters in the solutions. As an example, setting \(\{n=4,\varLambda =-0.02,k_w=M=\alpha =1\}\) that keeps only the \(r_1<r_4<r_2\) real, in the \(r_+\geqslant r_4\) region the heat capacity is negative until \(r_+=r_2\) and then becomes positive without any divergence. Also, as an another example, if one sets \(\{n=4,M=2,\varLambda =-0.01,k_w=0.1,\alpha =1\}\), the order of real radii is \(r_1<r_4<r_6<r_5<r_2\). Here, the solutions are unstable in \(r_4<r_+<r_5\) region, then become stable between two divergent points \(r_5\) and \(r_6\), and then there is an unstable phase as \(r_5<r_+<r_2\), which is followed by a stable phase in \(r_+>r_2\) region.
The second group of solutions for (49) is indicated by the f(r) function given by (50), where there is a relation of type (35) between n and \(\lambda \). To study the thermodynamic behavior of this kind of solutions, similar to what have been done in Sect. 4.1.3, we rewrite the action in terms of the new function F(r), defined by
which results in
whose equation of motion gives
The temperature of the black hole based on Euclidean regularity is given by
Also, from the variation of the Euclidean action, we find that the variation of the boundary term is given by
which, using (154), leads to
Satisfactions of the first law of thermodynamics by these thermodynamic quantities demands the \(C_2\) constant to have one of the following forms
Similar to what we had in (108), the positive sign is not an interesting case since substituting it into \(f(r_+)=0\) leads to \(C_1r_+^{\frac{3}{2}(n-2)}=0\). But, with the negative sign, the expression for \(C_2\) constant is identical to the expression given by the condition of degenerate horizon \(f(r)=f'(r)=0\) [36], where the \(C_1\) constant is given by
Then, we have \(T^{\mathrm{ex}}=0\) and
The near horizon geometry of the above solutions can be found by using the following change of the variables
where sending \(\epsilon \rightarrow 0\) and scaling of time gives the near horizon metric as a product space of \(AdS_2 \times H^2\times R\) with different radii
where
5 Conclusion
We have found black hole solutions to \(z=4\) Hořava–Lifshitz gravity in \((4+1)\) dimensions, assuming that the horizons possess Bianchi types II and III symmetries. These solutions can be regarded as topological black hole solutions whose negatively curved three-dimensional horizons are modeled on two types of Thurston’s closed 3-geometries, namely the Nil geometry and \(H^2 \times R\), which are twisted product and product of constant curvature type, respectively. The considered negatively curved geometries do not admit the constant curvature type metric on the horizon, i.e. the Einstein metric \(R_{\alpha \beta }=kg_{\alpha \beta }\). The solutions have been found for \(\beta =-\frac{1}{3}\) in two cases of \(\lambda =1\) and general \(\lambda \). The thermodynamic properties of the solutions have been investigated using the canonical Hamiltonian method. Interestingly, except for the differences in the coefficients, the solutions for two Bianchi types II and III have similar forms of metric component functions f(r) and thermodynamic behaviors.
Generally, the solutions and their thermodynamic quantities are given in terms of some constants, including negative cosmological constant \(\varLambda \), Hořava–Lifshitz constants \( k_w\), and M, the horizon Ricci scalar dependent parameter \(\alpha \) that appears similar to the k parameter of the topological black hole solutions with constant curvature horizons [26,27,28,29], the constant n of metric that is used to provide distinct classes of solutions, and the two integrating constant \(C_1\) and \(C_2\) which are not independent and can be given in terms of radius of horizon using the first law of thermodynamics. Also, the a and b constants in the metric, which can provide additional scaling, besides being interpreted in terms of \(\alpha \), have been used to establish generalized Lifshitz scaling invariance on the horizon and asymptotic region.
For \(\lambda =1\), one of the interesting outputs of the considered horizon geometries for \(z=4\) Hořava–Lifshitz gravity in \((1+4)\) dimensions was existence of a logarithmic branch in the solutions for metric. Even though, similar to the other \((1+4)\) dimensional \(z=4\) black hole solutions, their entropy does not contain logarithmic correction that appears in \(z=3\) black hole solutions in \((1+3)\) dimensions. Also, it has been shown that when the Hořava–Lifshitz terms are neglected at \(M\rightarrow \infty \) limit, the \(\lambda =1\) solutions can behave similar to the solutions obtained for vacuum Einstein equations with negative cosmological constant [58, 60, 64].
For general \(\lambda \), we first considered the special case of \(n=2\). In addition, allowing n to primarily have arbitrary value, we considered two cases using the asymptotic behavior of the solutions and imposing relations between n and \(\lambda \). Then, the appearing n constant in these classes of solutions refers actually to the general value of \(\lambda \). It turned out that for the solutions that possess two integrating constants \(C_1\) and \(C_2\), the energy in Hamiltonian formalism requires more information to be integrated, and the two integrating constants need to be subject to a boundary condition imposed as a functional relation between \(C_1\) and \(C_2\). In fact, this feature and the necessity of imposing the boundary condition were first observed in Einstein-Scalar theory [72], where in the Hamiltonian formalism of mass the functional relation between dilaton charge and the dilaton asymptotic value is required, which can be fixed uniquely if the asymptotic AdS symmetry is of interest [73, 75, 76], leading to satisfaction of first law without including the variation of the non-physical charge of Dilaton [63, 77]. Here, having only the mass as the physical characteristic of the black hole solutions, we employed the first law of thermodynamics to determine the suitable functional relation between \(C_1\) and \(C_2\), which enabled us to calculate the well-defined mass in terms of the radius of the horizon.
A generic feature of the obtained solutions is that the entropy for all classes of solutions with both horizon geometries of Nil and \(H^2\times R\), besides containing a term proportional to the area of horizon \(A_H\), receive two negative corrections of type \(A_H^{\frac{1}{3}}\) proportional to \(\varLambda ^{-1}\), and \(A_H^{-\frac{1}{3}}\) proportional to Hořava–Lifshitz constant \(k_w\). The latter one, which shows a divergent at \(r_+\rightarrow 0\) limit, is a particular consequence of the considered unusual horizon geometries and does not appear in the entropy of \((1+4)\) dimensional topological black hole solutions of \(z=4\) Hořava–Lifshitz gravity with spherical and hyperbolic horizons, obtained in [27, 43]. However, similar to the constant curvature horizon \((1+4)\) dimensional \(z=4\) solutions presented in [27, 43], the entropy for our obtained solutions with horizon geometries of Nil and \( H^2 \times R\) did not receive logarithm correction that is common in \((1+3)\) dimensional black hole solutions in Hořava–Lifshitz gravity [29, 36, 78]. Furthermore, investigating the behavior of heat capacity, it is found out that with proper choices of parameters, the locally stable or unstable phases can appear for all classes of solutions.
In addition, classes of extremal black hole solutions have been provided for both Bianchi types II and III models. We have shown that with general \(\lambda \) if there is a relation of type (90) between \(\lambda \) and n, the consistent solutions are restricted to be in the extremal cases. The near horizon geometries for these extremal black holes were obtained as \(AdS^2\times Nil\) and \(AdS^2\times H^2\times R\) for Bianchi types II and III solutions, respectively. These solutions possess finite entropy at zero temperature, similar to extreme near horizon Reissner–Nordstrom black hole solution. This is also similar to the behavior of Bianchi type II and III charged black hole solutions in extremal near horizon limit that we have studied in [63] in the context of string theory.
The \((4+1)\) dimensional black hole solutions for \(z=4\) Hořava–Lifshitz gravity with flat, hyperbolic and spherical horizons have been already studied in [29, 39, 43]. There is a correspondence between these geometries and Bianchi types I, V (isotropic expansion), and IX. It would be also desirable to investigate black hole solutions for Hořava–Lifshitz gravity with horizons modeled on the other Thurston type geometries of \(\widetilde{{SL_2R}}\) and solve geometry, which correspond to the homogeneous spaces with Bianchi types VIII and \(VI_{-1}\) symmetries. A difficulty in finding solutions with these symmetries is that the equations of motions contain higher derivative terms that can not be eliminated by suitable choices of constants, however, further work is under progress in this sense. Also, in view of applications of black holes with Thurston horizon geometries in AdS/CFT context, where the symmetry requirements on spatial directions are slightly relaxed considering homogeneity instead of usual translational symmetries [57, 64], it would be interesting to further analyze the \((1+4)\) dimensional black holes we obtained for \(z=4\) Hořava–Lifshitz gravity.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This work is entirely theoretical, so we have not used any specific data.]
Notes
It is worth mentioning that for black hole solutions with Nil geometry horizon the requirement of metric of type (20) to admit an additional isometry corresponding to Lifshitz scale invariance, constraints the n and m constants to \(n=2m\) [57, 60]. In this work, we will consider only the 3-isometries of Bianchi types, letting \(n=m\). However, if the Lifshitz scaling invariance on the horizon is the case of interest with \(m=n\), it can be admitted by setting \(a=\sqrt{r_H^{-n}}\).
However, as we will see in the following, a well-defined mass in the Hamiltonian approach needs \(\mu =0\), which practically leaves no difference between \(C_1\) and \(C_2\)-dependent terms in (32).
Similarly, for \(n<2\) we have \(s_1=0\), leading to the last two terms in f(r) in the form of \(-{ C_1}+{ C_2}{r}^{\frac{3}{2}n-3}\).
In fact, it was first observed in AdS context in [72] that for Einstein-Scalar models with scalar filed \(\phi =\frac{\alpha }{r}+\frac{\beta }{r}\) the integrability of energy in Hamiltonian formalism, which contains \(\delta Q_{\phi }=\int \beta \delta \alpha d\varOmega +\dots \) term, forces the coefficients in the asymptotic expansion of the scalar field \(\alpha \) and \(\beta \) to be functionally related.
For example with \(\{\varLambda = - \frac{1}{4}, M = \frac{1}{2}, k_w = \frac{1}{2}, \alpha = 1\}\).
For example with \(\{\varLambda = -0.1, M = 4, k_w = \alpha = 1\}\).
For example with \(\{\varLambda = - \frac{1}{2}, M = \frac{1}{2}, k_w = 0.6, \alpha = 1\}\).
For example with \(\{\varLambda = \frac{1}{40}, M = \frac{1}{3}, k_w = 4, \alpha = 1\}\)
For example with \(\{\varLambda = -0.05, M = 0.5, k_w = 0.6,\alpha = 1\}\).
For example with \(\{\varLambda = - \frac{1}{20}, M = \frac{1}{3}, k_w = 2,\alpha = 1\}\).
References
P. Hořava, J. High Energy Phys. 2009, 020 (2009). arXiv:0812.4287 [hep-th]
P. Hořava, Phys. Rev. D 79, 084008 (2009). arXiv:0901.3775 [hep-th]
P. Hořava, Phys. Rev. Lett. 102, 161301 (2009). arXiv:0902.3657 [hep-th]
N. Afshordi, Phys. Rev. D 80, 081502 (2009). arXiv:0907.5201 [hep-th]
A. Wang, Int. J. Mod. Phys. D 26, 1730014 (2017). arXiv:1701.06087 [gr-qc]
E. Kiritsis, G. Kofinas, Nucl. Phys. B 821, 467 (2009). arXiv:0904.1334 [hep-th]
R. Brandenberger, Phys. Rev. D 80, 043516 (2009). arXiv:0904.2835 [hep-th]
S. Nojiri, S.D. Odintsov, Phys. Rev. D 81, 043001 (2010). arXiv:0905.4213 [hep-th]
T. Christodoulakis, N. Dimakis, J. Geom. Phys. 62, 2401 (2012). arXiv:1112.0903 [gr-qc]
L. Giani, A.Y. Kamenshchik, Class. Quantum Gravity 34, 085007 (2017). arXiv:1606.03243 [gr-qc]
S. Mukohyama, J. Cosmol. Astropart. Phys. 2009, 001 (2009). arXiv:0904.2190 [hep-th]
Y.S. Piao, Phys. Lett. B 681, 1 (2009). arXiv:0904.4117 [hep-th]
X. Gao, Chin. Phys. C 43, 075103 (2019). arXiv:0904.4187 [hep-th]
A. Wang, D. Wands, R. Maartens, J. Cosmol. Astropart. Phys. 2010, 013 (2010). arXiv:0909.5167 [hep-th]
A. Wang, R. Maartens, Phys. Rev. D 81, 024009 (2010). arXiv:0907.1748 [hep-th]
A. Wang, Y. Wu, J. Cosmol. Astropart. Phys. 2009, 012 (2009). arXiv:0905.4117 [hep-th]
R.G. Cai, N. Ohta, Phys. Rev. D 81, 084061 (2010). arXiv:0910.2307v3 [hep-th]
G. Cognola et al., Class. Quantum Gravity 33, 225014 (2016). arXiv:1601.00102v3 [gr-qc]
E.N. Saridakis, Eur. Phys. J. C 67, 229 (2010). arXiv:0905.3532 [hep-th]
C. Bogdanos, E.N. Saridakis, Class. Quantum Gravity 27, 075005 (2010). arXiv:0907.1636 [hep-th]
G. Leon, E.N. Saridakis, J. Cosmol. Astropart. Phys. 2009, 006 (2009). arXiv:0909.3571 [hep-th]
J. Chagoya, G. Tasinato, Class. Quantum Gravity 36, 075014 (2019). arXiv:1805.12010 [hep-th]
M.I. Park, J. High Energy Phys. 2009, 123 (2009). arXiv:0905.4480 [hep-th]
A. Ghodsi, Int. J. Mod. Phys. A 26, 925 (2011). arXiv:0905.0836 [hep-th]
A. Ghodsi, E. Hatefi, Phys. Rev. D 81, 044016 (2010). arXiv:0906.1237 [hep-th]
H. Lü, J. Mei, C.N. Pope, Phys. Rev. Lett. 103, 091301 (2009). arXiv:0904.1595 [hep-th]
R.G. Cai, Y. Liu, Y.W. Sun, J. High Energy Phys. 2009, 010 (2009). arXiv:0904.4104 [hep-th]
R.G. Cai, L.M. Cao, N. Ohta, Phys. Rev. D 80, 024003 (2009). arXiv:0904.3670 [hep-th]
R.G. Cai, L.M. Cao, N. Ohta, Phys. Lett. B 679, 504 (2009). arXiv:0905.0751 [hep-th]
D. Blas, S. Sibiryakov, Phys. Rev. D 84, 124043 (2011). arXiv:1110.2195 [hep-th]
E. Barausse, T. Jacobson, T.P. Sotiriou, Phys. Rev. D 83, 124043 (2011). arXiv:1104.2889 [gr-qc]
C. Eling, Phys. Rev. D 94, 126017 (2016). arXiv:1610.05967 [hep-th]
B. Pourhassan et al., Nucl. Phys. B 928, 415 (2018). arXiv:1705.03005 [hep-th]
R. Bécar et al., Eur. Phys. J. C 80, 1 (2020). arXiv:1906.06654 [gr-qc]
S. Chen, J. Jing, Phys. Lett. B 687, 124 (2010). arXiv:0905.1409 [gr-qc]
Y.S. Myung, Phys. Lett. B 684, 158 (2010). arXiv:0908.4132 [hep-th]
S. Chen, J. Jing, Phys. Rev. D 80, 024036 (2009). arXiv:0905.2055 [gr-qc]
J.J. Peng, S.Q. Wu, Eur. Phys. J. C 66, 325 (2010). arXiv:0906.5121 [hep-th]
D.Y. Chen, H. Yang, X.T. Zu, Phys. Lett. B 681, 463 (2009). arXiv:0910.4821 [gr-qc]
H.W. Lee, Y.W. Kim, Y.S. Myung, Eur. Phys. J. C 68, 255 (2010). arXiv:0907.3568 [hep-th]
M. Wang et al., Phys. Rev. D 81, 083006 (2010). arXiv:0912.4832 [gr-qc]
A. Abdujabbarov, B. Ahmedov, A. Hakimov, Phys. Rev. D 83, 044053 (2011). arXiv:1101.4741 [gr-qc]
M. Liu et al., Phys. Rev. D 87, 024043 (2013). arXiv:1310.0153v1 [gr-qc]
J. Ambjørn, J. Jurkiewicz, R. Loll, Phys. Rev. Lett. 95, 171301 (2005)
M.B.J. Poshteh, R.B. Mann, Phys. Rev. D 103, 104024 (2021). arXiv:2103.04365 [hep-th]
W.P. Thurston, Bull. Am. Math. Soc. (N.S.) 6, 357 (1982)
G. Perelman (2003), arXiv:math/0303109
H.V. Fagundes, Phys. Rev. Lett. 54, 1200 (1985)
Y. Fujiwara, H. Ishihara, H. Kodama, Class. Quantum Gravity 10, 859 (1993). arXiv:gr-qc/9301019
M. Lachieze-Rey, J.P. Luminet, Phys. Rep. 254, 135 (1995). arXiv:gr-qc/9605010v2
G.F.R. Ellis, M.A.H. MacCallum, Commun. Math. Phys. 12, 108 (1969)
N.A. Batakis, A.A. Kehagias, Nucl. Phys. B 449, 248 (1995). arXiv:hep-th/9502007
M.P. Da̧browski, A.L. Larsen, Phys. Rev. D 57, 5108 (1998). arXiv:hep-th/9706020
F. Naderi, A. Rezaei-Aghdam, Nucl. Phys. B 923, 416 (2017). arXiv:1612.06074v4 [hep-th]
F. Naderi, A. Rezaei-Aghdam, F. Darabi, Phys. Rev. D 98, 026009 (2018). arXiv:1712.03581v3 [hep-th]
F. Naderi, A. Rezaei-Aghdam, Eur. Phys. J. C 81, 1 (2021). arXiv:2010.14157 [gr-qc]
N. Iizuka et al., J. High Energy Phys. 2012, 193 (2012). arXiv:1201.4861v2 [hep-th]
C. Cadeau, E. Woolgar, Class. Quantum Gravity 18, 527 (2001). arXiv:gr-qc/0011029
Y. Liu, J. High Energy Phys. 2012, 24 (2012). arXiv:1202.1748 [hep-th]
M. Hassaïne, Phys. Rev. D 91, 084054 (2015). arXiv:1503.01716v1 [hep-th]
M. Bravo-Gaete, M. Hassaïne, Phys. Rev. D 97, 024020 (2018). arXiv:1710.02720v2 [hep-th]
S. Hervik, J. Geom. Phys. 58, 1253 (2008). arXiv:0707.2755v3 [hep-th]
F. Naderi, A. Rezaei-Aghdam, Eur. Phys. J. C 79, 995 (2019). arXiv:1905.11302 [hep-th]
R.E. Arias, I.S. Landea, Phys. Rev. D 99, 106015 (2019). arXiv:1812.09108v2 [hep-th]
R.E. Arias, I.S. Landea, J. High Energy Phys. 2017 (2017). arXiv:1708.04335v2 [hep-th]
R.G. Cai, Y.Z. Zhang, Phys. Rev. D 54, 4891 (1996). arXiv:gr-qc/9609065
R.G. Cai, H.Q. Zhang, Phys. Rev. D 81, 066003 (2010). arXiv:0911.4867 [hep-th]
T.J. Li et al., Phys. Rev. D 90, 124070 (2014). arXiv:1405.4457 [hep-th]
M.P. Ryan, L.C. Shepley, Homogeneous Relativistic Cosmologies (Princeton University Press, 2015)
M. Bañados, C. Teitelboim, J. Zanelli, Phys. Rev. D 49, 975 (1994). arXiv:gr-qc/9307033
E. Kiritsis, G. Kofinas, J. High Energy Phys. 2010, 122 (2010). arXiv:0910.5487 [hep-th]
T. Hertog, G.T. Horowitz, Phys. Rev. Lett. 94, 221301 (2005). arXiv:hep-th/0412169v1
A. Anabalón, D. Astefanesei, C. Martínez, Phys. Rev. D 91, 041501 (2015). arXiv:1407.3296v1 [hep-th]
D. Birmingham, Class. Quantum Gravity 16, 1197 (1999). arXiv:hep-th/9808032v3
M. Henneaux et al., Ann. Phys. 322, 824 (2007). arXiv:hep-th/0603185v2
A. Anabalón et al., J. High Energy Phys. 2016, 117 (2016). arXiv:1511.08759v2 [hep-th]
D. Astefanesei et al., Phys. Lett. B 782, 47 (2018). arXiv:1803.11317 [hep-th]
Y.S. Myung, Phys. Lett. B 678, 127 (2009). arXiv:0905.0957 [hep-th]
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
In this appendix, we present Ricci scalars and the components of \(R_{ij}\), \(K_{ij}\), and \(L_{ij}\) tensors for both Bianchi types II and III models, where the i and j indices run over the radial coordinate r and the Bianchi space part indices \(\{1,2,3\}\).
1.1 Bianchi type II
For this Bianchi type, with the considered metric ansatz (20), the non-zero component of Ricci tensor are given by
Also, the Ricci scalar is
The extrinsic curvature tensor \(K_{ij}\), defined by (4), does not have non-zero components with the metric (20). Also, for \(L_{ij}\) defined by (11), we have the following components, considering \(\beta =-\frac{1}{3}\)
1.2 Bianchi type III
For Bianchi type III, with the metric ansatz (38), the non-zero components of Ricci tensor are
The Ricci scalar is given by
The extrinsic curvature \(K_{ij}\), defined by (4), vanishes with metric (38), and the non-zero components of tensor \(L_{ij}\), defined by (11), considering \(\beta =-\frac{1}{3}\), are as follows
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Naderi, F., Rezaei-Aghdam, A. & Mahvelati-Shamsabadi, Z. Spatially homogeneous black hole solutions in \(z=4\) Hořava–Lifshitz gravity in \((4+1)\) dimensions with Nil geometry and \(H^2\times R\) horizons. Eur. Phys. J. C 81, 865 (2021). https://doi.org/10.1140/epjc/s10052-021-09622-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-021-09622-7