1 Introduction

The no-hair theorem states that a black hole can be uniquely determined via three parameters, its mass, electric charge and angular momentum [1,2,3]. Although this theorem holds true in the Einstein–Maxwell field theory, it suffers from challenges due to the existence of hairy black holes possessing extra macroscopic degrees of freedom in other theories. In fact, various black hole solutions, e.g., hairy black holes in the Einstein–Yang–Mills theory [4,5,6], black holes with Skyrme hairs [7, 8] and black holes with dilaton hairs [9], have been discovered as counter-examples to the no-hair theorem. For a review, see [10].

Spontaneous scalarization typically occurs in models with non-minimal coupling terms of scalar fields, which can source the scalar fields to destabilize scalar-free black hole solutions and form scalarized hairy black holes. This phenomenon was first studied for neutron stars in scalar-tensor models by coupling scalar fields to the Ricci curvature [11]. It was demonstrated that there is a coexistence region for scalar-free and scalarized neutron star solutions, where the scalarized ones can be energetically preferred. Later, it was found that there also exists spontaneous scalarization of black holes in scalar-tensor models, provided that black holes are coupled to non-linear electrodynamics [12, 13] or surrounded by non-conformally invariant matter [14, 15].

Recently, the phenomenon of spontaneous scalarization has been studied in the extended scalar-tensor-Gauss–Bonnet (eSTGB) gravity [16,17,18,19,20,21,22]. In particular, asymptotically anti-de Sitter (AdS) scalarized black holes, as well as their applications to holographic phase transitions, have been studied in a scalar-tensor model with non-minimally coupling the scaler field to the Ricci scalar and the Gauss–Bonnet term [23]. In eSTGB models, the scalar field is non-minimally coupled to the Gauss-Bonnet curvature correction of the gravitational sector, which leads to numerical challenges for solving the evolution equations due to non-linear curvature terms. To better understand the dynamical evolution into scalarized black holes, a similar, but technically simpler, class of models, i.e., Einstein–Maxwell-scalar (EMS) models with non-minimal couplings between the scalar and Maxwell fields, has been put forward in [24], where fully non-linear numerical evolutions of spontaneous scalarization were presented. Subsequently, further studies of spontaneous scalarization in the EMS models were discussed in the context of various non-minimal coupling functions [25, 26], dyons including magnetic charges [27], axionic-type couplings [28], massive and self-interacting scalar fields [29, 30], horizonless reflecting stars [31], stability analysis of scalarized black holes [32,33,34,35,36], higher dimensional scalar-tensor models [37], quasinormal modes of scalarized black holes [38, 39], two U(1) fields [40], quasi-topological electromagnetism [41], topology and spacetime structure influences [42] and the Einstein–Born–Infeld-scalar theory [43]. Besides the above asymptotically flat scalarized black holes, spontaneous scalarization was also discussed in the EMS model with a positive cosmological constant [44]. Additionally, spontaneous vectorization of electrically charged black holes was also proposed [45], analytic treatments were applied to study spontaneous scalarization in the EMS models [46,47,48,49], and an infinite family of exact topological charged hairy black hole solutions was constructed in the EMS gravity system [50].

Studying thermodynamics of the EMS models not only provides evidence for endpoints of the dynamical evolution of unstable scalar-free black holes, but also is interesting per se. Understanding the statistical mechanics of black holes has been a subject of intensive study for several decades. In the pioneering work [51,52,53], Hawking and Bekenstein found that black holes possess the temperature and the entropy. However, asymptotically flat black holes are often thermally unstable since they have negative specific heats. To make black holes thermally stable, appropriate boundary conditions need to be imposed, e.g., putting the black holes in AdS space. Asymptotically AdS black holes become thermally stable since the AdS boundary acts as a reflecting wall. The thermodynamic properties of AdS black holes were first studied by Hawking and Page [54], who discovered the Hawking–Page phase transition between Schwarzschild AdS black holes and thermal AdS space. Later, motivated by AdS/CFT correspondence [55,56,57], there has been much interest in studying phase structure and transitions of AdS black holes [58,59,60,61,62,63,64,65,66,67]. In light of this, it is of great interest to study spontaneous scalarization of asymptotically AdS black holes and associated thermodynamic properties in the EMS models with non-minimal couplings of the scalar and electromagnetic fields.

The remainder of this paper is organized as follows. In Sect. 2, we introduce the EMS model with a negative cosmological constant and derive the free energy in a canonical ensemble. Section 3 is devoted to discussing linear perturbations in scalar-free and scalarized black hole solutions. In Sect. 4, we present our main numerical results, including the domain of existence, entropic preference, effective potentials for radial perturbations, and phase structure and transitions in a canonical ensemble. We summarize our results with a brief discussion in Sect. 5.

2 EMS Model in AdS space

In this section, we derive the equations of motion, asymptotic behavior, the Smarr relation and the Helmholtz free energy for asymptotically AdS scalarized black hole solutions in the EMS model. The action of the EMS model with a negative cosmological constant is

$$\begin{aligned} S_{\text {bulk}}&=-\frac{1}{16\pi }\int d^{4}x\sqrt{-g}\nonumber \\&\quad \times \left[ R-2\Lambda -2\left( \partial \phi \right) ^{2}-f\left( \phi \right) F_{\mu \nu }F^{\mu \nu }\right] , \end{aligned}$$
(1)

where we take \(G=1\) for simplicity throughout this paper. In the action (1) , the scalar field \(\phi \) is minimally coupled to the metric \(g_{\mu \nu }\) and non-minimally coupled to the gauge field \(A_{\mu }\), \(F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }\) is the electromagnetic field strength tensor, \(\Lambda =-3/L^{2}\) is the cosmological constant with the AdS radius L, and \(f\left( \phi \right) \) is the non-minimal coupling function of the scalar and gauge fields.

2.1 Equations of motion

Varying the action (1) with respect to the metric \(g_{\mu \nu }\), the scalar field \(\phi \) and the gauge field \(A_{\mu }\), one obtains the equations of motion,

$$\begin{aligned} R_{\mu \nu }-\frac{1}{2}Rg_{\mu \nu }-\frac{3g_{\mu \nu }}{L^{2}}&=2T_{\mu \nu },\nonumber \\ \square \phi -\frac{1}{4}{\dot{f}}\left( \phi \right) F_{\mu \nu }F^{\mu \nu }&=0,\nonumber \\ \partial _{\mu }\left( \sqrt{-g}f\left( \phi \right) F^{\mu \nu }\right)&=0, \end{aligned}$$
(2)

where \({\dot{f}}\left( \phi \right) \equiv df\left( \phi \right) /d\phi \). The energy-momentum tensor \(T_{\mu \nu }\) in Eq. (2) is given by

$$\begin{aligned} T_{\mu \nu }= & {} \partial _{\mu }\phi \partial _{\nu }\phi -\frac{1}{2}g_{\mu \nu }\left( \partial \phi \right) ^{2}\nonumber \\&+f\left( \phi \right) \left( F_{\mu \rho }F_{\nu }^{\;\rho }-\frac{1}{4}g_{\mu \nu }F_{\rho \sigma }F^{\rho \sigma }\right) . \end{aligned}$$
(3)

In the following, we focus on the spherically symmetric ansatz for the metric, the electromagnetic field and the scalar field,

$$\begin{aligned} ds^{2}&=-N\left( r\right) e^{-2\delta \left( r\right) }dt^{2}+\frac{1}{N\left( r\right) }dr^{2}\nonumber \\&\quad +r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\varphi ^{2}\right) ,\nonumber \\ A_{\mu }dx^{\mu }&=V\left( r\right) dt\text { and }\phi =\phi \left( r\right) . \end{aligned}$$
(4)

Plugging the above ansatz into the equations of motion (2) yields

$$\begin{aligned} N^{\prime }\left( r\right)&=\frac{1-N\left( r\right) }{r}-\frac{Q^{2} }{r^{3}f\left( \phi \left( r\right) \right) }\nonumber \\&\quad -rN\left( r\right) \phi ^{\prime 2}\left( r\right) +\frac{3r}{L^{2}},\nonumber \\ \left( r^{2}N\left( r\right) \phi ^{\prime }\left( r\right) \right) ^{\prime }&=-\frac{{\dot{f}}\left( \phi \left( r\right) \right) Q^{2} }{2f^{2}\left( \phi \right) r^{2}} -r^{3}N\left( r\right) \phi ^{\prime 3}\left( r\right) ,\nonumber \\ \delta ^{\prime }\left( r\right)&=-r\phi ^{\prime 2}\left( r\right) ,\nonumber \\ V^{\prime }\left( r\right)&=-\frac{Q}{r^{2}f\left( \phi \left( r\right) \right) }e^{-\delta \left( r\right) }, \end{aligned}$$
(5)

where primes denote the derivatives with respect to the radial coordinate r, and the integration constant Q can be interpreted as the electric charge of the black hole solution. For later use, we introduce the Misner-Sharp mass function \(m\left( r\right) \) by \(N\left( r\right) =1-2m\left( r\right) /r+r^{2}/L^{2}\).

2.2 Asymptotic behavior

To obtain non-trivial hairy black hole solutions of the non-linear ordinary differential equations (5) , one should impose appropriate boundary conditions at the event horizon and the spatial infinity. Accordingly, in the vicinity of the event horizon at \(r=r_{+}\), we find that the solutions can be approximated as power series expansions in terms of \(\left( r-r_{+}\right) \),

$$\begin{aligned} m\left( r\right)&=\frac{r_{+}}{2}\left( 1+\frac{r_{+}^{2}}{L^{2} }\right) +m_{1}\left( r-r_{+}\right) +\cdots ,\nonumber \\ \delta \left( r\right)&=\delta _{0}+\delta _{1}\left( r-r_{+}\right) +\cdots ,\nonumber \\ \phi \left( r\right)&=\phi _{0}+\phi _{1}\left( r-r_{+}\right) +\cdots ,\nonumber \\ V\left( r\right)&=v_{1}\left( r-r_{+}\right) +\cdots , \end{aligned}$$
(6)

where

$$\begin{aligned} m_{1}= & {} \frac{Q^{2}}{2r_{+}^{2}f\left( \phi _{0}\right) },\nonumber \\ \phi _{1}= & {} -\frac{{\dot{f}}\left( \phi _{0}\right) Q^{2}}{2\left[ f^{2}\left( \phi _{0}\right) r_{+}^{3}-f\left( \phi _{0}\right) r_{+}Q^{2}+3f^{2}\left( \phi _{0}\right) r_{+}^{5}/L^{2}\right] },\nonumber \\ \delta _{1}= & {} -r_{+}\phi _{1}^{2},\quad v_{1}=-\frac{Q}{r_{+}^{2}f\left( \phi _{0}\right) }e^{-\delta _{0}}. \end{aligned}$$
(7)

The two essential parameters, \(\phi _{0}\) and \(\delta _{0}\), can be determined after matching the asymptotic expansions of the solutions at the spatial infinity,

$$\begin{aligned} m\left( r\right)= & {} M-\frac{Q^{2}}{2r}+\cdots ,\quad \phi \left( r\right) =\frac{\phi _{+}}{r^{3}}+\cdots ,\nonumber \\ \delta \left( r\right)= & {} \frac{3\phi _{+}^{2} }{2r^{6}}+\cdots ,\quad V\left( r\right) =\Phi +\frac{Q}{r}+\cdots , \end{aligned}$$
(8)

where \(f\left( 0\right) =1\) is assumed, M is identified as the ADM mass, and \(\Phi \) is the electrostatic potential with \(\Phi =\int _{r_{+}}^{\infty }dre^{-\delta \left( r\right) }Q/\left( r^{2}f\left( \phi \left( r\right) \right) \right) \). Note that the scalar field falls off as \(\phi \left( r\rightarrow \infty \right) \sim Q_{s}/r\) in the asymptotically flat case, where \(Q_{s}\) is the scalar charge [24]. On the other hand, the interpretation of the asymptotic expansion of the scalar field is quite different for asymptotically AdS black holes. In general, the asymptotic scalar field solution of Eq. (5) is \(\phi \left( r\right) \sim \phi _{-}+\frac{\phi _{+}}{r^{3}}\), where, according to the gauge/gravity duality, \(\phi _{+}\) can be interpreted as the expectation value of the dual operator of the scalar field on the conformal boundary in the presence of the external source \(\phi _{-}\). In this paper, the non-normalizable mode of the scalar field is set to vanish, i.e., \(\phi _{-} =0\), corresponding to the absence of the external source in the conformal boundary theory [23, 68]. Interestingly, this type of boundary condition has important holographic applications in systems with spontaneous symmetry breaking, e.g., holographic superconductors [69] and holographic superfluids [70]. Consequently, we can use the shooting method to solve the non-linear differential equations (5) for solutions satisfying the asymptotic expansions at the boundaries. It is also noteworthy that there is a scaling symmetry among the physical quantities,

$$\begin{aligned} r\rightarrow \lambda r,\,M\rightarrow \lambda M,\,Q\rightarrow \lambda Q,\,L\rightarrow \lambda L, \end{aligned}$$
(9)

which allows us to solve Eq. (5) numerically in terms of redefined dimensionless quantities.

2.3 Smarr relation

The Smarr relation [71] can be used to test the accuracy of numerical scalarized black hole solutions, since it associates the black hole mass with other physical quantities. The Smarr relation can be derived from computing the Komar integral for a time-like Killing vector \(K^{\mu }=\left( 1,0,0,0\right) \) in a manifold M. Integrating the identity \(\nabla _{\mu }\left( \nabla _{\nu }K^{\mu }\right) =K^{\mu }R_{\mu \nu }\) over the time constant hypersurface \(\Sigma \), whose boundary \(\partial \Sigma \) consists of the event horizon \(r=r_{+}\) and the spatial infinity \(r=+\infty \), one can use Gauss’s law to obtain

$$\begin{aligned}&\int _{\partial \Sigma }dS_{\mu \nu }\nabla ^{\mu }K^{\nu }\nonumber \\&\quad =\int _{\Sigma }dS_{\mu }K_{\nu }\left( 2T_{\mu \nu }-Tg_{\mu \nu }-\frac{3g_{\mu \nu }}{L^{2}}\right) , \end{aligned}$$
(10)

where \(dS_{\mu \nu }\) is the surface element on \(\partial \Sigma \), and \(dS_{\mu }\) is the volume element on \(\Sigma \), accordingly. Making use of eqns. (3) and (5), we find that the Smarr relation is given by

$$\begin{aligned} M= & {} \frac{A_{H}T}{2}+Q\Phi -e^{-\delta _{0}}\frac{r_{+}^{3}}{L^{2}}\nonumber \\&+\int _{r_{+} }^{\infty }dre^{-\delta \left( r\right) }\delta ^{\prime }\left( r\right) \frac{r^{3}}{L^{2}}, \end{aligned}$$
(11)

where \(A_{H}=4\pi r_{+}^{2}\) is the horizon area, and \(T=N^{\prime }\left( r_{+}\right) e^{-\delta \left( r_{+}\right) }/4\pi \) is the Hawking temperature. For a RNAdS black hole with \(\delta \left( r\right) =0\), the Smarr relation (11) reduces to

$$\begin{aligned} M=\frac{A_{H}T}{2}+Q\Phi -\frac{r_{+}^{3}}{L^{2}}, \end{aligned}$$
(12)

where the last term is the PV term in the extended phase space of AdS black holes [72].

2.4 Free energy

Given a family of scalarized black holes, it is of interest to compute the Helmholtz free energy, which can be used to investigate phase structure and transitions in a canonical ensemble with fixed charge Q and temperature T. The free energy, which is identified as the thermal partition function of black holes, can be derived via constructing the Euclidean path integral. In the semiclassical approximation, the partition function is evaluated by exponentiating the on-shell Euclidean action \(S_{\text {on-shell}}^{E}\),

$$\begin{aligned} Z\sim e^{-S_{\text {on-shell}}^{E}}, \end{aligned}$$
(13)

where the on-shell action \(S_{\text {on-shell}}^{E}\) is obtained by substituting the classical solution into the action. However, the on-shell action \(S_{\text {on-shell}}^{E}\) normally diverges in asymptotically AdS spacetime.One then needs holographic renormalization to remove divergences appearing in the asymptotic region [73, 74]. There are several methods to regularize \(S_{\text {on-shell}}^{E}\), such as the background-subtraction method [60] and the Kounterterms method [75,76,77]. Here, we adopt the counterterm subtraction method to regularize the action by adding a series of boundary terms to the bulk action [78,79,80].

Specifically for the aforementioned bulk action \(S_{\text {bulk}}\) in Eq. (1) , the regularized action \(S_{R}\) is supplied with three boundary terms

$$\begin{aligned} S_{R}=S_{\text {bulk}}+S_{\text {GH}}+S_{\text {ct}}+S_{\text {surf}}\text {,} \end{aligned}$$
(14)

where \(S_{\text {GH}}\) is the Gibbon–Hawking boundary term to render the variational problem well-defined, \(S_{\text {ct}}\) includes counterterms to eliminate divergences on asymptotic boundaries, and \(S_{\text {surf}}\) is used to fix the charge rather than the electrostatic potential when the action is varied [65, 81]. The three boundary terms are given by

$$\begin{aligned} S_{\text {GH}}&=-\frac{1}{8\pi }\int d^{3}x\sqrt{-\gamma }\Theta ,\nonumber \\ S_{\text {ct}}&=\frac{1}{8\pi }\int d^{3}x\sqrt{-\gamma }\left( \frac{2}{L}+\frac{L}{2}R_{3}\right) ,\nonumber \\ S_{\text {surf}}&=-\frac{1}{4\pi }\int d^{3}x\sqrt{-\gamma }f\left( \phi \right) F^{\mu \nu }n_{\mu }A_{\nu }, \end{aligned}$$
(15)

where the integrals are performed on the hypersurface at the spatial infinity, \(\gamma \) is the determinant of the induced metric on the hypersurface, \(\Theta \) is the trace of the extrinsic curvature, \(R_{3}\) is the scalar curvature of the induced metric \(\gamma \), and \(n_{\mu }\) is the unit vector normal to the hypersurface. Using the equations of motion (2) and the asymptotic expansions (8), we obtain the on-shell Euclidean version of \(S_{\text {bulk}}\), \(S_{\text {GH}}\), \(S_{\text {ct}}\) and \(S_{\text {surf}}\),

$$\begin{aligned} S_{\text {bulk, on-shell}}^{E}&=\frac{1}{T}\left( \left. \frac{e^{-\delta \left( r\right) }r^{2}N^{\prime }\left( r\right) -2e^{-\delta \left( r\right) }r^{2}N\left( r\right) \delta ^{\prime }\left( r\right) }{4}\right| _{r=+\infty }\right. \nonumber \\&\quad \left. -TS-Q\Phi \right) ,\nonumber \\ S_{\text {GH, on-shell}}^{E}&=\left. -\frac{1}{T}\left[ \frac{e^{-\delta \left( r\right) }r^{2}N^{\prime }\left( r\right) -2e^{-\delta \left( r\right) }r^{2}\delta ^{\prime }\left( r\right) N\left( r\right) }{4}\right. \right. \nonumber \\&\quad \left. \left. +e^{-\delta \left( r\right) }\left( r-2M+\frac{r^{3}}{L^{2}}\right) \right] \right| _{r=+\infty },\nonumber \\ S_{\text {ct, on-shell}}^{E}&=\left. \frac{e^{-\delta \left( r\right) } }{T}\left( \frac{r^{3}}{L^{2}}+r-M\right) \right| _{r=+\infty },\nonumber \\ S_{\text {surf, on-shell}}^{E}&=\frac{Q\Phi }{T}, \end{aligned}$$
(16)

where \(S=\pi r_{+}^{2}\) is the entropy of the black hole. Consequently, the regularized on-shell Euclidean action for the black hole solution (4) is

$$\begin{aligned} S_{\text {on-shell}}^{E}= & {} S_{\text {bulk, on-shell}}^{E}+S_{\text {GH, on-shell} }^{E}+S_{\text {ct, on-shell}}^{E}\nonumber \\&+S_{\text {surf, on-shell}}^{E}\nonumber \\= & {} \frac{M-TS}{T}. \end{aligned}$$
(17)

The Helmholtz free energy F is related to the Euclidean action \(S_{\text {on-shell}}^{E}\) via

$$\begin{aligned} F=-T\ln Z=TS_{\text {on-shell}}^{E}, \end{aligned}$$
(18)

which gives

$$\begin{aligned} F=M-TS. \end{aligned}$$
(19)

3 Perturbations around Black hole solution

In this section, we investigate linear perturbations around black hole solutions, which can help us understand the stability of the solutions.

3.1 Scalar perturbation around RNAdS black holes

We first examine a scalar perturbation \(\delta \phi \) in a RNAdS black hole background. Note that if \({\dot{f}}\left( 0\right) =0\) is imposed, a RNAdS black hole, which is described by

$$\begin{aligned} N\left( r\right)= & {} 1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}+\frac{r^{2}}{L^{2} },\nonumber \\ A= & {} \frac{Q}{r}dt,\delta \left( r\right) =0,\phi \left( r\right) =0, \end{aligned}$$
(20)

is manifestly a solution of the equations of motion (2). In this scalar-free solution background, we can linearize the scalar equation in Eq. (2) with a scalar perturbation \(\delta \phi \),

$$\begin{aligned} \left( \square -\mu _{eff}^{2}\right) \delta \phi =0, \end{aligned}$$
(21)

where \(\mu _{eff}^{2}=-\ddot{f}\left( 0\right) Q^{2}/\left( 2r^{4}\right) \). In a \(\left( 3+1\right) \)-dimensional asymptotically AdS spacetime of AdS radius L, a scalar field can cause a tachyonic instability only if its mass-squared is less than the so-called Breitenlohner–Freedman (BF) bound \(\mu _{BF}^{2}=-9/\left( 4L^{2}\right) \) [82]. For the scalar perturbation \(\delta \phi \), one always has \(\mu _{eff}^{2}>\mu _{BF}^{2}\) for large enough r, and hence, asymptotically, the RNAdS black hole is stable against the formation of the scalar field, which guarantees that scalarized black holes induced by the tachyonic instability of the scalar field are asymptotically AdS. However, if \(\mu _{eff}^{2}<\mu _{BF}^{2}\) in some region (e.g., near the event horizon), a RNAdS black hole may evolve to a scalarized black hole under a scalar perturbation. Note that if \(\ddot{f}\left( 0\right) <0\), one always has \(\mu _{eff}^{2}>\mu _{BF}^{2}\), and hence a tachyonic instability can not occur.

To study how a scalarized black hole solution bifurcates from a scalar-free black hole solution, we calculate zero modes of the scalar perturbation in the scalar-free black hole background. For simplicity, the scalar perturbation \(\delta \phi \) is written as the decomposition with spherical harmonics functions,

$$\begin{aligned} \delta \phi =\sum _{l,m}Y_{lm}\left( \theta ,\phi \right) U_{l}\left( r\right) . \end{aligned}$$
(22)

With this decomposition, the scalar equation (21) then reduces to

$$\begin{aligned} \frac{1}{r^{2}}\frac{d}{dr}\left( r^{2}N\left( r\right) \frac{dU_{l}\left( r\right) }{dr}\right) -\left[ \frac{l\left( l+1\right) }{r^{2}}+\mu _{eff}^{2}\right] U_{l}\left( r\right) =0. \end{aligned}$$
(23)

Given the fixed values of l and \(\ddot{f}\left( 0\right) \), a family of discrete black hole solutions is selected by requiring that the radial field \(U_{l}\left( r\right) \) is regular at the event horizon and vanishes at the spatial infinity. The black hole solutions can be labelled by a non-negative integer node number n. In this paper, we focus on the \(l=0=n\) fundamental mode since it gives the smallest q of the black hole solutions [24]. Due to the tachyonic instability, scalarized RNAdS black holes may emerge from these zero modes, which compose bifurcation lines in the domain of existence for the scalarized black holes.

3.2 Time-dependent perturbation around scalarized black holes

To investigate the perturbative stability of the scalarized black hole solution (4), we then consider spherically symmetric and time-dependent linear perturbations. Specifically including the perturbations, the metric ansatz is written as [25]

$$\begin{aligned} ds^{2}&=-{\tilde{N}}\left( r,t\right) e^{-2{\tilde{\delta }}\left( r,t\right) }dt^{2}+\frac{dr^{2}}{{\tilde{N}}\left( r,t\right) }\nonumber \\&\quad +r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\varphi ^{2}\right) ,\nonumber \\ {\tilde{N}}\left( r,t\right)&=N\left( r\right) +\epsilon {\tilde{N}} _{1}\left( r\right) e^{-i\Omega t},\nonumber \\ {\tilde{\delta }}\left( r,t\right)&=\delta \left( r\right) +\epsilon {\tilde{\delta }}_{1}\left( r\right) e^{-i\Omega t}, \end{aligned}$$
(24)

where the time dependence of the perturbations is assumed to be Fourier modes with frequency \(\Omega \). Similarly, the ansatzes of the scalar and electromagnetic fields are given by

$$\begin{aligned} {\tilde{\phi }}\left( r,t\right)= & {} \phi \left( r\right) +\epsilon \phi _{1}\left( r\right) e^{-i\Omega t}\quad \text {and}\nonumber \\ {\tilde{V}}\left( r,t\right)= & {} V\left( r\right) +\epsilon V_{1}\left( r\right) e^{-i\Omega t}, \end{aligned}$$
(25)

respectively. Solving Eq. (2) with the ansatzes (24) and (25), we can extract a Schrodinger-like equation for the perturbative scalar field \(\phi _{1}\left( r\right) \),

$$\begin{aligned} -\frac{d^{2}\Psi \left( r\right) }{dr^{*2}}+U_{\Omega }\Psi \left( r\right) =\Omega ^{2}\Psi \left( r\right) , \end{aligned}$$
(26)

where \(\Psi \left( r\right) \equiv r\phi _{1}\left( r\right) \), and the tortoise coordinate \(r^{*}\) is defined by \(dr^{*}/dr\equiv e^{\delta \left( r\right) }N^{-1}\left( r\right) \). Here, the effective potential \(U_{\Omega }\) is given by

$$\begin{aligned} U_{\Omega }= & {} \frac{e^{-2\delta }N}{r^{2}}\Bigg \{ 1-N-2r^{2}\phi ^{\prime 2} -\frac{Q^{2}}{r^{2}f\left( \phi \right) }\Bigg ( 1-2r^{2}\phi ^{\prime 2} \nonumber \\&+\frac{\ddot{f}\left( \phi \right) }{2f\left( \phi \right) }+2r\phi ^{\prime }\frac{{\dot{f}}\left( \phi \right) }{f\left( \phi \right) }-\frac{{\dot{f}} ^{2}\left( \phi \right) }{f^{2}\left( \phi \right) }\Bigg ) \nonumber \\&\quad +\frac{3r^{2}\left( 1-2r^{2}\phi ^{\prime 2}\right) }{L^{2}}\Bigg \} . \end{aligned}$$
(27)

One can show that the effective potential \(U_{\Omega }\) vanishes at the event horizon, whereas approaches positive infinity at the spatial infinity. From quantum mechanics, the existence of an unstable mode with \(\Omega ^{2}<0\) requires the presence of \(U_{\Omega }<0\) in some regions. Nevertheless, a positive definite \(U_{\Omega }\) ensures that scalarized black hole solutions are stable against the spherically symmetric perturbations. It is noteworthy that the appearance of a negative region in \(U_{\Omega }\) cannot sufficiently guarantee the presence of an instability [29]. One can utilize other techniques, like the S-deformation method [83], to further discuss the stability of these solutions.

Alternatively, computing quasinormal modes of time-dependent perturbations can be used to check whether black hole solutions are stable against perturbations [13, 84]. Specifically for the radial perturbations (24) and (25), quasinormal frequencies of unstable modes have a positive imaginary part, while the absence of positive imaginary modes suggests that black holes are radially stable. Focusing on the scalar field perturbation \(\Psi \left( r\right) \), Eq. (26) can be solved for quasinormal modes with appropriate boundary conditions imposed at the event horizon and spatial infinity. In particular, we require that the solutions are purely incoming waves at the event horizon and vanish at the spatial infinity,

$$\begin{aligned} \Psi \left( r\rightarrow r_{+}\right) \sim e^{i\Omega r^{*}}\quad \text { and }\quad \Psi \left( r\rightarrow \infty \right) \sim \frac{1}{r^{2}}, \end{aligned}$$
(28)

which selects a discrete set of quasinormal modes. Moreover, it can show that unstable quasinormal modes of Eq. (26) are purely imaginary. In fact, multiplying Eq. (26) by \(\Psi ^{*}(r)\) and integrating it from the event horizon to the infinity gives

$$\begin{aligned} \Omega ^{2}\int _{r_{+}}^{r=\infty }dr^{*}\Psi \Psi ^{*}&=-i\Omega \left| \Psi \right| ^{2}|_{r=r_{+}}\nonumber \\&\quad +\int _{r_{+}}^{r=\infty }dr^{*}\left( \left| \frac{d\Psi }{dr^{*}}\right| ^{2}+U_{\Omega }\left| \Psi \right| ^{2}\right) , \end{aligned}$$
(29)

where the boundary conditions (28) are used. Denoting \(\Omega =\Omega _{R}+i\Omega _{I}\), the imaginary part of the above identity can be written as

$$\begin{aligned} \Omega _{R}\left( \left| \Psi \right| ^{2}|_{r=r_{+}}+2\Omega _{I}\int _{r_{+}}^{r=\infty }dr^{*}\left| \Psi \right| ^{2}\right) =0, \end{aligned}$$
(30)

which leads to \(\Omega _{R}=0\) for unstable modes with \(\Omega _{I}>0\).

4 Numerical results

In this section, we first study various properties of scalarized RNAdS black hole solutions and then investigate their phase structure and transitions in a canonical ensemble. After the non-linear differential equations (5) are expressed in terms of a new dimensionless coordinate

$$\begin{aligned} x=1-\frac{r_{+}}{r}\quad \text { with }\quad 0\le x\le 1\text {,} \end{aligned}$$
(31)

they are numerically solved for scalarized black hole solutions using the NDSolve function in Wolfram Mathematica. In the remainder of this paper, we focus on the coupling function \(f\left( \phi \right) =e^{\alpha \phi ^{2}}\) with \(\alpha >0\). For this coupling function, one has \(f\left( 0\right) =1\) and \({\dot{f}}\left( 0\right) =0\), which ensures that RNAdS black holes are solutions of the EMS model, and \(\ddot{f}\left( 0\right) >0\), which may trigger a tachyonic instability of the scalar field to induce scalarized black hole solutions. For later use, we define reduced quantities,

$$\begin{aligned} q= & {} \frac{Q}{M},\quad a_{H}=\frac{A_{H}}{16\pi M^{2}},\quad {\tilde{T}}=TL,\quad {\tilde{F}} =\frac{F}{L},\nonumber \\ {\tilde{r}}_{+}= & {} \frac{r_{+}}{L},\quad {\tilde{Q}}=\frac{Q}{L} ,\quad {\tilde{M}}=\frac{M}{L}, \end{aligned}$$
(32)

which are dimensionless and invariant under the scaling symmetry (9). To test the accuracy of our numerical method, we use the Smarr relation (11) and find that the numerical error can be maintained around the order of \(10^{-6}\).

Fig. 1
figure 1

Plots of tachyonically unstable region for RNAdS black holes, and the domain of existence, entropic preference and effective potentials for scalarized black holes. Here, we take \(Q/L=0.1\). Upper left: density plot of \(\left( \mu _{eff}^{2}-\mu _{BF} ^{2}\right) Q^{2}\) evaluated at the event horizon \(r=r_{+}\) as a function of q and \(\alpha \) for the scalar perturbation in RNAdS black holes. We only display the tachyonically unstable region, where \(\mu _{eff}^{2}<\mu _{BF}^{2}\), in the \(\alpha \text {-}q\) plane. The closer RNAdS black holes are to the extremal limit, the more unstable the scalar field becomes. The blue dashed line represents the bifurcation line, where tachyonic instabilities are strong enough to induce scalarized black holes. Upper right: domain of existence for scalarized RNAdS black holes in the \(\alpha \text {-}q\) plane, which is highlighted by the light blue region and bounded by the critical and bifurcation lines. The critical line is depicted by a red solid line, on which the reduced horizon area \(a_{H}\) vanishes. The horizontal dashed gray line denotes extremal RNAdS black holes, above which RNAdS black hole solutions do not exist. Lower left: reduced horizon area \(a_{H}\) against q for RNAdS and scalarized black holes. The scalarized black hole solutions are always entropically preferred, which means that they are globally stable in a micro-canonical ensemble. Lower right: effective potentials of scalarized black holes with \(\alpha =5\) for several values of q. Solid red lines denote positive definite effective potentials between the event horizon and the spatial infinity, while dashed red lines represent those possessing negative regions. When q is large enough, the scalarized black hole solutions are stable against radial perturbations

Full size image
Fig. 2
figure 2

Imaginary parts of the lowest-lying quasinormal modes of fundamental scalarized black holes (green) and unstable modes of RNAdS black holes (blue), and the first (orange) and second (red) excited scalarized black holes as functions of reduced charge q for \(\alpha =5\) (left) and functions of \(\alpha \) for \(q=0.8745\) (right). Solid lines correspond to black holes with strictly positive potentials, dotted lines to black holes without unstable radial modes although the potential is not strictly positive, and dashed lines to black holes possessing at least one unstable radial mode. Different branches of scalarized black hole solutions start from RNAdS black holes at the corresponding bifurcation points. The cusp on the dotted green line in the left panel corresponds to the transition between purely imaginary modes and complex ones. The green lines are negative, suggesting radial stability of the fundamental branch of scalarized black hole solutions

Full size image

4.1 Scalarized black holes

Here, we present the numerical results, e.g., the domain of existence, entropic preference and effective potentials, for scalarized black hole solutions, which are dynamically induced from RNAdS black holes. Without loss of generality, we focus on \({\tilde{Q}}=Q/L=0.1\) in this subsection. For a RNAdS black hole, a tachyonic instability of the scalar field occurs if \(\mu _{eff}^{2}<\mu _{BF}^{2}\) somewhere in the spacetime. Since the minimum value of \(\mu _{eff}^{2}\) occurs at the event horizon \(r=r_{+}\), we only need to check \(\mu _{eff}^{2}<\mu _{BF}^{2}\) at \(r=r_{+}\). The region in the \(\left( \alpha ,q\right) \) parameter space of RNAdS black holes where \(\mu _{eff} ^{2}<\mu _{BF}^{2}\) at \(r=r_{+}\) is plotted in the upper left panel of Fig. 1. The distribution of values of \((\mu _{eff}^{2}-\mu _{BF}^{2} )Q^{2}|_{r=r_{+}}\) is also displayed, which shows that the tachyonic instability region becomes larger as \(\alpha \) increases, and the scalar field suffers from a strong tachyonic instability when black holes are near-extremal. The bifurcation line is composed of the \(l=0=n\) zero modes of Eq. (23) for the scalar perturbation in RNAdS black holes, and represented by blue dashed lines in Fig. 1. When the tachyonic instability is strong enough, the scalar perturbation can lead to scalarized black holes with non-trivial scalar fields above the bifurcation line. In the upper right panel of Fig. 1, we display the domain of existence for scalarized black holes, which is exhibited by a light blue region. The domain of existence is bounded by the bifurcation and critical lines, and resembles that of RN scalarized black holes [24] . On the critical line, the mass and the charge of scalarized solutions remain finite, whereas its horizon radius vanishes. On the other hand, the mass-to-charge ratio q of RNAdS black holes reaches the maximum value in the extremal limit, which is shown by a horizontal dashed gray line. Moreover, there is a certain region bounded by the extremal and bifurcation lines, where scalarized and RNAdS black holes coexist.

The reduced area \(a_{H}\) as a function of reduced charge q is plotted for RNAdS and scalarized black holes in the lower left panel of Fig. 1, which demonstrates that scalarized black holes emerge from RNAdS black holes at the bifurcation points, marked by B, and eventually terminate on the critical line with zero \(a_{H}\). For a multiphase system in a micro-canonical ensemble with conserved energy, the phase of maximum entropy is globally stable and will be present at equilibrium. Therefore, in the scalarized and RNAdS black holes coexisting region, our numerical results show that scalarized solutions are entropically preferred over RNAdS black hole solutions, and hence are the globally stable phase in the micro-canonical ensemble.

To study the stability of scalarized solutions, the effective potentials \(U_{\Omega }\) of scalarized solutions with \(\alpha =5\) are plotted for several values of q in the lower right panel of Fig. 1, where solid and dashed colored lines correspond to potentials with and without negative regions, respectively. The scalarized solutions have positive effective potentials for a large enough value of q, and thus are free of radial instabilities. However, as q decreases towards the bifurcation line, there appear negative regions in the effective potentials, which means that radial instabilities cannot be excluded near the bifurcation line.

To further explore the stability of scalarized black holes, we numerically solve Eq. (26) with the boundary conditions (28) to find quasinormal modes of the scalar field perturbation. Specially, we consider two cases, one with fixed \(\alpha =5\) and the other with \(q=0.8745\). In this paper, we focus on scalarized black holes without nodes of the scalar field (\(n=0\)). It is found that, for this fundamental branch of black hole solutions, the scalar field perturbation does not possess quasinormal modes with positive imaginary parts in the two cases. Instead, we obtain a discrete set of complex frequencies with negative imaginary parts. Fig. 2 displays the imaginary parts of the lowest-lying quasinormal modes (i.e., with the largest imaginary part), which are denoted by green lines, for the \(n=0\) scalarized black holes of \(\alpha =5\) (left panel) and \(q=0.8745\) (right panel). The dotted/solid green lines correspond to black hole solutions with/without effective potentials possessing negative regions. In particular, our result shows that the quasinormal modes of the fundamental branch always have negative imaginary parts. It is noteworthy that the stable modes of fundamental scalarized black holes may not be purely imaginary with \(\Omega _{R}\ne 0\). In short, fundamental scalarized black holes seem free of unstable modes despite negative regions appearing in some effective potentials.

In addition, quasinormal modes of RNAdS black holes and excited scalarized black holes with one and two nodes of the scalar field (\(n=1\) and 2) are also calculated. Unlike fundamental scalarized black holes, these black holes are found to have unstable quasinormal modes, which are purely imaginary with positive imaginary parts. In Fig. 2, we present the imaginary parts of unstable modes of RNAdS black holes (dashed blue lines), and \(n=1\) (dashed orange lines) and 2 (dashed red lines) scalarized black holes in the \(\alpha =5\) (left panel) and \(q=0.8745\) (right panel) cases. Therefore, RNAdS and excited scalarized black holes are demonstrated to be unstable against radial perturbations, which may justify the neglection of the excited branches in our paper.

Fig. 3
figure 3

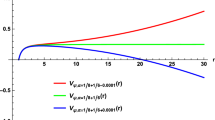
Effective potentials \(r_{+}^{2}U_{\Omega }\) of fundamental scalarized black holes with \(\alpha =5\) as functions of x for different values of q (left) and the corresponding dominant and subdominant quasinormal frequencies \(\Omega L\) (right). The solid/dashed lines represent the potentials with a barrier/dip near the event horizon, for which the complex/purely imaginary stable quasinormal modes dominate

Full size image

It is noteworthy that purely imaginary quasinormal modes are observed for the perturbative scalar field in scalarized black holes. The purely imaginary quasinormal modes correspond to a special set of purely damped modes, which are distinguished from regular complex ones with non-vanishing real part. Although purely imaginary quasinormal modes have not often been reported in the literature, their existence was found for various black holes [85,86,87,88,89,90,91]. Specifically, it was demonstrated that the type of purely imaginary modes can be used to characterize electromagnetic and axial perturbations of large asymptotically AdS black holes [85]. In the context of Kerr geometry, there is a set of quasinormal modes precisely existing on the negative imaginary axis [87]. Interestingly, purely imaginary quasinormal modes were found to play an important role in violating the strong cosmic censorship conjecture for near-extremal dS black holes [88, 90]. Similar to the cusp presented in Fig. 2, the transition between purely imaginary modes and complex ones was also observed in [90].

The authors of [86] argued that the presence of purely imaginary quasinormal modes can be related to the profile of the corresponding effective potential by considering a massless scalar perturbation on the 3D charged-dilaton black holes. It was found that a potential-step appearing outside the event horizon, which is similar to the case of the electromagnetic perturbations in the large Schwarzschild AdS black holes, can lead to a type of purely imaginary quasinormal modes. For a massless scalar field propagating in 4D Einstein–Gauss–Bonnet black holes, it showed that purely imaginary quasinormal modes dominate when the corresponding effective potential is a monotonically increasing function of the radius coordinate, whereas complex quasinormal modes dominate when the potential have a barrier near the outside horizon [92]. Motivated by these observations, we explore the relation between the purely imaginary modes of the scalar field perturbation around fundamental scalarized black holes and the profiles of the corresponding effective potentials. In the left and right panels of Fig. 3, we present the effective potentials and the dominant and subdominant quasinormal modes of the scalar field perturbation in fundamental scalarized black holes with \(\alpha =5\) for several values of q, respectively. When \(q=0.8862\) and 0.8966, the effective potentials are shown to possess a barrier near the event horizon. As exhibited in the table of Fig. 3, the dominant and subdominant quasinormal modes of this barrier-type potential are complex. However as q decreases, the barrier of the effective potential disappears, and instead a potential dip appears near the event horizon, e.g., the \(q=0.8631\) and 0.8734 cases in Fig. 3. In these two cases, the table of Fig. 3 displays that the dominant quasinormal modes are purely imaginary, while the subdominant ones are complex. Our numerical results suggest that the presence of a potential dip near the event horizon may induce a family of dominant purely imaginary modes.

Fig. 4
figure 4

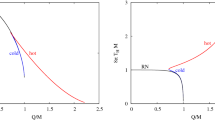
Plots of the reduced horizon radius \({\tilde{r}}_{+}\) (the upper row) and the reduced free energy \({\tilde{F}}\) (the lower row) versus the reduced temperature \({\tilde{T}}\) for RNAdS (blue lines) and scalarized (green lines) black holes with several fixed values of the reduced charge \({\tilde{Q}}\). Here, we focus on \(\alpha =5\). Bifurcation points are labeled by B. When \({\tilde{r}}_{+}({\tilde{T}})\) is multivalued, black hole solutions have more than one branch of different horizon radii in a canonical ensemble with fixed \({\tilde{T}}\) and \({\tilde{Q}}\). Left column: there is a band of temperatures where three branches of RNAdS black hole solutions coexist, and a first-order phase transition occurs between the large RNAdS BH phase (i.e., the branch with the largest horizon radius) and the small RNAdS BH phase (i.e., the branch with the smallest horizon radius). Scalarized black holes emerge from the bifurcation point. Nevertheless, they are not globally preferred since they always have a higher free energy than RNAdS black holes. Center column: RNAdS black hole solutions have only one branch, whose free energy is smaller than that of scalarized black holes. There is no phase transition. Right column: RNAdS black hole solutions have only one branch, whereas scalarized black hole solutions have two branches of different sizes. As \({\tilde{T}}\) increases, the globally stable phase jumps from RNAdS black holes to scalarized black holes (the branch with a larger horizon radius), corresponding to a zeroth-order phase transition at \({\tilde{T}}_{\min }\). Further increasing \({\tilde{T}}\), there would be a second-order phase transition returning to RNAdS black holes at the bifurcation point B. Here, we observe a RNAdS BH/scalarized BH/RNAdS BH reentrant phase transition

Full size image

4.2 Phase structure in a canonical ensemble

In this subsection, we consider phase structure and transitions of scalarized and RNAdS black holes in a canonical ensemble maintained at a given temperature of T and a given charge of Q. In a canonical ensemble, the globally stable phase of a multiphase system, which exists at equilibrium, has the lowest possible Helmholtz free energy F, which can be computed via Eq. (19). The rich phase structure of black holes usually comes from expressing the horizon radius \(r_{+}\) as a function of temperature T. If the function \(r_{+}\left( T\right) \) is multivalued, there will be more than one black hole phase, corresponding to different branches of \(r_{+}\left( T\right) \).

To illustrate phase structure and transitions, we plot the reduced horizon radius \({\tilde{r}}_{+}\) and the free energy \({\tilde{F}}\) as functions of reduced temperature \({\tilde{T}}\) for scalarized and RNAdS black holes with three representative values of \({\tilde{Q}}\) in Fig. 4, where we have \(\alpha =5\). In the left column of Fig. 4 with a small \({\tilde{Q}}\), the upper panel shows that three branches of the RNAdS black hole solution coexist in some range of \({\tilde{T}}\), and are dubbed as large, intermediate and small RNAdS BHs, respectively, based on their values of horizon radius. At a high (low) enough temperature, only the large (small) RNAdS BH phase exists. On the other hand, there is only one phase for the scalarized black hole solution, which bifurcates from the RNAdS black hole solution at the bifurcation point B, and does not exist at a low temperature. The reduced free energy \({\tilde{F}}\) is plotted against \({\tilde{T}}\) for these four phases in the lower panel, which shows that the scalarized black hole can not be the globally stable phase since there always exists some RNAdS black hole phase of a lower free energy at a given \({\tilde{T}}\). In the coexisting region of the RNAdS black hole phases, a first-order phase transition between large and small RNAdS BHs occurs at some point, where their free energies intersect each other.

The coexisting region of the RNAdS black hole phases shrinks as \({\tilde{Q}}\) increases until reaching a critical point, where a second-order phase transition occurs between large and small RNAdS BHs. Beyond the critical point, large RNAdS BH is indistinguishable from small RNAdS BH, hence RNAdS black hole solutions have a single phase. In the center column of Fig. 4, we depict \({\tilde{r}}_{+}({\tilde{T}})\) and \({\tilde{F}}({\tilde{T}})\) for the case with a value of \({\tilde{Q}}\) greater than the critical value. The upper panel shows that both RNAdS and scalarized black holes have a single phase. Moreover, as displayed in the lower panel, the RNAdS black hole always has a smaller free energy than the scalarized black hole, and hence is the globally stable phase. Consequently, there is no phase transition in this case.

However when \({\tilde{Q}}\) is large enough, phase structure of scalarized and RNAdS black holes becomes much richer. For example, \({\tilde{r}}_{+}({\tilde{T}})\) and \({\tilde{F}}({\tilde{T}})\) are plotted for scalarized and RNAdS black holes with a large enough \({\tilde{Q}}\) in the right column of Fig. 4. It shows in the upper panel that the RNAdS black hole solution possesses a single phase, whereas the scalarized solution can have two phases at some given \({\tilde{T}}\), namely large scalarized BH (i.e., the one with a larger horizon radius) and small scalarized BH (i.e., the one with a smaller horizon radius). In fact, the scalarized black hole solution has a minimum temperature \({\tilde{T}}_{\min }\), and large scalarized BH coexists with small scalarized BH between \({\tilde{T}}={\tilde{T}}_{\min }\) and the bifurcation point B, where large scalarized BH and the RNAdS black hole merge. The lower panel exhibits the free energy as a function of \({\tilde{T}}\) for the three phases. If we start increasing the temperature from \({\tilde{T}}=0\), the system follows the blue line of the RNAdS black hole until \({\tilde{T}}={\tilde{T}}_{\min }\), where the free energy has a discontinuity at its global minimum. Further increasing \({\tilde{T}}\), the inset shows that the system jumps to the lower green line of large scalarized BH, which corresponds to a zeroth-order phase transition between scalarized and RNAdS black holes. As \({\tilde{T}}\) continues to increase, the system follows the lower green line until it joins the blue line at the bifurcation point B, which corresponds to a second-order phase transition between scalarized and RNAdS black holes. Note that since scalarized and RNAdS black holes have the same entropy at the bifurcation point, a phase transition between them at the bifurcation point is second-order. In short, a RNAdS BH/scalarized BH/RNAdS BH reentrant phase transition is observed as \({\tilde{T}}\) increases.

In addition, it is interesting to consider the local thermodynamic stability of black hole phases against thermal fluctuations. In a canonical ensemble, the quantity of particular interest is the specific heat at constant charge,

$$\begin{aligned} C_{Q}= & {} T\left( \frac{\partial S}{\partial T}\right) _{Q}\nonumber \\= & {} 2L^{2}\pi \tilde{r}_{+}{\tilde{T}}\frac{\partial {\tilde{r}}_{+}}{\partial {\tilde{T}}}. \end{aligned}$$
(33)

Since the entropy is proportional to the size of the black hole, a positive specific heat means that black holes radiate less when they are smaller. Thus, the thermal stability of a phase follows from \(C_{Q}>0\) (or equivalently, \(\partial {\tilde{r}}_{+}/\partial {\tilde{T}}>0\)). From the upper row of Fig. 4, we notice that large and small RNAdS BHs in the left column, RNAdS black hole in the center column, and large scalarized BH and RNAdS black hole in the right column all have \(\partial {\tilde{r}}_{+}/\partial {\tilde{T}}>0\). In consequence, the globally stable phases of scalarized and RNAdS black holes possess a positive \(C_{Q}\), and are thermally stable.

Fig. 5
figure 5

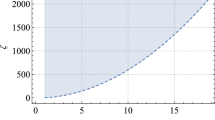
Phase diagram of RNAdS and scalarized black holes in a canonical ensemble with fixed temperature T and charge Q. Here, we take \(\alpha =5\). The phase diagram exhibits the globally stable phases, which have the lowest free energy, and the phase transitions between them. The light yellow and blue regions correspond to RNAdS and scalarized black holes, respectively. A first-order phase transition line (the purple line) separates the large RNAdS BH phase, which is above the line, and the small RNAdS BH phase, which is below the line. The first-order phase transition line terminates at the critical point, labelled by C. The scalarized black hole phase is delimited by a zeroth-order phase transition line (the red line) and a second-order one (the blue dashed line), which coincides with the bifurcation line

Full size image

To better illustrate the globally stable phases of lowest free energy and the associated phase transitions, we display the phase diagram of scalarized and RNAdS black holes in the \({\tilde{Q}}\)–\({\tilde{T}}\) plane in Fig. 5, where \(\alpha =5\). There is a first-order phase transition line (the purple line) separating large and small RNAdS BHs for small \({\tilde{Q}}\), which terminates at the critical point. This first-order phase transition is quite similar to the liquid/gas phase transition. When \({\tilde{Q}}\) is large enough, large scalarized BH (the light blue region) appears, and is bounded by zeroth-order (the red line) and second-order (the blue dashed line) phase transition lines.

5 Discussions and conclusions

In this paper, we investigated spontaneous scalarization of asymptotically AdS charged black holes in an EMS model, and studied phase structure of scalarized and RNAdS black holes in a canonical ensemble. We focused on a non-minimal coupling function \(f\left( \phi \right) =e^{\alpha \phi ^{2}}\), which leads to spontaneous scalarization due to the tachyonic instability of the scalar field near the event horizon. In practice, scalarized black holes can be induced from RNAdS black holes on the bifurcation line, which consists of zero modes of the scalar perturbation in RNAdS black holes. In the \(\alpha \text {-}q\) plane with a fixed \({\tilde{Q}}\), the domain of existence for scalarized RNAdS black holes is bounded by the bifurcation and critical lines, which resembles that of scalarized RN black holes very closely [24]. In a micro-canonical ensemble, we found that scalarized black hole solutions are always entropically preferred over RNAdS black holes, and hence the globally stable phase.

On the other hand, the system has much richer phase structure in a canonical ensemble. After the Helmholtz free energy of the EMS model was computed, we obtained the phase structure of scalarized and RNAdS black holes. In the small Q regime, scalarized black holes never globally minimize the free energy, and the corresponding phase diagram resembles that of the liquid/gas system closely. Nevertheless in the large Q regime, scalarized black holes can be the globally stable phase in some parameter region. As the temperature increases at a given charge, the system undergoes a RNAdS BH/scalarized BH/RNAdS BH reentrant phase transition, which consists of zeroth-order and second-order phase transitions.

The phenomenon of reentrant phase transition was first observed in a nicotine/water mixture, and later discovered in the context of black hole thermodynamics, e.g., Born–Infeld-AdS black holes [65, 93], higher dimensional singly spinning Kerr-AdS black holes [94], AdS black holes in Lovelock gravity [95], AdS black holes in dRGT massive gravity [96], hairy AdS black holes [97]. For these black holes, reentrant phase transitions were found to include zeroth-order and first-order phase transitions. In this paper, we present an example of a reentrant phase transition for black holes, which is composed of zeroth-order and second-order phase transitions. Furthermore, the second-order phase transition between scalarized and RNAdS black holes is of great interest since this implies that our results may provide an interesting model of holographic superconductors. We leave this for future work.

AdS black holes can also be studied in the context of extended phase space thermodynamics, where the cosmological constant is interpreted as a thermodynamic pressure \(P\equiv 6/L^{2}\) [63, 98]. In terms of P, the reduced quantities are expressed as

$$\begin{aligned} {\tilde{T}}= & {} T\sqrt{6/P},\quad {\tilde{F}}=F\sqrt{P/6},\quad {\tilde{r}}_{+}=r_{+}\sqrt{P/6},\nonumber \\ {\tilde{Q}}= & {} Q\sqrt{P/6},\quad {\tilde{M}}=M\sqrt{P/6}. \end{aligned}$$
(34)

Note that M and F are identified as the enthalpy and the Gibbs free energy, respectively, in extended phase space. With Eq. (34), our results can be generalized to extended phase space thermodynamics.