Properties of strange quark matter and strange quark stars

Abstract

A Polyakov chiral $\text {SU(3)}$ quark mean-field (PCQMF) model is applied to study the properties of strange quark matter (SQM) and strange quark star (SQS) in $\beta$-equilibrium. The effect of increasing the strength of vector interactions on the effective constituent quark mass, particle fractions, and the thermodynamical properties such as pressure, energy density, and the speed of sound is investigated. We investigate the above properties for the SQM relevant for various stages of star evolution, i.e., considering with/without trapped neutrinos and zero/finite entropy. The finite lepton fraction and the entropy of the medium is observed to cause the stiffness in the equation of state (EoS). Finally, we calculate the mass-radius relation and the dimensionless tidal deformability within the present model calculations and compare the results to the recent studies.

1 Introduction

Exploring the strong interaction physics of the QCD phase diagram over a wide range of temperature and baryon chemical potential (or baryonic density) is a fascinating topic of research. One of the reasons is the possibility of various phases over different ranges of temperature and baryonic density, hence, enthralling underlying physics. The phase of quark-gluon-plasma (QGP) can be realized when the hadronic matter is put through high temperature at low baryonic density. This is commonly referred to as heating of matter. Such a phase may have existed in the early stage of the universe or can be created in heavy-ion collision facilities. On the other hand, compression of the hadronic matter to high baryonic density, keeping temperature low, may also result in a phase of deconfined quarks, known as quark matter. The matter at a high baryonic density and low temperature may exist in the compact stars. The ‘compact star’ may refer to a pure neutron star that is gravitationally bound, a pure quark star which may result from very high compression such that quarks start overlapping and hadrons lose their identity, or a hybrid star comprising of crust as of a neutron star and the core of quark matter.

Witten et. al. anticipated a postulate that instead of nuclear matter, the strange quark matter (SQM) may be contemplated as the stable ground state due to the lowering of quark chemical potential of the strange quark, and this results in a value of energy per baryon less than 930 MeV for SQM at zero pressure [1,2,3]. Hence, there may be a possibility that the pulsars which are detected as neutron stars (NSs) may also be quark stars (QSs). SQM, if exist, may play a crucial role in the various remarkable fields such as hot and dense matter in heavy-ion collisions [4,5,6], compact stars structure [7], deconfinement phase transition [8,9,10,11,12,13] etc. The possibility for the existence or non-existence of various phases of compact stars is strongly constrained by the astrophysical data on pulsars.

Neutron star interior composition explorer (NICER), a mission of NASA, has become the first multi-messenger observation of binary neutron star merger, which allows the measurement of masses and radii of neutron stars [14, 15]. Moreover, there are several other facilities in terms of telescopes and satellites which describe the properties of dense matter [16]. Among them a few are: the radio telescope at the Parkes, Jodrell Bank, the Hubble space telescope, the x-ray satellites Chandra, a gigantic telescope of European Southern observatory, and the swift satellite.

Although the first discovery of a pulsar dated back to the year 1967 [17], the recent findings of pulsars with larger masses stimulated a lot of theoretical research in the field with a motivation to provide a concrete explanation of the experimental observations. The precise mass measurement of two solar mass pulsars named as PSR J1614-2230 ($1.928 \pm 0.017\ M_\odot$) [18, 19] and PSR J0348+0432 ($2.01 \pm 0.04\ M_\odot$) [20], has put strong constraints on EoS. Currently, the only pulsars whose masses are larger than $2\ M_{\odot }$ are PSR J0740+6620 ($2.14^{+0.10}_{-0.09}M_{\odot }$) [21] and PSR J2215+5135 ($2.27{}_{-0.15}^{+0.17}\ M_\odot$) [22]. The detection of gravitational waves can be a convenient method to collect the evidence for QSs [23, 24]. The detection of gravitational wave event by LIGO and VIRGO interferometer [25], has also put several constraints on EoS and the properties of NSs such as radii, masses, and tidal deformability [26,27,28].

The above observations of larger mass limit on the compact stars flavor the models with stiffer EoS. To date, there are no first principle calculations on the EoS, and it is highly model (and parameters used in the model) dependent. It was a general conjecture that an increase in the degree of freedom in the neutron stars would soften the equation of state. For example, within different theoretical studies, hyperons and kaon condensates cause the softening of the EoS and hence, will lead to a decrease in the mass of compact stars. Similarly, the transition from pure neutron stars to a hybrid or a mixed phase of nucleons and quarks or pure quark stars may also soften the EoS, and this may lead to the results on the mass-radius opposite to the expectations of earlier discussed large mass pulsars. However, as was debated in [29] (in response to conclusion of [30]), the strong interactions may lead to the stiffening of the EoS and hence, existence of pure quark stars or hybrid stars composed of quark matter core cannot be rejected [31,32,33] (also see the reply of $\ddot{\text {O}}$zel [34] and refs. [18, 35]).

In the present paper, we investigate the properties of strongly interacting strange quark matter to explore the mass-radius relation of strange quark stars, with and without trapped neutrinos. The non-perturbative lattice QCD calculations, which work fine at finite temperature and zero baryonic density, are not applicable at high baryonic density, which is a subject of present work. Therefore, several QCD enthused effective models are used widely to study the non-perturbative strongly interacting matter. Some of the examples are: MIT bag model [36, 37], Dyson-Schwinger equation approach [38,39,40,41], quark meson coupling (QMC) model [42], quark mass density dependent (QMDD) model [43,44,45,46,47], Nambu–Jona—Lasinio (NJL) model [37, 48], confined density dependent quark mass (CDDM) model [8, 49, 50], chiral $\text {SU(3)}$ quark mean field (CQMF) model [51, 52], Polyakov quark meson coupling (PQMC) model [53, 54] and Polyakov extended NJL (PNJL) model [55,56,57]. Many authors have studied the properties of pure SQM in $\beta$-equilibrium [58,59,60,61], proto-strange quark stars (PSQS) [62,63,64,65,66,67], as well as hybrid star with SQM in the core [68, 69] (also, see references therein).

In [36], the EoS of quark matter with color flavor locked (CFL) phase was studied using MIT bag and NJL model to understand the conditions which may lead to the mass of about $1.97 M_\odot$. Although in the MIT model, the stiff EoS can be observed if a larger value of gap parameter is used, in the NJL-CFL model, including gluonic effects, the stiffening of the EoS is very sensitive to the vector-vector coupling strength $G_V$ (large value of $G_V$ is required for stiff EoS). The presence of trapped neutrinos along with quarks is expected to cause an increase in the mass of stars as compared to the neutrino free phase [70]. In order to consider the PSR J0348+0432 ($2.01 \pm 0.04\ M_\odot$) and MSP J0740 + 6620 (2.14$^{+0.10}_{-0.09} M_\odot$) as quark stars, the importance of isospin effects and quark symmetry energy at finite temperature was explored in [65].

In our present study on the properties of SQM and SQS, the CQMF model is extended to include the gluonic degree of freedom through the Polyakov loop effect, i.e., we will use the Polyakov chiral quark mean field (PCQMF) model. In the CQMF model, quarks are confined within the baryons by a confining potential. The CQMF model is used in the past to study the properties of both hadronic and quark matter [51, 52, 71, 72].

Following is the process of evolution of a quark star (assuming pure quark star exist): in an early stage when proto-strange quark star (PSQS) starts forming lepton number per baryon with trapped neutrino and entropy per baryon will be approximately 0.4 and 1, respectively [48]. During the meantime of 10-20 seconds, the star matter gets heated by diffusing neutrinos, and entropy per baryon will increase to 2, while the neutrino fraction drops to almost zero. Following the heating condition, PSQS begins to cool down and finally reach to the stage of cold SQS. In the present work, we will investigate the properties of stars during above described stages of evolution. The questions, for example, CFL phase in SQS [36], the impact of finite magnetic field [64], and the inclusion of the hadronic degrees of freedom to investigate hybrid stars within the present PCQMF model will be addressed in the future work.

The present paper is organized as follows: In Sect. 2, we describe the Polyakov chiral $\text {SU(3)}$ quark mean field model, various thermodynamic relations, and the structure of SQS (Tolman-Oppenheimer-Volkov (TOV) equations). In Sect. 3, we explain the results of our analysis on SQM and SQSs for various situations of star evolution, and finally, in the Sect. 4, the results of the present work are summarized.

2 Methodology

2.1 Polyakov Chiral $\text {SU(3)}$ Quark Mean Field Model

The PCQMF model [73] is an extended version of CQMF model [51, 52] which is based on the quark degree of freedom, the non-linear realization of chiral symmetry [74,75,76], and the trace anomaly [77,78,79]. Through the spontaneous symmetry breaking, the constituent quarks and mesons (except for the pseudoscalars) obtain their masses, whereas the pseudoscalar mesons acquire their masses through the explicitly symmetry breaking. By including the gluonic degrees of freedom in the CQMF model through an effective Polyakov loop potential, it is possible to investigate both, the deconfinement and the chiral symmetry breaking together in the PCQMF model. The effective Lagrangian density of the PCQMF model for the SQM is written as

$$\begin{aligned} {{\mathcal {L}}}_{\mathrm{PCQMF}} \,= & {} \, {{\mathcal {L}}}_{q0} \, + \, {{\mathcal {L}}}_{qm} \, + \, {{\mathcal {L}}}_{\Sigma \Sigma } \,+\, {{\mathcal {L}}}_{VV} \,\nonumber \\&+\, {{\mathcal {L}}}_{SB}\, + \, {{\mathcal {L}}}_{\Delta m} \, + \, {{\mathcal {L}}}_{h} \, -U(\Phi ,{\bar{\Phi }},T), \end{aligned}$$

(1)

where ${{\mathcal {L}}}_{q0} = {\bar{q}} \, i\gamma ^\mu \partial _\mu q$ represents the free part of massless quarks, ${{\mathcal {L}}}_{qm}$ denotes the quark mesons interaction term that remains invariant under the chiral $\text {SU(3)}$ transformation and can be written as [72]

$$\begin{aligned} {{\mathcal {L}}}_{qm}= & {} g_s\left( \bar{q}_LM q_R+\bar{q}_RM^+q_L\right) \nonumber \\&- g_v\left( \bar{q}_L\gamma ^\mu l_\mu q_L+\bar{q}_R\gamma ^\mu r_\mu q_R\right) . \end{aligned}$$

(2)

In the above, $q=\left( \begin{array}{lcr} u \\ d \\ s \end{array}\right)$, and $g_s$ and $g_v$ are the scalar and vector coupling constants, respectively. The compact form of spin-0 scalar ($\Sigma$) and pseudoscalar ($\Pi$) meson nonets can be expressed as

$$\begin{aligned} M(M^{\dagger })=\Sigma \pm i\Pi =\frac{1}{\sqrt{2}}\sum _{a=0}^{8} \left( \sigma ^{a}\pm i \pi ^{a}\right) \lambda ^{a}, \end{aligned}$$

(3)

where $\sigma ^{a}$ and $\pi ^{a}$ represent the nonets of scalar and pseudoscalar mesons, respectively, $\lambda ^{a}$ are Gell-Mann matrices with $\lambda ^{0}=\sqrt{\frac{2}{3}}I$. Similarly, the spin-1 mesons are defined as

$$\begin{aligned} l_{\mu }(r_{\mu })=\frac{1}{2}\left( V_{\mu }\pm A_{\mu }\right) = \frac{1}{2\sqrt{2}}\sum _{a=0}^{8}\left( v_{\mu }^{a}\pm a^{a}_{\mu } \right) \lambda ^{a}. \end{aligned}$$

(4)

In the above, $v_{\mu }^a$ and $a_{\mu }^a$ are nonets of vector and pseudovector mesons, respectively. The expressions for physical states of scalar and vector meson nonets are

$$\begin{aligned} \Sigma= & {} \frac{1}{\sqrt{2}}\sum _{a=0}^8 \sigma ^a \, \lambda ^a\nonumber \\= & {} \left( \begin{array}{lcr} \frac{1}{\sqrt{2}}\left( \sigma +\delta ^0\right) &{} \delta ^{+} &{} \kappa ^{*+} \\ \delta ^- &{} \frac{1}{\sqrt{2}}\left( \sigma -\delta ^0\right) &{} \kappa ^{*0} \\ \kappa ^{*-} &{} {\bar{\kappa }}^{*0} &{} \zeta \end{array} \right) , \end{aligned}$$

(5)

and

$$\begin{aligned} V_\mu= & {} \frac{1}{\sqrt{2}}\sum _{a=0}^8 v_\mu ^a \, \lambda ^a\nonumber \\= & {} \left( \begin{array}{lcr} \frac{1}{\sqrt{2}}\left( \omega _\mu +\rho _\mu ^0\right) &{} \rho _\mu ^+ &{} K_\mu ^{*+}\\ \rho _\mu ^- &{} \frac{1}{\sqrt{2}}\left( \omega _\mu -\rho _\mu ^0\right) &{} K_\mu ^{*0}\\ K_\mu ^{*-} &{} \bar{K}_\mu ^{*0} &{} \phi _\mu \end{array} \right) , \, \end{aligned}$$

(6)

respectively.

The coupling between scalar mesons $\Sigma$ follows the $\mathrm {SU(3)_V}$ symmetry and leads to three independent invariants written as [78]

$$\begin{aligned} I_1=\mathrm{Tr}(\Sigma ), \quad I_2= \mathrm{Tr}(\Sigma )^2, \quad I_3=\det (\Sigma ) . \end{aligned}$$

(7)

These invariants are the building blocks of meson-meson interactions and higher order invariants can be written in the form of these three basic invariants. In terms of the above written invariants, the potential for scalar meson-meson interactions is written as

$$\begin{aligned} {{\mathcal {L}}}_{0}=-\frac{1}{2} \, k_0 \, \chi ^2 \,I_2 +k_1 \, (I_2)^2 + k_2 \, I_4 + 2 \, k_3 \, I_3 \, \chi , \end{aligned}$$

(8)

where $\chi$ represents the scalar dilaton field and is related to the trace anomaly (property of QCD) which is defined through the non-vanishing trace of the energy momentum tensor $\theta _{\mu }^{\mu }= \frac{ \beta _{QCD} }{2 g} {{\mathcal {G}}}_{\mu \nu }^a \mathcal{G}^{\mu \nu }_a$, (${{\mathcal {G}}}_{\mu \nu }$ is the gluon field strength tensor of QCD). The trace anomaly property is introduced in the present chiral model through the scale breaking potential

$$\begin{aligned} {{\mathcal {L}}}_{\mathrm {scale}}= & {} \frac{1}{2} (\partial _\mu \chi )(\partial ^\mu \chi )- k_4 \chi ^4 -\nonumber \\&\times \frac{1}{4}\chi ^4 \ln \frac{ \chi ^4 }{ \chi _0^4} +\frac{d}{3}\chi ^4 \ln \frac{(\sigma ^2-\delta ^2)\chi }{{\sigma _0}^2\chi }. \end{aligned}$$

(9)

Within the mean field approximation, the Lagrangian density of scalar meson self-interaction term, ${{\mathcal {L}}}_{\Sigma \Sigma }$ (the $3^{\text {rd}}$ term in Eq. (1)), including the effect of broken scale invariance, can be expressed as

$$\begin{aligned} {{\mathcal {L}}}_{\Sigma \Sigma }= & {} {{\mathcal {L}}}_{0} + {{\mathcal {L}}}_{scale}= -\frac{1}{2} \, k_0\chi ^2 \left( \sigma ^2+\zeta ^2+\delta ^2\right) \nonumber \\&+k_1 \left( \sigma ^2+\zeta ^2+\delta ^2\right) ^2 +k_2\Bigg (\frac{\sigma ^4}{2} +\frac{\delta ^4}{2}+3\sigma ^2\delta ^2\nonumber \\&+\zeta ^4\Bigg )+k_3\chi \left( \sigma ^2-\delta ^2\right) \zeta -k_4\chi ^4-\frac{1}{4}\chi ^4 \mathrm{ln}\frac{\chi ^4}{\chi _0^4} \nonumber \\&+ \frac{d}{3}\chi ^4 \mathrm{ln}\left( \left( \frac{\left( \sigma ^2{-}\delta ^2\right) \zeta }{\sigma _0^2\zeta _0}\right) \left( \frac{\chi ^3}{\chi _0^3}\right) \right) {+} \frac{1}{2} (\partial _\mu \chi )(\partial ^\mu \chi ). \nonumber \\ \end{aligned}$$

(10)

Here, d =6/33 (for $N_f=3$ and $N_c=3$), and $\sigma _0$, $\zeta _0$ and $\chi _0$ denote the vacuum expectation values of $\sigma$, $\zeta$ and $\chi$ fields. The scale invariant self-interaction terms for the vector mesons is written as [79]

$$\begin{aligned} {{\mathcal {L}}}_{vec}^{(1)}= \frac{1}{2} m_V^2 \frac{\chi ^2}{\chi _0^2} \mathrm{Tr}V_{\mu } V^{\mu } +2g_4 \mathrm{Tr}(V_\mu V^\mu )^2. \end{aligned}$$

(11)

The mass degeneracy of vector meson nonets is signified by the above equation. The property of scale invariance is satisfied on multiplying the square of the dilaton field, $\chi$ in the $1^{\text {st}}$ term of Eq. (11).

To split the masses, we need an addition chiral invariant term

$$\begin{aligned} {{\mathcal {L}}}_{vec}^{(2)} = \frac{1}{4} \mu \mathrm{Tr}\left[ V_{\mu \nu } V^{\mu \nu } \Sigma ^2 \right] . \end{aligned}$$

(12)

Combining Eqs. (11) and (12) along with the kinetic term of vector mesons, within the mean-field approximation, we obtain the Lagrangian density for the vector meson self interaction term, ${{\mathcal {L}}}_{VV}$ (the $4^{\text {th}}$ term in Eq. (1)) as

$$\begin{aligned} {{\mathcal {L}}}_{VV}= & {} \frac{1}{2} \, \frac{\chi ^2}{\chi _0^2} \left( m_\omega ^2\omega ^2+m_\rho ^2\rho ^2+m_\phi ^2\phi ^2\right) \nonumber \\&+g_4\left( \omega ^4+6\omega ^2\rho ^2+\rho ^4+2\phi ^4\right) . \end{aligned}$$

(13)

In Eq. (13), the density dependent vector meson masses can be written as [80]

$$\begin{aligned}&m^2_\omega = m_\rho ^2 = \frac{m_v^2}{1 - \frac{1}{2} \mu \sigma ^2}\, ,\quad \mathrm{and} \quad m^2_\phi = \frac{m_v^2}{1 - \mu \zeta ^2}\, . \end{aligned}$$

(14)

In the above equation, the vacuum value of the vector meson mass, $m_v$ = 673.6 MeV and the density parameter, $\mu$ = 2.34 fm$^2$ is considered in order to replicate ${m_\omega }$ = 783 MeV and ${m_\phi }$ = 1020 MeV. Furthermore, the last three terms ${{\mathcal {L}}}_{SB}$, ${{\mathcal {L}}}_{\Delta m}$ and ${{\mathcal {L}}}_{h}$ of Eq. (1) break the chiral symmetry explicitly. The relations between different quark meson coupling constants are given as [52]

$$\begin{aligned} \frac{g_s}{\sqrt{2}}= & {} g_{\delta }^u = -g_{\delta }^d = g_\sigma ^u = g_\sigma ^d \nonumber \\= & {} \ldots = \frac{1}{\sqrt{2}}g_\zeta ^s, \quad g_{\delta }^s = g_\sigma ^s = g_\zeta ^u = g_\zeta ^d = 0 \, , \end{aligned}$$

(15)

$$\begin{aligned} \frac{g_v}{2\sqrt{2}}= & {} g_{\rho ^0}^u = -g_{\rho ^0}^d = g_\omega ^u\nonumber \\= & {} g_\omega ^d = \ldots = \frac{1}{\sqrt{2}}g_\phi ^s, ~~~g_\omega ^s \nonumber \\= & {} g_{\rho ^0}^s = g_\phi ^u = g_\phi ^d = 0. \end{aligned}$$

(16)

The explicitly symmetry breaking term is introduced to exclude Goldstone modes of a chiral effective theory. It is written as

$$\begin{aligned} {{\mathcal {L}}}_{SB}= & {} -\frac{1}{2} m_{\eta _0}^2\mathrm{Tr}Y^2 \nonumber \\&-\frac{1}{2} \mathrm{Tr}A_p \left( u \Sigma u+u^{\dagger }\Sigma u^{\dagger }\right) \nonumber \\&-\mathrm{Tr}\left( A_s-A_p\right) \Sigma , \end{aligned}$$

(17)

where Y is pseudoscalar chiral singlet, $A_p=1/\sqrt{2}{\mathrm {diag}}(m_{\pi }^2 f_{\pi },m_\pi ^2 f_\pi , 2 m_K^2 f_K-m_{\pi }^2 f_\pi )$, $A_s=\mathrm {diag}(x,x,y)$. The first term of Eq. (17) provide mass to the pseudoscalar singlet, the second term is analogous to the explicit symmetry breaking term, and the third term is motivated by $SU(3)_V$ symmetry breaking term. In v(1), the Lagrangian density ${{\mathcal {L}}}_{SB}$ with mean field approximation results in non-vanishing masses for the pseudoscalar mesons and is written as

$$\begin{aligned} {{\mathcal {L}}}_{SB}=-\frac{\chi ^2}{\chi _0^2}\left[ m_\pi ^2f_\pi \sigma + \left( \sqrt{2}m_K^2f_K-\frac{m_\pi ^2}{\sqrt{2}}f_\pi \right) \zeta \right] . \end{aligned}$$

(18)

Above equation results in a non-vanishing divergence of the axial-vector current which fulfills the partial conserved axial-vector current (PCAC) relations for $\pi$ and K mesons (masses of $\pi$ and K mesons are non-zero). The parameters $\sigma _0$ and $\zeta _0$ are controlled by the spontaneous breaking of chiral symmetry and can be expressed in terms of kaon and pion decay constants

as

$$\begin{aligned} \zeta _0 = \frac{1}{\sqrt{2}} ( f_\pi - 2 f_K) \quad \mathrm{and} \quad \sigma _0 = - f_\pi , \end{aligned}$$

(19)

where $f_K$ = 115 MeV and $f_\pi$ = 93 MeV. To attain constituent mass of strange quark, an additional mass term is introduced through

$$\begin{aligned} {{\mathcal {L}}}_{\Delta m} = - \Delta m_s {\bar{q}} S q, \end{aligned}$$

(20)

where $S \, = \, \frac{1}{3} \, \left( I - \lambda _8\sqrt{3}\right) = \mathrm{diag}(0,0,1)$ stands for strange quark matrix and $\Delta m_s = 29$ MeV. In vacuum, relations for constituent quark masses can be written as

$$\begin{aligned} m_u=m_d=-\frac{g_s}{\sqrt{2}}\sigma _0, \quad m_s=-g_s \zeta _0 + \Delta m_s. \end{aligned}$$

(21)

The coupling constant $g_s$ and $\Delta m_s$ are chosen to yield the constituent quark masses. For reasonable values of hyperon potentials an additional symmetry breaking term should be added, which within mean field approximation is written as [52]

$$\begin{aligned} {{\mathcal {L}}}_h \, = \, (h_1 \, \sigma \, + \, h_2 \, \zeta ) \, \bar{s} s \, . \end{aligned}$$

(22)

The last term of Eq. (1), $U(\Phi ,{\bar{\Phi }}, T)$ is better known as temperature-dependent effective Polyakov loop potential which accounts for the deconfinement transition. The Polyakov line and the Polyakov loop are, respectively, defined as

$$\begin{aligned}&L(\mathbf {x})=\mathcal {P} exp\bigg [i\int _0^{\frac{1}{T}} d\tau A_4 (\mathbf {x},\tau ) \bigg ],\nonumber \\&\quad \Phi (\mathbf {x})=(Tr_c L)/N_C, \end{aligned}$$

(23)

Table 1 Parameters for Polyakov effective potential

Table 2 Parameters for PCQMF model used in the present work

where $\mathcal {P}$ is the path ordering operator and $A_4$ is the gluon field in the temporal direction [81].

In the present work, we consider the logarithmic Polyakov loop potential that satisfy the pure gauge $Z(N_C)$ symmetry and is expressed by [55, 82, 83]

$$\begin{aligned} \frac{U(\Phi ,{\bar{\Phi }},T)}{T^4}= & {} -\frac{a(T)}{2}{\bar{\Phi }}\Phi \nonumber \\&+b(T)\mathrm {ln}\big [1-6{\bar{\Phi }}\Phi +4({\bar{\Phi }}^3+\Phi ^3)-3({\bar{\Phi }}\Phi )^2\big ].\nonumber \\ \end{aligned}$$

(24)

In the above equation, the T-dependent parameters a(T) and b(T) can be inscribed as [55, 82]

$$\begin{aligned} a(T)=a_0+a_1\bigg (\frac{T_0}{T}\bigg )+a_2\bigg (\frac{T_0}{T}\bigg )^2,\ \ b(T)=b_3\bigg (\frac{T_0}{T}\bigg )^3. \end{aligned}$$

(25)

Parameters $a_0$, $a_1$, $a_2$ and $b_3$ summarized in Table 1 are precisely fitted as per result of lattice QCD thermodynamics in pure gauge sector [82]. The parameter $T_0$ is the confinement-deconfinement transition temperature in the pure Yang–Mills theory at vanishing chemical potential [84]. A rescaling of parameter $T_0$ from 270 to around 200 MeV is usually implemented when fermion fields are included [86,87,88,89].

Within mean field approximation, the thermodynamical potential density of SQM in the PCQMF model at finite baryon density and temperature can be elucidated as

$$\begin{aligned} \Omega =\mathcal {U}(\Phi ,{\bar{\Phi }},T) +\Omega _{q\bar{q}}-{{\mathcal {L}}}_M- {{\mathcal {V}}}_{vac}, \end{aligned}$$

(26)

where ${\Omega }_{q\bar{q}}$ exemplifies the contribution of quarks and antiquarks to the total thermodynamical potential and is given by

$$\begin{aligned} \Omega _{q\bar{q}}&=-\gamma _i k_BT\sum _{q, l}\int _0^\infty \frac{d^3k}{(2\pi )^3}\nonumber \\&\quad \times [\ln (1+e^{-3(E_i^*(k)-{\nu _i}^{*})/k_BT}+3\Phi e^{-(E_i^*(k)-{\nu _i}^{*})/k_BT} \nonumber \\&\quad +3{\bar{\Phi }}e^{-2(E_i^*(k)-{\nu _i}^{*})/k_BT})\nonumber \\&\quad +\ln (1+e^{-3(E_i^*(k)+{\nu _i}^{*})/k_BT} \nonumber \\&\quad + 3{\bar{\Phi }} e^{-(E_i^*(k)+{\nu _i}^{*})/k_BT} \nonumber \\&\quad +3\Phi e^{-2(E_i^*(k)+{\nu _i}^{*})/k_BT})]. \end{aligned}$$

(27)

In above equation, summation runs over constituent quarks (q=u, d, s) and leptons (l=e, $\mu$, $\nu _e$, $\nu _{\mu }$). Moreover, the value of spin degeneracy factor, $\gamma _i$, is 2 for quarks while 1 for leptons and $E_i^*(k)=\sqrt{m_i^{*2}+k^2}$ is the effective single particle energy of quarks. In Eq. (26), the term ${{\mathcal {L}}}_M = {{\mathcal {L}}}_{\Sigma \Sigma } +{{\mathcal {L}}}_{VV} +{{\mathcal {L}}}_{SB}$ defines the meson interaction. Also, the vacuum energy term, ${{\mathcal {V}}}_{vac}$, is subtracted to attain zero vacuum energy. Furthermore, the effective chemical potential, ${\nu _i}^{*}$, of quarks is defined by

$$\begin{aligned} {\nu _i}^{*}=\mu _i-g_\omega ^i\omega -g_\phi ^i\phi -g_\rho ^i\rho , \end{aligned}$$

(28)

where $\mu _i$ is usual quark chemical potential, $g^i_{\omega }$, $g^i_{\phi }$ and $g^i_{\rho }$ are the coupling strengths of quarks with vector meson fields.

Additionally, the effective constituent quark mass ${m_i}^{*}$ is defined as per the relation

$$\begin{aligned} {m_i}^{*} = -g_{\sigma }^i\sigma - g_{\zeta }^i\zeta - g_{\delta }^i\delta + {m_{i0}}. \end{aligned}$$

(29)

In the above equation, $g_{\sigma }^i$, $g_{\zeta }^i$ and $g_{\delta }^i$ signify the coupling strengths of various quarks with scalar fields. The model dependent parameters used in the present work and the parameters used for fixing them are given in Tables 2 and 3, respectively. The values of $g_{\sigma }^i$, $g_{\zeta }^i$ and ${m_{i0}}$ are approximated to fit the vacuum masses of constituent quarks with their values given as $m_u= m_d=313$ MeV and $m_s=490$ MeV [80].

Table 3 Values of different meson masses and decay constants (in MeV)

The model parameters, $k_0$, $k_1$, $k_2$, $k_3$, $k_4$, $g_v$, $g_4$ are determined using $\pi$-meson mass, K-meson mass and average mass of $\eta$ and $\eta ^{'}$ mesons which are further calculated by eigenvalues of mass matrix $M_{ij}=-\delta ^2{{\mathcal {L}}}(\phi )/\delta \phi _i\delta \phi _j$.

The vacuum expectation value of the dilaton field, $\chi _{0}$ and the parameter $g_4$, is constrained to obtain the effective nucleon mass around $0.61 m_N$ and compression modulus at around 252 MeV at nuclear saturation density $\rho _0=0.15$ fm$^{-3}$. Further, the constraint that binding energy of nuclear matter, $\epsilon _{0}/\rho -m_N$, at saturation density, $\rho _0$, should be near $-16$ MeV fix the parameter $g_v$. The vacuum values of $\sigma$ and $\zeta$ fields are calculated by applying the constraint on the values of decay constants of pion and kaon, respectively.

The fermion vacuum term, which is usually considered in the NJL and PNJL models, but neglected in Polyakov linear sigma (PLS) and PQMC models [53, 85], is not included in Eq. (27). This is because in the case of PLS, PQMC, and also in the present PCQMF model, the spontaneous breaking of chiral symmetry is done via mesonic potential; however, NJL and PNJL models use the ultraviolet cut-off parameter, $\Lambda$. In some of the studies within the PQM, such term is considered to study the properties of strongly interacting matter and is observed to change the nature of phase transition from first to second order [86, 87, 90].

The vector density, $\rho _{i}$, and scalar density, $\rho _{i}^{s}$, of quarks are defined as

$$\begin{aligned} \rho _{i} = 2N_c\int \frac{d^{3}k}{(2\pi )^{3}} \Big (f_i(k)-\bar{f}_i(k) \Big ), \end{aligned}$$

(30)

and

$$\begin{aligned} \rho _{i}^{s} = 2N_c\int \frac{d^{3}k}{(2\pi )^{3}} \frac{m_{i}^{*}}{E^{*}_i(k)} \Big (f_i(k)+\bar{f}_i(k) \Big ), \end{aligned}$$

(31)

respectively, where $f_i(k)$ and $\bar{f}_i(k)$ denote the Fermi distribution functions at finite temperature for quarks and anti-quarks and are expressed as

$$\begin{aligned} f_{i}(k)=\dfrac{\Phi e^{-(E_i^*(k)-{\nu _i}^{*})/k_BT}+2{\bar{\Phi }} e^{-2(E_i^*(k)-{\nu _i}^{*})/k_BT}+e^{-3(E_i^*(k)-{\nu _i}^{*})/k_BT}}{1+3\Phi e^{-(E_i^*(k)-{\nu _i}^{*})/k_BT}+3{\bar{\Phi }} e^{-2(E_i^*(k)-{\nu _i}^{*})/k_BT}+e^{-3(E_i^*(k)-{\nu _i}^{*})/k_BT}} , \end{aligned}$$

(32)

and

$$\begin{aligned} \bar{f}_{i}(k)=\dfrac{{\bar{\Phi }} e^{-(E_i^*(k)+{\nu _i}^{*})/k_BT}+2{\Phi } e^{-2(E_i^*(k)+{\nu _i}^{*})/k_BT}+e^ {-3(E_i^*(k)+{\nu _i}^{*})/k_BT}}{1+3{\bar{\Phi }} e^{-(E_i^*(k)+{\nu _i}^{*})/k_BT}+3{\Phi } e^{-2(E_i^*(k)+{\nu _i}^{*})/k_BT}+e^{-3(E_i^*(k)+{\nu _i}^{*})/k_BT}} . \end{aligned}$$

(33)

In order to evaluate the values of scalar fields $\sigma$, $\zeta$, $\delta$, and $\chi$, the vector fields $\omega$, $\rho$ and $\phi$ and the Polyakov field $\Phi$ and its conjugate ${\bar{\Phi }}$, we minimize $\Omega$ with respect to these fields, i.e.,

$$\begin{aligned} \frac{\partial \Omega }{\partial \sigma }= & {} \frac{\partial \Omega }{\partial \zeta }=\frac{\partial \Omega }{\partial \delta }\nonumber \\= & {} \frac{\partial \Omega }{\partial \chi }=\frac{\partial \Omega }{\partial \omega }=\frac{\partial \Omega }{\partial \rho }=\frac{\partial \Omega }{\partial \phi }\nonumber \\= & {} \frac{\partial \Omega }{\partial \Phi }=\frac{\partial \Omega }{\partial {{\bar{\Phi }}}}=0. \end{aligned}$$

(34)

This leads to the following set of coupled equations:

$$\begin{aligned} \frac{\partial \Omega }{\partial \sigma }&= k_{0}\chi ^{2}\sigma -4k_{1}\left( \sigma ^{2}+\zeta ^{2} +\delta ^{2}\right) \sigma -2k_{2}\nonumber \\&\quad \times \left( \sigma ^{3}+3\sigma \delta ^{2}\right) -2k_{3}\chi \sigma \zeta \nonumber \\&\quad -\frac{d}{3} \chi ^{4} \bigg (\frac{2\sigma }{\sigma ^{2}-\delta ^{2}}\bigg ) +\left( \frac{\chi }{\chi _{0}}\right) ^{2}m_{\pi }^{2}f_{\pi }\nonumber \\&\quad - \left( \frac{\chi }{\chi _0}\right) ^2m_\omega \omega ^2 \frac{\partial m_\omega }{\partial \sigma }\nonumber \\&\quad -\left( \frac{\chi }{\chi _0}\right) ^2m_\rho \rho ^2 \frac{\partial m_\rho }{\partial \sigma } -\sum _{i=u,d} g_{\sigma }^i\rho _{i}^{s} = 0 , \end{aligned}$$

(35)

$$\begin{aligned} \frac{\partial \Omega }{\partial \zeta }&= k_{0}\chi ^{2}\zeta -4k_{1}\left( \sigma ^{2}+\zeta ^{2}+\delta ^{2}\right) \zeta \nonumber \\&\quad -4k_{2}\zeta ^{3}-k_{3}\chi \left( \sigma ^{2}-\delta ^{2}\right) \nonumber \\&\quad -\frac{d}{3}\frac{\chi ^{4}}{{\zeta }} +\left( \frac{\chi }{\chi _{0}} \right) ^{2}\left[ \sqrt{2}m_{K}^{2}f_{K}-\frac{1}{\sqrt{2}} m_{\pi }^{2}f_{\pi }\right] \nonumber \\&\quad -\left( \frac{\chi }{\chi _0}\right) ^2m_\phi \phi ^2\frac{\partial m_\phi }{\partial \zeta } -\sum _{i=s} g_{\zeta }^i\rho _{i}^{s}&= 0 , \end{aligned}$$

(36)

$$\begin{aligned} \frac{\partial \Omega }{\partial \delta }&=k_{0}\chi ^{2}\delta -4k_{1}\left( \sigma ^{2}+\zeta ^{2}+\delta ^{2}\right) \nonumber \\&\quad \times \delta -2k_{2}\left( \delta ^{3}+3\sigma ^{2}\delta \right) +\mathrm {2k_{3}\chi \delta \zeta } \nonumber \\&\quad + \frac{2}{3} d \chi ^4 \left( \frac{\delta }{\sigma ^{2}-\delta ^{2}}\right) -\sum _{i=u,d} g_{\delta }^i\rho _{i}^{s} = 0 , \end{aligned}$$

(37)

$$\begin{aligned} \frac{\partial \Omega }{\partial \chi }&=\mathrm {k_{0}\chi } \left( \sigma ^{2}+\zeta ^{2}+\delta ^{2}\right) \nonumber \\&\quad -k_{3} \left( \sigma ^{2}-\delta ^{2}\right) \zeta \nonumber \\&\quad + \chi ^{3}\left[ 1 +\mathrm{{ln}}\left( \frac{\chi ^{4}}{\chi _{0}^{4}}\right) \right] +(4k_{4}-d)\chi ^{3} \nonumber \\&\quad -\frac{4}{3} d \chi ^{3} \mathrm{{ln}} \Bigg ( \bigg (\frac{\left( \sigma ^{2} -\delta ^{2}\right) \zeta }{\sigma _{0}^{2}\zeta _{0}} \bigg ) \bigg (\frac{\chi }{\mathrm {\chi _0}}\bigg )^3 \Bigg )+ \frac{2\chi }{\chi _{0}^{2}}\left[ m_{\pi }^{2} f_{\pi }\sigma \right. \nonumber \\&\quad \left. +\left( \sqrt{2}m_{K}^{2}f_{K}-\frac{1}{\sqrt{2}} m_{\pi }^{2}f_{\pi } \right) \zeta \right] \nonumber \\&\quad -\frac{\chi }{{\chi ^2}_0}({m_{\omega }}^2 \omega ^2+{m_{\rho }}^2\rho ^2) = 0, \end{aligned}$$

(38)

$$\begin{aligned} \frac{\partial \Omega }{\partial \omega }&=\frac{\chi ^2}{\chi _0^2}m_\omega ^2\omega +4g_4\omega ^3\nonumber \\&\quad +12g_4\omega \rho ^2 -\sum _{i=u,d}g_\omega ^i\rho _{i}^{v}=0, \end{aligned}$$

(39)

$$\begin{aligned} \frac{\partial \Omega }{\partial \rho }&=\frac{\chi ^2}{\chi _0^2}m_\rho ^2\rho +4g_4\rho ^3\nonumber \\&\quad +12g_4\omega ^2\rho - \sum _{i=u,d}g_\rho ^i\rho _{i}^{v}=0, \end{aligned}$$

(40)

$$\begin{aligned} \frac{\partial \Omega }{\partial \phi }&=\frac{\chi ^2}{\chi _0^2}m_\phi ^2\phi \nonumber \\&\quad +8g_4\phi ^3- \sum _{i=s}g_\phi ^i\rho _{i}^{v}=0, \end{aligned}$$

(41)

$$\begin{aligned} \frac{\partial \Omega }{\partial \Phi }&=\bigg [\frac{-a(T){\bar{\Phi }}}{2} -\frac{6b(T) ({\bar{\Phi }}-2{\Phi }^2+{{\bar{\Phi }}}^2\Phi ) }{1-6{\bar{\Phi }}\Phi +4({\bar{\Phi }}^3 +\Phi ^3)-3({\bar{\Phi }}\Phi )^2}\bigg ]T^4 -\sum _{i=u,d,s}\frac{2k_BTN_C}{(2\pi )^3} \nonumber \\&\quad \times \int _0^\infty d^3k \bigg [\frac{e^{-(E_i^*(k)-{\nu _i}^{*})/k_BT}}{(1+e^{-3(E_i^*(k)-{\nu _i}^{*})/k_BT}+3\Phi e^{-(E_i^*(k)-{\nu _i}^{*})/k_BT} +3{\bar{\Phi }}e^{-2(E_i^*(k)-{\nu _i}^{*})/k_BT})} \nonumber \\&\quad +\frac{e^{-2(E_i^*(k)+{\nu _i}^{*})/k_BT}}{(1+e^{-3(E_i^*(k)+{\nu _i}^{*})/k_BT} +3{\bar{\Phi }} e^{-(E_i^*(k)+{\nu _i}^{*})/k_BT}+3\Phi e^{-2(E_i^*(k)+{\nu _i}^{*})/k_BT})}\bigg ]=0, \end{aligned}$$

(42)

and

$$\begin{aligned} \frac{\partial \Omega }{\partial {\bar{\Phi }}}&=\bigg [\frac{-a(T)\Phi }{2}-\frac{6b(T) (\Phi -2{{\bar{\Phi }}}^2+{\Phi }^2{\bar{\Phi }}) }{{1-6{\bar{\Phi }}\Phi +4({\bar{\Phi }}^3+\Phi ^3) -3({\bar{\Phi }}\Phi )^2}}\bigg ]\times T^4 -\sum _{i=u,d,s}\frac{2k_BTN_C}{(2\pi )^3} \nonumber \\&\quad \times \int _0^\infty d^3k\ \bigg [\frac{e^{-2(E_i^*(k)-{\nu _i}^{*})/k_BT}}{1+e^{-3(E_i^*(k)-{\nu _i}^{*})/k_BT} +3\Phi e^{-(E_i^*(k)-{\nu _i}^{*})/k_BT} +3{\bar{\Phi }}e^{-2(E_i^*(k)-{\nu _i}^{*})/k_BT}} \nonumber \\&\quad +\frac{e^{-(E_i^*(k)+{\nu _i}^{*})/k_BT}}{1+e^{-3(E_i^*(k)+{\nu _i}^{*})/k_BT} +3{\bar{\Phi }} e^{-(E_i^*(k)+{\nu _i}^{*})/k_BT}+3\Phi e^{-2(E_i^*(k)+{\nu _i}^{*})/k_BT}}\bigg ]=0. \end{aligned}$$

(43)

The above equations are solved simultaneously under different situations of the medium to obtain the in-medium values of scalar and vector fields, which are further used to evaluate other thermodynamic properties and the EoS.

2.2 Thermodynamics of $\beta$-equilibrated SQM and structure of strange quark stars

The initial stage of SQS known as PSQS is composed of quarks (u, d, s) and leptons (e, $\mu$, $\nu _e$ and $\nu _{\mu }$) maintaining the weak $\beta$- equilibrium and the charge neutrality.

The weak $\beta$-equilibrium conditions are expressed as [45, 46]

$$\begin{aligned}&\mu _{d}=\mu _{s}=\mu _{u}+\mu _e-\mu _{\nu _e}, \end{aligned}$$

(44)

$$\begin{aligned}&\mu _{\mu }=\mu _e \quad \text {and}\quad \mu _{{\nu }_{\mu }}=\mu _{\nu _e}. \end{aligned}$$

(45)

Additionally, the condition for electric charge neutrality is written as

$$\begin{aligned} \frac{2}{3}\rho _u=\frac{1}{3}\rho _d+\frac{1}{3}\rho _s+\rho _e+\rho _{\mu }. \end{aligned}$$

(46)

The total baryon density can be articulated in terms of number density of quarks as

$$\begin{aligned} \rho _B=\frac{1}{3} (\rho _u+\rho _d+\rho _s). \end{aligned}$$

(47)

Using thermodynamical potential density, $\Omega$, one can evaluate the pressure, p, free energy density, F, and the energy density, $\epsilon$, through the relations

$$\begin{aligned} p= & {} -\Omega , \end{aligned}$$

(48)

$$\begin{aligned} F= & {} \Omega +\sum _{i=q, l} {\mu _i}^{*} {\rho _i}, \end{aligned}$$

(49)

and

$$\begin{aligned} \epsilon =\Omega +\sum _{i=q, l} {\mu _i}^{*} \rho _i+TS, \end{aligned}$$

(50)

respectively.

The EoS of quark matter calculated using the above relations can be used further to obtain the mass-radius relation of QSs by solving the Tolman-Oppenheimer-Volkov (TOV) equations (in units $G=c=1$) [91]

$$\begin{aligned} \frac{dM}{dr}= & {} 4\pi r^2 \epsilon (r), \end{aligned}$$

(51)

$$\begin{aligned} \frac{dp}{dr}= & {} -\frac{\epsilon (r)M(r)}{r^2}\bigg [1+\frac{p(r)}{\epsilon (r)}\bigg ] \bigg [1+\frac{4\pi p(r)r^3}{M(r)}\bigg ]\nonumber \\&\times \bigg [1-\frac{2GM(r)}{r}\bigg ]^{-1}. \end{aligned}$$

(52)

In above, M(r) is the total mass within the sphere of radius r, $\epsilon (r)$ is the corresponding energy density, p(r) is the pressure, and G is the Newton’s gravitational constant. In Eq. (52) the first two factors in the square brackets denote the special relativity corrections of order $v^2/c^2$, and these factors reduce to 1 in the non-relativistic limit. The last set of brackets is a general relativistic correction. The gravitational mass $M=M(r=R)$ of the star is the mass enclosed within the star’s radius.

The gravitational waves emitted from the merger of two compact stars serve as another probe to the study of the EoS of dense matter. To calculate the tidal deformability and Love number, along with TOV equations, we need to solve the differential equations [58, 92,93,94]

$$\begin{aligned} \frac{\mathrm {d}H(r)}{\mathrm {d}r}= & {} \beta , \end{aligned}$$

(53)

$$\begin{aligned} \frac{\mathrm {d} \beta (r)}{\mathrm {d} r}= & {} 2\left( 1-2 \frac{M}{r}\right) ^{-1} H\Bigg \{-2 \pi [5 \epsilon +9 P+f(\epsilon +P)] \nonumber \\&\left. +\frac{3}{r^{2}}+2\left( 1-2 \frac{M}{r}\right) ^{-1}\left( \frac{M}{r^{2}}+4 \pi r P\right) ^{2}\right\} +\frac{2 \beta }{r}\left( 1-2 \frac{M}{r}\right) ^{-1}\left\{ -1+\frac{M}{r}+2 \pi r^{2}(\epsilon -P)\right\} , \end{aligned}$$

(54)

where H(r) is the metric function and f is defined as $\mathrm {d}\epsilon /\mathrm {d}p$. The integration will start from the center with the expansions $H(r)=a_{0}r^{2}$ and $\beta (r)=2a_{0}r$ as the radius $r\rightarrow 0$. The love number measures the distortion of the shape of the surface of a star by an external tidal field. The tidal deformability, $\Lambda$, is related to the $l=2$ dimensional love number $k_2$ through the relation $\Lambda =\frac{2}{3}k_2\left( C\right) ^{-5}$, with $k_2$ given by [93, 95]

$$\begin{aligned} k_{2}&=\frac{8C^{5}}{5}(1-2C)^{2}[2+2C(y-1)-y]\nonumber \\&\quad \times \lbrace 2C[6-3y+3C(5y-8)] \nonumber \\&\quad +4C^{3}[13-11y+C(3y-2)+2C^{2}(1+y)] \nonumber \\&\quad +3(1-2C)^{2}[2-y+2C(y-1)]\ln (1-2C)\rbrace ^{-1}. \end{aligned}$$

(55)

In Eq. 55, $C \equiv M/R$ is the compactness of the compact star, and the parameter y is defined as [58, 94]

$$\begin{aligned} y=\frac{R\beta (R)}{H(R)}-\frac{4\pi R^{3}\epsilon _{0}}{M}, \end{aligned}$$

(56)

is related to the metric function H(R) and the surface energy density $\varepsilon _{0}$. The second term in the above equation is because of the non-zero value of the surface energy density $\varepsilon _{0}$.

3 Numerical results and discussion

In this section, numerical results on the study of the quark matter under the conditions of $\beta$-equilibrium and charge neutrality are presented. The solution of the non-linear coupled equation of motion (from Eqs. (35) to (43)) give rise to the scalar fields ($\sigma$, $\zeta$, $\delta$, $\chi$), vector fields ($\omega$, $\rho$, $\phi$), and Polyakov loop fields, ($\Phi$, ${\bar{\Phi }}$). As discussed in the introduction section, three situations are taken into consideration for evaluating various quantities of interest. In the first situation, neutrinos are assumed to be inside of a star with lepton fraction, $Y_l = 0.4$ $(Y_l=Y_e+Y_{\mu }+Y_{\nu _e}+Y_{\nu _{\mu }}=0.4)$ and entropy per baryon equals to 1, second stage comes into action just after the escape of neutrinos ($Y_{\nu _l}=0$) and the entropy per baryon increases to 2, and finally cold stars with zero entropy forms [67, 96, 97]. In Sect. 3.1, we present the discussion on the particle fraction, the effective constituent quark masses, and the EoS under consideration. At last, employing the EoS, the possible structure of SQSs is explored in Sect. 3.2.

Fig. 1

Particle fractions of quarks (u, d and s) and leptons (e, $\mu$) at $g_v=0$ and 10.92 for different snapshots of PQS as a function of baryonic density, $\rho _B$ (in units of nuclear saturation density $\rho _0$)

3.1 Thermodynamical properties of SQM

In Fig. 1, we show the particle fractions, $Y_i$, of quarks (u, d, s) and leptons (e, $\mu$) for different snapshots of PQS evolution at $g_v=0$ and 10.92, as a function of baryonic density, $\rho _B$. The population of d-quarks and electrons start decreasing when s-quark appearance is observed for each case. The density at which s-quarks start appearing is decreased with an increase in the entropy. The fraction of electrons and muons is larger at initial stage of the PQS evolution ($s=1$ and $Y_l=0.4$), as shown in Fig. 1a, b. This may occur due to the higher lepton fraction which provides a large number of electrons and decreases other negatively charged particles due to electric charge neutrality. At second stage of star evolution, the fraction of electron and muon decreased. At the final stage, where $s=0$ and $Y_{\nu _l}=0$, the muon almost disappears for the whole range of density, and the electron fraction is very small. For the finite vector interaction, s quarks appear at lower density as compared to the vanishing vector interaction.

Fig. 2

The effective constituent quark masses, $m_i^*$, for three snapshots of PQS evolution at $g_v=0$ and 10.92 as a function of baryonic density, $\rho _B$ (in units of nuclear saturation density $\rho _0$)

Fig. 3

a The sound velocity square, $c_s^2$, as a function of energy density $\epsilon$, b the entropy per baryon, s, as a function of baryonic density for strange quark matter at $T=10$, 30, 50 and 80 MeV

The constituent quark masses are generated via the coupling of scalar fields with the quarks in the medium. Figure 2 illustrates the variation of the constituent quark masses with the baryonic density, $\rho _B$, at $g_v=0$ and 10.92. It is observed that the effective constituent quark mass, $m_{i}^*$, in the SQM decreases with an increase in the value of baryon density for $g_v=0$ and 10.92. The variation in $m_{u}^*$ and $m_{d}^*$ is sharper than $m_{s}^*$ for lower density due to the absence of coupling between s-quark and scalar $\sigma$ field ($g^{s}_\sigma =0$). The values of $m_u^*$, $m_d^*$ and $m_s^*$ are observed as 140, 134 and 423 MeV at $2 \rho _0$ and can be compared to the vacuum masses 313 MeV for u, d and 498 MeV for s-quark. For a given density, an increase in the strength of vector interactions causes an increment in the $m_{i}^*$. Moreover, the effect of different values of the entropy and lepton fraction is minimal on $m_{d}^*$ due to almost same fraction of d-quark, however measurable change is observed in $m_{u}^*$ and $m_{s}^*$. As is visible from Fig. 2e, f, the sharp decrement in $m_{s}^*$ starts from different value of $\rho _B$ for evolution condition of PQS, because s-quark appear at different densities in each case. Increase in the lepton fraction causes an increase in the mass of s-quark and this shows that, for finite lepton fraction, the chiral restoration for s-quark is suppressed because of the large electron fraction. Further, with the increase in vector interaction, the sharp decrement in $m_{s}^*$ starts from lower density. Our results are consistent with work of Ref. [98], where the effects of varying the scalar-isovector coupling strength on the constituent quark masses and particle fractions were studied in the cold quark matter using NJL model. To further explore the impact of finite temperature on the quark matter properties, we present the discussion on the sound velocity square, $c_s^2$, and the entropy density, s. It is known that the square of the sound velocity ${c_{s}^2}$ $\left( =dp/d\epsilon \right)$ for strongly interacting liquid is typically smaller than 1/3 (ideal gas limit) and satisfies the causality constraint, $c_s<c$. Therefore, it becomes interesting to introduce and investigate the sound velocity in the proposed model for the physical verification of model parameters. In Fig. 3a, the sound velocity square is plotted against the energy density for the SQM without considering the case of neutrinos at $T=10$, 30, 50, and 80 MeV. From the attained figure, it is observed that ${c_{s}^2}$ of dense quark matter for each T will always be less than 1/3. If we increase the temperature from $T=10$ to 80 MeV, it is attained that ${c_{s}^2}$ shows decrement and for $T=80$ MeV, the peak of ${c_{s}^2}$ almost disappears. The results for the square of the sound velocity plotted here resemble the results predicted in the three flavor NJL model [48].

Fig. 4

The range of temperature achieved as a function of baryonic density for $s=1$, 2 with/without trapped neutrinos at different vector interaction

Fig. 5

The electron chemical potential as a function of baryonic density, $\rho _B$ (in units of nuclear saturation density $\rho _0$) for three snapshots of PQS evolution at $g_v=0$, 6 and 10.92

The variation of the entropy density as a function of baryon density at finite temperatures is depicted in Fig. 3b, without trapped neutrino matter. At finite temperature, entropy density, s, decreases with an increase in the baryonic density. This behavior may be because, when baryon density vanishes, an electron-positron pair is generated at a finite temperature, contributing to the entropy. Also, we noticed that with the increase in temperature, s becomes larger. These observations are also consistent with the calculations of Ref. [99] where properties of SQM at finite temperature were investigated using the MIT bag model with the density-dependent bag constant.

Fig. 6

The behavior of pressure at for different condition of PQS evolution as a function of baryonic density, $\rho _B$ (in units of nuclear saturation density $\rho _0$) at $g_v=0$, 6 and 10.92

Fig. 7

The EoS plotted as a function of baryonic density $\rho _B$ (in units of nuclear saturation density $\rho _0$), for various situation of PQS evolution at $g_v=0$, 6 and 10.92

In Fig. 4 we plot the variation of temperature, T, as a function of baryonic density for $(s, Y_l) = (1, 0.4)$ and $(s, Y_{\nu l}) = (2, 0)$, at $g_v=0$, 6 and 10.92. For both $s=1$ and 2, it is evident that temperature becomes almost constant and saturation is achieved at $4-6$ $\rho _0$. For both situations, the temperature of each curve increased gradually and attained a maximum value at 38 MeV and 76 MeV, for $s=1$ and 2, respectively. For a given value of entropy per baryon, if one compare the situations with and without neutrino cases, the temperature will be lower in the former situation. The reason is: the degrees of freedom will increase for fixed lepton fraction, and a lower value of temperature will be required to keep the entropy per baryon fixed [37]. Further, the effect of vector interaction can also be observed in the moderate density range, i.e., for an increment in $g_v$ at fixed density, the temperature is observed to decrease.

Lepton fraction plays an important role in studying the behavior of electron chemical potential. Figure 5 shows the variation of electron chemical potential, $\mu _e$, with the baryon density, at various vector interactions, for three star evolution snapshots of PQS. It is observed that for $Y_{\nu _ l}=0$, $\mu _e$ first increase, attain a maximum value and then decrease for $s=0$, 2 at $g_v=0$, 6 and 10.92. On the other hand, for a fixed value of the total lepton fraction with the finite number of neutrinos, $\mu _e$ increases gradually with the density. Comparing $s=0$ and $s=2$ curves, $\mu _e$ is observed to fall with an increase in the entropy, for each given $g_v$ value. Increasing the strength of vector interactions, keeping other parameters fixed, $\mu _e$ increases, and maxima of the curve (for $Y_{\nu _l}=0$) moves toward lower density. Focusing on the range of electron chemical potential, for $Y_{\nu _l}=0$ and $Y_{l}=0.4$, it is observed to be nearly 0 to 75 MeV and 0 to 300 MeV, respectively. The nature of $\mu _e$ is also studied in NJL and MIT bag model [37]. It was observed that in the MIT model, $\mu _e$ is always less than 20 MeV, whereas its range was about 100 MeV for the NJL model.

In Fig. 6, we plot the behavior of pressure density, P, of quarks with baryonic density for different conditions of PQS evolution at $g_v=0$, 6 and 10.92. It is observed that P shows a monotonic increment with an increase in the baryonic density for each configuration. For a given density, an increase in the strength of vector interactions results in the pressure increment.

In Fig. 7 we plot the EoS of quark matter for different conditions of the medium. Pressure is observed to increase smoothly with energy density for each combination of entropy and lepton fraction. An increase in the value of $g_v$ and as well as lepton fraction, increase the stiffness in the EoS. The effect of temperature on the EoS for different values of lepton fraction has been studied using the NJL model under the $\beta$-equilibrium and charge neutrality condition in Ref. [37]. Also, EoS for SQM for different coupling strengths of vector-isovector and scalar-isoscalar interaction have been computed in NJL model studies of Refs. [48, 98, 100].

3.2 Properties of strange quark stars (SQSs)

Solving the TOV equation for a specific EoS, one can find the radial dependency of the energy density and the pressure for a particular central pressure, $P_c$. With the variation in $P_c$, one can attain a sequence of compact star masses and radii as illustrated in Fig. 8.

Fig. 8

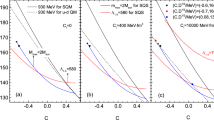
Mass-radius relation of SQSs for various vector interactions/moments of the star evolution defined by entropy and lepton fraction with the observational constraints for maximum mass required by PSR J0740-6620(2.14$^{+0.10}_{-0.09}M_\odot$) and PSR J0348+0432 ($2.01 \pm 0.04\ M_\odot$) [20]

Fig. 9

Relation between Love number, $k_2$ and the mass of SQS for different moments of the star evolution at $g_v=0$, 1 and 2

Fig. 10

Relation between tidal deformability and the mass of SQS for different moments of the star evolution at $g_v=0$, 1 and 2

This figure shows the effect of vector interactions on the mass-radius relation for different stages of PQS evolution. For an increase in the $g_v$ value, the EoS becomes stiffer and the maximum gravitational mass and radius of SQS increases. In case of cold quark star ($s = 0$ and $Y_{\nu _l}=0$), the maximum value of mass reaches upto 1.776$M_\odot$, 1.830$M_\odot$, and 1.934$M_\odot$ for $g_v=0$, 1 and 2, respectively. On increasing the entropy per baryon (keeping $Y_{\nu _l}=0$) from 0 to 2, the maximum mass of SQSs is also found to increase, for finite values of $g_v$. The inclusion of neutrinos further increase the gravitational mass for different vector interactions. For stars with trapped neutrinos and $g_v\ge 2$, the maximum mass can have a value larger than 2.0 $M_\odot$, which is consistent with the recently discovered large mass pulsar $J1614-2230$ $(1.97\pm 0.04M_\odot )$ and PSR J0740-6620 (2.14$^{+0.10}_{-0.09} M_\odot$) [18, 19], however the upper radius limit values for a 1.4$M_\odot$ from three recent works are $R\le 13.76$ km, $R\le 13.6$ km, and 8.9 $\le R\le 13.76$ km, respectively [26, 28]. From Fig. 8 one can observe that the upper radius limits of 1.4$M_\odot$ are smaller than our maximum radii except $s = 0$ and $Y_{\nu _l}=0$ for $g_v=2$. Table 2 shows the numeric values of maximum masses and radii for various conditions of PQS evolution at different $g_v$ values (Table 4).

Table 4 The values of maximum gravitational mass, $M/M_\odot$ and corresponding radius, R, for strange quark stars are tabulated.

Another important parameter Love number, $k_2$, is calculated using Eq. (55). Figure 9 depicts the variation of Love number as a function of SQS mass at $g_v=0$, 1, and 2. It is observed that $k_2$ increases at small SQS mass values, then reaches its maximum at around 1.1–1.4$M_\odot$, and later decays rapidly in the larger mass region.

The tidal deformability is an important quantity in the binary neutron star merger which can be derived using a gravitational wave detector. In Fig. 10, the tidal deformability, $\Lambda$, is plotted against the mass of SQS. It is perceived that the deformability decreases with an increase in the mass of star, as long as SQS is stable with increasing central density. Comparing the results attained for $g_v=2$, one can see that larger deformability of SQS is achieved at $s=2$. The recent investigation for binary neutron star merger GW170817 put tight constraints on mass and $\Lambda$, with corresponding range 1.00–1.89$M_\odot$ and 70–580, respectively. In our case, for 1.4$M_\odot$ star, the observed tidal deformabilities are 85–132 for $g_v=0$, 106–151 for $g_v=1$ and 160-200 for $g_v=2$ which show good agreement with the results obtained for GW170817. In Ref. [60], the author studied the tidal deformability in binary star mergers, considering the cases of udQS$-ud$QS and udQS-hadronic star. The obtained tidal deformabilities at ${1.4M\odot }$ and their average values are in good agreement with the experimental constraints of GW170817.

Fig. 11

The gravitational redshift versus gravitational mass of strange quark stars for different moments of the star evolution, at $g_v=0$, 1 and 2

The properties of proto-quark star are also explained in Ref. [102] using different models (QMDD model, MIT bag model, and NJL model) at different entropy and lepton fraction. Their results show that the QMDD model always reproduces massive stars than the MIT bag model due to the additional terms appearing in the thermodynamical potential. Bordbar et al. investigated the properties of SQSs considering the impact of finite entropy and temperature using MIT bag model [63] and NJL model [103]. It was concluded that the maximum mass and the radius of stars decreases with an increase in entropy, whereas an increment is observed as a function of temperature. The mass-radius relation for the above models obey the relation, $M\propto R^3$, for different cases at fixed central energy density.

Finally, we present the results on the gravitational redshift, Z, defined through the relation [63]

$$\begin{aligned} Z=\left( 1-\frac{2M}{Rc^{2}}\right) ^{-1/2}-1. \end{aligned}$$

(57)

The gravitational redshift of SQS as a function of gravitational mass is plotted in Fig. 11. It is observed that Z increases with an increase in the value of $g_v$ for different moments of star evolution, and Z has a larger value at finite lepton fraction. The maximum value of Z for SQS is observed as 0.210 at $g_v=2$, with $s=1$, $Y_{l}=0$ and minimum value as 0.174 at $g_v=0$ with $s=2$ and $Y_{\nu _l}=0$. The maximum gravitational redshift, $Z=0.192$, lies in the observed range of quark star candidate RXJ185635-3750 [104]. In Ref. [63], authors have studied the gravitational redshift using the MIT bag model for both fixed and density-dependent bag constant. They found that Z increases with an increase in the entropy value, and its maximum is attained by density-dependent bag constant with entropy $s=2.5k_B$. The behavior of gravitational redshift with temperature is also studied in the NJL model and observed that Z increases with an increase of temperature.

4 Summary and future outlook

In summary, employing Polyakov chiral $\text {SU(3)}$ quark mean-field model, we studied the properties of SQM/ SQSs under $\beta$-equilibrium, with/without trapped neutrinos. We studied the effect of finite entropy and lepton fraction on the population threshold of quarks and leptons, the effect of temperature on entropy density and sound velocity squared. We also observed the effect of vector interactions at different snapshots of PQS evolution on the EoS. It was found that the EoS becomes stiffer for a higher $g_v$ value in each case, and the presence of lepton fraction further enhanced this. The EoS was further used in TOV equation to calculate the mass-radius and tidal deformability for different stages of star evolution. The maximum mass of SQSs shows an increment with an increase in the vector interaction. In the case of cold star, the maximum gravitational mass of SQSs reached upto 1.776$M_\odot$, 1.830$M_\odot$ and 1.934$M_\odot$, for $g_v=0$, 1 and 2, respectively. We further evaluated the tidal deformability of SQSs and found that its magnitude has good compatibility with the constraint of the GW170817 event.

In our future work, the hadronic degrees of freedom will be incorporated in the present Polyakov model, and the EoS and other properties of hybrid stars will be explored as has been done in different studies [68, 105,106,107,108]. Several efforts have been made by the authors to study the effect of first-order phase transition on SQM in relation to compact stars [109,110,111]. Roark and Dexheimer applied a two-phase approach on the chiral mean-field model in order to explore the first-order phase transition for different leptonic degrees of freedom [109]. A similar approach was applied within MIT bag model to describe the properties of SQM and phase transition [110].

Extending the current model to situations beyond the mean-field approximation for the study of strongly interacting matter will also be of interest in the future work. To incorporate quantum fluctuations in the PCQMF model, calculations can be done using the functional renormalization group (FRG) approach. Recently, the QCD phase has been studied applying the FRG approach to the quark meson model [112,113,114,115]. Also, we will include the effect of finite magnetic field on the EoS and structural properties of compact objects [100, 116,117,118].