Abstract
We study the \(S_3\)-symmetric two Higgs doublet model by adding two generations of vector like leptons (VLL) which are odd under a discrete \(Z_2\)-symmetry. The lightest neutral component of the VLL acts as a dark matter (DM) whereas the full VLL set belongs to a dark sector with no mixings allowed with the standard model fermions. We analyse the model in light of dark matter and collider searches. We show that the DM is compatible with the current relic density data as well as satisfying all direct and indirect dark matter search constraints. We choose some representative points in the model parameter space allowed by all aforementioned dark matter constraints and present a detailed collider analysis of multi-lepton signals viz. the mono-lepton, di-lepton, tri-lepton and four-lepton along with missing transverse energy in the final state using both the cut-based analysis and multivariate analysis respectively at the high luminosity 14 TeV LHC run.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Standard Model (SM) particle spectrum appears to be complete after the Higgs discovery [1, 2], albeit the several shortcomings, both theoretical and experimental. The resolution to any of these shortcomings beg for an extension of the SM framework, which invariably lead us to scenarios with additional bosonic or fermionic degrees of freedom in the particle spectrum. One such possible scenario is an extension with vector like fermions, whose left- and right-chiral counterparts transform identically under the SM gauge symmetry. These VLLs can appear naturally in grand unified theories [3,4,5,6], theories with non-minimal supersymmetric extensions [7,8,9,10,11,12,13], warped or universal extra-dimension [14,15,16,17,18,19,20,21,22], composite Higgs model [23,24,25,26,27,28,29], little Higgs model [30,31,32,33,34], etc. VLLs can acquire masses from the gauge-invariant bilinear dimension-3 bare mass terms. Since they do not achieve masses from the Yukawa couplings alone, unlike fourth generation of chiral fermions, the vector like fermions are weakly constrained from electroweak precision observables and Higgs data [35]. Although the vector like quarks participate in both the production and decay of Higgs boson, only the decay of Higgs boson is modified in presence of vector like leptons (VLLs). The rate of the process where the Higgs decays to two photons receives additional contribution from the charged VLLs in loop and gets modified [36]. SM extended with one or more generations of VLLs have been studied earlier in [37,38,39]. The extensions of Higgs singlet [40], Higgs doublet [41,42,43,44], Higgs triplet [35, 45, 46], left right symmetric model [47,48,49] along with VLLs have been very popular in literature for dark matter (DM) and collider searches throughout.
In this work, we study the \(S_3\)-symmetric two Higgs doublet model (2HDM) [50, 51] augmented with two generations of VLLs. The need to add two generations of VLL instead of one, is to maintain an exact \(S_3\)-symmetry in the Yukawa sector. One of the primary motivations of the \(S_3\)-symmetric 2HDM is aimed at understanding the fermion mass hierarchy within the SM, as it provides a proper description of the mass hierarchy and mixing among the quarks. Non-zero quark masses and non-block-diagonal CKM matrix, compatible with the experiment, makes this special kind of 2HDM endowed with non-abelian \(S_3\) group very attractive. One also notes that unlike the general 2HDM, \(S_3\)-symmetric 2HDM naturally provides a 125 GeV SM-like Higgs boson, which we discuss later. As we want to study the DM phenomenology of the VLL in this model, we impose an additional \(Z_2\) symmetry in the model under which all the VLLs are odd while the SM particles along with the 2HDM is even. In Ref. [43], the authors have used a CP-conserving 2HDM along with one generation of VLLs to study the DM phenomenology. The difference in their study with ours lies not only in the particle spectrum due to the presence of an extra generation of VLL which is mandated by the \(S_3\)-symmetry, but also in the way these VLLs interact with the visible sector particles. To be more specific, the quartic part of the Yukawa Lagrangian being \(S_3\)-symmetric, there exist additional interactions with respect to the reference [43] due to the presence of an extra generation of VLLs. In addition, in our framework, \(S_3\)-symmetry is softly broken by the dimension-3 Dirac as well as Majorana mass terms unlike reference [43], where the authors considered only Dirac mass terms for soft breaking. In our framework the lightest neutral mass eigenstate of the VLL is a viable DM candidate, which produces the correct relic density, and its direct detection cross-sections and thermally averaged annihilation cross-sections in indirect detection are compatible with that of the experiments.
We choose some representative benchmark points from the multi-dimensional parameter space which satisfy the relic density, direct and indirect search constraints and perform collider analysis for some specific multi-lepton channels containing mono-lepton, di-lepton, tri-lepton and four leptons along with missing transverse energy in the final state. Multi-lepton signals have already been analysed in the context of additional VLLs [52, 53]. In addition, there already exists several searches by ATLAS and CMS, in the context of a few beyond SM models, for the final states comprising of mono-lepton [54,55,56], di-lepton [57], tri-lepton [58, 59] and four leptons along with missing transverse energy [60, 61]. We have considered the limits arising out of these studies in our work and highlight how the signals differ in each of our individual cases and the necessity to modify the cuts to optimise our signal events over the SM background.
The paper is structured as follows. In Sect. 2 we briefly discuss the necessary extensions over the \(S_3\)-symmetric 2HDM [50, 51] done in our model. Section 3 deals with the relevant theoretical and experimental constraints to be considered which is followed by the DM phenomenology in Sect. 4. Then we move on to Sect. 5 where we present the collider analysis of the model in the leptonic channels, namely the signals having mono-lepton, di-lepton, tri-lepton and four-lepton along with missing transverse energy in the final state. Finally we summarise and conclude in Sect. 6.
2 Model
We consider the \(S_3\)-symmetric 2HDM augmented with two generations of VLL. The reason for adding two generations of VLL is to ensure an \(S_3\)-symmetric Yukawa Lagrangian. Each generation of VLL consists of one left-handed lepton doublet \(L_{L_i}'\), one right-handed charged lepton singlet \(e_{R_i}'\), one right-handed singlet neutrino \(\nu _{R_i}'\) and their mirror counter parts with opposite chirality but same gauge charges, i.e. \(L_{R_i}'', e_{L_i}''\) and \(\nu _{L_i}''\) with \(i=2.\) These two generations of VLLs are doublets under \(S_3\)-symmetry. Different quantum numbers associated with the particles are shown in Tables 1 and 2. In Table 1, \(Q_{iL}, L_{iL}\) are left-handed quark and lepton doublets respectively in SM with \(i=1,2,3\). \(u_{iR}, d_{iR}\) are right-handed up-type and down-type quark singlets respectively with \(i=1,2,3\).
2.1 Scalar Lagrangian
In the \(S_3\)-symmetric 2HDM, there are two \(SU(2)_L\) doublets \(\phi _1\) and \(\phi _2\) with hypercharge \(Y= + 1\)Footnote 1, which collectively behave like a doublet under \(S_3\)-symmetry, i.e. \(\begin{pmatrix} \phi _1 \\ \phi _2 \end{pmatrix} = \Phi \). For this specific doublet representation, the elements of \(S_3\) is given by [62],
After symmetry breaking, \(\phi _i\) can be expressed as,
Here \(v_i\)’s are vacuum expectation values (VEV) and \(v_1 = v \cos \beta , ~v_2 = v \sin \beta , v = \sqrt{v_1^2 + v_2^2} = 246\) GeV. \(\tan \beta \) can be defined as the ratio of two vacuum expectation values: \(\tan \beta = \frac{v_2}{v_1}\).
The quartic part of the most general renormalisable \(S_3\)-symmetric scalar potential is given by [50],
The most general quadratic part of the scalar potential is [50]:
In Eq. (3), the quartic couplings \(\lambda _1, \lambda _2\) and \(\lambda _3\) are real owing to the hermiticity of the scalar potential. In the quadratic part of the potential in Eq. (4), \(m_{11}^2, m_{22}^2\) are real, \(m_{12}^2\) can be complex in principle. Throughout the analysis, we have taken \(m_{12}^2\) to be real to avoid CP-violation. Though \(m_{11}^2 = m_{22}^2\) and \(m_{12}^2 =\) 0 ensure that the quadratic part of the potential is \(S_3\)-symmetric, this configuration ends up with a massless scalar [50]. Thus for our analysis, we stick to the configuration \(m_{11}^2 = m_{22}^2\) and \(m_{12}^2 \ne \) 0 (which breaks the \(S_3\)-symmetry softly), which fixes the value of \(\tan \beta =1\), following the minimisation condition of the scalar potential:Footnote 2
The scalar sector of this model consists of SM-like Higgs (h), heavy Higgs (H), pseudoscalar Higgs (A) and charged Higgs (\(H^{\pm }\)). The limit at which h behaves as SM-like Higgs boson is defined as the alignment limit. This limit is naturally achieved in this model [50].
Transformations from flavour basis to mass basis of the scalars occur through the following \( 2 \times 2 \) orthogonal matrix:
\(w^\pm \) and z being the charged and neutral Golstone boson respectively.
The light Higgs and the heavy Higgs of the model are connected to there flavour eigenstates via,
In Eq. (3), the quartic couplings \(\lambda _1, \lambda _2, \lambda _3\) can be expressed in terms of the physical scalar masses as:
2.2 Yukawa Lagrangian
The dimension-4 terms in \(S_3\)-symmetric Yukawa Lagrangian involving two generations of VLLs can be written as,
Next we write down the dimension-3 Dirac and Majorana mass terms present in the Yukawa Lagrangian, which break \(S_3\)-symmetry softly:Footnote 3
Here the fields with superscript “c” are the charge conjugated fields. The subscripts of “\({\mathcal {L}}\)” in Eqs. (9) and (10) denote the mass dimensions of the operators. Thus whole Yukawa lagrangian can be written as the sum of \({\mathcal {L}}_3\) and \({\mathcal {L}}_4\) as:
Here we can construct eight neutral mass eigenstates (\(N_i , i = 1\)..8) out of two generations of vector leptons. To ensure that the lightest VLL \(N_1\) is the DM candidate, we impose a \(Z_2\)-symmetry (mentioned in Table 1) under which all the VLLs are odd and all the SM leptons are even. This forbids the mixing between the SM leptons and VLLsFootnote 4. The two Higgs doublets are assumed to be even under this \(Z_2\)-symmetry.
In this set up, \(8 \times 8 \) neutral VLL mass matrix in the basis \((\nu _{L_1}^{'c}, \nu _{R_1}', \nu _{R_1}'', \nu _{L_1}^{''c}, \nu _{L_2}^{'c}, \nu _{R_2}', \nu _{R_2}'', \nu _{L_2}^{''c})^T\) reads :
With
Since \(M_\nu \) is hermitian, it can be brought to diagonal form by the following transformation via unitary matrix V:
Among all states \(N_1\) is the lightest and \(M_{N{j+1}} > M_{N_j}\) for \(j = 1,2,\ldots 7\).
In the charged VLL sector, the mass matrix is,
where,
The non-hermitian \(M_c\) can be diagonalised by using the following bi-unitary transformation, with the unitary matrices \(U_L\) and \(U_R\),
Here we follow the same convention as the neutral sector, i.e. \(M_{E_{i+1}^+} > M_{E_{i}^+}\) for \(i= 1,2,3.\)
3 Constraints to be considered
The \(S_3\)-symmetric 2HDM model has an extended scalar sector and we have included VLLs in our model with some being \(SU(2)_L\) doublets . The addition of particles under a new symmetry which are not singlets under the SM gauge symmetry would lead to interactions and mixings that could affect several existing experimental observations. In addition, the new parameters in the model would also have to adhere to theoretical constraints to make the model mathematically consistent. We look at the most relevant ones and extract the constraints they could put on the model parameters.
3.1 Theoretical constraints
-
Perturbativity: The quartic couplings \(\lambda _1. \lambda _2, \lambda _3\) are taken to be perturbative: \(|\lambda _i| < 4 \pi ,~~ i=1,2,3.\) For Yukawa couplings the corresponding bound reads: \(|y_2|, |y_2'|, |y_4|, |y_4'| < \sqrt{4 \pi }.\)
-
Stability conditions of the potential: The quartic couplings \(\lambda _1, \lambda _2\) and \(\lambda _3\) are also constrained from the stability conditions, so that the potential remains bounded from below in any field direction:
$$\begin{aligned}&\lambda _1 + \lambda _3 \ge 0 \,, \nonumber \\&\lambda _1 \ge 0 \,, \nonumber \\&2 \lambda _1 - \lambda _2 + \lambda _3 \ge 0 \,. \end{aligned}$$(16) -
Higgs mass : We keep the SM-like Higgs mass within the range: 125.1 ± 0.14 GeV [64]. We have used the SM-like Higgs mass as an input parameter and fix its value to \(M_h = 125\) GeV throughout the analysis.
3.2 Constraints from electroweak precision observables
The additional extra scalars and VLLs that are not SM singlets would interact with the W and Z boson. There contributions in the self-energy correction diagrams would modify the mass of the weak gauge bosons and related electroweak precision observables parametrised by the oblique parameters S, T and U [65, 66]. Using \( M_h = 125\) GeV and top mass as 172.5 GeV, the allowed ranges [67] are
Notably the deviations in the T-parameter from its SM value enforces the mass splitting between the neutral and the charged scalar to be less than \(\sim 50-100\) GeV. Regarding the contributions coming from the VLL counterpart, the differences between the Yukawa couplings \(|y_2 - y_2'|\) and \(|y_4 - y_4'|\) should be small to evade the bound coming from T-parameter [35].
3.3 Higgs signal strength
Since we demand that the lightest CP-even scalar h is the SM like Higgs, it is imperative that we should check whether the production and decay of h in our model is consistent with the current experimental data. The compatibility can be checked by computing the signal strength in the ith decay mode of h as,
Assuming gluon-gluon fusion to be the most dominant Higgs production process at the LHC, one can rewrite the signal strength \(\mu _i\) as,
where \(\Gamma _{\mathrm{{tot}}}\) stands for the total decay width of SM like Higgs.
Since the Alignment limit is maintained naturally in this model, the signal strengths in the decay channels of h into WW [68, 69], ZZ [70, 71], \(b\overline{b}\) [72, 73], \(\tau ^+\tau ^-\) [74, 75] are satisfied without any loss of generality. On the other hand, the loop-induced decay mode of the \(h \rightarrow \gamma \gamma \) will get additional contribution from the charged vector leptons and the non-standard charged scalars. For the chosen benchmark points, the \(h \rightarrow \gamma \gamma \) signal strength remains within 2\(\sigma \)-range of the current experimental value [76, 77]. The detailed formula for the decay width of \(h \rightarrow \gamma \gamma \) channel is relegated to Appendix A.
4 Dark matter phenomenology
As mentioned earlier, the lightest neutral VLL \(N_1\) is a viable DM candidate due to its stable nature ensured by the imposed \(Z_2\)-symmetry. In this section we investigate the parameter space spanned by relevant and independent model parameters which are compatible with relic density [78], direct and indirect DM searches. Setting the mass of the SM-like Higgs to 125 GeV, we scan the independent parameters of the model in the following range:
For the analysis, we derive the interactions, mass and mixings in the model which is then implemented in FeynRules [79]. The CALCHEP [80] model files obtained from FeynRules is made compatible to use with micrOMEGAs [81]. The DM observables like relic density (\(\Omega _{\mathrm{DM}} h^2\))Footnote 5, spin-dependent (\(\sigma _\mathrm{SD}\)) and independent cross-sections (\(\sigma _{\mathrm{SI}}\)), thermally averaged annihilation cross-sections (\( \langle \sigma v \rangle \)) etc. are computed with the help of micrOMEGAs. The observed relic abundance obtained from the PLANCK experiment [78] lies in the band: \(0.1166 \le \Omega _\mathrm{DM} h^2 \le 0.1206\). Furthermore the parameter space is also constrained by the bounds coming from several direct detection experiments like LUX [82], PANDAX-II [83], Xenon-1T [84], PICO [85], etc. and from the indirect detection bounds coming from FERMI-LAT [86], MAGIC [87] and PLANCK [78] experiments.
Having discussed what could be the possible constraints coming from the DM sector, let us illustrate it more in a model specific manner. The relic density can be computed as the function of the thermally averaged DM pair annihilation cross-sections. Since the lightest neutral VLL \(N_1\) in this model is the admixture of SU(2) singlets and doublets, it has couplings with both \(W^\pm \) and Z-bosons. Depending on the mass of DM, the s-channel pair annihilation of the DM to \(W^+ W^-, ZZ, Zh, hh, f\overline{f}\) mediated by h, H, A and Z-boson can occur. Besides, t-channel annihilation to ZZ, Zh, hh (\(W^+ W^-\)) via \(N_i,~ i=1,2,\ldots ,8\) (\(E_j^\pm ,~ j= 1,2,..,4\)) as mediator also contribute to the \( \langle \sigma v \rangle \).
In Table 3, we present five representative points BP1, BP2, BP3, BP4 and BP5 with increasing DM mass, which satisfy the relic density constraints as well as the direct and indirect detection bounds. Corresponding values of \(\sigma _{\mathrm{SI}}\), \(\sigma _{\mathrm{SD}}\) and \(\langle \sigma v \rangle \) are also tabulated in the same table. Since the DM is Majorana-like, due to the Z-mediated process, for all the benchmarks \(\sigma _{\mathrm{SI}} < \sigma _{\mathrm{SD}}\). As mentioned earlier, from the minimisation conditions of the scalar potential of the \(S_3\)-symmetric 2HDM, with \(m_{11}^2 = m_{22}^2\) and \(m_{12}^2 \ne 0\), \(\tan \beta \) is fixed to 1. Now \(Hf \overline{f}\) and \(A f \overline{f}\) (“f” is SM fermion) couplings being proportional to \((\cos \beta -\sin \beta )\), vanish at \(\tan \beta = 1\) limit. Thus s-channel annihilations into SM fermions mediated by H or A are absent in this framework. The only surviving s-channel annihilation to SM fermions is mediated by h. For the first two points, since \(M_{N_1} < M_Z\), the DM pair dominantly annihilate into \(W^+ W^-\). After crossing the ZZ-threshold, the major annihilation occurs to the final state ZZ along with \(W^+ W^-\). Since the H, A-mediated s-channel annihilation to \(W^+ W^-\) and ZZ are forbidden at alignment limit, t-channel annihilation to \(W^+ W^-\) and ZZ via \(E_i^\pm \) becomes the major contributor. Moderate \(Z N_i N_j\) couplings (with \( i \ne j\)) participating in the annihilation come out to be the main reason behind this dominance. To put this in perspective, we list the dominant annihilation modes for the aforementioned five benchmark points in Table 3 too. We note that since the alignment limit is maintained naturally in this model, the s-channel H, A-mediated processes leading to \(W^+ W^-\) and ZZ final state will not contribute to \( \langle \sigma v \rangle \). The scattering of DM with the nuclei within the detector material mediated by Z or h, gives rise to spin-dependent and spin-independent cross-sections (\(\sigma _{\mathrm{SD}}\) and \(\sigma _\mathrm{SI}\)) respectively, which in turn are constrained from direct detection experiments. This forces \(h N_1 N_1\) and \(Z N_1 N_1\) couplings to be small enough to circumvent the direct detection bound. This is merely a choice and the smallness of the aforementioned couplings is achieved by tuning relevant parameters of the model. Due to the Majorana nature of the DM, the WIMP-nucleon cross-section is dominated by spin-dependent interactions mediated by Z boson. Hence we have to consider the direct detection bound on the \(\sigma _{\mathrm{SD}}\) coming from the PICO experiment [85].
In Fig. 1, we depict the variation of spin-independent cross-section (\(\sigma _{\mathrm{SI}}\)) with DM mass predicted by our model (magenta curve). The black line and the green band correspond to 90% confidence level (C.L.) and 2\(\sigma \) sensitivity predicted by Xenon-1T experiment. We can conclude that for the dark matter mass range allowed by relic density constraint, \(\sigma _{\mathrm{SI}}\) are smaller and allowed by the experimental limit shown by the black line in Fig. 1. Therefore the spin-independent cross-sections for all the chosen benchmarks evade the constraint coming from the direct detection experiments. As mentioned earlier, the strongest bound on spin-dependent cross-section comes from PICO experiment [85]. For the chosen benchmark points, the spin-dependent cross-section remain below the experimental limit as can be seen from Fig. 2.
Spin-dependent cross-section of proton as a function of the DM mass in our model (magenta curve), and the experimental upper bound from PICO-60 [85] experiment
Indirect detection experiments look for annihilation of the DM pair to SM particles through various channels that could produce distinctive signatures in cosmic rays. In Fig. 3, we show the variation of the thermally averaged annihilation cross-section as a function of dark matter mass. The magenta curve signifies the variation of annihilation cross-section for our model. Combined results from the FERMI-LAT and MAGIC experiments [87] are represented by the dashed lines. Here the blue, black, red and green dashed curves show the variation of \(\langle \sigma v \rangle \) with DM masses for the annihilation to \(\mu \mu , \, \tau \tau , \, b \overline{b}\) and \(W^+ W^-\) respectively. We find that the parameter space characterised by our benchmarks survive the bounds coming from the indirect detection experiments. We however note that for the DM mass range of 100-200 GeV lies quite close to the experimental bounds from the indirect detection and may become sensitive to future data from indirect detection experiments. We have also incorporated the experimental results obtained from PLANCK data [78] in our analysis, though we have not shown it in Fig. 3. We have checked that the curve representing our model in Fig. 3 lies well below the experimental limits from PLANCK.
Variation of thermally averaged annihilation cross-section with DM masses. The magenta and the dashed curves represent the variations of \(\langle \sigma v \rangle \) for the model and various annihilation cross-sections predicted by combined results of FERMI-LAT and MAGIC experiments [87] respectively. Colour coding is expressed in legends
5 Collider searches
In this section we focus on the collider phenomenology of our model. We study the most likely signals of the model that may manifest itself at the current and future runs of the large hadron collider (LHC). As the model consists of an extension of the spectrum in the electroweak and leptonic sector, it becomes quite clear that the production of these new exotic particles would be limited by their cross section if they are too heavy. In fact, the limits on weakly interacting BSM particles are still quite weak from LHC. In this model, VLLs with unbroken \(Z_2\)-symmetry have no mixing with the SM fermions. Thus, the production of these VLL’s will have to be in pairs and they would decay to a SM particle and a lighter component of the VLL. We therefore focus on the relatively lighter spectrum of the exotics whose lightest neutral component is the DM candidate, represented by the states for the five benchmark points (BP) shown in Table 3 and consistent with the DM phenomenology presented in the previous section. The mass of the remaining VLL components which correspond to the same five BP’s viz. \(M_{N_i}, \) with \(i=1,2,\ldots ,8\) and \(M_{E_j^\pm }\) with \(j=1,2,\ldots ,4\) are tabulated in Table 4.
The pair production of the VLL would give rise to lepton rich final states, that may include mono-lepton, di-leptons, tri-leptons and four-leptons along with  in the final states. Note that in the absence of any mixing between the SM leptons and VLL’s, the all hadronic multi-jet +
in the final states. Note that in the absence of any mixing between the SM leptons and VLL’s, the all hadronic multi-jet + is the dominant signal. However this signal would be swamped by huge SM backgrounds, which leads us to consider multi-lepton final states starting with at least one charged lepton (\(e/\mu \)) as a more useful signal for this model. We shall perform the analysis for the collider signals based on five benchmark points (BP1, BP2, BP3, BP4, BP5) given in Table 4. We tabulate the two-body and three-body decay branching ratios of the charged and neutral VLLs in Appendix B (Tables 18 and 19 and 20). We must however note that for all benchmark points, the relative mass splittings among the mother and daughter particles of the VLL in the cascade decays are not very large, leading to a somewhat compressed spectrum. This would imply relatively softer decay products in the final state for some of the benchmark points leading to challenges in signal-background discrimination, as we will see in our analysis. We therefore try to use machine learning methods in a few channels to check what kind of improvement one may achieve over the traditional cut-based analysis.
is the dominant signal. However this signal would be swamped by huge SM backgrounds, which leads us to consider multi-lepton final states starting with at least one charged lepton (\(e/\mu \)) as a more useful signal for this model. We shall perform the analysis for the collider signals based on five benchmark points (BP1, BP2, BP3, BP4, BP5) given in Table 4. We tabulate the two-body and three-body decay branching ratios of the charged and neutral VLLs in Appendix B (Tables 18 and 19 and 20). We must however note that for all benchmark points, the relative mass splittings among the mother and daughter particles of the VLL in the cascade decays are not very large, leading to a somewhat compressed spectrum. This would imply relatively softer decay products in the final state for some of the benchmark points leading to challenges in signal-background discrimination, as we will see in our analysis. We therefore try to use machine learning methods in a few channels to check what kind of improvement one may achieve over the traditional cut-based analysis.
To check that our choice of benchmark points do not conflict any existing LHC analysis in a given leptonic channel, we validate these points against existing multi-lepton searches by the ATLAS and CMS collaborations. For example, the final state containing  originated from the decay of \(W'\) has been studied by ATLAS at \(\sqrt{s} = 8\) TeV and integrated luminosity of 20.3 fb\(^{-1}\) in [54], with a similar study carried out by CMS both at \(\sqrt{s} = 8\) TeV and 13 TeV [55, 56]. The electroweak production of charginos and sleptons decaying into final states with
originated from the decay of \(W'\) has been studied by ATLAS at \(\sqrt{s} = 8\) TeV and integrated luminosity of 20.3 fb\(^{-1}\) in [54], with a similar study carried out by CMS both at \(\sqrt{s} = 8\) TeV and 13 TeV [55, 56]. The electroweak production of charginos and sleptons decaying into final states with  has been explored by ATLAS at 13 TeV LHC [57]. Similarly search results for
has been explored by ATLAS at 13 TeV LHC [57]. Similarly search results for  final state arising from the decay of pair produced chargino-neutralino with degenerate masses (with mass splitting at electroweak scale) has been reported by ATLAS at \(\sqrt{s} = 13\) TeV in Ref. [59] ( [58]). In addition, search for the more robust final state with four or more charged leptons in supersymmetric framework by ATLAS at 13 TeV LHC has also been summarised in Ref. [60]. Finally, a detailed study of the multi-lepton final state coming from the decay of doubly- and singly-charged Higgs bosons has also been performed by ATLAS at 13 TeV LHC [61]. Although the above studies are in context of other BSM scenarios, the overlap with our signal topology allows us to use these studies to check whether our representative points are allowed or not. The checks have been performed for the five benchmarks using the mono-lepton [88], di-lepton [89] and multi-lepton [90] searches in Madanalysis5 [91,92,93,94,95,96].
final state arising from the decay of pair produced chargino-neutralino with degenerate masses (with mass splitting at electroweak scale) has been reported by ATLAS at \(\sqrt{s} = 13\) TeV in Ref. [59] ( [58]). In addition, search for the more robust final state with four or more charged leptons in supersymmetric framework by ATLAS at 13 TeV LHC has also been summarised in Ref. [60]. Finally, a detailed study of the multi-lepton final state coming from the decay of doubly- and singly-charged Higgs bosons has also been performed by ATLAS at 13 TeV LHC [61]. Although the above studies are in context of other BSM scenarios, the overlap with our signal topology allows us to use these studies to check whether our representative points are allowed or not. The checks have been performed for the five benchmarks using the mono-lepton [88], di-lepton [89] and multi-lepton [90] searches in Madanalysis5 [91,92,93,94,95,96].
For the chosen benchmark points, we implement the model using FeynRules [79], which gives the required UFO that is fed in MG5aMC@NLO [97] to generate the signal and background events with the cross-section at the leading order (LO).
The LO production cross-sections at the LHC for signal and SM backgrounds are calculated using the NNPDF3.0 parton distribution functions (PDF). To simulate the showering and hadronisation, the parton level events are passed through Pythia8 [98]. Finally, we implement the detector effects in our analysis using the default CMS detector simulation card for LHC available in Delphes-3.4.1 [99]. For jet reconstruction, the anti-\(k_t\) clustering algorithm has been used throughout. Besides the traditional cut-based analysis to compute the signal significance, more sophisticated technique, i.e. Decorrelated Boosted Decision Tree (BDTD) algorithm is used for improvement. For such analysis, the Toolkit for Multivariate Data Analysis (TMVA) package [100] has been used. Details of the package will be discussed later in Sect. 5.1. The signal significance \({\mathcal {S}}\) is derived using \({\mathcal {S}} = \sqrt{2\Big [(S + B) \log \Big (\frac{S + B}{B}\Big )- S\Big ]}\), with S(B) denoting the number of signal (background) events surviving the cuts applied on the kinematical variables. The number of signal (S) and the background (B) events can be calculated as:
where \(\sigma _{S(B)},~{\mathcal {L}},~\epsilon _S (\epsilon _B)\)Footnote 6 denote the signal (background) cross-section, integrated luminosity and signal (background) cut-efficiency respectively. Following this strategy, let us proceed to perform the collider analysis of the aforementioned channels at 14 TeV high luminosity (HL)-LHC.
5.1 Mono-lepton final state
To include all possible processes leading to a signal containing mono-lepton and missing transverse energy ( ) in the final state, we take into account the pair production and associated production of the VLL’s:
) in the final state, we take into account the pair production and associated production of the VLL’s:
where \(i,j = 1\ldots 4\) and \( k,m = 1\ldots 8\). Following the decay cascades listed in Appendix B, of all the final states arising from the decay of VLLs, we choose the final states yielding one lepton \(\ell _1\) (electron or muon) with a minimum transverse momentum \(p_T^{\ell _1} > 10\) GeV and reject any additional lepton with \(p_T^{\ell } \ge 10\) GeV. We also put veto on any hadronic activity by rejecting all jets with \(p_T^{j} > 20\) GeV. This ensures that the signal consists of a single charged lepton with \(p_T^{\ell _1} > 10\) GeV and  .
.
The irreducible SM background for this final state is the W boson mediated \(p p \rightarrow \ell \nu \), with \(\ell = e, \mu \). There can be additional contributions from the di-boson productions, such as \(W^\pm \,Z, \, W^+ \,W^- \) and ZZ, which yield one or more charged leptons in the final state if only leptonic decays are allowed and where the additional charged leptons are missed. Similarly, the multi-jet QCD background could also be a source of the mono-lepton background provided one of the jets is mis-tagged as a charged lepton. Although the probability of mis-identifying a jet as a charged lepton is rather small (\(\lesssim 10^{-5}\)) [101], the sheer size of the QCD cross section makes it non-negligible. However, we also require a large missing transverse energy in the final state along with a jet veto which helps in suppressing the QCD background to negligible values. Thus in the study, we can afford to ignore this background completely.
To generate the signal and backgrounds, we apply the following criterion to identify the isolated objects (\(\Delta \, R_{ij}>0.4\)):
In Table 5, the cross-sections of the signal ( ) for the chosen benchmark points are tabulated for 14 TeV LHC.
) for the chosen benchmark points are tabulated for 14 TeV LHC.

To perform the cut-based analysis, we apply the following selection cuts on chosen kinematic variables to disentangle the signal from SM backgrounds:Footnote 7
-
\(A_1\): From Fig. 4a it can be seen that the \(p_T\)-distribution of the lepton for the SM background coming from the decay of W boson has the sharp Jacobian peak at \(\sim M_W/2\), whereas the corresponding distribution is smeared for the signal where the charged lepton comes from the cascade decays of the heavy VLLs. However, a large part of the signal overlaps where the background peaks. Thus we demand that the charged lepton has a minimum transverse momentum \(p_T^{\ell } > 20\) GeV to exclude a significant part of the sharply peaked background (magenta line) without losing too many signal events.
-
\(A_2\): A lower cut on the missing transverse energy, i.e.
 GeV helps to reduce the background drastically as the
GeV helps to reduce the background drastically as the  distribution for the background (magenta line) in Fig. 4b peaks sharply at lower value than the signal. Unlike the background where the neutrinos carry most of the imbalanced missing transverse energy, the signal gets contributions from neutrinos as well as from the much massive DM candidate (\(N_1\)) which is the end-product of all cascades giving rises to a much larger
distribution for the background (magenta line) in Fig. 4b peaks sharply at lower value than the signal. Unlike the background where the neutrinos carry most of the imbalanced missing transverse energy, the signal gets contributions from neutrinos as well as from the much massive DM candidate (\(N_1\)) which is the end-product of all cascades giving rises to a much larger  in the signal distribution.
in the signal distribution. -
\(A_3\): The next kinematic variables used for separating signal from background is transverse mass \((M_T)\) which is defined as [56],
 (24)
(24)where
 is the azimuthal angle between the lepton and
is the azimuthal angle between the lepton and  . In Fig. 4c, the \(M_T\) distribution sharply peaks around \(M_W\) for the background as expected, while the signal has a comparatively smeared distribution. Thus we demand \(M_T > 100\) GeV to eliminate the sharp background peak which in turn enhances the signal significance.
. In Fig. 4c, the \(M_T\) distribution sharply peaks around \(M_W\) for the background as expected, while the signal has a comparatively smeared distribution. Thus we demand \(M_T > 100\) GeV to eliminate the sharp background peak which in turn enhances the signal significance. -
\(A_4\): Distribution of \(M_{\mathrm{eff}}\) is depicted in Fig. 4d. \(M_{\mathrm{eff}}\) is defined by the scalar sum of the lepton \(p_T\) and
 . We find that putting a lower cut \(M_{\mathrm{eff}} > 110\) GeV for all the benchmark points helps enhance the signal over background.
. We find that putting a lower cut \(M_{\mathrm{eff}} > 110\) GeV for all the benchmark points helps enhance the signal over background.
 channel
channelWe summarize the cut flow for both signal and background and calculate the signal significances for all five benchmarks in Table 6. The table also shows the efficacy of the applied cuts for enhancing the signal significance. With 3 ab\(^{-1}\) integrated luminosity BP1, BP2 and BP3 can be probed with significances 7.0, 5.3, 2.4 respectively. Remaining two benchmarks BP4 and BP5 yield negligible significances owing to small signal cross-sections.
Having completed the cut-based analysis, we now proceed to perform the multivariate analysis (MVA) using Decorrelated Boosted Decision Tree (BDTD) algorithm within the Toolkit for Multivariate Data Analysis (TMVA) framework, with the hope of improvement in signal significance compared to the cut-based one. Before doing the BDTD analysis of the channels, let us present a brief overview of the method.
To classify the signal-like or background-like events, decision trees are used as classifier. One discriminating variable with an optimised cut value applied on it is associated with each node of the decision tree, to provide best possible separation between the signal-like and background-like events depending on the purity of the sample. Within TMVA, this can be done by tuning the BDTD variable NCuts. The training of the decision trees starts from the root node (zeroth node) and continues till a particular depth specified by the user is reached. This particular depth is termed as MaxDepth. Finally from the final nodes or the leaf nodes an event can be specified as signal or background according to their purity.Footnote 8 An event can be tagged as signal (background) when \(p > 0.5\) (\(p < 0.5\)).
Now the decision trees are termed as weak classifiers as they are prone to statistical fluctuations of the training sample. To circumvent this problem, one can combine a set of weak classifiers into a stronger one and create new decision trees by modifying the weight of the events. This procedure is termed as Boosting. For this analysis, we choose Adaptive boost with the input variables transforming in a decorrelated manner, since this is very useful for weak classifiers. In TMVA it is implemented as Decorrelated AdaBoost. Several BDTD parameters like the number of decision trees NTrees, the maximum depth of the decision tree allowed MaxDepth, the minimum percentage of training events in each leaf node MinNodeSize and NCuts for five benchmarks of our analysis have been tabulated in Table 7. To avoid over training of the signal and background samples, the results of the Kolmogorov–Smirnov test, i.e. Kolmogorov–Smirnov score (KS-score) should always be> 0.1Footnote 9 and stable.
 channel
channelAccording to the degree of discriminatory power between the signal and backgrounds, following are the kinematic variables of importance :

These relevant kinematic variables are constructed for each and every channel to discriminate between the signal and the backgrounds.
Figure 5 shows the KS-scores for both signal (blue distribution) and backgrounds (red distribution) for two representative benchmark points BP1 and BP3. For convenience, we have tabulated the KS-scores for both signal and background in the sixth column of Table 7 for all benchmark points. To make the KS-score stable, one can tune the BDTD parameters given in Table 7. With the aforementioned discriminating variables at hand, we tune the BDT cut value (BDT score) in such a way that the significance is maximized. We plot the Receiver’s Operative Characteristic (ROC) curve for all benchmarks in Fig. 6aFootnote 10, which classifies the degree of rejecting the backgrounds with respect to the signal. Variation of the signal significance with BDT cut value for all the benchmarks are shown in Fig. 6b. It can be clearly seen that the signal significance attains a maximum value for each benchmark at a particular value of BDT score.
Signal and background yields with 3 ab\(^{-1}\) integrated luminosity after performing BDTD analysis have been tabulated in Table 8. The significances for BP1, BP2, BP3, BP4 and BP5 are 7.8, 5.9, 2.6, 0.5 and 0.4 respectively. It becomes quite clear that compared to the cut-based analysis, the signal significances get typical improvements of \(11.4\, \%,\, 11.3 \,\%,\, 8.3\,\%,\, 25\,\%\) and \(33.3\, \%\) for BP1, BP2, BP3, BP4 and BP5 respectively. An integrated luminosity of \(\sim \)1232 fb\(^{-1}\) is required to achieve 5\(\sigma \) significance for BP1 after performing the BDTD analysis.
 channel after performing the BDTD analysis
channel after performing the BDTD analysis5.2 Di-lepton final state
We now consider the final states containing same or different flavour and opposite sign (OS) di-leptons along with  that can arise from the following subprocesses in our model:
that can arise from the following subprocesses in our model:
where \(i,j = 1,2,\ldots 4, k = 2,3,\ldots 8\). The dominant signal contribution comes from the pair production of the charged VLLs followed by their decay to DM and a lepton. Production of the vector like neutrino along with the DM can also give rise to the similar final state albeit small cross-section. However for the sake of completeness we take into account all such processes that may give rise to a di-lepton final state. The major SM background for the signal comes from the inclusive  process which includes contributions from \(W^{+}W^{-}\) and ZZ pair production. Due to large cross-section, \(t\overline{t}\) followed by the leptonic decay of top-quark (leading to
process which includes contributions from \(W^{+}W^{-}\) and ZZ pair production. Due to large cross-section, \(t\overline{t}\) followed by the leptonic decay of top-quark (leading to  final state) also contributes as one of the major background. Even after a b-jet veto along with a jet-veto, the small fraction of events surviving from the \(t \overline{t}\) process can still lead to a significant number of events in the
final state) also contributes as one of the major background. Even after a b-jet veto along with a jet-veto, the small fraction of events surviving from the \(t \overline{t}\) process can still lead to a significant number of events in the  final state. In addition, processes with smaller cross-sections such as \(W^{\pm }Z\), and \(W^+W^-Z\) followed by the leptonic decay of \(W^\pm \) and Z can also be a possible source of background for the
final state. In addition, processes with smaller cross-sections such as \(W^{\pm }Z\), and \(W^+W^-Z\) followed by the leptonic decay of \(W^\pm \) and Z can also be a possible source of background for the  final state, if one or more leptons escape detection. For the analysis, we consider the above three SM subprocesses as major contributions to the SM background. In Table 9 the LO signal cross-sections for the di-lepton final state are tabulated for all our benchmark points.
final state, if one or more leptons escape detection. For the analysis, we consider the above three SM subprocesses as major contributions to the SM background. In Table 9 the LO signal cross-sections for the di-lepton final state are tabulated for all our benchmark points.

To generate the signal and backgrounds we apply the same set of generation cuts as mentioned in Sect. 5.1. We select events with exactly two charged leptons with \(p_T^{\ell } > 10\) GeV and \(|\eta _{\ell }| < 2.5\) and reject any additional lepton with \(p_T^{\ell } > 10\) GeV. To ensure a hadronically quiet final state, we veto all light-jets, b-jets and \(\tau \)-jets with \(p_T > 20\) GeV. We then analyse the signal containing OS di-leptons and compute the signal significance using traditional cut-based method. To differentiate our signal from the SM background, we focus on the following kinematic variables:  and invariant mass of two OS same or different flavoured leptons \(M_{\ell ^{+} \ell ^{-}}\). We define the cuts applied on them as \(B_1, B_2, B_3, B_4\) respectively and we describe them below:
and invariant mass of two OS same or different flavoured leptons \(M_{\ell ^{+} \ell ^{-}}\). We define the cuts applied on them as \(B_1, B_2, B_3, B_4\) respectively and we describe them below:
-
\(B_1\): In Fig. 7a, b, we depict normalised \(p_T\) distribution for the leading and sub-leading leptons \(\ell _1\) and \(\ell _2\) for both signal and SM background. In can be seen that
the distributions have a significant overlap owing to their origin being from W decay. Thus we apply \(p_T^{\ell _1} > 20\) GeV suppress the SM backgrounds.
-
\(B_2\): The normalised distribution of missing transverse energy is shown in Fig. 7c. The
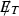 distributions for the BP1 and BP3 (green and blue lines) are much harder as in the mono-lepton case. Thus we demand
distributions for the BP1 and BP3 (green and blue lines) are much harder as in the mono-lepton case. Thus we demand  GeV, which helps to reduce the
GeV, which helps to reduce the  background. As the mass splitting between the VLLs become smaller for heavier DM, the
background. As the mass splitting between the VLLs become smaller for heavier DM, the  distribution is shifted towards the softer side.
distribution is shifted towards the softer side. -
\(B_3\): The normalised distribution of \(M_{\ell ^{+} \ell ^{-}}\) is shown in Fig. 7d. The distribution for the WZ background (red line) shows a peak at \(M_Z\), since two same flavour opposite sign leptons out of the three in the final state, originate from the Z-boson decay. As the signal does not have a Z peak in its distribution, we reject events \( 75< (M_{\ell ^+ \ell ^-})_{1,2} < 105\) GeV to exclude the Z-peak. This cut helps in suppressing the WZ background. Along with, we also demand \((M_{\ell ^+ \ell ^-})_{1,2} > 12\) GeV to reduce the Drell–Yan background contribution [102].
We sum up the number of surviving signal and background events after applying the aforementioned cuts in Table 10. It can be seen that with 3 ab\(^{-1}\) integrated luminosity, the significance reach for BP1 and BP2 is 6.7 and 2.5 respectively. The search prospect of this channel at the same integrated luminosity for BP3, BP4 and BP5 is considerably poor with the signal significances being 1.3, 0.8 and 0.3 respectively, owing not only to the small signal production cross-sections but also to the huge SM background which is not reducible. Note that for the di-lepton channel, the signal and background distributions have significant overlap in most kinematic variables, which makes it somewhat difficult to suppress the backgrounds without reducing the signal events.
 channel along with the significance for BP1, BP2, BP3, BP4 and BP5 at 14 TeV LHC for 3 ab\(^{-1}\) integrated luminosity
channel along with the significance for BP1, BP2, BP3, BP4 and BP5 at 14 TeV LHC for 3 ab\(^{-1}\) integrated luminosity
 channel after the BDTD analysis
channel after the BDTD analysisAfter discussing the cut-based analysis, let us move on to the multivariate (BDTD) analysis, which improves the signal significance by enhancing the discriminatory power between the signal and the backgrounds. For this analysis, we consider the following kinematic variables with maximal discerning ability:

Using these variables we train the signal and backgrounds so that the signal significance is maximized.
We present the set of tuned BDT parameters for all the benchmarks in Table 11 to make the KS-score stable following the criteria mentioned in Sect. 5.1. The KS-scores for BP1 and BP3 (both for signal and background) are given in Fig. 8. In the sixth column of Table 11 KS-scores for all benchmarks have been quoted. Having fixed the KS-score, we next proceed to tune the BDT score to yield maximum significance. Background rejection efficiency vs. signal efficiency have been plotted in the ROC curves in Fig. 9a using the aforementioned kinematic variables. From the ROC curves of the  channel, it is evident that the background rejection efficiency is somewhat poor compared to the
channel, it is evident that the background rejection efficiency is somewhat poor compared to the  channel. The significances have been plotted against BDT score for all benchmarks in Fig. 9b.
channel. The significances have been plotted against BDT score for all benchmarks in Fig. 9b.
Signal and background yields with 3 ab\(^{-1}\) integrated luminosity for our chosen benchmark points along with the significances are listed in Table 12. From Table 12 it can be inferred that the signal significance has improved a bit compared to the cut-based counter part. For BP1, BP2, BP3, BP4 and BP5 the improvements in signal significance are \(16.4\%, \, 60.0\%, \, 30.8\%, \, 12.5\%\) and \(6.7\%\) respectively.
5.3 Tri-lepton final state
The tri-lepton final state can originate from the following subprocesses:
We generate the events with tri-lepton final state using the same generation-level cuts and following the method discussed in Sect. 5.1. Among all possible decay products of the pair produced neutral and charged VLLs, we select only those events which have three charged leptons and missing transverse energy in the final state. We consider  with zero jets as the dominant irreducible SM background for our signal, which includes both on-shell and off-shell contributions from diboson and triboson production. In addition, the pair production of Z boson where \(ZZ \rightarrow 4\ell \) can also give rise to a similar final state if one of the leptons is missed. All LO cross-sections for this signal and backgrounds at 14 TeV LHC are given in Table 13Footnote 11.
with zero jets as the dominant irreducible SM background for our signal, which includes both on-shell and off-shell contributions from diboson and triboson production. In addition, the pair production of Z boson where \(ZZ \rightarrow 4\ell \) can also give rise to a similar final state if one of the leptons is missed. All LO cross-sections for this signal and backgrounds at 14 TeV LHC are given in Table 13Footnote 11.

For this channel with more leptons, which is cleaner with smaller SM background, we restrict ourselves to the cut-based analysis only. To discriminate the signal from background, we demand our final state to have exactly three charged leptons with \(p_T^\ell > 10\) GeV out of which two leptons are of the same sign and the third lepton is of opposite sign. Among these three leptons, at least two are expected to be of same flavour. We also impose b-jet veto (reject \(p_T(b) > 20\) GeV) to eliminate the b-jets in the final state coming from the \(t\overline{t}\) background. Next we identify a few kinematic variables which would help to discriminate the signal from background as follows:
 channel
channel-
\(C_1\): Out of two same sign leptons and one opposite sign lepton in the final state, one can construct two invariant mass system \((M_{\ell ^+ \ell ^-})_{1,2}\), considering one same and one opposite sign lepton at a time. Demanding \(((M_{\ell ^+ \ell ^-})_{1,2} < 75\) GeV and \((M_{\ell ^+ \ell ^-})_{1,2} > 105\) GeV one can get rid of the Z-peak, which in turn reduces the \(W^\pm Z\), ZZ background drastically. We also impose a lower cut \((M_{\ell ^+ \ell ^-})_{1,2} > 12\) GeV to suppress the Drell–Yan background [102].
-
\(C_2\): We define a variable \(M_{\mathrm{eff}}\) as the scalar sum of all the lepton \(p_T\)’s and the
 . In Fig. 10a the distribution of
. In Fig. 10a the distribution of  background (magenta line) is flatter and smeared with respect to the distributions of the signal (green and blue lines) and other background ZZ (brown line). Setting \(M_{\mathrm{eff}} < 500\) GeV helps in reducing the background.
background (magenta line) is flatter and smeared with respect to the distributions of the signal (green and blue lines) and other background ZZ (brown line). Setting \(M_{\mathrm{eff}} < 500\) GeV helps in reducing the background. -
\(C_3\): Since the background ZZ does not have
 in the final state explicitly, corresponding
in the final state explicitly, corresponding  distribution peaks at lower value than the signal as can be seen from Fig. 10b. Thus a minimum cut of
distribution peaks at lower value than the signal as can be seen from Fig. 10b. Thus a minimum cut of  GeV helps to reduce the ZZ background drastically as can be found in Table 14.
GeV helps to reduce the ZZ background drastically as can be found in Table 14. -
\(C_4\): We choose the vector sum of three leptons (\(p_{T, 3 \ell }^{\mathrm{vector}}\)) and the scalar sum of the same (\(p_{T, 3 \ell }^{\mathrm{scalar}}\)) and show their distributions in Fig. 10c, d respectively. We find that kinematic selections of \(p_{T, 3 \ell }^{\mathrm{vector}} < \) 200 GeV and \(p_{T, 3 \ell }^{\mathrm{scalar}}<\) 250 GeV helps to reduce the
 background efficiently.
background efficiently. -
\(C_5\): We also construct the azimuthal angle between the unpaired third lepton out of total three leptons in the final state and
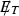 as
as  . Corresponding distributions are shown in Fig. 10e. We find that the choice
. Corresponding distributions are shown in Fig. 10e. We find that the choice  1.5 on the events help in eliminating the SM background further.
1.5 on the events help in eliminating the SM background further.
The number of events for signal and background, surviving after imposing the selection cuts on the aforementioned variables with 3 ab\(^{-1}\) integrated luminosity are quoted along with the significances in Table 14. For the five benchmarks BP1, BP2, BP3, BP4, BP5, using the cut-based analysis, the signal significances are 11.1, 4.5, 3.5, 1.2, 0.5 respectively. This is a substantial improvement over the previous two final state topologies considered earlier. In fact for BP1, \({\mathcal {L}} \sim \) 609 fb\(^{-1}\) of integrated luminosity is enough to achieve a 5\(\sigma \) significance in the tri-lepton channel.
5.4 Four-lepton final state
In this section, we analyse the final state comprising of  . The
. The  final state for the signal can be obtained from the following processes:
final state for the signal can be obtained from the following processes:

 channel
channelThe events are generated using the same generation-level cuts and following the same method discussed in Sect. 5.1. The most dominant SM background [60] that gives rise to the similar final state is \(VVV,(V= W^{\pm },Z\)). The next irreducible background that follows the signal is \(ZZ \rightarrow 4\ell \). In principle, \(t\overline{t}Z\) can also mimic the signal, but putting a b-veto( rejecting \(p_T(b) > 20\) GeV) kills the background. The other SM process \(Z+2~jets\) also results in the same topology if the jets are mis-tagged as leptons. However, we find out that this background can be reduced considerably when proper  cut is applied. Due to large cross-section, \(t\overline{t}\) could also be a possible background. But demanding four lepton with \(p_T^\ell > 10\) GeV and putting a b-jet veto reduces the background drastically. Thus from now on we shall only consider the dominant background VVV and \(ZZ \rightarrow 4\ell \)Footnote 12. In Table 15 we have tabulated the LO cross-sections for signal and background at 14 TeV LHC.
cut is applied. Due to large cross-section, \(t\overline{t}\) could also be a possible background. But demanding four lepton with \(p_T^\ell > 10\) GeV and putting a b-jet veto reduces the background drastically. Thus from now on we shall only consider the dominant background VVV and \(ZZ \rightarrow 4\ell \)Footnote 12. In Table 15 we have tabulated the LO cross-sections for signal and background at 14 TeV LHC.
To disentangle the signal and background, we select four leptons with \(p_T^\ell > 10\) GeV and \(|\eta _\ell | < 2.5\) and reject any additional charged lepton satisfying the same. We also apply a veto on light-jets and \(b-\)jet in the final state. We consider the following set of kinematic variables to improve the the signal sensitivity over the background:
-
\(D_1\): Out of total four leptons in the final state, we first select two pairs of leptons (pairwise of same flavour and opposite sign), performing all possible combinations. Then we calculate the invariant mass of the pairs and compare whether they are close to \(M_Z\) or not. Considering the invariant mass of the first and second pair as \((M_{\ell ^+ \ell ^-})_{1,2}\) respectively, we reject all events where \( 105> (M_{\ell ^+ \ell ^-})_{1,2} > 75\) GeV to exclude the Z-peak of ZZ-background. For the signal, the four charged leptons are not produced from the decay of two Z-bosons, which makes this cut very useful in boosting the signal significance.
-
\(D_2\): For the ZZ-background, the only source of
 is the mis-tagging of one or more leptons and so the
is the mis-tagging of one or more leptons and so the  distribution for the dominant ZZ background peaks at lower value than the signal which is expected as the
distribution for the dominant ZZ background peaks at lower value than the signal which is expected as the  in ZZ process mainly comes from mis-measurements. The VVV background on the other hand would still have a substantial overlap with the signal distribution which has a softer
in ZZ process mainly comes from mis-measurements. The VVV background on the other hand would still have a substantial overlap with the signal distribution which has a softer  due to the compression in the spectrum which leads to the cascade decays. Thus we choose a moderately low cut of
due to the compression in the spectrum which leads to the cascade decays. Thus we choose a moderately low cut of  GeV which helps to reduce the ZZ background significantly while not killing too many of the signal events as we can see in Table 16.
GeV which helps to reduce the ZZ background significantly while not killing too many of the signal events as we can see in Table 16. -
\(D_3\): We define the kinematic variable \(M_{\mathrm{eff}}\) as the sum of the transverse momenta of four leptons and
 . The background in this case seems to have a longish tail compared to the signal. To exclude the tail of the \(M_{\mathrm{eff}}\) distribution of the ZZ-background
. The background in this case seems to have a longish tail compared to the signal. To exclude the tail of the \(M_{\mathrm{eff}}\) distribution of the ZZ-backgroundwe demand \(M_{\mathrm{eff}} < 500\) GeV to enhance the signal significance.
The cuts applied on the aforementioned kinematic variables along with the significances are listed in Table 16. For the five benchmarks, the significances at the integrated luminosity 3 ab\(^{-1}\) are 10.1, 7.1, 5.2, 3.2, 1.0 respectively. Note that the first four benchmarks seem to achieve a significance \(> 3 \sigma \) (the first three having \({\mathcal {S}} > 5\sigma \)). Thus we find that the higher lepton multiplicity of the final states tend to achieve a more significant signal sensitivity in our model which is expected due to the addition of vector like fermions which decay to charged leptons.
Before concluding this section, let us present a comparative study among all the aforementioned channels according to the degree of performance. For convenience, we have tabulated the signal significances corresponding to all BPs for all channels at an integrated luminosity 3 ab\(^{-1}\) in Table 17. For  and
and  channels we present the signal significances both for by the BDTD and cut-based analysis, whereas for
channels we present the signal significances both for by the BDTD and cut-based analysis, whereas for  ,
,  channels we present the significances obtained from the cut-based analysis only. For all the benchmarks and all the channels there exist a generic pattern, which shows that the signal significance goes down with increasing DM masses. As mentioned earlier, smaller signal cross-section for larger DM masses are accountable for this particular pattern. According to the degree of performance, the
channels we present the significances obtained from the cut-based analysis only. For all the benchmarks and all the channels there exist a generic pattern, which shows that the signal significance goes down with increasing DM masses. As mentioned earlier, smaller signal cross-section for larger DM masses are accountable for this particular pattern. According to the degree of performance, the  channel fares the best among all for BP2, BP3, BP4 and BP5. With 3 ab\(^{-1}\) luminosity, first four benchmark points can be probed with significance > \(3 \sigma \). Next better performing channel after
channel fares the best among all for BP2, BP3, BP4 and BP5. With 3 ab\(^{-1}\) luminosity, first four benchmark points can be probed with significance > \(3 \sigma \). Next better performing channel after  is
is  for last four benchmarks. In fact for BP1,
for last four benchmarks. In fact for BP1,  channel turns out to be best performing with signal significance 11.1 at 3 ab\(^{-1}\) integrated luminosity. For
channel turns out to be best performing with signal significance 11.1 at 3 ab\(^{-1}\) integrated luminosity. For  and
and  channel the significance for BP1 are 7.0 and 6.7 respectively with cut-based analysis, which is improved to 7.8 using the BDTD analysis.
channel the significance for BP1 are 7.0 and 6.7 respectively with cut-based analysis, which is improved to 7.8 using the BDTD analysis.
6 Conclusion
In this work, we extend the \(S_3\)-symmetric 2HDM with two generations of VLLs. The introduction of two generations of VLLs in the minimal version of the model is essential to ensure \(S_3\)-symmetric Yukawa Lagrangian. Since the VLLs are odd under the imposed \(Z_2\)-symmetry and the SM fermions are even under the same, the mixing between the SM leptons and the VLLs is forbidden. Thus we end up with a dark sector in our model which talks to the SM matter fields only through the SM force mediators and the scalar sector. In this set up, the lightest neutral VLL mass eigenstate serves as a viable DM candidate.
Having satisfied the constraints like perturbativity, vacuum stability, electroweak precision data and Higgs signal strength, we show that a large portion of parameter space spanned by the model parameters is allowed from the observed relic density, direct and indirect detection experiments. We choose five representative points BP1, BP2, BP3, BP4 and BP5 according to the low, medium and high DM masses to perform the collider analysis of some particular channels with  and
and  in the final state at 14 TeV HL-LHC. We must point out here that our choice of benchmarks for the LHC analysis only represents a part of the parameter space allowed by DM data, as it gives a relatively lighter spectrum which can give appreciable signal sensitivity to our model at LHC. To highlight this, we have chosen a benchmark point (BP5) which represents a point near the threshold (for the spectrum) which will be out of reach at LHC, even with the very high luminosity (vHL-LHC) option.
in the final state at 14 TeV HL-LHC. We must point out here that our choice of benchmarks for the LHC analysis only represents a part of the parameter space allowed by DM data, as it gives a relatively lighter spectrum which can give appreciable signal sensitivity to our model at LHC. To highlight this, we have chosen a benchmark point (BP5) which represents a point near the threshold (for the spectrum) which will be out of reach at LHC, even with the very high luminosity (vHL-LHC) option.
To start with, we first analyse the final state containing  , which can originate from the pair production of the charged VLLs and neutral VLLs as well as from the associated production of the charged and neutral VLLs. The major background for this channel is
, which can originate from the pair production of the charged VLLs and neutral VLLs as well as from the associated production of the charged and neutral VLLs. The major background for this channel is  . With traditional cut-based analysis, we show that with 3 ab\(^{-1}\) luminosity BP1 and BP2 can be probed with significance \(> 5\sigma \), which in turn improves with multivariate (BDTD) analysis. Next we move on to perform the collider analysis of the final state comprising of
. With traditional cut-based analysis, we show that with 3 ab\(^{-1}\) luminosity BP1 and BP2 can be probed with significance \(> 5\sigma \), which in turn improves with multivariate (BDTD) analysis. Next we move on to perform the collider analysis of the final state comprising of  (di-lepton along with missing transverse energy), which mainly comes from the pair production of the charged VLLs and neutral VLLs individually. The main background is
(di-lepton along with missing transverse energy), which mainly comes from the pair production of the charged VLLs and neutral VLLs individually. The main background is  which takes care of \(W^{+}W^{-}, ZZ\) pair production. \(t\overline{t}\) and \(W^{\pm }Z\) also contribute as subdominant SM background for the di-lepton channel. After performing cut-based analysis we find that only BP1 can be probed with a significance \(> 5 \sigma \) while the sensitivity in the di-lepton channel diminishes for the rest of the benchmarks. The primary reason for this is the fact that the mass splittings amongst the VLL’s is not too large which leads to a relatively compressed spectrum. The resulting decay products in the cascade are therefore not very hard, leading to a significant overlap of the kinematic distributions with that of the SM background. This led to less signal significance in the di-lepton mode, though it can be improved marginally with a BDTD analysis. The final state containing tri-lepton with missing transverse energy can be generated from the associated production of the charged and neutral VLLs. Corresponding irreducible background originates from
which takes care of \(W^{+}W^{-}, ZZ\) pair production. \(t\overline{t}\) and \(W^{\pm }Z\) also contribute as subdominant SM background for the di-lepton channel. After performing cut-based analysis we find that only BP1 can be probed with a significance \(> 5 \sigma \) while the sensitivity in the di-lepton channel diminishes for the rest of the benchmarks. The primary reason for this is the fact that the mass splittings amongst the VLL’s is not too large which leads to a relatively compressed spectrum. The resulting decay products in the cascade are therefore not very hard, leading to a significant overlap of the kinematic distributions with that of the SM background. This led to less signal significance in the di-lepton mode, though it can be improved marginally with a BDTD analysis. The final state containing tri-lepton with missing transverse energy can be generated from the associated production of the charged and neutral VLLs. Corresponding irreducible background originates from  process. The situation is found to improve here as the SM background is now smaller compared to the di-lepton final state. With simple cut-based analysis we find out that with 3 ab\(^{-1}\) luminosity, BP1 can be probed with significance \(> 10\sigma \), while now even BP3 has a \(>3\sigma \) sensitivity. The situation improves further with an increase in charged lepton multiplicity, which we show with the analysis of
process. The situation is found to improve here as the SM background is now smaller compared to the di-lepton final state. With simple cut-based analysis we find out that with 3 ab\(^{-1}\) luminosity, BP1 can be probed with significance \(> 10\sigma \), while now even BP3 has a \(>3\sigma \) sensitivity. The situation improves further with an increase in charged lepton multiplicity, which we show with the analysis of  final state, arising mostly from neutral VLL pair production. The major SM background for this process is \( p p \rightarrow ZZ \rightarrow 4\ell \) and \(p p \rightarrow V\,V\,V \,\, (V\equiv W,Z)\) which have small cross-sections. We find that now the four benchmark points can be probed with significance > 3 \(\sigma \) with 3 ab\(^{-1}\) integrated luminosity. Thus comparing all four channels of the multi-lepton final states we find that
final state, arising mostly from neutral VLL pair production. The major SM background for this process is \( p p \rightarrow ZZ \rightarrow 4\ell \) and \(p p \rightarrow V\,V\,V \,\, (V\equiv W,Z)\) which have small cross-sections. We find that now the four benchmark points can be probed with significance > 3 \(\sigma \) with 3 ab\(^{-1}\) integrated luminosity. Thus comparing all four channels of the multi-lepton final states we find that  channel turns out to be the most promising among all owing to it being the most clean and background free final state.
channel turns out to be the most promising among all owing to it being the most clean and background free final state.
We conclude our discussion by stating that this model can provide a viable Majorana type DM candidate and that a part of the allowed parameter space (with DM masses up to \(\sim 300\) GeV) can be tested at the 14 TeV HL-LHC in the multi-lepton channel. The relative compression in the mass spectrum of the VLL’s do not allow very clean kinematic thresholds that could provide as a good discriminator for signal against the SM background. This limits the search sensitivity of the model to relatively light VLL masses of about 350 GeV, beyond which it is very difficult to achieve any signal sensitivity even with the HL-LHC option. To probe higher DM masses one may benefit by looking for such a model at the 1 TeV ILC which warrants a separate study in future [103].
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The data we used in our manuscript to compare with our model estimations are already public from the ATLAS, CMS, LUX, PANDAX-II, Xenon-1T, PICO, FERMI-LAT, MAGIC, PLANCK experiments.]
Notes
The hyper-charge Y has been computed by using the relation: \(Q = T_3 + \frac{Y}{2}\). Here \(T_3\) and Q are the weak isospin and electric charge respectively.
In Ref. [63], it has been shown that with the configuration \(m_{11}^2 = m_{22}^2\) and \(m_{12}^2 \ne \) 0, one can still achieve the correct mass hierarchy in the quark sector by computing the correction to the eigenvalues using first order (non-degenerate) perturbation theory.
Note that with exact \(S_3\)-symmetry, the mass of the vector like leptons will be proportional to the product of Yukawa coupling and the electroweak vacuum expectation value (VEV), which in turn will lead to non-perturbative Yukawa couplings (for vector lepton masses \(\sim \) 1 TeV). With \(S_3\) softly broken we can write down gauge-invariant bilinear dimension-3 interaction terms in the Lagrangian.
The couplings of the SM fermions with the scalar doublets \(\phi _1\) and \(\phi _2\) are also governed by \(S_3\)-symmetry. The most general \(S_3\)-symmetric Yukawa lagrangian containing dimension-4 interactions between the SM fermions and the scalar doublets can be found in [50].
\(\Omega _{\mathrm{DM}}\) is defined as the ratio of non-baryonic DM density to the critical density of the universe and h is the reduced Hubble parameter (not to be confused with SM Higgs h).
\(\epsilon = \frac{{\mathrm{Number\ of\ events\ surviving\ after\ applying\ cuts}}}{\mathrm{Total\ number\ of\ events\ generated}}.\)
We plot the relevant kinematic distributions for only BP1 and BP3 as representative points while only the dominant SM background via
 which is \(\sim {\mathcal {O}}(10^4)\) bigger than the rest is shown.
which is \(\sim {\mathcal {O}}(10^4)\) bigger than the rest is shown.The purity p can be defined as: \( p = \frac{S}{S+B}\).
KS-score > 0.01 will also serve the purpose if it remains stable even after changing the internal parameters of the algorithm.
ROC curve is a plot of signal efficiency (\(\epsilon _S\)) vs. efficiency of rejecting the backgrounds \((1-\epsilon _B)\), \(\epsilon _B\) being the background efficiency.
Before proceeding towards the analysis at 14 TeV, we first validate the chosen benchmarks using the existing search for chargino-neutralino pair production in final states with three leptons and missing transverse momentum at \(\sqrt{s} = 13\) TeV performed by the ATLAS detector [59].
The chosen benchmarks are also validated with an existing study by ATLAS at \(\sqrt{s} = 13\) TeV [60].
References
ATLAS collaboration, G. Aad et al., Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 716, 1–29 (2012). arXiv:1207.7214
CMS collaboration, S. Chatrchyan et al., Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 716, 30–61 (2012). arXiv:1207.7235
J.L. Rosner, Splitting between up type and down type quark masses via mixing with exotic fermions in E6. Phys. Rev. D 61, 097303 (2000)
K. Das, T. Li, S. Nandi, S.K. Rai, A new proposal for diphoton resonance from \(E_6\) motivated extra \(U(1)\). arXiv:1607.00810
A. Joglekar, J.L. Rosner, Searching for signatures of \(E_{{\rm 6}}\). Phys. Rev. D 96, 015026 (2017). arXiv:1607.06900
K. Das, T. Li, S. Nandi, S.K. Rai, New signals for vector-like down-type quark in \(U(1)\) of \(E_6\). Eur. Phys. J. C 78, 35 (2018). arXiv:1708.00328
T. Moroi, Y. Okada, Radiative corrections to Higgs masses in the supersymmetric model with an extra family and antifamily. Mod. Phys. Lett. A 7, 187–200 (1992)
T. Moroi, Y. Okada, Upper bound of the lightest neutral Higgs mass in extended supersymmetric Standard Models. Phys. Lett. B 295, 73–78 (1992)
S.P. Martin, Extra vector-like matter and the lightest Higgs scalar boson mass in low-energy supersymmetry. Phys. Rev. D 81, 035004 (2010). arXiv:0910.2732
K.S. Babu, I. Gogoladze, M.U. Rehman, Q. Shafi, Higgs boson mass, sparticle spectrum and little hierarchy problem in extended MSSM. Phys. Rev. D 78, 055017 (2008). arXiv:0807.3055
S.P. Martin, Raising the Higgs mass with yukawa couplings for isotriplets in vector-like extensions of minimal supersymmetry. Phys. Rev. D 82, 055019 (2010). arXiv:1006.4186
P.W. Graham, A. Ismail, S. Rajendran, P. Saraswat, A little solution to the little hierarchy problem: a vector-like generation. Phys. Rev. D 81, 055016 (2010). arXiv:0910.3020
J. Kang, P. Langacker, B.D. Nelson, Theory and phenomenology of exotic isosinglet quarks and squarks. Phys. Rev. D 77, 035003 (2008). arXiv:0708.2701
L. Randall, R. Sundrum, A large mass hierarchy from a small extra dimension. Phys. Rev. Lett. 83, 3370–3373 (1999). arXiv:hep-ph/9905221
L. Randall, R. Sundrum, An alternative to compactification. Phys. Rev. Lett. 83, 4690–4693 (1999). arXiv:hep-th/9906064
K. Agashe, G. Perez, A. Soni, Flavor structure of warped extra dimension models. Phys. Rev. D 71, 016002 (2005). arXiv:hep-ph/0408134
K. Agashe, G. Perez, A. Soni, Collider signals of top quark flavor violation from a warped extra dimension. Phys. Rev. D 75, 015002 (2007). arXiv:hep-ph/0606293
T. Li, Z. Murdock, S. Nandi, S.K. Rai, Quark lepton unification in higher dimensions. Phys. Rev. D 85, 076010 (2012). arXiv:1201.5616
G.-Y. Huang, K. Kong, S.C. Park, Bounds on the fermion-bulk masses in models with universal extra dimensions. JHEP 06, 099 (2012). arXiv:1204.0522
C. Biggio, F. Feruglio, I. Masina, M. Perez-Victoria, Fermion generations, masses and mixing angles from extra dimensions. Nucl. Phys. B 677, 451–470 (2004). arXiv:hep-ph/0305129
D.E. Kaplan, T.M.P. Tait, Supersymmetry breaking, fermion masses and a small extra dimension. JHEP 06, 020 (2000). arXiv:hep-ph/0004200
H.-C. Cheng, Doublet triplet splitting and fermion masses with extra dimensions. Phys. Rev. D 60, 075015 (1999). arXiv:hep-ph/9904252
R.S. Chivukula, B.A. Dobrescu, H. Georgi, C.T. Hill, Top quark seesaw theory of electroweak symmetry breaking. Phys. Rev. D 59, 075003 (1999). arXiv:hep-ph/9809470
B.A. Dobrescu, C.T. Hill, Electroweak symmetry breaking via top condensation seesaw. Phys. Rev. Lett. 81, 2634–2637 (1998). arXiv:hep-ph/9712319
H.-J. He, C.T. Hill, T.M.P. Tait, Top quark seesaw, vacuum structure and electroweak precision constraints. Phys. Rev. D 65, 055006 (2002). arXiv:hep-ph/0108041
R. Contino, L. Da Rold, A. Pomarol, Light custodians in natural composite Higgs models. Phys. Rev. D 75, 055014 (2007). arXiv:hep-ph/0612048
C. Anastasiou, E. Furlan, J. Santiago, Realistic composite Higgs models. Phys. Rev. D 79, 075003 (2009). arXiv:0901.2117
K. Kong, M. McCaskey, G.W. Wilson, Multi-lepton signals from the top-prime quark at the LHC. JHEP 04, 079 (2012). arXiv:1112.3041
M. Gillioz, R. Grober, C. Grojean, M. Muhlleitner, E. Salvioni, Higgs low-energy theorem (and its corrections) in composite models. JHEP 10, 004 (2012). arXiv:1206.7120
N. Arkani-Hamed, A.G. Cohen, E. Katz, A.E. Nelson, The littlest Higgs. JHEP 07, 034 (2002). arXiv:hep-ph/0206021
M. Perelstein, M.E. Peskin, A. Pierce, Top quarks and electroweak symmetry breaking in little Higgs models. Phys. Rev. D 69, 075002 (2004). arXiv:hep-ph/0310039
M. Carena, J. Hubisz, M. Perelstein, P. Verdier, Collider signature of T-quarks. Phys. Rev. D 75, 091701 (2007). arXiv:hep-ph/0610156
S. Matsumoto, T. Moroi, K. Tobe, Testing the littlest Higgs model with T-parity at the large hadron collider. Phys. Rev. D 78, 055018 (2008). arXiv:0806.3837
T. Han, H.E. Logan, B. McElrath, L.-T. Wang, Phenomenology of the little Higgs model. Phys. Rev. D 67, 095004 (2003). arXiv:hep-ph/0301040
S. Bahrami, M. Frank, Dark matter in the Higgs triplet model. Phys. Rev. D 91, 075003 (2015). arXiv:1502.02680
K. Das, S.K. Rai, 750 GeV diphoton excess in a U(1) hidden symmetry model. Phys. Rev. D 93, 095007 (2016). arXiv:1512.07789
N. Bizot, M. Frigerio, Fermionic extensions of the Standard Model in light of the Higgs couplings. JHEP 01, 036 (2016). arXiv:1508.01645
S. Beser, B.B. Oner, U. Kaya, S. Sultansoy, Possible discovery channel for fourth chiral family up-quark at the LHC. arXiv:1607.07623
N. Kumar, S.P. Martin, Vectorlike leptons at the large hadron collider. Phys. Rev. D 92, 115018 (2015). arXiv:1510.03456
N.F. Bell, M.J. Dolan, L.S. Friedrich, M.J. Ramsey-Musolf, R.R. Volkas, Electroweak baryogenesis with vector-like leptons and scalar singlets. JHEP 19, 012 (2020). arXiv:1903.11255
E. Osoba, Fourth generations with an inert doublet Higgs. arXiv:1206.6912
S.K. Garg, C.S. Kim, Vector like leptons with extended Higgs sector. arXiv:1305.4712
A. Angelescu, G. Arcadi, Dark matter phenomenology of SM and enlarged Higgs sectors extended with vector like leptons. Eur. Phys. J. C 77, 456 (2017). arXiv:1611.06186
A. Angelescu, A. Djouadi, G. Moreau, Scenarii for interpretations of the LHC diphoton excess: two Higgs doublets and vector-like quarks and leptons. Phys. Lett. B 756, 126–132 (2016). arXiv:1512.04921
S. Bahrami, M. Frank, Vector leptons in the Higgs triplet model. Phys. Rev. D 88, 095002 (2013). arXiv:1308.2847
S. Bahrami, M. Frank, Neutrino dark matter in the Higgs triplet model. In Meeting of the APS Division of Particles and Fields, vol. 9 (2015). arXiv:1509.04763
S. Chakdar, K. Ghosh, S. Nandi, S.K. Rai, Collider signatures of mirror fermions in the framework of a left-right mirror model. Phys. Rev. D 88, 095005 (2013). arXiv:1305.2641
S. Bahrami, M. Frank, D.K. Ghosh, N. Ghosh, I. Saha, Dark matter and collider studies in the left-right symmetric model with vectorlike leptons. Phys. Rev. D 95, 095024 (2017). arXiv:1612.06334
A. Patra, S.K. Rai, Lepton-specific universal seesaw model with left-right symmetry. Phys. Rev. D 98, 015033 (2018). arXiv:1711.00627
D. Das, U.K. Dey, P.B. Pal, Quark mixing in an \(S_3\) symmetric model with two Higgs doublets. Phys. Rev. D 96, 031701 (2017). arXiv:1705.07784
D. Cogollo, J.A.P. Silva, Two Higgs doublet models with an \(S_3\) symmetry. Phys. Rev. D 93, 095024 (2016). arXiv:1601.02659
F.F. Freitas, J.A. Gonçalves, A.P. Morais, R. Pasechnik, Phenomenology of vector-like leptons with deep learning at the large hadron collider. JHEP 01, 076 (2021). arXiv:2010.01307
S. Bißmann, G. Hiller, C. Hormigos-Feliu, D.F. Litim, Multi-lepton signatures of vector-like leptons with flavor. Eur. Phys. J. C 81, 101 (2021). arXiv:2011.12964
ATLAS collaboration, G. Aad et al., Search for new particles in events with one lepton and missing transverse momentum in \(pp\) collisions at \(\sqrt{s}\) = 8 TeV with the ATLAS detector. JHEP 09, 037 (2014). arXiv:1407.7494
CMS collaboration, V. Khachatryan et al., Search for physics beyond the standard model in final states with a lepton and missing transverse energy in proton-proton collisions at sqrt(s) = 8 TeV. Phys. Rev. D 91, 092005 (2015). arXiv:1408.2745
CMS collaboration, A.M. Sirunyan et al., Search for high-mass resonances in final states with a lepton and missing transverse momentum at \( \sqrt{s}=13 \) TeV. JHEP 06, 128 (2018). arXiv:1803.11133
ATLAS collaboration, G. Aad et al., Search for electroweak production of charginos and sleptons decaying into final states with two leptons and missing transverse momentum in \(\sqrt{s}=13\)TeV\(pp\) collisions using the ATLAS detector. Eur. Phys. J. C 80, 123 (2020). arXiv:1908.08215
ATLAS collaboration, G. Aad et al., Search for chargino-neutralino production with mass splittings near the electroweak scale in three-lepton final states in \(\sqrt{s}\)=13 TeV\(pp\) collisions with the ATLAS detector. Phys. Rev. D 101, 072001 (2020). arXiv:1912.08479
ATLAS collaboration, Search for chargino-neutralino pair production in final states with three leptons and missing transverse momentum in \(\sqrt{s}\) = 13 TeV p-p collisions with the ATLAS detector, ATLAS-CONF-2020-015
ATLAS collaboration, M. Aaboud et al., Search for supersymmetry in events with four or more leptons in \(\sqrt{s}=13\) TeV \(pp\) collisions with ATLAS. Phys. Rev. D 98, 032009 (2018). arXiv:1804.03602
ATLAS collaboration, G. Aad et al., Search for doubly and singly charged Higgs bosons decaying into vector bosons in multi-lepton final states with the ATLAS detector using proton-proton collisions at \(\sqrt{s}\) = 13 TeV. arXiv:2101.11961
D. Das, U.K. Dey, Analysis of an extended scalar sector with \(S_3\) symmetry. Phys. Rev. D 89, 095025 (2014). arXiv:1404.2491
N. Chakrabarty, I. Chakraborty, On the Higgs mass fine-tuning problem with multi-Higgs doublet models. Int. J. Mod. Phys. A 34, 1950025 (2019). arXiv:1801.05272
Particle Data Group collaboration, M. Tanabashi et al., Review of particle physics. Phys. Rev. D 98, 030001 (2018)
M.E. Peskin, T. Takeuchi, A new constraint on a strongly interacting Higgs sector. Phys. Rev. Lett. 65, 964–967 (1990)
M.E. Peskin, T. Takeuchi, Estimation of oblique electroweak corrections. Phys. Rev. D 46, 381–409 (1992)
J. Haller, A. Hoecker, R. Kogler, K. Mönig, T. Peiffer, J. Stelzer, Update of the global electroweak fit and constraints on two-Higgs-doublet models. Eur. Phys. J. C 78, 675 (2018). arXiv:1803.01853
ATLAS collaboration, G. Aad et al., Measurement of the production cross section for a Higgs boson in association with a vector boson in the \(H \rightarrow WW^{\ast } \rightarrow \ell \nu \ell \nu \) channel in \(pp\) collisions at \(\sqrt{s}\) = 13 TeV with the ATLAS detector. Phys. Lett. B 798, 134949 (2019). arXiv:1903.10052
CMS collaboration, A.M. Sirunyan et al., Measurements of properties of the Higgs boson decaying to a W boson pair in pp collisions at \(\sqrt{s}=\) 13 TeV. Phys. Lett. B 791, 96 (2019). arXiv:1806.05246
ATLAS collaboration, Measurements of the Higgs boson production, fiducial and differential cross sections in the \(4\ell \) decay channel at \(\sqrt{s}\) = 13 TeV with the ATLAS detector, ATLAS-CONF-2018-018
CMS collaboration, Measurements of properties of the Higgs boson in the four-lepton final state in proton-proton collisions at \(\sqrt{s}=13~{{\rm TeV}}\), cms-pas-hig-19-001
ATLAS collaboration, M. Aaboud et al., Search for Higgs bosons produced via vector-boson fusion and decaying into bottom quark pairs in \(\sqrt{s} = 13\)\({{\rm TeV}}\)\(pp\) collisions with the ATLAS detector. Phys. Rev. D 98, 052003 (2018). arXiv:1807.08639
CMS collaboration, VBF H to bb using the 2015 data sample, CMS-PAS-HIG-16-003
ATLAS collaboration, Cross-section measurements of the Higgs boson decaying to a pair of tau leptons in proton–proton collisions at \(\sqrt{s}=13\) TeV with the ATLAS detector, ATLAS-CONF-2018-021
CMS collaboration, A.M. Sirunyan et al., Observation of the Higgs boson decay to a pair of \(\tau \) leptons with the CMS detector. Phys. Lett. B 779, 283–316 (2018). arXiv:1708.00373
ATLAS collaboration, M. Aaboud et al., Measurements of Higgs boson properties in the diphoton decay channel with 36 fb\(^{-1}\) of \(pp\) collision data at \(\sqrt{s} = 13\) TeV with the ATLAS detector. Phys. Rev. D 98, 052005 (2018). arXiv:1802.04146
CMS collaboration, A.M. Sirunyan et al., Measurements of Higgs boson properties in the diphoton decay channel in proton-proton collisions at \(\sqrt{s} =\) 13 TeV. JHEP 11, 185 (2018). arXiv:1804.02716
Planck collaboration, N. Aghanim et al., Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 641, A6 (2020). arXiv:1807.06209
A. Alloul, N.D. Christensen, C. Degrande, C. Duhr, B. Fuks, FeynRules 2.0—a complete toolbox for tree-level phenomenology. Comput. Phys. Commun. 185, 2250–2300 (2014). arXiv:1310.1921
A. Belyaev, N.D. Christensen, A. Pukhov, CalcHEP 3.4 for collider physics within and beyond the Standard Model. Comput. Phys. Commun. 184, 1729–1769 (2013). arXiv:1207.6082
G. Bélanger, F. Boudjema, A. Pukhov, A. Semenov, micrOMEGAs4.1: two dark matter candidates. Comput. Phys. Commun. 192, 322–329 (2015). arXiv:1407.6129
LUX collaboration, D.S. Akerib et al., Results from a search for dark matter in the complete LUX exposure. Phys. Rev. Lett. 118, 021303 (2017). arXiv:1608.07648
PandaX-II collaboration, X. Cui et al., Dark matter results from 54-ton-day exposure of PandaX-II experiment. Phys. Rev. Lett. 119, 181302 (2017). arXiv:1708.06917
XENON collaboration, E. Aprile et al., Dark matter search results from a one ton-year exposure of XENON1T. Phys. Rev. Lett. 121, 111302 (2018). arXiv:1805.12562
PICO collaboration, C. Amole et al., Dark matter search results from the complete exposure of the PICO-60 C\(_3\)F\(_8\) bubble chamber. Phys. Rev. D 100, 022001 (2019). arXiv:1902.04031
T. Daylan, D.P. Finkbeiner, D. Hooper, T. Linden, S.K.N. Portillo, N.L. Rodd et al., The characterization of the gamma-ray signal from the central Milky Way: a case for annihilating dark matter. Phys. Dark Univ. 12, 1–23 (2016). arXiv:1402.6703
MAGIC, Fermi-LAT collaboration, M.L. Ahnen et al., Limits to dark matter annihilation cross-section from a combined analysis of MAGIC and fermi-LAT observations of dwarf satellite galaxies. JCAP 02, 039 (2016). arXiv:1601.06590
K. Park, U. Min, S.J. Lee, W. Jun, Implementation of the ATLAS-EXOT-2018-030 analysis in the MadAnalysis 5 framework (\(W^{\prime }\) boson into a lepton and a neutrino; 139 fb\(^{-1}\)). Mod. Phys. Lett. A 36, 2141001 (2021)
J.Y. Araz, B. Fuks, Implementation of the ATLAS-SUSY-2018-32 analysis (sleptons and electroweakinos with two leptons and missing transverse energy; 139 fb\(^{-1}\)). Mod. Phys. Lett. A 36, 2141005 (2021)
CMS collaboration, A.M. Sirunyan et al., Search for electroweak production of charginos and neutralinos in multilepton final states in proton-proton collisions at \(\sqrt{s}=\)13 TeV. JHEP 03, 166 (2018). arXiv:1709.05406
J.Y. Araz, B. Fuks, G. Polykratis, Simplified fast detector simulation in MadAnalysis 5. arXiv:2006.09387
J.Y. Araz, M. Frank, B. Fuks, Reinterpreting the results of the LHC with MadAnalysis 5: uncertainties and higher-luminosity estimates. Eur. Phys. J. C 80, 531 (2020). arXiv:1910.11418
E. Conte, B. Fuks, Confronting new physics theories to LHC data with MADANALYSIS 5. Int. J. Mod. Phys. A 33, 1830027 (2018). arXiv:1808.00480
B. Dumont, B. Fuks, S. Kraml, S. Bein, G. Chalons, E. Conte et al., Toward a public analysis database for LHC new physics searches using MADANALYSIS 5. Eur. Phys. J. C 75, 56 (2015). arXiv:1407.3278
E. Conte, B. Dumont, B. Fuks, C. Wymant, Designing and recasting LHC analyses with MadAnalysis 5. Eur. Phys. J. C 74, 3103 (2014). arXiv:1405.3982
E. Conte, B. Fuks, G. Serret, MadAnalysis 5, a user-friendly framework for collider phenomenology. Comput. Phys. Commun. 184, 222–256 (2013). arXiv:1206.1599
J. Alwall, R. Frederix, S. Frixione, V. Hirschi, F. Maltoni, O. Mattelaer et al., The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations. JHEP 07, 079 (2014). arXiv:1405.0301
T. Sjöstrand, S. Ask, J.R. Christiansen, R. Corke, N. Desai, P. Ilten et al., An introduction to PYTHIA 8.2. Comput. Phys. Commun. 191, 159–177 (2015). arXiv:1410.3012
DELPHES 3 collaboration, J. de Favereau, C. Delaere, P. Demin, A. Giammanco, V. Lemaître, A. Mertens et al., DELPHES 3, a modular framework for fast simulation of a generic collider experiment. JHEP 02, 057 (2014). arXiv:1307.6346
A. Hocker et al., TMVA—Toolkit for Multivariate Data Analysis. arXiv:physics/0703039
ATLAS collaboration, G. Aad et al., Expected performance of the ATLAS experiment—detector, trigger and physics. arXiv:0901.0512
CMS collaboration, S. Chatrchyan et al., Search for anomalous production of events with three or more leptons in \(pp\) collisions at \(\sqrt{(s)} =\) 8 TeV. Phys. Rev. D 90, 032006 (2014). arXiv:1404.5801
I. Chakraborty, D.K. Ghosh, N. Ghosh, S.K. Rai, Work in Progress
A. Djouadi, The anatomy of electro-weak symmetry breaking. II. The Higgs bosons in the minimal supersymmetric model. Phys. Rep. 459, 1–241 (2008). arXiv:hep-ph/0503173
Acknowledgements
IC acknowledges support from DST, India, under grant number IFA18-PH214 (INSPIRE Faculty Award). NG and SKR would like to acknowledge support from the Department of Atomic Energy, Government of India, for the Regional Centre for Accelerator-based Particle Physics (RECAPP). NG and SKR would like to thank Tousik Samui and Anjan Barik for computational help.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Decay width of \(h \rightarrow \gamma \gamma \)
Amplitude and decay width of the process \(h \rightarrow \gamma \gamma \) can be written as [104]:
where \(N_f, Q_f, G_F\) and \(\alpha \) are respectively color factor, charge of fermion, the Fermi constant and the QED fine-structure constant. For quarks \(N_f = 3\). \(\lambda _{h H^+ H^-}\) and \(\lambda _{h E_i^+ E_i^-} ~(i=1,2,3,4)\) are \(h H^+ H^-\) and \(h E_i^+ E_i^-\) couplings respectively. \(f_{hff}, f_{hVV}\) are scale factors of hff, hVV couplings with respect to SM. At exact alignment limit,
The loop functions can be written as,
where \(A_{1/2}(x), A_1(x)\) and \(A_0(x)\) are the respective amplitudes for the spin-\(\frac{1}{2}\), spin-1 and spin-0 particles in the loop respectively while \(\lambda _{h H^+ H^-} = 2 v~ (\lambda _1 - \lambda _3)\).
Appendix B: Decay modes of the charged and neutral VLLs
We list below the tables (Tables 18 and 19 and 20) which summarise the decay probabilities of the VLLs, both charged and neutral for the five benchmark points chosen for our analysis.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Chakraborty, I., Ghosh, D.K., Ghosh, N. et al. Dark Matter and Collider Searches in \(S_3\)-Symmetric 2HDM with Vector Like Lepton . Eur. Phys. J. C 81, 679 (2021). https://doi.org/10.1140/epjc/s10052-021-09446-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-021-09446-5




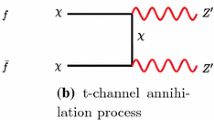




 , (c)
, (c)  channel at 14 TeV HL-LHC
channel at 14 TeV HL-LHC GeV helps to reduce the background drastically as the
GeV helps to reduce the background drastically as the  distribution for the background (magenta line) in Fig.
distribution for the background (magenta line) in Fig.  in the signal distribution.
in the signal distribution.
 is the azimuthal angle between the lepton and
is the azimuthal angle between the lepton and  . In Fig.
. In Fig.  . We find that putting a lower cut
. We find that putting a lower cut 
 channel
channel
 channel. b Variation of significance with BDT-score for
channel. b Variation of significance with BDT-score for  channel
channel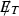 distributions for the BP1 and BP3 (green and blue lines) are much harder as in the mono-lepton case. Thus we demand
distributions for the BP1 and BP3 (green and blue lines) are much harder as in the mono-lepton case. Thus we demand  GeV, which helps to reduce the
GeV, which helps to reduce the 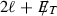 background. As the mass splitting between the VLLs become smaller for heavier DM, the
background. As the mass splitting between the VLLs become smaller for heavier DM, the  distribution is shifted towards the softer side.
distribution is shifted towards the softer side.
 for
for  channel at 14 TeV HL-LHC
channel at 14 TeV HL-LHC
 channel
channel
 channel. b BDT-scores corresponding to BP1, BP2, BP3, BP4 and BP5 for
channel. b BDT-scores corresponding to BP1, BP2, BP3, BP4 and BP5 for  channel
channel
 for
for  channel at 14 TeV HL-LHC
channel at 14 TeV HL-LHC . In Fig.
. In Fig.  background (magenta line) is flatter and smeared with respect to the distributions of the signal (green and blue lines) and other background ZZ (brown line). Setting
background (magenta line) is flatter and smeared with respect to the distributions of the signal (green and blue lines) and other background ZZ (brown line). Setting  in the final state explicitly, corresponding
in the final state explicitly, corresponding  distribution peaks at lower value than the signal as can be seen from Fig.
distribution peaks at lower value than the signal as can be seen from Fig.  GeV helps to reduce the ZZ background drastically as can be found in Table
GeV helps to reduce the ZZ background drastically as can be found in Table  background efficiently.
background efficiently.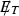 as
as  . Corresponding distributions are shown in Fig.
. Corresponding distributions are shown in Fig.  1.5 on the events help in eliminating the SM background further.
1.5 on the events help in eliminating the SM background further. is the mis-tagging of one or more leptons and so the
is the mis-tagging of one or more leptons and so the  distribution for the dominant ZZ background peaks at lower value than the signal which is expected as the
distribution for the dominant ZZ background peaks at lower value than the signal which is expected as the  in ZZ process mainly comes from mis-measurements. The VVV background on the other hand would still have a substantial overlap with the signal distribution which has a softer
in ZZ process mainly comes from mis-measurements. The VVV background on the other hand would still have a substantial overlap with the signal distribution which has a softer  due to the compression in the spectrum which leads to the cascade decays. Thus we choose a moderately low cut of
due to the compression in the spectrum which leads to the cascade decays. Thus we choose a moderately low cut of  GeV which helps to reduce the ZZ background significantly while not killing too many of the signal events as we can see in Table
GeV which helps to reduce the ZZ background significantly while not killing too many of the signal events as we can see in Table  . The background in this case seems to have a longish tail compared to the signal. To exclude the tail of the
. The background in this case seems to have a longish tail compared to the signal. To exclude the tail of the  which is
which is