Tetraquark state X(6900) and the interaction between diquark and antidiquark

Abstract

Recently LHCb declared a new structure X(6900) in the final state di-$J/\psi$ which is popularly regarded as a cc-$\bar{c}\bar{c}$ tetraquark state. Within the Bethe–Salpeter (B–S) framework we study the possible cc-$\bar{c}\bar{c}$ bound states and the interaction between diquark (cc) and antidiquark ($\bar{c}\bar{c}$). In this work cc ($\bar{c}\bar{c}$) is treated as a color anti-triplet (triplet) axial-vector so the quantum numbers of cc-$\bar{c}\bar{c}$ bound state are $0^+$, $1^+$ and $2^+$. Learning from the interaction in meson case and using the effective coupling we suggest the interaction kernel for the diquark and antidiquark system. Then we deduce the B–S equations for different quantum numbers. Solving these equations numerically we find the spectra of some excited states can be close to the mass of X(6900) when we assign appropriate values for parameter $\kappa$ introduced in the interaction (kernel). We also briefly calculate the spectra of bb-$\bar{b}\bar{b}$ bound states. Future measurement of bb-$\bar{b}\bar{b}$ state will help us to determine the exact form of effective interaction.

1 Introduction

Not long ago, LHCb declared a narrow structure about 6.9 GeV ( named as X(6900) or $T_{cc\bar{c}\bar{c}}$) and a broad structure about twice the $J/\psi$ mass in the final state di-$J/\psi$ [1]. Based on no-interference fit, the new state’s mass and width are $6905\pm 11\pm 7$ MeV and $80\pm 19\pm 33$ MeV, while based on the simple model with interference they are $6886\pm 11\pm 11$ MeV and $168\pm 33\pm 69$ MeV. In the past twenty years many exotic states named $X,\,Y,\,Z$ have been experimentally observed. However, X(6900) is a novel state, since it seems a fully-charmed multi-quark state. This new discovery has inspired many theoretical interests [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. Many authors suggest that the new resonance $T_{cc\bar{c}\bar{c}}$ can be a cc-$\bar{c}\bar{c}$ tetraquark state [10,11,12,13,14,15,16,17,18], a cc-G-$\bar{c}\bar{c}$ hybrid [19], a $c\bar{c}_\mathrm{octet}$-$c\bar{c}_\mathrm{octet}$ tetraquark [20], a dynamically generated resonance pole [21] or a light Higgs-like boson [22]. Few people believe $T_{cc\bar{c}\bar{c}}$ is a molecular state because the interaction between two charmonia is too weak to form a molecular state.

In fact some authors [24,25,26,27,28] had been explored the cc-$\bar{c}\bar{c}$ bound state before the measurement of LHCb. In this paper we will study the possible bound states between the diquark (cc) and antidiquark ($\bar{c}\bar{c}$) using the Bethe–Salpeter (B–S) equation which is a relativistic two-body bound state equation. We want to explore the interaction between diquark and antidiquark by this study. As we know, if the orbital angular momentum is zero, two c quarks constitute an axial-vector diquark, but it may be a color anti-triple state or sextet one. The one-gluon exchange potential is attractive for anti-triple state but repulsive for sextet one. Therefore, in this work we will only consider the axial-vector diquark (antidiquark) of color anti-triplet (color triplet). In quantum field theory, at the tree level, two particles interact with each other by exchanging an intermediary messenger particle. For the present case, the tetraquark state consists of one diquark and one antidiquark. Apparently cc in $\bar{3}_c$ presentation and $\bar{c}\bar{c}$ in $3_c$ one can be regards as an antiquark and a quark respectively, so gluons are exchanged between cc and $\bar{c}\bar{c}$. And one can employ a phenomenological potential similar to the meson case to study the diquark and antidiquark bound state. However, since diquark isn’t the fundamental particle, the coupling between diquark and gluon doesn’t exist in QCD Lagrangian. In Refs. [29, 30] the authors suggested an effective coupling between diquark and gluon, which is different from that between quark and gluon so one cannot use the phenomenological potential for the mesons (Cornell potential [31, 32]) directly. Therefore, we have to modify the form of potential between diquark and antidiquark. With that coupling in Ref. [30] we can modify the coulomb part in the potential, but we still lack a proper treatment for the confine part of the potential. To address this issue, we follow the approach in Refs. [33, 34] and introduce a parameter $\kappa$ for the confine part in the Cornell potential.

Initially B–S equation was used to explore the bound state of two fermions. Later some authors extended this approach to study the bound state composed of one fermion and one boson [34,35,36]. In Refs. [37, 38] the authors employed B–S equation to study the $K\bar{K}$ and BK molecular stated and their decays. Later we extended the method to explore some other systems [39, 40]. Diquark and antidiquark bound state is a novel system in this approach and the effective interaction hasn’t been studied in depth due to the lack of data. In this work, we will study the phenomenological potential between diquark and antidiquark, and establish the formalism of effective interaction for this bound state system.

Here we only concern the state where the orbital angular momentum between the two constituents (cc and $\bar{c}\bar{c}$) is zero ($l=0)$ so the $J^{P}$ of the molecular state can be $0^+$, $1^+$ or $2^+$. Following Ref. [34], we explore the potential between cc and $\bar{c}\bar{c}$ and then deduce the B–S equations for different quantum numbers. By solving these B–S equations numerically we obtain the spectra and B–S wave function of the cc-$\bar{c}\bar{c}$ bound states. We use experimental data to determine the free parameters in the expression of the effective potential.

This paper is organized as follows. In Sect. 2 we deduce the B–S equations for the $0^+$, $1^+$ and $2^+$ diquark–antidiquark states. Then in Sect. 3 we present our numerical results and explicitly display all input parameters. Section 4 is devoted to the summary and discussion. As indicated before, in this work we concentrate on the case of cc-$\bar{c}\bar{c}$ states, but we also briefly calculate the spectra of the bb-$\bar{b}\bar{b}$ states.

2 The bound states of diquark and antidiquark

Fig. 1

The tetraquark state of cc and $\bar{c}\bar{c}$

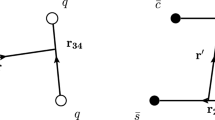
A diquark (cc) and an antidiquark ($\bar{c}\bar{c}$) can interact by exchanging gluon, and the scenario is depicted in Fig. 1. Since cc ($\bar{c}\bar{c}$) consists of two same quarks (antiquark), the ground state of cc ($\bar{c}\bar{c}$) possesses $1^+$ quantum number.

The relative and total momenta of the bound state in the equations are defined as

$$\begin{aligned} p= & {} \eta _2p_1 - \eta _1p_2,\quad p' = \eta _2p'_1 - \eta _1p'_2,\nonumber \\ P= & {} p_1 + p_2 = p'_1 + p'_2, \end{aligned}$$

(1)

where p and $p'$ are the relative momenta before and after the effective vertices, $p_1$ ($p'_1$) and $p_2$ ($p'_2$) are the momenta of the constituents before and after the effective vertices, P is the total momentum of the bound state, $\eta _i = m_i/(m_1+m_2)$ and $m_i\, (i=1,2)$ is the mass of the i-th constituent (diquark or antidiquark).

2.1 The B–S equation of $0^+$ state which is composed of two axial-vectors

The B–S wave function of $0^+$ state composed of two axial-vector can be defined as

$$\begin{aligned} \langle 0 | \mathrm{T}\,\phi _{1}^\alpha (x_1)\phi ^{\alpha '}_2(x_2) | \mathcal {S} \rangle ={\chi }_{{}_\mathcal {S}}^{}(x_1,x_2)g^{\alpha \alpha '}. \end{aligned}$$

(2)

The corresponding B–S equation can be written as

$$\begin{aligned}&\chi _{_{{}_\mathcal {S}}}({ p})g_{\beta \beta '}=\Delta _{1\mu \beta }\int {d^4{p}'\over (2\pi )^4}\,K^{\mu \mu '\nu \nu '}\nonumber \\&\quad \times ({ p},{ p}')\chi _{_{{}_\mathcal {S}}}^{}({ p}')\Delta _{2\mu '\beta '}g_{\nu \nu '}, \end{aligned}$$

(3)

where the propagators $\Delta _{1\mu \beta }=(-g_{\mu \beta }+p_{1\mu }p_{1\beta }/{m_1}^2)/({p_1}^2-{m_1}^2+i\epsilon )$ and $\Delta _{2\mu '\beta '}=(-g_{\mu \beta }+p_{2\mu '}p_{2\beta '}/{m_2}^2)/({p_2}^2-{m_2}^2+ i\epsilon )$.

Recall that the kernel between a quark and an antiquark [44] has the following form:

$$\begin{aligned} K({ p},{ p}')=K_v({ p},{ p}')\gamma ^\mu \bigotimes \gamma _\mu + K_s({ p},{ p}')I\bigotimes I \ , \end{aligned}$$

(4)

where $K_v({ p},{ p}')$ is called vector potential which comes from single gluon exchange, $K_s({ p},{ p}')$ is scalar potential which is responsible for the confinement and after taking instantaneous approximation $p_0'=p_0$

$$\begin{aligned} K_v(\mathbf {q})= & {} -\frac{16\pi \alpha _s}{3(\mathbf {q}^2+\alpha ^2)},\,\,\nonumber \\ K_s(\mathbf {q})= & {} -\frac{8\pi \lambda }{(\mathbf {q}^2+\alpha ^2)^2} +(2\pi )^3(\frac{\lambda }{\alpha }+V_0)\delta ^3(\mathbf {q}) \ , \end{aligned}$$

(5)

where q is equal to $p-p'$ ($\mathbf {q}$ is its three-momentum), $V_0$ is the zero-point energy term and $\alpha$ is a very small parameter. Since a diquark is in $\bar{3}_c$ presentation and an antiquark is in $3_c$ presentation, the interaction between diquark and antidiquark should be similar to that between quark and antiquark. However diquark and antidiquark are not the fundamental particles in standard model, so effective interaction vertex of the vector diquark–gluon coupling can be parameterized as

$$\begin{aligned}&-ig_s t^a[(p_1+{p'}_1)^\omega g^{\mu \nu }-k_vp_1^\mu g^{\omega \nu }-(1+k_v){p}_1^\nu g^{\mu \omega }\nonumber \\&\quad -k_v{p'}_1^\nu g^{\mu \omega }-(1+k_v){p'}_1^\mu g^{\omega \nu }]F_V(q^2), \end{aligned}$$

(6)

where $g_s$ is strong coupling constant, $t^a$ is color matrix, and $k_v$ is the anomalous magnetic momentum of vector diquark. In the non-relativistic quark model, $k_v$ should be 1. The form factor $F_V(q^2)$ is parametrized as $[Q_1^2/(Q_1^2 -q^2)]^2$ where $Q^2_1$ is a parameter which freezes $F_V(q^2)$ when $q^2$ is small. In Ref. [29] the authors fixed $Q^2_1$ and $k_v$ to be 1.58 GeV$^2$ and 1.16 by fitting the diquark model of nucleon based on the data of electron-proton and electron-neutron cross-sections [41, 42].

If only single gluon exchange is accounted, the kernel can be

$$\begin{aligned}&-\frac{16\pi \alpha _s}{3}[F_V(q^2)]^2 \left[ (p_1+{p'}_1)^\omega g^{\mu \nu }-k_vp_1^\mu g^{\omega \nu }\right. \nonumber \\&\quad \left. -(1+k_v){p}_1^\nu g^{\mu \omega }-k_v{p'}_1^\nu g^{\mu \omega }-(1+k_v){p'}_1^\mu g^{\omega \nu }\right] \nonumber \\&\quad \times \left[ (p_2+{p'}_2)^{\omega '} g^{\mu '\nu '}-k_vp_2^{\mu '} g^{\omega '\nu '}-(1+k_v){p}_2^{\nu '} g^{\mu '\omega '}\right. \nonumber \\&\quad \left. -k_v{p'}_2^{\nu '} g^{\mu '\omega '}-(1+k_v){p'}_2^{\mu '} g^{\omega '\nu '}\right] \frac{-ig_{\omega \omega '}}{q^2}. \end{aligned}$$

(7)

Compared with the kernel in Eq. (4) we have

$$\begin{aligned}&K^{\mu \mu '\nu \nu '}({ p},{ p}')=K_{v}(p,p')\Gamma ^{\omega \mu \nu }_1\bigotimes \Gamma ^{\omega '\mu '\nu '}_2\nonumber \\&\quad \times [F_V(q^2)]^2(-ig_{\omega \omega '})+ K_s({ p},{ p}')I\bigotimes Ig^{\mu \mu '}g^{\nu \nu '}\kappa \end{aligned}$$

where $\Gamma ^{\omega \mu \nu }_1=[(p_1+{p'}_1)^\omega g^{\mu \nu }-k_vp_1^\mu g^{\omega \nu }-(1+k_v){p}_1^\nu g^{\mu \omega }-k_v{p'}_1^\nu g^{\mu \omega }-(1+k_v){p'}_1^\mu g^{\omega \nu }]$, $\Gamma ^{\omega '\mu '\nu '}_2=[(p_2+{p'}_2)^{\omega '} g^{\mu '\nu '}-k_vp_2^{\mu '} g^{\omega '\nu '}-(1+k_v){p}_2^{\nu '} g^{\mu '\omega '}-k_v{p'}_2^{\nu '} g^{\mu '\omega '}-(1+k_v){p'}_2^{\mu '} g^{\omega '\nu '}]$ and $\kappa$ is a parameter introduced to compensate the dimension of the second term and its dimension is the quadratic of mass.

We need time $g_{\beta \beta '}$ on both sides in Eq. (3) and sum the same indexes. In order to achieve the three-dimensional Salpeter we take the instantaneous approximation $p'_0=p_0$ in the kernel and perform the integral over $p_0$ on both side of Eq. (3). The right hand side of expression is a contour integral in the complex place. By choosing a proper contour [37, 38] one can obtain the corresponding B–S equation in three-momentum space

$$\begin{aligned} \mathcal {\psi }_{{}_\mathcal {S}}^{}(\mathbf{|p|})= & {} \frac{ 1}{8E_1E_2[E^2-(E_1+E_2)^2](E+E_1-E_2)}\nonumber \\&\times \int {d^3\mathbf {p}'\over (2\pi )^3}\, \psi _{{}_\mathcal {S}}^{}(\mathbf{|p|}')\nonumber \\&\times \{E_2(E-E_1-E_2)[C_{\mathcal {S}1}|_{_{p_0=-E/2-E_1}}K_{v}(\mathbf {q})\nonumber \\&\times |F_V(\mathbf {q}^2)|^2+C_{\mathcal {S}2}|_{_{p_0=-E/2-E_1}}K_{s}(\mathbf {q})\kappa ]\nonumber \\&+E_1(E+E_1+E_2)[C_{\mathcal {S}1}|_{_{p_0=E/2-E_2}}K_{v}(\mathbf {q})\nonumber \\&\times |F_V(\mathbf {q}^2)|^2+C_{\mathcal {S}2}|_{_{p_0=E/2-E_2}}K_{s}(\mathbf {q})\kappa ]\}, \end{aligned}$$

(8)

where E is the total energy of the bound state, $E_i = \sqrt{\mathbf{p}^2 + m_i^2}$ and $\psi _{{}_\mathcal {S}}^{}(\mathbf{|p|})=\int {d{p_0}\over (2\pi )}\chi _{_{{}_\mathcal {S}}}^{}({ p})$ is the B–S wave function in the three-momentum space. The explicit expressions of $C_{\mathcal {S}1}$ and $C_{\mathcal {S}2}$ are presented in Appendix.

2.2 The B–S equation of $1^+$ state which is composed of two vectors

The B–S wave function of $1^+$ state composed of two axial-vectors is defined

$$\begin{aligned} \langle 0|T\phi _\alpha (x_1)\phi _{\alpha '}(x_2)|V\rangle =\frac{\varepsilon _{\alpha \alpha '\tau \tau '}}{\sqrt{6}M}\chi _{_\mathcal {V}}(x_1,x_2)\varepsilon ^\tau P^{\tau '} , \end{aligned}$$

(9)

where $\varepsilon$ is the polarization vector of $1^+$.

The corresponding B–S equation should be

$$\begin{aligned}&\varepsilon _{\beta \beta ' \omega \sigma }\chi _{_\mathcal {V}}(p)\varepsilon ^\sigma P^\omega =\Delta _{1\mu \beta }\nonumber \\&\times \int {d^4{q}\over (2\pi )^4}\,K^{\mu \mu '\nu \nu '}(P,p,q) \varepsilon _{\nu \nu '\omega '\sigma '}\chi _{_\mathcal {V}}(q)\varepsilon ^{\sigma '}P^{\omega '}\Delta _{2\mu '\beta '},\nonumber \\ \end{aligned}$$

(10)

and its form in three-momentum space

$$\begin{aligned} \psi _{{}_\mathcal {V}}^{}(\mathbf{|p|}) =&\frac{ 1}{12E^2E_1E_2[E^2-(E_1+E_2)^2](E+E_1-E_2)}\nonumber \\&\times \int {d^3\mathbf {p}'\over (2\pi )^3}\, \psi _{{}_\mathcal {V}}^{}(\mathbf{|p|}')\nonumber \\&\times \{E_2(E-E_1-E_2)[C_{\mathcal {V}1}|_{_{p_0=-E/2-E_1}}K_{v}(\mathbf {q})\nonumber \\&\times |F_V(\mathbf {q}^2)|^2+C_{\mathcal {V}2}|_{_{p_0=-E/2-E_1}}K_{s}(\mathbf {q})\kappa ]\nonumber \\&+E_1(E+E_1+E_2)[C_{\mathcal {V}1}|_{_{p_0=E/2-E_2}}K_{v}(\mathbf {q})\nonumber \\&\times |F_V(\mathbf {q}^2)|^2+C_{\mathcal {V}2}|_{_{p_0=E/2-E_2}}K_{s}(\mathbf {q})\kappa ]\} . \end{aligned}$$

(11)

The detailed expressions of $C_{\mathcal {V}1}$ and $C_{\mathcal {V}2}$ are also collected in Appendix.

2.3 The B–S equation of $2^+$ state which is composed of two vectors

The B–S wave-function of $2^+$ state composed of two axial-vectors can be written as

$$\begin{aligned} \langle 0|T\phi ^\alpha (x_1)\phi ^{\alpha '}(x_2)|V\rangle =\frac{1}{\sqrt{5}}\chi _{_\mathcal {T}}(x_1,x_2)\varepsilon ^{\alpha \alpha '} , \end{aligned}$$

(12)

where $\varepsilon$ is the polarization vector of $2^+$.

The B–S equation can be expressed as

$$\begin{aligned} \chi _{_\mathcal {T}}(p)\varepsilon _{\beta \beta '} =\Delta _{1\mu \beta }\int {d^4{q}\over (2\pi )^4}\,K^{\mu \mu '\nu \nu '}(P,p,q) \varepsilon _{\nu \nu '}\chi _{_\mathcal {T}}(q)\Delta _{2\mu '\beta '}.\nonumber \\ \end{aligned}$$

(13)

Similarly one can obtain its three-momentum form

$$\begin{aligned} \psi _{{}_\mathcal {T}}^{}(\mathbf{|p|}) =&\frac{ 1}{10E_1E_2[E^2-(E_1+E_2)^2](E+E_1-E_2)}\nonumber \\&\times \int {d^3\mathbf {p}'\over (2\pi )^3}\, \psi _{{}_\mathcal {T}}^{}(\mathbf{|p|}')\nonumber \\&\times \{E_2(E-E_1-E_2)[C_{\mathcal {T}1}|_{_{p_0=-E/2-E_1}}K_{v}(\mathbf {q})\nonumber \\&\times |F_V(\mathbf {q}^2)|^2+C_{\mathcal {T}2}|_{_{p_0=-E/2-E_1}}K_{s}(\mathbf {q})\kappa ]\nonumber \\&+E_1(E+E_1+E_2)[C_{\mathcal {T}1}|_{_{p_0=E/2-E_2}}K_{v}(\mathbf {q})\nonumber \\&\times |F_V(\mathbf {q}^2)|^2+C_{\mathcal {T}2}|_{_{p_0=E/2-E_2}}K_{s}(\mathbf {q})\kappa ]\} . \end{aligned}$$

(14)

The expressions of $C_{\mathcal {T}1}$ and $C_{\mathcal {T}2}$ can be found in Appendix.

3 Numerical results

The B–S equations in Eqs. (8, 11, 14) have integral forms. Generally the standard way to solve an integral equation is to discretize and perform algebraic operations. Concretely, we let $\mathbf |p|$ and $\mathbf |p'|$ take n ( n is sufficient large) discrete values $Q_1$, $Q_2,\ldots Q_n$ which distribute with equal gap, then the integral equation is transformed into n coupled algebraic equations. $\psi _{{}_\mathcal {N}}^{}(Q_1),\psi _{{}_\mathcal {N}}^{}(Q_2),\ldots \psi _{{}_\mathcal {N}}^{}(Q_n)$ ( the subscript $\mathcal {N}$ denotes $\mathcal {S}$, $\mathcal {V}$ or $\mathcal {T}$) constituents a column matrix so these algebraic equations can be regards as a matrix equation. We have explained how to solve the equation in detail in our earlier paper [40]. It is noted that here we must deal with the factor $E^2-(E_1+E_2)^2$ in the denominator to avoid the singularity when $E>m_1+m_2$. The following approach has been adopted : first, $E^2-(E_1+E_2)^2$ is timed on both side in Eq. (8), (11) and (14), and then $-(E_1+E_2)^2\psi _{_{\mathcal {N}}}(\mathbf |p|)$ ( the subscript $\mathcal {N}$ denotes $\mathcal {S}$, $\mathcal {V}$ or $\mathcal {T}$) is moved to right side of every equation, at last both sides of every equation are divided by $E^2$.

To solve the B–S equation numerically some input parameters are needed. At first we need to determine the masses of diquarks cc and bb. In Refs. [35, 36, 43] the theoretical values of heavy diquarks are presented. In [35] and [36] the authors fixed the mass of diquark cc from the mass of $\Xi _{cc}$ so the predicted diquark masses in [35] and [36] are very close. In this work we will use the values in [36] to do the calculations. The parameters $a=0.06$ GeV$^2$ and $\lambda =0.21$ GeV$^2$ are fixed in Ref. [44]. In principle the strong coupling constant $\alpha _s$ can be estimated using the expression $\alpha _s(Q^2)=\frac{12\pi }{33-2N_f}\frac{1}{\mathrm{ln}(\frac{Q^2}{\Lambda _{QCD}})}$ with $Q^2=m_D^2$ ($m_D$ is the mass of diquark ) and $\Lambda _{QCD}=0.27$ GeV [44]. We also need input value for the zero energy $V_0$. In Refs. [45, 46] for heavy quarkonia the value is about -0.4$\sim$-0.6 GeV so we will employ -0.5 GeV in our calculation. We know very little about the parameter $\kappa$. In Refs. [33, 34] the similar parameter for scalar potential has the dimension of mass and is proportional to $\Lambda _{QCD}$. Here we set it to be $\Lambda _{QCD}\times \Lambda _{QCD}$, $\Lambda _{QCD}\times E$ or $E\times E$ in our calculations (E is the spectrum of the bound state).

Table 1 The masses of diquarks in different references

Table 2 The spectra of the cc-$\bar{c}\bar{c}$ states with $m_{cc}=3.23$ GeV [36]

Fig. 2

The wave functions of the cc-$\bar{c}\bar{c}$ bound states

Table 3 The spectra of the cc-$\bar{c}\bar{c}$ states in different references

Table 4 The spectra of the bb-$\bar{b}\bar{b}$ states with $m_{bb}=9.8$ GeV

The spectra of the cc-$\bar{c}\bar{c}$ states we obtained are present in Table 2. One can find the spectra of $1^+$ and $2^+$ are degenerate for different parameters. The mass of the second radial excited state of $0^+$ is close to mass of X(6900) when the parameter $\kappa$ takes the value $E\times E$. In fact LHCb also observed a board structure, using the Fig. 3(b) in Ref. [1], the authors [15] estimated that its mass is $6490\pm 15$ GeV, which is close to that of the first radial excited state $0^+$. When one change the value of $\kappa$ the radial excited state of $1^+$ or 2 also can be consistent with data. In Fig. 2 the wave functions of the cc-$\bar{c}\bar{c}$ bound states are depicted. One can find that the wave shapes of state with different quantum numbers are almost the same. It is noted the wave functions in Fig. 2 are not normalized. Proper normalization is needed when one want to use them to calculate the decay rates.

In Table 3 we list some theoretical predictions [8,9,10, 25, 28] on cc-$\bar{c}\bar{c}$ states. One can notice that the numerical results covers a board range i.e., there is no conclusive answers about the spectra of $0^+$, $1^+$ and $2^+$. Certainly the changes of some input parameters can alter the numerical results markedly. For example if $m_{cc}=3.52$ GeV is used in our calculation all numerical results will increase about 550 MeV. We also find that the spectra of $1^+$ and $2^+$ are degenerate but there is a gap with $0^+$ in Ref. [8], which is consistent with ours. Nevertheless the mass splitting between $0^+$ and $1^+$ ( $2^+$) in our calculation is larger than those in Ref. [8].

The spectra of the bb-$\bar{b}\bar{b}$ bound states was also explored in Ref. [25]. We also present our predictions in Table 4. The wave functions are similar to those in Fig. 2 so we ignore them here. Future measurement of bb-$\bar{b}\bar{b}$ state will be crucial for us to determine the exact effective interaction between diquark and antidiquark.

4 Summary and discussion

In this paper we mainly explore the possible cc-$\bar{c}\bar{c}$ bound states within Bethe–Salpeter framework and we compare our theoretical result to the measurement of X(6900) when the parameters are properly chosen. Since the one-gluon exchange potential is attractive for color anti-triplet (triplet) state we only consider the ground axial-vector diquark (antidiquark) of color anti-triplet (triplet). The $J^P$ of the diquark–antidiquark state is $0^+$, $1^+$ or $2^+$. In order to deduce the B–S equation of diquark–antidiquark we need to know the interaction (kernel) between them. Since the coupling between diquark and gluon is not presented in fundamental QCD Lagrangian, in general it is different from that between quark and gluon, so the interaction (kernel) between quark and antiquark cannot be directly applied to diquark–antidiquark system. Instead, we employ the effective interaction to derive the tree level one-gluon exchange vortex for the diquark–antidiquark system. Then we modify the effective interaction kernel for meson to study the possible diquark–antidiquark bound state. Adopting the kernel, we deduce the B–S equations for $0^+$, $1^+$ and $2^+$ diquark–antidiquark system. Using the parameters based on previous studies of meson and baryon, we solve these equations in 3-dimensional momentum space. In our calculation, the parameter $\kappa$ we introduced in kernel is undetermined so we take different values in the calculation.

The spectra of $1^+$ and $2^+$ are degenerate for different parameters in our results. The mass of the second radial excited state $0^+$ is close to mass of X(6900) when the parameter $\kappa$ takes the value $E\times E$. In fact LHCb also observed a board structure whose mass is $6490\pm 15$ GeV, whcih is close to the first radial excited state $0^+$.

Theoretical results on cc-$\bar{c}\bar{c}$ bound states [9, 10, 25] indicate X(6900) maybe is the radial excited of $0^+$, $1^+$ or $2^+$ cc-$\bar{c}\bar{c}$ state. However, LHCb only reported two structures in the mass region of $J/\psi$ pair between 6.2 to 7.4 GeV, which are less than the theoretical prediction for the number of possible states in cc-$\bar{c}\bar{c}$ system. In principle, If X(6900) really is a cc-$\bar{c}\bar{c}$ bound state, other cc-$\bar{c}\bar{c}$ states predicted in theory should be seen in the experiment except that most states are degenerate. Due to the lack of experimental evidence of a definite diquark and antidiquark bound state, we are not able to completely fix free parameters in our model, which causes some uncertainties in the theoretical predictions. To overcome this issue, we will suggest our experimental colleagues to measure the structures in the mass region of $J/\psi$ pair between 6.2 to 7.4 GeV in depth. Using present parameters we also calculate the spectra of the bb-$\bar{b}\bar{b}$ bound states. In the future, more accurate data will help us to elucidate the exact form of effective interaction between diquark and antidiquark, and deepen our understanding of exotic bound state systems.

Appendix A: Some detailed expressions

$$\begin{aligned} C_{\mathcal {S}1}= & {} \frac{7 {k_v}^2 {E}^6}{16 {m_1}^2 {m_2}^2}+\frac{3 {k_v} {E}^6}{16 {m_1}^2 {m_2}^2}+\frac{3 {E}^6}{64 {m_1}^2 {m_2}^2}-\frac{21 {k_v}^2 {p_0}^2 {E}^4}{4 {m_1}^2 {m_2}^2}\nonumber \\&-\frac{9 {k_v} {p_0}^2 {E}^4}{4 {m_1}^2 {m_2}^2}-\frac{9 {p_0}^2 {E}^4}{16 {m_1}^2 {m_2}^2}\nonumber \\&-\frac{11 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}} {E}^4}{8 {m_1}^2 {m_2}^2}-\frac{15 {k_v} {\mathbf {p}\cdot \mathbf {q}} {E}^4}{8 {m_1}^2 {m_2}^2}-\frac{{\mathbf {p}\cdot \mathbf {q}} {E}^4}{4 {m_1}^2 {m_2}^2}\nonumber \\&+\frac{9 {k_v}^2 {\mathbf {p}^2} {E}^4}{16 {m_1}^2 {m_2}^2}+\frac{{k_v} {\mathbf {p}^2} {E}^4}{8 {m_1}^2 {m_2}^2}+\frac{{\mathbf {p}^2} {E}^4}{4 {m_1}^2 {m_2}^2}\nonumber \\&+\frac{{k_v}^2 {\mathbf {q}^2} {E}^4}{16 {m_1}^2 {m_2}^2}+\frac{{\mathbf {q}^2} {E}^4}{16 {m_1}^2 {m_2}^2}-\frac{7 {k_v}^2 {E}^4}{4 {m_1}^2}\nonumber \\&-\frac{3 {k_v} {E}^4}{4 {m_1}^2}-\frac{3 {E}^4}{16 {m_1}^2}-\frac{7 {k_v}^2 {E}^4}{4 {m_2}^2}-\frac{3 {k_v} {E}^4}{4 {m_2}^2}\nonumber \\&-\frac{3 {E}^4}{16 {m_2}^2}-\frac{7 {k_v}^2 {p_0} {E}^3}{{m_1}^2}-\frac{3 {k_v} {p_0} {E}^3}{{m_1}^2}\nonumber \\&-\frac{3 {p_0} {E}^3}{4 {m_1}^2}+\frac{7 {k_v}^2 {p_0} {E}^3}{{m_2}^2}+\frac{3 {k_v} {p_0} {E}^3}{{m_2}^2}+\frac{3 {p_0} {E}^3}{4 {m_2}^2}\nonumber \\&+\frac{21 {k_v}^2 {p_0}^4 {E}^2}{{m_1}^2 {m_2}^2}+\frac{9 {k_v} {p_0}^4 {E}^2}{{m_1}^2 {m_2}^2}+\frac{9 {p_0}^4 {E}^2}{4 {m_1}^2 {m_2}^2}+10 {k_v}^2 {E}^2\nonumber \\&+\frac{3 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}}^2 {E}^2}{2 {m_1}^2 {m_2}^2}+\frac{3 {k_v} {\mathbf {p}\cdot \mathbf {q}}^2 {E}^2}{2 {m_1}^2 {m_2}^2}\nonumber \\&+\frac{{\mathbf {p}\cdot \mathbf {q}}^2 {E}^2}{2 {m_1}^2 {m_2}^2}-\frac{3 {k_v}^2 \mathbf {p}^4 {E}^2}{{m_1}^2 {m_2}^2}-\frac{5 {k_v} \mathbf {p}^4 {E}^2}{2 {m_1}^2 {m_2}^2}\nonumber \\&+\frac{\mathbf {p}^4 {E}^2}{4 {m_1}^2 {m_2}^2}+6 {k_v} {E}^2-\frac{{k_v}^2 {p_0}^2 {\mathbf {p}\cdot \mathbf {q}} {E}^2}{{m_1}^2 {m_2}^2}\nonumber \\&+\frac{3 {k_v} {p_0}^2 {\mathbf {p}\cdot \mathbf {q}} {E}^2}{{m_1}^2 {m_2}^2}-\frac{{k_v}^2 {\mathbf {p}\cdot \mathbf {q}} {E}^2}{2 {m_1}^2}-\frac{{k_v} {\mathbf {p}\cdot \mathbf {q}} {E}^2}{2 {m_1}^2}\nonumber \\&-\frac{{\mathbf {p}\cdot \mathbf {q}} {E}^2}{2 {m_1}^2}-\frac{{k_v}^2 {\mathbf {p}\cdot \mathbf {q}} {E}^2}{2 {m_2}^2}-\frac{{k_v} {\mathbf {p}\cdot \mathbf {q}} {E}^2}{2 {m_2}^2}\nonumber \\&-\frac{{\mathbf {p}\cdot \mathbf {q}} {E}^2}{2 {m_2}^2}-\frac{33 {k_v}^2 {p_0}^2 {\mathbf {p}^2} {E}^2}{2 {m_1}^2 {m_2}^2}-\frac{5 {k_v} {p_0}^2 {\mathbf {p}^2} {E}^2}{{m_1}^2 {m_2}^2}\nonumber \\&-\frac{2 {p_0}^2 {\mathbf {p}^2} {E}^2}{{m_1}^2 {m_2}^2}-\frac{2 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2} {E}^2}{{m_1}^2 {m_2}^2}\nonumber \\&-\frac{6 {k_v} {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2} {E}^2}{{m_1}^2 {m_2}^2}-\frac{{\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2} {E}^2}{{m_1}^2 {m_2}^2}+\frac{3 {k_v}^2 {\mathbf {p}^2} {E}^2}{4 {m_1}^2}\nonumber \\&+\frac{{k_v} {\mathbf {p}^2} {E}^2}{2 {m_1}^2}+\frac{3 {\mathbf {p}^2} {E}^2}{4 {m_1}^2}+\frac{3 {k_v}^2 {\mathbf {p}^2} {E}^2}{4 {m_2}^2}+\frac{{k_v} {\mathbf {p}^2} {E}^2}{2 {m_2}^2} \end{aligned}$$

$$\begin{aligned}&+\frac{3 {\mathbf {p}^2} {E}^2}{4 {m_2}^2}-\frac{{k_v}^2 {p_0}^2 {\mathbf {q}^2} {E}^2}{2 {m_1}^2 {m_2}^2}-\frac{{p_0}^2 {\mathbf {q}^2} {E}^2}{2 {m_1}^2 {m_2}^2}\nonumber \\&+\frac{{k_v}^2 {\mathbf {p}^2} {\mathbf {q}^2} {E}^2}{2 {m_1}^2 {m_2}^2}+\frac{{\mathbf {p}^2} {\mathbf {q}^2} {E}^2}{2 {m_1}^2 {m_2}^2}-\frac{{k_v}^2 {\mathbf {q}^2} {E}^2}{4 {m_1}^2}\nonumber \\&-\frac{{\mathbf {q}^2} {E}^2}{4 {m_1}^2}-\frac{{k_v}^2 {\mathbf {q}^2} {E}^2}{4 {m_2}^2}-\frac{{\mathbf {q}^2} {E}^2}{4 {m_2}^2}+\frac{9 {E}^2}{2}\nonumber \\&+\frac{28 {k_v}^2 {p_0}^3 {E}}{{m_1}^2}+\frac{12 {k_v} {p_0}^3 {E}}{{m_1}^2}+\frac{3 {p_0}^3 {E}}{{m_1}^2}-\frac{28 {k_v}^2 {p_0}^3 {E}}{{m_2}^2}\nonumber \\&-\frac{12 {k_v} {p_0}^3 {E}}{{m_2}^2}-\frac{3 {p_0}^3 {E}}{{m_2}^2}-\frac{14 {k_v}^2 {p_0} {\mathbf {p}\cdot \mathbf {q}} {E}}{{m_1}^2}\nonumber \\&-\frac{10 {k_v} {p_0} {\mathbf {p}\cdot \mathbf {q}} {E}}{{m_1}^2}-\frac{3 {p_0} {\mathbf {p}\cdot \mathbf {q}} {E}}{{m_1}^2}+\frac{14 {k_v}^2 {p_0} {\mathbf {p}\cdot \mathbf {q}} {E}}{{m_2}^2}\nonumber \\&+\frac{10 {k_v} {p_0} {\mathbf {p}\cdot \mathbf {q}} {E}}{{m_2}^2}+\frac{3 {p_0} {\mathbf {p}\cdot \mathbf {q}} {E}}{{m_2}^2}-\frac{13 {k_v}^2 {p_0} {\mathbf {p}^2} {E}}{{m_1}^2}\nonumber \\&-\frac{2 {k_v} {p_0} {\mathbf {p}^2} {E}}{{m_1}^2}+\frac{{p_0} {\mathbf {p}^2} {E}}{{m_1}^2}+\frac{13 {k_v}^2 {p_0} {\mathbf {p}^2} {E}}{{m_2}^2}\nonumber \\&+\frac{2 {k_v} {p_0} {\mathbf {p}^2} {E}}{{m_2}^2}-\frac{{p_0} {\mathbf {p}^2} {E}}{{m_2}^2}-\frac{{k_v}^2 {p_0} {\mathbf {q}^2} {E}}{{m_1}^2}-\frac{{p_0} {\mathbf {q}^2} {E}}{{m_1}^2}\nonumber \\&+\frac{{k_v}^2 {p_0} {\mathbf {q}^2} {E}}{{m_2}^2}+\frac{{p_0} {\mathbf {q}^2} {E}}{{m_2}^2}-\frac{28 {k_v}^2 {p_0}^6}{{m_1}^2 {m_2}^2}\nonumber \\&-\frac{12 {k_v} {p_0}^6}{{m_1}^2 {m_2}^2}-\frac{3 {p_0}^6}{{m_1}^2 {m_2}^2}+\frac{28 {k_v}^2 {p_0}^4}{{m_1}^2}\nonumber \\&+\frac{12 {k_v} {p_0}^4}{{m_1}^2}+\frac{3 {p_0}^4}{{m_1}^2}+\frac{28 {k_v}^2 {p_0}^4}{{m_2}^2}+\frac{12 {k_v} {p_0}^4}{{m_2}^2}+\frac{3 {p_0}^4}{{m_2}^2}\nonumber \\&+\frac{7 {k_v}^2 \mathbf {p}^6}{{m_1}^2 {m_2}^2}-40 {k_v}^2 {p_0}^2-24 {k_v} {p_0}^2-18 {p_0}^2-\frac{6 {k_v}^2 {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}^2}{{m_1}^2 {m_2}^2}\nonumber \\&-\frac{6 {k_v} {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}^2}{{m_1}^2 {m_2}^2}-\frac{2 {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}^2}{{m_1}^2 {m_2}^2}\nonumber \\&+\frac{6 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}}^2}{{m_1}^2}+\frac{6 {k_v} {\mathbf {p}\cdot \mathbf {q}}^2}{{m_1}^2}+\frac{2 {\mathbf {p}\cdot \mathbf {q}}^2}{{m_1}^2}\nonumber \\&+\frac{6 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}}^2}{{m_2}^2}+\frac{6 {k_v} {\mathbf {p}\cdot \mathbf {q}}^2}{{m_2}^2}+\frac{2 {\mathbf {p}\cdot \mathbf {q}}^2}{{m_2}^2}-\frac{36 {k_v}^2 {p_0}^2 \mathbf {p}^4}{{m_1}^2 {m_2}^2}\nonumber \\&-\frac{6 {k_v} {p_0}^2 \mathbf {p}^4}{{m_1}^2 {m_2}^2}-\frac{{p_0}^2 \mathbf {p}^4}{{m_1}^2 {m_2}^2}+\frac{14 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}} \mathbf {p}^4}{{m_1}^2 {m_2}^2}\nonumber \\&+\frac{6 {k_v} {\mathbf {p}\cdot \mathbf {q}} \mathbf {p}^4}{{m_1}^2 {m_2}^2}+\frac{7 {k_v}^2 \mathbf {p}^4}{{m_1}^2}+\frac{7 {k_v}^2 \mathbf {p}^4}{{m_2}^2}+\frac{26 {k_v}^2 {p_0}^4 {\mathbf {p}\cdot \mathbf {q}}}{{m_1}^2 {m_2}^2}\nonumber \\&+\frac{18 {k_v} {p_0}^4 {\mathbf {p}\cdot \mathbf {q}}}{{m_1}^2 {m_2}^2}+\frac{4 {p_0}^4 {\mathbf {p}\cdot \mathbf {q}}}{{m_1}^2 {m_2}^2}+20 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}}-\frac{26 {k_v}^2 {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}}{{m_1}^2}\nonumber \\&-\frac{18 {k_v} {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}}{{m_1}^2}-\frac{4 {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}}{{m_1}^2}\nonumber \\&-\frac{26 {k_v}^2 {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}}{{m_2}^2}-\frac{18 {k_v} {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}}{{m_2}^2}\nonumber \\&-\frac{4 {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}}{{m_2}^2}+12 {k_v} {\mathbf {p}\cdot \mathbf {q}}+6 {\mathbf {p}\cdot \mathbf {q}}+\frac{57 {k_v}^2 {p_0}^4 {\mathbf {p}^2}}{{m_1}^2 {m_2}^2}\nonumber \\&+\frac{18 {k_v} {p_0}^4 {\mathbf {p}^2}}{{m_1}^2 {m_2}^2}+\frac{4 {p_0}^4 {\mathbf {p}^2}}{{m_1}^2 {m_2}^2}+10 {k_v}^2 {\mathbf {p}^2}-\frac{29 {k_v}^2 {p_0}^2 {\mathbf {p}^2}}{{m_1}^2}\nonumber \\&-\frac{6 {k_v} {p_0}^2 {\mathbf {p}^2}}{{m_1}^2}-\frac{{p_0}^2 {\mathbf {p}^2}}{{m_1}^2}-\frac{29 {k_v}^2 {p_0}^2 {\mathbf {p}^2}}{{m_2}^2}\nonumber \\&-\frac{6 {k_v} {p_0}^2 {\mathbf {p}^2}}{{m_2}^2}-\frac{{p_0}^2 {\mathbf {p}^2}}{{m_2}^2}+\frac{6 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}}^2 {\mathbf {p}^2}}{{m_1}^2 {m_2}^2} \end{aligned}$$

$$\begin{aligned}&+\frac{6 {k_v} {\mathbf {p}\cdot \mathbf {q}}^2 {\mathbf {p}^2}}{{m_1}^2 {m_2}^2}+\frac{2 {\mathbf {p}\cdot \mathbf {q}}^2 {\mathbf {p}^2}}{{m_1}^2 {m_2}^2}+6 {k_v} {\mathbf {p}^2}-\frac{40 {k_v}^2 {p_0}^2 {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{{m_1}^2 {m_2}^2}\nonumber \\&-\frac{24 {k_v} {p_0}^2 {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{{m_1}^2 {m_2}^2}-\frac{4 {p_0}^2 {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{{m_1}^2 {m_2}^2}\nonumber \\&+\frac{14 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{{m_1}^2}+\frac{6 {k_v} {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{{m_1}^2}+\frac{14 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{{m_2}^2}\nonumber \\&+\frac{6 {k_v} {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{{m_2}^2}+6 {\mathbf {p}^2}+\frac{{k_v}^2 {p_0}^4 {\mathbf {q}^2}}{{m_1}^2 {m_2}^2}+\frac{{p_0}^4 {\mathbf {q}^2}}{{m_1}^2 {m_2}^2}+10 {k_v}^2 {\mathbf {q}^2}\nonumber \\&-\frac{{k_v}^2 {p_0}^2 {\mathbf {q}^2}}{{m_1}^2}-\frac{{p_0}^2 {\mathbf {q}^2}}{{m_1}^2}-\frac{{k_v}^2 {p_0}^2 {\mathbf {q}^2}}{{m_2}^2}\nonumber \\&-\frac{{p_0}^2 {\mathbf {q}^2}}{{m_2}^2}+\frac{{k_v}^2 \mathbf {p}^4 {\mathbf {q}^2}}{{m_1}^2 {m_2}^2}+\frac{\mathbf {p}^4 {\mathbf {q}^2}}{{m_1}^2 {m_2}^2}+6 {k_v} {\mathbf {q}^2}\nonumber \\&-\frac{2 {k_v}^2 {p_0}^2 {\mathbf {p}^2} {\mathbf {q}^2}}{{m_1}^2 {m_2}^2}-\frac{2 {p_0}^2 {\mathbf {p}^2} {\mathbf {q}^2}}{{m_1}^2 {m_2}^2}\nonumber \\&+\frac{{k_v}^2 {\mathbf {p}^2} {\mathbf {q}^2}}{{m_1}^2}+\frac{{\mathbf {p}^2} {\mathbf {q}^2}}{{m_1}^2}+\frac{{k_v}^2 {\mathbf {p}^2} {\mathbf {q}^2}}{{m_2}^2}\nonumber \\&+\frac{{\mathbf {p}^2} {\mathbf {q}^2}}{{m_2}^2}+6 {\mathbf {q}^2} \end{aligned}$$

(A1)

$$\begin{aligned} C_{\mathcal {S}2}= & {} \frac{{E}^4}{16 {m_1}^2 {m_2}^2}-\frac{{E}^2 {p_0}^2}{2 {m_1}^2 {m_2}^2}+\frac{{E}^2 {\mathbf {p}^2}}{2 {m_1}^2 {m_2}^2}-\frac{{E}^2}{4 {m_1}^2}\nonumber \\&-\frac{{E}^2}{4 {m_2}^2}-\frac{{E} {p_0}}{{m_1}^2}+\frac{{E} {p_0}}{{m_2}^2}+\frac{{p_0}^4}{{m_1}^2 {m_2}^2}\nonumber \\&-\frac{2 {p_0}^2 {\mathbf {p}^2}}{{m_1}^2 {m_2}^2}+\frac{{\mathbf {p}^4}}{{m_1}^2 {m_2}^2}-\frac{{p_0}^2}{{m_1}^2}+\frac{{\mathbf {p}^2}}{{m_1}^2}\nonumber \\&-\frac{{p_0}^2}{{m_2}^2}+\frac{{\mathbf {p}^2}}{{m_2}^2}+4 \end{aligned}$$

(A2)

$$\begin{aligned} C_{\mathcal {V}1}= & {} \frac{{E}^4 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}}}{{m_1}^2}+\frac{{E}^4 {k_v}^2 {\mathbf {p}^2}}{{m_1}^2}+\frac{{E}^4 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}}}{{m_2}^2}+\frac{{E}^4 {k_v}^2 {\mathbf {p}^2}}{{m_2}^2}\nonumber \\&+\frac{3 {E}^4 {k_v} {\mathbf {p}\cdot \mathbf {q}}}{2 {m_1}^2}+\frac{{E}^4 {k_v} {\mathbf {p}^2}}{2 {m_1}^2}+\frac{3 {E}^4 {k_v} {\mathbf {p}\cdot \mathbf {q}}}{2 {m_2}^2}\nonumber \\&+\frac{{E}^4 {k_v} {\mathbf {p}^2}}{2 {m_2}^2}+\frac{5 {E}^4 {\mathbf {p}^2}}{2 {m_1}^2}+\frac{5 {E}^4 {\mathbf {p}^2}}{2 {m_2}^2}+6 {E}^4\nonumber \\&+\frac{4 {E}^3 {k_v}^2 {p_0} {\mathbf {p}\cdot \mathbf {q}}}{{m_1}^2}+\frac{4 {E}^3 {k_v}^2 {p_0} {\mathbf {p}^2}}{{m_1}^2}-\frac{4 {E}^3 {k_v}^2 {p_0} {\mathbf {p}\cdot \mathbf {q}}}{{m_2}^2}\nonumber \\&-\frac{4 {E}^3 {k_v}^2 {p_0} {\mathbf {p}^2}}{{m_2}^2}+\frac{10 {E}^3 {k_v} {p_0} {\mathbf {p}\cdot \mathbf {q}}}{{m_1}^2}+\frac{6 {E}^3 {k_v} {p_0} {\mathbf {p}^2}}{{m_1}^2}\nonumber \\&-\frac{10 {E}^3 {k_v} {p_0} {\mathbf {p}\cdot \mathbf {q}}}{{m_2}^2}-\frac{6 {E}^3 {k_v} {p_0} {\mathbf {p}^2}}{{m_2}^2}\nonumber \\&+\frac{4 {E}^3 {p_0} {\mathbf {p}\cdot \mathbf {q}}}{{m_1}^2}+\frac{2 {E}^3 {p_0} {\mathbf {p}^2}}{{m_1}^2}-\frac{4 {E}^3 {p_0} {\mathbf {p}\cdot \mathbf {q}}}{{m_2}^2}\nonumber \\&-\frac{2 {E}^3 {p_0} {\mathbf {p}^2}}{{m_2}^2}+\frac{4 {E}^2 {k_v}^2 {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}}{{m_1}^2}+\frac{4 {E}^2 {k_v}^2 {p_0}^2 {\mathbf {p}^2}}{{m_1}^2}\nonumber \\&-\frac{{E}^2 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}}^2}{{m_1}^2}-\frac{4 {E}^2 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{{m_1}^2}-\frac{2 {E}^2 {k_v}^2 \mathbf {p}^4}{{m_1}^2}\nonumber \\&-\frac{{E}^2 {k_v}^2 {\mathbf {p}^2} {\mathbf {q}^2}}{{m_1}^2}+\frac{4 {E}^2 {k_v}^2 {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}}{{m_2}^2}\nonumber \\&+\frac{4 {E}^2 {k_v}^2 {p_0}^2 {\mathbf {p}^2}}{{m_2}^2}-\frac{{E}^2 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}}^2}{{m_2}^2}-\frac{4 {E}^2 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{{m_2}^2}\nonumber \\&-\frac{2 {E}^2 {k_v}^2 \mathbf {p}^4}{{m_2}^2}-\frac{{E}^2 {k_v}^2 {\mathbf {p}^2} {\mathbf {q}^2}}{{m_2}^2}\nonumber \\&-8 {E}^2 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}}-4 {E}^2 {k_v}^2 {\mathbf {p}^2}-4 {E}^2 {k_v}^2 {\mathbf {q}^2}\nonumber \\&+\frac{14 {E}^2 {k_v} {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}}{{m_1}^2}+\frac{10 {E}^2 {k_v} {p_0}^2 {\mathbf {p}^2}}{{m_1}^2}\nonumber \\&-\frac{3 {E}^2 {k_v} {\mathbf {p}\cdot \mathbf {q}}^2}{{m_1}^2}-\frac{12 {E}^2 {k_v} {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{{m_1}^2}-\frac{6 {E}^2 {k_v} \mathbf {p}^4}{{m_1}^2}\nonumber \\&-\frac{3 {E}^2 {k_v} {\mathbf {p}^2} {\mathbf {q}^2}}{{m_1}^2}+\frac{14 {E}^2 {k_v} {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}}{{m_2}^2}\nonumber \\&+\frac{10 {E}^2 {k_v} {p_0}^2 {\mathbf {p}^2}}{{m_2}^2}-\frac{3 {E}^2 {k_v} {\mathbf {p}\cdot \mathbf {q}}^2}{{m_2}^2}-\frac{12 {E}^2 {k_v} {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{{m_2}^2}\nonumber \\&-\frac{6 {E}^2 {k_v} \mathbf {p}^4}{{m_2}^2}-\frac{3 {E}^2 {k_v} {\mathbf {p}^2} {\mathbf {q}^2}}{{m_2}^2}\nonumber \\&-24 {E}^2 {k_v} {\mathbf {p}\cdot \mathbf {q}}-12 {E}^2 {k_v} {\mathbf {p}^2}-12 {E}^2 {k_v} {\mathbf {q}^2}\nonumber \\&+\frac{8 {E}^2 {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}}{{m_1}^2}-\frac{6 {E}^2 {p_0}^2 {\mathbf {p}^2}}{{m_1}^2}-\frac{{E}^2 {\mathbf {p}\cdot \mathbf {q}}^2}{{m_1}^2}\nonumber \\&-\frac{2 {E}^2 {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{{m_1}^2}+\frac{{E}^2 {\mathbf {p}^2} {\mathbf {q}^2}}{{m_1}^2}+\frac{8 {E}^2 {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}}{{m_2}^2}\nonumber \\&-\frac{6 {E}^2 {p_0}^2 {\mathbf {p}^2}}{{m_2}^2}-\frac{{E}^2 {\mathbf {p}\cdot \mathbf {q}}^2}{{m_2}^2}-\frac{2 {E}^2 {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{{m_2}^2}\nonumber \\&+\frac{{E}^2 {\mathbf {p}^2} {\mathbf {q}^2}}{{m_2}^2}-24 {E}^2 {p_0}^2+2 {E}^2 {\mathbf {p}^2}+2 {E}^2 {\mathbf {q}^2} \end{aligned}$$

(A3)

$$\begin{aligned} C_{\mathcal {V}2}= & {} \frac{2 {E}^2 {\mathbf {p}^2}}{{m_1}^2}+\frac{2 {E}^2 {\mathbf {p}^2}}{{m_2}^2}+6 {E}^2 \end{aligned}$$

(A4)

$$\begin{aligned} C_{\mathcal {T}1}= & {} \frac{2 {k_v}^2 \mathbf {p}^6}{{m_1}^2 {m_2}^2}-\frac{4 {k_v} \mathbf {p}^6}{3 {m_1}^2 {m_2}^2}-\frac{2 \mathbf {p}^6}{3 {m_1}^2 {m_2}^2}-\frac{10 {k_v}^2 {p_0}^2 \mathbf {p}^4}{3 {m_1}^2 {m_2}^2}\nonumber \\&+\frac{4 {k_v} {p_0}^2 \mathbf {p}^4}{{m_1}^2 {m_2}^2}-\frac{4 {p_0}^2 \mathbf {p}^4}{3 {m_1}^2 {m_2}^2}+\frac{4 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}} \mathbf {p}^4}{{m_1}^2 {m_2}^2}\nonumber \\&-\frac{4 {k_v} {\mathbf {p}\cdot \mathbf {q}} \mathbf {p}^4}{3 {m_1}^2 {m_2}^2}-\frac{{k_v}^2 {\mathbf {q}^2} \mathbf {p}^4}{3 {m_1}^2 {m_2}^2}\nonumber \\&-\frac{2 {k_v} {\mathbf {q}^2} \mathbf {p}^4}{3 {m_1}^2 {m_2}^2}+\frac{{\mathbf {q}^2} \mathbf {p}^4}{3 {m_1}^2 {m_2}^2}+\frac{3 {k_v}^2 \mathbf {p}^4}{{m_1}^2}\nonumber \\&-\frac{7 {k_v} \mathbf {p}^4}{3 {m_1}^2}-\frac{2 \mathbf {p}^4}{3 {m_1}^2}+\frac{3 {k_v}^2 \mathbf {p}^4}{{m_2}^2}\nonumber \\&-\frac{7 {k_v} \mathbf {p}^4}{3 {m_2}^2}+\frac{{E}^2 \mathbf {p}^4}{{m_1}^2 {m_2}^2}-\frac{{E}^2 {k_v}^2 \mathbf {p}^4}{2 {m_1}^2 {m_2}^2}\nonumber \\&-\frac{{E}^2 {k_v} \mathbf {p}^4}{3 {m_1}^2 {m_2}^2}-\frac{2 \mathbf {p}^4}{3 {m_2}^2}+\frac{10 {k_v}^2 {\mathbf {p}^2}}{3}\nonumber \\&-\frac{10 {k_v}^2 {p_0}^2 {\mathbf {p}^2}}{3 {m_1}^2}+\frac{5 {k_v} {p_0}^2 {\mathbf {p}^2}}{{m_1}^2}\nonumber \\&-\frac{5 {p_0}^2 {\mathbf {p}^2}}{{m_1}^2}-\frac{10 {k_v}^2 {p_0}^2 {\mathbf {p}^2}}{3 {m_2}^2}+\frac{5 {k_v} {p_0}^2 {\mathbf {p}^2}}{{m_2}^2}-\frac{5 {p_0}^2 {\mathbf {p}^2}}{{m_2}^2}\nonumber \\&+\frac{7 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}}^2 {\mathbf {p}^2}}{3 {m_1}^2 {m_2}^2}+\frac{2 {k_v} {\mathbf {p}\cdot \mathbf {q}}^2 {\mathbf {p}^2}}{3 {m_1}^2 {m_2}^2}\nonumber \\&-\frac{{\mathbf {p}\cdot \mathbf {q}}^2 {\mathbf {p}^2}}{3 {m_1}^2 {m_2}^2}\nonumber \\&-\frac{10 {k_v} {\mathbf {p}^2}}{3}-\frac{10 {E} {k_v}^2 {p_0} {\mathbf {p}^2}}{3 {m_1}^2}+\frac{5 {E} {p_0} {\mathbf {p}^2}}{3 {m_1}^2}\nonumber \\&+\frac{5 {E} {k_v} {p_0} {\mathbf {p}^2}}{3 {m_1}^2}+\frac{10 {E} {k_v}^2 {p_0} {\mathbf {p}^2}}{3 {m_2}^2}\nonumber \\&-\frac{5 {E} {p_0} {\mathbf {p}^2}}{3 {m_2}^2}-\frac{5 {E} {k_v} {p_0} {\mathbf {p}^2}}{3 {m_2}^2}\nonumber \\&-\frac{4 {k_v}^2 {p_0}^2 {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{{m_1}^2 {m_2}^2}+\frac{8 {p_0}^2 {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{3 {m_1}^2 {m_2}^2}+\frac{6 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{{m_1}^2}\nonumber \\&-\frac{10 {k_v} {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{3 {m_1}^2}+\frac{{\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{{m_1}^2}+\frac{6 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{{m_2}^2}\nonumber \\&-\frac{10 {k_v} {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{3 {m_2}^2}-\frac{2 {E}^2 {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{3 {m_1}^2 {m_2}^2}-\frac{{E}^2 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{3 {m_1}^2 {m_2}^2}\nonumber \\&-\frac{2 {E}^2 {k_v} {\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{3 {m_1}^2 {m_2}^2}+\frac{{\mathbf {p}\cdot \mathbf {q}} {\mathbf {p}^2}}{{m_2}^2}+\frac{{k_v}^2 {p_0}^2 {\mathbf {q}^2} {\mathbf {p}^2}}{3 {m_1}^2 {m_2}^2}\nonumber \\&+\frac{2 {k_v} {p_0}^2 {\mathbf {q}^2} {\mathbf {p}^2}}{3 {m_1}^2 {m_2}^2}+\frac{{p_0}^2 {\mathbf {q}^2} {\mathbf {p}^2}}{3 {m_1}^2 {m_2}^2}+\frac{{k_v}^2 {\mathbf {q}^2} {\mathbf {p}^2}}{6 {m_1}^2}\nonumber \\&-\frac{7 {k_v} {\mathbf {q}^2} {\mathbf {p}^2}}{6 {m_1}^2}+\frac{5 {\mathbf {q}^2} {\mathbf {p}^2}}{6 {m_1}^2}+\frac{{k_v}^2 {\mathbf {q}^2} {\mathbf {p}^2}}{6 {m_2}^2}-\frac{7 {k_v} {\mathbf {q}^2} {\mathbf {p}^2}}{6 {m_2}^2}\nonumber \\&-\frac{{E}^2 {\mathbf {q}^2} {\mathbf {p}^2}}{12 {m_1}^2 {m_2}^2}-\frac{{E}^2 {k_v}^2 {\mathbf {q}^2} {\mathbf {p}^2}}{12 {m_1}^2 {m_2}^2}-\frac{{E}^2 {k_v} {\mathbf {q}^2} {\mathbf {p}^2}}{6 {m_1}^2 {m_2}^2} \end{aligned}$$

$$\begin{aligned}&+\frac{5 {\mathbf {q}^2} {\mathbf {p}^2}}{6 {m_2}^2}+\frac{25 {E}^2 {\mathbf {p}^2}}{12 {m_1}^2}-\frac{5 {E}^2 {k_v}^2 {\mathbf {p}^2}}{6 {m_1}^2}-\frac{5 {E}^2 {k_v} {\mathbf {p}^2}}{12 {m_1}^2}\nonumber \\&+\frac{25 {E}^2 {\mathbf {p}^2}}{12 {m_2}^2}-\frac{5 {E}^2 {k_v}^2 {\mathbf {p}^2}}{6 {m_2}^2}-\frac{5 {E}^2 {k_v} {\mathbf {p}^2}}{12 {m_2}^2}\nonumber \\&+\frac{5 {\mathbf {p}^2}}{3}+5 {E}^2-20 {p_0}^2-\frac{{k_v}^2 {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}^2}{{m_1}^2 {m_2}^2}-\frac{2 {k_v} {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}^2}{{m_1}^2 {m_2}^2}\nonumber \\&-\frac{{p_0}^2 {\mathbf {p}\cdot \mathbf {q}}^2}{{m_1}^2 {m_2}^2}+\frac{17 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}}^2}{6 {m_1}^2}+\frac{{k_v} {\mathbf {p}\cdot \mathbf {q}}^2}{6 {m_1}^2}\nonumber \\&-\frac{5 {\mathbf {p}\cdot \mathbf {q}}^2}{6 {m_1}^2}+\frac{17 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}}^2}{6 {m_2}^2}+\frac{{k_v} {\mathbf {p}\cdot \mathbf {q}}^2}{6 {m_2}^2}+\frac{{E}^2 {\mathbf {p}\cdot \mathbf {q}}^2}{4 {m_1}^2 {m_2}^2}\nonumber \\&+\frac{{E}^2 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}}^2}{4 {m_1}^2 {m_2}^2}+\frac{{E}^2 {k_v} {\mathbf {p}\cdot \mathbf {q}}^2}{2 {m_1}^2 {m_2}^2}-\frac{5 {\mathbf {p}\cdot \mathbf {q}}^2}{6 {m_2}^2}\nonumber \\&+\frac{20 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}}}{3}-\frac{10 {k_v}^2 {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}}{3 {m_1}^2}+\frac{5 {k_v} {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}}{3 {m_1}^2}\nonumber \\&+\frac{10 {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}}{3 {m_1}^2}-\frac{10 {k_v}^2 {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}}{3 {m_2}^2}+\frac{5 {k_v} {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}}{3 {m_2}^2}\nonumber \\&+\frac{10 {p_0}^2 {\mathbf {p}\cdot \mathbf {q}}}{3 {m_2}^2}-\frac{20 {k_v} {\mathbf {p}\cdot \mathbf {q}}}{3}-\frac{10 {E} {k_v}^2 {p_0} {\mathbf {p}\cdot \mathbf {q}}}{3 {m_1}^2}\nonumber \\&-\frac{5 {E} {k_v} {p_0} {\mathbf {p}\cdot \mathbf {q}}}{3 {m_1}^2}+\frac{10 {E} {k_v}^2 {p_0} {\mathbf {p}\cdot \mathbf {q}}}{3 {m_2}^2}+\frac{5 {E} {k_v} {p_0} {\mathbf {p}\cdot \mathbf {q}}}{3 {m_2}^2}\nonumber \\&-\frac{5 {E}^2 {\mathbf {p}\cdot \mathbf {q}}}{6 {m_1}^2}-\frac{5 {E}^2 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}}}{6 {m_1}^2}-\frac{5 {E}^2 {k_v} {\mathbf {p}\cdot \mathbf {q}}}{4 {m_1}^2}\nonumber \\&-\frac{5 {E}^2 {\mathbf {p}\cdot \mathbf {q}}}{6 {m_2}^2}-\frac{5 {E}^2 {k_v}^2 {\mathbf {p}\cdot \mathbf {q}}}{6 {m_2}^2}-\frac{5 {E}^2 {k_v} {\mathbf {p}\cdot \mathbf {q}}}{4 {m_2}^2}\nonumber \\&+\frac{20 {\mathbf {p}\cdot \mathbf {q}}}{3}+\frac{10 {k_v}^2 {\mathbf {q}^2}}{3}-\frac{10 {k_v} {\mathbf {q}^2}}{3}+\frac{5 {\mathbf {q}^2}}{3} \end{aligned}$$

(A5)

$$\begin{aligned} C_{\mathcal {T}2}= & {} \frac{2 {\mathbf {p}^4}}{3 {m_1}^2 {m_2}^2}+\frac{5 {\mathbf {p}^2}}{3 {m_1}^2}+\frac{5 {\mathbf {p}^2}}{3 {m_2}^2}+5 \end{aligned}$$

(A6)