Strong decays of the lowest bottomonium hybrid within an extended Born–Oppenheimer framework

Abstract

We analyze the decays of the theoretically predicted lowest bottomonium hybrid H(1P) to open bottom two-meson states. We do it by embedding a quark pair creation model into the Born–Oppenheimer framework which allows for a unified, QCD-motivated description of bottomonium hybrids as well as bottomonium. A new $^{1}\!P_{1}$ decay model for H(1P) comes out. The same analysis applied to bottomonium leads naturally to the well-known $^{3}\!P_{0}$ decay model. We show that H(1P) and the theoretically predicted bottomonium state $\varUpsilon (5S)$, whose calculated masses are close to each other, have very different widths for such decays. A comparison with data from $\varUpsilon (10860)$, an experimental resonance whose mass is similar to that of $\varUpsilon (5S)$ and H(1P), is carried out. Neither a $\varUpsilon (5S)$ nor a H(1P) assignment can explain the measured decay widths. However, a $\varUpsilon (5S)$–H(1P) mixing may give account of them supporting previous analyses of dipion decays of $\varUpsilon (10860)$ and suggesting a possible experimental evidence of H(1P).

1 Introduction

There is nowadays compelling theoretical evidence, from quenched (without light quarks) lattice QCD calculations, of the existence of quarkonium hybrids ($Q\overline{Q}g$ bound states where Q is a heavy quark, b or c, $\overline{Q}$ its antiquark, and g stands for a gluon) [1]. In contrast, there is not convincing experimental evidence of the existence of hybrids until now mostly due to the difficulty of identifying unambiguous distinctive signatures for them. As for any other predicted unstable system these signatures have to be looked at the decay products. Hence a thorough theoretical analysis of the dominant and/or exclusive decays of hybrids can be instrumental in unveiling their presence from data. In this regard the lowest bottomonium hybrid ($b\overline{b}g$ bound state) that we shall call henceforth H(1P) (the reason for this notation will be explained later on) may be an ideal system, in spite of its possible mixing with bottomonium ($b\overline{b}$ bound state), for trying to disentangle these signatures for several reasons.

First, the mass of the b quark, $M_{b}$, is much larger than the QCD scale, $\varLambda _{QCD}$. This, added to the assumption of no significant string breaking effects, supports the Born–Oppenheimer (B–O) approximation used for the description of H(1P) in QCD. In this approach, its mass corresponds to the lowest energy level of a Schrödinger equation for $b\overline{b}$ in an excited flavor-singlet B–O potential. This (deepest) hybrid potential, defined by the energy of an excited state of the gluon field in the presence of static b and $\overline{b}$ sources, has been calculated in quenched lattice QCD.

Second, the validity of the B–O approximation implies approximate heavy quark spin symmetry (HQSS) [2] which limits its possible hadronic transitions.

Third, being the lowest hybrid state it cannot decay to other hybrids. Moreover, as the deepest hybrid B–O potential is smaller than the sum of the ground-state flavor singlet B–O potential and the mass of a glueball (bound state of gg) with the appropriate quantum numbers, decay to a bottomonium state, which is an energy level of the ground-state flavor singlet B–O potential, plus a glueball is not expected. Hence, its strong decays are constrained to final states not involving hybrids or glueballs.

In this article we follow these reasonings to analyze the dominant decays of H(1P) to open-flavor meson-meson states. As this hybrid and the $\varUpsilon (5S)$ bottomonium state, both with the same quantum numbers $J^{PC}=1^{--}$, are predicted to have about the same mass in the B–O approximation, we study for comparison similar decays from $\varUpsilon (5S)$. In order to be consistent (and to make meaningful the comparison) we describe the decays, through pair creation, within an extended B–O framework. For the bottomonium states this description gives rise to the well-known $^{3}\!P_{0}$ decay model. For H(1P) a $^{1}\!P_{1}$ decay model comes out consistently. It is worth to emphasize that this $^{1}\!P_{1}$ decay model is essentially different from the decay models built from constituent glue or flux tube hybrid models, see [3, 4] and references therein. In brief, in these hybrid models pair creation is spin triplet whilst in the $^{1}\!P_{1}$ is spin singlet. This difference, directly related to the different hybrid descriptions, translates in very distinct selection rules for the forbidden and allowed decays from H(1P) to open bottom two-meson states.

These selection rules, and the ones that can be analogously derived for other hybrids whose disentanglement from data may be even more difficult, could be of great help for the analysis of upcoming data, in particular from JLab (GlueX) and Fair (PANDA), or for directing new experimental searches.

The decay width ratios for $\varUpsilon (5S)$ and H(1P), calculated from the $^{3}\!P_{0}$ and $^{1}\!P_{1}$ decay model respectively, are very different. None of these predicted ratios can explain by its own the measured ones for the only experimental candidate with a similar mass, the $1^{--}$ resonance $\varUpsilon (10860)$ [5]. In contrast, we show that a $\varUpsilon (5S)$–H(1P) mixed state could give reasonable account of data. This provides additional support to the mixing scenario proposed in [6] for $\varUpsilon (10860)$ from the study of its leptonic and dipion decays. This suggest that, altogether, the measured decay widths of $\varUpsilon (10860)$ might provide the first (indirect) experimental evidence of the existence of H(1P).

The contents of this article are organized as follows. In Sect. 2 the B–O framework for the description of bottomonium and bottomonium hybrids is briefly revisited. In Sect. 3 their dominant strong decays to open bottom two-meson states are described within an extended B–O framework. Next, in Sect. 4 we apply this description to the calculation of the widths of the lowest bottomonium hybrid H(1P) and the $\varUpsilon (5S)$ bottomonium state. The results obtained are compared with data from $\varUpsilon (10860)$ in Sect. 5. This comparison suggests that $\varUpsilon (10860)$ could be a mixing of these two components. Finally, in Sect. 6, our main conclusions are summarized.

2 Born–Oppenheimer approximation

The B–O approximation, initially developed for the description of molecules from electromagnetic interactions [7] has been shown to be also well suited for the description of heavy-quark meson bound states from strong interactions [1, 2]. The reason is that it allows for the implementation of the strong interaction theory (QCD) dynamics through quenched (with quarks and gluons but no light quarks) lattice QCD calculations. (For a connection of the B–O approximation with effective field theory, see [8].)

To understand how the B–O approximation works let us briefly recall the main steps in its construction. For this purpose let us consider a meson system containing a heavy quark–antiquark ($Q\overline{Q}$) interacting with light fields (gluons), with Hamiltonian

$$\begin{aligned} H=K_{Q\overline{Q}}+H_{Q\overline{Q}}^{\text {lf}} \end{aligned}$$

(1)

where $K_{Q\overline{Q}}$ is the $Q\overline{Q}$ kinetic energy operator and $H_{Q\overline{Q}}^{\text {lf}}$ includes the light field energy operator and the $Q\overline{Q}$ – light-field interaction. A bound state $|\psi \rangle$ is a solution of the characteristic equation

$$\begin{aligned} H|\psi \rangle =E|\psi \rangle \end{aligned}$$

(2)

where E is the energy of the state. Notice that $|\psi \rangle$ contains information on both the $Q\overline{Q}$ and light fields.

The first step in building the B–O approximation consists in solving the dynamics of the light fields by neglecting the $Q\overline{Q}$ motion, i.e., setting the kinetic energy term $K_{Q\overline{Q}}$ equal to zero (static limit). This corresponds to the limit where Q and $\overline{Q}$ are infinitely massive, what can be justified because the Q and $\overline{Q}$ masses, $m_{Q}$ and $m_{\overline{Q}}$, are much bigger than the QCD scale $\varLambda _{{QCD }}$, which is the energy scale associated with the light fields. In this limit the quark–antiquark relative position $\varvec{r}$ is fixed, ceasing to be a dynamical variable. Then, in the center of mass reference frame $H_{Q\overline{Q}}^{lf }$ depends operationally only on the light fields, and parametrically on $\varvec{r}$. We indicate this renaming it as $H_{static }^{lf }(\varvec{r})$.

The dynamics of the light fields for any fixed value of $\varvec{r}$ can then be solved from

$$\begin{aligned} (H_{\text {static}}^{\text {lf}}(\varvec{r})-V_{\alpha }(\varvec{r}))|\alpha ;(\varvec{r})\rangle =0 \end{aligned}$$

(3)

where $|\alpha ;(\varvec{r})\rangle$ are the light field eigenstates that depend parametrically on $\varvec{r}$ and are characterized by the quantum numbers $\alpha \equiv (\varLambda ,\eta ,\epsilon )$. These quantum numbers have been detailed elsewhere, see for example [2]. Thus, $\varLambda$ stands for the modulus of the eigenvalue of $\widehat{\varvec{r}}\cdot \varvec{J}_{lf }$, being $\varvec{J}_{\text {lf}}$ the total angular momentum of the light fields, $\eta$ for the eigenvalue of $C_{\text {lf}}P_{\text {lf}}$, being $C_{\text {lf}}$ the light field charge-conjugation operator and $P_{\text {lf}}$ the parity operator spatially inverting the light fields through the midpoint between Q and $\overline{Q}$, and $\epsilon$ for the eigenvalue of the operator reflecting the light fields through a plane containing Q and $\overline{Q}$.

As for the eigenvalues $V_{\alpha }(\varvec{r})$, depending parametrically on $\varvec{r}$, they correspond to the energies of stationary states of the light fields in the presence of static Q and $\overline{Q}$ sources placed at distance r. These eigenvalues have been calculated ab initio in quenched lattice QCD [1].

So, the ground state of the light fields is usually characterized through $\varSigma _{g}^{+}$ where $\varSigma$ stands for $\varLambda =0$, the subscript g for $\eta =+1$ and the superscript $+$ for $\epsilon =+1$, and the corresponding eigenvalue reads $V_{\varSigma _{g}^{+}}(\varvec{{r}})$. Up to spin dependent terms that we shall not consider this eigenvalue mimics the form of the phenomenological Cornell (central) potential, see for example [9]. As for the first excited state of the light fields, it is denoted through $\varPi _{u}^{+}$ where $\varPi$ stands for $\varLambda =1$ and the subscript u for $\eta =-1$, and its corresponding eigenvalue by $V_{\varPi _{u}^{+}}(\varvec{r})$ which, up to spin dependent terms, is also a central potential.

The second step in building the B–O approximation consists in reintroducing the $Q\overline{Q}$ motion and assuming that the light fields respond almost instantaneously to the motion of the quark and antiquark. This is the adiabatic approximation, in which non adiabatic coupling terms in the kinetic energy are neglected. Then the bound state equation factorizes in a set of decoupled single-channel Schrödinger like equations for $Q\overline{Q}$, one per each light field eigenstate $|\alpha ; (\varvec{r})\rangle$, where the potential is given by the corresponding eigenvalue $V_{\alpha }(\varvec{r})$. The bound state solutions $|\psi \rangle$ can be characterized as [2]

$$\begin{aligned}&|E,L,m_{L},s_{Q\overline{Q}},m_{s_{Q\overline{Q}}};\alpha \rangle \nonumber \\&\quad =\int \mathrm {d}{\varvec{r}^{\prime }}R_{nL}(r^{\prime })Y_{Lm_{L}} (\widehat{\varvec{r}}^{\prime })|\varvec{r}^{\prime }\rangle |s_{Q\overline{Q}}, m_{s_{Q\overline{Q}}}\rangle |\alpha ;(\varvec{r}^{\prime })\rangle \end{aligned}$$

(4)

where L and $m_{L}$ indicate that they are eigenstates of $\varvec{L}^{2}$ and $\varvec{L}_{z}$, being $\varvec{L}$ an angular momentum of the system defined as $\varvec{L}=\varvec{l}_{Q\overline{Q}}+\varvec{J}_{\alpha }$ where $\varvec{l}_{Q\overline{Q}}$ is the orbital angular momentum of $Q\overline{Q}$ and $\varvec{J}_{\alpha }$ is the total angular momentum of the light fields. $s_{Q\overline{Q}}$ and $m_{s_{Q\overline{Q}}}$ stand for the spin of $Q\overline{Q}$ and its third component, and $R_{nL}(r)Y_{Lm_{L}}(\widehat{\varvec{r}})$ for the wave function at $\varvec{r}$. Notice that the energy of the state E depends on the quantum numbers n and L.

From these solutions, which are also eigenstates of parity with eigenvalue

$$\begin{aligned} P=\epsilon (-1)^{\varLambda +L+1} \end{aligned}$$

(5)

and charge conjugation with eigenvalue

$$\begin{aligned} C =\eta \epsilon (-1)^{\varLambda +L+s_{Q\overline{Q}}}, \end{aligned}$$

(6)

one can easily build physical states $|E,L,s_{Q\overline{Q}},J,m_{J};\alpha \rangle$ characterized by quantum numbers $J^{PC}$ where $\varvec{J}=\varvec{L}+\varvec{s}_{Q\overline{Q}}$ is the total angular momentum of the system.

For $Q=b$, and the ground state of the light fields

$$\begin{aligned} \varSigma _{g}^{+}:\, (\varLambda =0,\eta =+1,\epsilon =+1), \end{aligned}$$

(7)

these $J^{PC}$ states correspond to bottomonium $b\bar{b}$. As $J_{\varSigma _{g}^{+}}=0$ one has $\varvec{L}=\varvec{l}_{b\bar{b}}$ and $\varvec{J}=\varvec{j}_{b\bar{b}}$ where $\varvec{j}_{b\bar{b}}$ is the total angular momentum of ${b\bar{b}}$. In particular, for $J^{PC}=1^{--}$ one has $s_{b\bar{b}}=1$ and $L=l_{b\bar{b}}=0,2$.

For $Q=b$, and the first excited state of the light fields

$$\begin{aligned} \varPi _{u}^{+}:\, (\varLambda =1,\eta =-1,\epsilon =+1) \end{aligned}$$

(8)

with $J_{\varPi _{u}^{+}}=1$, the $J^{PC}$ states correspond to bottomonium hybrids $b\bar{b}g$. The lower energy state has $J^{PC}=1^{--}$, $s_{b\bar{b}}=0$ and $L=1$. This is why we use H(1P) to denote this lowest bottomonium hybrid (H for hybrid and P for $L=1)$.

3 Strong decays to open bottom two-meson states

If allowed, the dominant strong decays of bottomonium and bottomonium hybrids are to open bottom two-meson states. Although the B–O approximation description of bottomonium and bottomonium hybrids incorporates QCD dynamics through quenched lattice results, the QCD treatment of these decays requires unquenched (with light quarks) lattice QCD inputs from which the mixing potentials with open bottom two-meson states can be derived. These mixing potentials are related to the non-adiabatic coupling terms which are neglected in the B–O approximation. Noticeable progress in the incorporation of the non-adiabatic coupling terms within a framework that goes beyond the B–O approximation has been recently reported [10, 11]. However, the calculation involving the non-adiabatic coupling terms requires more unquenched lattice data than currently at disposal [12, 13]. In particular, no lattice data for the mixing of bottomonium hybrids are available. This makes unaffordable such an ab initio treatment at present.

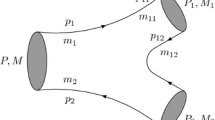
Instead, as the underlying physical mechanism is light-quark pair creation and string breaking, we shall assume that the decay proceeds first through light quark–antiquark ($q\overline{q}$) pair creation in a transition from an initial light field (gluon) B–O configuration to a light field (gluon and light quark) configuration given by the direct product of a B–O one and a $q\overline{q}$ state. We call this product an extended B–O configuration.

The application of general conservation arguments to this transition informs us of the possible quantum numbers of the emitted pair. Then, the recombination of $q\overline{q}$ with $b\bar{b}$ gives rise to an open bottom two-meson state (string breaking). Although this two-step process is only an approximation to the QCD mixing, it seems reasonable to think that, as this mixing takes place via pair creation, the quantum numbers of the pair will be the same that we derive from general conservation laws. These quantum numbers define the decay model, as we show in what follows.

3.1 Bottomonium

For bottomonium it is natural to assume, because of its $b\overline{b}$ content, that a flavor and color singlet $q\overline{q}$ is emitted within the hadronic medium. In the extended B–O framework this emission corresponds to a transition

$$\begin{aligned}&|E,l_{b\bar{b}},s_{b\bar{b}},J=j_{b\bar{b}},m_{J}=m_{j_{b\bar{b}}}; \varSigma _{g}^{+}\rangle \nonumber \\&\quad \rightarrow |E,(l_{b\bar{b}}^{\prime },s_{b\bar{b}},j_{b\overline{b}}^{\prime }), J,m_{J}; (l_{q\overline{q}},s_{q\overline{q}},j_{q\overline{q}}),\varSigma _{g}^{+}\rangle \end{aligned}$$

(9)

where we have used HQSS so that $s_{b\bar{b}}$ is conserved.

Conservation of parity implies

$$\begin{aligned}&\epsilon _{\varSigma _{g}^{+}}(-1)^{\varLambda _{\varSigma _{g}^{+}}+l_{b\bar{b}}+1} =\epsilon _{\varSigma _{g}^{+}}(-1)^{\varLambda _{\varSigma _{g}^{+}}+l_{b\bar{b}}^{\prime }+1} (-1)^{l_{q\overline{q}}+1}\nonumber \\&\quad \Rightarrow (-1)^{l_{b\bar{b}}+1}=(-1)^{l_{b\bar{b}}^{\prime }+l_{q\overline{q}}} \end{aligned}$$

(10)

and conservation of charge conjugation

$$\begin{aligned}&\eta _{\varSigma _{g}^{+}}\epsilon _{\varSigma _{g}^{+}}(-1)^{l_{b\bar{b}}+s_{b\bar{b}}} =\eta _{\varSigma _{g}^{+}}\epsilon _{\varSigma _{g}^{+}}(-1)^{l_{b\bar{b}}^{\prime } +s_{b\bar{b}}}(-1)^{l_{q\overline{q}}+s_{q\overline{q}}}\nonumber \\&\quad \Rightarrow (-1)^{l_{b\bar{b}}}= (-1)^{l_{b\bar{b}}^{\prime }}(-1)^{l_{q\overline{q}}+s_{q\overline{q}}} . \end{aligned}$$

(11)

By substituting (10) in (11) we have $(-1)^{s_{q\overline{q}}}=-1\Rightarrow s_{q\overline{q}}=\text {odd}$. Hence

$$\begin{aligned} s_{q\overline{q}}=1. \end{aligned}$$

(12)

If we reasonably assume that the most favored emission is for $j_{q\overline{q}}$ having its minimal value, $j_{q\overline{q}}=0$, then $l_{q\overline{q}}=1$ (and $l_{b\bar{b}}^{\prime }=l_{b\bar{b}})$, so that the emitted $q\overline{q}$ pair is in a $^{3}\!P_{0}$ or $0^{++}$ state.

Then, the recombination of the color singlet $q\overline{q}$ with the color singlet $b\bar{b}$ gives rise to the final $b\overline{q}$ and $\overline{b}q$ mesons.

This two step process defines the decay model for bottomonium within the extended B–O framework. Actually it corresponds to the so called $^{3}\!P_{0}$ decay model proposed long time ago [14, 15] within a constituent quark model framework. The $^{3}\!P_{0}$ model, detailed for bottomonium decays in [16], has been extensively applied in quarkonium (bottomonium and charmonium) decays to open flavor two-meson states.

This correspondence with the $^{3}\!P_{0}$ decay model is directly related to the equivalence of the B–O and the constituent quark model (with a Cornell potential) frameworks for the description of bottomonium. The nice feature of the extended B–O framework is that the possible quantum numbers for the $q\overline{q}$ pair are derived from general conservation arguments what also makes us confident in their validity despite our approximated treatment.

3.2 Lowest bottomonium hybrid

For the lowest bottomonium hybrid H(1P) it is natural to assume, because of its gluon content, that a color octet light quark–antiquark pair is emitted within the hadronic medium. In the extended B–O framework, the emission corresponds to a transition

$$\begin{aligned}&|E,L=1,s_{b\bar{b}}=0,J=1,m_{J};\varPi _{u}^{+}\rangle \nonumber \\&\quad \rightarrow |E,(l_{b\bar{b}}^{\prime },s_{b\bar{b}}=0,j_{b\overline{b}}^{\prime }),J=1,m_{J};\nonumber \\&\quad (l_{q\overline{q}},s_{q\overline{q}}, j_{q\overline{q}}),\varSigma _{g}^{+}\rangle . \end{aligned}$$

(13)

Conservation of parity implies

$$\begin{aligned}&\epsilon _{\varPi _{u}^{+}}(-1)^{\varLambda _{\varPi _{u}^{+}}+L+1}=\epsilon _{\varSigma _{g}^{+}} (-1)^{\varLambda _{\varSigma _{g}^{+}}+l_{b\bar{b}}^{\prime }+1}(-1)^{l_{q\overline{q}}+1}\nonumber \\&\quad \Rightarrow -1=(-1)^{l_{b\bar{b}}^{\prime }+l_{q\overline{q}}} \end{aligned}$$

(14)

so that $l_{b\bar{b}}^{\prime }+l_{q\overline{q}}=\text {odd}$, and conservation of charge conjugation

$$\begin{aligned}&\eta _{\varPi _{u}^{+}}\epsilon _{\varPi _{u}^{+}}(-1)^{\varLambda _{\varPi _{u}^{+}}+L+s_{b\bar{b}}}\nonumber \\&\quad =\eta _{\varSigma _{g}^{+}}\epsilon _{\varSigma _{g}^{+}}(-1)^{\varLambda _{\varSigma _{g}^{+}} +l_{b\bar{b}}^{\prime }+s_{b\bar{b}}}(-1)^{l_{q\overline{q}}+s_{q\overline{q}}}\nonumber \\&\quad \Rightarrow -1=(-1)^{l_{b\bar{b}}^{\prime }+l_{q\overline{q}}+s_{q\overline{q}}} \end{aligned}$$

(15)

so that $l_{b\bar{b}}^{\prime }+l_{q\overline{q}}+s_{q\overline{q}}=\text {odd}$, and $s_{q\overline{q}}=\text {even}$. Hence

$$\begin{aligned} s_{q\overline{q}}=0. \end{aligned}$$

(16)

Then, using $J_{\varSigma _{g}^{+}}=0$, the total angular momentum conservation reads $\varvec{J}=\varvec{l}_{b\bar{b}}^{\prime }+\varvec{l}_{q\overline{q}}$. As $\widehat{\varvec{r}}\cdot \varvec{l}_{b\bar{b}}^{\prime }=0$ because the orbital angular momentum of $b\bar{b}$ is orthogonal to the separation vector of b and $\bar{b}$, we have $\widehat{\varvec{r}}\cdot \varvec{J}=\widehat{\varvec{r}}\cdot \varvec{l}_{q\overline{q}}$. On the other hand $\varvec{J}=\varvec{L}+\varvec{s}_{b\bar{b}}=\varvec{L}=\varvec{l}_{b\bar{b}}+\varvec{J}_{\varPi _{u}^{+}}$ so that $\widehat{\varvec{r}}\cdot \varvec{J}=\widehat{\varvec{r}}\cdot \varvec{J}_{\varPi _{u}^{+}}$. Therefore $\widehat{\varvec{r}}\cdot \varvec{J}_{\varPi _{u}^{+}}=\widehat{\varvec{r}}\cdot \varvec{l}_{q\overline{q}}$. Recalling that the modulus of the eigenvalue of $\widehat{\varvec{r}}\cdot \varvec{J}_{\varPi _{u}^{+}}$ is $\varLambda _{\varPi _{u}^{+}}=1$ we conclude that $j_{q\overline{q}}=l_{q\overline{q}}\ge \varLambda _{\varPi _{u}^{+}}=1$. If we reasonably assume that the most favored emission is for $j_{q\overline{q}}$ having its minimal value then $j_{q\overline{q}}=1,s_{q\overline{q}}=0$ and $l_{q\overline{q}}=1$ so that the emitted color octet $q\overline{q}$ pair is in a $^{1}\!P_{1}$ or $1^{+-}$ state. Then, $l_{b\bar{b}}^{\prime }=\text {even}$. For the lowest hybrid transition it is quite natural to assign $j_{b\bar{b}}^{\prime }=l_{b\bar{b}}^{\prime }=0$ so that the color octet $b\bar{b}$ pair is in a $0^{-+}$ state.

Notice that the quantum numbers of the emitted pair $1^{+-}$ are the same of the ground state gluelump, which is the limit of the gluon configuration $\varPi _{u}^{+}$ when $r\rightarrow 0$ [2].

The second step is the recombination of the color octet $q\overline{q}$ with the color octet $b\bar{b}$ giving rise to $b\overline{q}$ and $\bar{b}q$ mesons.

This two step process defines the $^{1}\!P_{1}$ model for the decay of H(1P) into open bottom two-meson states within the extended B–O framework. Let us remark that the quantum numbers of the emitted pair $1^{+-}$ are different from the $1^{--}$ used in decay models of hybrids based on constituent glue, see [3, 4] and references therein. Otherwise said, the bottomonium hybrid descriptions provided by the B–O approximation in QCD and the constituent gluon models are not equivalent. This difference is crucial to establish the forbidden and allowed decays of H(1P) to open bottom two-meson states, as we show next.

4 Decay widths

Let us consider the decay $H(1P)\rightarrow C+F$ where C is a $b\overline{q}$ meson state $\overline{B}_{(s)}^{(*)}$, and F is a $\bar{b}q$ meson state $B_{(s)}^{(*)}$. In parallel with the $^{3}\!P_{0}$ decay model for bottomonium we shall characterize the $q\overline{q}$ emission by a real constant probability amplitude: $\sqrt{2}\gamma _{1}$ for $u\overline{u}$ or $d\overline{d}$ and $\sqrt{2}\gamma _{1}^{\prime }$ for $s\overline{s}$ where the $\sqrt{2}$ is a color normalization factor. Notice that the color matrix element in the recombination of the emitted $1^{+-}$ color octet $q\overline{q}$ with the $0^{-+}$ color octet $b\bar{b}$ is $1/\sqrt{2}$ so that the total (emission + recombination) color factor is $\sqrt{2}\frac{1}{\sqrt{2}}=1$ as it corresponds to the decay of an initial color singlet into final color singlet states. To complete the calculation of the amplitude for the recombination process (of $q\overline{q}$ with the color octet $b\overline{b}$) we need the radial wave function of the color octet $b\overline{b}$. We shall approximate it by that of the hybrid $R_{n=1,L=1}(r)$. This is justified in the limit $r\rightarrow 0$ where the r-dependent interaction potential between $b\overline{b}$ and the gluon field becomes negligible against the centrifugal barrier. As the orbital angular momentum of $b\overline{b}$ is zero the orbital part of the wave function is that of the gluon field and the radial part of the wave function is effectively that of the color octet $b\bar{b}$ configuration. This wave function approximation holds as long as the $\varPi _{u}^{+}$ configuration remains close to the gluelump, what may occur up to a distance around 0.5 fm [2].

The calculation of the width follows exactly the same procedure used in the $^{3}\!P_{0}$ model detailed in [14,15,16]. In the rest frame of H(1P) and for the emission of a $u\overline{u}$ or $d\overline{d}$ pair it can be expressed as (for the emission of $s\overline{s}$ one should substitute $\gamma$ by $\gamma ^\prime$)

$$\begin{aligned} \varGamma (H(1P)\rightarrow C+F) =\gamma _{1}^{2}2\pi \frac{E_{C}E_{F}}{M_{H}}k|{\mathcal {M}}|^{2} \end{aligned}$$

(17)

where $M_{H}$ is the mass of the hybrid, $E_{C}$ is the energy of the C meson given by $E_{C}=\sqrt{M_{C}^{2}+k^{2}}$ being k the modulus of the three-momentum of C (or F), and

$$\begin{aligned} |{\mathcal {M}}|^{2}= & {} \frac{1}{2\pi ^{2}} |\langle I_C m_{I_C} I_F m_{I_F} \vert I_{b\bar{b}} m_{I_{b\bar{b}}}\rangle |^{2}\! \begin{bmatrix} I_{b} &{} I_{\overline{b}} &{} I_{b\bar{b}}\\ I_{q} &{} I_{\overline{q}} &{} 0\\ I_{C} &{} I_{F} &{} I_{b\bar{b}} \end{bmatrix} ^{2}\nonumber \\&\times \begin{bmatrix} 1/2 &{} 1/2 &{} s_{b\bar{b}}\\ 1/2 &{} 1/2 &{} s_{q\bar{q}}\\ s_{C} &{} s_{F} &{} s_{CF} \end{bmatrix} ^{2}\begin{bmatrix} l_{b\bar{b}}^{\prime } &{} s_{b\bar{b}} &{} j_{b\bar{b}}^{\prime }\\ l_{q\bar{q}} &{} s_{q\bar{q}} &{} j_{q\bar{q}}\\ l_{b\bar{b}}^{\prime }+1 &{} s_{CF} &{} J_{H} \end{bmatrix} ^{2}|{\mathcal {J}}_{+}(k)|^{2}\nonumber \\ \end{aligned}$$

(18)

where I and $m_{I}$ stand for isospin and its third component, s for spin, J for total angular momentum of the initial state, $l_{b\bar{b}}^{\prime }=0$, $s_{b\bar{b}}=0$, $j_{b\bar{b}}^{\prime }=0$, $s_{q\bar{q}}=0$, $l_{q\bar{q}}=1$ and $j_{q\bar{q}}=1$. The square brackets are related to the 9j symbols:

$$\begin{aligned} \begin{bmatrix} j_{a} &{} j_{b} &{} j_{e}\\ j_{c} &{} j_{d} &{} j_{f}\\ j_{g} &{} j_{h} &{} j_{i} \end{bmatrix} \equiv \sqrt{\hat{\jmath }_{e}\,\hat{\jmath }_{f}\,\hat{\jmath }_{g}\,\hat{\jmath }_{h}} \begin{Bmatrix} j_{a}&j_{b}&j_{e}\\ j_{c}&j_{d}&j_{f}\\ j_{g}&j_{h}&j_{i} \end{Bmatrix} \end{aligned}$$

(19)

with $\hat{\jmath }\equiv 2j+1$. The spatial integral ${\mathcal {J}}_{+}$ is given by

$$\begin{aligned} {\mathcal {J}}_{+}(k)=i^{l_{b\bar{b}}^{\prime }} \sqrt{\frac{3(l_{b\bar{b}}^{\prime }+1)}{2l_{b\bar{b}}^{\prime }+3}}{\mathcal {I}}_{+}(k) \end{aligned}$$

(20)

with

$$\begin{aligned}&{\mathcal {I}}_{+}(k)=\int _{0}^{\infty }r^{2}\mathrm {d}{r}p^{2}\mathrm {d}{p} u_{C}^{*}(p)u_{F}^{*}(p) R_{H(1P)}(r)\nonumber \\&\quad \times \bigl [pj_{1}(pr)j_{l_{b\bar{b}}^{\prime }+1}(h_{b}kr)+h_{q}kj_{0}(pr) j_{l_{b\bar{b}}^{\prime }}(h_{b}kr)\bigr ], \end{aligned}$$

(21)

where $h_{b}\equiv \frac{M_{b}}{M_{q}+M_{b}}$, $h_{q}\equiv \frac{M_{q}}{M_{q}+M_{b}}$, and u stands for the Fourier transform of the radial wave function.

Notice that from these expressions one can easily recover the corresponding ones to the $^{3}\!P_{0}$ model for the decay of an S-wave $1^{--}$ bottomonium state $\varUpsilon$ by substituting $\gamma _{1}^{2}\rightarrow \gamma _{0}^{2}$, $s_{q\overline{q}}=0\rightarrow s_{q\overline{q}}=1$, $j_{q\overline{q}}=1\rightarrow j_{q\overline{q}}=0$, $s_{b\overline{b}}=0\rightarrow s_{b\overline{b}}=1$, $j_{b\bar{b}}^{\prime }=0\rightarrow j_{b\bar{b}}^{\prime }=1$, and $H\rightarrow \varUpsilon$.

For the sake of simplicity we shall use henceforth the notation:

$$\begin{aligned}&\varGamma _{H_{u}}\equiv \varGamma _{H(1P) \rightarrow B\overline{B}}, \quad \varGamma _{H_{s}}\equiv \varGamma _{H(1P) \rightarrow B_{s}\overline{B}_{s}}, \nonumber \\&\varGamma _{H_{u}^{*}}\equiv \varGamma _{H(1P) \rightarrow B\overline{B}^{*}},\quad \varGamma _{H_{s}^{*}}\equiv \varGamma _{H(1P) \rightarrow B_{s}\overline{B}_{s}^{*}}, \nonumber \\&\varGamma _{H_{u}^{**}}\equiv \varGamma _{H( 1P) \rightarrow B^{*}\overline{B}^{*}},\quad \varGamma _{H_{s}^{**}}\equiv \varGamma _{H(1P) \rightarrow B_{s}^{*} \overline{B}_{s}^{*}}. \end{aligned}$$

(22)

From (18) and taking into account that the three elements in the same column in the 9j symbol have to satisfy the triangular rule for the symbol not to vanish we immediately infer from $s_{q\overline{q}}=0$ that H(1P) can only decay to CF open bottom two-meson channels with $s_{CF}=s_{b\bar{b}}=0$. From this spin selection rule, the decays to $B\overline{B}^{*}$ and $B_{s}\overline{B}_{s}^{*}$ (we use this notation instead of $B\overline{B}^{*} + B^{*}\overline{B}$ and $B_{s}\overline{B}_{s}^{*} + B_{s}^{*}\overline{B}_{s}$), although kinematically allowed, are forbidden

$$\begin{aligned} \varGamma _{H_{u}^{*}}=0\qquad \varGamma _{H_{s}^{*}}=0. \end{aligned}$$

(23)

As for the calculation of the widths for the other kinematically allowed decays to $B\overline{B}$, $B^{*}\overline{B}^{*}$ and $B_{s}\overline{B}_{s}$, $B_{s}^{*}\overline{B}_{s}^{*}$ we shall use for H(1P) the mass 10888 MeV and the radial wave function calculated in reference [6]. Let us remind that the excited string potential used in [6] differs from the lattice QCD parametrization of the hybrid potential [2] only at short distances, where they are both dominated by the centrifugal barrier given by $L=1$. Therefore, the difference between these two parametrizations has no appreciable effect on the wave function of the lowest bottomonium hybrid. For the final mesons, we use their experimental masses and for simplicity, as usual, Gaussian radial wave functions with an average rms radius of 0.45 fm, as obtained from a Cornell potential model. For the heavy and light quark masses we have chosen standard values $M_{b}=4793$ MeV, $M_{s}=500$ MeV and $M_{u,d}=340$ MeV. Thus, we get

$$\begin{aligned}&\frac{\varGamma _{H_{u}}}{\gamma _{1}^{2}} =1.7~\text {MeV},\quad \frac{\varGamma _{H_{u}^{**}}}{\gamma _{1}^{2}}=25.7~\text {MeV} , \nonumber \\&\frac{\varGamma _{H_{s}}}{\gamma _{1}^{\prime 2}} =30.3~\text {MeV}, \quad \frac{\varGamma _{H_{s}^{**}}}{\gamma _{1}^{\prime 2}}=114.3~ \text {MeV}, \end{aligned}$$

(24)

so that

$$\begin{aligned} \frac{\varGamma _{H_{u}^{**}}}{\varGamma _{H_{u}}}=15.1,\quad \frac{\varGamma _{H_{s}^{**}}}{\varGamma _{H_{s}}}=3.8. \end{aligned}$$

(25)

Let us emphasize again that the hybrid decay pattern resulting from Eqs. (23) and (24) is very different from the one predicted by constituent glue or flux tube models. In these models, as a consequence of the assumption of a spin triplet light quark pair, $s_{q\overline{q}} = 1$, our selection rule (23) does not appear. Instead, a different selection rule establishing the suppression of the coupling of the $1^{--}$ hybrid with two S-wave mesons, e.g., $B^{(*)}\overline{B}^{(*)}$, comes out. More concretely, in [17] it has been proved that when $s_{q\overline{q}}=1$ the amplitude ${\mathcal {M}}$ in (17) for the decay into two S-wave mesons vanishes. As in our case $s_{q\overline{q}}=0$ this selection rule does not apply. On the other hand, in [18] the authors consider the same decay into two S-wave mesons and reach the same conclusion from their characterization of the hybrid as a bound state of a $0^{-+}$ $c\overline{c}$ and a gluon in P-wave, which is referred to as a $1^{+-}$ magnetic gluon. This magnetic gluon then decays into a color octet spin-one S-wave light $q\overline{q}$ pair. The fact that the orbital angular momentum of the gluon in the hybrid is $l_{g}=1$, determining the symmetry properties of the hybrid wave function entering in the calculation of the amplitude, is instrumental for the derivation of the selection rule.

A direct comparison of our B–O two-body description of the hybrid with the constituent model three-body description of this reference is not straightforward, but in this context we can observe that if instead one considered the hybrid as being made of a $0^{-+}$ $c\overline{c}$ and a $1^{+-}$ gluelump in an S-wave, with this gluelump decaying into a color octet spin-zero P-wave light $q\overline{q}$ pair as it is our case, then the orbital angular momentum of the gluelump would be zero and the selection rule would not appear.

It is very illustrative to compare these results with the corresponding decay widths from $\varUpsilon (5S)$ with a calculated mass of 10865 MeV, quite close to the hybrid one [6]. In this case, using the $^{3}\!P_{0}$ decay model and the same kind of self-explained simplified notation we get

$$\begin{aligned}&\frac{\varGamma _{\varUpsilon _{u}}}{\gamma _{0}^{2}}=0.8~\text {MeV},\quad \frac{\varGamma _{\varUpsilon _{u}^{**}}}{\gamma _{0}^{2}}=0.5~\text {MeV},\quad \frac{\varGamma _{\varUpsilon _{u}^{*}}}{\gamma _{0}^{2}}=1.9~\text {MeV},\nonumber \\&\frac{\varGamma _{\varUpsilon _{s}}}{\gamma _{0}^{\prime 2}}=0.5~\text {MeV},\quad \frac{\varGamma _{\varUpsilon _{s}^{**}}}{\gamma _{0}^{\prime 2}}= 0.3~\text {MeV},\nonumber \\&\frac{\varGamma _{\varUpsilon _{s}^{*}}}{\gamma _{0}^{\prime 2}} =1.4~\text {MeV}, \end{aligned}$$

(26)

from which

$$\begin{aligned} \frac{\varGamma _{\varUpsilon _{u}^{*}}}{\varGamma _{\varUpsilon _{u}}}=2.4,\quad \frac{\varGamma _{\varUpsilon _{s}^{*}}}{\varGamma _{\varUpsilon _{s}}}=2.8,\quad \frac{\varGamma _{\varUpsilon _{u}^{**}}}{\varGamma _{\varUpsilon _{u}}}=0.6,\quad \frac{\varGamma _{\varUpsilon _{s}^{**}}}{\varGamma _{\varUpsilon _{s}}}=0.6. \end{aligned}$$

(27)

The comparison of Eqs. (23), (25) with Eq. (27) makes clear the very different decay patterns for H(1P) and $\varUpsilon (5S)$. Next we analyze whether these patterns could provide or not an explanation for current data.

5 Comparison with data

The only experimental data available to possibly check our results come from $\varUpsilon (10860)$ [5], a $1^{--}$ bottomonium-like resonance produced in $e^{+}e^{-}$ annihilation at a c.o.m. energy of $10889.9_{-2.6}^{+3.2}$ MeV, pretty close to the calculated masses of the lowest bottomonium hybrid H(1P) and the $\varUpsilon (5S)$ bottomonium state, and not far from the $B_{s}^{*}\overline{B}_{s}^{*}$ threshold.

Although the measured leptonic width $\varGamma _{\varUpsilon (10860) \rightarrow e^{+}e^{-}}=0.31 \pm 0.07$ KeV is compatible within the errors with an assignment of this resonance to a pure $\varUpsilon (5S)$ state, this option is ruled out because $\varUpsilon (10860)$ has dipion decays to $\pi ^{+}\pi ^{-}h_{b}((1,2)P)$ and $\pi ^{+}\pi ^{-}\varUpsilon ((1,2,3)S)$ with a similar production rate. As $s_{h_{b}}=0$ and $s_{\varUpsilon }=1$, HQSS implies that $\varUpsilon (10860)$ must have $s_{b\bar{b}}=0$ and $s_{b\bar{b}}=1$ components.

As for the ratios of decay widths to open bottom two-meson states a comparison of the measured values (we do not list the ratio $\frac{\varGamma _{\varUpsilon (10860)\rightarrow B_{s}\overline{B}_{s}}}{\varGamma _{\varUpsilon (10860)\rightarrow B_{s}\overline{B}_{s}^{*}}}$ because data on $\varGamma _{\varUpsilon (10860)\rightarrow B_{s}\overline{B}_{s}}$ is very uncertain)

$$\begin{aligned}&\frac{\varGamma _{\varUpsilon (10860)\rightarrow B\overline{B}}}{\varGamma _{\varUpsilon (10860)\rightarrow B\overline{B}^{*}}} =0.40\pm 0.12 \end{aligned}$$

(28)

$$\begin{aligned}&\frac{\varGamma _{\varUpsilon (10860)\rightarrow B^{*}\overline{B}^{*}}}{\varGamma _{\varUpsilon (10860)\rightarrow B\overline{B}^{*}}}=2.8\pm 0.8 \end{aligned}$$

(29)

and

$$\begin{aligned} \frac{\varGamma _{\varUpsilon (10860)\rightarrow B_{s}^{*}\overline{B}_{s}^{*}}}{\varGamma _{\varUpsilon (10860)\rightarrow B_{s}\overline{B}_{s}^{*}}}=13\pm 5 \end{aligned}$$

(30)

to our results for $\varUpsilon (5S)$,

$$\begin{aligned} \frac{\varGamma _{\varUpsilon _{u}}}{\varGamma _{\varUpsilon _{u}^{*}}} = 0.4, \qquad \frac{\varGamma _{\varUpsilon _{u}^{**}}}{\varGamma _{\varUpsilon _{u}^{*}}} = 0.3,\quad \frac{\varGamma _{\varUpsilon _{s}^{**}}}{\varGamma _{\varUpsilon _{s}^{*}}} = 0.2, \end{aligned}$$

(31)

also supports a different assignment for $\varUpsilon (10860)$. In this respect, different proposals about its nature, incorporating $s_{b\bar{b}}=0$ and $s_{b\bar{b}}=1$ components, have been developed.

In Ref. [19], following HQSS arguments, a mixture of $\varUpsilon (5S)$ and a P-wave $B_{s}^{*}\overline{B}_{s}^{*}$ has been suggested. Taking into account that the decays $B_{s}^{*}\overline{B}_{s}^{*} \rightarrow B^{(*)}\overline{B}^{(*)}$ are suppressed, $\varUpsilon (10860)\rightarrow B^{(*)}\overline{B}^{(*)}$ should then proceed through the $\varUpsilon (5S)$ component. However, the comparison of our calculated ratio $\frac{\varGamma _{\varUpsilon _{u}^{**}}}{\varGamma _{\varUpsilon _{u}^{*}}}=0.3$ with data Eq. (29) seems not to support that mixing (notice that in [19] the predicted ratios are different than ours because the spatial integrals have not been taken into account).

In Ref. [20] an analysis of the decays through the incorporation of meson-meson components in the description of the $\varUpsilon (10860)$ has been carried out. A very strong disagreement between the calculated ratio $\frac{\varGamma _{\varUpsilon (10860)\rightarrow B_{s}^{*}\overline{B}_{s}^{*}}}{\varGamma _{\varUpsilon (10860)\rightarrow B_{s}\overline{B}_{s}^{*}}}$ and data has been observed.

As an alternative, in reference [6] it has been proposed that $\varUpsilon (10860)$ could be a mixing of H(1P) and $\varUpsilon (5S)$ (for mixing in nonrelativistic effective field theories see [21, 22])

$$\begin{aligned} \varUpsilon (10860)=\cos \theta |\varUpsilon (5S)\rangle +\sin \theta |H(1P)\rangle , \end{aligned}$$

(32)

where the probability of H(1P) should be at most of a few percent, $\sin ^{2}\theta \lesssim 0.1$, in order to get a good description of the leptonic widths. This proposal allows for an explanation of the observed dipion decays. Let us examine now whether it could give or not quantitative account of the observed decays of $\varUpsilon (10860)$ to open bottom meson-meson channels. For this purpose, we shall calculate the decay widths from the ones of its $\varUpsilon (5S)$ and H(1P) components in the form

$$\begin{aligned} \varGamma _{\varUpsilon (10860)\rightarrow B_{(s)}^{(*)}\overline{B}_{(s)}^{(*)}}=\left( \cos \theta \sqrt{\varGamma _{\varUpsilon _{u,s}^{(*)}}}+ \sin \theta \sqrt{\varGamma _{H_{u,s}^{(*)}}}\right) ^{2}. \end{aligned}$$

(33)

As $\varGamma _{H_{u}^{*}}=0$, from (26) and (33) we have

$$\begin{aligned} \varGamma _{\varUpsilon (10860) \rightarrow B\overline{B}^{*}}=1.9\gamma _{0}^{2}\cos ^{2}\theta ~\text {MeV}. \end{aligned}$$

(34)

Then from data

$$\begin{aligned} \varGamma _{\varUpsilon (10860)\rightarrow B\overline{B}^{*}}=7.0\pm 1.3 ~\text {MeV} \end{aligned}$$

(35)

we obtain

$$\begin{aligned} \gamma _{0}^{2}\cos ^{2}\theta =3.7\pm 0.7, \end{aligned}$$

(36)

where the quoted errors come from data uncertainty only.

If we use this information, together with the calculated widths (24) and (26), then compatibility with experimental data Eqs. (28) and (29) translates into two independent conditions to be satisfied:

$$\begin{aligned} \left\{ \begin{array}{l} (0.95\cdot x+0.65)^{2} =0.40\pm 0.12 \\ (3.68\cdot x+0.51)^{2} =2.8\pm 0.8 \end{array} \right. \end{aligned}$$

(37)

where $x\equiv \frac{\gamma _{1}}{\gamma _{0}} \tan \theta$.

Each of these conditions admits two solutions. Full consistency with existent data requires that there exist a pair of overlapping solutions, so that there is a value of x that reproduces both experimental ratios within the error bars. The fact that the two closest solutions are

$$\begin{aligned} \left\{ \begin{array}{l} x = 0.32 \pm 0.06 \\ x = -0.02 \pm 0.10 \end{array}\right. \end{aligned}$$

(38)

(errors from data uncertainty only) shows some tension (around $2 \sigma$) with data. This may be attributed to the approximations we have followed, among them having neglected the possible momentum dependence of $\gamma _{0}$ and $\gamma _{1}$.

Following a Bayesian approach, we work under the hypothesis that these two solutions are nevertheless two independent measurements of the same quantity, so we identify the best fit of x with the weighted average:

$$\begin{aligned} \frac{\gamma _{1}}{\gamma _{0}}\tan \theta =0.23\pm 0.14 \end{aligned}$$

(39)

where the weighted average error has been doubled in order to account for the aforementioned uncertainties.

As for the decays to bottom-strange mesons, we use $\varGamma _{H_{s}^{*}}=0$ and

$$\begin{aligned} \varGamma _{\varUpsilon (10860)\rightarrow B_{s}\overline{B}_{s}^{*}}= 1.4\gamma _{0}^{\prime 2}\cos ^{2}\theta =0.7\pm 0.3~\text {MeV} \end{aligned}$$

(40)

to obtain

$$\begin{aligned} \gamma _{0}^{\prime 2}\cos ^{2}\theta =0.5\pm 0.2. \end{aligned}$$

(41)

Then from the experimental ratio Eq. (30) we get

$$\begin{aligned} \frac{\gamma _{1}^{\prime }}{\gamma _{0}^{\prime }}\tan \theta =0.35\pm 0.16. \end{aligned}$$

(42)

Like before, we have doubled the error bar to account for uncertainty coming from our approximations.

Then, for example, for the maximum value of $\sin ^{2}\theta =0.1$ we would have for bottomonium $\gamma _{0}=2.0 \pm 0.2$ in good accord with the value commonly used in the literature, see for instance [16], and $\gamma _{0}^{\prime }=0.75 \pm 0.15$ so that $\gamma _{0}^{\prime }<\gamma _{0}$ as expected from the more probable emission of a $u\overline{u}$ or $d\overline{d}$ pair than a $s\overline{s}$ pair. From these values, one would have $\frac{\gamma _{1}}{\gamma _{0}}=0.7\pm 0.4$ and $\frac{\gamma _{1}^{\prime }}{\gamma _{0}^{\prime }}=1.0 \pm 0.5$, so that for H(1P) we would get $\gamma _{1}=1.4 \pm 0.9$ and $\gamma _{1}^{\prime }= 0.8 \pm 0.5$.

These results show that a fully consistent explanation of $\varUpsilon (10860)$ as mainly being a mixing of $\varUpsilon (5S)$ and the lowest bottomonium hybrid is feasible. It can be easily inferred that this mixing would be also necessary to explain data if an additional $\varUpsilon (5S)$–$\varUpsilon (4D)$ mixing were implemented, since the decays to $B^{*}\overline{B}^{*}$ and $B_{s}^{*}\overline{B}_{s}^{*}$ from $\varUpsilon (4D)$ are even more suppressed than from $\varUpsilon (5S)$.

Therefore, a $\varUpsilon (5S)$–H(1P) mixing may give reasonable account of the observed leptonic, dipion and open-bottom two-meson decays of $\varUpsilon (10860)$. We may tentatively interpret this as an indirect experimental evidence of the existence of the lowest bottomonium hybrid H(1P).

A remaining question is whether a direct detection of the hybrid dominated orthogonal combination, that we shall call H(10860):

$$\begin{aligned} H(10860)=-\sin \theta |\varUpsilon (5S)\rangle +\cos \theta |H(1P)\rangle \end{aligned}$$

(43)

is feasible or not. From $0<\sin ^{2}\theta \lesssim 0.1$ and our previous results we can easily evaluate a lower limit on the total width of H(10860) to two open-bottom mesons:

$$\begin{aligned} \varGamma (H(10860)\rightarrow B_{(s)}^{(*)}\overline{B}_{(s)}^{(*)})\gtrsim 300~\text {MeV}. \end{aligned}$$

(44)

This width of at least some hundreds of MeV, and an expected larger width for the 2P hybrid state with a calculated mass around 11080 MeV, makes very unlikely a clean experimental signature of H(10860) in the foreseeable future.

6 Summary

A thorough study of the decays of the lowest bottomonium hybrid, that we have called H(1P), to open bottom two-meson channels has been carried out by implementing light-quark pair creation within an extended B–O framework. The application of conservation laws for strong interactions fixates the possible quantum numbers of the pair. Thus, a $^{1}\!P_{1}$ decay model has been built. From it selection rules for the forbidden and allowed decays and quantitative ratios of decay widths have been predicted. These predictions differ greatly from the ones obtained from the $^{3}\!P_{0}$ decay model resulting for bottomonium decays within the same framework. In particular, the calculated ratios for H(1P) and for the bottomonium state $\varUpsilon (5S)$, with the same quantum numbers $J^{PC}=1^{--}$ and predicted masses in the B–O approximation close to each other, have been compared between them and with the measured widths of $\varUpsilon (10860)$, an experimental $1^{--}$ resonance with similar mass. This comparison indicates that $\varUpsilon (10860)$ should not be assigned to a pure $\varUpsilon (5S)$ state, in accord with the indications from Heavy Quark Spin Symmetry when applied to its observed dipion decays. The need for a heavy-quark spin zero component, apart from the $\varUpsilon (5S)$ spin one, has led to several proposals about the nature of $\varUpsilon (10860)$ in the literature. We have centered on a $\varUpsilon (5S)$–H(1P) mixing scenario that gives reasonable quantitative account of the dipion decay widths. We have shown that such a mixing could also explain the observed decays of $\varUpsilon (10860)$ to open bottom two-meson channels. It is worth to emphasize that many of our results, namely the selection rules and the impossibility to describe the $\varUpsilon (10860)$ as a pure bottomonium or bottomonium hybrid state, are not affected by any change in the hybrid wave function. These results make us tentatively conclude that current data on $\varUpsilon (10860)$ may be showing the presence of the lowest bottomonium hybrid.