Strong decays of $D_{3}^{*}(2760)$, $D_{s3}^{*}(2860)$, $B_{3}^{*}$, and $B_{s3}^{*}$

Abstract

In this paper, we study the OZI-allowed two-body strong decays of $3^-$ heavy–light mesons. Experimentally the charmed $D_{3}^{*}(2760)$ and the charm–strange $D_{s3}^{*}(2860)$ states with these quantum numbers have been discovered. For the bottomed B(5970) state, which was found by the CDF Collaboration recently, its quantum number has not been decided yet and we assume it is a $3^-$ meson in this paper. The theoretical prediction for the strong decays of bottom–strange state $B_{s3}^*$ is also given. The relativistic wave functions of $3^-$ heavy mesons are constructed and their numerical values are obtained by solving the corresponding Bethe–Salpeter equation with instantaneous approximation. The transition matrix is calculated by using the PCAC and low energy theorem, following which the decay widths are obtained. For $D_{3}^*(2760)$ and $D_{s3}^*(2860)$, the total strong decay widths are 72.6 and 47.6 MeV, respectively. For $B_3^*$ with $M=5978$ MeV and $B_{s3}^*$ with $M=6178$ MeV, their strong decay widths are 22.9 and 40.8 MeV, respectively.

1 Introduction

In the last few years, many new hadron states have been discovered experimentally, injecting new vitality to the study of hadron physics. Among these new states, some are thought to be tetraquark, pentaquark [1], or molecule states, while some are believed to have the usual quark–antiquark structure [2]. The observation of the second case improves the meson spectra predicted by the quark potential models and may bring about more insights into the nonperturbative properties of QCD. Among these particles, we are interested in the spin-3 heavy–light mesons in this paper, as more data about such states are collected recently. In 2006, the Babar Collaboration found the $D_{sJ}^*(2860)$ state [3], which was confirmed by LHCb [4]. This particle attracted much attention [8, 5,6,7, 9,10,11,12,13,14,15,16,17,18]. Theoretically it is thought to be a charm–strange meson with spin–parity quantum number $J^P=3^-$ or $1^-$ (S–D mixing). Both predict the correct partial decay widths within the experimental error. This uncertainty was eliminated in 2014 by the LHCb Collaboration [19, 20], which found that two particles, namely, $D_{s3}^*(2860)$ with spin-3 and $D_{s1}^*(2860)$ with spin-1, are around this mass region.

For the charmed meson, $D^*(2760)$ was discovered by the BaBar Collaboration [21] and $D_J^*(2760)$ was found by LHCb [22]. Both particles have similar masses and decay widths, so they are thought to be the same state. Just as $D_{sJ}^*(2860)$, they are also thought to be $3^-$ or $1^-$ state. Recently, LHCb [23] found the first spin-3 charmed meson $D_3^*(2760)$, whose decay width (for the isobar formalism, see Table 3) is about 30 MeV larger than that of $D_J^*(2760)$ [22]. Whether a $1^-$ partner with a similar mass to $D_3^*(2760)$ exists (as the charm–strange case) is an interesting question. In the bottomed (bottom–strange) meson sector, the $3^-$ state has not been found. However, very recently the CDF Collaboration reported the existence of B(5970) [24], which has been investigated by assuming it has the quantum number $1^-$ [25, 26] or $3^-$ [26]. The decay width still has a large experimental error (see Table 1), so more precise detection is needed.

Table 1 The experimental results of the mass (MeV) and decay width (MeV) for the candidates of the heavy–light states with quantum number $3^-$

Usually, if the strong decay channels of a meson are OZI-allowed, they will be dominant, and the sum of their partial widths can be used to estimate the total width of the meson. Beside that, those decays are also applied to determine the quantum number of particles. To study these decays, several theoretical methods could be applied, such as the chiral quark method [9, 29, 30, 27, 28], the heavy meson effective theory [31, 5, 26, 14], the QCD sum rules [15, 16], and the $^3P_0$ method [10, 35, 33, 36,37,38, 25, 12, 34, 18, 32, 39, 40]. The chiral quark model introduces an effective Lagrangian to describe the coupling between light quark fields and light meson, while for the heavy meson effective theory, the interaction lagrangian is constructed just by meson fields. The $^3P_0$ model is very popular in dealing with OZI-allowed strong decays. In this method, a $q\bar{q}$ with $J^{PC}=0^{++}$ is assumed to be created from the vacuum. For the heavy mesons, the simple harmonic oscillator (SHO) wave functions are usually adopted.

In our recent work [41], the weak production of $3^-$ heavy–light states from the $D(D_s)$ or $B(B_s,B_c)$ mesons have been studied. When these particles are produced, they will decay very quickly to the lighter final states which are used experimentally to reconstruct their mother particle. Here, by using the same formalism, we investigate the OZI-allowed two-body strong decays of these $3^-$ mesons, This may be helpful to gain more information of these high-spin states, especially for the undiscovered b-flavored ones.

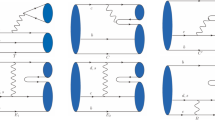
As Fig. 1 shows, the OZI-allowed two-body strong decays can be realized by introducing a scalar type interaction vertex. It can also be realized without that interaction vertex, that is, the light quark and antiquark are connected by a propagator, which is used in Ref. [42] and our previous work [43]. In the current situation, there is a light meson in the final states, whose wave function cannot be described by the instantaneous approximation. To deal with this difficulty, we take a different method, which is realized by using the reduction formula, PCAC and the low energy theorem. This method has been applied to deal with the strong decays of S-wave heavy–light mesons [44, 45], which get the results close to the experimental data. However, this method can only be applied to the case when the light meson being a pseudoscalar one. For the case when the light meson is vector, PCAC cannot be used. For those channels, we will adopt an effective lagrangian to describe the quark–meson coupling.

Fig. 1

Feynman diagram of the OZI-allowed two-body strong decay channel

Since the relativistic effects should be considered, especially for the state with high orbital angular momentum, using more appropriate wave functions to calculate the strong decays of these high-spin mesons is necessary. In this paper, the instantaneous Bethe–Salpeter equation [46, 47], namely, the full Salpeter equation is used to get the mass spectrum and corresponding wave functions of heavy–light mesons. The transition matrix can be written within Mandelstam formalism [48].

The paper is organized as follows. In Sect. 2, we present the theoretical formalism of the calculation. The wave function of the $3^-$ state is constructed. For the channels with a light pseudoscalar meson, the quark–meson coupling is introduced by two methods, while for the light vector case, an effective Lagrangian from other literature is adopted. In Sect. 3, we give the results of strong decays of four heavy–light mesons and compare them with those of other models. Finally, we draw the conclusion in Sect. 4.

2 Theoretical formalism

As the wave functions of heavy mesons will be used in the following to calculate the transition amplitude, it must be constructed as a starting point. In our previous work [50, 49, 41], the wave function of the $3^{-}$ state has been given as

(1)

where M and P are the mass and momentum of the meson, respectively; q is the relative momentum between the quark and antiquark; $q_\perp$ is defined as $q-\frac{P\cdot q}{M}P$; $f_i$s are functions of $q_\perp$ which will be obtained by solving the full Salpeter equation; $\epsilon _{\mu \nu \gamma }$ is the polarization tensor of the meson, which is totally symmetric and satisfies

$$\begin{aligned} g^{\mu \nu }\epsilon _{\mu \nu \gamma }=0, P^\mu \epsilon _{\mu \nu \gamma }=0. \end{aligned}$$

(2)

The completeness relation is given by [51]

$$\begin{aligned} \sum _{\lambda =-3}^{3} \epsilon ^{(\lambda )}_{abc}\epsilon ^{*(\lambda )}_{xyz}= & {} \frac{1}{6}(\mathcal {P}_{ax}\mathcal {P}_{by}\mathcal {P}_{cz} +\mathcal {P}_{ax}\mathcal {P}_{bz}\mathcal {P}_{cy}\nonumber \\&+\mathcal {P}_{ay}\mathcal {P}_{bx}\mathcal {P}_{cz} +\mathcal {P}_{ay}\mathcal {P}_{bz}\mathcal {P}_{cx}\nonumber \\&+\mathcal {P}_{az}\mathcal {P}_{by}\mathcal {P}_{cx}+\mathcal {P}_{az}\mathcal {P}_{bx} \mathcal {P}_{cy})\nonumber \\&-\frac{1}{15}(\mathcal {P}_{ab}\mathcal {P}_{cz}\mathcal {P}_{xy} +\mathcal {P}_{ab}\mathcal {P}_{cy}\mathcal {P}_{xz}\nonumber \\&+\mathcal {P}_{ab}\mathcal {P}_{cx}\mathcal {P}_{yz} +\mathcal {P}_{ac}\mathcal {P}_{bz}\mathcal {P}_{xy}\nonumber \\&+\mathcal {P}_{ac} \mathcal {P}_{by}\mathcal {P}_{xz}+\mathcal {P}_{ac}\mathcal {P}_{bx}\mathcal {P}_{yz}\nonumber \\&+\mathcal {P}_{bc}\mathcal {P}_{az}\mathcal {P}_{xy}+\mathcal {P}_{bc} \mathcal {P}_{ay}\mathcal {P}_{xz}\nonumber \\&+\mathcal {P}_{bc}\mathcal {P}_{ax}\mathcal {P}_{yz}), \end{aligned}$$

(3)

where we have defined $\mathcal {P}_{\mu \nu } \equiv -g_{\mu \nu } + \frac{P_\mu P_\nu }{M^2}$.

By using the reduction formula, the transition amplitude can be written as the production of the inverse propagator and the expectation value of the light meson field [52]. We take the process $D_{sJ}^{*}\rightarrow D^{(*)}K$ as an example, which has the form

$$\begin{aligned} \langle D^{(*)}(P_1)K(P_2)|D^{*+}_{sJ}(P)\rangle= & {} \int \mathrm{d}^4x\mathrm{e}^{iP_2\cdot x}(M_K^2-P_2^2)\nonumber \\&\times \langle D^{(*)}(P_1)|\Phi _K(x)|D^{*+}_{sJ}(P)\rangle .\nonumber \\ \end{aligned}$$

(4)

By using PCAC, the light meson field is expressed as the divergence of the axial-vector current divided by the decay constant of the light meson,

$$\begin{aligned} \Phi _K(x) = \frac{1}{M_K^2f_K}\partial ^\mu (\bar{q}\gamma _\mu \gamma _5 s). \end{aligned}$$

(5)

Combining Eqs. (4) and (5), we get

$$\begin{aligned}&\langle D^{(*)}(P_1)K(P_2)|D^{*+}_{sJ}(P)\rangle \nonumber \\&\quad = \frac{M_K^2-P_2^2}{M_K^2f_K} \int \mathrm{d}^4x\mathrm{e}^{iP_2\cdot x}\langle D^{(*)}(P_1)|\partial ^\mu (\bar{q}\gamma _\mu \gamma _5 s)|D^{*+}_{sJ}(P)\rangle \nonumber \\&\quad =\frac{-iP_2^\mu (M_K^2-P_2^2)}{M_K^2f_K} \int \mathrm{d}^4x\mathrm{e}^{iP_2\cdot x}\langle D^{(*)}(P_1)|\bar{q}\gamma _\mu \gamma _5 s|D^{*+}_{sJ}(P)\rangle ,\nonumber \\ \end{aligned}$$

(6)

where in the second equation partial integral is used. Finally, by using the low-energy theorem [52], we can get the form of the transition amplitude in the momentum space (see Fig. 2)

$$\begin{aligned}&\langle D^{(*)}(P_1)K(P_2)|D^{*+}_{sJ}(P)\rangle \approx (2\pi )^4\delta ^4(P{-}P_1{-}P_2)\frac{-iP_2^\mu }{f_K}\nonumber \\&\quad \times \langle D^{(*)}(P_1)|\bar{q}\gamma _\mu \gamma _5s|D^{*+}_{sJ}(P)\rangle . \end{aligned}$$

(7)

Fig. 2

Feynman diagram of the OZI-allowed two-body strong decay channel of the heavy–light meson with the interaction vertex being changed the form

This result can also be achieved by adopting the effective lagrangian method [29, 28],

$$\begin{aligned} \mathcal L_{qqP} = \frac{g}{\sqrt{2}f_h}\bar{q}_i\gamma _\mu \gamma _5q_j\partial ^\mu \phi _{ij}, \end{aligned}$$

(8)

where

$$\begin{aligned} \phi _{ij} = \sqrt{2}\left( \begin{array}{lll} \frac{1}{\sqrt{2}}\pi ^0 + \frac{1}{\sqrt{6}}\eta &{}\quad \pi ^+ &{}\quad K^+\\ \pi ^- &{}\quad -\frac{1}{\sqrt{2}}\pi ^0 + \frac{1}{\sqrt{6}}\eta &{}\quad K^0 \\ K^- &{}\quad \bar{K}^0 &{}\quad -\frac{2}{\sqrt{6}}\eta \\ \end{array} \right) \end{aligned}$$

(9)

is the chiral field of pseudoscalar mesons. The quark–meson coupling constant g is taken to be unity. $f_h$ is the decay constant.

In the Mandelstam formalism, the transition amplitude can be written as the overlapping integral over the Salpeter wave functions of the initial and final mesons [52],

(10)

where $m_1^\prime$ and $m_2^\prime$ are, respectively, the masses of quark and antiquark in the final $D^{(*)}$ meson; $\overline{\varphi }$ is defined as $\gamma ^0\varphi \gamma ^0$; $\varphi ^{++}$ is the positive energy part of the wave function. In the above equation, we have neglected the contributions of negative energy part of the wave function, which is very small compared with that of the positive one (less than $1\%$).

If the final light meson is $\eta$ or $\eta ^\prime$, we have to consider the $\eta$–$\eta ^\prime$ mixing

$$\begin{aligned} \left( \begin{array}{c} \phi _\eta \\ \phi _{\eta ^\prime } \\ \end{array} \right) = \left( \begin{array}{ll} \cos \theta &{}\quad \sin \theta \\ - \sin \theta &{}\quad \cos \theta \end{array} \right) \left( \begin{array}{c} \phi _{\eta _8}\\ \phi _{\eta _0} \end{array} \right) , \end{aligned}$$

(11)

where the mixing angle $\theta =19^\circ$ is used. The masses of the physical states are related to the masses of the flavor states by

$$\begin{aligned} \left( \begin{array}{c} M^2_{\eta _8} \\ M^2_{\eta _0} \\ \end{array} \right) = \left( \begin{array}{ll} \cos ^2\theta &{}\quad \sin ^2\theta \\ \sin ^2\theta &{}\quad \cos ^2\theta \end{array} \right) \left( \begin{array}{c} M^2_{\eta }\\ M^2_{\eta ^\prime } \end{array} \right) . \end{aligned}$$

(12)

By considering $\phi _{\eta _8}=(u\bar{u} + d\bar{d} -2s\bar{s})/\sqrt{6}$ and $\phi _{\eta _0}=(u\bar{u} + d\bar{d} + s\bar{s})/\sqrt{3}$, the transition amplitude of $D_{sJ}^*(2860)^+\rightarrow D_s^+\eta$ has the form [52]

$$\begin{aligned} \mathcal M= & {} P_2^\mu \left[ \frac{-2M_\eta ^2\cos \theta }{\sqrt{6}M_{\eta _8}^2f_{\eta _8}} + \frac{M_\eta ^2\sin \theta }{\sqrt{3}M_{\eta _0}^2f_{\eta _0}}\right] \nonumber \\&\times \,\langle D^{(*)}_s(P_1)|\bar{s}\gamma _\mu \gamma _5s|D^{*+}_{sJ}(P)\rangle , \end{aligned}$$

(13)

where $f_{\eta _0}$ and $f_{\eta _8}$ are the decay constants of $\eta _0$ and $\eta _8$, respectively.

The method above can only be applied to the processes when the light meson is a pseudoscalar. In the case when a light vector boson is involved, we use the effective lagrangian method which is adopted in Ref. [29]. The quark–meson coupling is described by the lagrangian

$$\begin{aligned} \mathcal {L}_{qqV} = \sum _{j}\bar{q}_j\left( a\gamma _\mu + \frac{ib}{2m_j}\sigma _{\mu \nu }P_2^\nu \right) V^\mu q_j, \end{aligned}$$

(14)

where $V^\mu$ is the field of the light vector meson with momentum $P_2$; $a=-3.0$ and $b=2.0$ represent the vector and tensor coupling strengths, respectively. In Ref. [29], this lagrangian is reduced to the nonrelativistic form and the harmonic oscillator wave functions are used. In our calculation, we use Eq. (14) directly, and the full Salpeter wave functions are applied which could provide some comparison with the results in Ref. [29].

After finishing the trace and integral in Eq. (10), we get the transition amplitudes which are expressed as several form factors,

$$\begin{aligned} \mathcal M_{D_{s3}^*(2860)\rightarrow DK} = \frac{-i}{f_K}\epsilon ^{\alpha \beta \gamma }P_{1\alpha } P_{1\beta } P_{1\gamma } t_1, \end{aligned}$$

(15)

$$\begin{aligned} \mathcal M_{D_{s3}^*(2860)\rightarrow D^*K} =\frac{-i}{f_K} \epsilon ^{\alpha \beta \gamma }\epsilon ^\delta _1\epsilon _{\alpha \delta \sigma \xi }P^\sigma P_{1}^{\xi }P_{1\beta }P_{1\gamma }t_2, \end{aligned}$$

(16)

$$\begin{aligned} \mathcal M_{D_{s3}^*(2860)\rightarrow DK^*} =\epsilon ^{\alpha \beta \gamma }\epsilon ^\delta _2\epsilon _{\alpha \delta \sigma \xi }P^\sigma P_{1}^{\xi }P_{1\beta }P_{1\gamma }t_3, \end{aligned}$$

(17)

$$\begin{aligned} \mathcal M_{D_3^*(2760)\rightarrow D_2^*(2460)\pi }= & {} \frac{-i}{f_\pi }\epsilon ^{\alpha \mu \sigma \delta }P_\sigma P_{1\delta }P_1^\beta \epsilon _{\alpha \beta \gamma }\epsilon _{1\mu \nu }\nonumber \\&\times \, (P_1^\gamma P^\nu t_4 + g^{\gamma \nu } M^2 t_5), \end{aligned}$$

(18)

$$\begin{aligned} \mathcal M_{D_3^*(2760)\rightarrow D_1(2420)\pi }= & {} \frac{-i}{f_\pi }\epsilon ^{\alpha \beta \gamma }\epsilon ^\mu _1 P_{1\beta } P_{1\gamma } (P_{1\alpha } P_\mu t_6\nonumber \\&+\, g_{\alpha \mu } M^2 t_7), \end{aligned}$$

(19)

$$\begin{aligned} \mathcal M_{B_{3}^*\rightarrow B^*\rho }= & {} \epsilon ^{\alpha \beta \gamma }P_{1\alpha }(P_{1\beta }\epsilon _1\cdot P\epsilon _{2\gamma }s_1+P_{1\beta }\epsilon _2\cdot P\epsilon _{1\gamma }s_2 \nonumber \\&+\,P_{1\beta }P_{1\gamma }\epsilon _1\cdot P\epsilon _2\cdot P s_3/M^2\nonumber \\&+\,P_{1\beta }P_{1\gamma }\epsilon _1\cdot \epsilon _2 s_4+ M^2 \epsilon _{1\beta }\epsilon _{2\gamma }s_5). \end{aligned}$$

(20)

In the above equations, $\epsilon ^{\alpha \mu \sigma \delta }$ is the totally antisymmetric tensor; $\epsilon$, $\epsilon _1$, and $\epsilon _2$ are the polarization vectors (tensor) of the initial meson, the final heavy meson, and the final light meson, respectively. The form factors $t_1\sim t_7$ and $s_1\sim s_5$ are integrals of $q_\perp$. For different channels, the integrations have different expressions. Thus the form factors have different values. Here we just take some channels of $D_{s3}$, $D_3$, and $B_3^*$ as examples. Other decay channels would have the same form of form factors as one of the above equations. For instance $\mathcal M_{D_3^*(2760)\rightarrow D_{1^\prime }(2420)\pi }$ would have the same expression as Eq. (19).

The two-body decay width is

$$\begin{aligned} \Gamma =\frac{|{\vec {P}}_1|}{8\pi M^2}\frac{1}{2J+1}\sum _\lambda |\mathcal M|^2, \end{aligned}$$

(21)

where $|{\vec {P}}_1| = \sqrt{[M^2-(M_1-M_2)^2][M^2-(M_1 + M_2)^2]}/2M$ is the momentum of the final meson; $J=3$ is the spin quantum number of the initial meson; $\lambda$ represents the polarization of both initial and final mesons.

Fig. 3

Two-body strong decay widths change with the mass of $3^-$ bottom and bottom–strange mesons. Only the dominant channels are considered. a is for $B_3^*$ and b is for $B_{s3}^*$

Table 2 Two-body strong decay widths (MeV) of $D_{s3}^{*}(2860)$. $^3P_0$ model is adopted in Refs. [34,35,36,37,38] and the chiral quark model is adopted by Ref. [29]

3 Results and discussions

The wave functions of mesons with different quantum numbers ($J^{PC}$) have different forms. So for each type of mesons, we have to construct the wave function first (such as Eq. (1)), and then deduce the full Salpeter equation fulfilled by this function [53, 50]. To solve this equation numerically, we should determine the values of parameters in the interaction potential, which in this work is phenomenologically written as the Coulomb-like term (comes from one-gluon exchange) plus a linear term. This form of the potential is used in most of the quark potential models, where one more free parameter $V_0$ is introduced to shift the whole spectrum, which makes the predicted spectrum consistent with the experimental values. Its value is fixed by fitting the mass of the ground state (that is, we treat this mass as an input parameter), which in this case is $D_{s3}^*(2860)$. Then the whole spectrum is fixed. In our previous work [54], we showed that, at least for the first few excited states, the prediction of the mass is consistent with the experimental data.

The parameters used in the calculation are as follows: $m_u=0.305$ GeV, $m_d=0.311$ GeV, $m_s=0.5$ GeV, $m_c=1.62$ GeV, and $m_b=4.96$ GeV. For the masses of $D_{s3}^*$ and $D_3^*$, we will use the experimental data as the input value. For $B_3^*$, we will study two cases: $M=5978$ MeV (to compare with experimental result) and $M=6015$ MeV (to compare with the results of other models). As to $B_{s3}^*$ meson, we will use 6178 MeV to compare with Refs. [25, 32]. When the transition amplitude is calculated, the following parameters are adopted: $f_\pi$= 130.4 MeV, $f_K$= 156.2 MeV [55], $f_{\eta _8} = 1.26 f_\pi$, $f_{\eta _0} = 1.07 f_\pi$, $M_{\eta _8} =604.7$ MeV, and $M_{\eta _0} = 923.0$ MeV [52].

The decay widths for $D_{s3}^*$ calculated by different models are listed in Table 2. The dominant channels are DK and $D^*K$, which in our calculation have partial widths 31.1 MeV and 14.6 MeV, respectively. Here we use $D^{(*)}K$ to represent $D^{(*)+}K^0+D^{(*)0}K^+$. Our results are close to those of other models, except that $\Gamma _{D^*K}$ in Ref. [35] is about two times of ours. References [36, 35, 34, 37, 38] use the $^3P_0$ model but with different parameter values, which causes diverse results. The chiral quark model is applied in Ref. [29]. In this work, for heavy mesons, the SHO wave function is adopted. One can see that their results are smaller than ours. For the $DK^*$ channel, we use the same effective lagrangian form as that in Ref. [29], whose result is about twice smaller than ours. The total decay width for our model is close to the central value of the LHCb’s result [19, 20], which is also at the same order with those of other models.

For $D_3^*$, the results of different models are presented in Table 3. In our calculation, the partial widths of two dominant channels $D\pi$ and $D^*\pi$ are, respectively, 33.1 MeV and 22.0 MeV, which are consistent with those of other models, especially the chiral quark model [30]. For the channels with light vector meson $D\rho$ and $D\omega$, our results are about 4 times of those in Ref. [30], but compatible with those of the $^3P_0$ model [33]. Reference [56] also uses the $^3P_0$ model, but one gets very large widths for these two channels, which makes the total width larger. In Table 3, the decay width of $D_J^*(2760)$ [22] is very close to our result, while for $D_3^*(2760)$ [23], as we pointed out before, its width is 30 MeV larger. Both results have large errors, which need more experimental observations.

Table 3 Two-body strong decay widths (MeV) of $D_{3}^{*}(2760)$. The $^3P_0$ model is adopted in Refs. [33, 34, 40, 56] and the chiral quark model is adopted by Ref. [30]

Table 4 Two-body strong decay widths (MeV) of the $B_{3}^{*}$ state with the mass 6.11 GeV. The second subrow of the first row is the mass (MeV) of the $B_{3}^*$ meson used in different models. The value a[b] represents $a\times 10^{-b}$. References [25, 32, 39] use the $^3P_0$ model. References [26, 27] use the heavy meson effective theory and chiral quark model, respectively

In Table 4, the decay width for $B_3^*$ is given. To compare with the results of other models, we consider two cases with different mass of $B_3^*$. For $M=5978$ MeV, the total decay width (22.9 MeV) is about 3 times smaller than the central value of the experimental data ($70^{+30}_{-20}\pm 30$ MeV) which has large errors. So we expect more data as regards this particle will be accumulated and more precise decay widths will be given. In Ref. [26], the effective theory is used. There the experimental value is used to deduce the effective coupling which is applied to calculate the partial decay widths, the first two of which are about 3 times as large as ours. Reference [27] gets the total decay width of 60 MeV, which is twice larger than ours. When M is taken to be 6105 MeV, our results increase by about two times, which is about 2 and 4 times of those in Ref. [32] and Ref. [25]. In our calculation, the $B^*_2\pi$ and $B_1^\prime \pi$ channels also give sizable contributions, which may be detected in the future to clarify the properties of this particle. For the mass of $B_2^*$, we take the value in PDG [55], which is 50 MeV smaller than that taken in Ref. [25] and Ref. [32]. Both references use the $^3P_0$ method and SHO wave functions. In Fig. 3a, we plot the total and main partial decay widths of $B_3^*$, where $M_{B_3^*}$ is taken to be 5950–6150 MeV. The total width changes from 18 to 89 MeV, which implies it depends strongly on the mass. One also notices that with the increase of mass, the decay width increases more and more quickly. When the mass of $B_3^*$ changes, the wave function actually changes not very much, and most of the changes come from the value of the overlap integral of wave functions, which is sensitive to the phase space. As the initial and final heavy mesons are, respectively, D wave and S wave for the two main decay channels, this makes the last point more important.

Table 5 Two-body strong decay widths (MeV) of the $B_{s3}^{*}$ state with the mass 6.18 GeV. The second subrow of the first row is the mass (MeV) of the $B_{s3}^*$ meson used in different models. The value a[b] represents $a\times 10^{-b}$. The $^3P_0$ model is used in Refs. [25, 32, 39], and the chiral quark model is used in Ref. [27]

Table 6 The ratios of decay widths of different channels

The result for $B_{s3}^*$ is given in Table 5. BK and $B^*K$ give the main contribution. For the total decay width, we get 40.8 MeV, which is larger than those in Refs. [25] and [32] but smaller than that in Ref. [39], where $^3P_0$ model is applied. Reference [27] uses the chiral quark model. One can see a result about twice of ours is obtained when M takes the same value. Figure 3b shows when M changes from 6050 to 6200 MeV, the total decay width increases from 11 to 49 MeV. As LHCb is running, we expect this state will be detected in the near future.

An experimentally measured quantity is the ratio of the partial widths of two dominant decay channels. In Table 6, we present both theoretical and experimental results for this quantity of four heavy–light mesons. For $\Gamma [D_{s3}^*\rightarrow D^*K]/\Gamma [D_{s3}^*\rightarrow DK]$, the theoretical models listed in Table 6 get results 0.43–0.75. In Ref. [57], the BaBar Collaboration gave

$$\begin{aligned} \frac{\Gamma [D_{sJ}^*(2860)\rightarrow D^{*}K]}{\Gamma [D_{sJ}^*(2860)\rightarrow DK]}=1.10\pm 0.15\pm 0.19, \end{aligned}$$

(22)

where the spin of this particle was not determined, while it was believed that $J=1$ or $J=3$, or a mixing of the former two states. This experiment result is apparently larger than the theoretical estimation of this ratio for $D_{s3}^*(2860)$, which implies $D_{sJ}^*(2860)$ is unlikely to be $D_{s3}^*(2860)$. This can be understood as follows. On the one hand, there are more than one particle around this mass region, such as $1D(3^-)$, $2S(1^-)$, $1D(1^-)$, $1D(2^-)$, and $1D^\prime (2^-)$. As Ref. [29] proposed, if the mass of $1D(3^-)$ and $1D^\prime (2^-)$ are close enough not to be distinguished experimentally, then BaBar’s results can be explained. One the other hand, the latest data published by the LHCb Collaboration [19, 20] indicate that there are two states $D_{s1}^*(2860)$ and $D_{s3}^*(2860)$ around this mass region. So a more precise measurement of this ratio is needed. We expect this can be achieved in the future by LHCb or the B factories. The ratio $\Gamma [D_{3}^*\rightarrow D^*\pi ]/\Gamma [D_{3}^*\rightarrow D\pi ]$ is close to that of the $D_{s3}^*$ case as a result of the $SU(3)_F$ symmetry. Our result is close to those of Refs. [34, 27]. For $\Gamma [B_{3}^*\rightarrow B^{*}\pi ]/\Gamma [B_{3}^*\rightarrow B\pi ]$, we present two results, which correspond $M_{B_{s3}^*}$= 6105 MeV and 5978 MeV (in the parentheses), respectively. One can see our result is close to those of Refs. [32, 27]. When $M_{B_3^*}$ takes values 5950–6150 MeV, this ratio changes from 0.85 to 1.03. The ratio $\Gamma [B_{s3}^*\rightarrow B^{*}\pi ]/\Gamma [B_{s3}^*\rightarrow B\pi ]$ is close to that of the $B_3^*$ case, which changes from 0.68 to 0.90 when $M_{B_{s3}^*}$ takes 6050–6200 MeV.

4 Summary

We have studied OZI-allowed two-body strong decays of $3^-$ heavy–light mesons. The instantaneous Bethe–Salpeter method is applied to get the wave functions of the heavy mesons. For $D_{s3}^*$ and $D_3^*$, the total decay widths are within the experimental error. For $B_3^*$ state, we present total and several main decay widths within the mass region 5950–6150 MeV. When $M_{B_3^*}=5978$ MeV, our result is much smaller than the central value of the decay width of the new discovered B(5970), while it is still within the experimental errors. So a more precise detection is needed. For the $B_{s3}^*$ state, there is no candidate in the experiments, and our calculations can provide some help for the future study of this particle. Our results also show that the decay widths of $B_3^*$ and $B_{s3}^*$ depend strongly on the particle mass.