Phase separation and exotic vortex phases in a two-species holographic superfluid

Abstract

At finite temperature, the stable equilibrium states of coupled two-component Bose Einstein condensations (BECs) with the same conformal mass in both non-rotating and rotating condition can be obtained by studying its real dynamics via holography. The equilibrium state is the state where the free energy reaches the minimum and does not change any more. In the case of no rotation, the spatial phase separated states of the two components become more stable than the miscible condensates state when the direct repulsive inter-component coupling constant $\eta>\eta _c>0$. Under rotation, the quantum fluid reveals four equilibrium structures of vortex states by varying the $\eta$ from the miscible region to the phase separated region. Among the four structures, the vortex sheet solution is the most exotic one that appears in the phase separated region.

1 Introduction

The gauge-gravity duality [1,2,3] which relates strongly interacting quantum field theories to theories of classic gravity in higher dimensions has provided a new scheme, which can not only study strongly interacting condensed matter systems in equilibrium [4, 5], but also study the real time dynamics when the system is far away from equilibrium [6,7,8,9,10]. Also, Schwinger-Keldysh propagators from AdS/CFT correspondence [11,12,13,14] has been studied in details in order to compute the real-time n-point functions from the partition function in the bulk. The first proposed model of a single component holographic superfluid/BEC was given in [15,16,17]. The array of vortices is known to happen in a rotating superfluid [18], which has been obtained in holography by studying the full dynamics of the single component holographic superfluid/BEC in a rotating disk as the final time-independent solutions [19, 20], while single vortex has been obtained in the same system as a static solution in the presence of rotation without the dynamic process [21,22,23,24,25,26]. Besides the superfluid/BEC with only one order parameter, a two-component superfluids/BECs with two coupled order parameters have become one of the most concerned topics in condensed matter physics, since it demonstrates novel quantum states which can not be observed in a single component system as confirmed in the frame work of two-component G–P equations [27]. The two components $\varPsi _1$ and $\varPsi _2$ are coupled through the direct coupling term $\eta |\varPsi _1|^2|\varPsi _2|^2$. In the case of no rotation, the two-component BECs will enter a spatial separation state due to the repulsive interaction $\eta >0$ between the two components [28,29,30,31]. In the presence of rotation, by solving the time dependent two-component Gross–Pitaevskii (G–P) equations where the two scalars have the same mass and the same intracomponent interaction, the equilibrium vortex structures can be obtained after a long time revolution, which reveal rich structures by varying the direct coupling between the two components [32]. As $\eta$ increase the interlocked vortex lattices undergo phase transitions from triangular to square, to double-core lattices, and eventually develop vortex sheets [33]. Vortex sheet is a state that the vortices are aligned to make up winding chains of single quantized vortices, and the chains of two components are interwoven alternately, or form as the cylindrical vortex sheets. Such a solution was proposed for the first time by Landau and Lifshitz [34] and has been observed experimentally in $^{3}$He A [35]. Vortex sheet has proved to be an important physical object with nontrivial topology, which has many physical applications [36].

Though the rotating single component superfluid has been studied thoroughly in holography, the holographic study on a rotating two component superfluid is still lacking. The purpose of this article is to study the equilibrium properties of strongly coupled two component BECs with and without rotation by using the holographic method. Indeed, continuous phase transition can not happen in 1D and 2D since the divergent fluctuation will destroy the long range correlation. However, the holographic model we used is in the large N limit while the fluctuations are suppressed, also the size of the system is much larger than the correlation length, we are not thinking of the holographic finite size effect [37] in the present work. The equilibrium states can be obtained by evolving the system from an initial homogeneous superfluid state under the disturbance of rotation or small fluctuation. Our treatment is very similar to the calculation of the time-dependent two-component G–P equation, where the static solution is also obtained as the final state that no longer changes with time anymore [32, 33]. When there is no rotation, the phase separation states was studied in detail for different temperatures and different values of coupling constants. We found that the phase separation states tend to occur in the case of low temperature and relatively high inter-components direct repulsive interaction, while Josephson coupling always prevents the system from phase separation. Under rotation, by turning off Josephson coupling, the holographic superfluid reveals four vortex structures corresponding to different direct coupling values between two components. The four structures include triangle lattice, square lattice, vortex stripe and vortex sheet. Vortex sheet solution is the result of phase separation. The vortex diagram in the intercomponent direct coupling $\eta$ versus rotation-frequency $\varOmega$ is also be obtained, which is similar to the simulation results of the two-component G–P equation [33]. Because of the nonlinear nature of the bulk theory, we will have to rely on numerical methods by solving a highly nonlinear partial differential bulk equations of motion.

This paper is organized as follows. Section 2 introduces the holographic superfluid model with two condensations, the equations of motion (EoMs) of the model and also the numerical method we adapted to solve the EoMs. Section 3 discusses the properties of the two-component system without rotation and the phase separation state is obtained with a large repulsive inter-components coupling. Section 4 presents the appearance of exotic vortex phases of the two-component system under rotation, and the vortex phase diagram is also obtained. The dynamic process of vortex evolution and corresponding free energy properties are also studied. Section 5 is devoted to the some discussions.

2 Holographic model and the time evolution equations of motion

The holographic model we use is a bottom-up construction contains two coupled charged scalar fields living in an AdS black hole background, which is an extension of the single component holographic superfluid model proposed in [16]. The action include two charged scalar fields and one U(1) gauge field [38]

$$\begin{aligned} S= & {} \int d^4x \sqrt{-g}\Bigg [-\frac{1}{4}F^2-\sum _{j=1}^2( |D\varPsi _j|^2+m_j^2|\varPsi _j|^2)\nonumber \\&+ V(\varPsi _1,\varPsi _2)\Bigg ], \end{aligned}$$

(1)

the inter-component coupling potential between the two charged scalar fields takes the form

$$\begin{aligned} V(\varPsi _1,\varPsi _2)=\eta |\varPsi _1|^2|\varPsi _2|^2, \end{aligned}$$

(2)

where $\eta$ is called the direct coupling. Note that the interaction potential takes the same form as the G–P equations for coupled two-component superfluid [32, 39, 40]. In the holography, there is another more complex model dual to a two-component superfluid with two gauge fields corresponding to two charged scalar fields respectively [41, 42].

Also in the action, $F_{\mu \nu }=\partial _\mu A_\nu -\partial _\nu A_\mu$, $D_\mu =\partial _\mu -iqA_\mu$ with q the charge. The metric of the $AdS_4$ black hole background adopts Eddington-Finkelstein coordinates,

$$\begin{aligned} ds^2=\frac{\ell ^2}{z^2}(-f(z)dt^2-2dtdz + dr^2+ r^2d\theta ^2). \end{aligned}$$

(3)

in which $\ell$ is the AdS radius, z is the AdS radial coordinate of the bulk and $f(z)=1-(z/z_h)^3$. Thus, $z=0$ is the AdS boundary while $z=z_h$ is the horizon; the Hawking temperature is $T=3/(4\pi z_h)$. r and $\theta$ are respectively the radial and angular coordinates of the dual $2+1$ dimensional boundary, which is a disk that suitable to study the properties of the two- component superfluid under rotation.

The axial gauge $A_z=0$ is adopted as in [7, 17]. Near the boundary $z=0$, by choosing that $m_1^2=m_2^2=-2$, the general solutions take the asymptotic form as,

$$\begin{aligned} A_\nu= & {} a_\nu + b_\nu z+\mathscr {O}(z^2), \end{aligned}$$

(4)

$$\begin{aligned} \varPsi _j= & {} \varPsi _j^1 z+ \varPsi _j^2 z^2+\mathscr {O}(z^3). \end{aligned}$$

(5)

$j=1,2$, the coefficients $a_{r,\theta }$ can be regarded as the superfluid velocity along $r, \theta$ directions while $b_{r,\theta }$ as the conjugate currents [21]. Coefficients $a_t$ and $b_t$ are respectively interpreted as chemical potential $\mu$ and charge density $\rho$ in the boundary field theory. Moreover, $\varPsi _j^1$ is a source term which is always set to be zero, $\varPsi _j^2$ is the vacuum expectation value $\langle O_j\rangle$ of the dual scalar operator in the boundary in the spontaneous symmetry broken phase. As the simplest case we set $m_1^2=m_2^2$, there is a discrete symmetry upon interchange of the two charged scalars. Such a discrete symmetry was also considered in the two-component G–P equations simulations [32, 33].

We take the superfluid interpretation of the holographic model, where the rotation is introduced by imposing the Dirichlet boundary condition for gauge fields on the boundary as [17, 22]

$$\begin{aligned} a_\theta =\varOmega r^2, \end{aligned}$$

(6)

where $\varOmega$ is the constant angular velocity of the disk and $a_\theta$ is the superfluid velocity along the $\theta$ direction. Since the system is only given rotational speed, and that the superfluid is confined to the container, so there is no radial velocity ($a_r=0$). In another word, the disk in the simulation should be static in the inertial frame, but the superfluid rotates relative to the disk with an angular velocity. Then the picture is that the disk is static while the superfluid is rotating, or equivalently we treat the superfluid as static while the disk is rotating. The radius of the boundary disk is set as $r=R$. The Neumann boundary conditions $\partial _r h_i=0$ are adopted both at $r=R$ and $r=0$, where $h_i$ represents all the fields except $a_\theta$.

Without loss of generality we rescale $\ell = z_h = q=1$. Therefore, by scaling $\varPsi _j= \psi _j z$ and using the axial gauge that $A_z=0$, the equations of motion (EoMs) can be written as

$$\begin{aligned} \partial _t\partial _z \psi _1&=\frac{1}{2}\Bigg \{-\eta \psi _1 |\psi _2|^2+i\Bigg [\psi _1\partial _z A_t+2A_t \partial _z \psi _1-\psi _1 \partial _r A_r\nonumber \\&\quad +2A_r \partial _r \psi _1-\frac{\psi _1\partial _\theta A_\theta +2A_\theta \partial _\theta \psi _1}{r^2}\Bigg ]\nonumber \\&\quad +\Bigg [(1-z^3)\partial _z^2 -3z^2\partial _z +\partial _r^2 +\frac{\partial _\theta ^2}{r^2}-z-A_r^2-\frac{A_\theta ^2}{r^2}\Bigg ]\psi _1\Bigg \}, \end{aligned}$$

(7)

$$\begin{aligned} \partial _t\partial _z \psi _2&=\frac{1}{2}\Bigg \{-\eta \psi _2 |\psi _1|^2+i\Bigg [\psi _2\partial _z A_t+2A_t \partial _z \psi _2-\psi _2 \partial _r A_r\nonumber \\&\quad +2A_r \partial _r \psi _2-\frac{\psi _2\partial _\theta A_\theta +2A_\theta \partial _\theta \psi _2}{r^2}\Bigg ]\nonumber \\&\quad +\Bigg [(1-z^3)\partial _z^2 -3z^2\partial _z +\partial _r^2 +\frac{\partial _\theta ^2}{r^2}-z-A_r^2-\frac{A_\theta ^2}{r^2}\Bigg ]\psi _2\Bigg \}, \end{aligned}$$

(8)

$$\begin{aligned} \partial _z^2 A_t&=-2\mathfrak {I}(\psi _1^*\partial _z\psi _1+\psi _2^*\partial _z\psi _2)+\partial _z\partial _r A_r+\frac{\partial _z\partial _\theta A_\theta }{r^2}, \end{aligned}$$

(9)

$$\begin{aligned} \partial _t\partial _z A_r&=\mathfrak {I}(\psi _1^*\partial _r\psi _1+\psi _2^*\partial _r\psi _2)-A_r(|\psi _1|^2+|\psi _2|^2)\nonumber \\&\quad +\frac{\partial _z\partial _r A_t}{2}+\frac{\partial _\theta ^2 A_r-\partial _r\partial _\theta A_\theta }{2r^2}+\frac{(1-z^3)\partial _z^2-3\partial _z}{2}A_r, \end{aligned}$$

(10)

$$\begin{aligned} \partial _t\partial _z A_\theta&=\mathfrak {I}(\psi _1^*\partial _\theta \psi _1+\psi _2^*\partial _\theta \psi _2)-A_\theta (|\psi _1|^2+|\psi _2|^2)\nonumber \\&\quad +\frac{\partial _r\partial _\theta A_r-\partial _r^2 A_\theta +\partial _z\partial _\theta A_t}{2}+\frac{(1-z^3)\partial _z^2-3\partial _z}{2}A_\theta . \end{aligned}$$

(11)

The EoMs are solved numerically by the Chebyshev spectral method in the z, r direction, while Fourier decomposition is adopted in the $\theta$ direction. The time evolution is simulated by the fourth order Runge–Kutta method. The GPU computing is used to speed up the calculation. The initial state at $t=0$ is always chosen to be a homogeneous solution for fixed $\eta$ when there is no rotation, which can be obtained by solving the time independent EoMs by fixing a chemical potential $\mu$ with the Newton–Raphson method. The solutions are considered to be the equilibrium states when the norm of changes of all fields become smaller than $10^{-5}$ for sufficient long time interval. Practically, a solutions at later time t is used to minus the solutions at $t-\delta t$, when the maximum of the change of the solution become smaller than $10^{-5}$ for a time interval ($\delta t=100$). In order to verify whether its stability, random perturbation of the order $\psi *10^{-2}$ is added to the order parameter. Then the system starts to evolve and will return to the same stable state in a short time, which is the state before the perturbation was added. The solution can remain unchanged at $t=20{,}000$ and beyond, so we think we attained a stable solution.

There is critical value $\mu _c(\eta )$ above which the two scalar fields will condense with the same value as a result of the discrete symmetry between the two components. From numerics we found that $\mu _c(0) \sim 4.07$, then the dimensionless critical temperature is $T_c^0 = \frac{3}{4\pi \mu _c(0)}=0.0587$. Turning on the direct coupling $\eta$ from $-\,0.5$ to 0.5 will not alter the critical temperature, though a positive/negative $\eta$ will reduce/increase the value of order parameter a bit. In all the dynamic simulation we set $T=0.82 T_c^0$, at which for every combination of $-\,0.5\le \eta \le 0.5$, the system always have a stable homogeneous solution with the two components have the same value of order parameter.

3 Phase separation and the effect of $\eta$

Phase separation is an inhomogeneous solution that the two condensates do not overlap spatially. The immiscible state can be more stable than the miscible state with a lower free energy, which is a result of the repulsive interaction between the two condensations when the positive $\eta$ is large enough and can be seen from the potential Eq. (2). Such an inhomogeneous stable solution can be obtained by solving the full time dependent equation. At initial time the system is in a homogeneous and miscible state with $\varPsi _1=\varPsi _2$ at fixed $\eta$, such a homogeneous state might be a metastable state which can evolve to a final stable inhomogeneous state, which will not change in time anymore, the real ground state. Without rotation, it is more convenient to adopt the Cartesian coordinate rather than the polar coordinate in the boundary theory, the metric is then $ds^2=\frac{\ell ^2}{z^2} (-f(z)dt^2-2dtdz + dx^2+ dy^2 )$. To study the phase separation just in x direction, we take the assumption that all fields are functions of t, z, x. At the boundary, we use periodic boundary conditions. To quantitatively describe the spatial overlap of the two condensations, we define an integral

$$\begin{aligned} \chi =\int _0^L dx \frac{|\langle O_1(x) \rangle ||\langle O_2(x) \rangle |}{|\langle O_h \rangle |.^2}, \end{aligned}$$

(12)

where $\langle O_h \rangle$ is the corresponding homogeneous order parameter at $t=0$ and the length of the x-axis is $L=50$. The system size L has no effect on the properties.

Fig. 1

a, b The overlap factor $\chi$ as a function of $\eta$. c, d The configuration of $\langle O_1(x)\rangle$ (black line) and $\langle O_2(x) \rangle$ (red line) in a phase separated phase

If $\chi = 1$, system shows no phase separation, and it stays in the initial homogeneous state. Otherwise, if $\chi \ll 1$, it would be fair to say the system shows phase separation. In the intermediate case, the system is partially phase-separated and partially phase-mixed. In Fig. 1a, we show that at three different temperatures, the overlapping integral $\chi$ as a function of $\eta$. The increase of $\chi$ along temperature when $\eta =0.5$ indicates that the system is harder to enter the phase separation phase, agrees with the increased correlation length of both condensations when T is approaching $T_c$. Two samples of $\langle O_{1,2}\rangle$ of a separated phase are illustrated in Fig. 1b, c. We tried to interchange the solutions of $\varPsi 1$ and $\varPsi 2$, and then substituted them into the equations to continue the simulation. We found that the solutions are still stable, so the solutions we obtained satisfy the commutative symmetry in the action. Such an exotic immiscible state has been experimentally observed in a two- [43] and a three- [44] component quantum fluid. In addition, the phase separated state can also be obtained from a holographic first order phase transition in an inhomogeneous black holes [45, 46].

4 Exotic vortex phases under rotation and phase diagram

In this section we are going to discuss the dynamics of the two-component BECs under rotation and also the phase diagram of final equilibrium vortex. We think of a physical process that begin with a stable homogeneous configuration without rotation corresponding to a fixed temperature (which can be obtained by solving the time independent EOMs by the Newton–Raphson method). Then, by applying the boundary condition Eq. (6), we increase the superfluid velocity along the $\theta$ direction to make the system suddenly rotate. The added velocity will drive the system to evolve and finally enter a stable state. To illustrate the stability of the long time static static states, one can also compute the free energy F of the system. We are working in the probe limit, which means that the fixed back ground black hole plays the role of a heat reservoir.

The temperature of the superfluid is fixed, then the free energy of the probe superfluid can evolve to the lowest value. At a fixed temperature, F can be computed from the renormalized on-shell action $S_{ren}$, which consists of two parts $S_{o.s.}$ and $S_{c.t.}$. Then one can get that $F=TS_{ren}=T(S_{o.s.}+S_{c.t.})$. $S_{o.s.}$ is the bare on-shell action obtained by subtracting the equation of motions from (1) and $S_{c.t.}=-\sum _{j=1}^2\int dtdrd\theta$ $\sqrt{-\gamma }\varPsi _j\varPsi _j^\star |_{z=0}$ is the term to remove the divergence near the boundary $z=0$, in which $\gamma$ is the determinant of the reduced metric. Therefore, the form of the renormalized on-shell action is

$$\begin{aligned} S_{ren}= & {} -\frac{1}{2}\int dtdzd\theta \left[ \frac{1}{r}A_\theta \partial _rA_\theta \right] |_{r=R}\nonumber \\&+\frac{1}{2}\int dtdrd\theta \left[ r\left( -a_tb_t+\frac{1}{r^2}a_\theta b_\theta \right. \right. \nonumber \\&\left. \left. +\sum _{j=1}^2(\varPsi _j^{1\star }\varPsi _j^2+\varPsi _j^{2\star }\varPsi _j^1)\right) \right] \nonumber \\&+\int dtdzdrd\theta [3\eta |\varPsi _1|^2|\varPsi _2|^2]\nonumber \\&+\frac{iq}{2}\int dtdzdrd\theta \Bigg [\frac{r}{z^4}A_\mu \sum _{j=1}^2(\varPsi _j^\star \partial ^\mu \varPsi _j\nonumber \\&-\varPsi _j\partial ^\mu \varPsi _j^\star )-2iqA^\mu |\varPsi _j|^2\Bigg ] \end{aligned}$$

(13)

Fig. 2

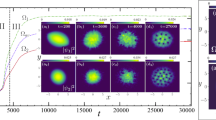
a The dynamical formation of two-component vortex lattice at separate times with $R=20$ , $\varOmega =0.1$ and $\eta =-0.2$. The temperature is $T=0.82 T_c^0$. The top row is component $\langle O_1\rangle$ and the second row is component $\langle O_2\rangle$. b The time evolution of average value of order parameter. c The time evolution of rescaled free energy under the same parameters as above

Fig. 3

Four typical vortex phases at $T=0.82 T_c^0$ and the corresponding radial profiles of $\langle O_{1,2}\rangle$ in the $\theta =\pi /2$ direction: a $\eta =-0.6,\varOmega =0.1$. b $\eta =-0.2,\varOmega =0.1$. c $\eta =-0.05,\varOmega =0.1$

In the presence of rotation, focusing on the case when the holographic two-component superfluid is at a temperature $T=0.82 T_c^0$, development of vortex lattices from $t=0$ to the final equilibrium state at $t=2000$ for $R=20$ , $\varOmega =0.1$ and $\eta =-0.2$ are shown in the above two rows of Fig. 2a. The Fig. 2b shows the dynamics for the average value of order parameters $\langle O_1\rangle$ and $\langle O_2\rangle$. After $t\simeq 1500$, the two averages are equal and do not change any more. The bottom row of Fig.2 shows the time evolution of the corresponding free energy $(F-F_n)/T$, in which $F_n$ is the free energy in the normal state, i.e., $\varPsi _j=0$. In the regime $30\lesssim t \lesssim 100$ the system is in a high free energy metastable state. At time $t\simeq 100$ the free energy begins to decrease, and at the same time the vortices begin to form at edge of the disk. After $t \gtrsim 200$, when vortices have fully formed and gradually move into the inner of the disk and align to the lattice structure, we can see the system is in a equilibrium state with constant lower free energy. Until the final square lattice is formed, the free energy always stays at this minimum, which confirms the stability of the final structure. Also in [47], the time dependent “free energy” was also plotted in the vortex dynamics in a type II superconductor under a periodic magnetical field.

Through the dynamic evolution of vortex under different coupling constants, we found several kinds of vortex phases. By increasing the inter-component interaction $\eta$ from $-\,0.6$, the system will approach the phase separated regime. Then the interlaced lattices are expected, where vortices in either component are filled by the other component. The sum of $\langle O_1 \rangle$ and $\langle O_2 \rangle$ is found to be an approximate constant with small fluctuation, this is the holographic realization of Thomas-Fermi distribution. In Fig. 3a–c, by increasing $\eta$ from $-\,0.6$ we see triangular lattices ($-\,0.6\le \eta \le -\,0.45$), square lattices ($-\,0.45\le \eta \le -\,0.1$) and vortex stripes ($-\,0.1<\eta <0.05$). The square lattice is stable, presumably due to the fact that each vortex in one component can have all its nearest-neighbor vortices to be in the other component [48].These various structures are similar to that obtained by two component G–P equations [33].

Fig. 4

Two typical perfect vortex sheet solutions and the corresponding radial profiles of $\langle O_{1,2}\rangle$ averaged in the $\theta$ direction at $T=0.82T_c^0$: a $\eta =0.2,\varOmega =0.15$. b $\eta =0.2,\varOmega =0.3$

In a classical turbulence, the vortex sheet is a thin interface across which the tangential component of the flow velocity is discontinuous. In quantum fluid, Landau and Lifshitz firstly proposed the vortex sheets scenario in rotating superfluid [34], almost at the same time when Feynman published his paper on quantized vortices in superfluid. A quantum vortex sheet solution is that the vorticity concentrated in line with the irrotational circulating flow stay between them. A typical picture of vortex sheet can be found in Fig. 1 of a review paper [36], where the vortices concentrated in circles with a uniform distance between the circles. As a novel quantum state, the vortex sheet had never been observed in superfluid $^4$He. However, vortex sheet has been observed in chiral superfluid $^3$He-A since it can be stable due to the confinement of the vorticity within the topologically stable solitons [35], which may has many physical applications. The other candidate to demonstrate vortex sheet is a quantum fluid with repulsive two order parameters, because the phase separation naturally provides a region of vanishing order parameters of one component and filled by the other component. Under rotation, the nucleated vortices merge to form a winding sheet structure like serpentine instead of forming a periodic lattice. As shown in Fig. 4, in the phase separation region $\eta >0.05$ (see the line corresponding to $0.82T_c^0$ in Fig. 1a), we find the expected exotic vortex sheet solutions. The vortices of the $\langle O_1\rangle$ are located at the region of the domains of $\langle O_2\rangle$ component. This can be understood from the fact that the condensate of one component works as a pinning potential for the vortices in the other component due to the phase separation nature [33]. By forming vortex sheets, the condensate achieves remarkable phase separation compared to a lattice. Furthermore, the vortex sheets nearly uniformly fill the disk, and the distance d between the layers are equal.

Fig. 5

(Top): the sheet distance d as a function of $\varOmega$ on a $\varOmega - d$ plot: $d = \frac{1}{0.95}\varOmega ^{-\frac{2}{3}}$. (Bottom): the sheet distance d as a function of $\varOmega$ on a Log–Log plot. The straight line is the best fit to $\ln d = a\ln \varOmega +b$ with $a=-\,0.655\pm 0.027$ and $b=0.060\pm 0.048$

According to the calculation by Landau and Lifshitz [34], the distance d between sheets is determined by the surface tension $\sigma$ of the soliton and the kinetic energy of the counterflow $(v_n-v_s)$ outside the sheet, where $v_n$ is the normal fluid velocity and $v_s$ is the vortex-free superfluid velocity. In unit volume, the counterflow energy is $\frac{1}{d}\int \frac{1}{2}\rho _s(v_n-v_s)^2dy = \frac{\rho _s\varOmega ^2d^2}{6}$, and the surface energy is $\frac{\sigma }{d}$, where $\rho _s$ is the superfluid density, which can be obtained from the conjugate current $J_\theta = \partial _z A_\theta |_{z=0}$, as [21]

$$\begin{aligned} \rho _s = \frac{J_\theta }{(\nabla arg[\varPsi _i])_\theta -A_{\theta }}, \end{aligned}$$

(14)

where $A_\theta =\frac{1}{2}\rho ^2 \varOmega$ and the denominator $(\nabla arg[\varPsi _i])_\theta - A_{\phi }$ is the gauge-invariant superfluid velocity along the angular direction.

By the minimization of energy, one obtains

$$\begin{aligned} d = \left( \frac{3\sigma }{\rho _s\varOmega ^2}\right) ^\frac{1}{3}. \end{aligned}$$

(15)

We confirm that the formula also hold in a two-component superfluid, a sample result when $\eta =0.2$ is plotted in Fig. 5.

Fig. 6

The profile of $\rho _s$ for the phase vortex sheet case $\eta =0.5$

We show in Fig. 6 the profile of $\rho _s$ in the x-direction for the vortex sheet case $\eta =0.5$. $\rho _s$ of one component has a constant value where the other one vanishes, we take the constant value of superfluid density in the Landau’s equation, then $\sigma$ can be written as $\sigma =\frac{1}{3} (\frac{\rho _s}{0.95})^3$.

Fig. 7

Vortex number of both components vs. angular velocity $\varOmega$. The straight line is the best fit to $N=a\varOmega$ where $a=272.78$ with $error=1.05\%$. The temperature is fixed to be $T=0.82T_c^0$

As another important properties of superfluid, the Feynman linear relation [18] between the excited vortex numbers and angular velocity in one component superfluid may can naturally generalizes to a two-component superfluid as

$$\begin{aligned} N_j=M_j\varOmega R^2, \end{aligned}$$

(16)

where N represents the number density of vortex and M is the atomic mass of BECs. Since the discrete symmetry upon interchange of the two charged scalars, the vortices numbers of the two components are expected to be the same. In the holographic model we also investigated the validity of the Feynman relation in the two-component system and found no deviations from it, also the numbers for the two components are the same, $N_1\approx N_2$. A sample result is given in Fig. 7 for $\eta =0.2,R=20$. By fitting we can get the value of the mass $M_1=M_2=0.6820$. We also computed the cases where R is 15, 20, 22, 25, the linear Feynman relations between rotating velocity and vortices still holds and we got that M is equal to 0.67, 0.68, 0.7, 0.69 respectively. This means that the radius has no effect on the vortices number density as confirmed in the single component superfluid under rotation [19].

At last, we investigate the phase diagram of the vortex structures in the intercomponent direct coupling $\eta$ versus rotation-frequency $\varOmega$ as plotted in Fig. 8. The upper limit of the rotation frequency is set by $\varOmega =0.1$ while the bottom limit is set by $\varOmega =0.05$. The diagram show a transition from triangular lattices to square lattices and then stripe and sheet for all angular velocities. The triangle lattices locate at the region when the coupling constant $\eta$ is negative, where the two components prefer to attract each other. Keep increasing $\eta$ to zero, square lattices appear and the vortices arrange in line then the vortex stripes appear at $\eta =0$. When $\eta >0.05$, where is the region of phase separation, it always presents a sheet solution, that shows that the sheet solution under rotation is a result of phase separation.

Fig. 8

$\varOmega -\eta$ phase diagram of the vortex states, where $\triangle$ symbolize triangular lattice, $\square$ symbolize square lattice, $\times$ stripe vortex and $\circ$ vortex sheet lattice

5 Discussions

In order to study the properties of rotating multi-components BECs, a two-components Einstein–Maxwell–Higgs model defined in a fixed black hole background is used while the charged scalars and gauge fields are just a probe to the gravity background. The probe limit corresponds to neglecting the effect of the bulk stress–energy due to the scalar field and gauge fields on the space-time geometry. In the dual fluid, this corresponds to neglecting the effect of the superfluid condensate on the normal component of the fluid [7, 8]. We don’t consider the effect of the superfluid onto the normal fluid. So our hypothesis is similar to the G–P equation, in which vortex lattice and phase separation do not occur in normal fluid components. Furthermore, it is extremely important to extend present work to the back-reaction case, as long as we are going to study the how the dynamics change as we incorporate the back reaction of the superfluid on the normal component and also the change of condition for “phase separation”.

The vortex phase diagram obtained from AdS/CFT correspondence in the simulation are very similar to that shown in the two-component GP equations [32, 33], the similarities include also four vortex states and also the phase transitions from triangular lattices to square lattices, to double-core lattices, and eventually develop vortex sheets. The results can also related to some experiments, for example, in ref [48], the interlaced square lattice similar to Fig. 3b was observed. Also in the same experiment, the vortex core size of the interlocked are bigger than the one of single component, which we can also observe in Fig. 3. The sheet solution is expected in the highly separated region, which may can be observed experimentally in a two-component BECs with tunable intercomponent interactions, which can be deeply in a phase separate region [49, 50]. The two species are of the same mass, then the vortex core size are the same as shown in Figa. 3 and 4. Using of different masses for the two components then the discrete symmetry upon interchange of the two charged scalars will not be reserved, one will realize a coexistence system of vortices with different vortex-core sizes, then the lattice structure shown in this work may be changed, which deserves to be studied in future.