1 Introduction

The Heisenberg uncertainty principle immediately implies that identical particles cannot be distinguished anymore in scattering amplitudes. Indeed, in elastic electron-electron scatterings, we loose predictive power in determining specifically the scattered electron detected by the experiment. Instead, we have to account for two possible interfering amplitudes, with electron pair exchanges. If the interference of the amplitudes is destructive, i.e. if their permutation symmetry encodes a minus sign, the two particles are fermions that retain spin \(\frac{1}{2}\) (electrons in our case).

On the other hand, identical particles with integer spin, namely bosons, undergo scattering amplitudes with constructive interference. This is certainly suggesting us how intimately the spin statistics is related to the Heisenberg Uncertainty Principle (HUP). Therefore, a natural question would be: what would happen if we modify the very foundations of quantum mechanics, deforming the standard HUP so to account for new physics? May this turn into a modification of the Spin Statistics and the Pauli Exclusion Principle (PEP)?

Recently, we have shown how constraints on possible transitions that violate the PEP can provide strong bounds [1,2,3] on a large class of non-commutative quantum gravity models that are based either on \(\theta \)-Poincaré deformed space-time symmetries [4,5,6] or on the \(\kappa \)-Poincaré deformed space-time symmetries [7,8,9,10,11,12,13]. It has been shown that many of these models can be actually ruled-out up to the second order in the Planck energy scale, as a byproduct of the amplification effect for the signal provided by the large mass sensitivity of the underground experiments. Sharing the same attitude, in this paper we will explore possible implications of the generalization of the HUP. We may take inspiration from the seminal work by Amati, Ciafaloni and Veneziano, who realized that polynomial momenta dependent corrections to HUP arise from string perturbation theory, accounting for the formal replacement of the standard bracket \([X,P]=i \hbar \) into \([X,P]=i\hbar (1\pm \beta P^{2}+...)\) [15,16,17]. This deformation of HUP is commonly referred to the literature as Generalized Uncertainty Principle (GUP) - see e.g. Ref. [18] for a modern review on this subject.

Whenever perturbation theory breaks down, we cannot anymore control all the infinite new contributions to the HUP. Nevertheless, this can turn out into a natural opportunity to exploit novel non-linear GUP models, bearing in mind that the whole power series of perturbative terms can be actually re-summed into a complete non-analytical function f(P). Therefore, we may reverse the logical pathway, namely “from scattering to GUP”, into “from GUP to scattering”: we can suggest reasonable effective GUP models, and then study their different predictions for what concerns their transition amplitudes, transitions probabilities, decay rates and so on. A posteriori, high precision data from underground experiments will phenomenologically suggest what are the “viable roads” towards quantum gravity. In this sense, we are here inaugurating a new effective quantum mechanical approach toward quantum gravity phenomenology. This is rooted at the theoretical level, on the very deep structure of the symplectic phase-space of the quantum theories of fields [19,20,21], and thus on their non-relativistic Galilean limit. Changing the very same pilasters of quantum mechanics, a large class of non-perturbative GUP models violates the Spin Statistics rules. This leads to Pauli Exclusion Principle-violating (PEPV) rare processes, which can in principle destabilize nuclear matter. Here, we will mainly focus on the DAMA/LIBRA data, inspired by the analysis shown in Refs. [23, 24]. PEPV transitions that emit energetic protons from nuclear level transitions can be indeed tested by the DAMA/LIBRA detectors with high precision, setting severe bounds on the GUP parameter spaces.

The plan of the paper is as follows. In Sect. 2 we review previous insights from the symplectic geometry side that shed light on the intrinsic link between the symplectic structure of the phase space of theories of fields, the space-time symmetries that label their representations and their co-algebra structure. In Sect. 3 we specify a particular phenomenological framework, inspired by string perturbation theory, and particularly suited to account for data from underground experiments. In Sect. 4 we discuss phenomenological constraints that arise from the inspection of data provided by the DAMA/LIBRA high precision detectors. Finally, in Sect. 5 we spell some preliminary conclusions and spare outlooks on forthcoming refinements of this analysis.

2 From the Heisenberg principle to space-time symmetries and statistics, and vice-versa

In the 80’s, a formalism for the covariant treatment of the field theories’ phase-space was developed by Crnkovic and Witten in [19,20,21]. The main idea was to express the symplectic form of field theories’ Lagrangians in terms of the space-time symmetries that are employed in labelling the solutions of the equation of motion. This simple idea allowed to unveil the intimate relations that links the phase-space structure of the theory to its symmetry structure.

The approach can be illustrated moving from a generic Lagrangian L of a scalar field \(\Phi \). The theory then casts

$$\begin{aligned} {S}=\int _{\mathcal {M}} {L}(\Phi , \partial _\alpha \Phi )dt\,, \end{aligned}$$
(2.1)

with \(\mathcal {M}\) space-time manifold. The phase space of the theory is then an infinite dimensional manifold \(\Gamma \) accounting for the pairs \(\{ \Phi , \Pi \}\), with \(\Pi =\frac{\delta {L}}{\delta \dot{\Phi }}\) momentum canonically conjugated to \(\Phi \), the dot “\(\,^{\dot{\,}}\,\)” denoting as usual time derivative. Points of the classical phase-space are then determined thanks to the one-to-one correspondence with the space of solutions \(\mathcal {A}\) of the equation of motion, namely the Euler Lagrange equation

$$\begin{aligned} \partial ^\alpha \left( \frac{\delta {L}}{\delta \, \partial _\alpha \Phi }\right) -\frac{\delta {L}}{\delta {\Phi }}=0\,. \end{aligned}$$
(2.2)

Within this geometrical description, the points of the phase-space are then identified with the solutions of the Euler Lagrange equation, or in other words, \(\Gamma \) is identified with \(\mathcal {S}\).

We may then introduce the tangent and cotangent elements of \(\mathcal {A}\). These are respectively the vectors \(\delta \Phi \in T\mathcal {A}\), which as small fields displacements still fulfill Eq. (2.2), and the associated one-form \(\delta \Phi (x) \in T*\mathcal {A}\), defined at each point \(x\in \mathcal {M}\). A general p-form can be then defined to be \(F=\int dx_1 \dots dx_p \,f_{x_1 \dots x_p} \delta \Phi (x_1) \wedge \dots \wedge \Phi (x_p)\). This enables us to see \(\delta \) as a mapping that satisfies \(\delta ^2\) and \(\delta (FG)=\delta (F)\,G + (-1)^{r(F)} F\, \delta (G)\), with r(F) rank of F.

It is now possible to specify a non-degenerate (symplectic) two-form \(\omega \), which casts as

$$\begin{aligned} \omega =\delta \left( \int _\Sigma d\sigma _\alpha \mathcal {J}^\alpha \right) \,, \end{aligned}$$
(2.3)

in terms of the conserved current \(\mathcal {J}^\alpha \) that arises from L, namely

$$\begin{aligned} \mathcal {J}^\alpha = \frac{\delta {L}}{\delta \, \partial _\alpha \Phi (x)}\, \delta \Phi (x)\,. \end{aligned}$$
(2.4)

Poincaré invariance automatically follows from the definition in Eq. (2.3). Labelling with s any independent symmetry generator, for the vector fields \(V_s \in T\mathcal {S}\) that are tangent to the orbits of the space-time symmetries, the evaluation of the two-forms provides \(\omega (V_s)=-\delta (Q_s)\), where \(Q_s\) is the generator of the symmetry. On \(\Sigma _t\) (the space-like hypersurfaces \(\Sigma \) at t fixed), this latter relation reduces to the integration on the three-dimensional space volume of a two-form expression

$$\begin{aligned} \omega =\frac{1}{2} \int _{\Sigma _t} \left( \delta \Pi \wedge \delta \Phi \right) , \end{aligned}$$
(2.5)

which evaluated on the vectors that are tangent to the spacetime symmetry orbits provides the one-form

$$\begin{aligned} \omega (V_s)=\frac{1}{2} \int _{\Sigma _t} \left( \delta \Pi (V_s) \delta \Phi - \delta \Pi \delta \Phi (V_s) \right) \,. \end{aligned}$$
(2.6)

Eqs. (2.5)–(2.6) respectively provide bilinear and linear functionals on \(\mathcal {S}\). Accounting for the covariant conjugated momenta \(\Pi _\alpha =\partial _\alpha \Phi \), these can be directly expressed in a covariant form on any spacial hypersurface \(\Sigma _t\) as [22]

$$\begin{aligned} \omega (\Phi _1,\Phi _2)=\frac{1}{2} \int _{\Sigma _t} \left( \Pi _1 \Phi _2 - \Phi _1 \Pi _2 \right) \,, \end{aligned}$$
(2.7)

providing the symplectic product of the theory, and (on a space-like surface \(\Sigma \) covariantly chosen)

$$\begin{aligned} -Q_s= & {} \omega (V_s)\left( \Phi \right) =\frac{1}{2} \int _\Sigma d\sigma _\alpha \left( (\mathcal {L}_{V_s} \Pi ^\alpha ) \, \Phi \right. \nonumber \\&\left. - \Pi ^\alpha \, (\mathcal {L}_{V_s} \Phi ) \right) \,, \end{aligned}$$
(2.8)

namely a symmetry generator, having introduced the Lie derivative \(\mathcal {L}\), which on a general p-form G reads \(\mathcal {L}_{V_s}\,G=(\delta G)(V_s)\), while on a 0-form f, i.e. a function, reads \(\mathcal {L}_{V_s} f=(\delta f)(V_s)\).

This brief summary sheds light on the link between the effective action L, its conserved current, and then the symplectic structure of the theory. As a matter of fact, it is not unconceivable to realize that a redefinition of the conjugated momenta to the fields that enter the symplectic structure, actually amounts to a change in the symplectic structure of the theory. But stepping out of the canonicity of theory actually amounts to change one of the fundamental pillars of quantum mechanics, namely the HUP.

Furthermore, it was shown in [10] that the relationship between symplectic structure and symmetry structure actually extends to the co-algebraic structure of the field theories’ symmetries: in other words, the link with between the HUP and the space-time symmetries extends to the statistics. This realization opened the pathway to the formulation in the symplectic geometry approach of the Hopf algebras symmetries, which are associated to non-commutative space-times/effective backgrounds instantiations of several quantum gravity models. Specifically, the approach made use of the Poisson map, which preserves the symmetry structure of the theory, even when considering a deformed space-time symmetries. In [10], the authors deepened the case of \(\kappa \)-Poincaré, but similar arguments can be extended in general, to any deformed space-time symmetry algebra.

On the other hand, the fact that a deformation of the space-time symmetries, and thus the effective Lagrangian, might induce a deformation of the statistics, arises naturally when reviewing a very simple, but rigorous and decisive argument developed by Schwinger to prove the spin-statistics theorem. Considering that more than relativistic quantum field theory the proof of the spin-statistics theorem requires Lorentz invariance, Schwinger realized that the kinetic part of the Lagrangian is the fundamental ingredient to be invoked. Therefore, crucial at this purpose are the requirements that, besides being derivable form a Lorentz invariant theory, the kinetic term for a real scalar field \(\Phi =\Phi ^\dagger \) encodes at most linear first derivatives of the field, and is bilinear in it. Labelling the spin of the field with l, m, Schwinger then considered a Lagrangian of the form

$$\begin{aligned} L= & {} \frac{i}{2} \left( \Phi _l \dot{\Phi }_m - \dot{\Phi }_l {\Phi }_m \right) K^0_{lm} \nonumber \\&- \frac{i}{2} \sum \limits _{j=1,2,3} \left( {\Phi }_l (\nabla _j \Phi _m) - (\nabla _j \Phi _l) \Phi _m \right) K^0_{lm} - M_{lm} \,{\Phi }_l {\Phi }_m,\nonumber \\ \end{aligned}$$
(2.9)

where the sum of j run over the space indices, and \(K^0_{lm} \), \(K^j_{lm} \) and \(M_{lm}\) are matrices of the field Lagrangian. Thus the Lagrangian in Eq. (2.9) can be recast in the compact form

$$\begin{aligned} L=\sum \limits _{lm} {\Phi }_l \Lambda _{lm} {\Phi }_m\,, \quad \Lambda _{lm} = \frac{i}{2} K^0 {\mathop {\partial }\limits ^{\leftrightarrow }}_t - \frac{i}{2} K_0 {\mathop {\partial }\limits ^{\leftrightarrow }}_j -M\,,\nonumber \\ \end{aligned}$$
(2.10)

which, as an aside, we notice is intimately connected to the definition of the internal symplectic product of the theory.

Now the argument develops very straightforwardly. We first consider that the Lagrangian must be invariant under the change of order of any two fields, since this is redundant and the spin-label is summed over. Then we take into account the properties of the SO(3) group, namely that representations labelled by a semi-integer spin have a bilinear antisymmetric internal product, while representations labelled by an integer spin retain a bilinear symmetric internal product. As a consequence, to ensure invariance of the Lagrangian under the swap of fields, namely

$$\begin{aligned}&{\Phi }_l \Lambda _{lm} {\Phi }_m + {\Phi }_m \Lambda _{ml} {\Phi }_l \rightarrow \nonumber \\&\quad \pm {\Phi }_m \Lambda _{lm} {\Phi }_l \pm {\Phi }_l \Lambda _{ml} {\Phi }_m\,, \quad \mathrm{for} \qquad \Phi _l \leftrightarrow \Phi _m\,, \end{aligned}$$
(2.11)

the infinite-dimensional \(\Lambda \) operator must satisfy

$$\begin{aligned} \Lambda _{lm}=\pm \Lambda _{ml}\,. \end{aligned}$$
(2.12)

Relation (2.12) imposes restrictions on the matrix M, which must be symmetric for integer-spin fields (Bose–Einstein statistics), and anti-symmetric for half integer spin (Fermi-Dirac statistics). Then, it is immediate to ponder that a deformation of the algebra of rotation will affect the internal product symmetries, and thus the statistics of the theory. It is also straightforward to realize that considering either non-local or non Lorentz-invariant Lagrangian functionals will amount to change the symplectic product of the theory, thus the very fundamental pillar of the HUP.

In forthcoming investigations, we will be back to this topic with the aim to further clarify the link between deformation of the HUP, deformation of the algebra and deformation of the statistics [25].

3 Generalized uncertainty principle and quantum gravity effects

We now specify the phenomenological framework, necessary to make contact with underground experiments. We may start from considering the specific class of GUP models, defined by the brackets

$$\begin{aligned}&[ X_i, P_j] = \frac{ i\hbar \delta _{ij} }{ (1 - (\beta P^2)^{m'})^{k} }\,\,,~~~ [ P_i, P_j]=0\,\,, ~~ \nonumber \\&[ X_i , X_j ] =\frac{ 2i\hbar \beta }{ (1 - (\beta P^2)^{m'})^{2k} }( P_i X_j - P_j X_i), \end{aligned}$$
(3.1)

where \(\beta \) is related to the GUP critical energy scale \(\Lambda \) as \(\beta =\Lambda ^{-2}\), and as usual X, P denote the position and the momentum operators, while \(m',k\) are two free index-parameters.

This class of models encodes a natural solution to several quantum gravity problems: when \(P=1/\sqrt{\beta }=\Lambda \), uncertainties diverge, i.e. \(\lim _{P\rightarrow \Lambda }\Delta X \Delta P\rightarrow \infty \) and \(\lim _{P\rightarrow \Lambda }\Delta X_{i} \Delta X_{j}\rightarrow \infty \). This implies that at a critical UV scale, space-time singularities cannot be formed, and thus becomes impossible to probe length shorter than \(\bar{l}=1/\Lambda \). On the other hand, commutativity of space coordinates is fully lost around \(P=\Lambda \). This is also suggesting that the angular-momentum operators may loose certainty around the UV fixed energy. Indeed, Eq. (3.1) implies a deformation of the standard angular-momentum generators algebra, namely

$$\begin{aligned}{}[ L_i, L_j]= & {} \frac{i \hbar }{(1-(\beta P^2)^{m'})^{k}}\left( X_i P_j-X_j P_i\right) \nonumber \\= & {} \frac{i \hbar }{(1-(\beta P^2)^{m'})^{k}}\epsilon _{ijk}L_{k}\,\, , \end{aligned}$$
(3.2)

which is compatible with a new definition of the angular-momentum operators,

$$\begin{aligned} L_{i}=\frac{1}{(1-(\beta P^2)^{m'})^{k}}\epsilon _{ijk}r_{j}p_{k}\, . \end{aligned}$$
(3.3)

Similarly, also the \([X_i,X_j]\) bracket can be cast in terms of the \(L_{ij}\) generators, namely

$$\begin{aligned}{}[X_i,X_j]= & {} \frac{ -2i \hbar \beta }{(1 - (\beta P^2)^{m'})^{k}}L_{ij}. \end{aligned}$$
(3.4)

This implies that space coordinates cannot commute anymore, but are rather proportional to a linear superposition of the angular-momentum generators. Within this framework, the scale of non-commutativity is individuated by \(\beta =1/\Lambda ^{2}\).

Conservation of the angular-momentum components in presence of a central interaction potential is also ensured from considering the average expectation of Eq. (3.2), namely \(\langle [L^{2},H]\rangle =\langle [L_{z},H]\rangle =0\). Nonetheless, Eq. (3.2) implies that \(\Delta L_{i}\Delta L_{j}\rightarrow \infty \) for \(p\rightarrow \Lambda \), i.e. quantum fluctuations may become extremely relevant even while considering eigenstates of the angular-momentum operators, if the corresponding energies do approach the UV scale \(\Lambda \). The uncertainty of the orbital angular-momentum operators at the UV scale \(\Lambda \) would amount to an uncertainty of the total angular momentum, and thus therefore would imply a spin uncertainty. Actually, a similar argument holds in general, even without accounting for GUP modifications at the UV-scale, and explains why the simple but crystal-clear argument by Schwinger is successful in proving the spin-statistic theorem.

Coming back to the phenomenological consequences, we take into account a generic bound-state of fermions (e.g. a Fermi nuclear hole model) endowed with two levels, characterized by the eigenvalues \(j_{1},m_{1}\) and \(j_{2},m_{2}\). In standard quantum mechanics, one can measure both \(J_{z}\) and \(J^{2}\) with theoretical infinite resolution, the only price to pay being the complete uncertainty on the components \(J_{x}\), \(J_{y}\). But according to Eqs. (3.1)–(3.2), this is impossible within the framework of the non-perturbative GUP. Indeed, \(J_{z}\) and \(J^{2}\) can only be measured with finite resolution, even theoretically, and the uncertainty on the z-component grows as \(\Delta J_{z}\ge k(\beta P^{2})^{m'}\hbar /2+\) higher-orders. If for a certain value of P it happens that \(\Delta J_{z}>|J^{(1)}_{z}-J^{(2)}_{z}|\) for any two different levels, then it is impossible to distinguish the level in which fermions are localized. In other words, the wave-functions of the fermion angular-momentum operators cast as linear combinations of the levels that undergo the uncertainty. In our previous example, this corresponds to considering the superposition of the two eigenstates \(|J,M\rangle \simeq \alpha (P)|j_{1},m_{1}\rangle +\beta (P) |j_{2},m_{2}\rangle \), with \(|\alpha (p)|^{2}+|\beta (p)|^{2}=1\). In the low-energy limit, one of the coefficients of the two-levels superposition in the fermion wave-function would vanish polynomially, as \(k(\beta P)^{m'}\).

In compliance with the aforementioned considerations, we shall consider a simple low-energy, single-fermion state, which results as a super-position of two eigenstates, i.e.

$$\begin{aligned} |J',M'\rangle \simeq (1-k(\beta P^2)^{m'})|j_{1},m_{1}\rangle +k(\beta P^2)^{m'}|j_{2},m_{2}\rangle ,\nonumber \\ \end{aligned}$$
(3.5)

being the normalization factor power-series negligible. According to Eq. (3.5), each fermion wave-function results in an energy-dependent mixing of several angular-momentum eigenstates, each one labelled by different quantum numbers. Therefore, for each fermionic particle there exists an energy-dependent probability to transit from a level with a certain angular-momentum eigenvalue to another one characterized by a different eigenvalue. Correspondingly, this can violate not only the very conservation of the angular-momentum, but also the Pauli exclusion principle.

To further clarify this point, we may inspect another relevant example and account for a wave-function that is almost localized on the second level, namely

$$\begin{aligned} |J,M\rangle \simeq \big [k(\beta \tilde{P}^2)^{m'}|j_{1},m_{1}\rangle +(1-k(\beta \tilde{P}^2)^{m'})|j_{2},m_{2}\rangle \big ]\, .\nonumber \\ \end{aligned}$$
(3.6)

It is then easy to show that the transition amplitude probability is not vanishing, but that instead

$$\begin{aligned}&\langle J,M|J',M'\rangle |_{J,M\ne J',M'}\nonumber \\&\quad = [k(\beta \tilde{P}^{2})^{m'}(1-k(\beta P^{2})^{m'})\nonumber \\&\qquad +k(\beta P^{2})^{m'}(1-n(\beta \tilde{P}^{2})^{m'})]\, . \end{aligned}$$
(3.7)

This transition amplitude goes to zero either for \(P,\tilde{P}\rightarrow 0\) or for \(\beta \rightarrow 0\) (\(\Lambda \rightarrow \infty \)). If the two states are degenerate in the energy, the leading order transition amplitude would be

$$\begin{aligned} \langle J,M|J',M'\rangle \simeq 2k (\beta P)^{m}\, . \end{aligned}$$
(3.8)

Equation (3.7) then implies that two nucleons can have a tiny overlap probability, and both stay in levels characterized by the same quantum numbers, hence violating the PEP.

4 Constraints from DAMA/LIBRA high precision data

We now give a closer look to what Nature can tell us, and inspect the high precision data provided the DAMA/LIBRA experiment. Of course, the probabilities associated to transitions that violate the PEP are much smaller than the Standard Model total rate. Keeping this in mind, we can parametrize PEPV transitions rate as

$$\begin{aligned} \Gamma _{PEPV}=n (\Lambda ^{-1}P)^{m}\Gamma _{SM}\, , \end{aligned}$$
(4.1)

where \(n=4k^{2}\), \(m=4m'\).

This parameterization is directly computed inserting the squared amplitude of Eq. (3.8) in the low energy limit, as a PEPV dressing suppression factor to the SM transition rate. The DAMA/LIBRA collaboration set strong limits on the PEPV nuclear level transitions [24]. The DAMA/LIBRA experiment is indeed sensitive to PEPV nuclear processes of \(\,^{23} Na\) and \(\,^{127}I\), emitting protons with an energy of about \(E_{p}\ge 10\, \mathrm{MeV}\). Since this process has not been observed, this amounts to the possibility to set limits on the transition time of \(\tau _{p}>1.63\times 10^{33}\,s\,(90\%\, \mathrm{C.L.})\) — see again Ref. [24]. Such a limit corresponds to \(n(\Lambda ^{-2}P)^{m}< 4\times 10^{-55}\,(90\%\, \mathrm{C.L.})\). For a complete nuclear modeling of the proton emission, we refer to Ref.  [23].

Fig. 1
figure 1

Excluded parameter space \((\Lambda ,m)\) from DAMA experiment: the four contour limits correspond to fix \(n=1,2,10,100\) respectively

Full size image

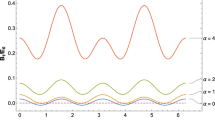
Limits on the parameter space (n, m, \(\Lambda \)(GeV )) can be worked out. In particular, Fig. 1 shows the excluded parameter space (\(\Lambda \), m) from DAMA/LIBRA experiment for four different values of \(n = 1, 2, 10, 100\). As we can see, very remarkably a large part of parameter space are already excluded at energies above the Planck scale and, in particular, for \(m \lesssim 2.7\) nearly independently on the n value. This argument is confirmed studying the dependence of \(\Lambda \) from n, which is reported for three sample values of \(m=1, 2, 3\) in Figs. 2, 3, 4, respectively. The region above the Planck scale is excluded for \(m=1,2\).

Fig. 2
figure 2

Excluded parameter space \((\Lambda ,n)\) from DAMA experiment, fixing \(m=1\)

Full size image
Fig. 3
figure 3

Excluded parameter space \((\Lambda ,n)\) from DAMA experiment, fixing \(m=2\)

Full size image
Fig. 4
figure 4

Excluded parameter space \((\Lambda ,n)\) from DAMA experiment, fixing \(m=3\)

Full size image

The DAMA/LIBRA constraints can be compared to other underground experiments based on different experimental techniques. Interesting comparative analysis can be performed considering experiments searching for PEPVs in atomic transitions rather than nuclear ones. The VIP experiment is dedicated on searches of PEPV atomic transitions in Copper atoms [26].

5 Conclusion

In conclusion, we have shown that a large class of non-perturbative GUP models, endowed with three free parameters, can be constrained/ruled out by the DAMA/LIBRA experiment, within a large parameter space region. We notice that the specific framework we analyzed predicts angular momentum violating transitions, as well as PEP violations. Exotic nuclear transitions can be tested with high precision by the DAMA/LIBRA experiment, having a background clean window for the detection of either the proton or the neutron with momentum of about \(10\, \mathrm{MeV}\).

The characteristic GUP energy scale \(\Lambda =1/\sqrt{\beta }\) can be then constrained to be larger than the Planck energy scale. For example, the case considered in Ref. [27] is already ruled out by the data, up to the Planck scale (corresponding to \(n=m=1\)).

On the other hand, it is also conceivable that matter stabilization would be guaranteed by either discrete symmetries or selection rules. In this case, it is important within a complementary strategy to test PEPV from recombination scattering processes, as suggested by the VIP collaboration [26].