1 Introduction

The existence of molecules made of heavy baryons is a hot topic in nowadays hadronic physics [1,2,3,4,5,6,7]. The observation in 2017 by the LHCb Collaboration of a doubly charmed baryon [8] increased the interest in exotic states containing pairs of charmed quarks. Right now, the LHCb Collaboration has reported two structures matching the lineshape of a resonance just above twice the \(J/\Psi \) mass, that could originate from a hadron containing two charm quarks [9]. Although the existence of exotic structures containing pairs of heavy quarks is a long-term challenge [10], it has recently been noticed, for example in Refs. [11,12,13], that doubly charmed tetraquarks are the first to be at the edge of binding.

On general grounds, the main motivation to wonder about the existence of heavy-baryon molecules is rooted in the reduction of the kinetic energy due to larger reduced masses. However, such molecular states could be the concatenation of several effects and not just a fairly attractive interaction. The coupling between nearby channels, conflicts between different terms of the interaction, and non-central forces often play a significant role. Some of these contributions may be reinforced by the presence of heavy quarks while others may become weaker [14, 15].

Behind all this there is the understanding of the hadron-hadron interaction governed by the dynamics of quarks and gluons, which is a topical issue. To encourage new experiments and analysis of existing data it is essential to have detailed theoretical investigations. Despite some uncertainty in contemporary interaction models, the possible existence of bound states or resonances is a key element, because their signs might be clear enough to be identified in the experimental data [9]. Thus, it is the purpose of this work to study the possible existence of hadronic molecules or resonances in two- and three-baryon systems with two units of charm, in particular, \(\Lambda _c\Lambda _c\), \(\Sigma _c\Sigma _c\), \(N\Lambda _c\Lambda _c\) and \(N\Sigma _c\Sigma _c\) states. When tackling this problem, one has to manage with an important difficulty, namely the complete lack of experimental data. Therefore, the generalization of models describing two-hadron interactions in the light-flavor sector could offer insight about the unknown interaction of hadrons with heavy flavors.

Following these ideas, we will make use of a constituent quark model (CQM) tuned on the description of the NN interaction [16] as well as the meson [17] and baryon [18, 19] spectra in all flavor sectors, to obtain parameter-free predictions that will hopefully be testable in future experiments. Let us note that the study of the interaction between charmed baryons has become an interesting subject in several contexts [9, 20,21,22,23] and it may shed light on the possible existence of exotic nuclei with heavy flavors [24,25,26,27,28,29].

The paper is organized as follows. In Sect. 2 we describe and analyze particular aspects of the S wave two-body subsystems: \(N\Lambda _c\), \(N\Sigma _c\), \(\Lambda _c\Lambda _c\) and \(\Sigma _c\Sigma _c\). Section 3 is devoted to the study of the lightest \(N\Lambda _c\Lambda _c\) and \(N\Sigma _c\Sigma _c\) three-body systems. Finally, in Sect. 4 we summarize our main conclusions.

2 Two-baryon systems

The two-body interactions that are necessary to study the charm \(+2\) two- and three-baryon systems have been discussed at length in the literature [30, 31]. They are derived from the CQM [16,17,18,19]. The capability of the model is endorsed by the nice description of the NN phase shifts, as can be seen in figs. 2, 3 and 4 of Ref. [32]. The \(N\Lambda _c\) and \(N\Sigma _c\) interactions have been presented and discussed in detail in Ref. [30], in comparison with the other approaches available in the literature, in particular recent lattice QCD studies [29]. The \(\Lambda _c\Lambda _c\) and \(\Sigma _c\Sigma _c\) interactions have been consistently derived within the CQM in Ref. [31], also in comparison with the alternative approaches available in the literature. We refer the reader to Refs. [30, 31] for a thorough description of the derivation and analysis of the two-body interactions. As can be seen in table 1 of Ref. [30] and table 2 of Ref. [31] all two-body interactions are consistently derived with the same set of parameters. In the following we highlight some peculiarities of the two-body interactions that are relevant to the purpose of the present work.

We summarize in Table 1 the low-energy parameters of the two-body systems in the charm \(+1\) and \(+2\) sectors. The scattering length becomes complex for those two-body channels with open lower mass two-body states. The two-body interactions are in general attractive but not sufficient for having bound states, in agreement with lattice QCD estimations [29]. The singlet isospin 1/2 and triplet isospin 3/2 \(\Sigma _c N\) interactions are the only repulsive ones. The last line of Table 1 presents the results for the uncoupled \(\Sigma _c\Sigma _c\) isosinglet system.Footnote 1 It can be seen how the scattering length is positive and larger than the range of the interaction, see Fig. 1, pointing to existence of a bound state that will be discussed further below.

Table 1 CQM results for the \(^1S_0\) and \(^3S_1\) scattering lengths (\(\mathrm {a}_s\) and \(\mathrm {a}_t\)) and effective range parameters (\(r_s\) and \(r_t\)) in fm for the different S wave \(Y_c N\) and \(Y_cY_c\) systems (\(Y_c = \Lambda _c\) or \(\Sigma _c\)). The results shown in the last line, marked by a \(\dagger \), correspond to the uncoupled \(\Sigma _c\Sigma _c\) system
Full size table
Fig. 1
figure 1

Charm \(+2\) \((I,J^P)=(0,0^+)\) two-body interactions

Full size image

Of particular interest are the results for the lightest charm \(+2\) channel, with quantum numbers \((I,J^P)=(0,0^+)\). We show in Fig. 1 the two-body potentials involved in this channel. The \(\Lambda _c\Lambda _c\) interaction is slightly attractive at intermediate distances but, however, repulsive at short range. It is decoupled from the closest two-baryon threshold, the \(N\Xi _{cc}\) state [31], which is relevant for the possible existence of a resonance in the strange sector [33, 34]. There is a general agreement on the overall attractive character of the \(\Sigma _c\Sigma _c\) interaction [1, 2, 5]. Finally, the CQM coupling between the \(\Lambda _c\Lambda _c\) and \(\Sigma _c\Sigma _c\) channels is a bit stronger than in hadronic theories, based solely on a one-pion exchange potential [2], due to quark-exchange effects [31]. All of this fits the scenario of the strange sector, as can be seen by comparing with fig. 1b of Ref. [35], but the absence of the one-kaon exchange potential gives rise to a less attractive interaction.

Fig. 2
figure 2

Fredholm determinant of the two-body \((I,J^P)=(0,0^+)\) charm \(+2\) channel. The dashed line corresponds to the \(\Lambda _c\Lambda _c - \Sigma _c\Sigma _c\) coupled system, whereas the solid line considers only the \(\Sigma _c\Sigma _c\) channel. The zero energy represents the mass of the lowest threshold, \(2m_{\Lambda _c}\) for the dashed line and \(2m_{\Sigma _c}\) for the solid line

Full size image

In Fig. 2 we present the Fredholm determinant [36] for the two-body \((I,J^P)=(0,0^+)\) charm \(+2\) channel in two different cases. The dashed line corresponds to the result considering the full coupling between the \(\Lambda _c\Lambda _c\) and \(\Sigma _c\Sigma _c\) states, whereas the solid line considers only the \(\Sigma _c\Sigma _c\) channel. The coupled channel calculation shows an attractive character but not sufficient to generate a bound state, the Fredholm determinant does not become negative for energies below threshold. This result is in agreement with other estimations in the literature [1, 2, 5] in which in spite of the attractive character of the \(\Lambda _c\Lambda _c\) interaction, the central potential alone is not enough to generate a bound state. The coupling to larger mass channels could be important for the existence of a bound state or a resonance. However, due to the large mass difference between the two coupled channels in the \((I,J^P)=(0,0^+)\) partial wave, 338 MeV, the coupled channel effect is weakened. Let us just note that, for example, in the strange sector the coupling to the \(N\Sigma \) state is relevant for the \(N\Lambda \) system [37] due to a smaller mass difference, \(M(\Sigma ) - M(\Lambda )=\) 77 MeV. Heavier mass channels play a minor role, such as the \(\Delta \Delta \) channel (584 MeV above the NN threshold) in the NN system [38]. Thus, one does not expect higher channels, as it could be \(\Sigma _c^*\Sigma _c^*\) (468 MeV above the \(\Lambda _c\Lambda _c\) threshold) to play a relevant role, as it has been explicitly checked in the literature [5].

Due to the large mass difference between the \(\Lambda _c\Lambda _c\) and \(\Sigma _c\Sigma _c\) channels, we have studied the uncoupled \(\Sigma _c\Sigma _c\) system. The dynamics could be dominated by the attraction in the \(\Sigma _c\Sigma _c\) channel in a way that the \(\Lambda _c\Lambda _c\) channel would be mainly a tool for detection. This mechanism is somewhat related to the ’synchronization of resonances’ proposed by D. Bugg [39]. A similar situation could be the case of the \(d^*(2380)\) resonance in the \(\Delta \Delta \) system, see Ref. [40] for a recent review. The result is depicted in Fig. 2 by the solid line, showing a bound state 16.2 MeV below the \(\Sigma _c\Sigma _c\) threshold, corresponding to the scattering length given in the last line of Table 1. However, since the \(\Lambda _c\Lambda _c\) channel is open, the \(\Sigma _c\Sigma _c\) state would decay showing a resonance behavior. This scenario, a two-body coupled channel problem showing a bound state in the upper channel but not in the coupled channel calculation has been studied in detail in Ref. [41]. It was demonstrated how the width of the resonance does not come only determined by the available phase space for its decay to the detection channel, but it greatly depends on the relative position of the mass of the resonance with respect to the masses of the coupled-channels generating the state.Footnote 2

Thus, making use of the interactions given in Fig. 1, we have studied the width of the resonance produced in between the two thresholds, \(\Lambda _c\Lambda _c\) and \(\Sigma _c\Sigma _c\). The Lippmann–Schwinger equation in the case of S-wave interactions is written as,

$$\begin{aligned} t^{ij}(p,p';E)= & {} V^{ij}(p,p')+\sum _{k=1,2} \int _0^\infty {p^{\prime \prime }}^2 dp^{\prime \prime } \nonumber \\&\times V^{ik}(p,p^{\prime \prime })\, \frac{1}{E-\Delta E \,\, \delta _{2,k}-{p^{\prime \prime }}^2/2\mu _k+i\epsilon }\,\nonumber \\&\times t^{kj}(p^{\prime \prime },p';E)\, , \,\,\,\,\,\,\,\, i,j =1,2, \end{aligned}$$
(1)

where \(\mu _1=m_{\Lambda _c}/2\), \(\mu _2=m_{\Sigma _c}/2\), and \(\Delta E=2 m_{\Sigma _c} - 2 m_{\Lambda _c}\). The interactions in momentum space are given by,

$$\begin{aligned} V^{ij}(p,p')=\frac{2}{\pi }\int _0^\infty r^2dr\; j_0(pr)V^{ij}(r)j_0(p'r) \, , \end{aligned}$$
(2)

where \(V^{ij}(r)\) are the two-body potentials in Fig. 1. The resonance exists at an energy \(E=E_R\) such that the phase shift \(\delta (E_R)=90^\circ \), for energies between the \(\Lambda _c\Lambda _c\) and \(\Sigma _c\Sigma _c\) thresholds, i.e., \(0< E_R < \Delta E\). The mass of the resonance is given by \(W_R=E_R + 2 m_{\Lambda _c}\). The width of the resonance is calculated using the Breit–Wigner formula as [43,44,45],

$$\begin{aligned} \Gamma (E) =\lim \limits _{E \rightarrow E_R}\, \frac{2(E_R-E)}{\text {cotg}[\delta (E)]} \, . \end{aligned}$$
(3)

Although the Breit–Wigner formula is not very accurate close to threshold, however, we have explicitly checked by analytic continuation of the S matrix on the second Riemann sheet that at low energy the width follows the expected \(\Gamma \sim E^{1/2}\) behavior.

Using the formalism described above we have calculated the width of the \(\Sigma _c\Sigma _c\) state. We found a resonance 331.8 MeV above the \(\Lambda _c\Lambda _c\) threshold, 6.2 MeV below the \(\Sigma _c\Sigma _c\) threshold, with a width of 4.7 MeV. As a consequence of the coupling to the lower \(\Lambda _c\Lambda _c\) channel, the pole approaches the threshold moving from \(-16.2\) MeV in the real axis to the complex plane, \((-6.2 - i \, 4.7/2)\) MeV. The mechanism we have discussed helps in understanding the narrow width of experimental resonances found in the heavy hadron spectra with a large phase space in the decay channel. The observation of a small width for the decay to a low-lying channel could thus point to a dominant contribution of some upper channel to the formation of the resonance.

3 The three-baryon system

The \(\Lambda _c\Lambda _c - \Sigma _c\Sigma _c\) system in a pure S wave configuration has quantum numbers \((I,J^P)=(0,0^+)\) so that adding one more nucleon, the \(N\Lambda _c\Lambda _c\) system has necessarily quantum numbers \((I,J^P)=(1/2,1/2^+)\). It is coupled to the \(N\Sigma _c\Sigma _c\) channel. A detailed description of the Faddeev equations of the three-body system can be found in Ref. [46]. It has been explained how to deal with coupled channels containing identical particles of various types in the upper and lower channels. We show in Table 2 the different two-body channels that contribute to the \(N\Lambda _c\Lambda _c - N\Sigma _c\Sigma _c\) \((I,J^P)=(\frac{1}{2},\frac{1}{2}^+)\) three-body system. Notice that the charm \(+2\) S wave channels \(\Lambda _c\Sigma _c\) and \(\Sigma _c\Sigma _c\) with isospin 1 are not considered since they do not couple to the isosinglet \(\Lambda _c\Lambda _c\) two-body subsystem. Therefore, the Faddeev equations of the \((I,J^P)=(1/2,1/2^+)\) three-body system are of the form,

$$\begin{aligned} T_{N\Lambda _c}^{\Lambda _c}= & {} -t_{N\Lambda _c}^{\Lambda _c} G_0 T_{N\Lambda _c}^{\Lambda _c} \nonumber \\&+2 \, t_{N\Lambda _c}^{\Lambda _c} G_0T_{\Lambda _c\Lambda _c}^N \nonumber \\&+ t_{N\Lambda _c-N\Sigma _c}^{\Lambda _c} G_0T_{N\Lambda _c}^{\Sigma _c} \nonumber \\ T_{N\Lambda _c}^{\Sigma _c}= & {} t_{N\Lambda _c}^{\Sigma _c} G_0T_{N\Sigma _c}^{\Lambda _c} \nonumber \\&+2 \, t_{N\Lambda _c-N\Sigma _c}^{\Sigma _c} G_0T_{\Sigma _c\Sigma _c}^N \nonumber \\&+ t_{N\Lambda _c-N\Sigma _c}^{\Sigma _c} G_0T_{N\Sigma _c}^{\Sigma _c} \nonumber \\ T_{N\Sigma _c}^{\Lambda _c}= & {} t_{N\Sigma _c}^{\Lambda _c} G_0T_{N\Lambda _c}^{\Sigma _c}\nonumber \\&+2 \, t_{N\Sigma _c-N\Lambda _c}^{\Lambda _c} G_0T_{\Lambda _c\Lambda _c}^N \nonumber \\&+ t_{N\Sigma _c-N\Lambda _c}^{\Lambda _c} G_0T_{N\Lambda _c}^{\Lambda _c} \nonumber \\ T_{N\Sigma _c}^{\Sigma _c}= & {} -t_{N\Sigma _c}^{\Sigma _c} G_0T_{N\Sigma _c}^{\Sigma _c} \nonumber \\&+2 \, t_{N\Sigma _c}^{\Sigma _c} G_0T_{\Sigma _c\Sigma _c}^N \nonumber \\&+ t_{N\Sigma _c-N\Lambda _c}^{\Sigma _c} G_0T_{N\Sigma _c}^{\Lambda _c} \nonumber \\ T_{\Lambda _c\Lambda _c}^N= & {} t_{\Lambda _c\Lambda _c}^N G_0T_{N\Lambda _c}^{\Lambda _c}\nonumber \\&+t_{\Lambda _c\Lambda _c-\Sigma _c\Sigma _c}^N G_0T_{N\Sigma _c}^{\Sigma _c} \nonumber \\ T_{\Sigma _c\Sigma _c}^N= & {} t_{\Sigma _c\Sigma _c}^N G_0T_{N\Sigma _c}^{\Sigma _c}\nonumber \\&+t_{\Sigma _c\Sigma _c-\Lambda _c\Lambda _c}^N G_0T_{N\Lambda _c}^{\Lambda _c} \, , \end{aligned}$$
(4)

where \(t_{ij}^k\) are the two-body t-matrices that already contain the coupling among all two-body channels contributing to a given three-body state, see Table 2. \(G_0\) is the propagator of three free particles. The superscript of the amplitudes indicates the spectator particle and the subscript the interacting pair.

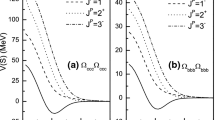
Table 2 S wave two-body channels (i, j) of the various subsystems that contribute to the \(N\Lambda _c\Lambda _c - N\Sigma _c\Sigma _c\) \((I,J^P)=(\frac{1}{2},\frac{1}{2}^+)\) three-body system
Full size table

The results are presented in Fig. 3. We have performed three different calculations. First, we have included the three-body amplitudes of the first two lines of Table 2 that do not contain the \(\Sigma _c\) baryon, the result being depicted by the dotted line. As it could have been expected, there exists attraction due to the attractive character of the \(N\Lambda _c\) and \(\Lambda _c\Lambda _c\) interactions discussed in Sect. 2. However, the attraction is not sufficient for having a bound state. Then, we have included the amplitudes containing the \(\Sigma _c\Sigma _c\) two-body subsystem, third line in Table 2, and all isospin 1/2 three-body amplitudes containing a \(\Sigma _c\) baryon either as spectator or as a member of the interacting pair, lines 4 to 6 of Table 2. The result corresponds to the dashed-dotted line. The coupled channel effect induces some additional attraction, reducing the value of the Fredholm determinant. Finally, we added the isospin 3/2 \(N\Sigma _c\) amplitudes indicated in the last line of Table 2, the result is depicted by the solid line. Although the singlet amplitudes increase the attraction, the repulsive triplet isospin 3/2 \(N\Sigma _c\) amplitude, discussed in Sect. 2, induces an overall repulsion in the three-body system, increasing the value of the Fredholm determinant.

Fig. 3
figure 3

Fredholm determinant of the \(N\Lambda _c\Lambda _c - N\Sigma _c\Sigma _c\) \((I,J^P)=(\frac{1}{2},\frac{1}{2}^+)\) three-body state. See text for details

Full size image
Fig. 4
figure 4

Fredholm determinant of the \(N\Lambda _c\Lambda _c - N\Sigma _c\Sigma _c\) \((I,J^P)=(\frac{1}{2},\frac{1}{2}^+)\) three-body state for two different values of the Gaussian size parameter of the charm quark wave function, \(b_c\)

Full size image

We have studied the dependence of the results on the only free parameter of the interacting potential, the Gaussian size parameter of the charm quark wave function, \(b_c\). It has been illustrated in fig. 4 of Ref. [30] how the central \(Y_c N\) interactions become more attractive for smaller values of \(b_c\). However, the weakening of the non-central contributions generates a slightly less attractive systems in the presence of coupled-channel effects, see right panel of fig. 5 of Ref. [31]. It was argued in Ref. [47] that the smaller values of \(b_c\) are preferred to get consistency with calculations based on infinite expansions, as hyperspherical harmonic expansions [48], where the quark wave function is not postulated. This also agrees with simple harmonic oscillator relations \(b_c=b_n\sqrt{\frac{m_n}{m_c}}\),Footnote 3 leading to the best suited value \(b_c=0.2\) fm for the study of the charm sector [47]. Thus, in Fig. 4 we show the Fredholm determinant for two different values of \(b_c\), 0.5 and 0.2 fm. As can be seen, the attraction increases for smaller values of \(b_c\), the effect not being enough to generate a bound state. Such tiny contributions might well be of importance for states at the edge of binding, as discussed in the following.

Guided by the resonance found in the \(\Sigma _c\Sigma _c\) system, we have finally studied the \(N\Sigma _c\Sigma _c\) system without coupling to \(N\Lambda _c\Lambda _c\), looking for a three-body resonance. The results are promising if the triplet isospin 3/2 amplitude is not considered. Thus, considering only the isospin 1/2 amplitudes we obtain a bound state with a separation energy of 0.6 MeV. If the singlet isospin 3/2 amplitude is included, the separation energy increases to 0.7 MeV. If the repulsive triplet isospin 3/2 \((N\Sigma _c)\Sigma _c\) amplitude is considered, the signal of the resonance is lost. However, adopting the best suited value for the charm sector, \(b_c=0.2\) fm, the \(N\Sigma _c\Sigma _c\) three-body resonance is still there with a separation energy of 0.2 MeV.

4 Summary

In short, we have studied two- and three-baryon systems with two units of charm looking for possible bound states or resonances. All two-baryon interactions are consistently derived from a constituent quark model tuned in the light-flavor hadron phenomenology. Our results show a narrow two-body resonance with quantum numbers \((I,J^P)=(0,0^+)\). It is located 6.2 MeV below the \(\Sigma _c\Sigma _c\) threshold and has a width of 4.7 MeV. A detailed study of the coupled \(N\Lambda _c\Lambda _c - N\Sigma _c\Sigma _c\) three-body system as well as the uncoupled \(N\Sigma _c\Sigma _c\) system shows that the foregoing two-body state contributes to generate a \(N \Sigma _c\Sigma _c\) resonance with quantum numbers \((I,J^P)=(1/2,1/2^+)\) and a separation energy of 0.2 MeV.

Weakly bound states and resonances are usually very sensitive to potential details and therefore theoretical investigations with different phenomenological models are highly desirable. The existence of these states could be scrutinized in the future at the LHC, J-PARC and RHIC providing a great opportunity for extending our knowledge to some unreached part in our matter world.