1 Introduction

The investigation of DE objects has turned into an interesting subject due to the phenomenon that the expansion of the Universe is accelerating. This phenomenon was proposed by the High-z supernova Search Team in 1998 by observing type Ia supernovae [1,2,3,4,5,6,7,8,9], which was subsequently confirmed by checking of the Cosmic Microwave Background Radiation [10, 11] and Large-scale structure [12,13,14,15,16,17]. DE is the most agreeable hypothesis to clarify this accelerating expansion of the Universe.

In Einstein’s general relativity, to explain the rate of accelerating expansion of the Universe, it is necessary to define a dark component with the matter distribution obeying a strong negative pressure. This dark component normally refers to DE. Cosmic perceptions show that the Universe is flat and currently contains about 1/3 DM (dark matter) and 2/3 DE. The dark sector concept (DE and DM) is obscure, and many very diverse models have been suggested, for instance, DGP branes, a small positive cosmological constant [18, 19], quintessence [20,21,22], the non-linear F(R) models [23,24,25], and DE in brane Universes [26, 29].

Then again, another essential problem in the physics of gravity concerns black holes (BHs) and their development in our world. In spite of the fact that it is, for the most part, trusted believed to considerably littler than the horizon extent, the DE variances itself are insignificant [30], their consequences for developing the complications of the matter might be huge [31, 32]. At that point, a characteristic inquiry is the manner by which DE influences the procedure of the star attraction’s gravity.

It is understood that DE applies an offensive force on its encompassing, and this later can restrain the object from collapsing. In reality, there are theories demonstrate that a gigantic object doesn’t just fall to shape a BH, rather for the development of objects that comprise DE. Mazur and Mottola [33,34,35] proposed a model unraveled keeping in mind the ultimate goal of having an answer with the last object without any scenario of singularity or horizons, which they so-called gravastar (GRAvitational VAcuum STAR). In this circumstance, the object (gravastar) is a framework represented by the presence of a thin layer yet not microscopic made of a solid matter, which isolates the interior region through the Schwarzschild outside of outer space. Disposal of the clear horizon is achieved by using an appropriate choice from the inside and outside the radius of the thin envelope, so that the internal radius is shorter than the horizontal range of the de-Sitter and the outer range is longer than the Schwarzschild horizon. In a past action, Visser and Wiltshire [36] estimated that the gravastar was gradually stabilized. The presence of elements such as gravastar brings both exchanges to the inevitable way that gravity collapse always forms a BH.

The configuration and gravitational collapse of BHs in the existence of DE and DM was first addressed by various works [37,38,39,40]. Chan et al. [41], motivated by the gravastars picture, have recently shown that these kinds of gases with anisotropic pressure, are possessed to a spherically symmetric objects typical script and gravity collapse, imposes a careful analysis of the anisotropy which is a very important parameter in this case. In the same context, they suggested generalizing the limits of the situation of the anisotropic fluids. This generalization comes directly from the strong state of energy.

In view of the talks about the gravastar picture a few theorists have proposed elective models [42,43,44,45,46]. Among them, we can discover a gravastar with anisotropic and continuous pressure [47], the gravastar supporting by nonlinear electrical dynamics [48], and a Chaplygin dark star [49]. Next to them, Lobo [50] has examined two DE models. One depicts a homogeneous energy density and another uses a particularly low diminishing energy density, both of them with the anisotropic pressure. With a specific end goal to coordinate an outside Schwarzschild space-time he has presented a thin layer in the space separating the inside and the outside space-times.

In the current procedure, we suggest a model for an anisotropic gravastar of DE or simply a DE object in agreement with Chaplin’s definition [51] based on the EoS, \(p=\gamma \rho -\rho \) with \(\gamma <{2}/{3}\), where we suppose that the radial pressure applied to the framework due to the nearness of DE is immediately proportional to the matter density for the perfect isotropic fluid. In our model, the energy density, as well as pressure, diminishes with radial coordinates, as anticipated for well-known star models and the mass function is a physical result of the EFEs. In order to remove the current central uniqueness, we have taken into consideration a center with an energy density of homogeneous, to find the central solution for modeling a DE object with a repulsive gravitational force. In this respect, we assume that the fluid governed by the EoS in the following form \(p_r=\lambda {\rho }_c\) with \(\lambda <0\). The junction along the space separating the interior and Schwarzschild has forced out of space-time a thin envelope. We are going to investigate diverse configurations, with impressive specific choices for the mass function in order to resolve the EFEs. The behavior of this mass function in the star interior represents an increase of the energy density interestingly with usual models. The primary electromagnetic mass model of Tiwari et al. [52] complying with an EoS \(p=-\rho \), infers which the gravitational mass goes as a high intensity of their radius interior the star. For the model of a star of anisotropic fluid in the DE scenario, where a repulsive gravitational is necessary, it is interesting to suggest a model with this anonymous dependence. In this respect, the fluid encloses inside a shell is considered so as to assess the behavior of stability and the physical properties. In the line of thought such as the dependence formalities of Lobo and Crawford [53], we find the stability profile.

The paper is organized as follows: In Sect. 2 we discuss the interior space-time and EFEs of stellar models of astrophysical objects. In Sect. 3 we demonstrate the junction conditions for the shell between the inside and the outside space-time, and then the energy conditions have been analyzed in Sec 4. In Sect. 5 we explored the equilibrium condition below various forces of compact object for a physically reasonable model. In Sect. 6 we discuss some characteristic comments about mass function, mass-radius relationship, and surface redshift function. A stability analysis is given in Sect. 7. Concluding remarks close this paper.

2 Interior space-time and EFEs of anisotropic fluid distributions

We are going to consider a static spherically symmetric anisotropic matter distribution, reported in the following metric, in curvature parameters [54]:

$$\begin{aligned} {ds}^2= & {} -exp\left\{ -2\int ^{\infty }_r{g\left( \tilde{r}\right) d\tilde{r}}\right\} {dt}^2 \nonumber \\&+{\left\{ 1-2m(r)/r\right\} }^{-1}{dr}^2+ r^2{d\Omega }^2, \end{aligned}$$
(1)

where \({d\Omega }^2={d\vartheta }^2+{sin}^2\vartheta {d\varphi }^2\) is the metric on the unit 2-sphere, g(r) and m(r) are two random expressions of the radial parameter r. And having an energy-momentum tensor represented for an anisotropic matter distribution by

$$\begin{aligned} T_{\mu \nu }=\left( \rho +p_t\right) u_{\mu }u_{\nu } +p_tg_{\mu \nu }+\left( p_r-p_t\right) v_{\mu }v_{\nu }, \end{aligned}$$
(2)

where \(\rho \) is the energy density, \(p_r\) is the radial pressure measured in the direction of \(v_{\mu }\), \(p_t\) is the transverse pressure measured in the orthogonal direction of \(v_{\mu }\), \(u_{\mu }\) is the vector 4-velocity, \(v_{\mu }\) is the space-like vector in the radial direction, i.e., \(v_{\mu }=\sqrt{1-2m(r)/r}\times g(r)\). The element g(r) is called the gravity profile, which symbolizes the locally weighted gravity acceleration. For g(r) is strictly positive, gravitational attraction is inward, and for g(r) is strictly negative, we find a gravitational repulsion outward.

The EFEs is given by

$$\begin{aligned} G_{\mu \nu }={8\pi T}_{\mu \nu }, \end{aligned}$$
(3)

where \(G_{\mu \nu }\) is the Einstein tensor, we get the following relationship

$$\begin{aligned} m'= & {} 4\pi r^2\rho , \end{aligned}$$
(4)
$$\begin{aligned} g= & {} \left( m+4\pi r^3p_r\right) {\left( r\left( r-2m\right) \right) }^{-1}, \end{aligned}$$
(5)
$$\begin{aligned} p_r'= & {} -\left( \rho +p_r\right) \left( m+4\pi r^3p_r\right) \nonumber \\&\times {\left( r\left( r-2Gm\right) \right) }^{-1}+\frac{2}{r}\left( p_t-p_r\right) , \end{aligned}$$
(6)

where primes represent differentiation with respect to the parameter, r. In generating the above field equations, we used geometric units where the coupling constant and the speed of light are considered as units (\(G=c=1\)). Equation (6) matching Bianchi’s identity means that \({\Delta }_{\mu }T^{\mu \nu }\), has also been found by using the Tolman–Oppenheimer–Volkoff (TOV) equation for the relativistic anisotropic pressure. It is clear that in the isotropic situation i.e. (\(p_t=p_r\)) the Eq. (6) correspond to the usual TOV equation, which restricts the structure of the internal equilibrium of general relativistic, isotropic, static ideal gas objects and it is constituted in basis textbooks of gravity [55, 56].

At this stage, we have a system of equations constituted by three equations, specifically, the field Eqs. (4)–(6), and 5 nameless variables of radial coordinate, r, i.e., \(\rho (r)\), \(p_r(r)\), \(p_t(r)\), g(r) and m(r). Along these lines, it is greatly hard to do to get a specific solution of EFEs. However as in previously mentioned discussion, we are concerned in closely realistic case where the mass expression is uniform and field distributions are basically acquired for deciding the physical highlights of a compact star. With this objective into account, let us suppose that a EoS \(p=p(\rho )\) and the mass density which is increment from the core to the surface of the star.

It is helpful now to present the mass and gas with the EoS in the specific shape

$$\begin{aligned} m\left( r\right)= & {} \ \frac{{\alpha }_1}{2}r+\frac{{\alpha }_2}{2}r^3, \end{aligned}$$
(7)
$$\begin{aligned} p_r= & {} \gamma \rho -\rho . \end{aligned}$$
(8)

For the choice of relation of the mass gives a behavior of monotonic increasing in kind and regular at the focal point of the star. At a similar time it supplies a matter density which gives a profile of monotonic diminishing in kind and gives a limited an incentive at the focal point of the star. So our chosen mass function is physically acceptable. Presently, considering the Eqs. (4) and (5) and utilizing the EoS of DE (8), we acquire

$$\begin{aligned} g(r)=\ {\left( {\alpha }_1\gamma +{\alpha }_2\left( 3\gamma -2\right) r^2\right) }/{\left( 2r\left( 1-{\alpha }_1 -{\alpha }_2r^2\right) \right) }.\nonumber \\ \end{aligned}$$
(9)

To investigate the nature of DE for local stellar manifestation has attracted a lot of interest and for fantastic surveys on this subject sees Refs. [57, 58]. The existence of DE sphere makes us expect that it is a generalization of the gravastar picture with an inside solution governed by the EoS of DE and such objects have gotten impressive consideration in astrophysics although some steps have been already taken in this direction.

Solving the above system Eqs. (4)–(6), utilizing the EoS of DE \(p_r=\gamma \rho -\rho \), we acquire the physical parameters for this model are written as:

$$\begin{aligned} {\rho }= & {} \ \frac{{\alpha }_1}{8\pi r^2}+\frac{3{\alpha }_2}{8\pi }, \end{aligned}$$
(10)
$$\begin{aligned} p_r= & {} \left( \gamma -1\right) \left( \frac{{\alpha }_1}{8\pi r^2}+\frac{3{\alpha }_2}{8\pi }\right) , \end{aligned}$$
(11)
$$\begin{aligned} {p_t}= & {} \ \frac{1}{8\pi }\left\{ \gamma \left( {\alpha }_1 +3{\alpha }_2r^2\right) \left( {\alpha }_1\gamma +{\alpha }_2 \left( 3\gamma -2\right) r^2\right) \right. \nonumber \\&\left. \times {\left( r^2\left( 1-{\alpha }_1-{\alpha }_2r^2\right) \right) }^{-1} +3{\alpha }_2\left( \gamma -1\right) \right\} , \end{aligned}$$
(12)

and using Eqs. (11) and (12) we get

$$\begin{aligned} \Delta= & {} \frac{1}{8\pi r^2}\left\{ \gamma \left( {\alpha }_1+3{\alpha }_2r^2\right) \left( {\alpha }_1\gamma +{\alpha }_2\left( 3\gamma -2\right) r^2\right) \right. \nonumber \\&\left. \times {\left( r^2\left( 1-{\alpha }_1-{\alpha }_2r^2\right) \right) }^{-1} -{\alpha }_1\left( \gamma -1\right) \right\} , \end{aligned}$$
(13)

\(\Delta =p_t-p_r\) is signified as the anisotropic parameter. It is a measure of the anisotropic pressure of the gas including the star of DE. \(\Delta =0\) matching to the special situation of a isotropic pressure DE object [50]. Notice that \(\Delta /r\) symbolizes a force appropriate to the anisotropic kind of the astrophysical form, which is repulsive, i.e., being outward directed if \(\Delta >0\), and attractive if \(\Delta <0\).

We will currently analyze the energy density is positive and limited at all focuses in the inside of the spherical object and some physical criterion which are important for the inside solution. In this respect, it is important to impose the restrictions on the constants appearing in the metric functions, so that all criteria for physical availability are fulfilled and well-behaved at all the inner points of strange compacts objects. Now we follow closely the Buchdahl limit, \(2m\left( r\right) -r<0\) and using the Eq. (7) we get \(1-{\alpha }_1-{\alpha }_2r^2>0\), which supply a restriction on the variables \({\alpha }_1\), \({\alpha }_2\), and radius r, so according to the last we can write

$$\begin{aligned} r<\sqrt{{\left( 1-{\alpha }_1\right) }/{{\alpha }_2}}. \end{aligned}$$
(14)

This gives the constraint on \({\alpha }_1\), \({\alpha }_2\) of \({\alpha }_1<1\) and \({\alpha }_2>0\). According to this restriction one can choose values of \({\alpha }_1=0.45\) and \({\alpha }_2={10}^{-3}\) which is very close with the choice of Dev and Gleiser [56]. Now, using the Eq. (9) provided that g(r) is strictly positive we find

$$\begin{aligned} \gamma >{2{\alpha }_2r^2}/{\left( {\alpha }_1+3{\alpha }_2r^2\right) }. \end{aligned}$$
(15)

By using the Eq. (14) in (15), and for a big value of r we can find the expression in the maximum limit in the following form as

$$\begin{aligned} \gamma >{2\left( 1-{\alpha }_1\right) }/{\left( 3-2{\alpha }_1\right) }. \end{aligned}$$
(16)

For a little value of r, from the Eq. (15) we get \(\gamma >0\), thus

$$\begin{aligned} \gamma >max\left( 0,\ 2\frac{\left( 1-{\alpha }_1\right) }{3-2{\alpha }_1}\right) . \end{aligned}$$
(17)

For our choice, \({\alpha }_1=0.45\), \(max\left( 0,\ 2\frac{\left( 1-{\alpha }_1\right) }{3-2{\alpha }_1}\right) =0.55\) i.e., \(\gamma =0.55\).

Once more, utilizing the condition (9) gave that g(r) is entirely negative we obtain

$$\begin{aligned} \gamma <{2{\alpha }_2r^2}/{\left( {\alpha }_1+3{\alpha }_2r^2\right) }. \end{aligned}$$
(18)
Fig. 1
figure 1

Variation of the gravity profile,\(\ g(r)\), with the radial coordinate when \(\gamma =+0.9\) and \(\gamma =-0.2\) for spherical object PSR J1614-2230

Full size image

For a little value of r, Eq. (18) gives \(\gamma <0\), and for big r i.e., in the maximum limit leads to

$$\begin{aligned} \gamma <{2\left( 1-{\alpha }_1\right) }/{\left( 3-2{\alpha }_1\right) }. \end{aligned}$$
(19)

Therefore,

$$\begin{aligned} \gamma <min\left( 0,\ 2\frac{\left( 1-{\alpha }_1\right) }{3-2{\alpha }_1}\right) . \end{aligned}$$
(20)

For the above choice of \({\alpha }_1\), we get \(min\left( 0,\ 2\frac{\left( 1-{\alpha }_1\right) }{3-2{\alpha }_1}\right) =0\) i.e., \(\gamma =0\). In this way, we need to decide for \(\gamma \) either \(\gamma >0.55\) and \(\gamma <0\) for the plots, which satisfies these two cases corresponding respectively to the normal and ghost phases.

The behaviors of the gravity profile g(r) are shown in Fig. 1 for \(\gamma =+0.9\) and \(\gamma =-0.2\) respectively. From this figure, we observe that gravity profile g(r) is strictly positive when \(\gamma =+0.9\) and strictly negative when \(\gamma =-0.2\) for our above choice of \({\alpha }_1\) and \({\alpha }_2\).

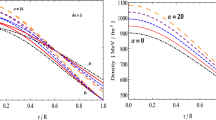
The behaviors of the matter density \(\rho \), transverse pressure \(p_t\), and radial pressure \(p_r\) are plotted in Fig. 2 are all monotonically decreasing expressions of the radial parameter r.

In Fig. 3, we show the variation of the force due to the anisotropic pressure with the radius within the sphere for different values of \(\gamma \) for fixed values of parameters \({\alpha }_1\) and \({\alpha }_2\). It explains that this force will be attractive in nature i.e. in the interior direction if \(p_t<p_r\) and repulsive if \(p_t>p_r\) or on the other hand \(\Delta >0\). For our astrophysical model configuration (see Fig. 3) \(\Delta >0\) for both the situations when \(\gamma =+0.9\) and the ghost phase, i.e. for \(\gamma =-0.2\).

Fig. 2
figure 2

Variation of the matter density \(\rho \), radial pressure \(p_r\) and transverse pressure \(p_t\) with the radial coordinate of the DE model for spherical object PSR J1614-2230

Full size image
Fig. 3
figure 3

Variation of the anisotropy parameter, \(\Delta =p_t-p_r\), with the radial coordinate r when \(\gamma =+0.9\) and \(\gamma =-0.2\) for spherical object PSR J1614-2230

Full size image

In fact, we can see that there are a number of problems in the model. For instance, the divergence of pressure and energy density in the center of the spherical object. In order, to solve these problems for modeling a spherical object. We assume that the spherical object has a center extending to the finite radius. So to stay away from this singularity in the center, we cut the space-time metric (1) close to its center where we place the anisotropy fluid of constant density \({\rho }_c\). Now, to find the central solution that can model a DE object with a repetitive gravitational force. In this respect, we assume that the fluid governed by the radial EoS in the following form:

$$\begin{aligned} p_r=\lambda {\rho }_c\ , \lambda <0. \end{aligned}$$
(21)

Here, the mass function m(r) becomes

$$\begin{aligned} m\left( r\right) =\frac{4\pi {\rho }_c}{3}r^3. \end{aligned}$$
(22)

Using this last expression (22), we obtain, with the help of Eq. (5),

$$\begin{aligned} g(r)=\ \frac{8\pi {\rho }_c}{3}\frac{\left( 1+3\lambda \right) }{\left( 1-\frac{8\pi {\rho }_c}{3}r^2\right) }r. \end{aligned}$$
(23)

Therefore, the space-time metric of the center is given by

$$\begin{aligned} {ds}^2= & {} {\left\{ 1-\frac{8\pi {\rho }_c}{3}r^2\right\} }^{-\frac{1}{2} \left( 1+3\lambda \right) }{dt}^2\nonumber \\&+{\left\{ 1-\frac{8\pi {\rho }_c}{3}r^2\right\} }^{-1}{dr}^2+r^2{d\Omega }^2. \end{aligned}$$
(24)

Note that with Eq. (22), the metric (24) does not diverge at the center \(r=0\). The transverse pressure can be obtained as

$$\begin{aligned} p_t=\ \lambda \left[ 1+\left( 1+\lambda \right) \left( 1+3\lambda \right) \frac{2\pi {\rho }^2_cr^2}{\left( 3-8\pi {\rho }_cr^2\right) }\right] {\rho }_c, \end{aligned}$$
(25)

and the anisotropy factor \(\Delta \) can be obtained in the form

$$\begin{aligned} \Delta =\ \left( 1+\lambda \right) \left( 1+3\lambda \right) \frac{2\pi {\rho }^2_cr^2}{\left( 3-8\pi {\rho }_cr^2\right) }, \end{aligned}$$
(26)

From the above expression of the anisotropy factor \(\Delta \), we must clearly observe that \(\Delta >0\) if \(\lambda <-1\) and \(\Delta <0\) if \(-1<\lambda <{-1}/{3}\). In the center of the spherical object, \(\Delta =0\), which is expected for a physically acceptable solution. We can also note that for \(\lambda =-1\) and \(\lambda ={-1}/{3}\), the anisotropic pressure of the center is reduced to the isotropic pressure.

3 Junction condition for the shell

The spherical object shell is a hypersurface of constant radius \(r=R\) in 3+1 dimensional space-time along which the space-time dedicated to the matching of the Schwarzschild metric outside the shell with \(p=\rho =0\) at the junction interface \(r=R\), with radius of junction R. The metric of the hypersurface is given by

$$\begin{aligned} ds^2= & {} -\left( 1-2M/r\right) {dt}^2+\frac{1}{\left( 1-2M/r\right) }{dr}^2\nonumber \\&+r^2\left( {d\theta }^2{{+sin}^2 \theta {d\phi }^2\ }\right) , \end{aligned}$$
(27)

describes a pointmass in space-time, with a singularity at the origin, where the singularity at \(r=2M\) is just a result of choice of coordinates [63]. We have taken the value of the radius of junction \(R>2M\) to stay away from the existence of such singularities i.e., the radius of junction lies exterior 2M, where M can be defined as the total mass of the DE star. At present using the Darmois-Israel formalism [64, 65], the special function for the shell stress-energy tensor \(S^i_j\) on a space-time hypersurface is given by the Lanczos equations

$$\begin{aligned} S^i_j=-\frac{1}{8\pi }\left( {\kappa }^i_j-{\delta }^i_j{\kappa }^k_k\right) , \end{aligned}$$
(28)

where the term \({\kappa }^i_j\) symbolize the extrinsic curvatures discontinuity, \(K^i_j\) beyond the hypersurface, i.e., \({\kappa }^i_j =K^+_{ij}-K^-_{ij}\). The extrinsic curvature is defined as [64, 65]:

$$\begin{aligned} K_{ij}\equiv n_{\mu ;\nu }e^{\mu }_{(i)}e^{\nu }_{(j)}, \end{aligned}$$
(29)

where \(n_{\mu }\) is the unit normal quadric-vector of the hypersurface \(\Sigma \), and \(e^{\mu }_{(i)}\) are the parts of the holonomic premise vectors tangent of the hypersurface \(\Sigma \). Now, we can utilizing the metrics (1) and (27), we conclude the non-trivial parts of the extrinsic curvature are given by on the following form

$$\begin{aligned} K^{\tau +}_{\tau }= & {} \frac{1}{R^2}\frac{M+\ddot{R}R^2}{\sqrt{1-\frac{2M}{R}+{\dot{R}}^2}}, \end{aligned}$$
(30)
$$\begin{aligned} K^{\tau -}_{\tau }= & {} \frac{\left( {\alpha }_1\gamma +{\alpha }_2 \left( 3\gamma -2\right) R^2\right) \left( 1-{\alpha }_1-{\alpha }_2 R^2\right) }{2R\left( 1-{\alpha }_1-{\alpha }_2R^2\right) \sqrt{1-{\alpha }_1-{\alpha }_2R^2+{\dot{R}}^2}}\nonumber \\&+\frac{2\ddot{R}R\left( 1-{\alpha }_1-{\alpha }_2R^2\right) -\gamma {\dot{R}}^2}{2R\left( 1-{\alpha }_1-{\alpha }_2R^2\right) \sqrt{1-{\alpha }_1-{\alpha }_2R^2+{\dot{R}}^2}},\nonumber \\ \end{aligned}$$
(31)

and

$$\begin{aligned} K^{\vartheta +}_{\vartheta }= & {} \frac{1}{R}\sqrt{1-\frac{2M}{R}+{\dot{R}}^2}, \end{aligned}$$
(32)
$$\begin{aligned} K^{\vartheta -}_{\vartheta }= & {} \frac{1}{R}\sqrt{1-{\alpha }_1 -{\alpha }_2R^2+{\dot{R}}^2}. \end{aligned}$$
(33)

where the dot signifies a derivative with respect to the correct time, \(\tau \). Therefore, from the equations of Lanczos [48, 50] one can write the surface stresses of the thin shell, as follows:

$$\begin{aligned} \sigma =-\frac{1}{4\pi R}\left\{ \sqrt{1-\frac{2M}{R} +{\dot{R}}^2}-\sqrt{1-{\alpha }_1-{\alpha }_2R^2+{\dot{R}}^2}\right\} , \end{aligned}$$
(34)

and

$$\begin{aligned} {\mathcal {P}}&=\frac{1}{4\pi R}\left\{ \frac{R^2\ddot{R}+R{\dot{R}}^2+R-M}{R\sqrt{1-\frac{2M}{R}+{\dot{R}}^2}} -\frac{\left( {\alpha }_1\gamma R+{\alpha }_2 \left( 3\gamma -2\right) R^3\right) \left( 1-{\alpha }_1-{\alpha }_2R^2\right) +\left( R\ddot{R}+1\right) \left( 1-{\alpha }_1-{\alpha }_2R^2\right) +2{\alpha }_2R^3{\dot{R}}^2}{2R\left( 1-{\alpha }_1-{\alpha }_2 R^2\right) \sqrt{1-{\alpha }_1-{\alpha }_2R^2+{\dot{R}}^2}}\right\} , \end{aligned}$$
(35)

\(\sigma \) and \({\mathcal {P}}\) are the energy density of surface and the transverse surface pressure, respectively.

We will likewise utilize the conservation law [48, 50] given by

$$\begin{aligned} S^i_{j,i}=-\frac{1}{8\pi }{\left[ T_{\mu \nu }e^{\mu }_{(j)}n^{\nu }\right] }^+_-, \end{aligned}$$
(36)

this equation provides us with

$$\begin{aligned} {\sigma }^{'}=-\frac{2}{R}\left( \sigma +{\mathcal {P}}\right) +\varXi . \end{aligned}$$
(37)

Where \(\varXi \), for notational convenience, we have defined as

$$\begin{aligned} \varXi =-\frac{1}{4\pi R}\frac{\gamma \left( {\alpha }_1 +3{\alpha }_2R^2\right) }{2R\left( 1-{\alpha }_1-{\alpha }_2R^2\right) } \sqrt{1-{\alpha }_1-{\alpha }_2R^2+{\dot{R}}^2}. \end{aligned}$$
(38)

Using the relationship (7) evaluated at R, it is clear to see that the transition phase \(\varXi \) is zero when \(\gamma =0\), which reduces to the examination inspected by Visser and Wiltshire [36]. The static solution is given to take into account \(\dot{R}=\ddot{R}=0\). The aggregate mass of the DE object, for the fixed solution, with the interface of junction R, is given by

$$\begin{aligned} M=m\left( R\right) +m_s(R)\left( \sqrt{1-\frac{m\left( R\right) }{R}} -\frac{m_s(R)}{2R}\right) , \end{aligned}$$
(39)

Where \(m_s\) is the mass of the surface of the thin layer is defined as

$$\begin{aligned} m_s(R)=4\pi R^2\sigma . \end{aligned}$$
(40)

Substituting the expression of \(\sigma \) in de static case into Eq. (40), and, with the assistance of condition (39), we get

$$\begin{aligned} M=\frac{1}{2}R\left( {\alpha }_1+{\alpha }_2R^2\right) +m_s\left( R\right) \sqrt{1-{\alpha }_1-{\alpha }_2R^2}-\frac{m^2_s(R)}{2R}, \end{aligned}$$
(41)

with

$$\begin{aligned} m_s\left( R\right) =R\left( \sqrt{1-{\alpha }_1-{\alpha }_2R^2} -\sqrt{1-\frac{2M}{R}}\right) . \end{aligned}$$
(42)

On the other hand, we can differentiate two times the relation in (40), and we take into consideration the radial component of the derivative of \({\sigma }'\), we can be rewrite expression (37) in the following form

$$\begin{aligned} {\left( \frac{m_s(R)}{2R}\right) }^{''}=\Upsilon -4\pi R{\sigma }{'}\eta , \end{aligned}$$
(43)

where \(\Upsilon \) and \(\eta \) are two unknown parameters defined respectively by

Fig. 4
figure 4

Variation of the velocity of the sound, \(\eta \), with the radial coordinate r, for tow values of mass M and when the parameter of DE \(\gamma \) is fixed for spherical object PSR J1614-2230

Full size image
$$\begin{aligned} \Upsilon =\frac{4\pi }{R}\left( \sigma +{\mathcal {P}}\right) +2\pi R{\varXi }{'}, \end{aligned}$$
(44)

and

$$\begin{aligned} \eta ={\frac{{{\mathcal {P}}}'}{{\sigma }'}}. \end{aligned}$$
(45)

where the prime indicates the derivative concerning R.

The equation found above will assume an essential role in deciding the stability area of the static arrangements. We use \(\eta \) as a parametrization of the stable equilibrium and using to establish the stability of the system, so that there is no necessity to identify a EoS of the surface [50]. We introduce \(\eta \) in Eq. (43), one deduces the idea proposed by Poisson and Visser [66] and Ishak and Lake [67], which consist that \(\sqrt{\eta }\) is described as the speed of the sound [50, 53]. At that point, the estimations of \(\eta \) are compelled to \(0<\eta \le 1\) on the surface layer, considering the prerequisite that the speed of sound ought not surpass the speed of light. The behavior of parameter of the stable equilibrium \(\eta \) is shown in Fig. 4.

With a specific end goal to acquire impression we investigate our framework by evolution identity defined by

$$\begin{aligned} {\left[ T_{\mu \nu }n^{\mu }_{(j)}n^{\nu }\right] }^+_-={\overline{K}}^i_jS^j_i, \end{aligned}$$
(46)

where

$$\begin{aligned} {\overline{K}}^i_j=\frac{1}{2}\left( K^{j+}_i+K^{j-}_i\right) , \end{aligned}$$
(47)

The above relationship of the evolution identity (46), with the help of expressions (37)–(40), one can provides the following relationship

$$\begin{aligned}&p_r+\frac{\left( \rho +p_r\right) {\dot{R}}^2}{1-{\alpha }_1-{\alpha }_2R^2} =\left\{ -\frac{1}{R}\left\{ \sqrt{1-\frac{2M}{R}+{\dot{R}}^2} +\sqrt{1-{\alpha }_1-{\alpha }_2R^2+{\dot{R}}^2}\right\} {\mathcal {P}}\right. \nonumber \\&\qquad +\frac{1}{2}\left\{ \frac{1}{R^2}\frac{M+\ddot{R}R^2}{\sqrt{1-\frac{2M}{R}+{\dot{R}}^2}} \left. +\frac{\left( {\alpha }_1\gamma +{\alpha }_2 \left( 3\gamma -2\right) R^2\right) \left( 1-{\alpha }_1-{\alpha }_2R^2\right) +2\ddot{R}R\left( 1-{\alpha }_1-{\alpha }_2R^2\right) -\gamma {\dot{R}}^2}{2R\left( 1-{\alpha }_1-{\alpha }_1R^2\right) \sqrt{1-{\alpha }_1-{\alpha }_2R^2 +{\dot{R}}^2}}\right\} \sigma \right\} , \end{aligned}$$
(48)

In order to considering the static case at \(R=R_0\) with \(\ddot{R}=\dot{R}=0\). From the above condition of the radial pressure we have the following pressure adjust equation in terms of the stress of surface as

$$\begin{aligned} p_r(R_0)&=\left\{ -\frac{1}{R_0}\left\{ \sqrt{1-\frac{2M}{R_0}} +\sqrt{1-{\alpha }_1-{\alpha }_2R^2_0}\right\} {\mathcal {P}}\right. \nonumber \\&\quad \left. +\frac{1}{2}\left\{ \frac{1}{R^2_0}\frac{M}{\sqrt{1-\frac{2M}{R_0}}} +\frac{\left( {\alpha }_1\gamma +{\alpha }_2\left( 3\gamma -2\right) R^2_0\right) }{2R_0\sqrt{1-{\alpha }_1-{\alpha }_2R^2_0}}\right\} \sigma \right\} , \end{aligned}$$
(49)

After this above equation, we can see that \(\sigma <0\) and the pressure of the shell acting from the inside is refuting \(p_r<0\), which implies that the stress is in a direction of radial. Consequently, if a positive transversal surface pressure \({\mathcal {P}}\) is necessary to maintain the shell stable.

4 Energy conditions on the junction

Located on the current section, let us analyze the energy conditions within the foundation of general relativity relating to the inside of the star. Presently, taking into consideration the standard description of this energy conditions for anisotropic fluids, we analyze: the Weak Energy Condition (WEC), the Null Energy Condition (NEC), the Strong Energy Condition (SEC), and the Dominant Energy Condition (DEC), at every point inside the fluid sphere. More accurately, we have the following suggestion

$$\begin{aligned}&NEC\ :\ \rho (r)+p_r(r)\ge 0, \end{aligned}$$
(50)
$$\begin{aligned}&WEC\ :\ \rho \left( r\right) +p_r\left( r\right) \ge 0,\ \rho (r)\ge 0, \end{aligned}$$
(51)
$$\begin{aligned}&SEC\ :\ \rho \left( r\right) +p_r\left( r\right) \ge 0, \ \rho \left( r\right) +p_r\left( r\right) +2p_t(r)\ge 0, \nonumber \\\end{aligned}$$
(52)
$$\begin{aligned}&DEC\ :\ \rho \left( r\right)>\left| p_r(r)\right| , \ \rho \left( r\right) >\left| p_t(r)\right| , \end{aligned}$$
(53)

Utilizing the above inequalities hold simultaneously for all terms of the inside region, one can easily confirm the kind of energy condition for the particular stellar configuration developed here. The profiles of the inequalities (50)–(53) have been demonstrated with the help of graphical depicted in Fig. 5. As an outcome, it is exceptionally obvious from Fig. 5 that all energy conditions (WEC), (NEC), (SEC), and (DEC) are satisfied for our suggested DE model.

5 Equilibrium condition

For exploring the equilibrium condition below various forces of compact object for a physically suitable model we examine the forces of gravity and other forces of fluid. If we take into account the generalized Tolman–Oppenheimer–Volkoff (TOV) [68], equation one can explain the context of the distribution of anisotropic fluid, which is given by

$$\begin{aligned} -{\frac{M_G(r)}{r^2}\left( \rho +p_r\right) exp \left( \frac{\lambda -\nu }{2}\right) }\ -\frac{dp_r}{dr} +\frac{2}{r}\left( \rho -p_r\right) =0, \end{aligned}$$
(54)

where \(M_G(r)\) is the successful gravitational mass interior a object of radius r given by the Tolmam–Whittaker procedure which is given by

$$\begin{aligned} M_G\left( r\right) =\frac{1}{2}r^2{\nu }^{'}{exp\left( \frac{\nu -\lambda }{2}\right) }\ . \end{aligned}$$
(55)

Substituting the Eq. (55) into (54) we find finally the modified TOV equation in a simply form

$$\begin{aligned} -{\frac{{\nu }'}{2}\left( \rho +p_r\right) }\ -\frac{dp_r}{dr}+\frac{2}{r} \left( \rho -p_r\right) =0, \end{aligned}$$
(56)

given this above equation from an equilibrium condition for anisotropic fluid spheres, the three forces are reactivated, namely, the gravitational (\(F_g\)), the hydrostatics (\(F_h\)) and the anisotropic (\(F_a\)) forces are given by :

$$\begin{aligned} F_g+F_h+F_a=0, \end{aligned}$$
(57)
Fig. 5
figure 5

Behaviour of the energy condition when \({\alpha }_1=0.45\), \({\alpha }_2={10}^{-3}\) as functions of r for fixed value of DE parameter \(\gamma =+0.9\) for spherical object PSR J1614-2230

Full size image
Fig. 6
figure 6

Behavior of different forces vs. radial coordinates r for \(\gamma =+0.9\) for spherical object PSR J1614-2230

Full size image

where

$$\begin{aligned} F_g= & {} -\frac{{\nu }'}{2}\left( \rho +p_r\right) , \end{aligned}$$
(58)
$$\begin{aligned} F_h= & {} -\frac{dp_r}{dr}, \end{aligned}$$
(59)
$$\begin{aligned} F_a= & {} +\frac{2}{r}\left( \rho -p_r\right) , \end{aligned}$$
(60)

To simplify these Eqs. (58)–(60) mentioned above, we have drawn the profiles of \(F_g\), \(F_h\), and \(F_a\) are demonstrate in Fig. 6. This figure shows that our DE model is in static equilibrium is feasible because to pressure gravitational, hydrostatic and anisotropy forces.

6 Some characteristics

6.1 Mass function

The mass expression inside the radius\(\ r\) which is mentioned in section 2 by Eq. (7) as,

$$\begin{aligned} m\left( r\right) =4\pi \int ^r_0{\rho \left( \omega \right) {\omega }^2d\omega } =\frac{{\alpha }_2}{2}r^3+\frac{{\alpha }_1}{2}r, \end{aligned}$$
(61)

As \({\mathop {\mathrm{lim}}_{r\rightarrow 0} m(r)\ }=0\), imply that the mass function is regular at the core of the the DE object. The behavior of the mass function is plotted in Fig. 7, which demonstrates that mass function is positive and monotonic expanding physical quantity according to the radial coordinates r.

Fig. 7
figure 7

Behaviour of the mass function when \({\alpha }_1=0.45\), \({\alpha }_2={10}^{-3}\) as functions of the radial coordinates r for spherical object PSR J1614-2230

Full size image
Fig. 8
figure 8

Behaviour of the compactness function when \({\alpha }_1=0.45\), \({\alpha }_2={10}^{-3}\) as functions of the radial coordinates r for spherical object PSR J1614-2230

Full size image
Table 1 Physical parameters for different anisotropic astrophysical models for \({\alpha }_1=0.45\) and \({\alpha }_2=0.001\)
Full size table

6.2 Mass-radius function

The mass-radius relationship of a compact object can not be arbitrarily big. Buchdahl [69] demonstrated that for a (\(3+1\))-dimensional fluid sphere \(\frac{2M}{R}<\frac{8}{9}\) (where R is the star radius) where \(R>2M\). The relationship mass-radius of our model is given in explicit form by

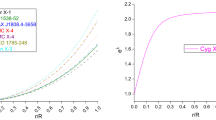
$$\begin{aligned} u(r)=\frac{m(r)}{r}=\frac{{\alpha }_2}{2}r^2+\frac{{\alpha }_1}{2}, \end{aligned}$$
(62)

The behavior of the compactification factor is represented in in Fig. 8. The factor \(u=m(R)/R=M/R\) characterizes the relationship mass-radius (the compactification factor) of the astrophysical configuration. The figure demonstrates that the compactification factor is a monotonic increasing relation according to the radial coordinates r. To see maximum value permissible the mass-radius ratio M/R is determined as \({M}/{R}=0.2719\) for our current model which lies in the normal framework of Buchdahl [69]. The impact of the mass-radius ratio on the EoS has been considered by Carvalho et al. [74] for white dwarfs and neutron stars, by Swift et al. [75] for exoplanets and for the nuclear center by Lattimer [76]. Similarly supposing the estimated masses and radii for several compact spherical objects: five X-ray binaries, namely Vela X-1, Cen X-3, 4U 1538-52, SAX J1808.4-3658 and Her X-1, analysis by Rawls et al. [77]; Abubekerov et al. [78]; Elebert et al. [79] and two binary millisecond pulsars, namely PSR J16142230 and PSR J1903+327 analysis by Demorest et al. [80]; Freire et al. [81], we have performed a comparative study of the values of the physical parameters which is shown in Table I, and are closely equal to the observed values of most of the compact spherical objects. Once again, we compared our solution of mass-radius relation for the compact neutron and quarks stars in one paradigmatic extension of general relativity, namely the realistic models of relativistic stars in \(f(R)=R+\alpha R^2\) gravity studied by Astashenok et al. [82]. The same behavior of the mass-radius relation was previously have been analyzed to model compact objects in the framework of f(R) gravity in [82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106], which do not cross the proposed range by Buchdahl in [69].

6.3 Surface redshift function

The surface redshift function \(z_s\) of a compact object can be given by the through expression

$$\begin{aligned} 1+z_s=\frac{1}{\sqrt{1-2u}}, \end{aligned}$$
(63)

substituting Eq. (62) into (63), thus, we get \(z_s\) as,

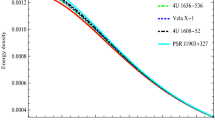
$$\begin{aligned} z_s={\left( 1-{\alpha }_1-{\alpha }_2R^2\right) }^{-{{\frac{1}{2}}}}-1, \end{aligned}$$
(64)

The values of the surface redshift parameter for various astrophysical structures are given in Table 1. For an isotropic spherical object, in the absence of a cosmological constant, Buchdahl [69] and Straumann [107] have demonstrated that \(z_s\le 2\). Böhmer and Harko [108] indicated that for an anisotropic spherical object, in the presence of a cosmological constant, the surface redshift can take a lot higher value \(z_s\le 5\). The limitation was thusly modified by Ivanov [109] who demonstrated that the most extreme admissible value could be as high as \(z_s=5.211\). In our situation, we have \(z_s\le 1\) for various compact spherical object models developed in this paper.

7 Stability analysis

We will then focus on Lobo and Crawford’s approach [53] to successfully consider dynamic thin shells that can radially move to the limit point of the star and examine under what conditions the star arrangement will be stable. A dynamic thin-shell associating two global static spherically symmetric space-times have additionally as of late been thought about [53] in a slightly different context.

We will portray the approach quickly, points of interest can be found in ref. [53]. It is appealing to note that Eq. (27), can be modified to get a condition of movement of the thin layer, as takes the follows,

$$\begin{aligned} V\left( R\right) +{\dot{R}}^2=0, \end{aligned}$$
(65)

with \(V\left( R\right) \) defined as

$$\begin{aligned} V\left( R\right) =1-\frac{M+m(R)}{R}-{\left( \frac{m_s(R)}{2R}\right) }^2 -{\left( \frac{M-m(R)}{m_s(R)}\right) }^2,\nonumber \\ \end{aligned}$$
(66)

Note that the resulting potential \(V\left( R\right) \) leads us to decide the stability analysis for the thin layer within our linear disturbance. Now we are going to consider the Taylor extension around the radius of the equilibrium \(R_0\) of the static arrangement, to the second order, we get

$$\begin{aligned} V\left( R\right)= & {} V\left( R_0\right) +\left( R-R_0\right) V^{'}\left( R_0\right) \nonumber \\&+\frac{{\left( R-R_0\right) }^2}{2}V^{''}\left( R_0\right) +O\left[ {\left( R-R_0\right) }^3\right] , \end{aligned}$$
(67)

where “ \('\) ” signified the derivative concerning R. As indicated by the standard technique we are linearizing around the static radius \(R=R_0\) we should have \(V\left( R_0\right) =0\), \(V^{'}\left( R_0\right) =0\). The solution will be stable if and only if the resulting potential \(V\left( R\right) \) has a minimum of locality at \(R_0\) and \(V^{''}\left( R_0\right) >0\) is checked.

Now, it is easy to see that the condition \(V^{'}\left( R_0\right) =0\) gives the following expression

$$\begin{aligned} \phi\equiv & {} {\left( \frac{m_s(R_0)}{2R_0}\right) }{'} =-\left( \frac{R_0}{m_s(R_0)}\right) {\left( \frac{M+m(R_0)}{R_0}\right) }^{'}\nonumber \\&-2\left( \frac{R_0}{m_s(R_0)}\right) \left( \frac{M-m(R_0)}{m_s(R_0)}\right) {\left( \frac{M-m(R_0)}{m_s(R_0)}\right) }^{'}.\nonumber \\ \end{aligned}$$
(68)

With this last description the second derivative \(V^{''}\left( R_0\right) \) can be composed as

$$\begin{aligned} V^{''}\left( R_0\right)&=-{\left( \frac{M+m\left( R_0\right) }{R_0}\right) }^{''} -2{\left( {\left( \frac{m_s\left( R_0\right) }{2R_0}\right) }'\right) }^2 \nonumber \\&\quad -2\left( \frac{m_s\left( R_0\right) }{2R_0}\right) {\left( \frac{m_s\left( R_0\right) }{2R_0}\right) }^{''} -2{\left( {\left( \frac{M-m(R_0)}{m_s(R_0)}\right) }'\right) }^2 \nonumber \\&\quad -2\left( \frac{M-m(R_0)}{m_s(R_0)}\right) {\left( \frac{M-m(R_0)}{m_s(R_0)}\right) }^{''}. \end{aligned}$$
(69)

In this way, a static solution asks for that the initial two relations of the Taylor development vanish, and the principal non-zero relation in the extension for the expression of the movement of the thin layer might be composed as (thinking about the Eq. (69))

$$\begin{aligned} {\dot{R}}^2+\frac{1}{2}V^{''}\left( R_0\right) {\left( R-R_0\right) }^2+O\left[ {\left( R-R_0\right) }^3\right] =0. \end{aligned}$$
(70)
Fig. 9
figure 9

Plots of the dimensionless parameter \({d{\sigma }^2}/{dR}\) as function of R for spherical object PSR J1614-2230

Full size image

To guarantee the static solution stabilities at \(R=R_0\), the second differential of the resulting potential shall be strictly positive, i.e., \(V^{''}\left( R_0\right) >0\). In order to simplicity were returning the formula (69), which appears

$$\begin{aligned} V^{''}\left( R_0\right) =\Theta -2{\phi }^2-\frac{m_s\left( R_0\right) }{R_0}{\left[ \Upsilon -4\pi R{\sigma }^{'}\eta \right] }_{R_0}, \end{aligned}$$
(71)

with

$$\begin{aligned} \Theta= & {} -{\left( \frac{M+m\left( R_0\right) }{R_0}\right) }^{''} -2{\left( {\left( \frac{M-m(R_0)}{m_s(R_0)}\right) }'\right) }^2 \nonumber \\&-2\left( \frac{M-m(R_0)}{m_s(R_0)}\right) {\left( \frac{M-m(R_0)}{m_s(R_0)}\right) }^{''}. \end{aligned}$$
(72)

Now from this last expression the second derivative (71) for \(V^{''}\left( R_0\right) >0\) , and assuming \(\eta \left( R_0\right) ={\eta }_0\), we have

$$\begin{aligned} {\eta }_0{\left. \frac{d{\sigma }^2}{dR}\right| }_{R_0} >\frac{\sigma }{2\pi }\left\{ \Upsilon +\frac{R_0}{m_s\left( R_0\right) } \left( 2{\phi }^2-\Theta \right) \right\} . \end{aligned}$$
(73)

Currently, from this last Eq. (73), we get stable equilibrium regions to be managed by the following inequalities

$$\begin{aligned}&{\eta }_0>\frac{\sigma }{2\pi }\left\{ \Upsilon +\frac{R_0}{m_s\left( R_0\right) }\left( 2{\phi }^2-\Theta \right) \right\} {\left\{ {\left. \frac{d{\sigma }^2}{dR}\right| }_{R_0}\right\} }^{-1},\nonumber \\&\qquad if\qquad {\left. \frac{d{\sigma }^2}{dR}\right| }_{R_0}>0, \end{aligned}$$
(74)
$$\begin{aligned}&{\eta }_0<\frac{\sigma }{2\pi }\left\{ \Upsilon +\frac{R_0}{m_s\left( R_0\right) }\left( 2{\phi }^2-\Theta \right) \right\} {\left\{ {\left. \frac{d{\sigma }^2}{dR}\right| }_{R_0}\right\} }^{-1}, \nonumber \\&\qquad if \qquad {\left. \frac{d{\sigma }^2}{dR}\right| }_{R_0}<0. \end{aligned}$$
(75)

We will currently model the astrophysical object by picking particular mass functions, and thusly, decide the equilibrium regions of the stability managed by the inequalities (74) and (75). As it was emphasized out in [48, 50], one can discover the stability regions graphically. The outcome is outlined in Fig. 9, which shows that the region of stability is given beneath the surface by Eq. (75).

8 Concluding remarks

BHs are well settled and generally acknowledged in relativity due to its strong cosmic proof for their reality, however, principal significance connects with horizons of BH present various hypothetical problems which have not yet to be agreeably settled. Along these lines, it has been contended by a few authors that after the gravity collapse of heavy objects, the various body could be shaped other than BHs. Among the proposals that have been put forward recently to disintegrate the problem of the horizon and singularity is the gravastar model suggested by Mazur and Mottola [33,34,35], has a successful stage change at/close where the event horizon is relied upon to be formed. It has as of late demonstrated that the ideal would be to generalize the gravastar picture by corresponding an inside solution matching to a EoS of DE to an outside solution of Schwarzschild at an interface of the junction. Such a spherically symmetrical model ought not to have a horizon and it should deal with a solution of static equilibrium, at some point alluded as a DE object [48, 50, 70,71,72,73].

We have contemplated a relativistic static and spherically symmetric astrophysical configuration living in a space filled with anisotropy fluid described by a EoS of DE. From this EoS of DE, we adapted our inner space-time to the Schwarzschild outer space-time within the sight of a thin shell where we have expected a positive pressure of surface to maintain the thin shell opposite to collapse. We have examined the configuration of stellar by commanding a particular choice of mass function in the inside of compact objects. Therefore we additionally broadened our analysis by studying the energy conditions, hydrostatic equilibrium under various forces, and velocity of sound. We have found through our investigation that all energy conditions are fulfilled at the inside of the configuration and hold equilibrium between various forces because of anisotropy, as should be obvious from Figs. 5 and 6. Besides, we underline the outcomes in more details, with observational data by Rawls et al. [75]; Abubekerov et al. [76]; Elebert et al. [77]; Demorest et al. [78]; Freire et al. [79] of some well-known pulsars like Vela X-1, Cen X-3, 4U 1538-52, SAX J1808.4-3658, Her X-1, PSR J16142230 and PSR J1903+327. For this purpose, we produce information sheet for the purpose of comparison between present model spherical objects and the known compact objects in Table I. As one can see, the outcomes extracted in this theory is especially perfect with the outcomes acquired through the observations and the got mass-radius ratio for various strange spherical objects lies in the proposed range by Buchdahl [69]. Next, we analyzed the surface redshift (\(Z_s\)) of the various compact spherical objects are of finite values and vanishes outside of the spherical object (see Table I), which lies in the proposed range by Buchdahl [69]; Straumann [103]; Böhmer and Harko [102]; Ivanov [104], are physically satisfactory with those of observations. We have note that the surface redshift is increasing with mass-radius ratio. The stability analysis was also discussed under a small radial disorder. As a finale comment, it is conceivable to get the existence of DE spherical objects; however, it is critical to comprehend the nature and general properties of compact objects by through fine tuning.