Note on the mass–radius relations for spherical compact objects in general relativity with semi-classical corrections

Abstract

We consider the effects that modifications to general relativity (GR) at high densities may have on the structure of spherical compact objects. Such effects can be modeled via semi-classical corrections that are manifest in an additional effective (i.e. non-physical) term in the energy momentum tensor. In particular, we consider two kinds of effective corrections that are quadratic in the density: one inspired by loop quantum gravity (LQG) and one inspired by Einstein–Cartan Theory (ECT). For both corrections, we consider two standard toy models of compact objects, one with polytropic equation of state and the other described by the MIT-bag model. We show that the LQG-inspired corrections can produce objects with greater radius and total mass, while the ECT-inspired corrections produce objects that are smaller and less massive than their counterparts in GR.

1 Introduction

The description of massive gravitating sources plays a fundamental role in general relativity (GR) since Schwarzschild’s derivation of the constant density interior solution in 1916 [1]. The subsequent works of Tolman [2] and Oppenheimer and Volkoff [3] paved the way for the study of relativistic stellar structure (e.g. [4,5,6]) that led to our modern understanding of the structure of neutron stars (NSs) (e.g. [7,8,9]) and the formation of black holes. By solving the Tolman–Oppenheimer–Volkoff (TOV) equation we are able to study the properties of theoretical compact objects depending on choices made for the equation of state (EoS) describing the matter content of the object. Such models have proven to be extremely useful in the description of existing astrophysical sources such as NSs as well as other objects, such as quark stars [10, 11], hybrid quark stars [12, 13], boson stars [14, 15], and gravastars [16,17,18].

The questions regarding the existence and properties of compact objects are closely related to the behavior of matter and gravity under extreme conditions: namely high density and strong curvature. Observations until now have shown no conclusive proof of the existence of another island of stability beyond NSs; however, it has been argued that stable configurations may occur for other matter models beyond the NS limit, with the quark star model being one of the candidates [19, 20].

As densities increase the issue is made more complicated by our ignorance regarding the behavior of matter fields under such extreme conditions and the eventual failure of classical GR to describe the behavior of gravity at high curvature. For this reason modifications to GR in the strong curvature regime have been considered as well, and these may affect the pressure and density profiles for a given EoS.

Typically, modifications to GR lead to modified versions of the TOV equation. The literature regarding compact objects in alternative theories of gravity is vast (e.g. [21,22,23,24,25,26,27,28,29,30]). Despite the large variety of models proposed, there are some common underlying features that appear in almost every approach. In fact, a good classical limit for any modified theory of gravity has a critical energy scale (corresponding to a critical density or a critical length) around which deviations from GR become non-negligible. For example, the TOV equation in f(R) gravity with $f(R)=R+\alpha R^2$ (where R is the Ricci scalar) has been considered for various EoS in [31, 32], where the authors found that relation between the mass–radius relation for the modified theory and the mass–radius relation in pure GR has a turning point about a characteristic central density, leading to objects of higher masses and radii at lower central densities. Also, in [33] the authors considered the TOV equation obtained from a quantum-improved Einstein theory obtained by allowing for variations of Newton’s constant at high energies and showed that the corresponding mass–radius relation leads to smaller and less massive objects.

Modifications coming from other quantum-improved theories, such as loop quantum gravity (LQG) have been shown to induce quadratic corrections to the density in the strong field (see [34, 35] for an application to cosmology) and models of gravitational collapse inspired by LQG have been shown to have repulsive effects that halt collapse and turn it into a bounce (e.g. [36]).

However, it is important to notice that this model dependent critical scale need not be related to the Planck scale. In fact, the general belief that the threshold for the appearance of quantum-gravity effects must be at the Planck scale is based mostly on geometrical arguments involving G, c and ${\bar{h}}$. This belief may be questioned, due to the lack of experimental evidence and to the possible existence of other fundamental scales (e.g. [37]). Then it is possible to argue that deviations from classical GR may appear at density scales other than the Planck density. For example, in Einstein–Cartan Theory of gravity (ECT) [38,39,40,41,42,43], the relaxation of the assumption that the space-time be torsion-free leads to a theory of gravity coupled to spin. This naturally resolves the occurrence of singularities, such as the black hole [44] and big bang singularities [45]. The critical density arising within ECT for the simplest spin models is several orders of magnitudes lower than the Planck density. Compact objects in ECT and in theories of gravity with torsion have been considered in [46,47,48,49,50], while rotating fluids with torsion have been investigated in [51]. More recently Bohmer et al. [52] and independently Luz and Carloni [53] have studied modifications to the TOV equation coming from ECT and determined the upper mass bound for some class of compact objects.

In the present article we consider two classes of semi-classical modifications to GR and investigate the role that these modifications may play in producing measurable effects in astrophysical compact objects. In particular, we focus on semi-classical corrections that arise naturally in LQG-inspired and ECT-inspired models and induce corrections that are quadratic in the density. We implement such modifications into two well known toy models for compact objects: A polytropic fluid model describing a NS and a MIT-bag model [54] describing an hypothetical quark star. By obtaining the mass–radius relation, we investigate the range of critical densities at which such effects may be detected via observations and how they may alter the size and mass of the compact objects.

The paper is organized as follows: In Sect. 2 we review the classical setup for the interior of compact objects in GR and introduce the semi-classical corrections that lead to the modified TOV equation. Section 3 will present the mass–radius relations for some simple toy models for NSs and compare them with the corresponding mass–radius relations obtained in the classical setup (the corresponding results for quark stars are presented in Appendix A). Finally Sect. 4 is devoted to a brief discussion of the possible implications of the results for models of astrophysical compact objects.

All the results presented in this work can be reproduced by running the Python notebook file available publicly at github.com/AyanNB/TOVSolver_py/.

2 Compact objects with effective corrections

The metric for a static, spherically symmetric gravitating object can be written in diagonal form as

$$\begin{aligned} ds^2= -e^{2\varPhi (r)}c^2\mathrm{d}t^2+\frac{\mathrm{d}r^2}{1-\frac{2Gm(r)}{c^2r}}+r^2\mathrm{d}\varOmega ^2, \end{aligned}$$

(1)

where $\varPhi (r)$ and m(r) need to be determined from Einstein’s equations and $\mathrm{d}\varOmega ^2$ is the usual line element on the unit two-sphere. Considering the matter source to be of the form of a perfect fluid $T^{\mu \nu }=(\rho +p/c^2)u^\mu u^\nu +pg^{\mu \nu }$, with $u^\mu$ the four-velocity of the fluid, $\rho (r)c^2$ the total energy density and p(r) the isotropic pressure, Einstein’s equations take the form

$$\begin{aligned} \frac{\mathrm{d}\varPhi }{\mathrm{d}r}= & {} \frac{m+4\pi r^3p/c^2}{r(r-2Gm/c^2)}, \end{aligned}$$

(2)

$$\begin{aligned} \frac{\mathrm{d}p}{\mathrm{d}r}= & {} -G(\rho +p/c^2)\frac{\mathrm{d}\varPhi }{\mathrm{d}r}, \end{aligned}$$

(3)

$$\begin{aligned} \frac{\mathrm{d}m}{\mathrm{d}r}= & {} 4\pi r^2 \rho , \end{aligned}$$

(4)

where Eqs. (2) and (3) can be combined in the TOV equation

$$\begin{aligned} \frac{\mathrm{d}p}{\mathrm{d}r}=-G(\rho +p)\frac{m+4\pi r^3p/c^2}{r(r-2Gm/c^2)}. \end{aligned}$$

(5)

The total density can be expressed as

$$\begin{aligned} \rho ={\tilde{\rho }}\left( 1+\frac{\varepsilon }{c^2}\right) , \end{aligned}$$

(6)

where ${\tilde{\rho }}$ is rest mass density and $\varepsilon$ is the internal energy density which can be obtained from the first law of thermodynamics for an adiabatic process as

$$\begin{aligned} \frac{\mathrm{d}\varepsilon }{\mathrm{d}{\tilde{\rho }}}=\frac{p}{{\tilde{\rho }}^2}. \end{aligned}$$

(7)

The internal energy density typically amounts to a few percent of the total energy density of the system and it is not affected by modifications at high densities. Since we are interested in a qualitative estimate of the effects of strong gravity on compact objects, for simplicity in the following we will focus on the total density of the system $\rho$. The system is closed once an Equation of State (EoS)

$$\begin{aligned} p=f(\rho ), \end{aligned}$$

(8)

relating the pressure to the density is provided. The pressure profile p(r) is then obtained from the integration of Eq. (5) with the integration constant fixed by the value of the central pressure $p_0=p(0)$, as obtained from the central density $\rho (0)=\rho _0$ via $p_0=f(\rho _0)$. The central value for Eq. (4) is naturally chosen as $m(0)=0$. The boundary of the compact object $R_b$ is given by the condition $p(R_b)=0$ and the total mass of the object M can be obtained from Eq. (4) as

$$\begin{aligned} M=4\pi \int _0^{R_b}r^2\rho (r)\mathrm{d}r. \end{aligned}$$

(9)

This, in turn, implies for the boundary condition for Eq. (2) $e^{2\varPhi (R_b)}=1-2GM/(c^2R_b)$, which matches to an exterior Schwarzschild geometry with mass parameter M.

Assuming that departures from GR will appear at some critical energy scale we may consider an effective theory in which Einstein’s equations are replaced by

$$\begin{aligned} G_{\mu \nu }+\langle G_{\mu \nu } \rangle =8\pi \kappa T_{\mu \nu }, \end{aligned}$$

(10)

where $\kappa =G/c^4$, and the term $\langle G_{\mu \nu } \rangle$, describing the modifications that the effective theory entails for the geometry, becomes negligible at low curvatures. Then we can take the corrections to the geometry due to the effective theory to the right-hand-side of Eq. (10) and define an effective energy momentum tensor from $8\pi \kappa T_{\mu \nu }^\mathrm{eff}=8\pi \kappa T_{\mu \nu }-\langle G_{\mu \nu }\rangle$ and write

$$\begin{aligned} G_{\mu \nu }=8\pi \kappa T_{\mu \nu }^{\mathrm{eff}}. \end{aligned}$$

(11)

In this manner the problem becomes equivalent to solving the classical set of Einstein’s field equations for an effective (i.e. non-physical) matter source which encompasses both the physical matter and the geometric modifications. The choice of $\langle G_{\mu \nu }\rangle$ (and therefore of the effective energy momentum tensor) depends on the specific model for the modifications to GR that one wishes to consider. In the following we will study two simple approaches that are inspired by two effective theories of gravity, namely LQG and ECT. However, one may consider semi-classical corrections per se without any reference to the original alternative theory.

The procedure then is the following: We use the effective energy momentum tensor to write the TOV equation for the non-physical effective matter source. We shall call this equation the effective Tolman Oppenheimer Volkoff (eTOV) equation. This equation is formally identical to the original TOV equation with effective quantities in place of the physical ones. For a given value of the central density $\rho _0$ we find the corresponding value of the effective central density $\rho _0^{\mathrm{eff}}$. The integration of the eTOV equation yields the effective pressure profile $p^{\mathrm{eff}}(r)$ which is then used to find the boundary radius from $p^{\mathrm{eff}}(R_b)=0$. The total mass of the object is then obtained from the integration of the classical (not effective) Eq. (4), between zero and $R_b$. The obtained model can then be compared with the corresponding classical one, obtained from the integration of the classical TOV equation with the same central density.

LQG-inspired corrections

The simplest effective correction that can be considered is a quadratic negative term to be added to the rest mass density. This can be written as

$$\begin{aligned} \rho ^{\mathrm{eff}}=\rho \left( 1-\frac{\rho }{\rho _{\mathrm{cr}}}\right) , \end{aligned}$$

(12)

where $\rho _{\mathrm{cr}}$ is a constant depending on the energy scale at which the modifications become important and for convenience now $\rho$ denotes the rest mass energy density. This type of correction originated in the context of loop quantum cosmology [55] and has been considered also in LQG-inspired models for collapse. In the case of LQG the critical density $\rho _{\mathrm{cr}}$ must be of the order of the Planck density (namely around $\rho _\mathrm{Pl}\simeq 10^{93}\ \mathrm{g}/\mathrm{cm}^3$). However, for a generic quadratic correction, the value of $\rho _{\mathrm{cr}}$ describes merely the scale at which repulsive effects become important and so in principle it can take values lower than the Planck density (see for example [56] where the observed amplitude for scalar perturbations suggests a critical density of the order of $10^{-9}\rho _\mathrm{Pl}$).

The effective pressure can be obtained via an EoS formally identical to Eq. (8) as

$$\begin{aligned} p^{\mathrm{eff}}=f(\rho ^{\mathrm{eff}}). \end{aligned}$$

(13)

Note that the eTOV equation obtained in this manner is identical to the classical TOV equation with effective density and pressure in place of their classical counterparts. However, differences in the object’s structure do appear, and they do manifest in the mass–radius relation. The reason is that, for calculating the object’s mass in the semi-classical case, one has to use Eq. (9) with the physical density $\rho$ while the boundary radius $R_b$ is obtained from integration of the effective eTOV equation.

ECT-inspired corrections

A similar approach can be constructed within a theory of gravity with torsion such as ECT. Here we shall follow a simple procedure to relate the spin-density of the fluid to the torsion contribution to the gravitational field (see [38,39,40,41,42,43] for details). We will assume that the spin properties of the fluid can be described by an antisymmetric tensor $s_{\mu \nu }$ which is related to the torsion $t^\lambda _{\mu \nu }=(\varGamma ^\lambda _{\mu \nu }-\varGamma ^\lambda _{\nu \mu })/2$ via

$$\begin{aligned} t^\lambda _{\mu \nu }=8\pi \kappa u^\lambda s_{\mu \nu }, \end{aligned}$$

(14)

where $u^\lambda$ is the four-velocity of the fluid. Then the spin-density is simply defined as

$$\begin{aligned} s^2=\frac{1}{2}s_{\mu \nu } s^{\mu \nu }. \end{aligned}$$

(15)

Notice that in the torsion-free case the affine connection $\varGamma ^\lambda _{\mu \nu }$ is symmetric and thus $t^\lambda _{\mu \nu }$ and $s^2$ vanish. A model for collapse with repulsion originating from torsion effects due to fermion interaction was studied in [57]. In the case of ECT-inspired compact objects, in order to close the system of Einstein’s equations, one needs to specify an EoS together with a prescription for the spin-density $s^2$ for the fluid’s particles. Here we will follow the most common approach to matter fluids with spin for which the spin-density can be obtained from a characterization of the fermion gas [45]. Then the effective density and pressure take the form

$$\begin{aligned} \rho ^{\mathrm{eff}}= & {} \rho -8\pi \kappa s^2, \end{aligned}$$

(16)

$$\begin{aligned} p^{\mathrm{eff}}= & {} p-8\pi \kappa c^2 s^2. \end{aligned}$$

(17)

Note that in order for the effective pressure to vanish at the surface of the object the spin-density should also vanish. Different choices of $s^2$ are possible (e.g. [52]). Here we shall consider the simple case of an ideal gas with no spin polarization for which the spin-density $s^2$ takes the form

$$\begin{aligned} s^2=\frac{\hbar ^2}{8}\langle n^2 \rangle , \end{aligned}$$

(18)

where $\hbar$ is the reduced Planck constant and n is the particle density of the fluid. Then the simplest model for the spin-density is obtained for $s^2\simeq \rho ^2$ [58] and we can rewrite Eqs. (16) and (17) as

$$\begin{aligned} \rho ^{\mathrm{eff}}= & {} \rho -\frac{\rho ^2}{\rho _{\mathrm{cr}}}, \end{aligned}$$

(19)

$$\begin{aligned} p^{\mathrm{eff}}= & {} p-\frac{\rho ^2}{\rho _{\mathrm{cr}}}c^2, \end{aligned}$$

(20)

where the classical density and pressure are related via the EoS and the critical density $\rho _{\mathrm{cr}}$ is model dependent.

3 Polytropic equation of state

We now apply the above formalism to a simple toy model describing a NS with polytropic equation of state of the kind

$$\begin{aligned} p=k\rho ^\gamma . \end{aligned}$$

(21)

The aim is to characterize how effective corrections affect a polytropic compact object. The value chosen for k is $7.454\times 10^{-3}$ (with appropriate units in the cgs system depending on the value of $\gamma$). Then for $\gamma =2.5$ we obtain a maximum NS mass of value of the order of $2.1M_\odot$, which is consistent with observations [59, 60].

LQG-inspired corrections

In order to qualitatively understand the effect of introducing LQG-inspired corrections, we first look at the case with $\gamma =2$. In this case, the equations simplify and we can obtain analytic estimates. By combining Eqs. (12) and (21), we can write the effective pressure as a function of the classical pressure as

$$\begin{aligned} p^{\mathrm{eff}}=p\left( 1-\frac{2\sqrt{p}}{\sqrt{k}\rho _\mathrm{cr}}+\frac{p}{k\rho _{\mathrm{cr}}^2}\right) . \end{aligned}$$

(22)

When $p\ge 4k/\rho _{\mathrm{cr}}^2$, the effective pressure is greater than the classical pressure, which leads to a larger boundary radius, and therefore a more massive compact object (for a fixed central density). Other values of $\gamma$ exhibit a similar behavior, as seen in Fig. 1 and in Fig. 2 for $\gamma =2.5$. Figure 1 shows the comparison between the mass–radius relation for NSs with polytropic EoS (21) and the mass–radius relation for the corresponding NSs once semi-classical corrections given by Eqs. (12) and (13) are included with different values of $\rho _{\mathrm{cr}}$.

Fig. 1

Mass–radius relation for compact objects with LQG-inspired corrections and polytropic EoS with $\gamma =2.5$ and $k=7.454\times 10^{-3}$ (in cgs units). The solid curve (1) shows the purely relativistic case. The dashed curve (2) is obtained for $\rho _{\mathrm{cr}}=10^{17} \ \mathrm{g}/\mathrm{cm}^3$, the dotted curve (3) is obtained for $\rho _{\mathrm{cr}}=4\times 10^{16} \ \mathrm{g}/\mathrm{cm}^3$, the dash-dotted curve (4) is obtained for $\rho _\mathrm{cr}=1.5\times 10^{16} \ \mathrm{g}/\mathrm{cm}^3$. See Table 1 for details

Fig. 2

Pressure profile for compact objects with LQG-inspired corrections and polytropic equation of state with $k=7.454\times 10^{-3}$ and $\gamma =2.5$. The central density is chosen as $\rho _0=1.65\times 10^{15} \ \mathrm{g}/\mathrm{cm}^3$ and critical densities are the same as in Fig. 1. See Table 1 for details

If the critical density is set at Planck scale, namely $\rho _\mathrm{cr}=\rho _{\mathrm{pl}}\simeq 5\times 10^{93}\ \mathrm{g}/\mathrm{cm}^3$, then semi-classical corrections to NSs are bound to be negligible. As expected, the critical density at which repulsive corrections start to become significant is only slightly higher than the NS density. We see that, for $\rho _{\mathrm{cr}}\simeq 1.5\times 10^{16}\ \mathrm{g}/\mathrm{cm}^3$, the mass–radius curve is distinguished from the classical case, giving an $\simeq 300$ m increase in the radius of a $2.1M_\odot$-mass NS. This amounts to $\sim 3\%$ difference, which, however, is too small to be measurable with current techniques (e.g. [61]). For $\rho _{\mathrm{cr}}\simeq 4\times 10^{16} \ \mathrm{g}/\mathrm{cm}^3$ and higher, the influence of semi-classical corrections become $<1\%$, which is practically negligible.

Figure 2 shows the pressure profiles for $\gamma =2.5$ for a NS model with the classical central density of $\rho _0=1.65\times 10^{15} \ \mathrm{g}/\mathrm{cm}^3$. The increase in the boundary radius corresponds to a higher total mass by, e.g., $\sim 3\%$ for the case with $\rho _{\mathrm{cr}}\simeq 1.5\times 10^{16}\ \mathrm{g}/\mathrm{cm}^3$).

For completeness, we investigated the robustness of the above conclusions against different values of $\gamma$ in the EoS. In these models, the value of k is chosen in such a way that a given central density corresponds to the same central pressure. We observe that the variations in the total mass and boundary radius for the NS are more significant for larger values of $\gamma$, as can be gleaned from Table 1. In all cases considered, we find that the qualitative behavior shown in Fig. 1 does not change.

Table 1 The masses and radii of the compact objects with polytropic EoS and central density $1.65\times 10^{15} \ \mathrm{g}/\mathrm{cm}^3$ for different values of $\gamma$ in the LQG-inspired gravity. The case with $\gamma =2.5$ is illustrated in Fig. 2. Masses are in units of solar masses, radii are in km, densities are in $\mathrm{g}/\mathrm{cm}^3$

ECT-inspired corrections

Similarly to the previous case, the effects of ECT-inspired corrections can be estimated by writing the effective pressure in terms of the classical pressure by combining Eqs. (20) and (21). In this case, for $\gamma =2.5$, we obtain

$$\begin{aligned} p^{\mathrm{eff}}=p\left( 1-\frac{1}{k\sqrt{\rho }\rho _\mathrm{cr}}\right) =p\left( 1-\frac{1}{k^{4/5}p^{1/5}\rho _{\mathrm{cr}}}\right) \end{aligned}$$

(23)

which is always smaller than the classical pressure. This implies that, for ECT-inspired modifications, the boundary radius and the total mass of the compact object will always be smaller than their classical counterparts. We also see that the difference between the effective model and the classical model becomes smaller for larger densities. This behavior occurs for $\gamma >2$, as can be seen from the fact that, for $\gamma =2$, the above equation becomes $p^{\mathrm{eff}}=p-p/(k\rho _{\mathrm{cr}})$, which is linear in p (i.e. it does not depend on $\rho$).

Fig. 3

Mass–radius relation for compact objects with ECT-inspired corrections and polytropic equation of state with $k=7.454\times 10^{-3}$ and $\gamma =2.5$. The solid curve (1) shows the purely relativistic case. The dashed curve (2) is obtained for $\rho _{\mathrm{cr}}=8\times 10^{17} \mathrm{g}/\mathrm{cm}^3$, the dotted curve (3) is obtained for $\rho _{\mathrm{cr}}=4\times 10^{17}\mathrm{g}/\mathrm{cm}^3$, the dash-dotted curve (4) is obtained for $\rho _\mathrm{cr}=2\times 10^{17}\mathrm{g}/\mathrm{cm}^3$. See Table 2 for details

In Fig. 3, we show the mass–radius relation for NSs with polytropic EoS and ECT-inspired corrections given by Eqs. (19) and (20) with $\gamma =2.5$ and different values of the critical density. Again, as expected, in the case where the critical density is set at natural spin-density for neutrons, namely $\rho _{\mathrm{cr}}\simeq 5\times 10^{54}\ \mathrm{g}/\mathrm{cm}^3$, then ECT corrections to NSs are negligible. As in the previous case, the critical density at which repulsive corrections start to become significant is slightly higher than the NS density, namely of the order of $\rho _{\mathrm{cr}}\simeq 10^{17}\ \mathrm{g}/\mathrm{cm}^3$ (see Table 2 for details).

Table 2 Comparison of the radii of ECT-inspired compact objects with polytropic EoS and central density $\rho _0=6.5\times 10^{14} \ \mathrm{g}/\mathrm{cm}^3$ for different values of the polytropic index. The case of $\gamma =2.5$ is illustrated in Fig. 4. Masses are in units of solar masses, radii are in km, densities are in $\mathrm{g}/\mathrm{cm}^3$

Fig. 4

Pressure profile for compact objects with ECT-inspired corrections and polytropic equation of state with $k=7.454\times 10^{-3}$, $\gamma =2.5$. All models have the same classical central density $\rho _0=6.5\times 10^{14}\mathrm{g}/\mathrm{cm}^3$. See Table 2 for details

Interestingly, in this case, the torsion-induced repulsive effects to the polytropic EoS model do not affect the maximum mass that can be achieved by NSs, which is determined by the values of k and $\gamma$, with effective corrections playing a negligible role. As a consequence, in contrast with what happens in the LQG-inspired case, for ECT-inspired corrections we see that significant deviations from the classical case in the mass–radius relation occur only for low central densities. In fact, as can be seen from Eq. (23), effective corrections become smaller at larger densities in this case. Therefore, changes in the boundary radius of the object are more significant for NSs with central density of the order of $\simeq 5\times 10^{14} \ \mathrm{g}/\mathrm{cm}^3$ than those with higher values.

Figure 4 shows the pressure profiles for this model for a classical central density of $\rho _0=6.5\times 10^{14}\ \mathrm{g}/\mathrm{cm}^3$. The boundary radius changes by roughly 1% with the introduction of ECT-inspired corrections with $\rho _\mathrm{cr}=2\times 10^{17}\ \mathrm{g}/\mathrm{cm}^3$ and variations of the total mass are comparable, as can be seen in Table 2. For robustness we have checked the above result for different values of $\gamma >2$, again choosing k in such a way that in each case with a given central density would correspond to the same central pressure. We see that the qualitative behavior shown in Fig. 3 does not depend on the value of $\gamma >2$, as can also be seen in Table 2.

It is worth noticing that since in the LQG-inspired case repulsive effects produce NSs with larger boundary radius, while in the ECT-inspired model we always obtain a smaller boundary radius, it could be possible to distinguish the two types of modifications, at least in principle.

Finally, we studied the effect of LQG- and ECT-inspired correction on quark stars using MIT-bag model EOS and we find qualitatively similar corrections. See Appendix A for a detailed discussion.

4 Discussion

In the present article we studied how semi-classical corrections to general relativity (GR) may alter the mass–radius relations of toy models describing neutron stars and quark stars. We considered two kinds of modifications that give negative quadratic corrections to the density, one inspired by LQG and the other inspired by Einstein–Cartan Theory (ECT), and allowed for the critical densities to take any value above the object’s central density.

We have shown that these modifications to Einstein’s equations bear different consequences for the structure of compact objects. In fact, LQG- and ECT-inspired modifications induce opposite changes in the mass–radius relations: LQG-inspired correction are more significant at high central densities and induce larger boundary radii for the objects. ECT-inspired corrections are more significant at low central densities and induce smaller boundary radii.

It must be noted that this is a qualitative study and there are other effects that do influence the maximum mass and boundary radius achievable by a compact object with a given EoS. The most important one is, of course, rotation (e.g. [62,63,64]), which can account for an increase of the maximum mass of up to 25% in the case of uniform rotation (see [65] for a recent review of rotating compact stars).

One of the most interesting issues of the current ongoing discussion on the limits of GR concerns the possible observational effects that modifications to the theory may bear on astrophysical phenomena. Is it possible to experimentally detect a signature of the departure from classical GR? And is it possible to use such signature to validate or invalidate different alternative approaches to gravity? While until some years ago the answer to both questions was in the negative, in recent times the possibility to test the regime where the relativistic description may fail has come within our experimental reach. This is thanks to the observation of gravitational waves from binary mergers [66,67,68,69] by the LIGO collaboration and the ’image’ of a supermassive black hole candidate by the Event Horizon Telescope collaboration [70]. In particular, the observation of neutron stars mergers is already providing data on the nature and properties of compact objects [71,72,73]. For example, in [74,75,76] constraints on the neutron star EoS were obtained from the observational data while in [77,78,79] the observed merger was used to constrain the validity of alternative theories of gravity. In [80] the data was used to investigate the role played by vacuum energy at the core of neutron stars, in order to test the properties of vacuum energy independently from the expansion rate of the universe. Similarly in [81] the authors investigated the role played by the presence of the cosmological constant at the core of compact objects.

At present there is great interest in the theoretical possibility of finding departures from classical GR in some astrophysical phenomena. The idea that deviations from the classical theory may be observable in the vicinity of compact objects has been suggested in [82]. In [83] it was shown that gravitational waves detected by LIGO may carry information as regards exotic compact objects. Also, the idea that such effects may be observable at ordinary energy scales and more in general the idea that repulsive effects may appear at high densities have been suggested (e.g. [84]), while the idea that torsion effects may be observable at ordinary energy scales (like solar system tests of gravity) was investigated in [85].

Here we have shown that it is possible for certain kinds of modifications to GR, occurring at low enough densities, to have observable consequences on the mass and radii of compact objects. Similar results have been found in other approaches such as in f(R) gravity (see [31, 32]) and in asymptotic safe gravity (see [33]). However, each approach bears its own unique features that, in principle, could be tested by future astrophysical observations. For example, in [31, 32] the authors found that for several choices of the EoS the mass–radius relation obtained in f(R) gravity with $f(R)=R+\alpha R^2$ leads to an increase of the total mass for low central densities and to a decrease of the total mass for high central densities with respect to the GR case. This modification of the mass–radius relation with respect to the pure GR scenario is different from the one obtained here, suggesting that the two approaches can be distinguished. At present, given our ignorance of the EoS for realistic neutron stars and quark stars, it is not possible to determine which approach, if any, is more viable. However, we have seen that the effects of the modifications to GR depend both on the modified theory and on the EoS and are therefore distinguishable, at least in principle. In the newly opened era of multi-messenger astronomy, it is reasonable to expect that future measurements of the masses and radii of neutron stars will determine more accurately the valid range of equations of state and thus constrain the allowed models and values for modifications to appear.

Appendix A: MIT-bag equation of state

We consider here a simple toy model for matter constituting a strange quark star as given by the MIT-bag model. The EoS, with the simplifying assumption of neglecting the quark mass, takes the form

$$\begin{aligned} p=\frac{\rho c^2-4B}{3}, \end{aligned}$$

(A.1)

where typically the bag constant B ranges between 58.926 and $91.5\ \mathrm{MeV}/\mathrm{fm}^3$ (see [86] for details). While this is an idealized model, the aim here is to study the effect of modifications to GR, which are expected to have qualitatively similar impact in more sophisticated models. As we will see below, when considering semi-classical corrections, larger values of B imply smaller departures from the classical case. Therefore in the following, in order to bring out the effects of the semi-classical corrections, we shall use a lower bound conservative assumption for the bag constant taking the value $B=50\ \mathrm{MeV}/\mathrm{fm}^3$ [87] and investigate the effects of repulsive corrections on the mass–radius relation of quark stars.

LQG-inspired corrections

In Fig. 5 we show the mass–radius relation for quark stars with MIT-bag EoS and LQG-inspired corrections given by Eq. (12) with different values of the critical density. We see that the presence of repulsive effects in the bag model allows for the maximum mass of the quark star to be higher than the corresponding classical case. This is somewhat similar to the repulsive effects obtained by adding a distribution of electric charge to the quark star (e.g. [88]). For a critical density of the order of $\rho _{\mathrm{cr}}\simeq 10^{16} \ \mathrm{g}/\mathrm{cm}^3$, the maximum allowed mass for the quark star can be $\simeq 5 \%$ larger than the corresponding classical case.

Fig. 5

Mass–radius relation for compact objects with LQG-inspired corrections and MIT-bag equation of state $B=50\ \mathrm{MeV}/\mathrm{fm}^3$. The solid curve (1) shows the purely relativistic case. The dashed curve (2) is obtained for $\rho _{\mathrm{cr}}= 10^{17} \ \mathrm{g}/\mathrm{cm}^3$, the dotted curve (3) is obtained for $\rho _\mathrm{cr}=4\times 10^{16} \ \mathrm{g}/\mathrm{cm}^3$, the dash-dotted curve (4) is obtained for $\rho _{\mathrm{cr}}=1.5\times 10^{16} \ \mathrm{g}/\mathrm{cm}^3$

Fig. 6

Pressure profile for compact objects with LQG-inspired corrections and MIT-bag EoS $B=50\ \mathrm{MeV}/\mathrm{fm}^3$. The comparison is done for models that have the same classical central density $\rho _0=1.65\times 10^{15} \ \mathrm{g}/\mathrm{cm}^3$. See Table 3 for details

Table 3 Comparison of the radii of the LQG-inspired compact objects with MIT-bag model EoS and central density $\rho _0=1.65\times 10^{15} \ \mathrm{g}/\mathrm{cm}^3$ for different values of the bag constant B in units $\mathrm{MeV}{/}\mathrm{fm}^3$. Masses are in units of solar masses, radii are in km, densities are in $\mathrm{g}/\mathrm{cm}^3$

Figure 6 shows the comparison of the pressure profiles for this model for different choices of the critical density. We take the same value of the classical central density as $\rho _0=1.65\times 10^{15} \ \mathrm{g}/\mathrm{cm}^3$ and for different values of $\rho _{\mathrm{cr}}$ we obtain objects with different size and total mass. Then a critical density of the order of $\rho _\mathrm{cr}=1.5\times 10^{16} \ \mathrm{g}/\mathrm{cm}^3$ produces an increase of roughly 1% in the radius of the object while the mass increases by roughly 5% (see Table 3).

The robustness of the result can be checked by choosing different values of the bag constant B of 60 and $70 \ \mathrm{MeV}/\mathrm{fm}^3$. We see from Table 3 that the qualitative behavior presented in Fig. 5 does not change for these values of B. The values of the NS mass and radius summarized in Table 3 are consistent with this behavior.

Fig. 7

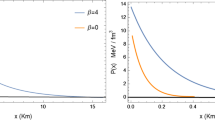
Mass–radius relation for compact objects with ECT-inspired corrections and MIT-bag equation of state $B=50\ \mathrm{MeV}/\mathrm{fm}^3$. The solid curve (1) shows the purely relativistic case. The dashed curve (2) is obtained for $\rho _{\mathrm{cr}}= 5\times 10^{17} \ \mathrm{g}/\mathrm{cm}^3$, the dotted curve (3) is obtained for $\rho _{\mathrm{cr}}=2.5\times 10^{17} \ \mathrm{g}/\mathrm{cm}^3$, the dash-dotted curve (4) is obtained for $\rho _{\mathrm{cr}}= 10^{17} \ \mathrm{g}/\mathrm{cm}^3$

Table 4 Comparison of the radii of ECT-inspired compact objects with MIT-bag model EoS and central density $\rho _0=6.5\times 10^{14} \ \mathrm{g}/\mathrm{cm}^3$ for different values of the bag constant B in units $\mathrm{MeV}{/}\mathrm{fm}^3$. Masses are in units of solar masses, radii are in km, densities are in $\mathrm{g}/\mathrm{cm}^3$

ECT-inspired corrections

Similarly to the LQG-inspired case, the introduction of ECT-inspired effects to the mass–radius relation for a quark star with MIT-bag EoS may alter the maximum allowed mass for the compact objects. However, similarly to what was found in the polytropic case, the maximum allowed mass for a compact object with ECT-inspired corrections becomes lower with respect to the purely classical case. This is again due to the fact that the effective pressure takes the form given in Eq. (20).

Fig. 8

Pressure profile for compact objects with ECT-inspired corrections and MIT-bag equation of state $B=50\ \mathrm{MeV}/\mathrm{fm}^3$. The comparison is done for models that have the same classical central density $\rho _0=6.5\times 10^{14} \ \mathrm{g}/\mathrm{cm}^3$. See Table 4 for details

In Fig. 7 we show the mass–radius relation for quark stars with MIT-bag model EoS and ECT-inspired corrections given by Eqs. (19) and (20) with different values of the critical density. Critical densities $\rho _{\mathrm{cr}}$ of $\simeq 10^{17} \ \mathrm{g}/\mathrm{cm}^3$ are enough to induce changes of $\sim 3\%$ in the mass and $\sim 1\%$ in the radius of the object (see Table 4 for details; Fig. 8).

Again, the qualitative behavior described in Fig. 7 above is not altered by changing the value of the bag constant and the comparison of models with different values of B is given in Table 4.