1 Introduction

The late-time accelerated expansion of the Universe is known as the most mysterious ideology of the cosmology. The standard hot big-bang phenomenon is the most engaging cosmological model to date. The study of the universe through different strategies revealed that currently the universe is undergoing through accelerating expansion. It was 1998 when this expansionary phenomenon was (firstly) traced by Type Ia Supernova observations [1] and then later confirmed by Cosmic Microwave Background (CMB) observations [2]. This phenomenon is expected to be occurred due to an extraordinary sort of energy component with negative pressure. As the origin and nature of such component is still a mystery, it is dubbed as dark energy (DE).

Cosmological constant is the simplest candidate to explain DE phenomenon thus the cosmological constant model \((\Lambda CDM)\) is consistent with current observations. But \(\Lambda CDM\) model suffered from the cosmological constant issue [3]. What is the reason behind the fact that vacuum energy is less than its estimated amount? In order to inspect the issue, two versatile approaches were adopted, one of which is the modification in geometric part of Einstein–Hilbert action (known as modified theories of gravity). Secondly, different dynamical DE models have also been proposed in context of quantum gravity and general relativity (GR) to describe DE. The matter modification facilitates with various DE models such as phantom, Chaplygin gas, k-essence, quintessence, holographic etc. [4].

In the background of quantum gravity, Holographic DE (HDE) model have been proposed on the basis of Holographic principal [5] the energy density of which is given by \(\mu _{d}=3h^{2}m_{p}^{2}L^{-2}\). Where \(m_{p}=(8\pi G)^{-\frac{1}{2}}\) exhibits reduced Plank’s mass, L denotes the infrared (IR) cutoff which describes the universe mass and h is dimensionless HDE constant parameter introduced for convenience.

The proposal of Veneziano ghost DE (\(\rho _{\Lambda }=\alpha H\), where \(\alpha \) is a constant having dimension \([energy]^{3}\)) lies in the category of dynamical DE models which plays a crucial role in the accelerated expansion of the universe [6, 7]. The incentive of this model comes from Veneziano ghost of quantum chromodynamics (QCD) that is beneficial to solve U(1) problem in QCD. The fundamental characteristic of this model is that Veneziano ghost (being unphysical in quantum field theory development in the Minkowski spacetime) gives non-trivial physical impacts in Friedmann Robertson–Walker (FRW) universe [8].

Vacuum energy is ghost field which can be utilized to describe the time varying cosmological constant in a space-time [9]. In vacuum ghost field, the energy density is directly proportional to \(\Lambda ^{3}_{QCD}\), where \(\Lambda ^{3}_{QCD}\) is QCD mass scale and H is Hubble parameter, is known as ghost dark energy (GDE) [10]. In QCD, the general vacuum energy of veneziano ghost field have the form \(H+O(H^{2})\) [11] is known as generalized GDE (GGDE). It is important to note that by taking the second order term, one can obtain the preferable compatibility with observational data as compare to GDE. In GGDE, the energy density is of the form \(\mu _{d}={\zeta }H +{\beta }H^{2}\), where \(\zeta \) and \(\beta \) are constants [12]. The ordinary ghost DE can be helpful in describing the early evolution of the universe. Wei [13] reconsidered this as pilgrim DE (PDE). In accordance with the Wei, the creation of black hole (BH) can be prevented through fitting resistive force that is able to anticipate the matter collapse. In this scenario, phantom-like DE can perform significant role that contains strong repulsive force as compare to the quintessence DE. Moreover, the useful role of phantom-like DE in case of BH’s mass has been examined in numerous ways. One of them is the accretion phenomenon which favors the possibility of prevention of BH creation due to the existence of phantom-like DE in the universe. The GGDE density after the addition of PDE parameter becomes

$$\begin{aligned} \mu _{d}=({\zeta }H +{\beta }H^{2})^{{\eta }}. \end{aligned}$$

The generalized ghost version of PDE is used to describe the fate of BH in the presence of great amount of phantom energy in the universe [14].

There exist so many past related work based on our analysis. Nojiri and Odintsov [15,16,17] worked on different modified gravities for dark energy. They considered the different forms of cosmological parameters in order to study the f(R), f(G) and f(R, G). Barrow and Liddle [18] studied the generalization of intermediate inflation model with the help of scale factor to analyze the early universe.

Fernandez [19] examined an association between interacting and non interacting GDE, dark sector components as well as the kinetic k-essence field. He evaluated that cosmic evolution of the GDE dominated universe can perfectly narrate a kinetic k-essence scalar field. In order to investigate the current cosmic expansion, Malekjani [20] examined the GGDE model from a statefinder diagnostic analysis in the background of a flat FRW universe. Sharif and Jawad [21, 22] investigated the evolution of PDE model regarding same universe model while considering a relation between DE and cold dark matter (CDM). The same authors [23, 24] studied the dynamics of interacting/non interacting GGPDE model with basic cosmological parameters and investigated the stability of DE model while considering FRW model. Sharif and Zubair [25] discussed the PDE model by considering f(R) gravity with infrared (IR) cut-offs.

Jawad and Rani [26] considered Horava–Lifshitz f(R) to reconstructed the GGPDE model and the same authors reconstructed PDE model in the background of f(G) gravity, respectively. They conclude that the recontracted dynamical model points out towards different DE scenarios. Zubair and Abbas [27] reconstructed the f(R, T) theory (T represents trace of energy momentum tensor) by taking into account Garcia–Salcedo GDE models. They examined the stability criteria of ghost f(R, T) models and observed that the newly constructed model shows correspondence with to quintessence and phantom regions. Fayaz et al. [28] when considered the same model in the background of anisotropic f(R, T) gravity they also concluded similar DE regions. Sharif and Nazir [29] extended the work for same DE model while considering f(T) gravity in addition to which they studied thermodynamical law and the behavior of entropy production term. Sharif and Nazir [30] considered well known scale factors to study the cosmological consequences of the reconstructed GGPDE \(F(T, T_{g})\) models. They graphically analyzed the influence of reconstructed models and EoS parameters by considering scale factors. They presumed that all of the outcomes are in concurrence with PDE phenomenon.

Sharif and Nazir [31] analyzed the cosmological conditions of GGPDE with \(F(\mathcal {T},\mathcal {T}_{g})\) in terms of red-shift parameter. They considered power-law scale factor, scale factor for unified phases and intermediated scale factor to study the reconstructed models. They evaluated the reconstructed models and their corresponding equation of state (EoS) parameter for the different choices of scale factors. They also explored the behavior of deceleration parameter, \(\omega -\acute{\omega }\) plane and state-finder parameters. Sharif and Nawazish [32] explored the interacting and non-interacting GGPDE in f(R) gravity through some standard cosmological parameters. They examined the cosmic evolution for FRW universe using red-shift parameter. They studied the current cosmic expansion with flat and non-flat geometry for interacting models.

In the paper, we study cosmological behavior of reconstructed GGPDE f(R) models with respect to red-shift parameter z. We study these reconstructed f(R) models by squared speed od sound, EoS parameters, \(\omega \)–\(\omega '\) and r–s planes. Also, we formulate both DE as well as ordinary matter density parameters. The paper is arranged as follows. In the next section, we provide basic introduction to f(R) gravity along with GGPDE and FRW universe models. In Sects. 3 and 4, we graphically analyze the behavior of reconstructed GGPDE f(R) model through cosmological parameters. Finally, we summarize the results in the last section.

2 f(R) gravity

The line element of standard FRW model can be given as

$$\begin{aligned} d\check{s}^{2}=dt^{2}-\hat{a}^{2}(t)\left[ \frac{dr^{2}}{1-k r^{2}}+r^{2}d\theta ^{2} +r^{2}\sin ^{2}\theta d\phi ^{2}\right] ,\nonumber \\ \end{aligned}$$
(1)

here \(\hat{a}(t)\) is the scale factor and k defines the curvature index that classifies universe as open \((k=-1)\), flat \((k=0)\) and closed \((k=1)\). Recent observations provide evidences about the flat geometry but there also exist some arguments that support the idea of closed geometry (non-flat geometry) due to the contribution of small fraction of positive curvature. In non-flat geometry, the closed models exhibit substantially higher lensing amplitudes than in \(\Lambda CDM\), so combining with the lensing reconstruction (which is consistent with a flat model) pulls parameters back into consistency with a spatially flat universe [33]. The f(R) theory of gravity modifies Einstein–Hilbert action as

$$\begin{aligned} \check{S}=\int d^{4}x\sqrt{-g}\frac{f(R)}{2\kappa ^{2}}+\check{l_{m}}~, \end{aligned}$$
(2)

where f(R) represents the function of Ricci scalar R, g is the determinant of the metric tensor \(g_{\mu \nu }\) and \(\check{l_{m}}\) denotes the matter Lagrangian. Varying the above action w.r.t metric tensor yields following fourth order field equation

$$\begin{aligned} \frac{1}{2}f(R)g_{\mu \nu }-F_{R}R_{\mu \nu }-\nabla _{\mu }\nabla _{\nu }F_{R} +g_{\mu \nu }\nabla ^{\delta }\nabla _{\delta }F_{R}+\kappa ^{2}\hat{T}_{\mu \nu }^{(m)},\nonumber \\ \end{aligned}$$
(3)

where, \(F_{R}\) defines the derivative of general function f with respect to R, \(\nabla _{\mu }\) is the covariant derivative, \(\Box =\nabla ^{\delta }\nabla _{\delta }\) and \(\hat{T}_{\mu \nu }^{(m)}\) is the energy–momentum tensor. For perfect fluid energy–momentum tensor is of the form

$$\begin{aligned} \hat{T}_{\mu \nu }^{(m)}=(\hat{\mu }_{m}+\hat{p}_{m})\upsilon _{\mu }\upsilon _{\nu }+\hat{p}_{m}g_{\mu \nu }, \end{aligned}$$

Fluid particles have four velocity as \(\upsilon _{\mu }=(1, 0, 0, 0)\) while \(\hat{\mu }_{m}\) is the energy density and \(\hat{p}_{m}\) represents the pressure of byronic matter and CDM. Following is the equivalent form of above field Eq. (3)

$$\begin{aligned} \hat{G}_{\mu \nu }=\kappa ^{2}\hat{T}_{\mu \nu }^{eff}=\frac{\kappa ^{2}}{F_{R}}\left( \hat{T}_{\mu \nu }^{(m)}+\hat{T} _{\mu \nu }^{(c)}\right) , \end{aligned}$$

where \(\hat{T}_{\mu \nu }^{eff}\) denotes Einstein effective energy–momentum tensor and higher order curvature terms \(\hat{T}_{\mu \nu }^{(c)}\) are defined by

$$\begin{aligned} \hat{T}_{\mu \nu }^{(c)}=\left( \frac{f(R)-RF_{R}}{2}\right) g_{\mu \nu }+\nabla _{\mu }\nabla _{\nu }F_{R} -g_{\mu \nu }\nabla ^{\delta }\nabla _{\delta }F_{R}.\nonumber \\ \end{aligned}$$
(4)
Fig. 1
figure 1

Plots of power-law reconstructed GGPDE f(R) model for \(k=1\) (upper plane) and \(k=-1\) (lower plane) with \(\eta = 0.99\) (left) and \(\eta = -0.99\) (right)

Full size image

Using Eqs. (1) and (3), the Friedmann equations become

$$\begin{aligned} H^{2}+\frac{k}{\hat{a}^{2}}= & {} \frac{\kappa ^{2}}{3}(\mu _{m}+\mu _{c}),\end{aligned}$$
(5)
$$\begin{aligned} H^{2}+\frac{2\ddot{\hat{a}}}{a}+\frac{k}{\hat{a}^{2}}= & {} -\kappa ^{2}(\rho _{m}+\rho _{c}), \end{aligned}$$
(6)

where \(H=\frac{\dot{\hat{a}}}{\hat{a}}\), \(\mu _{m}=\frac{\hat{\mu _{m}}}{F_{R}}\) , \(\rho _{m}=\frac{\hat{\rho }_{m}}{F_{R}}\) and the contribution of higher order curvature terms in energy density and pressure are respectively given below

$$\begin{aligned} \mu _{c}= & {} \frac{1}{F_{R}}\left( \frac{R F_{R}-f(R)}{2}-3H\dot{R}F_{RR}\right) , \end{aligned}$$
(7)
$$\begin{aligned} \rho _{c}= & {} \frac{1}{F_{R}}\left( \frac{f(R)-R F_{R}}{2}+\ddot{R}F_{RR}+\dot{R}^{2}F_{RRR}+2H\dot{R}F_{RR}\right) .\nonumber \\ \end{aligned}$$
(8)

The total energy density is given by \(\mu _{T}=\mu _{m}+\mu _{c}\) while \(\rho _{T}=\rho _{m}+\rho _{c}\) is the total pressure. Both preserve total energy conservation as follows

$$\begin{aligned} \dot{\mu _{T}}+3H(\mu _{T}+\rho _{T})=0. \end{aligned}$$

Now, in order to explore the cosmic expansion and current acceleration we reconstruct general f(R) model by simply equating the energy densities of f(R) gravity and GGPDE model as follows

$$\begin{aligned} (\zeta H+\beta H^{2})^{\eta }=\frac{RF_{R}-f(R)}{2}+3H\dot{R}F_{RR}. \end{aligned}$$
(9)

The above equation in terms of t, becomes

$$\begin{aligned} (\zeta H+\beta H^{2})^{\eta }=\frac{R\dot{f}(t)-\dot{R}f(t)}{2\dot{R}} +3H\left( \frac{\dot{R}\ddot{f}(t)-\ddot{R}\dot{f}(t)}{\dot{R}^{2}}\right) .\nonumber \\ \end{aligned}$$
(10)

3 Power-law scale factor

The mathematical form of this scale factor is given by [15]

$$\begin{aligned} \hat{a}(t)= & {} c_{0}t^{n}, \end{aligned}$$

where \(n > 0\), \(c_{0} > 0\). This significant scale factor is consistent with accelerating universe for \(n>1\) while it corresponds to decelerating phase for \(n<1\). In particular, it characterizes radiation and matter dominated epochs of decelerating cosmos for \(n=0.5\) and \(n=0.66\), respectively. Here we obtain the corresponding Hubble parameter, Ricci scalar and energy density of GGPDE model as

$$\begin{aligned} H= & {} \frac{n}{t},\quad R=\frac{12n^{2}}{t^{2}}-\frac{6n}{t^{2}}+\frac{k}{\hat{a}^{2}}\\ \mu _{d}= & {} (\zeta (nt^{-1}) +\beta (nt^{-1})^{2})^{{\eta }}={\zeta }^{\eta } (nt^{-1})^{\eta }+\eta {\zeta }^{\eta -1}\beta (nt^{-1})^{\eta +1}. \end{aligned}$$

In order to evaluate reconstructed GGPDE f(R) model, we substitute corresponding GGPDE density in Eq. (10) with \(\hat{a} = a_{0}(1 + z)^{-1}\) and obtain a differential equation. Upon numerically solving this differential equation, we get reconstructed GGPDE f(R) model in terms of z. To examine the evolution of this model, we consider two values of PDE parameter, i.e., \(\eta =0.99\) and \(\eta = -0.99\) and three distinct values of \(n=0.5\), 0.66, 1.5 in the background of closed as well as open universe models. The rest of the parameters are taken as \(\zeta =0.5\), \(\beta =-0.5\), \(a_{0}=2.5\) and \(c_{0}=1.9\).

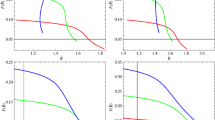
The plots for f(R) model versus red-shift parameter z are displayed in Fig. 1 for both closed and open universe models. The upper plane of Fig. 1 identifies positively increasing trajectories of GGPDE f(R) model for \(k=1\) with \(\eta =0.99\) (left panel) and \(\eta =-0.99\) (right panel). In the lower panel, the left plot incorporates negatively increasing curves of f for \(k=-1\) and all considered values of n. In the right plot, the GGPDE f(R) model evolves negatively for \(n=0.5\) whereas a transition appears from positive to negative regime for \(n=0.66\) and 1.5. In order to analyze the stable/unstable behavior of reconstructed GGPDE f(R) model, we consider squared speed of sound parameter defined as

$$\begin{aligned} \nu _{s}^{2}=\frac{\dot{\mu _{c}}}{\dot{\rho _{c}}}. \end{aligned}$$
(11)
Fig. 2
figure 2

Plots for Power-law squared speed of sound versus z

Full size image

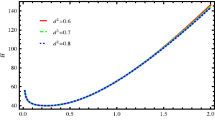
For positive values of \(\nu _{s}^{2}\), the stable behavior of model appears whereas in case of negative values, the parameter identifies instability of the model. In Fig. 2, the upper plane exhibits behavior of squared speed of sound parameter for \(k=1\) with \(\eta =0.99\) (left plot) and \(\eta =-0.99\) (right plot). In both left and right plots, the model remains stable in the surrounding of matter dominated era while in the background of radiation dominated era, the GGPDE model experiences a transition from stable to unstable state. In the presence of DE, the GGPDE model gets stable after crossing the limit \(z=1\) (left plot) whereas negatively increasing trajectory identifies model instability. In lower plane, the trajectories of \(\nu _{s}^{2}\) are plotted against z for \(k=-1\) with \(\eta =0.99\) (left plot) and \(\eta =-0.99\) (right plot). For \(n=0.5\), the curve evolves from positive to negative region implying transition from stable to unstable state (left plot) whereas positively increasing trajectory specifies stable GGPDE f(R) model (right plot). When \(n=0.66\), the model remains unstable as PDE parameter is positive (left plot) whereas for negative PDE parameter (right plot), the model ia found to be unstable initially and gets stable as z increases. In case of \(n=1.5\), the squared speed of sound parameter specifies model’s stability (left panel) and instability (right panel) for positive and negative values of PDE parameter, respectively.

The EoS parameter identifies various stages of accelerating as well as decelerating cosmos such as when \(\omega = \frac{1}{3}\), 0 and \(-1\), it preserves consistency with radiation, matter and DE eras. Furthermore, this parameter splits DE era into quintessence and phantom phases for \(-1<\omega \le -\frac{1}{3}\) and \(\omega <-1\), respectively. For higher order curvature terms, it is defined as

$$\begin{aligned} \omega =\frac{{\mu _{c}}}{{\rho _{c}}}, \end{aligned}$$

where \(\omega \) represents effective EoS parameter. This parameter not only distinguishes the cosmos into different eras but also determines the rate of expansion with the help of \(\omega '\). Caldwell and Linder [34] used this strategy for the first time to explore the behavior of quintessence DE model. They suggested that \(\omega \)–\(\omega '\) plane corresponds to freezing region if \(\omega<0, \omega '<0\) and for \(\omega <0 , \omega '>0\), thawing regions is appeared. Recent observational analysis interpret that the cosmos experiences a greater rate of expansion in freezing region as compared to thawing region.

Fig. 3
figure 3

Plots for power-law EoS parameter versus z

Full size image
Fig. 4
figure 4

Plots for power-law \(\omega \)–\(\omega '\) versus z

Full size image
Fig. 5
figure 5

Plots for r–s versus z

Full size image

The evolution of both closed as well as open cosmos from decelerating to accelerating phase of expansion is given in Fig. 3. The effective EoS parameter determines a decelerated phase of expansion when \(z\le 0.9\), \(z\le 0.85\) in the upper left plot and \(z\le 1\), \(z\le 0.82\) in the lower left plot, respectively. The accelerated phase of expansion is identified for \(z\ge 0.78\) and \(z\ge 0.6\) in both upper as well as lower left plots. In the upper right plot, the negatively increasing trajectories correspond to phantom phase for both \(n=0.5\) and \(n=0.66\). In the lower right plot, the effective EoS parameter is compatible with phantom phase for \(n=0.5\) whereas in case of \(n=0.66\), the parameter specifies both decelerated and accelerated phases. In the context of DE era, a smooth transition from decelerated to accelerated phase is appeared for both positive as well as negative values of PDE parameter in the background of closed and open universe models. In Fig. 4, we discuss the rate of accelerated expanding cosmos through \(\omega \)–\(\omega '\) plane in the background of closed and open universe models with positive and negative PDE parameter. In the upper plane, the negative trajectories of \(\omega '\) ensure the presence of freezing region for \(n=0.5\) and \(n=0.66\) while thawing region is identified for \(n=1.5\). In the lower plane when \(n=0.5\), the parameter \(\omega '\) evolves negatively with \(\omega <0\) implying the existence of freezing region while the positive variation of \(\omega \)–\(\omega '\) plane leads to incompatible result for \(n=0.66\). In case of \(n=1.5\), \(\omega \)–\(\omega '\) plane locates thawing region as \(\omega '>0\) when \(\omega <0\).

The deceleration parameter q measures the rate of expansion and defined as

$$\begin{aligned} q=\frac{1}{2}+\frac{3}{2}\omega . \end{aligned}$$

The positive value \((q>0)\) exhibits decelerating behavior while \(q = 0\) indicates constant expansion and for negative values \((q<0)\), it corresponds to accelerating rate of expansion. Sahni et al. [35] described state-finder parameters given by

$$\begin{aligned} r=q+2q^{2}-\frac{\dot{q}}{H},\quad s=\frac{r-\Omega _T}{3q-\frac{3\Omega _T}{2}}. \end{aligned}$$

These are two dimensionless parameters which evaluate the compatibility of reconstructed models with standard cosmological models. The CDM limit is indicated by \((r, s)=(1, 1)\) whereas for \((r, s)=(1, 0)\), the model preserves consistence with \(\Lambda \)CDM model. The Chaplygin gas model is appeared for \(s < 0, r > 1\) while \(s > 0, r < 1\) region defines quintessence and phantom phases. Figure 5 determines correspondence between reconstructed GGPDE f(R) and standard cosmological models. In the upper left plot, the GGPDE f(R) is compatible with Chaplygin gas model as for \(r>1\), \(s<0\) for all considered values of n. For \(n=0.5\) and \(n=0.66\), the consistency between Chaplygin gas and GGPDE models is established while the reconstructed model is incompatible to any standard cosmological model for \(n=1.5\) in the right upper plot. The GGPDE model corresponds to Chaplygin gas model for \(n=0.5\) and 1.5 while this compatibility disturbed for \(n=0.6\) (left lower plot). For \(n=0.5\), the reconstructed model preserves consistency with Chaplygin gas model while the trajectories for \(n=0.66\) and \(n=1.5\) leads to some new model (lower right plot).

Fig. 6
figure 6

Evolution of matter density parameter versus z

Full size image
Fig. 7
figure 7

Evolution of dark energy density parameter versus z

Full size image

The evaluation of fractional densities corresponding to ordinary matter and DE plays a vital role to measure the contribution of these elements in the cosmos as for flat universe model, the densities define \(\Omega _m+\Omega _c=1\) whereas for non-flat universe model, this equality becomes \(\Omega _m+\Omega _c=1+\Omega _k\). According to some recent observations, there are some evidences in favor of closed universe model with fractional density \(\Omega _k\simeq 0.01\). From observations of Planck 2018, it is suggested that \(\Omega _m\simeq 0.3111\) and \(\Omega _c\simeq 0.6889\). In Fig. 6, we discuss the contribution of ordinary matter fractional density in the background of radiation, matter and DE dominated eras. The graphical interpretation indicates that when \(z=0\), the trajectories of fractional density provide \(\Omega _m=0.7\), 0.5 and 0.2 for \(n=0.5\), 0.66 and 1.5, respectively. In this regard, fractional density parameter of ordinary matter preserves consistency with Planck’s 2018 constraints in the presence of DE. Figure 7 explores the behavior of DE fractional density parameter in the context of closed and open universe models. In the upper plane, the positively increasing curves show that the DE fractional density is consistent with Planck constraints for \(n=0.66\), 1.5 (left plot) while in case of \(n=0.5\), \(\Omega _c=0.28\) implying inconsistent result. In the right plot, the Planck’s suggested value of \(\Omega _c\) is obtained for all considered values of n. In the lower plane, the compatibility is preserved in the presence of radiation and DE dominated eras (left plot) while \(\Omega _c\) is consistent for all chosen values of n (right plot).

4 Unified scale factor

The scale factor for unified phases discusses both matter as well as DE dominated eras. It is defined as [16]

$$\begin{aligned} {\hat{a}}(t)= & {} m_{0}t^{h_{2}}\exp (h_{1}t), \end{aligned}$$

where \(h_{1}\) and \(h_{2}\) are arbitrary constants. The corresponding Hubble parameter, Ricci scalar and GGPDE density are given by

$$\begin{aligned} H= & {} h_{1}+\frac{h_{2}}{t}\quad R=12\left( h_{1}+\frac{h_{2}}{t}\right) ^{2}-6\left( \frac{h_{2}}{t^{2}}\right) +\frac{k}{\hat{a}^{2}},\\ \mu _{d}= & {} {\zeta }^{\eta }\left( h_{1}+\frac{h_{2}}{t})^{\eta }+\eta \zeta ^{\eta -1}\beta (h_{1}+\frac{h_{2}}{t}\right) ^{\eta +1}. \end{aligned}$$

For very small value of t, we obtain \(H(t)\sim \frac{h_{2}}{t}\) exhibiting the existence of perfect fluid with \(\omega =\frac{2}{3}h_{2}^{-1}-1\). However, when t is extremely large, \(H\rightarrow h_{1}\) resulting constant Hubble parameter represents the de Sitter universe. Such a Hubble parameter provides a transition from matter to DE dominated era. For unified scale factor, in order to examine the behavior of reconstructed f(R) models, we substitute corresponding values of Hubble parameter, Ricci scalar and energy density in Eq. (10) with \(\hat{a} = a_{0}(1 + z)^{-1}\) and upon numerically solving the differential equation, we get reconstructed GGPDE f(R) model in terms of z. The evolution of this reconstructed model is examined for two values of PDE parameter, i.e., \(\eta =0.99\) and \(\eta = -0.99\) and three distinct values of \(h_{2} = 0.75, 1.5, 2.5\).

Fig. 8
figure 8

Plots of unified phase reconstructed GGPDE f(R) model for \(k=1\) (upper panel) and \(k=-1\) (lower panel) with \(\eta = 0.99\) and \(\eta = -0.99\)

Full size image

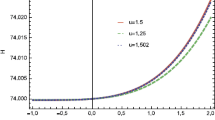
The variation of GGPDE f(R) model versus red-shift parameter z for \(\eta =0.99\) (left) and \(-0.99\) (right) along closed and open universe models is displayed in Fig. 8. In both upper and lower left plots, the function f tends to increase positively while trajectories of f evolve positive to negative in both upper and lower right plots for all values of \(h_2\). Figure 9 represents the stability analysis of GGPDE f(R) model against red-shift parameter. The positively increasing behavior of \(\nu _s^2\) indicates that the reconstructed model is stable in the background of both closed and open universe models. Figure 10 describes the behavior of reconstructed model through effective EoS parameter. For all considered values of \(h_2\), the parameter identifies decelerated expanding phase for large values of z while crossing the quintessence phase, it finally corresponds to the phantom phase near \(z=0\) which is current state of the cosmos.

Fig. 9
figure 9

Plots for squared speed of sound versus z

Full size image
Fig. 10
figure 10

Unified phase EoS parameter versus z

Full size image
Fig. 11
figure 11

Evolution of \(\omega \)–\(\omega '\) versus z

Full size image
Fig. 12
figure 12

Trajectories of r–s plane versus z

Full size image

In Fig. 11, the existence of thawing/freezing regions is examined via \(\omega \)–\(\omega '\) plane. In the upper left plot, the trajectories of \(\omega \)–\(\omega '\) ensure the presence of thawing and freezing regions for \(h_2=0.75,~1.5\) and 2.5, respectively. In upper right plot, there is a transition from thawing to freezing region when \(h_2=0.75\) and 1.5 while for \(h_2=2.5\), the variation of \(\omega \)–\(\omega '\) plane locates thawing region. For open universe model with positive PDE parameter (lower left plot), the graphical interpretation corresponds to thawing region for all chosen values of \(h_2\) whereas in the right plot, freezing and thawing regions exist for \(h_2=0.75\) and \(h_2=1.5,~2.5\), respectively. Figure 12 measures the compatibility of GGPDE f(R) model with standard cosmological models through r–s parameters. In the context of closed universe with positive PDE parameter (upper left plot), the reconstructed model admits consistence with chaplygin gas model for \(h_2=0.75\) and 1.5. For \(h_2=2.5\) with \(z\ge -10\), it corresponds to quintessence and phantom phases whereas the compatibility with Chaplygin gas model is preserved for negative PDE parameter (upper and lower right plots). The same behavior appears in the background of open universe with positive PDE parameter for \(h_2=0.75\) and 1.5 while the GGPDE model lost its compatibility for \(h_2=2.5\).

Figure 13 evaluates the consistence of fractional density parameter relative to ordinary matter against red-shift parameter. For \(h_2=0.75\) (left plot), \(\Omega _m=0.31\) at \(z=0\) (current stage of cosmos) implying consistency with Planck’s observations whereas the fractional density parameter attains much smaller value for \(h_2=1.5\) and 2.5 (right plot). Figure 14 measures the variation of DE fractional density parameter versus z in the context of closed universe with positive PDE parameter. The graphical analysis represents that fractional density parameter admits consistency with Planck’s constraints for \(h_2=0.75\) at \(z=1\) (left plot) while this consistency is disturbed for \(h_2=1.5\) and 2.5 (right plot) due to extreme small values of \(\Omega _c\). For negative PDE parameter, the DE fractional density remains small in the background of closed and open universe models (Fig. 15). In Fig. 16, the fractional density parameter of DE is found to be compatible with Planck 2018 data for \(h_2=1.5\) (right plot) whereas for \(h_2=0.75\) and \(h_2=2.5\) (left plot), the compatibility is lost due to small values of \(\Omega _c\).

Fig. 13
figure 13

Evolution of matter density parameter versus z

Full size image
Fig. 14
figure 14

Evolution of dark energy density parameter versus z

Full size image
Fig. 15
figure 15

Evolution of dark energy density parameter versus z

Full size image
Fig. 16
figure 16

Evolution of dark energy density parameter versus z

Full size image

5 Conclusion

In this paper, we have discussed cosmic evolution of non-flat FRW universe GGPDE model in the background of f(R) gravity. For this purpose, we have reconstructed f(R) model using two well known scale factors, i.e., power-law and unified scale factors in terms of red-shift parameter. In order to determine the stability/instability of reconstructed GGPDE f(R) models, we have considered squared speed of sound parameter. We have investigated the behavior of reconstructed GGPDE models via standard cosmological parameter such as effective EoS parameter. We have also explored the variation of \(\omega '\) along \(\omega \) to analyze the rate of accelerated expansion. The compatibility of new models with standard cosmological models is discussed through state-finder parameters. Furthermore, we have evaluated fractional densities of ordinary matter and DE to measure the ratio of universe constituents. The results for both power-law and unified reconstructed GGPDE f(R) models are summarized as follows.

5.1 Power-law GGPDE f(R) model

  • The f(R) model evolves positively for \(k=1\) with \(\eta =0.99\) and \(\eta =-0.99\) while it tends to increase negatively \(k=1\) with \(\eta =0.99\) and experiences transition from positive to negative region for \(\eta =-0.99\).

  • When \(k=1\) and \(\eta =0.99\), the model is found to be stable initially but becomes unstable as z increases for \(n=0.5\) and \(n=0.66\). When \(n=1.5\), the reconstructed model admits a transition from stable to unstable state. For \(\eta =-0.99\), the GGPDE f(R) model gets stable and unstable at \(z=0\) for \(n=0.5,~0.66\) and \(n=1.5\), respectively. For \(k=-1\) with \(\eta =0.99\), the model is found to be stable in the present cosmos while prior to this stage, it gets unstable whereas it remains unstable for all z in the presence of decelerated epoch. In case of accelerated expansion, the model is unstable at the present stage while stability is achieved in the earlier phase. When \(\eta =-0.99\), the reconstructed model remains stable and unstable for \(n=0.5\) and \(n=1.5\), respectively while a transition from unstable to stable behavior appears for \(n=0.66\).

  • For \(k=1\) and \(k=-1\) with \(\eta =0.99\), the effective EoS parameter corresponds to both decelerated and accelerated phases for \(n=0.5\) and \(n=0.66\). For \(k=1\) and \(\eta =-0.99\) , it coincides with phantom phase for both \(n=0.5\) and \(n=0.66\) whereas in case of \(k=-1\), the parameter seems to be consistent with phantom phase for \(n=0.5\). For \(n=0.66\), it characterizes both accelerated (initially) and decelerated phases. When \(n=1.5\), the parameter experiences a phase transition from decelerated to accelerated phase of expansion for \(k=1\) and \(k=-1\).

  • When \(n=0.5\), the variation of \(\omega \)–\(\omega '\) plane specifies freezing region for both \(k=1\) and \(k=-1\). For \(k=1\), the existence of freezing region is assured whereas incompatible results appeared for \(k=-1\) in the presence of matter dominated epoch. When \(n=1.5\), the \(\omega \)–\(\omega '\) plane locates thawing region for both \(k=1\) and \(k=-1\).

  • When \(k=1\), the reconstructed GGPDE f(R) model is compatible with Chaplygin gas model for all values of n and \(\eta =0.99\) while this compatibility is preserved for \(n=0.5\) and 0.66 with \(\eta =-0.99\). For \(k=-1\), the correspondence between reconstructed and Chaplygin gas models is established for \(n=0.5\) and 1.5 with \(\eta =0.99\) whereas in case of \(n=0.5\) and \(\eta =-0.99\), the model remains compatible with Chaplygin gas model.

  • When \(n=1.5\), the ordinary matter fractional density parameter turns out to be \(\Omega _m=0.28\) whereas for \(n=0.5\) and 0.66, the value exceeds from Planck’s suggested constraints at 68%CL given as [33]

    $$\begin{aligned} \Omega _m= & {} 0.289^{+0.026}_{-0.033}\quad \text {(EE+lowE)},\\ \Omega _m= & {} 0.3153\pm 0.0073\\&\text {(Planck TT,TE,EE+lowE+lensing)},\\ \Omega _m= & {} 0.3111\pm 0.0056\\&\text {(Planck TT,TE,EE+lowE+lensing+BAO)}. \end{aligned}$$

  • For \(k=1\) and \(\eta =0.99\), the DE fractional density is consistent with Planck constraints for \(n=0.66\), 1.5 as \(\Omega _c=0.68\) and 0.66, respectively while in case of \(n=0.5\), \(\Omega _c=0.28\) implying inconsistent result. When \(\eta =-0.99\), the Planck’s suggested value of \(\Omega _c\) is obtained for all considered values of n. In case of \(k=-1\) and \(\eta =0.99\), the compatibility is preserved in the presence of radiation and DE dominated eras while for \(\eta =-0.99\), \(\Omega _c\) is consistent for all chosen values of n. Recent observations of Planck 2018 proposed different values of \(\Omega _c\) at 68%CL given by [33]

    $$\begin{aligned} \Omega _c= & {} 0.711^{+0.033}_{-0.026}\quad \text {(EE+lowE)},\\ \Omega _c= & {} 0.6847\pm 0.0073\\&\hbox {(Planck TT,\;TE,\;EE+lowE+lensing)},\\ \Omega _c= & {} 0.6889\pm 0.0056\\&\hbox {(Planck TT,\;TE,\;EE+lowE+lensing+BAO)}. \end{aligned}$$

5.2 Unified GGPDE f(R) Model

  • When \(k=1\) and \(k=-1\) with \(\eta =0.99\), the function f tends to increase positively while trajectories of f evolve positive to negative for \(\eta =-0.99\) and all values of \(h_2\).

  • The squared speed of sound parameter identifies stable behavior of reconstructed GGPDE f(R) model for both choices of PDE parameter in the context of closed and open universe models.

  • For \(k=1\) and \(k=-1\) with all considered values of \(h_2\), the effective EoS parameter identifies decelerated expanding phase for large values of z while crossing the quintessence phase, it finally corresponds to the phantom phase near \(z=0\) which is current state of the cosmos.

  • When \(k=1\) and \(\eta =0.99\), thawing and freezing regions exist for \(h_2=0.75,~1.5\) and 2.5, respectively. For \(\eta =-0.99\), there is a transition from thawing to freezing region when \(h_2=0.75\) and 1.5 while for \(h_2=2.5\), \(\omega \)–\(\omega '\) plane locates thawing region. For \(k=-1\) and \(\eta =0.99\), the thawing region is determined for all chosen values of \(h_2\) whereas when \(\eta =-0.99\), freezing and thawing regions appear for \(h_2=0.75\) and \(h_2=1.5,~2.5\), respectively.

  • The reconstructed model is consistent with chaplygin gas model for \(k=1\), \(\eta =0.99\) and \(h_2=0.75\) and 1.5 while it corresponds to quintessence and phantom phases for \(h_2=2.5\) with \(z\ge -10\). When \(\eta =-0.99\), the compatibility with Chaplygin gas model is preserved for both \(k=1\) and \(k=-1\). The same behavior appears when \(k=-1\) and \(\eta =0.99\) for \(h_2=0.75\) and 1.5 while the GGPDE model lost its compatibility for \(h_2=2.5\).

  • For \(h_2=0.75\), \(\Omega _m=0.31\) at \(z=0\) (current stage of cosmos) implying consistency with Planck’s observations whereas the fractional density parameter attains much smaller value for \(h_2=1.5\) and 2.5.

  • In case of \(k=1\) and \(\eta =0.99\), the DE fractional density parameter admits consistency with Planck’s constraints for \(h_2=0.75\) at \(z=1\) while this consistency is disturbed for \(h_2=1.5\) and 2.5. For \(\eta =-0.99\), the DE fractional density remains small in the background of closed and open universe models. When \(k=-1\) and \(\eta =0.99\), \(\Omega _c\) is found to be compatible with Planck 2018 data for \(h_2=1.5\) whereas for \(h_2=0.75\) and \(h_2=2.5\), the compatibility is lost due to small values of \(\Omega _c\).

The reconstructed GGPDE model is stable as well as consistent with Chaplygin gas model for both power-law and unified scale factors in most of the cases. In the background of open and closed universe models, the analysis of fractional density parameter of matter and DE reveals that the power-law GGPDE f(R) model is consistent with Planck’s 2018 data for both choices of PDE parameter. In case of unified GGPDE f(R) model, this consistency is preserved only for positive PDE parameter. We conclude that the power-law GGPDE f(R) model significantly explains the cosmic journey from decelerated to accelerated epoch.