Modified cosmology models from thermodynamical approach

Abstract

We apply the first law of thermodynamics to the apparent horizon of the universe with the power-law corrected and non-extensive Tsallis entropies rather than the Bekenstein–Hawking one. We examine the cosmological properties in the two entropy models by using the CosmoMC package. In particular, the first numerical study for the cosmological observables with the power-law corrected entropy is performed. We also show that the neutrino mass sum has a non-zero central value with a relaxed upper bound in the Tsallis entropy model comparing with that in the $\Lambda$CDM one.

1 Introduction

According to the current cosmological observations, our universe is experiencing a late time accelerating expansion. Although the $\Lambda$CDM model can describe the accelerating universe by introducing dark energy [1], it fails to solve the cosmological constant problem, related to the “fine-tuning” [2, 3] and “coincidence” [4, 5] puzzles. A lot of efforts have been made to understand these issues. For example, one can modify the gravitational theory to obtain viable cosmological models with dynamical dark energy to explain the accelerating universe [6].

On the other hand, one can reconstruct the Friedmann equations through the implications of thermodynamics. It has been shown that the Einstein’s equations can be derived by considering the Clausius’ relation of a local Rindler observer [7]. In particular, this idea has been applied to cosmology, while the Friedmann equations have been obtained by using the first law of thermodynamics in the horizon of the universe [8]. It has been also demonstrated that the modified Friedmann equations can be acquired from the thermodynamical approach by just replacing the entropy-area relation with a proper one in a wide variety of gravitational theories [8,9,10,11,12,13]. Thus, as long as there is a new entropy area relation, thermodynamics gives us a new way to determine the modified Friedmann equations without knowing the underlying gravitational theory. Furthermore, since the entropy area relation obtained from the modified gravity theory can be useful to extract the dark energy dynamics along with the modified Friedmann equations, it is reasonable to believe that even if we do not know the underlying theory of modified gravity, some modifications of the entropy relation will still give us additional information for modified Friedmann equations as well as the dynamics of dark energy, which would be different from $\Lambda$CDM. As a result, we expect that the modification of the entropy is also relevant to the cosmological evolutions.

It is known that a power-law corrected term from the quantum entanglement can be included in the black hole entropy near its horizon [14]. Interestingly, one can apply it to cosmology by taking it as the entropy on the horizon of the universe. On the other hand, the universe is regarded as a non-extensive thermodynamical system, so the Boltmann–Gibbs entropy should be generalized to a non-extensive quantity, the Tsallis entropy, while the standard one can be treated as a limit [15,16,17]. The Tsallis entropy has been widely discussed in the literature. In the entropic-cosmology scenario [18], the Tsallis entropy model predicts a decelerating and accelerating universe [19]. In addition, a number of works on the Tsallis holographic dark energy have been proposed and investigated [20,21,22,23,24]. In addition, the Tsallis entropy has also been used in many different dark energy models, such as the Barboza–Alcaniz and Chevalier–Polarski–Linder parametric dark energy and Wang–Meng and Dalal vacuum decay models [25]. Moreover, it is shown that modified cosmology from the first law of thermodynamics with varying-exponent Tsallis entropy can provide a description of both inflation and late-time acceleration with the same parameter choices [27]. In particular, the Tsallis entropy is proportional to a power of the horizon area, i.e. $S_T \propto A^{\delta }$, when the universe is assumed to be a spherically symmetric system [28].

Although it is possible to modify Friedmann equations by just considering fluid with an inhomogeneous equation of state of the corresponding form [29], we still choose the thermo-dynaimical approach as that in Ref. [30], in which the authors considered the first law of thermodynamics of the universe with fixed-exponent Tsallis entropy and showed that the cosmological evolution mimics that of $\Lambda$CDM and are in great agreement with Supernovae type Ia observational data. In this paper, we examine the features of the modified Friedmann equations obtained by replacing the usual Bekenstein–Hawking entropy-area relation, $S=A/4G$, with the power-law correction and Tsallis entropies [14,15,16,17, 19,20,21,22,23,24,25,26,27,28, 30], where G is the gravitational constant.

This paper is organized as follows. In Sect. 2, we consider the power-law corrected and Tsallis entropy models and derive the modified Friedmann equations and dynamical equation of state parameters by applying the first law of thermodynamics to the apparent horizon of the universe. In Sect. 3, we present the cosmological evolutions of the two models and compare them with those in $\Lambda$CDM. Finally, the conclusions are given in Sect. 4. The paper is written in units of $c=\hbar =k_B=1$.

2 The models

We use the flat Friedmann–Lemaître–Robertson–Walker (FLRW) metric:

$$\begin{aligned} ds^2=-dt^2+a^{2}(t)\Big (dr^2+r^2 d\Omega ^2\Big ), \end{aligned}$$

(2.1)

where a(t) is the scale factor. The modified Friedmann equations can be constructed by considering the first law of thermodynamics in the apparent horizon of the universe and using the new entropy area relation rather than the Bekenstein–Hawking one. We concentrate on two models: power law corrected entropy (PLCE) and Tsallis entropy cosmological evolution (TECE) models.

2.1 Power law corrected entropy (PLCE) model

In the PLCE model, the entropy has the form [14]

$$\begin{aligned} S_{pl}= \frac{A}{4L_p^2}\bigg (1 - K_\nu A^{1-\frac{\nu }{2}}\bigg ), \end{aligned}$$

(2.2)

where $\nu$ is a dimensionless constant parameter and $K_\nu =\nu (4 \pi )^{(\nu -2)/2}(4-\nu )^{-1}r_c^{\nu -2}$ with $r_c$ the crossover scale, A corresponds to the area of the system, and $L_p$ represents the Planck length. With the method described in Ref. [30], one is able to extract the modified Friedmann equations:

$$\begin{aligned} H^2&=\frac{8\pi G}{3}(\rho _m +\rho _r + \rho _{DE}),\nonumber \\ {\dot{H}}&=-4\pi G(\rho _m +\rho _r+ \rho _{DE}+p_m +p_r+p_{DE}), \end{aligned}$$

(2.3)

where $\rho _{DE}$ and $p_{DE}$ are the dark energy density and pressure, given by

$$\begin{aligned} \rho _{DE}&= \frac{3}{8 \pi G}\frac{1}{r^{2-\nu }_c}\big (H^{\nu }-1\big ) + \frac{\Lambda }{8 \pi G}, \end{aligned}$$

(2.4)

$$\begin{aligned} p_{DE}&=\frac{-\nu }{8 \pi G}\frac{\dot{H}}{r^{2-\nu }_c}\big (H^{\nu }-1\big )- \frac{3}{8 \pi G}\frac{1}{r^{2-\nu }_c}\big (H^{\nu }-1\big ) \nonumber \\&-\frac{\Lambda }{8 \pi G}, \end{aligned}$$

(2.5)

respectively. To discuss the evolution of dark energy, it is convenient to define the equation of state parameter, $w_{DE} \equiv p_{DE}/\rho _{DE}$, which is found to be

$$\begin{aligned} w_{DE} = -1 + \frac{-\nu \dot{H}H^{\nu -2}}{3(H^{\nu }-1) + \Lambda r^{2-\nu }_c}. \end{aligned}$$

(2.6)

2.2 Tsallis entropy cosmological evolution model

In the TECE model, we have [28]

$$\begin{aligned} S_T=\frac{\tilde{\alpha }}{4G}A^{\delta }, \end{aligned}$$

(2.7)

where A is the area of the system with dimension [$L^2$], $\tilde{\alpha }$ is a positive constant with dimension [$L^{2-2\delta }$], and $\delta$ denotes the non-additivity parameter. Similarly, by following the procedure in Ref. [30], we obtain

$$\begin{aligned} H^2&=\frac{8\pi G}{3}(\rho _m +\rho _r + \rho _{DE}),\nonumber \\ \dot{H}&=-4\pi G(\rho _m +\rho _r+ \rho _{DE}+p_m +p_r+p_{DE}), \end{aligned}$$

(2.8)

with

$$\begin{aligned} \rho _{DE}&=\frac{3}{8 \pi G}\bigg [\frac{\Lambda }{3}+ H^2\bigg (1-\alpha \frac{\delta }{2-\delta } H^{2(1-\delta )}\bigg )\bigg ], \end{aligned}$$

(2.9)

$$\begin{aligned} p_{DE}&=-\frac{1}{8 \pi G}\bigg [\Lambda +2 \dot{H}(1-\alpha \delta H^{2(1-\delta )})\nonumber \\&\quad +3H^2\bigg (1-\alpha \frac{\delta }{2-\delta }H^{2(1-\delta )}\bigg )\bigg ] \end{aligned}$$

(2.10)

where $\alpha = (4 \pi )^{\delta -1}\tilde{\alpha }$, and $\Lambda$ is a constant related to the present values of $H_0, \rho _{m0}$ and $\rho _{r0}$, given by

$$\begin{aligned} \Lambda&=\frac{3\alpha \delta }{2-\delta }H_0^{2(2-\delta )}-8\pi G(\rho _{m0} +\rho _{r0}). \end{aligned}$$

(2.11)

Thus, the equation of state parameter for the TECE model is evaluated to be

$$\begin{aligned} w_{DE} = \frac{p_{DE}}{\rho _{DE}} =-1 + \frac{2\dot{H}(\alpha \delta H^{2\dot{H}(1-\delta )}-1)}{3H^2\bigg (1-\frac{\alpha \delta }{2-\delta }H^{2(1-\delta )}\bigg )+\Lambda }. \end{aligned}$$

(2.12)

3 Cosmological evolutions

3.1 Power law corrected entropy model

Since $\rho _{DE}$ and $w_{DE}$ are determined by the Hubble parameter H(z), we use the Newton–Raphson method [31] to obtain the cosmological evolutions of the PLCE model.

Fig. 1

Evolutions of the equation-of-state parameter $w_{DE}$ in $\Lambda$CDM and PLCE models

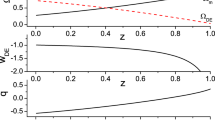
Because the PLCE model goes back to $\Lambda$CDM when $\nu = 0$, we choose $\nu =\pm 0.02$ to compare the differences between the two models. We also take a larger value of $\nu = 0.2$ to check the sensitivity of $\nu$. The results in Fig. 1 show that $w_{DE}$ does not overlap or cross $-1$ in any non-zero value of $\nu$. In addition, it maintains its value in the early universe, and only trends to $-1$ for $z<2$.

Fig. 2

CMB power spectra of the TT mode in $\Lambda$CDM and PLCE models along with the Planck 2018 data

Fig. 3

The change $\Delta D_{\ell }^{TT}$ of the TT mode of CMB power spectra between PLCE and $\Lambda$CDM, where the legend is the same as Fig. 1

Fig. 4

CMB TE power spectra in the $\Lambda$CDM and PLCE models along with the Planck 2018 data

In Fig. 2, we display the CMB power spectra in the $\Lambda$CDM and PLCE models along with the data from Planck 2018. Since the TT spectra of PLCE and $\Lambda$CDM are almost identical to the data from Planck 2018 for the high values of the multipole l, we focus on the differences between the two models and the data when $l<100$ as depicted in Fig. 3. The TT power spectrum in the PLCE model for $\nu > 0$ is larger than that of $\Lambda$CDM when $l < 100$ with the error in the allowable range of the observational data.

For the TE mode, the spectra in PLCE for the different parameters $\nu$ are always close to that in $\Lambda$CDM as well as the observational data of Planck 2018, as shown in Fig. 4. However, when we carefully compare the differences between the results in PLCE and $\Lambda$CDM in Fig. 5, we notice that those of PLCE are closer to the Planck 2018 data, comparing to that in $\Lambda$CDM.

Fig. 5

The change $\Delta D_{\ell }^{TE}$ of the TT mode of CMB power spectra between PLCE and $\Lambda$CDM, where the legend is the same as Fig. 4

3.2 Tsallis entropy cosmological evolution model

Fig. 6

Evolutions of the equation-of-state parameter $w_{DE}$ in $\Lambda$CDM and TECE models

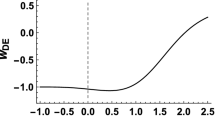
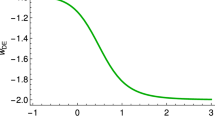
Equation (2.7) of TECE becomes the one in $\Lambda$CDM when $\delta =\tilde{\alpha }=1$. In our study, we only focus on the effects when $\delta \ne 1$ so we set $\tilde{\alpha }=1$ and $\delta =1+\xi$. In Fig. 6, we find that the equation of state, $w_{DE}$, behaves differently for different values of $\xi$. In particular, it is larger (smaller) than $-1$ when $\xi$ is larger (smaller) than zero without crossing $-1$ in anytime.

In Figs. 7 and  8, we see that the TT Power spectra of TECE and $\Lambda$CDM have a large difference in the large scale structure. Note that there is a significant discrepancy between $\Lambda$CDM and the data at $l\sim 20-27$. However, the spectrum of TECE for $\xi =0.002$ and $l\sim 20-27$ is below that in $\Lambda$CDM, and closer to the observational data of Planck 2018. The shifts of the TE mode between PLCE and $\Lambda$CDM are shown in Figs. 9 and 10.

Fig. 7

Legend is the same as Fig. 2 but in the TECE model with a set of $\xi$

Fig. 8

Legend is the same as Fig. 3 but in the TECE model with a set of $\xi$

Fig. 9

Legend is the same as Fig. 4 but in the TECE model with a set of $\xi$

Fig. 10

Legend is the same as Fig. 5 but in the TECE model with a set of $\xi$

Table 1 H(z) data points

3.3 Global fits

We use the modified $\mathbf{CAMB}$ and CosmoMC program [32] to do the global cosmological fits for the PLCE and TECE models from the observational data with the MCMC method. The dataset includes those of the CMB temperature fluctuation from Planck 2015 with TT, TE, EE, low-l polarization and CMB lensing from SMICA [45,46,47], the weak lensing (WL) data from CFHTLenS [48], and the BAO data from 6dF Galaxy Survey [49] and BOSS [50]. In particular, we include 35 points for the H(z) measurements in our fits, which are listed in Table 1. The $\chi ^2$ fit is given by

$$\begin{aligned} {\chi ^2}={\chi ^2_{CMB}}+{\chi ^2_{WL}}+{\chi ^2_{BAO}}+{\chi ^2_{H(z)}}, \end{aligned}$$

(3.1)

with

$$\begin{aligned} \chi ^2_c = \sum _{i=1}^n \frac{(T_c(z_i) - O_c(z_i))^2}{E^i_c} \,, \end{aligned}$$

(3.2)

where the subscript of “c” denotes the category of the data, n represents the number of the dataset, $T_c$ is the prediction from CAMB, and $O_c$ ($E_c$) corresponds to the observational value (covariance). The priors of the various cosmological parameters are given in Table 2.

Table 2 Priors for cosmological parameters in the PLCE and TECE models

Fig. 11

One and two-dimensional distributions of $\Omega _b h^2$, $\Omega _c h^2$, $\sum m_\nu$, $\nu$, $H_0$, and $\sigma _8$ in the PLCE and $\Lambda$CDM models, where the contour lines represent 68$\%$  and 95$\%$  C.L., respectively

Fig. 12

Legend is the same as Fig. 11 but for the TECE and $\Lambda$CDM models

Table 3 Fitting results for the PLCE and $\Lambda$CDM models, where the limits are given at 68$\%$ and 95$\%$ C.L., respectively

Table 4 Fitting results for the TECE and $\Lambda$CDM models, where the limits are given at 68$\%$ and 95$\%$ C.L., respectively

In Fig. 11, we present our fitting results of PLCE (red) and $\Lambda$CDM (blue). Although the PLCE model has been discussed in the literature, it is the first time to illustrate its numerical cosmological effects. In particular, we find that $\nu$ $=$ $( 0.0240^{+0.0110}_{-0.0085})$ in 68$\%$ C.L., which shows that PLCE and $\Lambda$CDM can be clearly distinguished. It is interesting to note that the value of $\sigma _8=0.814^{+0.023}_{-0.026}$ (95$\%$ C.L.) in PLCE is smaller than that of $0.815^{+0.023}_{-0.025}$ (95$\%$ C.L.) in $\Lambda$CDM. As shown in Table 3, the best fitted $\chi ^2$ value in PLCE is 3017.12, which is also smaller than 3018.32 in $\Lambda$CDM. Although the cosmological observables for the best $\chi ^2$ fit in PLCE do not significantly deviate from those in $\Lambda$CDM, it indicates that the PLCE model is closer to the observational data than $\Lambda$CDM.

Similarly, we show our results for TECE (red) and $\Lambda$CDM (blue) in Fig. 12. Explicitly, we get that $\xi$ = $( 3.8\pm {2.7})\times 10^{-4}$ in 68$\%$ C.L. In addition, the TECE model can relax the limit of the total mass of the active neutrinos. In particular, we have that $\Sigma m_\nu$ $< 0.317$ eV, comparing to $\Sigma m_\nu$ $< 0.195$ eV in $\Lambda$CDM at 95$\%$ C.L. In addition, the value of $H_0$ in TECE equals to $68.42\pm {0.71}$ $(68.4\pm {1.4})$, which is larger than $68.05^{+0.60}_{-0.54}$ $(68.1^{+1.1}_{-1.2})$ in $\Lambda$CDM with 68$\%$ (95$\%$) C.L.

As shown in Table 4, the best fitted $\chi ^2$ value in the TECE model is 3018.96, which is smaller than 3019.28 in $\Lambda$CDM model. Although the difference between the value of $\chi ^2$ in TECE and $\Lambda$CDM is not significant, it still implies that the TECE model can not be ignored. Clearly, more considerations and discussions are needed in the future.

4 Conclusions

We have calculated the cosmological evolutions of $\rho _{DE}$ and $w_{DE}$ in the PLCE and TECE models. We have found that the EoS of dark energy in PLCE (TECE) does not cross $-1$. We have shown that the CMB TE power spectrum of the PLCE model with a positive $\nu$ is closer to the Planck 2018 data than that in $\Lambda$CDM, while the CMB TT spectrum in the TECE model has smaller values around $l\sim 20-27$, which are lower than that in $\Lambda$CDM, but close to the data of Planck 2018. By using the Newton method in the global fitting, we have obtained the first numerical result in the PLCE model with $\nu =0.0240^{+0.0110}_{-0.0085}$ in 68$\%$ C.L., which can be distinguished well with $\Lambda$CDM. Our Fitting results indicate that the PLCE model gives a smaller value of $\sigma _8$ with a better $\chi ^2$ value than $\Lambda$CDM. In the TECE model, we have gotten that $\xi =(3.8\pm 2.7)^{-4}$ and $\Sigma m_\nu$ $< 0.186$ eV in 68$\%$ C.L., while $H_0$ is closer to 70. The best fitted value of $\chi ^2$ is 3018.96 in the TECE model, which is smaller than 3019.28 in $\Lambda$CDM. These results have demonstrated that the TECE model deserves more attention and research in the future.