1 Introduction

Surface operators in 4d gauge theories are natural two dimensional generalizations of Wilson and ’t Hooft loops which can provide valuable information about the phase structure of the gauge theories [1]. In this paper we study the low-energy effective action of surface operators in pure \({{\mathcal {N}}}=2\) 4d gauge theories from two distinct points of view, namely as monodromy defects [2, 3] and as coupled 2d/4d quiver gauge theories [4, 5]. In the first approach, one specifies how the 4d gauge fields are affected by the presence of the surface operator by imposing suitable boundary conditions in the path-integral. In this framework the non-perturbative effects are described in terms of ramified instantons [2] whose partition function can be computed using equivariant localization methods [5,6,7,8,9,10]. From the ramified instanton partition function one can extract two holomorphic functions [11, 12]: one is the prepotential \(\mathcal {F}\) that governs the low-energy effective action of the 4d \({\mathcal {N}}=2\) gauge theory on the Coulomb branch; the other is the twisted chiral superpotential \({\mathcal {W}}\) that describes the 2d dynamics on the defect.

In the second description of the surface operators, one considers coupled 2d/4d theories that are (2, 2) supersymmetric sigma models with an ultraviolet description as a gauged linear sigma model (GLSM). The low-energy dynamics of such a GLSM is completely determined by a twisted chiral superpotential \({{{\mathcal {W}}}}(\sigma )\) that depends on the twisted chiral superfields \(\sigma \) containing the 2d vector fields [13]. By giving a vacuum expectation value (vev) to the adjoint scalar of the 4d \({\mathcal {N}}=2\) gauge theory, one introduces twisted masses in the 2d quiver theory [14, 15]. At a generic point on the 4d Coulomb branch, the 2d theory is therefore massive in the infrared and the 2d/4d coupling mechanism is determined via the resolvent of the 4d gauge theory [5]. The resulting massive vacua of the GLSM are solutions to the twisted chiral ring equations, which are obtained by extremizing \({{\mathcal {W}}}(\sigma )\) with respect to the twisted chiral superfields.

The main goal of this work is to clarify the precise relationship between the above two descriptions of the surface operators. In our previous works [9, 10] the first steps in this direction were already taken by showing that there is a precise correspondence between the massive vacua of the 2d/4d gauge theory and the monodromy defects in the \({{{\mathcal {N}}}}=2\) gauge theory. In fact, the effective twisted chiral superpotential of the 2d/4d quiver gauge theory evaluated in a given massive vacuum exactly coincides with the one computed from the 4d ramified instanton partition function [9, 10]. This equality was shown in a specific class of models that are described by oriented quiver diagrams. Recently, this result has been proven in full generality in [16, 17].

An important feature of the (2, 2) quiver theories that was not fully discussed in our previous papers is Seiberg duality [18, 19]. This is an infrared equivalence between two gauge theories that have different ultraviolet realizations. In this work we fill this gap and consider all possible quivers obtained from the oriented ones by applying 2d Seiberg duality. While all such quivers have different gauge groups and matter content, once the 4d Coulomb vev’s are turned on, it is possible to find a one-to-one map between their massive vacua. Therefore it becomes clear that they must describe the same surface operator from the point of view of the 4d gauge theory; indeed, the different twisted chiral superpotentials, evaluated in the respective vacua, all give the same result. This equality of superpotentials gives a strong hint that the choice of a Seiberg duality frame might have an interpretation as distinct contours of integration on the localization side: the equality of the superpotentials would then be a simple consequence of multi-dimensional residue theorems.

In this work we show that this expectation is correct and provide a detailed map between a given quiver realization of the surface operator and a particular choice of contour in the localization integrals. This contour prescription can be conveniently encoded in a Jeffrey-Kirwan (JK) reference vector [20], whose coefficients turn out to be related to the Fayet-Iliopoulos (FI) parameters of the 2d/4d quiver. While the twisted superpotentials are equal irrespective of the choice of contour, the map relates the individual residues on the localization side to the individual terms in the solutions to the twisted chiral ring equations, thereby allowing us to identify in an unambiguous way which quiver arises from a given contour prescription and vice-versa.

This paper is organized as follows. In Sect. 2 we review and extend our earlier work [8,9,10], and in particular we show how to map the oriented quiver to a particular contour by studying the solution of the chiral ring equations and the precise correspondence to the residues of the localization integrand. In Sect. 3 we discuss the basics of 2d Seiberg duality and how it acts on the quiver theories we consider. In Sect. 4 we apply the duality moves to the oriented quiver of interest and show in detail (for the 4-node quiver), how it is possible to map each quiver to a particular integration contour on the localization side without explicitly solving the chiral ring equations. We also discuss how this integration contour can be specified in terms of a JK reference vector. In Sect. 5 we give a simple solution for the JK vector associated to a generic linear 2d/4d quiver with arbitrary number of nodes. Finally, we summarize our main results in Sect. 6 and collect the more technical material in the appendices.

2 Review of earlier work

To set the stage for the discussion in the next sections and also to introduce our notation, we briefly review the results obtained in our earlier work [10] where we studied surface operators both as monodromy defects in 4d and as coupled 2d/4d gauge theories.

2.1 Surface operators as monodromy defects

As a monodromy defect, a surface operator in a 4d SU(N) theory is specified by a partition of N, denoted by \(\varvec{n}=(n_1, n_2, \ldots n_M)\), which corresponds to the breaking of the gauge group to a Levi subgroup

$$\begin{aligned} {\mathbb {L}} = \mathrm {S}\left[ \mathrm {U}(n_1)\times \mathrm {U}(n_2)\times \cdots \mathrm {U}(n_M) \right] \end{aligned}$$
(1)

at the location of the defect [2, 3]. This also gives a natural partitioning of the classical Coulomb vev’s of the adjoint scalar \(\varPhi \) of the \({\mathcal {N}}=2\) SU(N) theory as follows:

$$\begin{aligned} \langle \varPhi \rangle = \big \{a_1,\ldots , a_{r_1}|\!\ldots \!\big | a_{r_{I-1}+1}, \ldots a_{r_{I}}\big |\! \ldots \!|a_{r_{M-1} +1}, \ldots , a_N \big \}.\nonumber \\ \end{aligned}$$
(2)

Here we have defined the integers \(r_I\) according to

$$\begin{aligned} r_I = \sum _{J=1}^{I} n_J ~, \end{aligned}$$
(3)

so that the Ith partition in (2) is of length \(n_I\). Introducing the following set of numbers with cardinality \(n_I\):

$$\begin{aligned} {\mathcal {N}}_I \equiv \{ r_{I-1}+1, r_{I-1}+2,\ldots , r_I \} ~, \end{aligned}$$
(4)

we define the \(n_I \times n_I\) block-diagonal matrices \(\mathcal {A}_I\) according to

$$\begin{aligned} \mathcal {A}_I \equiv \mathrm {diag}\,\left( a_{s\in {{\mathcal {N}}}_I} \right) = \begin{pmatrix} a_{r_{I-1}+1} &{}0 &{} 0 &{} \ldots \\ 0 &{} \ddots &{} 0 &{} \ldots \\ \vdots &{} \vdots &{} \ddots \\ 0 &{} 0 &{} \ldots &{} a_{r_{I}} \end{pmatrix}~. \end{aligned}$$
(5)

With these conventions, the splitting in (2) can be written as

$$\begin{aligned} \langle \varPhi \rangle = {{\mathcal {A}}}_1 \oplus {{\mathcal {A}}}_2 \oplus \ldots \oplus {{\mathcal {A}}}_M ~. \end{aligned}$$
(6)

The instanton partition function in the presence of such a surface operator, also known as the ramified instanton partition function, takes the following form [6, 10]:

$$\begin{aligned} Z_{\text {inst}}[\varvec{n}] = \sum _{\{d_I\}}Z_{\{d_I\}}[\varvec{n}] \end{aligned}$$
(7)

with

$$\begin{aligned} Z_{\{d_I\}}[\varvec{n}]= \prod _{I=1}^M \left[ \frac{(-q_I)^{d_I}}{d_I!} \int \prod _{\sigma =1}^{d_I} \frac{d\chi _{I,\sigma }}{2\pi \mathrm {i}}\right] ~ z_{\{d_I\}} \end{aligned}$$
(8)

where

$$\begin{aligned} z_{\{d_I\}}&= \,\prod _{I=1}^M \prod _{\sigma ,\tau =1}^{d_I}\, \frac{\left( \chi _{I,\sigma } - \chi _{I,\tau } + \delta _{\sigma ,\tau }\right) }{\left( \chi _{I,\sigma } - \chi _{I,\tau } + \epsilon _1\right) }\nonumber \\&\quad \times \prod _{I=1}^M \prod _{\sigma =1}^{d_I}\prod _{\rho =1}^{d_{I+1}}\, \frac{\left( \chi _{I,\sigma } - \chi _{I+1,\rho } + \epsilon _1 + {\hat{\epsilon }}_2\right) }{\left( \chi _{I,\sigma } - \chi _{I+1,\rho } + {\hat{\epsilon }}_2\right) } \nonumber \\&\quad \times \prod _{I=1}^M \prod _{\sigma =1}^{d_I} \frac{1}{\prod _{s\in {\mathcal {N}}_I}\left( a_{s}-\chi _{I,\sigma } + \frac{1}{2} (\epsilon _1 + {\hat{\epsilon }}_2)\right) } \nonumber \\&\quad \times \prod _{I=1}^M \prod _{\sigma =1}^{d_I} \frac{1}{\prod _{t\in {\mathcal {N}}_{I+1}}\left( \chi _{I,\sigma } - a_{t} + \frac{1}{2} (\epsilon _1 + {\hat{\epsilon }}_2)\right) }~. \end{aligned}$$
(9)

Here, the M positive integers \(d_I\) count the numbers of ramified instantons in the various sectors, the variables \(q_I\) are the ramified instanton weights, and the parameters \(\epsilon _1\) and \({\hat{\epsilon }}_2=\epsilon _2/M\) specify the \(\varOmega \)-background [21, 22] which is introduced to localize the integrals over the instanton moduli space.Footnote 1

There is one more ingredient that is needed to calculate the partition function (8), namely the contour of integration for the \(\chi _I\) variables. A convenient way to specify it and to select which poles of the integrand contribute and which do not, is to treat the Coulomb vev’s a as real variables and assign an imaginary part to the \(\varOmega \)-deformation parameters according to

$$\begin{aligned} 0<\text {Im}(\hat{\epsilon }_2)\ll \text {Im}(\epsilon _1) \ll 1~. \end{aligned}$$
(10)

Then, the contour is specified by integrating \(\chi _{I,\sigma }\) in the upper or lower half-plane and by choosing a definite order in the successive integrations. Equivalently, as we will see in the following sections, the contour of integration can be selected by specifying a Jeffrey-Kirwan reference vector [20].

In the limit \(\epsilon _1,{\hat{\epsilon }}_2\rightarrow 0\), the low-energy effective action of the gauge theory with the 2d defect is specified by two holomorphic functions: the prepotential \(\mathcal {F}\) and the twisted chiral superpotential \({\mathcal {W}}\). Each of these functions can be written as a sum of the classical, the one-loop, and the instanton contributions. The latter can be extracted from the ramified instanton partition function as follows [11, 12]:

$$\begin{aligned} \log \big (1+Z_{\text {inst}}\big ) = -\frac{{\mathcal {F}}_{\text {inst}}}{\epsilon _1{\hat{\epsilon }}_2} + \frac{{\mathcal {W}}_{\text {inst}}}{\epsilon _1} + \ldots \end{aligned}$$
(11)

where the ellipses refer to regular terms. In Appendix A we list the one-instanton contribution to \({{{\mathcal {W}}}}_{\text {inst}}\) calculated for various choices of contours in the case \(M=4\). As we will show in the following, the different contour prescriptions can be given a precise meaning by associating them to specific 2d/4d quiver gauge theories.

2.2 Surface operators as coupled 2d/4d quivers

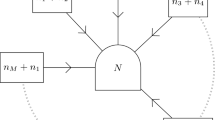
The prepotential \(\mathcal {F}\) governs the 4d gauge theory dynamics at a generic point on the Coulomb branch. The twisted chiral superpotential \({\mathcal {W}}\), instead, is best understood as the low-energy effective description of a 2d non-linear sigma model. For a surface operator with a Levi subgroup \({\mathbb {L}}\) in a 4d theory with a gauge group G, the relevant sigma model is defined on the target space \(G/{\mathbb {L}}\) [2, 3]. Such a space is, in general, a flag variety which can be realized as the low-energy limit of a GLSM [13, 15], whose gauge and matter content can be summarized in the quiver diagram of Fig. 1.

Fig. 1
figure 1

The quiver which describes the generic surface operator in pure SU(N) gauge theory

Full size image

Each circular node represents a 2d gauge group \(\mathrm {U}(r_I)\) where the ranks \(r_I\) are as in (3), whereas the last node on the right hand side represents the 4d gauge group SU(N) which acts as a flavour symmetry group for the \((M-1)^{\mathrm {th}}\) 2d node. The arrows correspond to matter multiplets which are rendered massive by non-zero v.e.v’s of the twisted scalars \(\sigma ^{(I)}\) of the \(I^{\mathrm {th}}\) node and of the 4d adjoint scalar \(\varPhi \). The orientation of the arrows specifies whether the matter is in the fundamental (out-going) or in the anti-fundamental (in-going) representation.

The effective action for the twisted chiral multiplets is obtained by integrating out the massive matter multiplets and, thanks to supersymmetry, can be encoded in the effective twisted chiral superpotential. For the quiver of Fig. 1, this is given by:

$$\begin{aligned} {\mathcal {W}} =&~2\pi \mathrm {i}\sum _{I=1}^{M-1}\sum _{s=1}^{r_I} \tau _I\,\sigma ^{(I)}_s-\! \sum _{I=1}^{M-2} \sum _{s=1}^{r_{I}} \sum _{t=1}^{r_{I+1}} \varpi \big (\sigma ^{(I)}_s - \sigma ^{(I+1)}_t\big ) \nonumber \\&-\!\sum _{s=1}^{r_{M-1}}\!\Big \langle \mathrm {Tr}\,\varpi \big (\sigma ^{(M-1)}_s - \varPhi \big ) \Big \rangle \end{aligned}$$
(12)

where

$$\begin{aligned} \varpi (x) = x\,\Big (\log \frac{x}{\mu } -1\Big )~, \end{aligned}$$
(13)

\(\mu \) is the UV cut-off scale, and \(\tau _I\) is the complexified FI parameter of the Ith node at the scale \(\mu \), namely

$$\begin{aligned} \tau _I=\frac{\theta _I}{2\pi }+\mathrm {i}\,\zeta _I \end{aligned}$$
(14)

with \(\theta _I\) and \(\zeta _I\) being, respectively, the \(\theta \)-parameter and the real FI parameter of the Ith gauge node. Finally, the angular brackets in the last term of (12) correspond to a chiral correlator in the 4d SU(N) theory. This correlator implies that the coupling between the 2d and 4d theory is via the resolvent of the SU(N) gauge theory [5], which in turn depends on the 4d dynamically generated scale \(\varLambda _{\text {4d}}\).

The running of the FI parameters leads to introducing 2d low-energy scales \(\varLambda _I\) at each node by the relation

$$\begin{aligned} \varLambda _I^{b_I}= \mathrm {e}^{\,2\pi \mathrm {i}\,\tau _I} \,\mu ^{b_I} \end{aligned}$$
(15)

where \(b_I\) is the corresponding \(\beta \)-function coefficient, which in this case is

$$\begin{aligned} b_I= n_I+ n_{I+1}~. \end{aligned}$$
(16)

Of course, we can rewrite (15) as

$$\begin{aligned} \left| \frac{\varLambda _I}{\mu }\right| = \mathrm {e}^{-2\pi \,\frac{\zeta _I}{b_I}} \end{aligned}$$
(17)

which implies that

$$\begin{aligned} \frac{\zeta _I}{b_I}>0~. \end{aligned}$$
(18)

Since for the quiver represented in Fig. 1, all \(b_I\) are positive (see (16)), we deduce that

$$\begin{aligned} \zeta _I>0~. \end{aligned}$$
(19)

Once the 4d Coulomb vev’s are given, the 2d Coulomb branch is completely lifted except for a finite number of discrete vacua. These are found by extremizing the twisted chiral superpotential \({\mathcal {W}}\), i.e. they are solutions of the twisted chiral ring equations [23, 24]

$$\begin{aligned} \exp \left( \frac{\partial {{\mathcal {W}}}}{\partial \sigma ^{(I)}_s}\right) =1~. \end{aligned}$$
(20)

In order to make contact with the partition of the vev’s in (2), we solve (20) about the following classical vacuum:

$$\begin{aligned} \sigma ^{(I)}_{\text {cl}} = {{\mathcal {A}}}_1\oplus {{\mathcal {A}}}_2\oplus \cdots \oplus {{\mathcal {A}}}_I ~. \end{aligned}$$
(21)

Once the solutions to the twisted chiral ring equations are obtained (order by order in the low-energy scales of the 2d/4d theories), we evaluate the effective twisted chiral superpotential \({\mathcal {W}}\) on this particular solution, and verify that the non-perturbative contributions exactly coincide with the \({{\mathcal {W}}}_{\text {inst}}\) calculated using localization. In essence, this match provides a one-to-one map between \(\frac{1}{2}\)-BPS defects in the 4d gauge theory and massive vacua in the coupled 2d/4d gauge theory.

2.3 A contour from the twisted chiral ring

We now consider in detail the case \(M=4\) corresponding to the quiver in Fig. 2. This is the simplest example that is general enough to contain all relevant features of a generic linear quiver, and thus it serves as a prototypical case.

Fig. 2
figure 2

The 4-node linear quiver that corresponds to the partition \([n_1, n_2, n_3, n_4]\)

Full size image

The twisted chiral ring Eq. (20) can be compactly written in terms of a characteristic gauge polynomial for each U\((r_I)\) node, given by

$$\begin{aligned} {\mathcal {Q}}_{I}(z) = \prod _{s=1}^{r_{I}} (z - \sigma ^{(I)}_s)~, \end{aligned}$$
(22)

and the characteristic polynomial of the 4d SU(N) node, namely

$$\begin{aligned} {\mathcal {P}}_N(z) =z^N +\sum _{i=2}^N (-1)^{k}\, u_k \, z^{N-k} ~. \end{aligned}$$
(23)

Here \(u_k\) are the gauge invariant coordinates on the moduli space, which can be calculated at weak coupling using localization methods [25,26,27,28,29]. In terms of these polynomials, the twisted chiral equations (20) become [10]

$$\begin{aligned} \begin{aligned} {{\mathcal {Q}}}_{2}(\sigma ^{(1)}_s)&= \varLambda _1^{n_1+n_2}~,\\ {{\mathcal {Q}}}_{{3}}(\sigma ^{(2)}_t)&= (-1)^{n_1} \,\varLambda _{2}^{n_2+n_3}\,{{\mathcal {Q}}}_{{1}}(\sigma ^{(2)}_t)~,\\ {\mathcal {P}}_N(\sigma ^{(3)}_u)&=(-1)^{n_1+n_2}\bigg (\varLambda _{3}^{n_3+n_4}\, {{\mathcal {Q}}}_{{2}}(\sigma ^{(3)}_u) \\&\quad +\frac{\varLambda _{\text {4d}}^{2N}}{\varLambda _{3}^{n_3+n_4}\, {{\mathcal {Q}}}_{{2}}(\sigma ^{(3)}_u)}\bigg )~, \end{aligned} \end{aligned}$$
(24)

for \(s\in {{{\mathcal {N}}}}_1\), \(t\in {{{\mathcal {N}}}}_1\cup {{{\mathcal {N}}}}_2\), and \(u\in {{{\mathcal {N}}}}_1\cup {{{\mathcal {N}}}}_2 \cup {{{\mathcal {N}}}}_3\), respectively. We look for solutions of these equations that are of the form

$$\begin{aligned} \sigma ^{(I)}_{\star } = \sigma ^{(I)}_{\text {cl}} + \delta \sigma ^{(I)}~, \end{aligned}$$
(25)

where the classical part is as in (21) for \(I=1,2,3\). A detailed derivation of the solution at the one-instanton level is presented in Appendix B. Here we merely write the expressions for the non-vanishing first-order corrections, that are

$$\begin{aligned} \delta \sigma ^{(1)}_s&=\frac{\varLambda _1^{n_1+n_2}}{\prod _{r\in {\widehat{{\mathcal {N}}}}_1\cup {\mathcal {N}}_2}(a_s-a_r)} \nonumber \\&\quad +\frac{(-1)^{n_2}\varLambda _{\text {4d}}^{2N}}{\varLambda _1^{n_1+n_2}\varLambda _2^{n_2+n_3} \varLambda _3^{n_3+n_4} \prod _{r\in {\mathcal {N}}_4\cup {\widehat{{\mathcal {N}}}}_1}(a_s-a_r)}~, \nonumber \\ \delta \sigma ^{(2)}_s&=\,\delta \sigma ^{(3)}_s = \frac{(-1)^{n_2} \varLambda _{\text {4d}}^{2N}}{\varLambda _1^{n_1+n_2}\varLambda _2^{n_2+n_3}\varLambda _3^{n_3+n_4} \prod _{r\in {\mathcal {N}}_4\cup {\widehat{{\mathcal {N}}}}_1}(a_s-a_r)} \end{aligned}$$
(26)

for \(s\in {\mathcal {N}}_1\),

$$\begin{aligned} \delta \sigma ^{(2)}_t=\frac{(-1)^{n_1}\varLambda _2^{n_2+n_3}}{ \prod _{r\in {\widehat{{\mathcal {N}}}}_2\cup {\mathcal {N}}_3}(a_t-a_r)} \end{aligned}$$
(27)

for \(t\in {\mathcal {N}}_2\), and

$$\begin{aligned} \delta \sigma ^{(3)}_u=\frac{(-1)^{n_1+n_2}\varLambda _3^{n_3+n_4}}{ \prod _{r\in {\widehat{{\mathcal {N}}}}_3\cup {\mathcal {N}}_4}(a_u-a_r)} \end{aligned}$$
(28)

for \(u\in {\mathcal {N}}_3\). In these formulas, the symbol \({\widehat{{\mathcal {N}}}}_I\) means that one has to omit from the set \({\mathcal {N}}_I\) the indices that would yield a vanishing denominator.

In [10] it was shown that

$$\begin{aligned} \mathrm {Tr}\,\sigma ^{(I)}_\star = \frac{1}{b_I}\varLambda _I \frac{\partial {\mathcal {W}}}{\partial {\varLambda _I}}\bigg |_{\sigma _\star }~. \end{aligned}$$
(29)

Integrating in this relation, one can obtain the twisted superpotential in the chosen vacuum, which in the one-instanton approximation is

$$\begin{aligned} {\mathcal {W}}\big |_{\sigma _\star }\!= & {} \!\sum _{s\in {\mathcal {N}}_1} \frac{\varLambda _1^{n_1+n_2}}{ \prod _{r\in {\widehat{{\mathcal {N}}}}_1\cup {\mathcal {N}}_2}(a_s-a_r) }\nonumber \\&+ \sum _{t\in {\mathcal {N}}_2}\frac{(-1)^{n_1}\varLambda _2^{n_2+n_3}}{ \prod _{r\in {\widehat{{\mathcal {N}}}}_2\cup {\mathcal {N}}_3}(a_t-a_r) }\nonumber \\&+ \sum _{u\in {\mathcal {N}}_3}\frac{(-1)^{n_1+n_2}\varLambda _3^{n_3+n_4}}{ \prod _{r\in {\widehat{{\mathcal {N}}}}_3\cup {\mathcal {N}}_4}(a_u-a_r) }\nonumber \\&+\sum _{s\in {\mathcal {N}}_1}\frac{(-1)^{n_2+1}\varLambda _{\text {4d}}^{2N}}{\varLambda _1^{n_1+n_2}\varLambda _2^{n_2+n_3}\varLambda _3^{n_3+n_4} \prod _{r\in {\mathcal {N}}_4\cup {\widehat{{\mathcal {N}}}}_1}(a_s - a_r)}. \nonumber \\ \end{aligned}$$
(30)

We now compare this expression with the result of the localization analysis at the one ramified instanton level. From (8) and (9), specified to the partition \([n_1,\ldots ,n_4]\), we find

$$\begin{aligned} Z_{1-\text {inst}}&= -\sum _{I=1}^4 q_I\! \int \!\frac{d\chi _I}{2\pi \mathrm {i}}\, \frac{1}{\epsilon _1}\prod _{s\in {\mathcal {N}}_I} \frac{1}{\left( a_{s}-\chi _I + \frac{1}{2} (\epsilon _1 + {\hat{\epsilon }}_2)\right) }\nonumber \\&\quad \times \prod _{t\in {\mathcal {N}}_{I+1}}\frac{1}{\left( \chi _I - a_{t} + \frac{1}{2} (\epsilon _1 + {\hat{\epsilon }}_2)\right) }. \end{aligned}$$
(31)

In view of the prescription (10), it is clear that the number of poles that contribute to a given \(\chi _I\)-integral depends upon whether we close the contour in the upper or lower half-planes. Closing the contour in the upper half-plane leads to \(n_I\) poles that contribute, while closing the contour in the lower half-plane leads to \(n_{I+1}\) poles that contribute. Furthermore, the mass dimensions of each \(q_I\) is fixed to be \(n_I+n_{I+1}\), since the partition function itself is dimensionless. These two facts immediately help us in relating the localization results with the chiral ring analysis.Footnote 2 Indeed, the dimensional argument allows us to express the ramified instanton counting parameters in terms of the 2d effective scales as follows [10] Footnote 3:

$$\begin{aligned} \begin{aligned} q_1&=(-1)^{n_1}\varLambda _1^{n_1+n_2}~,\\ q_2&=(-1)^{n_1+n_2}\varLambda _2^{n_2+n_3}~,\\ q_3&=(-1)^{n_1+n_2+n_3}\varLambda _3^{n_3+n_4}~,\\ q_4&=\frac{(-1)^{n_2+n_4}\varLambda _{\text {4d}}^{2N}}{\varLambda _1^{n_1+n_2}\varLambda _2^{n_2+n_3}\varLambda _3^{n_3+n_4}}~. \end{aligned} \end{aligned}$$
(32)

Using (15), the first three \(q_I\) can also be written in terms of the bare complexified FI parameters \(\tau _I\) of the three 2d nodes as

$$\begin{aligned} \begin{aligned} q_1&=\mathrm {e}^{2 \pi \mathrm {i}\, \tau _1}\,(-1)^{n_1} \,\mu ^{n_1+n_2}~,\\ q_2&=\mathrm {e}^{2 \pi \mathrm {i}\, \tau _2}\,(-1)^{n_1+n_2}\,\mu ^{n_2+n_3}~,\\ q_3&=\mathrm {e}^{2 \pi \mathrm {i}\, \tau _3}\,(-1)^{n_1+n_2+n_3}\,\mu ^{n_3+n_4}~. \end{aligned} \end{aligned}$$
(33)

Once the identification (32) is made, we can match the number and the structure of the terms that appear in (30) by closing the contours for \(\chi _1\), \(\chi _2\) and \(\chi _3\) in the upper half-plane, and the contour of \(\chi _4\) in the lower half-plane. We denote this choice of contours as \(\big (\chi _1|_+,\chi _2|_+,\chi _3|_+,\chi _4|_-\big )\). Indeed, computing the corresponding residues and extracting the one-instanton twisted superpotential from (11) and (31), we find

$$\begin{aligned} \begin{aligned} {\mathcal {W}}_{1-\text {inst}}&=\sum _{s\in {\mathcal {N}}_1}\frac{(-1)^{n_1}q_1}{ \prod _{r\in {\widehat{{\mathcal {N}}}}_1\cup {\mathcal {N}}_2}(a_s-a_r)}\\&\quad +\sum _{t\in {\mathcal {N}}_2}\frac{(-1)^{n_2}q_2}{ \prod _{r\in {\widehat{{\mathcal {N}}}}_2\cup {\mathcal {N}}_3}(a_t-a_r)}\\&\quad +\sum _{u\in {\mathcal {N}}_3}\frac{(-1)^{n_3}q_3}{ \prod _{r\in {\widehat{{\mathcal {N}}}}_3\cup {\mathcal {N}}_4}(a_u-a_r)}\\&\quad +\sum _{s\in {\mathcal {N}}_1} \frac{(-1)^{n_4+1}q_4}{\prod _{r\in {\mathcal {N}}_4\cup {\widehat{{\mathcal {N}}}}_1}(a_s-a_r)} \end{aligned} \end{aligned}$$
(34)

which, term by term, exactly matches the superpotential (30) obtained by solving the twisted chiral ring equations.

3 2d Seiberg duality

The notion of Seiberg duality in 4d gauge theories [18] can be generalized to two dimensions (see for example [19]). Thus, by applying 2d Seiberg duality it is possible to obtain distinct quiver theories in the UV that have the same IR behaviour.

Let us first consider the simplest case, shown in Fig. 3.

Fig. 3
figure 3

A single 2d gauge node of rank r with \(N_F\) fundamental and \(N_A\) anti-fundamental flavours attached to it

Full size image

This is a 2d U(r) gauge theory with \(N_F\) fundamental flavours and \(N_A\) anti-fundamental flavours. For definiteness we take \(N_F > N_A\), and call this system “theory A”. Its classical twisted superpotential is simply

$$\begin{aligned} {\mathcal {W}}^{\text {A}}_{\text {cl}}=2\pi \mathrm {i}\tau \,\mathrm {Tr}\,\sigma ~. \end{aligned}$$
(35)

We now perform a Seiberg duality, and obtain “theory B”, which is described by the quiver in Fig. 4.

Fig. 4
figure 4

The theory obtained after a 2d Seiberg duality on the gauge node in Fig. 3

Full size image

Under the duality, the rank of the gauge group changes as

$$\begin{aligned} r\longrightarrow r'&=\text {max}(N_F,N_A)-r =N_F-r ~, \end{aligned}$$
(36)

and the roles of the fundamental and anti-fundamental flavours are exchanged as denoted by the reversal of the arrows. The classical twisted superpotential for “theory B” is Footnote 4

$$\begin{aligned} {\mathcal {W}}^{\text {B}}_{\text {cl}}=-2\pi \mathrm {i}\,\tau \,\mathrm {Tr}\,\sigma '+2\pi \mathrm {i}\,\tau \sum _{f=1}^{N_F}m_f \end{aligned}$$
(37)

where \(\sigma '\) denotes the twisted chiral superfield in the vector multiplet of the dualized node and \(m_f\) are the twisted masses that completely break the flavour symmetry to its Cartan subgroup.

We now apply this basic duality rule to the quiver theories that describe surface operators. Since for a given 2d node the flavour symmetry is realized by the adjacent nodes, we can encounter three kinds of configurations. The first one is when we dualize a gauge node with both fundamental and anti-fundamental fields in an oriented sequence, as shown in Fig. 5.

Fig. 5
figure 5

2d Seiberg duality on a node with both fundamental and anti-fundamental matter with \(r_2>r_1\). The rank of the dualized node is max\((r_1, r_2)-r = r_2-r\). The blue and red colours indicate the node before and after the duality

Full size image

Before the duality, the classical superpotential for the three relevant nodes is

$$\begin{aligned} {\mathcal {W}}^{\text {A}}_{\text {cl}}&= \cdots +2\pi \mathrm {i}\,\tau _{1}\,\mathrm {Tr}\,\sigma ^{(1)} +2\pi \mathrm {i}\,\tau \,\mathrm {Tr}\,\sigma \nonumber \\&\quad +2\pi \mathrm {i}\,\tau _{2}\,\mathrm {Tr}\,\sigma ^{(2)} +\cdots ~, \end{aligned}$$
(38)

while, after duality, it becomes

$$\begin{aligned} {\mathcal {W}}^{\text {B}}_{\text {cl}}&= \cdots +2\pi \mathrm {i}\,\tau _{1}\,\mathrm {Tr}\,\sigma ^{(1)} -2\pi \mathrm {i}\,\tau \,\mathrm {Tr}\,{\sigma '}\nonumber \\&\quad +2\pi \mathrm {i}\,(\tau _{2}+\tau )\,\mathrm {Tr}\,\sigma ^{(2)} +\cdots ~. \end{aligned}$$
(39)

Here we have taken into account the fact that the role of the twisted masses for the dualized node is played by the \(\sigma \)-variables of the \(r_2\) node. This explains why the FI parameter \(\tau _2\) is shifted by \(\tau \).

The second possibility is when we dualize a node with only fundamental matter, as shown in Fig. 6. In this case the classical superpotential before the duality is still given by (38), but after the duality it becomes

$$\begin{aligned} {\mathcal {W}}^{\text {B}}_{\text {cl}}&= \cdots +2\pi \mathrm {i}\, (\tau _{1}+\tau )\,\mathrm {Tr}\,\sigma ^{(1)} -2\pi \mathrm {i}\,\tau \,\mathrm {Tr}\,{\sigma '}\nonumber \\&\quad +2\pi \mathrm {i}\,(\tau _{2}+\tau )\,\mathrm {Tr}\,\sigma ^{(2)} +\cdots \end{aligned}$$
(40)

because both adjacent nodes provide fundamental matter for the dualized node, and hence both FI parameters \(\tau _1\) and \(\tau _2\) get shifted by \(\tau \).

Fig. 6
figure 6

2d Seiberg duality on a node with only chiral fundamental matter realized by adjacent 2d gauge nodes. In this case there are no mesonic fields introduced in this case

Full size image

In the third possibility, we dualize a node that has only anti-fundamental matter as shown in Fig. 7. In this case the classical superpotential before the duality is given again by (38), but after the duality it becomes

$$\begin{aligned} {\mathcal {W}}^{\text {B}}_{\text {cl}}&= \cdots +2\pi \mathrm {i}\,\tau _{1}\,\mathrm {Tr}\,\sigma ^{(1)} -2\pi \mathrm {i}\,\tau \,\mathrm {Tr}\,{\sigma '}\nonumber \\&\quad +2\pi \mathrm {i}\,\tau _{2}\,\mathrm {Tr}\,\sigma ^{(2)} +\cdots \end{aligned}$$
(41)

with no shifts in \(\tau _1\) and \(\tau _2\) since the dualized node has no fundamental matter.

Fig. 7
figure 7

2d Seiberg duality on a node with only anti-chiral fundamental matter realized by adjacent 2d gauge nodes. There are no mesonic fields introduced in this case

Full size image

4 Relating quivers and contours

In this section we discuss different 2d/4d theories related by Seiberg duality to the oriented quiver represented in Fig. 2. To any of these theories we can associate a system of twisted chiral ring equations that are distinct from the ones we have discussed in Sect. 2.3. However, being related by Seiberg duality, there is a simple one-to-one map among them and their solutions. Then, a natural question arises: how is this duality map reflected on the localization side?

To answer this question, consider again the oriented quiver of Fig. 2, which we now denote by \(Q_0\). From it we can generate equivalent quivers by dualizing any of the 2d nodes. We first carry out a very specific sequence of dualities that are shown in Fig. 8: at each step of the duality chain, the node being dualized has only fundamental matter. Therefore, Seiberg duality always acts as in (40).Footnote 5

For each quiver in the chain, we can proceed as we did in Sect. 2.3 for \(Q_0\). We integrate out the matter multiplets to obtain the effective twisted chiral superpotential, derive from it the twisted chiral ring equations, solve them about a particular massive vacuum order by order in the strong coupling scales, evaluate the superpotential on the corresponding vacuum and finally compare the result with the ramified instanton calculation with a specific integration contour for the \(\chi _I\) variables. In this program, the choice of the classical vacuum is the first important piece of information which we have to provide.

4.1 Classical vacuum

The classical twisted superpotential for the quiver \(Q_0\) is

$$\begin{aligned} {\mathcal {W}}_{\text {cl}}^{\,Q_0}=2\pi \mathrm {i}\,\tau _1\, \text {Tr}\,\sigma ^{(1)}+2\pi \mathrm {i}\,\tau _2\,\text {Tr}\,\sigma ^{(2)} +2\pi \mathrm {i}\,\tau _3\,\text {Tr}\,\sigma ^{(3)}~. \end{aligned}$$
(42)

Applying to it the duality rule (40), we obtain the classical superpotential for the quiver \(Q_1\). With a further duality we obtain the classical superpotential for the quiver \(Q_2\) and so on along the duality chain of Fig. 8.

Fig. 8
figure 8

A sequence of Seiberg dualities obtained by dualizing the node that has only fundamental flavours attached to it at each step. The node that is dualized is indicated by the blue arrow. The reason why in the list of names for the quivers we skipped \(Q_3\) will become clear later on

Full size image

Explicitly these superpotentials are Footnote 6:

$$\begin{aligned} {\mathcal {W}}_{\text {cl}}^{\,Q_1}&=-2\pi \mathrm {i}\,\tau _1\,\text {Tr}\, \sigma ^{(1)}+2\pi \mathrm {i}\,(\tau _1+\tau _2)\, \text {Tr}\,\sigma ^{(2)}\nonumber \\&\quad +2\pi \mathrm {i}\,\tau _3\,\text {Tr}\,\sigma ^{(3)}~,\end{aligned}$$
(43)
$$\begin{aligned} {\mathcal {W}}_{\text {cl}}^{\,Q_2}&=2\pi \mathrm {i}\,\tau _2\,\text {Tr}\,\sigma ^{(1)} -2\pi \mathrm {i}\,(\tau _1+\tau _2)\,\text {Tr}\,\sigma ^{(2)}\nonumber \\&\quad + 2\pi \mathrm {i}\,(\tau _1+\tau _2+\tau _3)\,\text {Tr}\,\sigma ^{(3)}~, \end{aligned}$$
(44)
$$\begin{aligned} {\mathcal {W}}_{\text {cl}}^{\,Q_4}&=2\pi \mathrm {i}\,\tau _2\,\text {Tr}\, \sigma ^{(1)}+2\pi \mathrm {i}\,\tau _3\, \text {Tr}\,\sigma ^{(2)}\nonumber \\&\quad -2\pi \mathrm {i}\,(\tau _1+\tau _2+\tau _3)\,\text {Tr}\,\sigma ^{(3)}~,\end{aligned}$$
(45)
$$\begin{aligned} {\mathcal {W}}_{\text {cl}}^{\,Q_5}&=-2\pi \mathrm {i}\,\tau _2\,\text {Tr}\,\sigma ^{(1)} +2\pi \mathrm {i}\,(\tau _2+\tau _3)\,\text {Tr}\,\sigma ^{(2)}\nonumber \\&\quad - 2\pi \mathrm {i}\,(\tau _1+\tau _2+\tau _3)\,\text {Tr}\,\sigma ^{(3)}~,\end{aligned}$$
(46)
$$\begin{aligned} {\mathcal {W}}_{\text {cl}}^{\,Q_6}&=2\pi \mathrm {i}\,\tau _3\,\text {Tr}\,\sigma ^{(1)}- 2\pi \mathrm {i}\,(\tau _2+\tau _3)\,\text {Tr}\,\sigma ^{(2)}\nonumber \\&\quad -2\pi \mathrm {i}\,\tau _1\text {Tr}\,\sigma ^{(3)}~,\end{aligned}$$
(47)
$$\begin{aligned} {\mathcal {W}}_{\text {cl}}^{\,Q_7}&=-2\pi \mathrm {i}\,\tau _3\,\text {Tr}\, \sigma ^{(1)}-2\pi \mathrm {i}\,\tau _2\, \text {Tr}\,\sigma ^{(2)}\nonumber \\&\quad -2\pi \mathrm {i}\,\tau _1\,\text {Tr}\,\sigma ^{(3)}~. \end{aligned}$$
(48)

From these expressions we can read the map between the FI parameters of any quiver and those of the initial quiver \(Q_0\). For example, for \(Q_1\) we have

$$\begin{aligned} \begin{aligned} \tau _1^{Q_1} = -\tau _1~,~~ \tau _2^{Q_1} = \tau _1 + \tau _2~,~~ \tau _3^{Q_1} = \tau _3~, \end{aligned} \end{aligned}$$
(49)

while for the quiver \(Q_2\) we have

$$\begin{aligned} \tau _1^{Q_2} = \tau _2~,~~ \tau _2^{Q_2} = -\tau _1 - \tau _2~ , ~~ \tau _3^{Q_2} = \tau _1+\tau _2+\tau _3~. \end{aligned}$$
(50)

The next step is to identify the classical vacuum for each quiver. We already know that for \(Q_0\) the vacuum that respects the partition \([n_1, \ldots , n_4]\) associated to the surface operator, is (see (21))

$$\begin{aligned} \sigma ^{(1)}_{\text {cl}} = {{\mathcal {A}}}_1~,~~ \sigma ^{(2)}_{\text {cl}} = {{\mathcal {A}}}_1\oplus {{\mathcal {A}}}_2~,~~ \sigma ^{(3)}_{\text {cl}} = {{\mathcal {A}}}_1\oplus {{\mathcal {A}}}_2\oplus {{\mathcal {A}}}_3~. \nonumber \\ \end{aligned}$$
(51)

Since Seiberg duality is an exact infrared equivalence, the classical superpotentials of two dual quivers, evaluated in the respective vacua, should be identical. This requirement immediately fixes the structure of the classical vacuum for all quivers. For instance, for \(Q_1\) one can check that

$$\begin{aligned} \sigma ^{(1)}_{\text {cl}} = {{\mathcal {A}}}_2~,~~ \sigma ^{(2)}_{\text {cl}} = {{\mathcal {A}}}_1\oplus {{\mathcal {A}}}_2~,~~ \sigma ^{(3)}_{\text {cl}} = {{\mathcal {A}}}_1\oplus {{\mathcal {A}}}_2\oplus {{\mathcal {A}}}_3~, \nonumber \\ \end{aligned}$$
(52)

leads to the desired match; indeed

$$\begin{aligned} {{{\mathcal {W}}}}_{\text {cl}}^{\,Q_1}= & {} -2\pi \mathrm {i}\,\tau _1 \,\mathrm {Tr}\,{{\mathcal {A}}}_2 + 2\pi \mathrm {i}\,(\tau _1+\tau _2)\, \big (\mathrm {Tr}\,{{\mathcal {A}}}_1+\mathrm {Tr}\,{{\mathcal {A}}}_2\big )\nonumber \\&+ 2\pi \mathrm {i}\,\tau _3\, \big (\mathrm {Tr}\,{{\mathcal {A}}}_1+\mathrm {Tr}\,{{\mathcal {A}}}_2 +\mathrm {Tr}\,{{\mathcal {A}}}_3\big )\nonumber \\= & {} +2\pi \mathrm {i}\,\tau _1 \,\mathrm {Tr}\,{{\mathcal {A}}}_1 + 2\pi \mathrm {i}\,\tau _2\, \big (\mathrm {Tr}\,{{\mathcal {A}}}_1+\mathrm {Tr}\,{{\mathcal {A}}}_2\big ) \nonumber \\&+ 2\pi \mathrm {i}\,\tau _3\,\big (\mathrm {Tr}\,{{\mathcal {A}}}_1+\mathrm {Tr}\,{{\mathcal {A}}}_2+ \mathrm {Tr}\,{{\mathcal {A}}}_3\big )\nonumber \\= & {} {{{\mathcal {W}}}}_{\text {cl}}^{\,Q_0} ~. \end{aligned}$$
(53)

This calculation can be easily generalized to all other quivers in the duality chain and the results are summarized in Table 1.

Table 1 For each of the quivers in Fig. 8, we list the classical expectation values of the twisted chiral fields in each of the three 2d nodes. Using them in the classical twisted chiral superpotentials given in (43), one finds identical expressions
Full size table

4.2 The q vs \(\varLambda \) map

The next necessary ingredient is the relation between the ramified instanton parameters \(q_I\) and the strong coupling scales \(\varLambda _I^{Q_i}\) of a given quiver.

For the first quiver \(Q_0\), the q vs \(\varLambda \) map was already derived and written in (32). If we now consider the second quiver \(Q_1\), from the running of the FI parameters we find

$$\begin{aligned} \begin{aligned} \big (\varLambda ^{Q_1}_1\big )^{-n_1-n_2} \,&=\, \mathrm {e}^{2\pi \mathrm {i}\, \tau _1^{Q_1}}\,\mu ^{-n_1-n_2}~,\\ \big (\varLambda ^{Q_1}_2\big )^{n_1+2n_2+n_3} \,&=\, \mathrm {e}^{2\pi \mathrm {i}\, \tau _2^{Q_1}}\,\mu ^{n_1+2n_2+n_3}~,\\ \big (\varLambda ^{Q_1}_3\big )^{n_3+n_4}\,&=\, \mathrm {e}^{2\pi \mathrm {i}\, \tau _3^{Q_1}}\,\mu ^{n_3+n_4}~. \end{aligned} \end{aligned}$$
(54)

Using the relations (49) and the definitions (33), it is easy to obtain (up to inessential signs) the q vs \(\varLambda \) map in this case, namely

$$\begin{aligned} \begin{aligned} q_1&\sim \big (\varLambda ^{Q_1}_1\big )^{n_1+n_2}~,\\ q_2&\sim \frac{\big (\varLambda ^{Q_1}_2\big )^{n_1+2n_2+n_3}}{\big (\varLambda ^{Q_1}_1\big )^{n_1+n_2}}~,\\ q_3&\sim \big (\varLambda ^{Q_1}_3\big )^{n_3+n_4}~. \end{aligned} \end{aligned}$$
(55)

Applying the same procedure to \(Q_2\) and using (50), we find

$$\begin{aligned} \begin{aligned} q_1&\sim \frac{\big (\varLambda ^{Q_2}_2\big )^{n_1+2n_2+n_3}}{\big (\varLambda ^{Q_2}_1\big )^{n_2+n_3}}~,\\ q_2&\sim \big (\varLambda ^{Q_2}_1\big )^{n_2+n_3}~,\\ q_3&\sim \frac{\big (\varLambda ^{Q_2}_3\big )^{N+n_2+n_3}}{\big (\varLambda ^{Q_2}_2\big )^{n_1+2n_2+n_3}}~. \end{aligned} \end{aligned}$$
(56)

Repeating this analysis for all quivers of Fig. 8, we obtain the results collected in Table 2.

Table 2 For each quiver of Fig. 8, we list the q vs \(\varLambda \) map (up to sign factors, which can be found in Appendix B). The exponent of each strong coupling scale is determined by the number of effective flavours at that node in the quiver and is related to the \(\beta \)-function coefficient of the corresponding FI parameter
Full size table

We finally recall that the following relation

$$\begin{aligned} q_4 \sim \frac{\varLambda _{\text {4d}}^{2N}}{q_1\,q_2\,q_3} \end{aligned}$$
(57)

holds for all quivers.

From Table 2, we observe that except for the oriented quivers \(Q_0\) and \(Q_7\), in all other cases the contributions of a single ramified instanton can be proportional to a ratio of strong coupling scales. It would be interesting to understand the origin of this fact from the perspective of vortex solutions in 2d quivers with bi-fundamental matter. However, for our present purposes it is important to keep in mind that the ramified instanton partition function is a power series in \(q_I\). This means that, except for the quivers \(Q_0\) and \(Q_7\), we are forced to have some hierarchy among the scales \(\varLambda _I^{Q_i}\) in order for the q vs \(\varLambda \) map to be consistent with the power series expansion of the ramified instanton partition function. For instance for the quiver \(Q_1\), we see from Table 2 that if we want that both \(q_1\) and \(q_2\) be “small”, it is necessary to have

$$\begin{aligned} 1 > \left| \frac{\varLambda ^{Q_1}_1}{\mu } \right| ^{n_1+n_2} \!\gg \left| \frac{\varLambda ^{Q_1}_2}{\mu } \right| ^{n_1+2n_2+n_3} ~. \end{aligned}$$
(58)

Using (54) and the fact that the \(\beta \)-function coefficient of the first node is negative, we can easily see that (58) is equivalent to

$$\begin{aligned} 0<-\zeta _1^{Q_1} \ll \zeta _2^{Q_1}~. \end{aligned}$$
(59)

Notice that this inequality follows from the duality relations (49): indeed, \(\zeta _1^{Q_1}=-\zeta _1\) and \(\zeta _2^{Q_1}=\zeta _1+\zeta _2\), with \(\zeta _I>0\) as indicated in (19).

In a similar way, for quiver \(Q_2\) we see from Table 2 that in order for the instanton weights \(q_I\) to be “small”, we must have

$$\begin{aligned} 1 > \left| \frac{\varLambda ^{Q_2}_1}{\mu } \right| ^{n_2+n_3} \!\gg \left| \frac{\varLambda ^{Q_2}_2}{\mu } \right| ^{n_1+2n_2+n_3} \!\gg \left| \frac{\varLambda ^{Q_2}_3}{\mu } \right| ^{N+n_2+n_3}, \nonumber \\ \end{aligned}$$
(60)

which, taking into account the signs of the \(\beta \)-function coefficients, in this case implies that

$$\begin{aligned} 0<\zeta _1^{Q_2} \ll -\zeta _2^{Q_2} \ll \zeta _3^{Q_2}~. \end{aligned}$$
(61)

Again we can check that this hierarchy just follows from the duality relations (50), since \(\zeta _1^{Q_2}=\zeta _2\), \(\zeta _2^{Q_2}=-\zeta _1-\zeta _2\) and \(\zeta _3^{Q_2}=\zeta _1+\zeta _2+\zeta _3\), with \(\zeta _I>0\).

We can repeat this analysis for all linear quivers of the sequence, and always find the same pattern: when a hierarchy of scales is needed in order to have a meaningful ramified instanton expansion, this is automatically guaranteed by the duality relations among the real FI parameters of the various quivers. Moreover, the 4d low-energy scale \(\varLambda _{\text {4d}}\) is always the smallest scale in view of (57).

4.3 Contour prescriptions for dual quivers

We now address the question of how the non-perturbative superpotential associated to each quiver can be obtained from the ramified instanton partition function (8) using a suitable contour prescription for the \(\chi _I\)-integrals. In Sect. 2.3 we answered this question for the oriented quiver \(Q_0\) by comparing each term of the solution of the chiral ring equations with the localization results. Here we provide a general argument that allows one to derive the appropriate contour prescription for any quiver of the duality chain, without explicitly solving the twisted chiral ring equations and integrating them in. We perform a detailed analysis at the one-instanton level, but our conclusions are valid also at higher instantons.

Let us first consider only the three 2d nodes and neglect for the moment the contribution of the 4d node by setting \(\varLambda _{\text {4d}}\rightarrow 0\) and hence, according to (57), \(q_4\rightarrow 0\). Using the partition function (31), the one-instanton superpotential in this case can be written as

$$\begin{aligned} {{{\mathcal {W}}}}_{\text {1-inst}}= \sum _{I=1}^3 q_I\, w_I \end{aligned}$$
(62)

where

$$\begin{aligned} w_I= & {} - \lim _{\epsilon _1,\hat{\epsilon }_2\rightarrow 0}\int \!\frac{d\chi _I}{2\pi \mathrm {i}}\, \prod _{s\in \mathcal {N}_I} \frac{1}{\left( a_{s}-\chi _I + \frac{1}{2} (\epsilon _1 + \hat{\epsilon }_2)\right) }\nonumber \\&\times \prod _{t\in \mathcal {N}_{I+1}}\frac{1}{\left( \chi _I - a_{t} + \frac{1}{2} (\epsilon _1 + \hat{\epsilon }_2)\right) }~. \end{aligned}$$
(63)

From this we immediately see that \(w_I\) can have either \(n_I\) or \(n_{I+1}\) terms depending on whether the \(\chi _I\)-contour is closed in the upper or lower half plane, respectively. On the other hand, exploiting the relation [10]

$$\begin{aligned} \mathrm {Tr}\,\sigma ^{(I)}_{\star }= \mathrm {Tr}\,\big (\sigma ^{(I)}_{\text {cl}}+\delta \sigma ^{(I)}\big ) = \frac{1}{b_I}\varLambda _I \frac{\partial {{\mathcal {W}}}}{\partial {\varLambda _I}}\bigg |_{\sigma _\star }~, \end{aligned}$$
(64)

and the maps in Table 2, we can understand which type of ramified instantons contributes to each term proportional to \(\mathrm {Tr}\,\sigma ^{(I)}\). For example, for \(Q_0\) using the map (32), we find

$$\begin{aligned} \begin{aligned} \mathrm {Tr}\,\delta \sigma ^{(1)}&= q_1\, w_1~,\\ \mathrm {Tr}\,\delta \sigma ^{(2)}&= q_2\, w_2~,\\ \mathrm {Tr}\,\delta \sigma ^{(3)}&= q_3\, w_3~. \end{aligned} \end{aligned}$$
(65)

These relations establish a natural correspondence between the nodes of the quiver and the instanton counting parameters \(q_I\) and the corresponding \(\chi _I\) fields for \(I=1,2,3\): indeed, the first node is associated to \(\chi _1\), the second node to \(\chi _2\) and the third node to \(\chi _3\). Furthermore, exploiting the fact that \(\delta \sigma ^{(I)}\) must have the same structure of the classical part \(\sigma ^{(I)}_{\text {cl}}\) and hence that their entries can only arise in any of the blocks that make up the rank of the corresponding 2d gauge node, we conclude that we have to close the integration contour in the upper-half plane for all \(\chi _I\), so that \(\mathrm {Tr}\,\delta \sigma ^{(1)}\) has \(n_1\) contributions, \(\mathrm {Tr}\,\delta \sigma ^{(2)}\) has \(n_2\) contributions and \(\mathrm {Tr}\,\delta \sigma ^{(3)}\) has \(n_3\) contributions. We indicate this choice of integration contour with the notation \(\big (\chi _1|_+,\chi _2|_+,\chi _3|_+\big )\). In this way we have retrieved the same contour prescription of Sect. 2.3, without explicitly solving the twisted chiral ring equations.

The same strategy can be used for the other quivers of the duality chain. Let us consider for example \(Q_1\). From (64) and the map (55), we find

$$\begin{aligned} \begin{aligned} \mathrm {Tr}\,\delta \sigma ^{(1)}&= q_1\, w_1-q_2\, w_2 ~,\\ \mathrm {Tr}\,\delta \sigma ^{(2)}&= q_2\, w_2 ~,\\ \mathrm {Tr}\,\delta \sigma ^{(3)}&= q_3\, w_3 ~. \end{aligned} \end{aligned}$$
(66)

In this case, the correspondence between the second node and \(\chi _2\) and between the third node and \(\chi _3\) is again obvious, but since now there are two \(w_I\) contributing to the first trace, we need to use the hierarchy of scales (58) to disentangle the linear combination. In particular we see that the contribution proportional to \(q_2\) is sub-dominant and thus can be neglected at leading order. This allows us to conclude that the first node must be unambiguously associated to \(\chi _1\). However, the number of terms contributing to \(\mathrm {Tr}\,\delta \sigma ^{(1)}\) must be \(n_2\), since for \(Q_1\) we have \(\sigma ^{(1)}_{\text {cl}}=\mathcal {A}_2\) (see (52)). Thus, the \(\chi _1\)-integral should be closed in the lower half-plane to provide this number of terms, while the integrations over \(\chi _2\) and \(\chi _3\) must be carried out in the upper half-plane as before. In conclusion, to \(Q_1\) we assign the contour prescription \(\big (\chi _1|_-,\chi _2|_+,\chi _3|_+\big )\). It can be checked that with this choice the localization results perfectly agree, term by term, with the solution of the appropriate chiral ring equations (see Appendix B for details).

Comparing \({\mathcal {W}}_{\text {cl}}^{\,Q_0}\) and \({\mathcal {W}}_{\text {cl}}^{\,Q_1}\) given in (42) and (43), we notice that an indication for the flipping of the \(\chi _1\) integration contour between \(Q_0\) and \(Q_1\) can be traced to the change in sign of the term containing \(\mathrm {Tr}\,\sigma ^{(1)}\), or equivalently to the change in sign of the \(\beta \)-function coefficient and of the FI parameter of the first node under the duality map from \(Q_0\) to \(Q_1\). We propose that this is in fact the rule, and that it is the sign of the \(\beta \)-function coefficient for a given node (or of its FI parameter) that determines whether the contour of integration for the corresponding \(\chi \) variable has to be closed in the upper or in the lower half-plane.

As a simple and non-trivial check of this proposal we consider the quiver \(Q_2\). Here, using the q vs \(\varLambda \) map of Table 2 into (64), we find

$$\begin{aligned} \begin{aligned} \mathrm {Tr}\,\delta \sigma ^{(1)}&= q_2\, w_2-q_1\, w_1~,\\ \mathrm {Tr}\,\delta \sigma ^{(2)}&= q_1\, w_1~,\\ \mathrm {Tr}\,\delta \sigma ^{(3)}&= q_3\, w_3~. \end{aligned} \end{aligned}$$
(67)

From the second and third relations respectively, we see that \(\chi _1\) is associated to the second node and \(\chi _3\) to the third node. To decide which \(\chi \)-variable is associated to the first node, we again exploit the hierarchy of scales (60), which for the case at hand implies that \(q_1\) is sub-dominant with respect to \(q_2\). Thus, the \(q_1\)-term in the first relation of (50) can be neglected at leading order, implying that \(\chi _2\) must be associated to the first node. Notice that it is the second node of \(Q_2\) that has a negative \(\beta \)-function, and hence a negative FI parameter, and so it is again \(\chi _1\) that has to be integrated in the lower half-plane. We then conclude that to the quiver \(Q_2\) we must assign the contour prescription \(\big (\chi _2|_+,\chi _1|_-,\chi _3|_+\big )\). A similar analysis can be done for all other quivers of the sequence in Fig. 8.

Let us now turn to the contour for the last integration variable \(\chi _4\). To specify it, we have to switch on the dynamics on the 4d node of the quiver, since the corresponding parameter \(q_4\) is non-zero only when \(\varLambda _{\text {4d}}\) is non-zero (see (57)). Thus, \(q_4\) and hence \(\chi _4\) cannot be associated to any of the 2d nodes and must be related to the 4d node. By observing the duality chain, we see that the third node, which is the only 2d node connected to the 4d node, is dualized precisely once. Until this point the 4d node provides fundamental matter to the third 2d node, while from this point on it provides anti-fundamental matter. Given that we know that for the initial quiver \(Q_0\) the variable \(\chi _4\) has to be integrated in the lower half-plane, we are naturally led to propose that the contour for \(\chi _4\) remains in the lower plane \((-)\) until the third node is dualized, i.e. for \(Q_0\), \(Q_1\) and \(Q_2\), and then it flips to the upper half-plane \((+)\), remaining unchanged for the rest of the duality chain, i.e. for \(Q_4\), \(Q_5\), \(Q_6\) and \(Q_7\). We have verified the validity of this proposal by explicitly solving the twisted chiral ring equations for all seven quivers to obtain the corresponding twisted superpotentials, and checking that these agree term by term with what the ramified instanton partition function yields with the proposed integration prescriptions (see Appendix B for details). Our results on the contour assignments for the various quivers are summarized in Table 3.Footnote 7

Table 3 For each quiver \(Q_i\) in Fig. 8, we list the signs of the \(\beta \)-function coefficients \(b_I^{Q_i}\) for the three 2d nodes, which are also the signs of the corresponding FI parameters \(\zeta _I^{Q_i}\). These signs determine whether the integration contour for the corresponding \(\chi \)-variable has to be closed in the upper (\(+\)) or lower (−) half-plane. The last column displays the contour prescription from which we can also read which \(\chi \)-variable is associated to which node of the quiver. The variable \(\chi _4\) is always the last one to be integrated
Full size table

4.4 The Jeffrey-Kirwan prescription for dual quivers

At one-instanton it is sufficient to specify whether the contours of integration for \(\chi _{I}\) are closed in the upper or lower half-planes to completely specify the prescription. However, at higher instantons this may be no longer sufficient since also the order in which the integrations are performed may become relevant to have a one-to-one correspondence between the terms appearing in the superpotential derived from the twisted chiral ring equations and the residues contributing in the localization integrals.

An elegant way to fully specify the contour of integration for all variables (including the order in which they are integrated) is using the Jeffrey-Kirwan (JK) residue prescription [20] (see also, for example, [7, 31, 32] for recent applications to gauge theories). The essential point of this prescription is that the set of poles chosen by a contour is completely specified by the so-called JK reference vector \(\eta \).

As we have seen before, for the oriented quiver \(Q_0\) the variable \(\chi _4\) associated to the 4d gauge node has to be integrated as the last one in the lower-half plane, while the variables \(\chi _1\), \(\chi _2\) and \(\chi _3\), associated to the first, second and third node respectively, have to be integrated in the upper-half plane but no particular order of integration is required in this case. This means that the JK vector for the quiver \(Q_0\) can be written as

$$\begin{aligned} \eta _{Q_0}=-\zeta _1\,\chi _1-\zeta _2\,\chi _2-\zeta _3\,\chi _3+\zeta _4\,\chi _4 \end{aligned}$$
(68)

where \(\zeta _I\), with \(I=1,2,3\), are the FI parameters of the three 2d nodes of the quiver and \(\zeta _4\) is a positive real number such that

$$\begin{aligned} \zeta _4~\gg ~\zeta _I \end{aligned}$$
(69)

for \(I=1,2,3\). As remarked in (19), the FI parameters are positive, so that, given our sign conventions, the vector (68) indeed selects a contour in the upper-half plane for \(\chi _I\) with \(I=1,2,3\). The JK prescription corresponding to (68) requires that these integrals are successively performed according to the magnitudes of \(\zeta _I\). However, the order of integration does not affect the final result, and thus this prescription always gives the correct answer no matter how the FI parameters are ordered. The inequality (69) implies, instead, that the integral over \(\chi _4\) is the last one to be performed and, because of the \(+\) sign in the last term of \(\eta _{Q_0}\), this integral must be computed along a contour in the lower-half plane.

Let us now consider the quiver \(Q_1\). In this case, the JK vector that selects the appropriate contour of integration can be written as

$$\begin{aligned} \begin{aligned} \eta _{Q_1}&=+\big |\zeta _1^{Q_1}\big |\,\chi _1-\big |\zeta _2^{Q_1}\big |\,\chi _2 -\big |\zeta _3^{Q_1}\big |\,\chi _3+\zeta _4\,\chi _4 \\&=-\zeta _1^{Q_1}\,\chi _1-\zeta _2^{Q_1}\,\chi _2-\zeta _3^{Q_1}\,\chi _3+\zeta _4\,\chi _4 \end{aligned} \end{aligned}$$
(70)

where \(\zeta _I^{Q_1}\), with \(I=1,2,3\), are the FI parameters of the the three 2d nodes of \(Q_1\) and \(\zeta _4\) is a positive number such that

$$\begin{aligned} \zeta _4~\gg ~\big |\zeta _I^{Q_1}\big |~. \end{aligned}$$
(71)

We recall that in the quiver \(Q_1\) the FI parameters satisfy the inequality (59). Consequently, the JK vector (70) implies that the integral over \(\chi _1\) must be computed in the lower-half plane before the integral over \(\chi _2\), which instead must be computed along a contour in the upper-half plane. The last integral is the one over \(\chi _4\) which must be computed along a contour in the lower half-plane. The order of integration over \(\chi _1\) and \(\chi _2\) is crucial at higher instantons to achieve a one-to-one correspondence between the superpotential obtained from the chiral ring equations and the one computed using the ramified instantons. Some details on this fact at the two-instanton level are provided in Appendix C.

For the quiver \(Q_2\) one can see that the appropriate integration contour corresponds to the following JK vector

$$\begin{aligned} \begin{aligned} \eta _{Q_2}&= -\big |\zeta _1^{Q_2}\big |\, \chi _2+\big |\zeta _2^{Q_2}\big |\, \chi _1 -\big |\zeta _3^{Q_2}\big |\, \chi _3+\zeta _4\, \chi _4\\&= -\zeta _1^{Q_2}\, \chi _2-\zeta _2^{Q_2}\, \chi _1 -\zeta _3^{Q_2}\, \chi _3+\zeta _4\, \chi _4 \end{aligned} \end{aligned}$$
(72)

where the FI parameters satisfy the inequality (61) and the last parameter \(\zeta _4\) is such that

$$\begin{aligned} \zeta _4~\gg ~\big |\zeta _I^{Q_2}\big |~. \end{aligned}$$
(73)

Using this, we can see a precise correlation with the prescription \(\big (\chi _2|_+,\chi _1|_-,\chi _3|_+,\chi _4|_-\big )\) which we discussed above for \(Q_2\). Notice that in this case the integrals are performed in a specific order, starting form \(\chi _2\) and finishing with \(\chi _4\). This order is essential at higher instantons to obtain a perfect match, term by term, between the results from the chiral ring equations and those from localization (see Appendix C for some details at the two-instanton level).

This procedure can be systematically applied to all quivers in the duality chain of Fig. 8, and the corresponding JK reference vectors are listed in Table 4.Footnote 8

Table 4 For each quiver we list the JK reference vector that picks the appropriate contour on the localization side. The parameter \(\zeta _4\) is always positive and bigger in magnitude than any of the FI parameters. If \(\zeta _I^{Q_i}>0\) the associated \(\chi \)-variable is integrated along a contour in the upper-half plane, while if \(\zeta _I^{Q_i}<0\) it is integrated in the lower-half plane, in agreement with the prescription in the last column of Table 3
Full size table

4.5 New quivers and the corresponding contours

The chain of Seiberg dualities shown in Fig. 8 is of a very special kind, since the 2d gauge node being dualized at each step always has only fundamental flavours attached to it. This ensures that the resulting quivers are always linear. We now relax this condition and consider an alternative duality chain with the same initial and final points, but in which we start by dualizing the second node of the quiver \(Q_0\) that has both fundamental and anti-fundamental flavours attached to it. This duality leads to the quiver \({\widehat{Q}}_{1}\) which contains a loop, as shown in Fig. 9. Proceeding all the way down as indicated in this figure, we encounter the quivers \(Q_2\) and \(Q_4\), which were also part of the earlier sequence, but we also find two new quivers, which we call \(Q_{3}\) and \({\widehat{Q}}_{5}\). The latter, like \({\widehat{Q}}_{1}\), contains a loop.

Fig. 9
figure 9

Another chain of dualities to proceed from \(Q_0\) to \(Q_7\)

Full size image

We can repeat the same analysis as before and derive the contour prescription for all quivers in this sequence, including the non-linear ones. The first step is obtaining the classical part of the superpotential. Starting from \({\mathcal {W}}_{\text {cl}}^{Q_0}\) given in (42) and applying the duality rule (39) to the second node, we find that the classical part of the superpotential for \({\widehat{Q}}_{1}\) is

$$\begin{aligned} \begin{aligned} {\mathcal {W}}_{\text {cl}}^{{\widehat{Q}}_{1}}&=2\pi \mathrm {i}\,\tau _1\, \text {Tr}\,\sigma ^{(1)}-2\pi \mathrm {i}\,\tau _2\,\text {Tr}\,\sigma ^{(2)}\\&\quad +2\pi \mathrm {i}\,(\tau _2+\tau _3)\,\text {Tr}\,\sigma ^{(3)}~. \end{aligned} \end{aligned}$$
(74)
Table 5 For the quivers \({\widehat{Q}}_{1}\), \(Q_{3}\) and \({\widehat{Q}}_{5}\) drawn in Fig. 9, we list the classical expectation values of the twisted chiral fields in each of the 2d nodes, about which one finds the solution to the twisted chiral ring. Using this vacuum, along with the FI couplings in the classical twisted chiral superpotentials for each quiver, one finds identical expressions at leading order. The vacuum for the other quivers of the duality chain, namely \(Q_0\), \(Q_2\), \(Q_4\) and \(Q_7\), can be read from Table 1
Full size table
Table 6 For the quivers \({\widehat{Q}}_{1}\), \(Q_{3}\) and \({\widehat{Q}}_{5}\) drawn in Fig. 9, we list the relations (up to signs) between the ramified instanton counting parameters \(q_I\) and the strong coupling scales \(\varLambda _I\), and also the JK reference vector that selects the contour prescription needed to compute the ramified instanton partition function using the localization formula
Full size table

If we now dualize the first node of \({\widehat{Q}}_{1}\) we obtain a new linear quiver \(Q_{3}\). Here it is natural to relabel the nodes in such a way that the dualized node corresponds to \(I=2\), thus respecting the order shown in Fig. 9. Taking this into account and applying the duality map to (74), we then obtain

$$\begin{aligned} \begin{aligned} {\mathcal {W}}_{\text {cl}}^{Q_{3}}&=-2\pi \mathrm {i}\,\tau _2\, \text {Tr}\,\sigma ^{(1)}-2\pi \mathrm {i}\,\tau _1\,\text {Tr}\,\sigma ^{(2)}\\&\quad +2\pi \mathrm {i}\,(\tau _1+\tau _2+\tau _3)\,\text {Tr}\,\sigma ^{(3)}~. \end{aligned} \end{aligned}$$
(75)

In the next two duality steps we find the quivers \(Q_2\) and \(Q_4\) whose classical superpotentials are given in (43). Dualizing the second node of \(Q_4\), we obtain the non-linear quiver \({\widehat{Q}}_{5}\), whose classical superpotential is

$$\begin{aligned} \begin{aligned} {\mathcal {W}}_{\text {cl}}^{{\widehat{Q}}_{5}}&=-2\pi \mathrm {i}\,\tau _3\, \text {Tr}\,\sigma ^{(1)}+2\pi \mathrm {i}\,\tau _2\,\text {Tr}\,\sigma ^{(2)}\\&\quad -2\pi \mathrm {i}\,(\tau _1+\tau _2)\,\text {Tr}\,\sigma ^{(3)}~. \end{aligned} \end{aligned}$$
(76)

Here we have again renamed indices in such a way that the labelling of the \(\sigma \)-variables follows the same order in which the gauge nodes are drawn in Fig. 9.

Next, we determine the classical vacuum for the quivers in this duality chain by equating the classical twisted chiral superpotentials for each dual pairs. In Table 5 we report the results for the three new quivers \({\widehat{Q}}_{1}\), \(Q_{3}\) and \({\widehat{Q}}_{5}\) of this sequence.

Using this information and following the same procedure described above, we can find the q vs \(\varLambda \) map and the contour prescription that has to be used in the localization formula in order to match term-by-term the superpotential with the one obtained from solving the twisted chiral ring equations. Of course, we do not repeat the derivation of these results since the calculations are a straightforward generalization of what we did for the other duality chain, and we simply collect our findings for the three new quivers \({\widehat{Q}}_{1}\), \(Q_{3}\) and \({\widehat{Q}}_{5}\) in Table 6. We have checked the validity of our proposal up to two instantons, while some details on the results at the one-instanton level can be found in Appendix B.

5 Proposal for generic linear quivers

The detailed analysis of the previous section shows that in the 4-node case there are eight linear quivers related to each other by duality: the seven ones found in the sequence of Fig. 8, and the quiver \(Q_3\) in the sequence of Fig. 9. If we consider these eight linear quivers all together, a nice structure emerges as illustrated in Fig. 10 where we exhibit the ranks of the nodes of the various quivers and their connections.

Fig. 10
figure 10

The linear quivers that are Seiberg-dual to the oriented quiver \(Q_0\). To each link we associate 0 or 1 depending whether it is rightward or leftward

Full size image

We recall that the ranks of the nodes of the initial oriented quiver \(Q_0\) can be obtained from the vector \(\varvec{n}=(n_1,n_2,n_3,n_4)\) as discussed in Sect. 2 (see (3)). Then, given the action of Seiberg duality, it is easy to realize that the ranks of the nodes of the other quivers can be obtained from vectors that are a permutation of the entries of \(\varvec{n}\). For example, for the quiver \(Q_2\) the ranks can be obtained from \((n_2,n_3,n_1,n_4)\), while for quiver \(Q_6\) they are obtained from \((n_3,n_4,n_2,n_1)\). It is not difficult to realize that all these permuted vectors can be written as

$$\begin{aligned} P_2^{s_3}\,P_3^{s_2}\, P_4^{s_1} \, \varvec{n}~, \end{aligned}$$
(77)

where \(s_i=0,1\) and \(P_k\) is the cyclic permutation on the first k elements out of 4. In matrix form, we have

$$\begin{aligned} \begin{aligned} P_{2}&= \begin{pmatrix} ~0 &{} ~1 &{} ~0 &{} ~0 ~\\ ~1 &{} ~0 &{} ~0 &{} ~0 ~\\ ~0 &{} ~0 &{} ~1 &{} ~0~ \\ ~0 &{} ~0 &{} ~0 &{} ~1~ \end{pmatrix}~,\\ P_{3}&= \begin{pmatrix} ~0 &{} ~1 &{} ~0 &{} ~0~\\ ~0 &{} ~0 &{} ~1 &{} ~0~ \\ ~1 &{} ~0 &{} ~0 &{} ~0~ \\ ~0 &{} ~0 &{} ~0 &{} ~1~ \end{pmatrix}~,\\ P_{4}&= \begin{pmatrix} ~0 &{} ~1 &{} ~0 &{} ~0~ \\ ~0 &{} ~0 &{} ~1 &{} ~0~ \\ ~0 &{} ~0 &{} ~0 &{} ~1~ \\ ~1 &{} ~0 &{} ~0 &{} ~0~ \end{pmatrix}~. \end{aligned} \end{aligned}$$
(78)

We therefore see that each linear quiver \(Q_i\) can be labelled by the set \(\mathbf {s}=(s_1,s_2,s_3)\) identifying the permutation

$$\begin{aligned} P[\mathbf {s}\,]=P_2^{s_3}\, P_3^{s_2}\, P_4^{s_1} \end{aligned}$$
(79)

which determines the ranks of the various nodes. For example, the quiver \(Q_3\) corresponds to (0, 1, 1) and the quiver \(Q_5\) to (1, 0, 1). For any quiver, its corresponding \(\mathbf {s}\) can be easily read from Fig. 10 by looking at the labels 0 and 1 on the links connecting the nodes, starting from the rightmost one and moving leftwards. Notice that, with the conventions we have chosen, the quiver \(Q_i\) turns out to be labelled by the vector \(\mathbf {s}\) that represents the number i written in binary notation.

The permutation \(P[\mathbf {s}\,]\) can be represented in an irreducible way in terms of \(3\times 3\) matrices as follows

$$\begin{aligned} {\widehat{P}}\,[\mathbf {s}\,]={\widehat{P}}_2^{s_3}\, {\widehat{P}}_3^{s_2}\, {\widehat{P}}_4^{s_1} \end{aligned}$$
(80)

where

$$\begin{aligned} \begin{aligned} {\widehat{P}}_{2}&= \begin{pmatrix} -1&{} ~0 &{} ~0 ~\\ ~1 &{} ~1 &{} ~0~ \\ ~0 &{} ~0 &{} ~1~ &{} \end{pmatrix}~,\\ {\widehat{P}}_{3}&= \begin{pmatrix} ~0 &{} ~1 &{} ~0 ~ \\ -1 &{} -1 &{} ~0 ~\\ ~1 &{} ~1&{} ~1~ \end{pmatrix}~,\\ {\widehat{P}}_{4}&= \begin{pmatrix} ~0 &{} ~1 &{} ~0~ \\ ~0 &{} ~0 &{} ~1~ \\ -1 &{} -1 &{} -1 ~ \end{pmatrix}~. \end{aligned} \end{aligned}$$
(81)

This defines the action on the FI couplings. Indeed, if we introduce the vector \(\mathbf {\zeta }=(\zeta _1,\zeta _2,\zeta _3)\) with the FI parameters of the first quiver \(Q_0\), then it is easy to check that

$$\begin{aligned} \big (\zeta _1^{Q_i}\,,\,\zeta _2^{Q_i}\,,\,\zeta _3^{Q_i}\big ) ={\widehat{P}}\,[\mathbf {s}\,]\,\mathbf {\zeta }~. \end{aligned}$$
(82)

For example, for \(Q_4\) we have

$$\begin{aligned} {\widehat{P}}\,[(1,0,0)]\,\mathbf {\zeta } = {\widehat{P}}_4\,\mathbf {\zeta } =\big (\,\zeta _2\,,\,\zeta _3\,,\,-\zeta _1-\zeta _2-\zeta _3\,\big )~, \end{aligned}$$
(83)

which indeed are the FI parameters of \(Q_4\), as one can see from the superpotential \({\mathcal {W}}_{\text {cl}}^{\,Q_4}\) in (43).

This formalism can be nicely used also to describe how the variables \(\chi _I\) appearing in the localization integrals are associated to the various nodes of the quiver. From the detailed analysis of Sect. 4, we see that \(\chi _4\) is always associated to the last 4d node of the quiver, while the other three variables \(\chi _1\), \(\chi _2\) and \(\chi _3\) are associated to the first three 2d nodes in a permutation determined by the q vs \(\varLambda \) map. Moreover, we see that two quivers whose vectors \(\mathbf {s}\) only differ by the value of \(s_3\) have the same permutation and that this permutation involves only cyclic rearrangements of the first two or the first three variables described by \(P_2\) and \(P_3\). In particular, introducing the vector \(\mathbf {\chi }=(\chi _1,\chi _2,\chi _3,\chi _4)\), we can check that

$$\begin{aligned} \mathbf {\chi }\,[\mathbf {s}\,]= P_2^{s_2}\, P_3^{s_1}\,\mathbf {\chi } \end{aligned}$$
(84)

correctly describes the correspondence between the nodes of the quiver and the \(\chi \)-variables. For example, for \(Q_6\) we find that \(\mathbf {\chi }\,[(1,1,0)]=P_2\, P_3\,\mathbf {\chi }=(\chi _3,\chi _2,\chi _1,\chi _4)\), which is indeed the correct sequence of \(\chi \)-variables for \(Q_6\) as one can see from Table 3.

We are now in the position of using this formalism to write the JK reference vector for any linear quiver in a compact form. To this aim, we first extend the three-component vector (82) by adding to it a fourth component according to

$$\begin{aligned} \mathbf {\zeta }\,[\mathbf {s}\,] = \big ({\widehat{P}}\,[\mathbf {s}\,]\,\mathbf {\zeta }\,,\,\pm \,\zeta _4\big )\,=\, \big (\zeta _1^{Q_i}\,,\,\zeta _2^{Q_i},\zeta _3^{Q_i}\,,\,\pm \,\zeta _4\big ) \end{aligned}$$
(85)

Here \(\zeta _4\) is a positive parameter that is always bigger than \(\big |\zeta _I^{Q_i}\big |\) for \(I=1,2,3\). The sign in (85) depends whether the 4d node of the quiver provides fundamental (\(+\)) or anti-fundamental (−) matter to the last 2d node. By considering the detailed structure of the various quivers, we see that in the first four quivers from \(Q_0\) to \(Q_3\) the 4d node provide anti-fundamental matter, while in the last four ones from \(Q_4\) to \(Q_7\) it provides fundamental flavors. This means that the sign in (85) can also be written as \((-1)^{s_1+1}\). With these positions, it is easy to realize that the JK vectors described in the previous section can all be compactly written as follows:

$$\begin{aligned} \eta _{Q_i}= -\mathbf {\zeta }\,[\mathbf {s}\,]\cdot \mathbf {\chi }\,[\mathbf {s}\,]~. \end{aligned}$$
(86)

This analysis can be extended to linear quivers with M nodes in a straightforward manner. In this case we have \((M-1)\) binary choices corresponding to \(2^{M-1}\) linear quivers that are related to each other by Seiberg duality. Therefore, they can be labelled by a vector \(\mathbf {s}=(s_1,s_2,\ldots ,s_{M-1})\) with \(s_i=0,1\). For each choice, the ranks of the M nodes are determined by the permutation

$$\begin{aligned} \begin{aligned} P[\mathbf {s}\,]=P_2^{s_{M-1}}\, P_3^{s_{M-2}}\cdots P_{M-1}^{s_2}\, P_M^{s_{1}} \end{aligned} \end{aligned}$$
(87)

where \(P_k\) permutes the first k numbers, while the FI parameters of the \((M-1)\) nodes are obtained using \({\widehat{P}}\,[\mathbf {s}\,]\), which represents the permutation \(P[\mathbf {s}]\) in an irreducible way in an \((M-1)\)-dimensional space. Generalizing (85) to the M-node case in an obvious way, and defining

$$\begin{aligned} \mathbf {\chi }\,[\mathbf {s}\,]= P_2^{s_{M-2}}\, P_3^{s_{M-3}}\cdots P_{M-2}^{s_2}\, P_{M-1}^{s_1}\, \mathbf {\chi } \end{aligned}$$
(88)

where \(\mathbf {\chi }=(\chi _1,\ldots ,\chi _M)\), it is natural to propose that the JK reference vector for a generic quiver \(Q_i\) is

$$\begin{aligned} \eta _{Q_i}= -\mathbf {\zeta }\,[\mathbf {s}\,]\cdot \mathbf {\chi }\,[\mathbf {s}\,] = - \sum _{I=1}^{M-1} \zeta _I^{Q_i}\,\chi _{\alpha (I)}\pm \zeta _4\,\chi _4 \end{aligned}$$
(89)

where \(\alpha (I)\) is determined by the permutation in (88). We have verified in several examples the validity of this proposal.

6 Summary of results

In this paper we have discussed in detail the relation between two distinct realizations of surface operators: as monodromy defects and as coupled 2d/4d quiver gauge theories. The main features of these two points of view and their relations are summarized in Table 7.

Table 7 The dictionary between the various features of surface operators in the two descriptions, as monodromy defects and as coupled 2d/4d quivers
Full size table

Establishing a precise correspondence between different integration contour prescriptions in the ramified instanton partition function for a monodromy defect and different quiver theories related to each other by a Seiberg duality has been the main focus of our present work. Dual quivers have different ultraviolet realizations but share the same infrared physics and thus the (massive) vacua of their low-energy theories can be mapped onto each other. These massive vacua are obtained by extremizing the effective twisted chiral superpotential of the 2d/4d quiver. The evaluation of the effective superpotential in a particular vacuum is in turn mapped to the twisted superpotential which is extracted from the ramified instanton partition function with a specific contour of integration.

For surface operators in pure \({{{\mathcal {N}}}}=2\) gauge theories, like the ones we have considered in this paper, residue theorem ensures that one always obtains the same superpotential irrespective of the contour of integration chosen. Nevertheless, by a careful study of the individual residues that contribute to the superpotential, we have been able to map distinct contours on the localization side to distinct Seiberg-dual 2d quivers coupled to the same 4d SU(N) flavour group. The duality frame one chooses affects the details of the other entries in the table above, such as the choice of the classical vacuum and the map between the ramified instanton counting parameters \(q_I\) and the strong coupling scales \(\varLambda _I\). We initially restricted ourselves to systems with four nodes to exhibit our explicit results, but in the end we have generalized our analysis to linear quivers with an arbitrary number of nodes providing the map between the data of the quiver and the corresponding JK prescription, which takes a universal form.

There is one caveat to our analysis. All quivers we have studied so far, have only a single 2d node that is connected to the flavour node that is gauged in 4d. It is only for such cases that the coupling of the 2d degrees of freedom to the 4d theory via its resolvent gives results that are consistent with those obtained using localization methods in the monodromy defect approach. It would be very interesting to understand whether quivers with more 2d nodes connected to the 4d node also have an interpretation as surface operators in a 4d gauge theory. Furthermore, there are many worthwhile but yet unexplored directions to pursue, such as the extension of our analysis to (conformal) SQCD models for which the integrands of ramified instanton partition function may have non-vanishing residues at infinity, or the lift of our techniques to five dimensions to study surface operators from the point of view of 3d/5d coupledsystems, with possible Chern-Simons interactions. We leave these extensions and generalizations to future work.