1 Introduction

The status of the no-hair theorem in general relativity is still a subject of current research ever since Penrose conjectured it in 1969 (see, e.g., a recent work by Cuzinatto et al. [1]). Specific examples of spinning spacetimes have also been studied in the literature testing the theorem (see, e.g., [2]). However, to our knowledge, no generic spinning spacetime has been considered for such studies until Johannsen [3] proposed a new spinning metric that departs from the Kerr black hole (BH) by an infinite number of dimensionless deviation parameters such that non-zero value of any of them would indicate violation of the no-hair theorem. The metric is not a solution of any known modified gravity theory but nonetheless shares the Kerr horizon defined by the BH mass M and spin a. Special features of the Johannsen metric include its regularity properties and the absence of closed time-like curves. Hence it provide an ideal setting for measuring the deviations, for instance, by observing the deformation of Kerr BH photon rings [3,4,5]. Possible deviations has been suggested also via the Blandford-Zjanek mechanism responsible for BH jets [6] (see also the review [7]).

The motivation of the present paper is guided by the possible determination of the Johannsen deviation parameters, hence the status of the no-hair theorem, from a completely different perspective, namely, the effect of relative time delay (RTD) (which is not Shapiro time delay). The concept of RTD is defined as follows [8, 9]: two light rays emanate from a variable source S behind a spinning lens L (with mass M), pass on either side of it with different times of arrival (TOA) at the observer O. The difference is caused by the frame dragging due to the intervening spinning lens that in turn causes light path lengths on either side of the lens to differ, shorter on the co-rotating side and longer in the counter-rotating side (see Fig. 1). An example of such an effect could be the early observation of extremely rapid fluctuations in the brightness of quasar \( 1525+227\) with characteristic time scale \(\sim \) 200 sec speculated to be caused by the relative delay of signals due to a spinning BH of mass \(M\sim 5\times 10^{8}M_{\odot }\) situated between the quasar and the observer [10].

The purpose of the present paper is to argue for gravitational lensing as a method to determine the influence of deviation parameters on the RTD. We shall work in the thin-lens approximation in first order in spin a and apply the result to different astrophysical lenses assuming an aligned setting of source, lense and observer. It will also be shown that the spinning lens can be degenerate to a artificial “static” lensFootnote 1, which would enable us to re-express the relative time delay components in terms of the spin a measured from the observed brightness of images. Numerical values are tabulated for three astrophysical lens systems. Note that there are also other regular metrics (see, e.g., [12,13,14,15,16,17]), that could equally well be treated within the framework of the present analysis.We shall take \(G=1\), \(c=1\) unless specifically restored.

The paper is organized as follows. In Sect. 2, we shall derive the equation for the relative time delay and in Sect. 3, integrate it in the thin-lens approximation. Section 4 contains the equivalent static lens system and the corresponding magnification of images. Section 5 presents indicative numerical estimates for three lens systems and Sect. 6 concludes the paper.

2 Johannsen metric and relative time delay

The gravitational field of a spinning lens of mass M described by axisymmetric, stationary and asymptotically flat spacetime, which we call here the spinning chargeless Johannsen metric [3], is given by

$$\begin{aligned} d\tau ^{2}=g_{tt}dt^{2}+2g_{t\phi }dtd\phi +g_{rr}dr^{2}+g_{\theta \theta }d\theta ^{2}+g_{\phi \phi }d\phi ^{2} \end{aligned}$$
(1)

where

$$\begin{aligned}&g_{tt}=-\frac{{\tilde{\varSigma }}\left[ \varDelta -a^{2}A_{2}(r)^{2}\sin ^{2}{\theta }\right] }{\left[ (r^{2}+a^{2})A_{1}(r)-a^{2}A_{2}(r)\sin ^{2}{\theta } \right] ^{2}}, \end{aligned}$$
(2)
$$\begin{aligned}&g_{t\phi }=-\frac{a\left[ (r^{2}+a^{2})A_{1}(r)A_{2}(r)-\varDelta \right] {\tilde{\varSigma }}\sin ^{2}{\theta }}{\left[ (r^{2}+a^{2})A_{1}(r)-a^{2}A_{2}(r) \sin ^{2}{\theta }\right] ^{2}}, \end{aligned}$$
(3)
$$\begin{aligned}&g_{rr}=\frac{{\tilde{\varSigma }}}{\varDelta A_{5}(r)}, \end{aligned}$$
(4)
$$\begin{aligned}&g_{\theta \theta }={\tilde{\varSigma }}, \end{aligned}$$
(5)
$$\begin{aligned}&g_{\phi \phi }=\frac{{\tilde{\varSigma }}\sin ^{2}{\theta }\left[ (r^{2}+a^{2})^{2}A_{1}(r)^{2}-a^{2}\varDelta \sin ^{2}{\theta }\right] }{\left[ (r^{2}+a^{2})A_{1}(r)-a^{2}A_{2}(r)\sin ^{2}{\theta }\right] ^{2}}, \end{aligned}$$
(6)
$$\begin{aligned}&A_{1}(r)=1+\sum \limits _{n=3}^{\infty }\alpha _{1n}\left( \frac{M}{r}\right) ^{n}, \end{aligned}$$
(7)
$$\begin{aligned}&A_{2}(r)=1+\sum \limits _{n=2}^{\infty }\alpha _{2n}\left( \frac{M}{r}\right) ^{n}, \end{aligned}$$
(8)
$$\begin{aligned}&A_{5}(r)=1+\sum \limits _{n=2}^{\infty }\alpha _{5n}\left( \frac{M}{r}\right) ^{n}, \end{aligned}$$
(9)
$$\begin{aligned}&{\tilde{\varSigma }}=r^{2}+a^{2}\cos ^{2}{\theta }+f(r), \end{aligned}$$
(10)
$$\begin{aligned}&f(r)=\sum \limits _{n=3}^{\infty }\epsilon _{n}\frac{M^{n}}{r^{n-2}}, \end{aligned}$$
(11)
$$\begin{aligned}&\varDelta =r^{2}-2Mr+a^{2}. \end{aligned}$$
(12)

The parameter a is the specific angular momentum of the lens defined by \( a=J/M\). The outer event horizon appears at (\(\varDelta =0\)):

$$\begin{aligned} r_{+}=M+\sqrt{M^{2}-a^{2}}. \end{aligned}$$
(13)

While the BHs have the constraint \(a\le M\), spinning galaxies tabulated by Romanowsky and Fall [18] have \(a>M\) (see an example in Table 3 below) but these constraints will not affect our analysis since in the weak field form of the metric these parameters can be freely specified.

The infinite number of deviation parameters are denoted by \(\alpha _{1n}\), \( \alpha _{2n}\), \(\alpha _{5n}\) and \(\epsilon _{n}\) for specified ranges of n as shown above. The metric is asymptotically flat, has the correct Newtonian limit, and is consistent with the current post-Newtonian constraints. At the first nonvanishing order in the deviation parameters, the metric depends only on four parameters in addition to the mass M and the spin a, which are \(\alpha _{13}\), \(\alpha _{22}\), \(\alpha _{52}\) and \(\epsilon _{3}\). These parameters are dimensionless numbers without dynamical interpretations except that lower limits on them have been worked out in [3] on the basis of certain requirements such as the existence of event horizon, the signature protection, positivity of the determinant, absence of closed time-like curves. At the extreme limit \(a=\pm M\), all of these have lower limit \(-1\). This limit in turn would induce lower limits to redefined deviation parameters (see below).

To derive the equation for relative time delay, consider the light trajectory on the equatorial plane (\(\theta =\pi /2\)) is given by \(d\tau ^{2}=0\), so that the coordinate time required for light rays along an infinitesimal null world line is given by

$$\begin{aligned} dt_{\pm }=\frac{d\phi }{g_{tt}}[-g_{t\phi }\pm h(r,\phi )], \end{aligned}$$
(14)

where

$$\begin{aligned} h(r,\phi )\equiv \sqrt{g_{t\phi }^{2}-g_{tt}\left\{ g_{rr}\left( \frac{dr}{ d\phi }\right) ^{2}+g_{\phi \phi }^{2}\right\} }. \end{aligned}$$
(15)

We assume the passage of coordinate time to be positive for both ± sides of the lens identifying \(d\phi >0\), for light rays passing the lens by the co-rotating side (\(+\)) and \(d\phi <0\) for the counter-rotating side (−), so that \(dt_{+}\) and \(dt_{-}\) are both positive. The net arrival time difference between the two light rays at the observer is also positive:

$$\begin{aligned} dt= & {} dt_{-}-dt_{+} = \frac{\left| d\phi \right| }{g_{tt}}[g_{t\phi }+h(r,\phi )] \nonumber \\&-\frac{\left| d\phi \right| }{g_{tt}}[-g_{t\phi }+h(r,\phi )] = \frac{2g_{t\phi }}{g_{tt}}\left| d\phi \right| . \end{aligned}$$
(16)

This delay dt is due to the frame-dragging effect characterized by\(\left( \frac{2g_{t\phi }}{g_{tt}}\right) \), which we are going to compute in this paper. We consider that the source, lens and the observer are perfectly aligned, that is, they are situated on a straight line (see Fig. 1). When the lens is not spinning, the path lengths of the light ray on both sides of the lens would be the same and there would be no arrival time difference at the observer. However, when the lens is spinning the path lengths will differ - shorter for co-rotating and longer for counter-rotating rays - giving rise to the time delay effect.Footnote 2

Fig. 1
figure 1

The generic thin-lens configuration (scales exaggerated). S, L and O are the source, lens and observer respectively aligned on a straight line (\(\beta =0\)), b is the closest approach distance and a is the spin. The arbitrary angles are as shown

Full size image

We shall consider deviation parameters that appear in the lowest order of expansion in \(\left( \frac{a}{cr}\right) \) of the function \(\left( \frac{ 2g_{t\phi }}{g_{tt}}\right) \), since for the metric (1), the next order appears only in \((\frac{a}{cr})^{3}\), reduced further by smaller order multiplicative terms like \(\left( M/r\right)<<1\) valid in the weak field. In this approximation, the expansion up to third order in \(\left( M/r\right) \) is:

$$\begin{aligned} dt=|d\phi |\left( \frac{1}{c}\right) \left[ \frac{4aM}{r}+\frac{8aM^{2}}{ r^{2}}\lambda _{1}+\frac{2aM^{3}}{r^{3}}\lambda _{2}\right] , \end{aligned}$$
(17)

where

$$\begin{aligned} \lambda _{1}=1+\frac{\alpha _{22}}{4},\quad \lambda _{2}=8+\alpha _{13}+2\alpha _{22}+\alpha _{23} \end{aligned}$$
(18)

are the redefined deviation parameters. Three results are already immediate: (1) The number of deviation parameters has reduced from three to two, viz., \( \lambda _{1}\) and \(\lambda _{2}\), the term containing \(\epsilon _{3}\) has canceled out between the numerator and dinominator of \(\left( \frac{ 2g_{t\phi }}{g_{tt}}\right) \). (2) The absence of \(a^{2}\) terms implies that the moment \(M_{2}\) does not contribute to observables in the asymptotic limit.Footnote 3 (3) The lowest limit \(-1\) on \(\alpha _{22}\), \(\alpha _{13}\) and \(\alpha _{23}\) corresponding to the extreme case yields lower limits \(\lambda _{1}>\frac{3}{4}\), \(\lambda _{2}>4\).

The total time delay \(\varDelta t\) between two light rays traveling from the source to observer along two opposite sides of the intermediate spinning lens is

$$\begin{aligned} \varDelta t= & {} \left( \frac{1}{c}\right) \int \limits _{0}^{\pi }d\phi \left[ \frac{4aM}{r}+\frac{8aM^{2}}{r^{2}}\lambda _{1}+\frac{2aM^{3}}{r^{3}}\lambda _{2}\right] \end{aligned}$$
(19)
$$\begin{aligned}\equiv & {} \frac{1}{c}\left( I_{1}+I_{2}+I_{3}\right) =\varDelta t_{1}+\varDelta t_{2}+\varDelta t_{2}. \end{aligned}$$
(20)

We compute the integral locating the spinning lens at the origin of a polar system of coordinates on the equatorial plane (\(\theta =\pi /2\)). As can be seen, the deviation parameters do not influence the leading order delay contribution \(\varDelta t_{1}\). In the following, we shall derive explicit expressions for \(\varDelta t_{1}\), \(\varDelta t_{2}\) and \(\varDelta t_{2}\) within the thin-lens approximation.

3 Thin-lens approximation

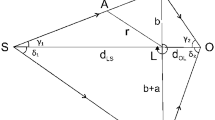
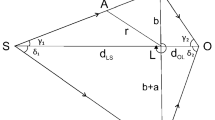
Thin-lens approximation means that the light deflection takes place only at the lens approximated as a point, while elsewhere the rays travel in straight lines and the relevant angles are small. In this approximation, Dymnikova [8] has shown that the rays emerging from S, after passing by either side of spinning lens L on the equatorial plane, will meet at O only if the corresponding closest approach distances are b and \(b+a\) as shown in Fig. 1.

Table 1 Relative time delay components \(\varDelta t_{1},\varDelta t_{2}, \varDelta t_{3}\) in microseconds (\(\mu \)s) calculated from Eqs. (30, 32, 33) for a typical BH sample with \(M=20M_{\odot }\), \(a=0.998M\) and \(d_{OL}=5\) kpc, \(r_{ \text {ph}}^{+}=1.18\times 10^{7}\) cm. The source distances \(d_{LS}=\chi d_{OL}\) in Fig. 1 are varied ensuring that the angles remain small in the lensing geometry: \(\gamma _{1}\simeq \) tan\(\gamma _{1}=b/d_{LS}\simeq \delta _{1}\simeq \) tan\(\delta _{1}\). The Kerr metric is obtained by setting the deviation parameters \(\alpha _{22},\alpha _{13}\) and \(\alpha _{23}\) to zero so that, from Eq. (18), the last two columns in the table below should be multiplied by \(\lambda _{1}=1,\lambda _{2}=8\) respectively
Full size table
Table 2 Relative time delay components \(\varDelta t_{1},\varDelta t_{2},\varDelta t_{3}\) in seconds calculated from Eqs. (30, 32, 33) for SgrA* with values given by Kato et al. [34], viz., \(M=4.2\times 10^{6}M_{\odot }\), \( d_{OL}=7.6\) kpc and a unique \(a=0.44M\) so that \(r_{\text {ph} }^{+}=2.48\times 10^{12}\) cm. The source distances \(d_{LS}=\chi d_{OL}\) in Fig. 1 are varied ensuring that the angles remain small: \(\gamma _{1}\simeq \) tan\(\gamma _{1}=b/d_{LS}\simeq \delta _{1}\simeq \) tan\(\delta _{1}\). The Kerr metric is obtained by setting the deviation parameters \(\alpha _{22},\alpha _{13}\) and \(\alpha _{23}\) to zero so that, from Eq. (18), the last two columns in the table below should be multiplied by \(\lambda _{1}=1,\lambda _{2}=8\) respectively
Full size table

At this stage, an important issue needs to be addressed. Note that major deflection does not occur in the weak field, hence it is necessary to quantify exactly how close to the lens the light rays should pass so that the weak field expansion for the metric does not incur significant errors. We shall quantify the closeness by using a natural characteristic length peculiar to the lens. For instance, we recall that there occurs photon spheres around BHs and the deflection angle becomes logarithmically divergent at that radius, as a result of which the light rays get captured there [23,24,25]. This radius therefore demarcates a natural strong field limit. We also recall that Bardeen [26] has shown that a spinning BH has two photon spheres centered at the lens with radii \(r=r_{ph}^{\pm }=2M\left[ 1\pm \cos \left\{ \frac{2}{3}\cos ^{-1}\left( \frac{a}{M}\right) \right\} \right] \). We shall consider the larger of the two photon spheres \(r_{ph}^{+} \), and define \(b\approx 10^{n}r_{ph}^{+}\) with n an integer. Our idea is to march b towards \(r_{ph}^{+}\), with the rays still moving in the weak field preserving the smallness of the involved angles. This algorithm will be exercised in Tables 1 and 2 below.

As a specific illustration right now, consider a small BH with \(M=20M_{\odot }\), \(a=0.99M\) (PSR-BH system, Table 1), then \(r_{ph}^{+}\approx 10^{7}\) cm. Choosing \(n=2\), so that \(b\approx 10^{9}\)cm, it can be seen that the expansion of \(g_{\mu \nu }\) contains typical terms having magnitudes much smaller than unity: \(\frac{M}{b}\approx 10^{-4}\), \(\frac{a^{2}}{b^{2}} \approx 10^{-7}\), \(\frac{aM}{b^{2}}\approx 10^{-7}\), \(\frac{aM^{2}}{b^{3}} \approx 10^{-10}\), \(\frac{M^{3}}{b^{3}}\approx 10^{-10},\frac{aM^{3}}{b^{4}} \approx 10^{-13}\), \(\frac{a^{2}M^{3}}{b^{5}}\approx 10^{-16}\) etc (assuming the deviation parameters to be of the order of unity). Thus, when the light rays pass about a hundred times farther than the photon sphere, \(b\approx 10^{2}r_{ph}^{+}\), it would produce a measurable leading order microsecond level delay as also anticipated in the literature using a different approach [9]. The values would be considerably higher in the two other systems considered in Tables 2 and 3.

Returning to Fig. 1, we have by construction \(d_{LS}=\chi d_{OL}\), where \( \chi \) is a constant, \(PLQ\perp OLS\), arbitrary angles \(\measuredangle LSP=\) \(\gamma _{1}\), \(\measuredangle LOP=\gamma _{2}\), \(\measuredangle LSQ=\delta _{1}\), \(\measuredangle LOQ=\delta _{2}\), thus allowing for a most general thin-lens configuration. With r denoting an arbitrary point A, we can write for the co-rotating light motion, where \(\measuredangle LSP=\) \(\gamma _{1}\), \(\measuredangle LOP=\gamma _{2}\), the equation of the straight line corresponding to the polar angle segment \(\pi \ge \phi \ge \pi /2\) as:

$$\begin{aligned} \frac{1}{r_{\text {cor}}}=\frac{1}{d_{LS}}\cos {\phi }+\frac{1}{d_{LS}}\cot \left( {\gamma }_{1}\right) \sin {\phi }, \end{aligned}$$
(21)

where \(d_{LS}=LS\), the distance between the lens and source and the subscript “cor” denotes corotating side. Similarly, for the remaining segment \(\pi /2\ge \phi \ge 0\), we have

$$\begin{aligned} \frac{1}{r_{\text {cor}}}=\frac{1}{d_{OL}}\cos {\phi }+\frac{1}{d_{OL}}\cot \left( {\gamma }_{2}\right) \sin {\phi }, \end{aligned}$$
(22)

where \(d_{OL}=OL\), the distance of the observer to the lens and the closest approach distance b is given by

$$\begin{aligned} \frac{\cot \left( {\gamma }_{1}\right) }{d_{LS}}=\frac{\cot \left( {\gamma } _{2}\right) }{d_{OL}}=\frac{1}{b}\text { at }\phi =\pi /2. \end{aligned}$$
(23)

For the counter-rotating light motion, denoted by the subscript “cou”, where \(\measuredangle LSQ=\delta _{1}\), \(\measuredangle LOQ=\delta _{2}\), the equation in the segment \(-\pi /2\le \phi \le -\pi \) is

$$\begin{aligned} \frac{1}{r_{\text {cou}}}=\frac{1}{d_{LS}}\cos {\phi }+\frac{1}{d_{LS}}\cot \left( {\delta }_{1}\right) \sin {\phi }, \end{aligned}$$
(24)

and in the segment \(-\pi /2\le \phi \le 0\), it is

$$\begin{aligned} \frac{1}{r_{\text {cou}}}=\frac{1}{d_{OL}}\cos {\phi }+\frac{1}{d_{OL}}\cot \left( {\delta }_{2}\right) \sin {\phi }, \end{aligned}$$
(25)

with the closest approach distance (\(a+b\)) given by

$$\begin{aligned} \frac{\cot \left( {\delta }_{1}\right) }{d_{LS}}=\frac{\cot \left( \delta _{2}\right) }{d_{OL}}=-\frac{1}{a+b}\text { at }\phi =-\pi /2. \end{aligned}$$
(26)

Inserting the expressions for 1 / r in Eq. (19) for the relevant segments and carrying out the angular integrations on the co-rotating and counter-rotating sides using

$$\begin{aligned} d_{LS}= & {} \chi d_{OL},\gamma _{1}=\cot ^{-1}\left[ d_{LS}/b\right] , \nonumber \\ \gamma _{2}= & {} \cot ^{-1}\left[ d_{OL}/b\right] , \end{aligned}$$
(27)
$$\begin{aligned} \delta _{1}= & {} \cot ^{-1}\left[ -d_{LS}/\left( a+b\right) \right] , \nonumber \\ \delta _{2}= & {} \cot ^{-1}\left[ -d_{OL}/\left( a+b\right) \right] , \end{aligned}$$
(28)

we get the final result by subtracting between the path lengths, viz., \(SQO-SPO\):

$$\begin{aligned} I_{1}= & {} 4aM\left[ \int \limits _{\pi /2}^{\pi }\frac{1}{r_{\text {cor}}}d\phi +\int \limits _{0}^{\pi /2}\frac{1}{r_{\text {cor}}}d\phi \right] \nonumber \\&-\,4aM\left[ \int \limits _{-\pi /2}^{-\pi }\frac{1}{r_{\text {cou}}}d\phi +\int \limits _{0}^{-\pi /2}\frac{1}{r_{\text {cou}}}d\phi \right] , \end{aligned}$$
(29)
$$\begin{aligned} \varDelta t_{1}= & {} \frac{I_{1}}{c}=\frac{8a^{2}M\left\{ b\left( \chi -1\right) +\chi d_{OL}\right\} }{b(a+b)\chi d_{OL}} \nonumber \\&+\,\frac{8abM\left\{ b\left( \chi -1\right) +2\chi d_{OL}\right\} }{b(a+b)\chi d_{OL}}. \end{aligned}$$
(30)

Equation (30) generalizes the expression used by Laguna and Wolszczan [9]

$$\begin{aligned} \varDelta t_{1}\simeq \frac{16aM}{cb}, \end{aligned}$$
(31)

to finite distance scale lensing geometry. In the same way, we can calculate the integrals \(I_{2}\) and \(I_{3}\) which, to leading orders in \(\left( \frac{M }{b}\right) ^{2}\) and \(\left( \frac{M}{b}\right) ^{3}\), work out to

$$\begin{aligned} \varDelta t_{2}= & {} \frac{I_{2}}{c}=\frac{4aM^{2}\left[ a^{2}F_{1}+2abF_{2}+b^{2}F_{3}\right] }{cb^{2}(a+b)^{2}\left( \chi d_{OL}\right) ^{2}}\lambda _{1}, \end{aligned}$$
(32)
$$\begin{aligned} \varDelta t_{3}= & {} \frac{I_{3}}{c}=\frac{2aM^{3}\left[ G_{1}+G_{2}-G_{3}-G_{4} \right] }{3cb^{3}d_{OL}^{3}}\lambda _{2}, \end{aligned}$$
(33)

where

$$\begin{aligned} F_{1}\equiv & {} 2b(\chi -1)\chi d_{OL}+\pi \left( \chi d_{OL}\right) ^{2}\nonumber \\&+\,\pi b^{2}\left( 1+\chi ^{2}\right) , \end{aligned}$$
(34)
$$\begin{aligned} F_{2}\equiv & {} 3b(\chi -1)\chi d_{OL}+\pi \left( \chi d_{OL}\right) ^{2}\nonumber \\&+\,\pi b^{2}\left( 1+\chi ^{2}\right) , \end{aligned}$$
(35)
$$\begin{aligned} F_{3}\equiv & {} 4b(\chi -1)\chi d_{OL}+2\pi \left( \chi d_{OL}\right) ^{2}\nonumber \\&+\,\pi b^{2}\left( 1+\chi ^{2}\right) , \end{aligned}$$
(36)
$$\begin{aligned} G_{1}\equiv & {} \left[ b+d_{OL}\right] \left( 2b^{2}+bd_{OL}+2d_{OL}^{2}\right) , \end{aligned}$$
(37)
$$\begin{aligned} G_{2}\equiv & {} \left[ \frac{a+b+d_{OL}}{\left( 1+a/b\right) ^{3}}\right] \left[ 2\left( a+b\right) ^{2}+\left( a+b\right) d_{OL}\right. \nonumber \\&\left. +\,2d_{OL}^{2}\right] , \end{aligned}$$
(38)
$$\begin{aligned} G_{3}\equiv & {} \left[ \frac{b-\chi d_{OL}}{\chi ^{3}}\right] \left[ 2b^{2}-b\chi d_{OL}+2(\chi d_{OL})^{2}\right] , \end{aligned}$$
(39)
$$\begin{aligned} G_{4}\equiv & {} \left[ \frac{1}{\left( 1+a/b\right) ^{3}\chi ^{3}}\right] \left[ 2\left( a+b\right) ^{3}-3\left( a+b\right) ^{2}\chi d_{OL}\right. \nonumber \\&\left. +\,3(a+b)\left( \chi d_{OL}\right) ^{2}- 2(\chi d_{OL})^{3}\right] . \end{aligned}$$
(40)

The Eqs. (30, 32, 33) are central to the calculation of the delay. We shall plug the lens parameter values a, M, distance values b, \(d_{OL}\), \(\chi =d_{LS}/d_{OL}\) into these equations, take care to preserve small angles \( b/d_{OL}\), \(b/d_{LS}<<1\), and estimate the total time delay \(\varDelta t\) containing the Johannsen deviation parameters \(\lambda _{1}\) and \(\lambda _{2}\) for spinning BHs and lens galaxies (Tables 1, 2 and 3). While one manifestation of a spinning lens is relative time delay, another manifestation could be in the form of magnification of images, to which we turn next.

4 Magnification of images

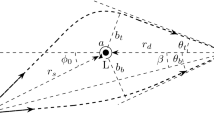
By measuring image positions in a static system, the Einstein angle \(\theta _{E}\) can be inferred. We shall replace the spinning lens system by a fictitious static system with \(\beta \ne 0\) effectively equivalent to the spinning lens system with \(\beta =0\) in the weak field limit. As deduced by Hartle [27], in a static lens system with \(\beta \ne 0\), the arrival times of the two images are different because of the difference \( \varDelta D\) in path length given in first order in \(\beta \) by \(\varDelta D\simeq \left( \frac{16\beta }{\theta _{E}}\right) M\). This yields a first order time difference \(\varDelta D/c\). The advantage of this static equivalent is that it facilitates the computation of the observable image shapes, individual and total magnifications, which are useful since a fluctuation in the magnification of the source will produce later fluctuation in the image, when it arrives at Earth.

If the lens were truly static, and the observer O, lens L, source S are perfectly aligned (\(\beta =0\)) along a line OLS, there would be no frame dragging, the rays from the source would traverse equal length to the observer, so there will be no time delay since the images would be placed symmetrically about the line OLS. However, due to the spinning, and consequent frame dragging, the incoming rays along the two different angles \( \gamma _{2}\) and \(\delta _{2}\) would now produce two images \(\theta _{\pm }\) situated asymmetrically on either side of the line OLS.

Fig. 2
figure 2

Fictitious “static lens” with \(\beta \ne 0\) equivalent to the spinning lens of Fig. 1 with \(\beta =0\). The images appear at \(I_{\pm }\) at two angular locations \(\theta _{\pm }\)

Full size image

Imagine a static lens with \(\beta \ne 0\),where \(\beta \) is the unlensed position angle of the source and \(\theta _{\pm }\) are the measured angular positions of the images (see Fig. 2), which are roots of the quadratic lens equation [27]

$$\begin{aligned} \theta ^{2}-\beta \theta -\theta _{E}^{2}=0. \end{aligned}$$
(41)

where \(\theta _{E}\) is the “Einstein angle” for some fictious distances in the static lens configuration (having “non-aligned” \(\beta \ne 0\)) that are different from \(d_{LS}\), \(d_{OS}\), \(d_{OL}\) used in the spinning configuration (having \(\beta =0\)). However, a value of \(\theta _{E}\) can be inferred from the observations of the image angles \(\theta _{\pm }\). Thus, we can identify from Figs. 1 and 2 that

$$\begin{aligned} \theta _{+}\equiv & {} \gamma _{2}=\cot ^{-1}\left( \frac{d_{OL}}{b}\right) , \end{aligned}$$
(42)
$$\begin{aligned} \theta _{-}\equiv & {} \delta _{2}=\cot ^{-1}\left( -\frac{d_{OL}}{a+b}\right) . \end{aligned}$$
(43)

so that we can write, from Eq. (42),

$$\begin{aligned} \theta _{+}+\theta _{-}= & {} \beta , \end{aligned}$$
(44)
$$\begin{aligned} \sqrt{-\theta _{+}\theta _{-}}= & {} \theta _{E}. \end{aligned}$$
(45)

It can be verified that the above values of \(\beta \) and \(\theta _{E}\) numerically yield the time delay deduced by Hartle [27]:

$$\begin{aligned} \varDelta t_{1}\simeq \varDelta D/c\simeq \left( \frac{\beta }{\theta _{E}}\right) \left( \frac{16M}{c}\right) . \end{aligned}$$
(46)

Comparing Eq. (31) for \(\varDelta t_{1}\) with \(\varDelta D/c\), we get \(a/b=\beta /\theta _{E}\), which then very nearly yields the other contributions \(\varDelta t_{2}\) and \(\varDelta t_{3}\) as well. The slight deviation is due to thin-lens approximation that can be improved. Note that time delay in a static system has been calculated by Virbhadra and Ellis [28] with the Einstein angle determined by the lens mass. In contrast, here \(\theta _{E}\) is determined from the lens geometry.

The values of \(\beta \) and \(\theta _{E}\) allow us to compute the shapes and magnifications (or ratios of brightness) of the images. Note that, while the azimuthal width \(\varDelta \phi \) is unchanged, the polar width \(\varDelta \theta _{\pm }\) of the images change and its magnitude can be obtained by differentiating Eq. (41):

$$\begin{aligned} \varDelta \theta _{\pm }=\left( \frac{1}{2}\right) \left[ 1\pm \frac{\beta }{ \sqrt{\beta ^{2}+4\theta _{E}^{2}}}\right] \varDelta \beta . \end{aligned}$$
(47)

Since the angular width of the source \(\varDelta \beta \ne 0\), this result implies a distorted and elongated shape of the images that have been confirmed by observations.

The ratio of the brighness of the individual images \(\mu _{\pm }\) to the unlensed brightness \(\mu _{*}\) at the angular positions \(\theta _{\pm }\) is given by the magnifications [27]

$$\begin{aligned} \frac{\mu _{\pm }}{\mu _{*}}= & {} \left| \left( \frac{\theta _{\pm }}{ \beta }\right) \left( \frac{d\theta _{\pm }}{d\beta }\right) \right| \nonumber \\= & {} \frac{1}{4}\left[ \frac{\beta }{\sqrt{\beta ^{2}+4\theta _{E}^{2}}}+\frac{ \sqrt{\beta ^{2}+4\theta _{E}^{2}}}{\beta }\pm 2\right] . \end{aligned}$$
(48)

We can draw a very interesting conclusion from here: Since from Eqs. (44) and (45) it follows that \(\beta <0\), we have \(\left| \mu _{-}\right| >\mu _{+}\) showing that the the image \(\theta _{-}\) on the counter-rotating side is brighter than the image \(\theta _{+}\) on the co-rotating side. Such observations would indicate that the intervening lens is spinning and provide determination of spin a if all other parameters are independently known. However, the magnitudes of brightness in any given sample do not differ very greatly thus making the individual measurements difficult. In this case, another very useful quantity is the total magnification over the background \(\mu _{*}\), called the magnification factor defined by

$$\begin{aligned} \frac{\mu _{\text {tot}}}{\mu _{*}}= & {} \frac{\mu _{+}-\mu _{-}}{\mu _{*}}=\frac{1}{2}\left| \frac{\beta }{\sqrt{\beta ^{2}+4\theta _{E}^{2}}}+\frac{\sqrt{\beta ^{2}+4\theta _{E}^{2}}}{\beta }\right| \nonumber \\= & {} \frac{1}{2}\left| \frac{\left( \beta /\theta _{E}\right) }{\sqrt{ \left( \beta /\theta _{E}\right) ^{2}+4}}+\frac{\sqrt{\left( \beta /\theta _{E}\right) ^{2}+4}}{\left( \beta /\theta _{E}\right) }\right| , \end{aligned}$$
(49)

the ratio being always greater than unity. Especially, when the equivalent \( \beta \) is small, that is, the source is very close to the optical axis OLS , the total magnification could be quite large that should be observable. The measurement of magnification can lead to the determination of \(\beta /\theta _{E}\). It is then possible to re-express the time delay components \( \varDelta t_{1},\varDelta t_{2},\varDelta t_{3}\) of Eqs. (30, 32, 33) in terms of the observable \(\beta /\theta _{E}\) using \(a/b=\beta /\theta _{E}\).

5 Numerical estimates

A possible scenario for detection of relative time delay would be provided by variable sources like pulsars, quasars, GRBs etc giving out signals at the instant they are behind the spinning lens on the optical axis OLS. Below we present some numerical estimates of the delay in different lensing situations.

(a) PSR-BH binaries

PSR-BH binary systems provide the best laboratory for testing the time delay predictions [9]. Though a concrete example of PSR-BH binary is yet to be detected, the prospects for discovery seem quite promising. Early estimate was that, of all pulsars discovered so far, only a small but significant number of them belong to a PSR-BH category with BH masses \(\sim 20M_{\odot }\) [29].

As is evident from the first two rows of the Table 1, the light rays pass very close to photon sphere \(b\approx 10^{0}r_{\text {ph}}^{+}\) so that all the delay components could be measurable but in this case the validity of the weak field metric expansion becomes doubtful since \(\frac{M}{b}\sim 10^{-1}\). In the 3rd and 4th row, \(\frac{M}{b}\sim 10^{-2}\) and the expansion could be just marginally valid. From the 5th to the last row, it is evident that as b continue to become larger than \(r_{\text {ph}}^{+}\), the leading order delays \(\varDelta t_{1}\) become comparable to those obtained in [30]. High precision measurement is best possible in the case of millisecond pulsars, and a precision of \(0.1\mu \)sec was obtained by van Straten et al. [31] for \(PSRJ0437-4715\), a bright millisecond pulsar in a White Dwarf-Neutron Star (WD-NS) binary system. However, unless the accuracy of measurement of total observed delay is raised to pico-second level, which is absurd today, there is no hope to estimate the values of the deviation parameters \(\lambda _{1}\) and \(\lambda _{2}\) by curve fitting.

(b) PSR-SgrA* lensing system

It is estimated that there are probably \(\sim 100\) pulsars surrounding the supermassive spinning BH SgrA* with orbital periods \(\lesssim \) 10 years [32] and a few among them are expected to form PSR-BH binaries with stellar sized BH companions residing within \(\sim 1\) parsec of SgrA* [33]. We shall assume the possibility that some of the pulsars (in binaries or not) may cross the optical axis OLS behind SgrA*.

We see that the delay could be as large as \(\sim 10\) s, when b is closest to \(r_{\text {ph}}^{+}\) allowed by the thin-lens condition for small angles. The weak field expansion of the metric is also valid since \(\frac{M}{ b}=7.1\times 10^{-3}\). All the components of the delay should be measurable provided an appropriate pulsar is identified in the future missions.

(c) Quasar–Galaxy lensing system

The Hubble Space Telescope has imaged the angular size of the Einstein rings of a number of lens galaxies, the observed Einstein angles are given in [30]. Also, more than 200,000 quasars are known, most from the Sloan Digital Sky Survey. The magnitude of all quasars have long been known to be intrinsically varying [35]. Therefore, there is good possibility that one one such quasar can be detected behind any lens galaxy. The observed time delay on Earth would be modified by the red-shift factor \((1+z_{L})\) of the lens such that \(\varDelta t=\left( \varDelta t_{1}+\lambda _{1}\varDelta t_{2}+\lambda _{2}\varDelta t_{3}\right) (1+z_{L})\) [36].

Table 3 below shows relative time delay components \(\varDelta t_{1},\varDelta t_{2},\varDelta t_{3}\) in seconds calculated from Eqs. (30, 32, 33) for a typical spiral galaxy NGC 224 chosen from the 67 samples tabulated by Romanowsky and Fall (see Table 4, p.47 in [18]). The valuesFootnote 4 are: \(d_{OL}=0.70\) Mpc, \(\log _{10}\left( M/M_{\odot }\right) =11.6\), \(a=2290\) km s\(^{-1}\)kpc (hence \(a/M=1.38\times 10^{3}\)), \( R_{d}=5.9\) kpc, \(z_{L}=\left( \frac{H}{c}\right) d_{OL}=1.68\times 10^{-4}\) (using linear Hubble law with the WMAP value of the Hubble constant \(H=72\) km sec\(^{-1}\)Mpc), \(\frac{\mu _{\text {tot}}}{\mu _{*}}=3.869\times 10^{3} \). Since there is no photon sphere for galaxies, the natural characteristic length here is the galactic disk scale length \(R_{d}\) specific to each sample and so we shall identify b to be \(R_{d}\) and multiples of it. Here \( \frac{M}{R_{d}}=9.33\times 10^{-7}\), hence metric expansion is valid. The red-shift correction to delay is too small. The source distances \( d_{LS}=\chi d_{OL}\) in Fig. 1 are varied ensuring that the angles remain small: \(\gamma _{1}\simeq \) tan\(\gamma _{1}=b/d_{LS}\simeq \delta _{1}\simeq \) tan\(\delta _{1}\)

Table 3 Table shows that for a chosen b, and for a range of source distances \( d_{LS}\) designated by \(\chi \), the delay components do not vary much. The leading order term \(\varDelta t_{1}\) is in hours, measurement of the next order \(\varDelta t_{2}\) requires an accuracy at \(\mu \)sec level, while that of \( \varDelta t_{3}\) requires nano-sec level accuracy. The Kerr metric is obtained by setting the deviation parameters \(\alpha _{22},\alpha _{13}\) and \(\alpha _{23}\) to zero so that, from Eq. (18), the last two columns in the table below should be multiplied by \(\lambda _{1}=1,\lambda _{2}=8\) respectively
Full size table

6 Conclusions

In the above, we had used RTD based on gravitational lensing as a possible dignostic for determining the status of the Penrose no-hair conjecture. To that end, we considered the generic metric of Johannsen and calculated the influence of its deviation parameters on the RTD. The Eqs. (30, 32, 33) generic in the weak field thin-lens approximation have been obtained on the basis of an analytical treatment of RTD within a realistic finite lensing system (Fig. 1). The derived equations have the flexibility to include different input values of lens mass M, spin a, distances of closest approach b and source distances \(d_{LS}\) within the stipulated approximations. We estimated not only the leading order delay \(\varDelta t_{1}\) but also other correction terms that are proportional to the redefined Johannsen deviation parameters \(\lambda _{1}\) and \(\lambda _{2}\) to be eventually determined by curve fitting to the observed data. They are constrained by lower limits \(\lambda _{1}>\frac{3}{4}\), \(\lambda _{2}>4\). If the fitted parameters are found to have exactly the Kerr values \(\lambda _{1}=1\) and \(\lambda _{2}=8\), then the observed delay would constitute a support for the no-hair theorem of general relativity. If they have values other than the Kerr values, the theorem would be falsified. However, either conclusion is still premature as the corresponding lens configurations are yet to be observationally identified and precise observational data obtained.

To our knowledge, so far RTD [a.k.a. different times of arrival (TOA) of pulses at the observer] calculations were carried out for two types of scenarios: One scenario considered TOA of the pulses sent out from diametrically opposite points on a fast spinning pulsar itself [37]. The other scenario considered a pulsar orbiting around a BH companion and used orbit parameters to determine b in Eq. (30), while the delay was obtained by numerically integrating the null geodesics in a Kerr background geometry [9]. The merit of the present work is that it belongs to neither of the two scenarios but presents an alternative perspective via a finite lensing configuration allowing the light rays to approach the photon sphere of the BHs (for galaxies, the disk radius) reasonably closely without violating the weak field thin-lens approximation.

Further, devising a “static” lens equivalent to a spinning lens (Fig. 2), a useful conclusion can be drawn from Eq. (48), viz., the image \(\theta _{-}\) on the counter-rotating side is brighter than the image \(\theta _{+} \) on the co-rotating side. Apart from this, it was shown how by measuring the magnification ratio, one could measure the RTD components. The components were estimated for three lensing systems using Eqs. ((30, 32, 33). The first system consists of anticipated PSR-BH binaries with stellar sized BH companion as considered in [9]. Table  1 shows that the expected \(\mu \)sec level delay can be predicted also from the lensing system with the adjustment of relevant distances and angles. The second one is the PSR-SgrA* lensing system for which the delays have been found to be at the level of seconds as shown in Table 2. The third one is the Quasar-Galaxy lensing system, where the leading order delay appears at the level of hours, although measurement of \(\varDelta t_{2}\) and \(\varDelta t_{3}\) would require nano-second and pico-second level accuracy respectively (Table 3). It must be emphasized that the values in the Tables are only indicative subject to the accurate detection of aligned lenses and variable sources. Currently planned astrophysical missions are expected to throw up a wealth of data that could tell us about the detectibility of such lensing systems.

Finally, even though the weak field effects could be reasonably large that can sample lens spin as a potential test of general relativity, the strong field effects are expected to reveal unforeseen characteristics. To discover these, one should ideally consider strong field deflection, where light rays pass very close to the photon spheres without being captured. In the spinning lens, the deflection angles of rays grazing the two photon spheres on either side of the lens will be highly asymmetric and large, resulting from the multiple winding of rays around the spheres before escaping away to observer. Further, the formula for the exact strong field deflection angle even in the Kerr BH metric has its own problems. The analytical expansion of the angle involving elliptic functions even at the zeroth order (Schwarzschild BH) already shows a logarithmic divergence at the photon sphere [25]. It would still be worthwhile to pursue this challenging task, perhaps numerically, in a future work.

An open question is whether it is possible to detect the inner structure of black holes, such as the existence of singularities, by using the outer effects of relative time delay or gravitational lens or any other astrophysical effect.Footnote 5 In our opinion, this possibility cannot a priori be ruled out since the hairs or deviation parameters \(\alpha _{22},\alpha _{13}\) and \(\alpha _{23}\) (or the redefined \(\lambda _{1}\) and \(\lambda _{2}\)) do contain information also of the inner structure of spacetime, notably the central singularity. The parameter values fitted to observations could indirectly detect the existence or otherwise of the singularity although the experimental accuracy required for this purpose would be quite challenging.