1 Introduction

Nowadays research in physics focused a lot attention on the evolution of the Universe and particularly on black holes and strange phenomena enclosed to it.The behavior of the matter and fields surrounding a black hole not only tells us about its presence but also helps us determine its parameters. The evolution of external field perturbation around black holes leads to damped oscillations called quasinormal modes (QNMs) [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. The QNMs of a black hole are defined as proper solutions of the perturbation equations belonging to certain complex characteristic frequencies, which satisfy the boundary conditions, appropriate for purely ingoing waves at the event horizon and purely outgoing waves at infinity [20]. QNMs of black holes are in general not complete and though insufficient to fully describe the dynamics, but contain a great amount of information. It is shown that QNMs can provide a direct way to identify a black hole existence in the universe since they carry the characteristic information of black holes [21, 22]. The QN frequencies are directly connected to the parameters of the black hole (mass, charge and angular momentum) and that means that QNMs will carry a unique “fingerprint” which would lead to the direct identification of the black hole existence. Clearly, the presence of perturbations affects the photon trajectories, causing some of the photons that would have crossed the horizon to escape and vice versa. This will significantly influence the shape and size of the shadow cast by the black hole on the surrounding emission. Moreover, the radial character of these perturbations causes light rays with different impact parameters to periodically bundle up and diverge, which will alter the brightness amplification introduced by gravitational lensing and lead to bright structures in the resulting images [23].

From recent measurements, we can see that our universe is dominated by a mysterious form of energy called “Dark Energy”. This kind of energy is responsible of the accelerated expansion of our universe. Today, inflation is quite well understood in terms of its phenomenology, but it still has a number of unresolved foundational questions. Despite these, it is certainly clear that cosmic inflation requires a period of cosmic acceleration that cannot be described by a cosmological constant [24, 25]. Cosmic inflation is understood to be driven by some matter field typically called the “inflaton”, which exhibits an equation of state \(p=\rho _q\omega _q\), where p is the pressure, \(\rho _q\) is the density of energy and \(\omega _q\) is the state parameter. In this category, we can find quintessence [26, 27], phantom [28], k-essence [29], and quintom [30, 31] models.

In 1968, the first example of a black hole with regular non-singular geometry with an event horizon satisfying weak energy condition was constructed by Bardeen [32]. The solution was obtained introducing an energy-momentum tensor interpreted as the gravitational field of some sort of nonlinear magnetic monopole charge \(\beta \). Recently, the quasinormal modes of the regular Bardeen black hole were investigated for gravitational perturbation [33], scalar perturbation [34,35,36], and Dirac perturbation [37]. Ghaderi and Malakolkalami [38] investigated the effects of quintessence on the thermodynamics of the black hole. In this paper, quasinormal modes of gravitational perturbation are investigated for the regular Bardeen black hole surrounded by quintessence.

The paper is organized as follows. In Sect. 2, the regular Bardeen black hole surrounded by quintessence is presented. In Sect. 3, we derive the wave equation for gravitational perturbation of the black hole using the Regge-Wheeler gauge. In Sect. 4, the quasinormal frequencies were evaluated by the help of third order WKB approximation. The last section is devoted to a conclusion.

2 The regular Bardeen black hole surrounded by quintessence

The spherically symmetric Bardeen regular black hole metric is given by

$$\begin{aligned} ds^2=-f(r)dt^2+f^{-1}(r)dr^2+r^2d\theta ^2+r^2\sin ^2\theta d\varphi ^2,\nonumber \\ \end{aligned}$$
(1)

where the lapse function \(f(r)=1-\frac{2M(r)}{r}\) depends on the specific form of underlying matter. With the following particular value of the mass function,

$$\begin{aligned} M(r)=\frac{mr^3}{(r^2+\beta ^2)^{3/2}}, \end{aligned}$$
(2)

where \(\beta \) is the monopole charge of a self-gravitating magnetic field described by a nonlinear electrodynamics source, and m is the mass of the black hole, the metric (1) reduces to the Bardeen regular black hole metric [32, 39,40,41].

Quintessence is a scalar field whose equation of state parameter, \(\omega _q\), is defined as a ratio of its pressure, p, and its energy density, \(\rho \) [42]. The pressure and the energy density of quintessence are given by \(p={\dot{\phi }}^2/2-V(\phi )\) and \(\rho ={\dot{\phi }}^2/2+V(\phi )\) [43]. The equation of state for quintessence is

$$\begin{aligned} \omega _q=\frac{p}{\rho }=\frac{{\dot{\phi }}^2/2-V(\phi )}{{\dot{\phi }}^2/2+V(\phi )}, \end{aligned}$$
(3)

with \(-1\le \omega _q\le -1/3\).

According to Kiselev’s investigations on quintessence and black holes [26], the general metric for static and spherically symmetric spacetime can be written as

$$\begin{aligned} ds^2=-\,e^\nu dt^2+e^\lambda dr^2+r^2d\theta ^2+r^2\sin ^2\theta d\varphi ^2, \end{aligned}$$
(4)

\(\lambda \) and \(\nu \) being functions of r.

Setting \(\lambda =-\ln (1+g)\), the energy-momentum tensor for homogeneous and isotropic matter field can be written as

$$\begin{aligned} T^t_t= & {} T^r_r=\rho =\frac{1}{2r^2}(g+rg'), \end{aligned}$$
(5)
$$\begin{aligned} T^\theta _\theta= & {} T^\phi _\phi =-\frac{1}{2}\rho (3\omega _q+1)=\frac{-1}{4r^2}(2g'+rg''). \end{aligned}$$
(6)

These expressions lead to the following equation,

$$\begin{aligned} (3\omega _q+1)g+3(\omega _q+1)rg'+r^2g''=0, \end{aligned}$$
(7)

which has as solution

$$\begin{aligned} g(r)=-\frac{r_g}{r}-\frac{c}{r^{3\omega _q+1}}, \end{aligned}$$
(8)

with \(c\ge 0\) and \(r_g\) the normalization factors.

Taking into account these statements, the metric of the black holes surrounded by the quintessence can be obtained by adding the quintessence term \(-\frac{c}{r^{3\omega _q+1}}\) to the metric of the black holes [38]. The metric of the regular Bardeen black hole in quintessence field can be expressed as

$$\begin{aligned} ds^2=-f(r)dt^2+f^{-1}(r)dr^2+r^2d\theta ^2+r^2\sin ^2\theta d\varphi ^2,\nonumber \\ \end{aligned}$$
(9)

with

$$\begin{aligned} f(r)=1-\frac{2mr^2}{(r^2+\beta ^2)^{3/2}}-\frac{c}{r^{3\omega _q+1}}, \end{aligned}$$
(10)

c is the normalization constant related to the density of quintessence \(\rho _q=-\frac{c}{2}\frac{3\omega _q}{r^{3\omega _q+3}}\), \(\omega _q\) is the state parameter of the quintessence \(-1\le \omega _q\le -1/3\).

3 Wave equation for Gravitational perturbation of the black hole

For the gravitational perturbation, we will deal with the Regge-Wheeler gauge [22]. In this gauge, the gravitational perturbation is regarded as perturbation to the background metric. We assume the perturbed background metric (\({\bar{g}}_{\mu \nu }\)) to be as the sum of the unperturbed metric (\(g_{\mu \nu }\)) and the perturbation in it (\(h_{\mu \nu }\))

$$\begin{aligned} {\bar{g}}_{\mu \nu }=g_{\mu \nu }+h_{\mu \nu }. \end{aligned}$$
(11)

The perturbations \(h_{\mu \nu }\) are supposed to be very small compared with \(g_{\mu \nu }\). The \(h_{\mu \nu }\) can be calculated from \(g_{\mu \nu }\), and \(R_{\mu \nu }+\delta R_{\mu \nu }\) from \(g_{\mu \nu }+h_{\mu \nu }\). The quantity \(\delta R_{\mu \nu }\) can be expressed in the form [44]

$$\begin{aligned} \delta {R}_{\mu \nu }=\delta {\varGamma }^{\alpha }_{\mu \alpha ,\nu }-\delta {\varGamma }^{\alpha }_{\mu \nu ,\alpha }, \end{aligned}$$
(12)

where

$$\begin{aligned} \delta {\varGamma }^{k}_{\mu \nu }=\frac{1}{2}g^{k\alpha }\big (h_{\alpha \nu ,\mu }+h_{\alpha \mu ,\nu }-h_{\mu \nu ,\alpha }\big ). \end{aligned}$$
(13)

Similarly, we will use the unperturbed Christoffel symbols in computing covariant derivatives of perturbation quantities. From Eq. (11), it follows that

$$\begin{aligned} {\bar{g}}^{\mu \nu }\simeq {g}^{\mu \nu }-h^{\mu \nu }. \end{aligned}$$
(14)

The perturbed Christoffel symbols are given by

$$\begin{aligned} {\bar{{\varGamma }}}^{k}_{\mu \nu }=\frac{1}{2}{\bar{g}}^{k\alpha }({\bar{g}}_{\alpha \nu ,\mu }+{\bar{g}}_{\alpha \mu ,\nu }-{\bar{g}}_{\mu \nu ,\alpha })={\varGamma }^{k}_{\mu \nu }+\delta {\varGamma }^{k}_{\mu \nu }, \end{aligned}$$
(15)

where

$$\begin{aligned} \delta {\varGamma }^{k}_{\mu \nu }=\frac{1}{2}g^{k\alpha }(h_{\alpha \nu ,\mu }+h_{\alpha \mu ,\nu }-h_{\mu \nu ,\alpha }). \end{aligned}$$
(16)

The last Eq. (16) reveals that the variation of the Christoffel symbols, \(\delta {\varGamma }^{k}_{\mu \nu }\), forms a tensor, even though the Christoffel symbols themselves do not.

Since the QNMs of a black hole undergo complex frequencies, they can easily be studied in the case of odd perturbations as they involve a simple differential equation [45]. Adopting the matching of Ref. [22], the final canonical form for an odd wave is then

$$\begin{aligned} h_{\mu \nu }= & {} \left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{} h_{0}(r) \\ 0 &{} 0 &{} 0 &{} h_{1}(r) \\ 0 &{} 0 &{} 0 &{} 0 \\ sym &{} sym &{} 0 &{} 0 \\ \end{array}\right) \nonumber \\&\exp (-ikT) (sin\theta \partial _{\theta })P_{l}(\cos \theta ). \end{aligned}$$
(17)

This form represents the perturbation of a spherically symmetric black hole in Regge-Wheeler gauge.

The radial wave equation is the final equation which gives us the behavior of the perturbation’s oscillation. It can be reduced to a simple linear differential equation.

In vacuum, the perturbed field equations are simply reduced to [46]

$$\begin{aligned} \delta {R}_{\mu \nu }=0. \end{aligned}$$
(18)

Using that and the background metric, we get from \(\delta {R}_{23}=0\),

$$\begin{aligned} f(r)^{-1}i\omega {h}_{0}+\frac{d}{dr}\Big [\Big (1-\frac{2mr^2}{(r^2+\beta ^2)^{3/2}}-\frac{c}{r^{3\omega _q+1}}\Big )h_{1}\Big ]=0,\nonumber \\ \end{aligned}$$
(19)

and from \(\delta {R}_{13}=0\),

$$\begin{aligned} f(r)^{-1}i\omega \Big (\frac{dh_{0}}{dr}+i\omega {h_{1}}-\frac{2h_{0}}{r}\Big )+(l-1)(l+2)\frac{h_{1}}{r^{2}}=0.\nonumber \\ \end{aligned}$$
(20)

Defining

$$\begin{aligned} \phi (r)=\Big (1-\frac{2mr^2}{(r^2+\beta ^2)^{3/2}}-\frac{c}{r^{3\omega _q+1}}\Big )h_{1}/r, \end{aligned}$$
(21)

and the tortoise coordinate \(r_*\),

$$\begin{aligned} \frac{dr_{*}}{dr}=\Big (1-\frac{2mr^2}{(r^2+\beta ^2)^{3/2}}-\frac{c}{r^{3\omega _q+1}}\Big )^{-1}, \end{aligned}$$
(22)

and eliminating \(h_{0}\), we then get

$$\begin{aligned} \Big (\frac{d^{2}}{dr^{2}_{*}}+\omega ^{2}\Big )\phi (r)=V\phi (r), \end{aligned}$$
(23)

where

$$\begin{aligned} V\!=\!f(r)\Big (\frac{(l-1)(l+2)}{r^{2}}-\frac{6mr^2}{(r^2+\beta ^2)^{3/2}}-\frac{3c(\omega _q+1)}{r^{3\omega _q+3}}\Big ).\nonumber \\ \end{aligned}$$
(24)

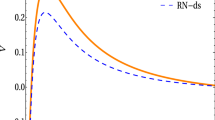
Equation (23) is a second order linear differential equation which represents a perturbation equation. The potential V depends explicitly on the radius r. Its behavior is represented on Fig.1.

Fig. 1
figure 1

Black hole’s effective potential

Full size image

Through this figure, we can see that the potential decreases with increasing c. That implies that the presence of quintessence reduces the magnitude of the gravitational potential.

Table 1 Quasinormal frequencies of gravitational perturbation of regular Bardeen black hole without quintessence
Full size table

4 Quasinormal frequencies

The wave equation ( 23) can be rewritten as:

$$\begin{aligned} \frac{d^{2}\psi }{dr^{2}_{*}}+Q(r_*)\psi =0, \end{aligned}$$
(25)

where \(Q(r_*)=\omega ^2-V(r_*)\). For a black hole, the QN frequencies correspond to solution of perturbation equation which satisfy the boundary conditions appropriate for purely ingoing waves at the horizon and purely outgoing waves at infinity. Incoming and outgoing waves correspond to the radial solution proportional to \(e^{-i\omega r_{*}}\) and \(e^{i\omega r_{*}}\), respectively. Only a discrete set of complex frequencies satisfies these conditions.

To evaluate the QN frequencies, we applied here the third order WKB approximation method derived by Schutz, Will [47] and Iyer [48] to the above equation and these QN frequencies are given by [49]

$$\begin{aligned} \omega ^{2}= & {} [V_{0}+(-2V''_{0})^{1/2}{\tilde{{\varLambda }}}] \nonumber \\&-i\left( n+\frac{1}{2}\right) (-2V''_{0})^{1/2}[1+{\tilde{{\varOmega }}}], \end{aligned}$$
(26)

where

$$\begin{aligned} {\tilde{{\varLambda }}}= & {} \frac{1}{(-2V''_{0})^{1/2}}\bigg \{\frac{1}{8} \bigg (\frac{V^{(4)}_{0}}{V''_{0}}\bigg ) \bigg (\frac{1}{4}+\alpha ^{2}\bigg )\\&-\frac{1}{288}\bigg (\frac{V'''_{0}}{V''_{0}}\bigg )^{2}(7+60\alpha ^{2})\bigg \}, \\ {\tilde{{\varOmega }}}= & {} \frac{1}{-2V''_{0}}\bigg \{\frac{5}{6912} \bigg (\frac{V'''_{0}}{V''_{0}}\bigg )^{4}(77+188\alpha ^{2})\\&-\frac{1}{384} \bigg (\frac{V'''^{2}_{0}V^{(4)}_{0}}{V''^{3}_{0}}\bigg ) (51+100\alpha ^{2})\\&-\frac{1}{288} \bigg (\frac{V^{(6)}_{0}}{V''_{0}}\bigg ) (5+4\alpha ^{2})\\&+\frac{1}{288}\bigg (\frac{V'''_{0}V^{(5)}_{0}}{V''^{2}_{0}}\bigg )(19+28\alpha ^{2})\\&+\frac{1}{2304}\bigg (\frac{V^{(4)}_{0}}{V''_{0}}\bigg )^{2} (67+68\alpha ^{2})\bigg \}, \end{aligned}$$

with \(\alpha =n+\frac{1}{2}\), and \(V^{(n)}_{0}=\frac{d^{n}V}{dr^{n}_{*}}|_{r_{*}=r_{*}(r_{p})}\).

Using Eq. (12), we calculated numerically the QN frequencies of the scalar field perturbation for \(M=1\) without and with quantum correction of the black hole. The results are shown in Tables 1, 2 and 3, where l is the harmonic angular index, n is the overtone number, \(\omega \) is the complex QN frequency, \(\beta \) is the monopole charge, \(\omega _q\) is the state parameter of the quintessence and c is the normalization constant related to the density of quintessence.

Table 2 Quasinormal frequencies of gravitational perturbation of regular Bardeen black hole surrounded by quintessence for \(\beta =0.5\) and \(c=0.01\)
Full size table
Table 3 Quasinormal frequencies of gravitational perturbation of regular Bardeen black hole surrounded by quintessence for \(\beta =0.5\) and \(c=0.02\)
Full size table

Through these tables, we can see that in the absence of quintessence, for \(\beta =0\), the obtained results coincide with those of the Schwarzschild black hole [50]. When increasing \(\beta \), the real parts of the quasinormal frequencies increase while the absolute values of the imaginary parts decrease and that is in agreement with the results of Ref. [33].

In the presence of quintessence, we can see that the real parts as well as the absolute value of the imaginary parts of the quasinormal frequencies decrease when increasing c or decreasing \(\omega _q\).

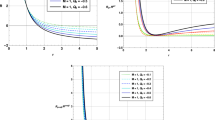
The relationship between the real and imaginary parts of quasinormal frequencies of the gravitational perturbation in the background of the black hole is plotted in Fig.2. We also plot the behavior of the gravitational perturbation for some frequencies. The results are shown in Fig. 3.

Fig. 2
figure 2

Behavior of the quasinormal frequencies for \(l=2\)

Full size image
Fig. 3
figure 3

Behavior of the gravitational perturbation for \(\beta =0.5\), \(c=0.02\) and \(l=2\)

Full size image

These figures show that when increasing c, the imaginary parts of the quasinormal frequencies increase while the real parts decrease. The gravitational perturbation damps more slowly when decreasing \(\omega _q\) and oscillates more slowly.

5 Conclusion

In summary, QNMs of graviatational perturbation have been investigated for the regular Bardeen black hole surrounded by quintessence. The quasinormal frequencies were evaluated using the third order WKB approximation. The results of Table 1 were obtained without considering any dark energy, while those of Tables 2 and 3 were obtained when considering the presence of quintessence dark energy in the background metric of the black hole. Through these tables, we can remark that the absolute values of the imaginary parts as well as the real parts of the quasinormal frequencies with quintessence are smaller compared to those without quintessence, for fixed set of l and n. Moreover, we can also remark that these values decrease when increasing c or when decreasing \(\omega _q\). That can be clearly seen through Figs. 2 and 3. On the other hand, increasing c or decreasing \(\omega _q\) implies increasing the density of quintessence. Thus, we can conclude that, due to the presence of quintessence, the quasinormal modes of gravitational perturbation of the regular Bardeen black hole damp more slowly and oscillate more slowly and this behavior increases when increasing the density of quintessence. That means that quintessence reduces the dissipative effect of the black hole on its neighborhood.