Neutrino mass, leptogenesis and FIMP dark matter in a $\mathrm{U}(1)_{B-L}$ model

Abstract

The Standard Model (SM) is inadequate to explain the origin of tiny neutrino masses, the dark matter (DM) relic abundance and the baryon asymmetry of the Universe. In this work, to address all three puzzles, we extend the SM by a local U$(1)_{B-L}$ gauge symmetry, three right-handed (RH) neutrinos for the cancellation of gauge anomalies and two complex scalars having non-zero U$(1)_{B-L}$ charges. All the newly added particles become massive after the breaking of the U$(1)_{B-L}$ symmetry by the vacuum expectation value (VEV) of one of the scalar fields $\phi _H$. The other scalar field, $\phi _\mathrm{DM}$, which does not have any VEV, becomes automatically stable and can be a viable DM candidate. Neutrino masses are generated using the Type-I seesaw mechanism, while the required lepton asymmetry to reproduce the observed baryon asymmetry can be attained from the CP violating out of equilibrium decays of the RH neutrinos in TeV scale. More importantly within this framework, we study in detail the production of DM via the freeze-in mechanism considering all possible annihilation and decay processes. Finally, we find a situation when DM is dominantly produced from the annihilation of the RH neutrinos, which are at the same time also responsible for neutrino mass generation and leptogenesis.

1 Introduction

The presence of non-zero neutrino mass and mixing has been confirmed by observing neutrino oscillations [1, 2] among its different flavours. Neutrino experiments have measured the three intergenerational mixing angles ($\theta _{12}, \theta _{23}, \theta _{13}$) and the two mass square differences ($\Delta m_{21}^{2}$ and $\Delta m_{32}^{2}$)¹ with an unprecedented accuracy [3,4,5,6,7,8,9,10]. Neutrinos are massless in the Standard Model (SM) of particle physics because in the SM there is no right-handed (RH) counterpart of the left-handed (LH) neutrinos. To generate tiny neutrino masses and their intergenerational mixing angles, as suggested by different experiments, we have to think of some new interactions and/or new particles beyond the Standard Model (BSM). Moreover, there are still some unsolved problems in the neutrino sector. For example, we do not know the exact octant of the atmospheric mixing angle $\theta _{23}$ i.e. whether it lies in the lower octant ($\theta _{23} < 45^{\circ }$) or in the higher octant ($\theta _{23} > 45^{\circ }$), the exact sign of $\Delta m^2_{32}$, which is related to the mass hierarchy between $m_2$ and $m_3$ (for the normal hierarchy (NH) $\Delta m^2_{32}>0$, while for the inverted hierarchy (IH) $\Delta m^2_{32}<0$) and as regards the Dirac CP phase $\delta$, responsible for the CP violation in the leptonic sector. Recently, T2K and No$\nu$A experiments have reported their preliminary result which predicts that the value of Dirac CP phase is around $\delta _\mathrm{CP} \sim 270^{\circ }$ [11]. Besides these, we do not know whether the neutrinos are Dirac or Majorana fermions. Observation of neutrino-less double $\beta$ decay [12,13,14,15,16,17] will confirm the Majorana nature of neutrinos and might also provide important information as regards the Majorana phases, which could be the other source of CP violation in the leptonic sector, if the SM neutrinos are Majorana fermions.

Besides these unsolved problems in the neutrino sector, another well-known puzzle in recent times is the presence of dark matter (DM) in the Universe. Many pieces of indirect evidence suggest the existence of DM. Among the most compelling pieces of evidence of DM are the observed flatness of rotation curves of spiral galaxies [18], gravitational lensing [19], the observed spatial offset between DM and visible matter in the collision of two galaxy clusters (e.g. the Bullet cluster [20], the Abell cluster [21, 22]) etc. The latter also imposes an upper bound on the ratio between self interaction and mass of DM particles, which is $\frac{\sigma _\mathrm{DM}}{M_\mathrm{DM}} \lesssim 1\,\mathrm{barn}/\mathrm{GeV}$ [23]. Moreover, satellite borne experiments like WMAP [24] and Planck [25] have made a precise measurement of the amount of DM present in the Universe from the cosmic microwave background (CMB) anisotropy and the current measured value of this parameter lies in the range $0.1172\le \Omega _\mathrm{DM} h^2\le 0.1226$ at 67% C.L. [25].

Despite the compelling observational evidence for DM due to its gravitational interactions, our knowledge about its particle nature is very limited.  The only thing we know about the DM is that it is very weakly interacting and electromagnetically blind.  The SM of particle physics does not have any fundamental particle which can play the role of a cold dark matter (CDM), consequently a BSM scenario containing new fundamental stable particle(s) is required. There are earth based ongoing DM direct detection experiments, namely Xenon-1T [26], LUX [27], CDMS [28, 29] amongst others, which have been trying to detect the weakly interacting massive particle (WIMP) [30,31,32] type DM by measuring recoil energies of the detector nuclei scattered by the WIMPs. However, no convincing DM signal has been found yet and hence the $M_\mathrm{DM}$–$\sigma _\mathrm{SI}$ plane for a WIMP type DM is now getting severely constrained. Therefore, invoking particle DM models outside the WIMP paradigm seems to be pertinent at this stage [33]. In the present work we study one of the possible alternatives of WIMP, namely, the feebly interacting massive particle (FIMP) [34,35,36,37,38,39,40,41,42,43]. A major difference between the WIMP and FIMP scenarios is that, while in the former case the DM particle is in thermal equilibrium with the plasma in the early Universe and freezes-out when the Hubble expansion rate becomes larger than its annihilation cross section, in the FIMP case the DM is never in thermal equilibrium with the cosmic soup. This is mainly ensured by its extremely weak couplings to other particles in the thermal bath. Therefore, the number density of the FIMP is negligible in the early Universe and increases when the FIMP is subsequently produced by the decays and annihilations of other particles to which it is coupled (very feebly). This process is generally known as freeze-in [34].

In addition to the above two unsolved problems, another long standing enigma is the presence of more baryons over anti-baryons in the Universe, which is known as the baryon asymmetry or the matter–antimatter asymmetry in the Universe. The baryon asymmetry observed in the Universe is expressed by a quantity $Y_{B}=\dfrac{\eta _{B}\,n_{\gamma }}{\mathrm{s}}$, where $\eta _{B}=n_{B}-n_{\bar{B}}$ is the excess in the number density for baryon over anti-baryon while $n_{\gamma }$ and $\mathrm{s}$ are the photon number density and the entropy density of the Universe, respectively. At the present epoch, $\eta _{B}= \left( 5.8--6.6 \right) \times 10^{-10}$ at 95% C.L. [44] while at $T\sim 2.73$ K, the photon density $n_{\gamma }=410.7\,\,\mathrm{cm}^{-3}$ [44] and the entropy density $\mathrm{s}=2891.2\,\,\mathrm{cm}^{-3}$ [44] (in natural unit with Boltzmann constant $K_\mathrm{B}=1$). Therefore, the observed baryon asymmetry at the present Universe is $Y_{B}=(8.24$–$9.38)\times 10^{-10}$, which, although small, is sufficient to produce the $\sim 5\%$ energy density (visible matter) of the Universe. To generate the baryon asymmetry in the Universe from a matter–antimatter symmetric state, one has to satisfy three necessary conditions, known as the Sakharov conditions [45,46,47,48]. These are: i) baryon number (B) violation, ii) C and CP violation and iii) departure from thermal equilibrium. Since the baryon number (B) is an accidental symmetry of the SM (i.e. all SM interactions are B conserving) and also the observed CP violation in quark sector is too small to generate the requited baryon asymmetry, like the previous cases, here also one has to look for some additional BSM interactions which by satisfying the Sakharov conditions can generate the observed baryon asymmetry in an initially matter–antimatter symmetric Universe.

In this work, we will try to address all of the three above mentioned issues. The non-observation of any BSM signal at LHC implies the concreteness of the SM. However, to address all the three problems, we need to extend the particles list and/or gauge group of SM because as already mentioned, the SM is unable to explain either of them. In our model, we extend the SM gauge group $\mathrm{SU}(3)_\mathrm{c}\times \mathrm{SU}(2)_\mathrm{L} \times \mathrm{U}(1)_\mathrm{Y}$ by a local $\mathrm{U}(1)_{B-L}$ gauge group. The ${B-L}$ extension of the SM [49,50,51,52] has been studied earlier in the context of DM phenomenology [53,54,55,56,57,58,59,60,61,62,63] and baryogenesis in the early Universe in Refs. [64,65,66]. Since we have imposed a local U(1) symmetry, consequently an extra gauge boson ($Z_\mathrm{BL}$) will arise. To cancel the anomaly due to this extra gauge boson we need to introduce three RH neutrinos ($N_{i}, i=1$, 2, 3) to make the model anomaly free. Apart from the three RH neutrinos, we also introduce two SM gauge singlet scalars namely $\phi _{H}$ and $\phi _\mathrm{DM}$, both of them are charged under the proposed $\mathrm{U}(1)_{B-L}$ gauge group. The $\mathrm{U}(1)_{B-L}$ symmetry is spontaneously broken when the scalar field $\phi _{H}$ takes a non-zero vacuum expectation value (VEV) and thereby generates the masses for the three RH neutrinos as well as the extra neutral gauge boson $Z_\mathrm{BL}$, whose mass terms are forbidden initially due to the $\mathrm{U}(1)_{B-L}$ invariance of the Lagrangian. The other scalar $\phi _\mathrm{DM}$ does not acquire any VEV and by choosing appropriate ${B-L}$ charge $\phi _\mathrm{DM}$ becomes naturally stable and therefore, can serve as a viable DM candidate. As mention above, anomaly cancellation requires the introduction of three RH neutrinos in the present model. Therefore we can easily generate the neutrino masses by the Type-I seesaw mechanism after ${B-L}$ symmetry is broken. Diagonalising the light neutrino mass matrix ($m_{\nu }$, for details see Sect. 3.1), we determine the allowed parameter space by satisfying the $3\sigma$ bounds on the mass square differences ($\Delta m_{12}^{2}$, $\Delta m_\mathrm{atm}^{2}$), the mixing angles ($\theta _{12}, \theta _{13}, \theta _{23}$) [67] and the cosmological bound on the sum of three light neutrinos masses [25]. We also determine the effective mass $m_{\beta \beta }$, which is relevant for neutrino-less double beta decay and compare it with the current bound on $m_{\beta \beta }$ from the GERDA phase I experiment [13].

Next, we explain the possible origin of the baryon asymmetry at the present epoch from an initially matter–antimatter symmetric Universe via leptogenesis. We first generate the lepton asymmetry (or ${ B-L}$ asymmetry, $Y_{B-L}$) from the out of equilibrium, CP violating decays of the RH neutrinos. The lepton asymmetry thus produced has been converted into the baryon asymmetry by the ($B+L$) violating sphaleron processes, which are effective before and during electroweak phase transition [68,69,70]. When the sphaleron processes are in thermal equilibrium ($10^{12}\,\mathrm{GeV} \,\lesssim T \lesssim 10^2$ GeV, T being the temperature of the Universe), the conversion rate is given by [71]

$$\begin{aligned} Y_{B} = - \frac{8 N_{f} + 4 N_{\phi _{h}}}{22 N_{f} + 13 N_{\phi _{h}}} Y_{B-L}\,\,, \end{aligned}$$

(1)

where $N_{f}= 3$ and $N_{\phi _{h}}= 1$, are the number of fermionic generations and number of Higgs doublet in the model, respectively.

Finally, in order to address the DM issue, we consider the singlet scalar $\phi _\mathrm{DM}$ as a DM candidate. Since the couplings of this scalar to the rest of the particles of the model are free parameters, they could take any value. Depending on the value of these couplings, we could consider $\phi _\mathrm{DM}$ as a WIMP or a FIMP. Detailed study on the WIMP type scalar DM in the present $\mathrm{U}(1)_{B-L}$ framework has been done in Refs. [59, 60, 72]. In most of the earlier works, it has been shown that the WIMP relic density is mainly satisfied around the resonance regions of the mediator particles. Moreover, the WIMP parameter space has now become severely constrained due to non-observation of any “real” signal in various direct detection experiments. Thus, as discussed earlier, in this situation the study of scalar DM other than WIMP is worthwhile. Therefore in this work, we consider the scalar field $\phi _\mathrm{DM}$ as a FIMP candidate which, depending on its mass, is dominantly produced from the decays of heavy bosonic particles such as $h_1$, $h_2$, $Z_\mathrm{BL}$ and from the annihilations of bosonic as well as fermionic degrees of freedom present in the model (e.g. $N_i$, $Z_\mathrm{BL}$, $h_i$ etc.). In particular, in Ref. [43], we have also studied a SM singlet scalar as the FIMP type DM candidate in a $L_{\mu } - L_{\tau }$ gauge extension of the SM. In that work, we have considered the extra gauge boson mass in MeV range to explain the muon $(g-2)$ anomaly. Consequently, the production of $\mathcal {O}$(GeV) DM from the decay of $Z_{\mu \tau }$ is forbidden. Additionally, in that model due to the considered $L_{\mu } - L_{\tau }$ flavour symmetry the neutrino mass matrices (both light and heavy neutrinos) have a particular shape. On the other hand, in the present work, we extensively study the FIMP DM production mechanism from all possible decays and annihilations other particles present in the model. Moreover, we have found that depending on our DM mass, a sharp correlation exists between the three puzzles of astroparticle physics, namely neutrino mass generation, leptogenesis and DM. Furthermore, in Ref.  [40], one of us, along with collaborators, has studied the freeze-in DM production mechanism in the framework of U(1)$_{B-L}$ extension of the SM. However, in that article one has considered an MeV range RH neutrino as the FIMP DM candidate. Thus, in the context of DM phenomenology the current work is vastly different from Ref.  [40].

In the non-thermal scenario, most of the production of the FIMP from the decay of a heavy particle occurs when $T\sim M$, where M is the mass of the decaying mother particle, which is generally assumed to be in thermal equilibrium. Therefore, the non-thermality condition of the FIMP demands that $\dfrac{\Gamma }{H}<1\bigg |_{T\sim M}$ [73], which in turn imposes a severe upper bound on the coupling strengths of the FIMP. Thus the non-thermality condition requires an extremely small coupling of $\phi _\mathrm{DM}$ with the thermal bath ($\lesssim 10^{-10}$) and, hence, FIMP DM can easily evade all the existing bounds from DM direct detection experiments [26,27,28].

The rest of the paper has been arranged in the following manner. In Sect. 2 we discuss the model in detail. In Sect. 3 we present the main results of the paper. In particular, we discuss the neutrino phenomenology in Sect. 3.1, baryogenesis via leptogenesis in Sect. 3.2 and non-thermal FIMP DM $\phi _\mathrm{DM}$ production in Sect. 3.3. Finally in Sect. 4 we end with our conclusions.

2 Model

The gauged $\mathrm{U}(1)_{B-L}$ extension of the SM is one of the most extensively studied BSM models so far. In this model, the gauge sector of the SM is enhanced by imposing a local $\mathrm{U}(1)_{B-L}$ symmetry to the SM Lagrangian, where B and L represent the respective baryon and lepton number of a particle. Therefore, the complete gauged group is $\mathrm{SU}(3)_\mathrm{c}\times \mathrm{SU}(2)_\mathrm{L} \times \mathrm{U}(1)_\mathrm{Y}\times \mathrm{U}(1)_{B-L}$. Since the $\mathrm{U}(1)_{B-L}$ extension of the SM is not an anomaly free theory, we need to introduce some chiral fermions to cancel the anomaly. In order to achieve this, we consider three extra RH neutrinos to make the proposed ${ B-L}$ extension anomaly free. Besides the SM particles and three RH neutrinos, we introduce two SM gauge singlet scalars $\phi _H$, $\phi _\mathrm{DM}$ in the theory with suitable ${B-L}$ charges. One of the scalar fields, namely $\phi _H$, breaks the proposed $\mathrm{U}(1)_{B-L}$ symmetry spontaneously by acquiring a non-zero VEV $v_\mathrm{BL}$ and thereby generates masses to all the BSM particles. We choose the ${ B-L}$ charge of $\phi _\mathrm{DM}$ in such a way that the Lagrangian of our model before the $\mathrm{U}(1)_{B-L}$ symmetry breaking does not contain any interaction term involving odd powers of $\phi _\mathrm{DM}$. When $\phi _H$ gets a non-zero VEV, this $\mathrm{U}(1)_{B-L}$ symmetry breaks spontaneously into a remnant $\mathbb {Z}_2$ symmetry under which only $\phi _\mathrm{DM}$ becomes odd. The $\mathbb {Z}_2$ invariance of the Lagrangian will be preserved as long as the parameters of the Lagrangian are such that the scalar field $\phi _\mathrm{DM}$ does not get any VEV. Under this condition, the scalar field $\phi _\mathrm{DM}$ becomes absolutely stable and, in principle, can serve as a viable DM candidate. The respective SU(2)$_\mathrm{L}$, U(1)$_\mathrm{Y}$ and $\mathrm{U}(1)_{B-L}$ charges of all the particles in the present model are listed in Table 1.

Table 1 Charges of all particles under various symmetry groups

The complete Lagrangian for the model is as follows:

$$\begin{aligned} \mathcal {L}= & {} \mathcal {L}_\mathrm{SM} + \mathcal {L}_\mathrm{DM} + (D_{\mu }\phi _{H})^{\dagger } (D^{\mu }\phi _{H}) -\frac{1}{4} {F_\mathrm{BL}}_{\mu \nu } {F_\mathrm{BL}}^{\mu \nu } \nonumber \\&+ \frac{i}{2}\bar{N_i}\gamma ^{\mu }D_{\mu } N_{i} -V(\phi _{h},\phi _{H})\nonumber \\&-\sum _{i=1}^3 \frac{y_{N_{i}}}{2} \phi _{H} \bar{N^{c}_{i}} N_{i} -\sum _{i,\,j=1}^3 y_{ij}^{\prime } \bar{L_{i}} \tilde{\phi _{h}} N_{j} +h.c.\,, \end{aligned}$$

(2)

with $\tilde{\phi _h} = i \sigma _2 \phi ^*_h$. The term $\mathcal {L}_\mathrm{SM}$ and $\mathcal {L}_\mathrm{DM}$ represent the SM and dark sector Lagrangian, respectively. The dark sector Lagrangian $\mathcal {L}_\mathrm{DM}$ containing all possible gauge invariant interaction terms of the scalar field $\phi _\mathrm{DM}$ has the following form:

$$\begin{aligned} \mathcal {L}_\mathrm{DM}= & {} (D^{\mu }\phi _\mathrm{DM})^{\dagger } (D_{\mu }\phi _\mathrm{DM}) - \mu _\mathrm{DM}^{2} (\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM})\nonumber \\&-\lambda _\mathrm{DM}\,(\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM})^{2} -\lambda _{Dh}\,(\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}) (\phi _{h}^{\dagger } \phi _{h}) \nonumber \\&-\lambda _{DH}\,(\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}) (\phi _{H}^{\dagger } \phi _{H})\,, \end{aligned}$$

(3)

where the interactions of $\phi _\mathrm{DM}$ with $\phi _h$ and $\phi _H$ are proportional to the couplings $\lambda _\mathrm{Dh}$ and $\lambda _\mathrm{DH}$, respectively. The fourth term in Eq. (2) represents the kinetic term for the additional gauge boson $Z_\mathrm{BL}^{\mu }$ in terms of field strength tensor ${F_\mathrm{BL}}_{\mu \nu }$ of the $\mathrm{U}(1)_{B-L}$ gauge group. The covariant derivatives involving in the kinetic energy terms of the BSM scalars and fermions, $\phi _H$, $\phi _\mathrm{DM}$ and $N_i$ (Eq. (2)), can be expressed in a generic form

$$\begin{aligned} D_\mu \psi = (\partial _{\mu } + i\,g_\mathrm{BL}\,Q_\mathrm{BL}(\psi ) \,{Z_\mathrm{BL}}_{\mu })\,\psi \,, \end{aligned}$$

(4)

where $\psi = \phi _\mathrm{DM}, \phi _H$, $N_i$ and $Q_\mathrm{BL}(\psi )$ represents the ${B-L}$ charge of the corresponding field (listed in Table 1). The quantity $V(\phi _h, \phi _H)$ in Eq. (2) contains the self interaction terms of $\phi _{H}$ and $\phi _h$ as well as the mutual interaction term between the two scalar fields. The expression of $V(\phi _h, \phi _H)$ is given by

$$\begin{aligned} V(\phi _h, \phi _H)= & {} \mu _{H}^{2} \phi _{H}^{\dagger } \phi _{H} + \mu _{h}^{2} \phi _{h}^{\dagger } \phi _{h} + \lambda _{H} (\phi _{H}^{\dagger } \phi _{H})^{2} \nonumber \\&+ \lambda _{h} (\phi _{h}^{\dagger } \phi _{h})^{2} + \lambda _{hH}(\phi _{h}^{\dagger } \phi _{h}) (\phi _{H}^{\dagger } \phi _{H})\,. \end{aligned}$$

(5)

After the symmetry breaking, the SM Higgs doublet $\phi _{h}$ and the BSM scalar $\phi _{H}$ take the following form:

$$\begin{aligned} \phi _{h}= \begin{pmatrix} 0 \\ \dfrac{v+H}{\sqrt{2}} \end{pmatrix} \,\,\,\,\,\,\,\,\, \phi _{H}= \begin{pmatrix} \dfrac{v_\mathrm{BL}+H_{BL}}{\sqrt{2}} \end{pmatrix}\,\,, \end{aligned}$$

(6)

where $v = 246$ GeV is the VEV of $\phi _{h}$, which breaks the SM gauge symmetry into a residual U(1)$_\mathrm{EM}$ symmetry. The remaining terms in Eq. (2) are the Yukawa interaction terms for the LH and RH neutrinos. As mentioned in the beginning of this section, when the extra scalar field $\phi _H$ gets a non-zero VEV $v_\mathrm{BL}$, the proposed $\mathrm{U}(1)_{B-L}$ gauge symmetry breaks spontaneously. As a result, the Majorana mass terms for the RH neutrinos, proportional to the Yukawa couplings $y_{N_i}$, are generated. In general, for three generations of RH neutrinos, we will have a $3\times 3$ Majorana mass matrix $\mathcal {M_{R}}$ with all off-diagonal terms present. However, in the present scenario for calculational simplicity we choose a basis for the $N_i$ fields with respect to which $\mathcal {M_{R}}$ is diagonal. The diagonal elements, representing the masses of $N_i$s, are given by

$$\begin{aligned} M_{N_i}= & {} \dfrac{y_{N_i}}{\sqrt{2}} v_\mathrm{BL} \,. \end{aligned}$$

(7)

Like the three RH neutrinos, the extra neutral gauge boson also becomes massive through Eq. (4) when $\phi _H$ picks up a VEV. The mass term $Z_\mathrm{BL}$ is given by

$$\begin{aligned} M_{Z_\mathrm{BL}}= & {} 2\,g_\mathrm{BL}\,v_\mathrm{BL}\,. \end{aligned}$$

(8)

When both $\phi _h$ and $\phi _H$ obtain their respective VEVs, there will be a mass mixing between the states H and $H_\mathrm{BL}$. The mass matrix with respect to the basis H and $H_\mathrm{BL}$ looks as follows:

$$\begin{aligned} \mathcal {M}^2_{scalar} = \left( \begin{array}{cc} 2\lambda _h v^2 &{} \lambda _{hH}\,v_\mathrm{BL}\,v \\ \lambda _{hH}\,v_\mathrm{BL}\,v ~~&{}~~ 2 \lambda _H v^2_\mathrm{BL} \end{array}\right) \,\,. \end{aligned}$$

(9)

Rotating the basis states H and $H_\mathrm{BL}$ by a suitable angle $\alpha$, we can make the above mass matrix diagonal. The new basis states ($h_1$ and $h_2$), with respect to which the mass matrix $\mathcal {M}^2_{scalar}$ becomes diagonal, are some linear combinations of earlier basis states H and $H_\mathrm{BL}$. The new basis states, now representing the two physical states, are defined as

$$\begin{aligned} h_{1}= & {} H \cos \alpha + H_\mathrm{BL} \sin \alpha \,, \nonumber \\ h_{2}= & {} - H \sin \alpha + H_\mathrm{BL} \cos \alpha \,, \end{aligned}$$

(10)

where we denote by $h_1$ the SM-like Higgs boson, while $h_2$ is playing the role of a BSM scalar field. The mixing angle between H and $H_\mathrm{BL}$ can be expressed in terms of the parameters of the Lagrangian (cf. Eq. (2)):

$$\begin{aligned} \tan 2\alpha = \dfrac{\lambda _{hH}\,v_\mathrm{BL}\,v}{\lambda _h v^2 - \lambda _H v^2_\mathrm{BL}}\,. \end{aligned}$$

(11)

Besides the two physical scalar fields $h_1$ and $h_2$, as mentioned earlier, there is another scalar field ($\phi _\mathrm{DM}$) in the present model, which can play the role of a DM candidate. The masses of these three physical scalar fields $h_1$, $h_2$ and $\phi _\mathrm{DM}$ are given by

$$\begin{aligned} M^2_{h_1}= & {} \lambda _h v^2 + \lambda _H v_\mathrm{BL}^2 \nonumber \\&- \sqrt{(\lambda _h v^2 - \lambda _H v_\mathrm{BL}^2)^2 + (\lambda _{hH}\,v\,v_\mathrm{BL})^2} \ ,\nonumber \\ M^2_{h_2}= & {} \lambda _h v^2 + \lambda _H v^2_s \nonumber \\&+ \sqrt{(\lambda _h v^2 - \lambda _H v_\mathrm{BL}^2)^2 + (\lambda _{hH}\,v\,v_\mathrm{BL})^2}\,, \nonumber \\ M^2_\mathrm{DM}= & {} \mu ^2_\mathrm{DM} + \frac{\lambda _{Dh} v^2}{2} + \frac{\lambda _{DH} v^2_\mathrm{BL}}{2}\,, \end{aligned}$$

(12)

where $M_{x}$ ² denotes the mass of the corresponding scalar field x.

In this work, we choose $M_{h_2}$, $M_\mathrm{DM}$, $n_\mathrm{BL}$, $M_{N_i}$, $M_{Z_\mathrm{BL}}$, $g_\mathrm{BL}$, $\alpha$, $\lambda _\mathrm{Dh}$, $\lambda _\mathrm{DH}$ and $\lambda _\mathrm{DM}$ as our independent set of parameters. The other parameters in the Lagrangian, namely $\lambda _{h}$, $\lambda _{H}$, $\lambda _{hH}$, $\mu _{\phi _{h}}^{2}$ and $\mu _{\phi _{H}}^{2}$, can be expressed in terms of these variables as follows [72]:

$$\begin{aligned} \lambda _{H}= & {} \dfrac{M_{h_{1}}^{2} + M_{h_{2}}^{2} + (M_{h_{2}}^{2} - M_{h_{1}}^{2})\cos 2 \alpha }{4\,v_\mathrm{BL}^{2}}\,,\nonumber \\ \lambda _{h}= & {} \dfrac{M_{h_{1}}^{2} + M_{h_{2}}^{2} + (M_{h_{1}}^{2} - M_{h_{2}}^{2})\cos 2 \alpha }{4\,v^{2}}\,,\nonumber \\ \lambda _{hH}= & {} \dfrac{(M_{h{1}}^{2}-M_{h_{2}}^{2}) \cos \alpha \sin \alpha }{v\,v_\mathrm{BL}}\,,\nonumber \\ \mu _{\phi _{h}}^{2}= & {} - \dfrac{(M_{h_1}^{2}+M_{h_2}^{2})v +(M_{h_1}^{2}-M_{h_2}^{2})(v \cos 2 \alpha + v_\mathrm{BL} \sin 2 \alpha )}{4\,v} \,,\nonumber \\ \mu _{\phi _{H}}^{2}= & {} \dfrac{-(M_{h_1}^{2}+M_{h_2}^{2})v_\mathrm{BL} + (M_{h_1}^{2}-M_{h_2}^{2})(v_\mathrm{BL}\cos 2 \alpha - v \sin 2 \alpha )}{4\,v_\mathrm{BL}}\,,\nonumber \\ \mu ^2_\mathrm{DM}= & {} {M}^2_\mathrm{DM}- \frac{\lambda _{Dh} v^2}{2} - \frac{\lambda _{DH} v^2_\mathrm{BL}}{2}\,, \end{aligned}$$

(13)

where $v_\mathrm{BL}$ is defined in terms of $M_{Z_\mathrm{BL}}$ and $g_\mathrm{BL}$ in Eq. (8).

As we already know, in the present scenario two of the three scalar fields, namely $\phi _h$ and $\phi _H$, obtain VEVs. On the other hand, the remaining scalar field $\phi _\mathrm{DM}$ does not have any VEV, which ensures its stability by preserving its $\mathbb {Z}_2$ odd parity. Therefore, the ground state of the system is ($\langle \phi _h\rangle$, $\langle \phi _H\rangle$, $\langle \phi _\mathrm{DM}\rangle$) = (v, $v_\mathrm{BL}$, 0). Now, such a ground state (vacuum) will be bounded from below when the following inequalities are satisfied simultaneously [72]:

$$\begin{aligned}&\mu ^2_{\phi _h}< 0, \mu ^2_{\phi _H} < 0 , \mu ^2_\mathrm{DM} > 0\,,\nonumber \\&\lambda _h \ge 0, \lambda _H \ge 0, \lambda _\mathrm{DM} \ge 0,\nonumber \\&\lambda _{hH} \ge - 2\sqrt{\lambda _h\,\lambda _H},\nonumber \\&\lambda _{Dh} \ge - 2\sqrt{\lambda _h\,\lambda _\mathrm{DM}},\nonumber \\&\lambda _{DH} \ge - 2\sqrt{\lambda _H\,\lambda _\mathrm{DM}},\nonumber \\&\sqrt{\lambda _{hH}+2\sqrt{\lambda _h\,\lambda _H}}\sqrt{\lambda _{Dh}+ 2\sqrt{\lambda _h\,\lambda _\mathrm{DM}}} \sqrt{\lambda _{DH}+2\sqrt{\lambda _H\,\lambda _\mathrm{DM}}} \nonumber \\&+ 2\,\sqrt{\lambda _h \lambda _H \lambda _\mathrm{DM}} + \lambda _{hH} \sqrt{\lambda _\mathrm{DM}} + \lambda _{Dh} \sqrt{\lambda _H} + \lambda _{DH} \sqrt{\lambda _h} \ge 0. \end{aligned}$$

(14)

Besides the lower limits of $\lambda$s as described by the above inequalities, there are also upper limits on the Yukawa and quartic couplings arising from the perturbativity condition, which demands that the Yukawa and scalar quartic couplings have to be less than $\sqrt{4\,\pi }$ ($y<\sqrt{4\,\pi }$) and $4\,\pi$ ($\lambda < 4\,\pi$), respectively [74].

3 Results

3.1 Neutrino masses and mixing

As mentioned earlier, the cancellation of both axial vector anomaly [75, 76] and gravitational gauge anomaly [77, 78], in $\mathrm{U}(1)_{B-L}$ extended SM, requires the presence of extra chiral fermions. Hence, in the present model to cancel these anomalies we introduce three RH neutrinos ($N_{i}$, $i=1$–3). The Majorana masses for the RH neutrinos are generated only after spontaneous breaking of the proposed ${B-L}$ symmetry by the VEV of $\phi _H$. Also, in the present scenario, as stated earlier, we are working in a basis where the Majorana mass matrix for the three RH neutrinos are diagonal, i.e. $\mathcal {M_{R}}= \mathrm{diag}\,(M_{N_1}, M_{N_2}, M_{N_3})$. The expression for the mass of the ith RH neutrino ($M_{N_i}$) is given in Eq. (7). On the other hand, the Dirac mass terms involving both left chiral and right chiral neutrinos originate when the electroweak symmetry is spontaneously broken by the VEV of the SM Higgs doublet $\phi _h$, giving rise to a $3\times 3$ complex matrix $\mathcal {M_{D}}$. In general, one can take all the elements of matrix $\mathcal {M_{D}}$ as complex but for calculational simplicity and keeping in mind that only three physical phases (one Dirac phase and two Majorana phases) exist for three light neutrinos (Majorana type), we consider only three complex elements in the lower triangle part of the Dirac mass matrix $\mathcal {M_{D}}$. However, the results we shall present later in this section will not change significantly if we consider all the elements of $\mathcal {M_{D}}$ to be complex. The Dirac mass matrix $\mathcal {M_{D}}$ we assume has the following structure:

$$\begin{aligned} \mathcal {M}_{D} = \left( \begin{array}{ccc} y_{ee} &{} y_{e\mu } &{}y_{e\tau } \\ y_{\mu e} + i\,\tilde{y}_{\mu e} &{} y_{\mu \mu } &{} y_{\mu \tau }\\ y_{\tau e} + i\,\tilde{y}_{\tau e} &{} y_{\tau \mu } + i\,\tilde{y}_{\tau \mu } &{} y_{\tau \tau } \\ \end{array}\right) \,, \end{aligned}$$

(15)

where $y_{ij} = \dfrac{y_{ij}^{\prime }}{\sqrt{2}} v$ ($i,j =$ e, $\mu$, $\tau$) and the Yukawa coupling $y_{ij}^{\prime }$ has been defined in Eq. (2).

Now, with respect to the Majorana basis $\left( \overline{{\nu _\alpha }_L} \,\,\overline{({N_{\alpha }}_R)^c}\right) ^T$ and $\left( ({\nu _\alpha }_L)^c ~~{N_{\alpha }}_R\right) ^T$ one can write down the Majorana mass matrix for both left and right chiral neutrinos using $\mathcal {M_{D}}$ and $\mathcal {M_{R}}$ matrices in the following way:

$$\begin{aligned} M = \left( \begin{array}{cc} 0 &{} \mathcal {M_{D}}\\ \mathcal {M_{D}}^{T} &{} \mathcal {M_{R}}\end{array}\right) \,\,. \end{aligned}$$

(16)

Since $M_{D}$ and $M_{R}$ are both $3\times 3$ matrices (for three generations of neutrinos), the resultant matrix M will be of order $6\times 6$ and it is a complex symmetric matrix which reflects its Majorana nature. Therefore, after diagonalisation of the matrix M, we get three light and three heavy neutrinos, all of which are Majorana fermions. If we use the block diagonalisation technique, we can write the light and heavy neutrino mass matrices in the leading order as

$$\begin{aligned} m_{\nu }\simeq & {} -\mathcal {M_{D}}\,\mathcal {M_{R}}^{-1} \mathcal {M_{D}}^T\,, \end{aligned}$$

(17)

$$\begin{aligned} m_N\simeq & {} \mathcal {M_{R}}\,. \end{aligned}$$

(18)

Here $M_{R}$ is a diagonal matrix and the expression of all the elements of $m_{\nu }$ in terms of the elements of $\mathcal {M_{D}}$ and $\mathcal {M_{R}}$ matrices are given in Appendix A. After diagonalising the ${m_{\nu }}$ matrix we get three light neutrino masses ($m_i$, $i=1,\,2,\,3$), three mixing angles ($\theta _{12}$, $\theta _{13}$ and $\theta _{23}$) and one Dirac CP phase $\delta$.

We use the Jarlskog invariant $J_\mathrm{CP}$ [79] to determine the Dirac CP phase $\delta$, which is defined as

$$\begin{aligned} J_\mathrm{CP} = \frac{1}{8} \sin 2\theta _{12} \sin 2\theta _{23} \sin 2\theta _{13} \cos \theta _{13} \sin \delta . \end{aligned}$$

(19)

Moreover, the quantity $J_\mathrm{CP}$ is related to the elements of the Hermitian matrix $h=m_{\nu }m^{\dagger }_{\nu }$ in the following way:

$$\begin{aligned} J_\mathrm{CP} = \frac{\mathrm{Im}\,(h_{13} h_{23} h_{31})}{\Delta m^{2}_{21}\, \Delta m^{2}_{32}\, \Delta m^{2}_{31}}\,\,, \end{aligned}$$

(20)

where in the numerator $\mathrm{Im} (X)$ represents the imaginary part of X, while in the denominator $\Delta m^{2}_{ij} = m^{2}_{i} - m^{2}_{j}$. Once we determine the quantity $J_\mathrm{CP}$ (from Eq. (20)) and the intergenerational mixing angles of neutrinos, one can easily determine the Dirac CP phase using Eq. (19).

In the present scenario we have 12 independent parameters coming from the Dirac mass matrix. The RH neutrino mass matrix, in principle, should bring about three additional parameters. However, as we will discuss in detail in Sect. 3.2, two of the RH neutrino masses are taken to be nearly degenerate. In particular, the condition of resonant leptogenesis requires that $M_{N_2}-M_{N_1}=\Gamma _1/2$, where $\Gamma _1$ is the tree level decay width of $N_1$ and is seen to be $\sim 10^{-11}$ GeV. Therefore, for all practical purposes we have $M_{N_1}\simeq M_{N_2}$, and the RH neutrino mass matrix only brings about two independent parameters, $M_{N_1}$ and $M_{N_3}$. Thus, we have 14 independent parameters, which we vary in the following ranges:

$$\begin{aligned} \begin{array}{cccccc} 1 \,\,\mathrm{TeV}&{} \le &{} M_{N_1}&{} \le &{} 3\,\,\mathrm{TeV}\,,&{}\\ M_{N_1}\,\,&{} < &{} M_{N_3}&{} \le &{} 15\,\,\mathrm{TeV}\,,&{}\\ 1\,&{}\le &{}\dfrac{\sqrt{2}\,\,y_{ij}}{v}\,\times 10^{8} &{} \le &{} 1000\, &{} (i,j= e,\,\mu ,\,\tau , i=j\ne e)\,,\\ 1\,&{}\le &{}\dfrac{\sqrt{2}\,\,y_{ee}}{v}\,\times 10^{10} &{} \le &{} 100\,,&{}\\ 1\,&{}\le &{}\dfrac{\sqrt{2}\,\,\tilde{y}_{ij}}{v}\,\times 10^{8} &{} \le &{} 1000\,&{}(i= \tau , j=e,\,\mu )\,,\\ 1\,&{}\le &{}\dfrac{\sqrt{2}\,\,\tilde{y}_{\mu e}}{v}\,\times 10^{9} &{} \le &{} 1000\,.&{} \end{array} \end{aligned}$$

(21)

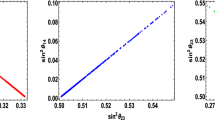
We try to find the allowed parameter space which satisfies the following constraints on three mixing angles ($\theta _{ij}$) and two mass square differences ($\Delta m_{ij}^{2}$), $J_\mathrm{CP}$ obtained from neutrino oscillation data and the cosmological bound on the sum of three light neutrino masses. These experimental/observational results are listed below.

• Measured values of three mixing angles in $3\sigma$ range [67]:

  $30^{\circ }<\,\theta _{12}\,<36.51^{\circ }$, $37.99^{\circ }<\,\theta _{23}\,<51.71^{\circ }$ and $7.82^{\circ }<\,\theta _{13}\,<9.02^{\circ }$.

• Allowed values of two mass squared differences in $3\sigma$ range [67]:

  $6.93<\dfrac{\Delta m^2_{21}}{10^{-5}}\,{\text {eV}^2} < 7.97$ and $2.37<\dfrac{\Delta m^2_{31}}{10^{-3}}\,{\text {eV}^2} < 2.63$ in $3\sigma$ range.

• The above-mentioned values of the neutrino oscillation parameters also put an upper bound on the absolute value of $J_\mathrm{CP}$ from Eq. (19), which is $|J_\mathrm{CP}|\le \,0.039$.

• Cosmological upper bound on the sum of three light neutrino masses i.e. $\sum _i m_{i} < 0.23$ eV at $2\sigma$ C.L. [25].

While it is possible to obtain both normal hierarchy (NH) ($m_1<m_2<m_3$) and inverted hierarchy (IH) ($m_3<m_1<m_2$) in this scenario, we show our results only for NH for brevity. Similar results can be obtained for IH.

Fig. 1

Left panel: Variation of $J_\mathrm{cp}$ with $\delta$. Right panel: Variation of neutrino-less double $\beta$ decay parameter ${m_{\beta \beta }}$ with $m_1$

In the left panel of Fig. 1, we show the variation of the $J_\mathrm{CP}$ parameter (as defined in Eq. (19)) with the Dirac CP phase $\delta$. From this plot one can easily notice that there are two allowed ranges of the Dirac CP phase, $0^{\circ }\le \delta \le 90^{\circ }$ and $270^{\circ }\le \delta \le 360^{\circ }$, respectively, which can reproduce the neutrino oscillation parameters in the $3\sigma$ range. Since the Jarlskog invariant $J_\mathrm{CP}$ is proportional to $\sin \delta$ (Eq.  19), we get both positive and negative values of $J_\mathrm{CP}$, symmetrically placed in the first and fourth quadrants. However, the absolute values of $J_\mathrm{CP}$ always lie below 0.039. Also, here we want to mention that, from the recent results of the T2K [80] experiment, the values of $\delta$ lying in the fourth quadrant are favourable compared to those in the first quadrant. In the right panel of Fig.  1, we show the variation of the neutrino-less double $\beta$ decay parameter, $m_{\beta \beta }$, with the mass of lightest neutrino, $m_1$. $m_{\beta \beta }$ is an important quantity for the study of neutrino-less double $\beta$ decay as the cross section of this process is proportional to $m_{\beta \beta } = \left| \sum _{i=1}^3 ({U_\mathrm{PMNS}})^2_{\,e\,i}\,\,m_i\right| =(m_{\nu })_{e\,e}$ (see Appendix B for details), where $(m_{\nu })_{e\,e}$ (Eq.  (A1)) is the (1,1) element of the light neutrino mass matrix $m_{\nu }$. The nature of this plot is very similar to the usual plot in the $m_{\beta \beta }$–$m_1$ plane for the normal hierarchical scenario [81]. In the same plot, we also show the current bound on $m_{\beta \beta }$ from the KamLand-Zen experiment [17].

3.2 Baryogenesis via resonant leptogenesis

As we have three RH neutrinos in the present model, in this section we study the lepton asymmetry generated from the CP violating out of equilibrium decays of these heavy neutrinos at the early stage of the Universe. The ${B-L}$ asymmetry thus produced is converted into the baryon asymmetry through sphaleron transitions which violate the ${B+L}$ quantum number, while conserving the ${ B-L}$ charge. The sphaleron processes are active between temperatures of $\sim 10^{12}$ GeV and $\sim 10^2$ GeV in the early Universe. At high temperatures the sphalerons are in thermal equilibrium and subsequently they freeze out at around $T\simeq 100$–200 GeV [82, 83], just before electroweak symmetry breaking (EWSB). To produce sufficient lepton asymmetry, which would eventually be converted into the observed baryon asymmetry, one requires RH neutrinos with masses $\gtrsim 10^{8}-10^{9}$ GeV [82, 84]. This is the well-known scenario of the “normal” or “canonical” leptogenesis. However, detection of these very massive RH neutrinos is beyond the reach of LHC and other future colliders. Here we consider the RH neutrinos to be in the TeV mass range to allow for their detection at collider experiments. It has been shown that with RH neutrinos in the TeV mass-scale range, it is possible to generate adequate lepton asymmetry by considering the two lightest RH neutrinos, $N_1$ and $N_2$, to be almost degenerate. More specifically, we demand that $M_{N_2}-M_{N_1}\simeq {\Gamma _1}/{2}$, where $\Gamma _1$ ³ is the total decay width of the lightest RH neutrino, $N_1$. This scenario is known as resonant leptogenesis [83, 85,86,87].

Fig. 2

Feynman diagrams for the decay of lightest RH neutrino $N_1$

Fig. 3

Left panel: Variation of the CP asymmetry parameter $\varepsilon _1$ with the mass of $N_1$. Right panel: Variation of total decay width of $N_1$ with $M_{N_1}$. A black solid line represents the upper bound of $\Gamma _1$ coming from out of equilibrium condition of $N_1$. All the points in both plots satisfy the neutrino oscillation data in the $3\sigma$ range

Figure  2 shows the tree level as well as one loop decay diagrams of the lightest RH neutrino, $N_1$. These diagrams are applicable for all the three RH neutrinos. Here L represents the SM lepton, which can either be a charged lepton or a left chiral neutrino, depending on the nature of the scalar field (charged⁴ or neutral) associated in the vertex, while $N_j$ denotes the remaining two RH neutrinos, $N_2$ and $N_3$, for the case of $N_1$ decay. In order to produce baryon asymmetry in the Universe we need both C and CP violating interactions, which is one of the three necessary conditions (see the Sakharov conditions [45] given in Sect. 1) for baryogenesis. Lepton asymmetry generated from the out of equilibrium decay of the RH neutrinos is determined by the CP asymmetry parameter ($\varepsilon _{i}$), which is given by (for details see Appendix C)

$$\begin{aligned} \varepsilon _2\simeq & {} -\dfrac{1}{2} \frac{\mathrm{Im} \left[ (\mathcal {M_{D}} \mathcal {M_{D}}^{\dagger })^{2}_{12}\right] }{(\mathcal {M_{D}} \mathcal {M_{D}}^{\dagger })_{11}\,(\mathcal {M_{D}} \mathcal {M_{D}}^{\dagger })_{22}} \,, \end{aligned}$$

(22)

$$\begin{aligned} \varepsilon _1\simeq & {} -\dfrac{\Gamma _1\,\Gamma _2}{\Gamma ^2_1+\Gamma ^2_2}\, \frac{\mathrm{Im} \left[ (\mathcal {M_{D}} \mathcal {M_{D}}^{\dagger })^{2}_{12}\right] }{(\mathcal {M_{D}} \mathcal {M_{D}}^{\dagger })_{11}\,(\mathcal {M_{D}} \mathcal {M_{D}}^{\dagger })_{22}} \,, \end{aligned}$$

(23)

$$\begin{aligned}\simeq & {} \dfrac{2\,\Gamma _1\,\Gamma _2}{\Gamma ^2_1+\Gamma ^2_2}\,\varepsilon _2\,. \end{aligned}$$

(24)

In the left panel of Fig.  3, we show the variation of the CP asymmetry parameter, $\varepsilon _1$, generated from the decay of the RH neutrino $N_1$, with the mass of $N_1$. Here we see that, for the considered ranges of $M_{N_1}$ ($1000\,\mathrm{GeV}\le M_{N_1} \le 10{,}000\,\mathrm{GeV}$) and other relevant Yukawa couplings (see Eq. (21)), the CP asymmetry parameter $\varepsilon _1$ can be as large as $\sim 10^{-2}$, which is significantly large compared with $\varepsilon _1$ in the “normal” leptogenesis case ($\varepsilon _1\sim 10^{-8}$ for $M_{N_1}\sim 10^{10}$ GeV) [82]. In the right panel of Fig.  3, we plot the variation of total decay width of $N_1$ with $M_{N_1}$. From this plot, one can easily notice that in the present scenario, $\Gamma _1$ lies between $\sim 10^{-12}$ and $10^{-9}$ GeV for the entire considered range of $M_{N_1}$. All the points in the two panels satisfy the neutrino oscillations data in the $3\sigma$ range, while the black solid line in the right panel provides the upper bound on $\Gamma _1$, obtained from the out of equilibrium conditions for $N_1$ i.e. $\Gamma _1<3\,H(M_{N_1})$ [82] where H is the Hubble parameter at $T=M_{N_1}$.

Fig. 4

Feynman diagrams for the annihilations of RH neutrinos

Next, we calculate the ${B-L}$ asymmetry generated from the decays as well as the pair annihilations of the RH neutrinos $N_1$ and $N_2$. In order to calculate the net ${B-L}$ asymmetry produced from the interactions of $N_1$ and $N_2$ at a temperature of the the Universe of $T\simeq 150$ GeV (freeze-out temperature of sphaleron), we have to solve a set of three coupled Boltzmann equations. The relevant Boltzmann equations [82, 83] for calculating $Y_{N_i}$ and $Y_{B-L}$ are given by

$$\begin{aligned} \frac{\mathrm{d} Y_{N_1}}{\mathrm{d} z}= & {} -\dfrac{M_{pl}}{1.66\,M^2_{N_1}} \dfrac{z\,\sqrt{g_{\star }(z)}}{g_\mathrm{s}(z)} \,\langle \Gamma _{1} \rangle \,\left( Y_{N_1}-Y_{N_{1}}^\mathrm{eq} \right) \nonumber \\&-\dfrac{2\,\pi ^2}{45}\,\dfrac{M_{pl}\,M_{N_1}}{1.66} \dfrac{\sqrt{g_{\star }(z)}}{z^2} \nonumber \\&\times \left( {\langle \sigma \mathrm{v}\rangle }_{N_1,\,Z_\mathrm{BL}} + {\langle \sigma \mathrm{v}\rangle }_{N_1,t,H_\mathrm{BL}}\right) \, \left( Y_{N_1}^2-(Y_{N_{1}}^\mathrm{eq})^2\right) , \nonumber \\ \end{aligned}$$

(25)

$$\begin{aligned} \frac{\mathrm{d} Y_{N_2}}{\mathrm{d} z}= & {} -\dfrac{M_{pl}}{1.66\,M^2_{N_1}} \dfrac{z\,\sqrt{g_{\star }(z)}}{g_\mathrm{s}(z)} \,\langle \Gamma _{2} \rangle \,\left( Y_{N_2}-Y_{N_{2}}^\mathrm{eq} \right) \nonumber \\&-\dfrac{2\,\pi ^2}{45}\,\dfrac{M_{pl}\,M_{N_1}}{1.66} \dfrac{\sqrt{g_{\star }(z)}}{z^2} \nonumber \\&\times \left( {\langle \sigma \mathrm{v}\rangle }_{N_2,\,Z_\mathrm{BL}} + {\langle \sigma \mathrm{v}\rangle }_{N_2,t,H_\mathrm{BL}}\right) \, \left( Y_{N_2}^2-(Y_{N_{2}}^\mathrm{eq})^2\right) , \nonumber \\ \end{aligned}$$

(26)

$$\begin{aligned} \frac{\mathrm{d}Y_{B-L}}{\mathrm{d} z}= & {} -\dfrac{M_{pl}}{1.66\,M^2_{N_1}} \dfrac{z\,\sqrt{g_{\star }(z)}}{g_\mathrm{s}(z)} \nonumber \\&\times \left[ \sum _{j = 1}^{2} \left( \frac{Y_{B-L}}{2}\, \frac{Y_{N_{j}^{eq}}}{Y_{L}^\mathrm{eq}} + \varepsilon _{j} \left( Y_{N_j}-Y_{N_{j}^{eq}}\right) \right) \langle \Gamma _{j}\rangle \right] \,, \nonumber \\ \end{aligned}$$

(27)

where $Y_{X} = \dfrac{n_X}{\mathrm{s}}$ denotes the comoving number density of X, with $n_X$ being the actual number density and $z=\dfrac{M_{N_1}}{T}$. The Planck mass is denoted by $M_{pl}$. The quantity $g_{\star }(z)$ is a function of $g_\rho$ and $g_\mathrm{s}$, the effective degrees of freedom related to the energy and entropy densities of the Universe, respectively, and it obeys the following expression [30]:

$$\begin{aligned} \sqrt{g_{\star }(z)} = \dfrac{g_\mathrm{s}(z)}{\sqrt{g_{\rho }(z)}}\,\left( 1 -\dfrac{1}{3} \dfrac{\mathrm{d}\,\mathrm{ln}\,g_\mathrm{s}(z)}{\mathrm{d} \,\mathrm{ln} z}\right) \,. \end{aligned}$$

(28)

Before EWSB, the variation of $g_s(z)$ with respect to z is negligible compared to the first term within the brackets and hence one can use $\sqrt{g_{\star }(z)} \simeq \dfrac{g_\mathrm{s}(z)}{\sqrt{g_{\rho }(z)}}$. The equilibrium comoving number density of X ($X=N_i$, L), obeying the Maxwell–Boltzmann distribution, is given by [30]

$$\begin{aligned} Y^\mathrm{eq}_{X}(z) = \dfrac{45\,g_X}{4\,\pi ^4}\, \left( \dfrac{M_X\,z}{M_{N_1}}\right) ^2 \,\dfrac{\mathrm{K}_2\left( \frac{M_{X}}{M_{N_1}}\,z\right) }{g_s\left( \frac{M_{N_1}}{z}\right) }\,, \end{aligned}$$

(29)

where $g_{X}$ and $M_{X}$ are the internal degrees of freedom and mass of X, respectively, while $g_s\left( \frac{M_{N_1}}{z}\right)$ is the effective degrees of freedom related to the entropy density of the Universe at temperature $T=\dfrac{M_{N_1}}{z}$. $\mathrm{K}_2\left( \frac{M_{X}}{M_{N_1}}\,z\right)$ is the modified Bessel function of order 2. The relevant Feynman diagrams, including both decay and annihilation of $N_i$, are shown in Figs.  2 and 4. The expression of thermal averaged decay width $\langle {\Gamma _i} \rangle$, which is related to the total decay width $\Gamma _i$ of $N_i$, is given as

$$\begin{aligned} \langle {\Gamma }_i \rangle = \Gamma _i\ \,\dfrac{\mathrm{K}_1\left( \frac{M_{N_i}}{M_{N_1}}\,z\right) }{\mathrm{K}_2\left( \frac{M_{N_i}}{M_{N_1}}\,z\right) }\,. \end{aligned}$$

(30)

The thermally average annihilation cross sections ${\langle \sigma \mathrm{v} \rangle }_{N_i,\,Z_\mathrm{BL}}$ and ${\langle \sigma \mathrm{v} \rangle }_{N_i,\,Z_\mathrm{BL}}$, appearing in the Boltzmann equations (Eqs. (25) and (26)) for the processes shown in Fig.  4, can be defined in a generic form,

$$\begin{aligned} {\langle \sigma \mathrm{v} \rangle }_{N_i,\,x}= & {} \dfrac{z}{16\,M^4_{N_i}\,M_{N_1}\,g^2_{N_i}\, \mathrm{K_2}\left( \frac{M_{N_i}}{M_{N_1}}\,z\right) ^2}\nonumber \\&\times \int _{4\,M^2_{N_i}}^{\infty } \hat{\sigma }_{N_i,\,x} \,\mathrm{K_1}\left( \dfrac{\sqrt{s}}{M_{N_1}}\,z\right) \,\sqrt{s}\,\mathrm{d}s \,, \end{aligned}$$

(31)

where $\hat{\sigma }_{N_i,\,x}$ is related to the actual annihilation cross section ${\sigma }_{N_i,\,x}$ by the following relation:

$$\begin{aligned} \hat{\sigma }_{N_i,\,x} = 2\,g^2_{N_i}\,\left( s-4\,M^2_{N_1}\right) \, {\sigma }_{N_i,\,x}\,, \end{aligned}$$

(32)

where $g_{N_i}=2$ is for the internal degrees of freedom of the RH neutrino $N_i$. The expression of $\hat{\sigma }_{N_i,\,Z_\mathrm{BL}}$ and $\hat{\sigma }_{N_i,\,t,\,H_\mathrm{BL}}$ for the present model is given in Ref. [83].

To calculate the ${B-L}$ asymmetry at around $T\simeq 150$ GeV, we have to numerically solve the set of three coupled Boltzmann equations (Eqs. (25)–(27)) using Eqs. (28)–(32). However, we can reduce the two flavour analysis (when both $N_2$ and $N_1$ are separately considered) into one flavour case by considering the parameters of the $\mathcal {M_{D}}$ matrix in such a way that the decay widths of $N_1$ and $N_2$ are of the same order, i.e. $\Gamma _{1}\sim \Gamma _{2}$. Hence, the CP asymmetry generated from the decays of both $N_1$ and $N_2$ are almost identical ($\varepsilon _1\sim \varepsilon _2$; see Eqs. (C9)–(C10)). In this case, the net ${B-L}$ asymmetry is equal to twice of that is being generated from the CP violating interactions of the lightest RH neutrino $N_1$ [83]. Hence instead of solving three coupled differential equations we now only need to solve Eqs. (25) and (27). The results we have found by numerically solving Eqs. (25) and (27) are plotted in Fig.  5. In this plot, we show the variation of $Y_{N_1}$ and $Y_{B-L}$ with z for $M_{N_1}=2000$ GeV, $\alpha _\mathrm{BL}=3\times 10^{-4}$ and $M_{Z_\mathrm{BL}}=3000$ GeV.⁵ While solving the coupled Boltzmann equations we consider the following initial conditions: $Y_{N_1}(T_\mathrm{in}^{B}) =Y^\mathrm{eq}_{N_1}$ and $Y_{B-L}=0$ with $T_\mathrm{in}^B$ being the initial temperature, which we take as 20 TeV. Thereafter, the evolutions of $Y_{N_1}$ and $Y_{B-L}$ are governed by their respective Boltzmann equations. From Fig.  5, one can notice that initially up to $z\sim 1$ ($T\sim M_{N_1}$), the comoving number density of $Y_{N_1}$ does not change much as a result of the ${B-L}$ asymmetry produced from the decay, and the annihilation of $N_1$ is also less. However, as the temperature of the Universe drops below the mass of $M_{N_1}$, there is a rapid change in the number density of $N_1$, which changes around six orders of magnitude between $z=1$ and $z=20$. Consequently, the large change in $Y_{N_1}$ significantly enhances the ${B-L}$ asymmetry $Y_{B-L}$ and finally $Y_{B-L}$ saturates to the desired value around $\sim 10^{-10}$, when there are practically no $N_1$ left to produce any further ${B-L}$ asymmetry.

Fig. 5

Variation of $Y_{N_1}$ (green dashed line) and $Y_{B-L}$ (blue dashed-dotted line) with z where the other parameters have been kept fixed at $M_{N_1} = 2000$ GeV, $\alpha _\mathrm{BL} \left( = \frac{g_\mathrm{BL}^{2}}{4 \pi }\right) = 3 \times 10^{-4}$, $M_{Z_\mathrm{BL}} = 3000$ GeV

The produced $B-L$ asymmetry is converted to net baryon asymmetry of the Universe through the sphaleron transitions while they are in equilibrium with the thermal bath. The quantities $Y_{B-L}$ and $Y_{B}$ are related by the following equation [71]:

$$\begin{aligned} Y_{B} = -\,2\times \dfrac{28}{79}\,Y_{B-L} (T_\mathrm{f})\,, \end{aligned}$$

(33)

where $T_\mathrm{f}\simeq 150$ GeV is the temperature of the Universe up to which the sphaleron process, converting $B-L$ asymmetry to a net B asymmetry, maintains its thermal equilibrium. The extra factor of 2 in the above equation is due to the equal contribution to $Y_{B-L}$ arising from the CP violating interactions of $N_2$ as well. Finally, we calculate the net baryon asymmetry $Y_{B}$ for three different masses of the RH neutrino $N_1$ and CP asymmetry parameter $\varepsilon _1$. The results are listed in Table 2. In all three cases, the final baryon asymmetry lies within the experimentally observed range for $Y_B$, i.e. (8.239–$9.375)\times 10^{-11}$ at 95% C.L. [44].

Table 2 Baryon asymmetry of the Universe generated for three different values of $M_{N_1}$ and $\varepsilon _1$

Table 3 Couplings of FIMP ($\phi _\mathrm{DM}$) with $Z_\mathrm{BL}$, $h_1$ and $h_2$

Fig. 6

Feynman diagrams for all the possible production modes of $\phi _\mathrm{DM}$ before EWSB

3.3 FIMP dark matter

In the present section we explore the FIMP scenario for DM in the Universe, by considering the complex scalar field $\phi _\mathrm{DM}$ as a corresponding candidate. As described in Sect. 2, the residual $\mathbb {Z}_2$ symmetry of $\phi _\mathrm{DM}$ makes the scalar field absolutely stable over the cosmological time scale and hence can play the role of a DM candidate. Since $\phi _\mathrm{DM}$ has a non-zero ${B-L}$ charge $n_\mathrm{BL}$, DM talks to the SM as well as the BSM particles through the exchange of extra neutral gauge boson $Z_\mathrm{BL}$ and two Higgs bosons present in the model; one is the SM-like Higgs, $h_{1}$, while the other one is the BSM Higgs, $h_{2}$. The corresponding coupling strengths, in terms of the gauge coupling $g_\mathrm{BL}$, ${B-L}$ charge $n_\mathrm{BL}$, mixing angle $\alpha$ and $\lambda$s, are listed in Table  3. As the FIMP never enters into thermal equilibrium, these couplings have to be extremely feeble in order to make the corresponding interactions non-thermal. For the case of the $\phi _\mathrm{DM}\,\phi ^\dagger _\mathrm{DM} \,{Z_\mathrm{BL}}_{\mu }$ coupling, we will make the ${B-L}$ charge of $\phi _\mathrm{DM}$ extremely tiny so that this interaction enters into the non-thermal regime. In principle, one can also choose the gauge coupling $g_\mathrm{BL}$ to be very small; however, in the present case we will keep the values of $g_\mathrm{BL}$ and $M_{Z_\mathrm{BL}}$ fixed at 0.07 and 3 TeV, respectively, as these values reproduce the observed baryon asymmetry of the Universe (see Sect. 3.2). Also, there is another advantage of choosing tiny $n_\mathrm{BL}$: this will make only $\phi _\mathrm{DM}$ out of equilibrium, while keeping $Z_\mathrm{BL}$ in equilibrium with the thermal bath. Moreover, due to the non-thermal nature, the initial number density of FIMP is assumed to be negligible and as the temperature of the Universe begins to fall down, they start to be produced dominantly from the decays and annihilation of other heavy particles.

In the present scenario, we consider all the particles except $\phi _\mathrm{DM}$ to be in thermal equilibrium. Before EWSB, all the SM particles are massless.⁶ In this regime, production of $\phi _\mathrm{DM}$ occurs mainly from the decay and/or annihilation of BSM particles, namely $Z_\mathrm{BL}$, $H_\mathrm{BL}$, and $N_i$. Also, before EWSB the annihilation of all four degrees of freedom of the SM Higgs doublet, $\phi _h$, can produce $\phi _\mathrm{DM}$. Feynman diagrams for all the production processes of $\phi _\mathrm{DM}$ before EWSB are shown in Fig. 6.

After EWSB, all the SM particles become massive and consequently, besides the BSM particles, $\phi _\mathrm{DM}$ can now also be produced from the decay and/or annihilation of the SM particles. The corresponding Feynman diagrams are shown in Fig. 7. In generating the vertex factors for the different vertices to compute the Feynman diagrams as listed in Fig. 6 and Fig. 7, we use the LanHEP [88] package.

Fig. 7

Production processes of $\phi _\mathrm{DM}$ from both SM as well as BSM particles after EWSB

In order to compute the relic density of a species at the present epoch, one needs to study the evolution of the number density of the corresponding species with respect to the temperature of the Universe. The evolution of the number density of $\phi _\mathrm{DM}$ is governed by the Boltzmann equation containing all possible number changing interactions of $\phi _\mathrm{DM}$. The Boltzmann equation of $\phi _\mathrm{DM}$ in terms of its comoving number density $Y_{\phi _\mathrm{DM}}=\dfrac{n_{\phi _\mathrm{DM}}}{\mathrm{s}}$, where n and $\mathrm{s}$ are the actual number density and entropy density of the Universe, is given by

$$\begin{aligned} \dfrac{\mathrm{d}Y_{\phi _\mathrm{DM}}}{\mathrm{d}z}= & {} \dfrac{2 M_{pl}}{1.66 M_{h_1}^{2}} \dfrac{z \sqrt{g_{\star }(z)}}{g_\mathrm{s}(z)}\nonumber \\&\times \Bigg [\sum _{X = Z_\mathrm{BL},\,h_1,\,h_2} \langle \Gamma _{X\rightarrow \phi _\mathrm{DM} \phi ^\dagger _\mathrm{DM}} \rangle (Y_{X}^\mathrm{eq} - Y_{\phi _\mathrm{DM}})\Bigg ]\nonumber \\&+\dfrac{4 \pi ^{2}}{45} \dfrac{M_{pl} M_{h_1}}{1.66} \dfrac{\sqrt{g_{\star }(z)}}{z^{2}}\nonumber \\&\times \Bigg [\sum _{p} \langle \sigma \mathrm{v}_{p\bar{p}\rightarrow \phi _\mathrm{DM} \phi ^\dagger _\mathrm{DM}}\rangle (Y_{p}^\mathrm{eq\,\,2} - Y_{\phi _\mathrm{DM}}^{2})\nonumber \\&+ \langle \sigma \mathrm{v}_{h_{1} h_{2}\rightarrow \phi _\mathrm{DM} \phi ^\dagger _\mathrm{DM}}\rangle (Y_{h_1}^\mathrm{eq} Y_{h_2}^\mathrm{eq} - Y_{\phi _\mathrm{DM}}^{2})\Bigg ]\,, \end{aligned}$$

(34)

where $z=\dfrac{M_{h_1}}{T}$, while $\sqrt{g_{\star }(z)}$, $g_\mathrm{s}(z)$ and $M_{pl}$ are the same as those in Eqs. (25)–(27) of Sect. 3.2. In the above equation (Eq. (34)), the first term represents the contribution coming from the decays of $Z_\mathrm{BL}$, $h_1$ and $h_2$. The expressions of equilibrium number density, $Y^\mathrm{eq}_{X}(z)$ (X is any SM or BSM particle except $\phi _\mathrm{DM}$), and the thermal averaged decay width, $\langle \Gamma _{X \rightarrow \phi _\mathrm{DM}\phi _\mathrm{DM}}\rangle$, can be obtained from Eqs. (29) and (30), respectively, by only replacing $M_{N_1}$ with $M_{X}$, the mass of the decaying mother particle. As mentioned above, before EWSB, the summation in the first terms is over $h_2$ and $Z_\mathrm{BL}$ only, as there will be no contribution from the SM Higgs decay, as such a trilinear vertex ($h_1\phi _\mathrm{DM}\phi _\mathrm{DM}^{\dagger }$) is absent before EWSB and after EWSB there will be contributions to the relic density of $\phi _\mathrm{DM}$ from all the decaying particles. The DM production from the pair annihilations of the SM and BSM particles are described by the second term of the Boltzmann equation. Here, summation over p includes all possible pair annihilation channels, namely $W^+W^-,\,ZZ,\,Z_\mathrm{BL}Z_\mathrm{BL},\,N_iN_i,\,h_ih_i,\,t\bar{t}$. However before EWSB, pair annihilations of the BSM particles and the SM Higgs doublet, $\phi _h$, contribute to the production processes (i.e. $p=Z_\mathrm{BL},\,N_i,\,H_\mathrm{BL},\,\phi _h$; see Fig.  6). The third term, which is present only after EWSB, is another production mode of $\phi _\mathrm{DM}$ from the annihilation of $h_1$ and $h_2$. The expressions of all the relevant cross sections and decay widths for computing the DM number density are given in Appendix E. The most general form of thermally averaged annihilation cross section for two different annihilating particles of mass $M_A$ and $M_B$ is given by [43]

$$\begin{aligned}&f_{1} = \sqrt{s^{2} + (M_{A}^{2} - M_{B}^{2})^{2} - 2\,s\,(M_{A}^{2} + M_{B}^{2})}\,,\nonumber \\&f_{2} = \sqrt{s - (M_{A} - M_{B})^{2}} \,\,\sqrt{s - (M_{A} + M_{B})^{2}}\,\,, \nonumber \\&\langle \sigma v_{A\,B \rightarrow \phi _\mathrm{DM} \phi _\mathrm{DM}}\rangle \nonumber \\&\quad = \dfrac{1}{8 \,M_{A}^{2}\, M_{B}^{2}\,T\, \mathrm{K}_{2}\left( \dfrac{M_{A}}{T}\right) \,\mathrm{K}_{2}\left( \dfrac{M_{B}}{T}\right) } \nonumber \\&\qquad \times \int _{(M_{A} + M_{B})^{2}}^{\infty } \dfrac{\sigma _{A\,B\rightarrow } \phi _\mathrm{DM} \phi _\mathrm{DM}}{\sqrt{s}}\,f_{1}\,f_{2}\,\mathrm{K}_{1} \left( \dfrac{\sqrt{s}}{T}\right) \,\mathrm{d}s \,. \nonumber \\ \end{aligned}$$

(35)

Fig. 8

Left (right) panel: Variation of relic density $\Omega h^{2}$ with z for different initial temperature (contributions to $\Omega h^2$ coming from decay and annihilation), where the other parameters are fixed at $\lambda _{Dh} = 8.75\times 10^{-13}$, $\lambda _{DH} = 5.88\times 10^{-14}$, $n_\mathrm{BL} = 1.33 \times 10^{-10}$, $M_\mathrm{DM} = 50$ GeV, $M_{Z_\mathrm{BL}}= 3000$ GeV, $g_\mathrm{BL}$ = 0.07, $M_{h_{1}} = 125.5$ GeV and $M_{h_{2}} = 500$ GeV, $\alpha = 10^{-4}$

Finally, the relic density of $\phi _\mathrm{DM}$ is obtained using the following relation between $\Omega h^2$ and $Y_{\phi _\mathrm{DM}}(0)$ [89, 90]:

$$\begin{aligned} \Omega h^2 = 2.755 \times 10^8 \left( \dfrac{M_\mathrm{DM}}{\mathrm{GeV}}\right) \,Y_{\phi _\mathrm{DM}}(0)\,, \end{aligned}$$

(36)

where $Y_{\phi _\mathrm{DM}}(0)$ is the value of the comoving number density at the present epoch, which can be obtained by solving the Boltzmann equation.

The contribution to DM production processes from decays as well as annihilations of various SM and BSM particles depends on the mass of $\phi _\mathrm{DM}$. Accordingly, we divide the rest of our DM analysis into four different regions, depending on $M_\mathrm{DM}$ and the dominant production modes of $\phi _\mathrm{DM}$.

3.3.1 $M_\mathrm{DM} < \dfrac{M_{h_1}}{2}$,  $\dfrac{M_{h_2}}{2}$, $\dfrac{M_{Z_\mathrm{BL}}}{2}$, the SM and BSM particles decay dominated region

In this case DM is dominantly produced from the decays of all three particles, namely $h_1$, $h_2$ and $Z_\mathrm{BL}$. Therefore, in this case the $\mathrm{U}(1)_{B-L}$ part of the present model directly enters into DM production. Moreover, in this mass range, $\phi _\mathrm{DM}$ can also be produced from the annihilations of the SM and BSM particles, however, we find that their contributions are not as significant as those from the decays of $h_1,\,h_2$ and $Z_\mathrm{BL}$. In the left panel and right panel of Fig. 8, we show the variation of DM relic density with z. In the left panel, we show the dependence of DM relic density with the initial temperature $T_{in}$. The initial temperature ($T_{in}$) is the temperature up to which we assume that the number density of DM is zero and its production processes start thereafter. We can clearly see from the figure that, as long as the initial temperature is above the mass of the BSM Higgs ($M_{h_2} \sim 500$ GeV), the final relic density does not depend on the choice of the initial temperature and reproduces the observed DM relic density of the Universe for the chosen values of the model parameters as written in the caption of Fig. 8. If we reduce the initial temperature from 500 GeV, i.e. for $T_{in} = 251$ GeV, the decay contribution of the BSM Higgs, $h_{2}$, becomes less, since the corresponding number density of $h_2$ for $T_{in}<M_{h_2}$ is Boltzmann suppressed (exponentially suppressed), which is clearly shown by the blue dashed-dotted line. Hence, if we reduce the initial temperature ($T_{in}$) further, i.e. $T_{in}<M_{h_2}, M_{h_1}$ $\sim 42$ GeV, then the number densities of both SM-like Higgs $h_1$ and BSM Higgs $h_{2}$ become Boltzmann suppressed and, hence, a smaller amount of DM production will occur, which is evident from the left panel of Fig. 8 (represented by the yellow dashed-dotted line). On the other hand in the right panel of Fig. 8, we show the contributions to the DM relic density coming from decay and annihilation. The magenta dotted horizontal line represents the present day observed DM relic density of the Universe. The green dashed line represents the total decay contribution arising from the decays of both $h_1$, $h_2$ and $Z_\mathrm{BL}$, whereas the net annihilation contribution coming from the annihilation of all the SM as well as BSM particles is shown by the blue dashed-dotted line. There is a sudden rise in the annihilation contribution which occurs around the Universe temperature $T \sim 154$ GeV (i.e. the EWSB temperature). After the EWSB temperature, all the SM particles become massive and hence the sudden rise in the annihilation part because of the appearance of the annihilation channels $W^{+}\,W^{-}$, $Z\,Z$, $h_{1}\,h_{1}$, $h_{1}\,h_{2}$. The plot clearly implies that the lion share of the contribution comes from the decay of the two Higgses $h_1$, $h_2$ and of $Z_\mathrm{BL}$, while for the considered values of the model parameters the annihilation contribution is subdominant. Moreover, in this case we cannot enhance the annihilation contribution by increasing the parameters $\lambda _\mathrm{Dh}$, $\lambda _\mathrm{DH}$ and $n_\mathrm{BL}$ as these changes will result in the over-production of DM from the decays of $h_1$, $h_2$ and $Z_\mathrm{BL}$.

Fig. 9

Left panel: variation of decay contributions of the two Higgs bosons to $\Omega h^2$ separately with z. Right panel: Variation of relic density $\Omega h^{2}$ with z for different values of the DM mass $M_\mathrm{DM}$. Other parameters value have been kept fixed at $\lambda _{Dh} = 8.75\times 10^{-13}$, $\lambda _{DH} = 5.88\times 10^{-14}$, $n_\mathrm{BL} = 1.33 \times 10^{-10}$, $M_\mathrm{DM} = 50$ GeV (for the left panel), $M_{Z_\mathrm{BL}}= 3000$ GeV, $g_\mathrm{BL}= 0.07$, $M_{h_{1}} = 125.5$ GeV and $M_{h_{2}} = 500$ GeV, $\alpha = 10^{-4}$

In the left panel of Fig. 9, we show how the individual decay contribution from each scalar varies with z. Here we consider the values of the scalar quartic couplings $\lambda _{Dh} = 8.75 \times 10^{-13}$ and $\lambda _{DH} = 5.88 \times 10^{-14}$ and the ($B-L$) charge of $\phi _\mathrm{DM}$ $n_\mathrm{BL} = 1.33 \times 10^{-10}$. From this plot we can see that before EWSB the SM-like Higgs $h_1$ cannot decay to a pair of $\phi _\mathrm{DM}$ as in this epoch it has no coupling with the latter. In this regime the decay of the BSM Higgs $h_2$ and $Z_\mathrm{BL}$ contribute, while after EWSB even the SM-like Higgs starts contributing to the DM production and hence we get an increased relic density (right side of EWSB). Its worth mentioning here that while generating the plot in the left panel of Fig.  9, we take the scalar quartic couplings $\lambda _{Dh}$, $\lambda _{DH}$ and ${B-L}$ charge of $\phi _\mathrm{DM}$ $n_\mathrm{BL}$ of different strengths such that the contributions of the two scalars ($h_1$ and $h_2$) and the extra gauge boson to the DM relic density are of equal order. This is because for the case of the BSM Higgs $h_{2}$ decay the coupling $\lambda _{DH}$ multiplied by the ${B-L}$ symmetry breaking VEV $v_\mathrm{BL}$ is relevant, while for the decay of the SM-like Higgs $h_{1}$, the product of the parameter $\lambda _{Dh}$ and the EWSB VEV v is relevant and the contribution from the decay of $Z_\mathrm{BL}$, DM charge $n_\mathrm{BL}$ is relevant. Since in the present case $v_\mathrm{BL}>v$, the magnitudes of the two quartic couplings $\lambda _{Dh}$ and $\lambda _{DH}$ are of different order (see Table 3). On the other hand, in the right panel of Fig.  9, we show the variation of the relic density with z for four different values of the DM mass $M_\mathrm{DM}$. From Eq. (36), one can see that the DM relic density is directly proportional to the mass $M_\mathrm{DM}$ and as a result when the other relevant couplings remain unchanged $\Omega h^2$ increases with $M_\mathrm{DM}$. This feature is clearly visible in the right panel for the cases with $M_\mathrm{DM}=10$ GeV (black solid line), $M_\mathrm{DM}=30$ GeV (red dashed line) and 50 GeV (green dashed line), respectively. However, for $M_\mathrm{DM} = 75$ GeV (blue dashed-dotted line) $\Omega h^2$ does not rise equally because for this value of the DM mass the decay of $h_1$ to a pair of $\phi _\mathrm{DM}$ and $\phi _\mathrm{DM}^{\dagger }$ becomes kinematically forbidden and hence, there is no equal increment in this case.

In the left panel and right panel of Fig. 10, we show how the relic density varies with z for different values of scalar quartic couplings $\lambda _{Dh}$ and $\lambda _{DH}$, respectively. In each panel, one can easily notice that there exists a kink around the EWSB region. However, in the left panel, the kink occurs for a higher value of $\lambda _{Dh}$ while in the right panel, the situation is just opposite. We have already seen in the left panel of Fig. 9 that before EWSB only $h_{2}$ decay is contributing to the DM relic density and at the EWSB region SM-like Higgs $h_1$ also starts contributing. A kink will always appear in the relic density curve when contribution of the SM-like Higgs boson $h_1$ to $\Omega h^2$ is larger compared to that of the BSM Higgs $h_2$ and extra gauge boson $Z_\mathrm{BL}$ i.e. $\Gamma _{h_1\rightarrow \phi _\mathrm{DM}\phi _\mathrm{DM}^{\dagger }}> \Gamma _{h_2\rightarrow \phi _\mathrm{DM}\phi _\mathrm{DM}^{\dagger }}$, $\Gamma _{Z_\mathrm{BL}\rightarrow \phi _\mathrm{DM}\phi _\mathrm{DM}^{\dagger }}$. The values of scalar quartic couplings $\lambda _\mathrm{Dh}$ and $\lambda _\mathrm{DH}$ in the left panel of Fig.  9 are such that $\Gamma _{h_2\rightarrow \phi _\mathrm{DM}\phi _\mathrm{DM}^{\dagger }}$ and $\Gamma _{Z_\mathrm{BL}\rightarrow \phi _\mathrm{DM}\phi _\mathrm{DM}^{\dagger }}$ always remain large compared to $\Gamma _{h_1\rightarrow \phi _\mathrm{DM}\phi _\mathrm{DM}}$ and hence no kink is observed in the total relic density curve. However, in the present figure (in the left panel of Fig.  10) we do have kinks around the EWSB region, because in the left panel with $\lambda _\mathrm{DH}=8.316\times 10^{-14}$ and $n_\mathrm{BL} = 1.33 \times 10^{-10}$, $\Gamma _{h_1\rightarrow \phi _\mathrm{DM}\phi _\mathrm{DM}^{\dagger }}> \Gamma _{h_2\rightarrow \phi _\mathrm{DM}\phi _\mathrm{DM}^{\dagger }}$, $\Gamma _{Z_\mathrm{BL}\rightarrow \phi _\mathrm{DM}\phi _\mathrm{DM}^{\dagger }}$ condition is satisfied only for the case with larger value of $\lambda _\mathrm{Dh}=1.237\times 10^{-11}$ ($\lambda _\mathrm{Dh}>>\lambda _\mathrm{DH}$) while in the right panel with a fixed value of $\lambda _\mathrm{Dh}=1.237\times 10^{-12}$, the above condition is not maintained because the $Z_\mathrm{BL}$ decay channel dominates.

Fig. 10

Left (Right) panel: Variation of relic density $\Omega h^{2}$ with z for three different values of $\lambda _{Dh}$ ($\lambda _{DH}$), where the other parameters are fixed at $\lambda _{DH} = 5.88\times 10^{-14}$ ($\lambda _{Dh} = 8.75\times 10^{-13}$), $n_\mathrm{BL} = 1.33 \times 10^{-10}$, $M_\mathrm{DM} = 50$ GeV, $M_{Z_\mathrm{BL}}= 3000$ GeV, $g_\mathrm{BL}= 0.07$, $M_{h_{1}} = 125.5$ GeV and $M_{h_{2}} = 500$ GeV, $\alpha = 10^{-4}$

Fig. 11

Left (Right) panel: Allowed region in the $\lambda _{Dh}$–$\lambda _{DH}$ ($M_{h_2}$–$\alpha$) plane where other parameters are fixed at $M_{Z_\mathrm{BL}}= 3000$ GeV, $g_\mathrm{BL}= 0.07$, $n_\mathrm{BL} = 1.33 \times 10^{-10}$, $M_{h_{1}} = 125.5$

In the left panel of Fig. 11, we show the allowed region in the coupling plane ($\lambda _{Dh}$–$\lambda _{DH}$) which reproduces the observed DM relic density ($0.1172\le \Omega h^2\le 0.1226$). In this figure, we clearly indicate the dominant DM production processes when $M_\mathrm{DM}$ varies between 10 GeV to 100 GeV i.e.  DM production from the decays of $h_1$, $h_2$ or both or entirely from the annihilations of the SM particles like $W^\pm ,\,\,Z,\,\,h_1$ etc. The parameters which are related to the $Z_\mathrm{BL}$ decay ($g_\mathrm{BL}$, $n_\mathrm{BL}$) have been kept fixed at 0.07 and $1.33\times 10^{-10}$, respectively, so at every time an equal amount of $Z_\mathrm{BL}$ decay contribution remains present. As illustrated in the figure, when the parameter $\lambda _\mathrm{Dh}$ is small compared to the other parameter $\lambda _\mathrm{DH}$ then among the two scalars it is the BSM Higgs $h_2$ which is mainly contributing to the DM production, while for the opposite case, the production of $\phi _\mathrm{DM}$ becomes $h_1$ dominated and in between the two scalars contribute equally. Apart from that, if the mass of $\phi _\mathrm{DM}$ is greater than the half of the SM-like Higgs mass (i.e. $M_\mathrm{DM} > \dfrac{M_{h_1}}{2}$), then DM production from $h_1$ decay becomes kinematically forbidden. In this case, however, the production from the decays of $h_2$ and $Z_\mathrm{BL}$ is still possible. Now, the deficit in DM production can be compensated by the production from self annihilation of the SM particles like $h_1$, $W^\pm$ and Z; for this we need to increase the parameter $\lambda _\mathrm{Dh}$. Moreover, by increasing $\lambda _\mathrm{Dh}$ (decreasing $\lambda _\mathrm{DH}$ simultaneously) we can arrive at a situation where DM production is entirely dominated by the annihilations of the SM particles and this situation has been indicated by a pink coloured arrow in the left panel of Fig. 11. On the other hand, in the right panel of Fig. 11 we present the allowed region in the $M_{h_2}$–$\alpha$ plane which satisfies the relic density bound. From this figure one can see that with the increase of $M_{h_2}$, the allowed values of mixing angle $\alpha$ decrease. The reason behind this decrement is the vacuum stability conditions as given in Eq. (14). The region satisfying both the relic density bound and the vacuum stability conditions is shown by the green dots, while in the other part of the $M_{h_2}$–$\alpha$ plane the quantity $\mu _{\phi _{h}}^{2}$ becomes positive which is undesirable in the context of the present model (see Eq. (14)).

Fig. 12

Variation of the DM relic density $\Omega h^2$ with z. The other parameter values have been kept fixed at $\lambda _{Dh} = 6.364\times 10^{-12}$, $\lambda _{DH} = 7.637\times 10^{-14}$, $n_\mathrm{BL} = 8.80 \times 10^{-11}$, $M_\mathrm{DM} = 70$ GeV, $M_{Z_\mathrm{BL}}= 3000$ GeV, $g_\mathrm{BL}= 0.07$, $M_{h_{1}} = 125.5$ GeV, $M_{h_{2}} = 500$ GeV, $\alpha = 10^{-5}$, $M_{N_2}$ $\approx$ $M_{N_1} = 2000$ GeV and $M_{N_3} = 2500$ GeV

Fig. 13

Left (Right) panel: Variation of the DM relic density $\Omega h^2$ with z. The other parameter values have been kept fixed at $\lambda _{Dh} = 2.574\times 10^{-12}$ ($7.212\times 10^{-14}$), $\lambda _{DH} = 3.035\times 10^{-11}$ ($8.316\times 10^{-14}$), $n_\mathrm{BL} = 3.4 \times 10^{-11}$ $(6.2 \times 10^{-11})$, $M_\mathrm{DM} = 450$ GeV (600 GeV), $M_{Z_\mathrm{BL}}= 3000$ GeV, $g_\mathrm{BL}= 0.07$, $M_{h_{1}} = 125.5$ GeV, $M_{h_{2}} = 500$ GeV, $\alpha = 10^{-5}$, $M_{N_2} \approx M_{N_1} = 2000$ GeV and $M_{N_3} = 2500$ GeV

3.3.2 $\dfrac{M_{h_1}}{2}<M_{\phi _\mathrm{DM}} <\dfrac{M_{h_2}}{2},\,\dfrac{M_{Z_\mathrm{BL}}}{2}$, BSM particles decay and SM particles annihilation dominated region

Clearly in this mass region, DM production from the decay of the SM-like Higgs $h_1$ is kinematically forbidden and hence DM has been produced from the decays of $h_2$, $Z_\mathrm{BL}$ only. However, unlike the previous case, here we find significant contribution to DM relic density arising from the self annihilation of the SM particles namely, $h_1$, $W^\pm$, Z and t. On the other hand, the annihilations of BSM particles like $Z_\mathrm{BL}$, $h_2$ and $N_i$ have negligible effect on DM production processes. In Fig. 12, we have shown the variation of the DM relic density with z for $\dfrac{M_{h_1}}{2}<M_{\phi _\mathrm{DM}} <\dfrac{M_{h_2}}{2},\,\dfrac{M_{Z_\mathrm{BL}}}{2}$. Since now the decay of the $h_1$ to $\phi _\mathrm{DM}{\phi _\mathrm{DM}}^\dagger$ is kinematically forbidden, hence we can increase the parameter $\lambda _{Dh}$ safely and this will not overproduce DM in the Universe. Due to this moderately large value of $\lambda _{Dh}$, the annihilation channels become important. From Fig. 12 it is clearly seen that in this case the annihilation channel $h_1 h_1 \rightarrow \phi _\mathrm{DM}\phi _\mathrm{DM}^{\dagger }$ (Green dashed line) contributes significantly to the DM production. Therefore in the present case, production of DM has been controlled by the decays of $h_2$, $Z_\mathrm{BL}$ and the self annihilations of the SM particles and thus directly relates to the $\mathrm{U}(1)_{B-L}$ sector of this model.

3.3.3 $\dfrac{M_{h_1}}{2},\, \dfrac{M_{h_2}}{2}<M_{\phi _\mathrm{DM}}<\dfrac{M_{Z_\mathrm{BL}}}{2}$, BSM particles decay and annihilation dominated region

In this regime of the DM mass, the only surviving decay mode is the decay of the ${B-L}$ gauge boson $Z_\mathrm{BL}$ to a pair of $\phi _\mathrm{DM}$. Apart from that, depending on the choice of the mass of $\phi _\mathrm{DM}$ a significant fraction of DM has been produced from the self annihilation of either BSM Higgs $h_2$. In other words, we can say that in this region the production of DM is BSM particles dominated. In the left panel of Fig. 13 we show the relative contribution of dominant production modes of DM to $\Omega h^2$ for a chosen value of $M_\mathrm{DM}=450$ GeV. From this plot one can easily notice that in the case when $M_\mathrm{DM}<M_{h_2}$, the almost entire fraction of DM is produced from the decay of $Z_\mathrm{BL}$ (green dashed line) and self annihilation of the BSM Higgs $h_2$ (solid turquoise line). This is because, as in this case the production of $\phi _\mathrm{DM}$ from $h_2$ decay is kinematically forbidden, one can increase the parameter $\lambda _\mathrm{DH}$ so that the annihilation channel $h_2h_2 \rightarrow \phi _\mathrm{DM}{\phi _\mathrm{DM}}^\dagger$, which is mainly proportional to $\lambda _\mathrm{DH}^2$ (due to four point interaction), becomes significant.

Fig. 14

Allowed region in the $M_{Z_\mathrm{BL}}$–$g_\mathrm{BL}$ plane which produces observed DM relic density. Solid lines (black and red) are the upper limits on the gauge coupling $g_\mathrm{BL}$ for a particular mass of $Z_\mathrm{BL}$ obtained from LHC and LEP, respectively. Other relevant parameters used in this plot are $250\,\mathrm{GeV}\le M_\mathrm{DM}\le 5000\,\mathrm{GeV}$, $\lambda _{Dh} = 7.212\times 10^{-14}$, $\lambda _{DH} = 8.316\times 10^{-14}$, $M_{h_{2}} = 500$ GeV, $\alpha = 10^{-5}$, $M_{N_2}$ $\approx$ $M_{N_1} = 2000$ GeV and $M_{N_3} = 2500$ GeV

On the other hand, in the right panel we consider a situation where almost the entire DM has been produced from the decay of ${B-L}$ gauge boson. For this purpose, we choose $M_\mathrm{DM}>M_{h_2}$ and a larger value of $n_\mathrm{BL}= 6.2\times 10^{-11}$. Similar to the previous case (i.e. $M_\mathrm{DM}< M_{h_2}$) here also, the production of $\phi _\mathrm{DM}$ from $h_2$ decay still remains forbidden. However, as the sum of the final state particles masses is larger than that of the initial state, in this case the $h_2 h_2$ annihilation mode becomes suppressed. Moreover, to make the contribution of the $h_2$ annihilation even more suppressed we reduce the quartic couplings $\lambda _\mathrm{Dh}$ and $\lambda _\mathrm{DH}$ accordingly. As a result other annihilation channels, e.g. $Z_\mathrm{BL}Z_\mathrm{BL}$, $N_iN_i$, also become inadequate as these channels are mediated by the exchange of $h_1$ and $h_2$. Although RH neutrinos can annihilate to $\phi _\mathrm{DM}{\phi _\mathrm{DM}}^{\dagger }$ via $Z_\mathrm{BL}$, we cannot increase the contribution of $Z_\mathrm{BL}$ mediated diagrams because for that one has to further increase the ${B-L}$ charge of $\phi _\mathrm{DM}$ ($n_\mathrm{BL}$), which results in an over production of DM in the Universe from $Z_\mathrm{BL}$ decay. From the right panel of Fig. 13, one can easily notice that in this situation $Z_\mathrm{BL}$ decay is the most dominant DM production channel (red dashed line), while the total contributions from the annihilations of $h_2$, $Z_\mathrm{BL}$ and $N_i$ are negligible. Therefore, for the entire mass range of $\phi _\mathrm{DM}$, i.e. $\dfrac{M_{h_1}}{2},\,\dfrac{M_{h_2}}{2}<M_{\phi _\mathrm{DM}}<\dfrac{M_{Z_\mathrm{BL}}}{2}$, the DM production processes are always related to the $\mathrm{U}(1)_{B-L}$ sector of the present model by receiving a sizeable contribution from $Z_\mathrm{BL}$ decay.

In Fig.  14, we show the allowed region (green coloured points) in the $M_{Z_\mathrm{BL}}$–$g_\mathrm{BL}$ plane, which reproduces the observed DM relic density. While generating this plot we vary $250\,\mathrm{GeV}\le M_\mathrm{DM}\le$ 5000 GeV and $10^{-11}\le n_\mathrm{BL}\le 10^{-8}$. In this region, as mentioned above, dominant contributions to the DM relic density arise from $Z_\mathrm{BL}$ decay and annihilation of the BSM Higgs $h_2$. In this figure, the black solid line represents the current upper bound [59, 91, 92] on $g_\mathrm{BL}$ for a particular mass of $Z_\mathrm{BL}$ from LHC,⁷ while the limit [95,96,97] from LEP⁸ has been indicated by the red solid line respectively. Therefore, the region below the red and black solid line is allowed by the collider experiments like LHC and LEP. The benchmark value of $g_\mathrm{BL}$, $M_{Z_\mathrm{BL}}$ (= 0.07, 3000 GeV) for which we have computed the baryon asymmetry in the previous section (Sect. 3.2) is highlighted by a blue coloured star. Hence, in this regime the extra gauge boson $Z_\mathrm{BL}$ immensely takes part in achieving the correct ballpark value of the DM relic density and also at the same time $Z_\mathrm{BL}$ plays a significant role in obtaining the observed value of the matter–antimatter asymmetry of the Universe.

3.3.4 $M_{\phi _\mathrm{DM}}>\dfrac{M_{h_1}}{2},\, \dfrac{M_{h_2}}{2},\,\dfrac{M_{Z_\mathrm{BL}}}{2}$, BSM particles annihilation dominated region

Finally, in this range of the DM mass the entire production of $\phi _\mathrm{DM}$ from the decays of $h_1$, $h_2$ and $Z_\mathrm{BL}$ becomes kinematically inaccessible. Therefore, in this case all three parameters, namely $\lambda _\mathrm{Dh}$, $\lambda _\mathrm{DH}$ and $n_\mathrm{BL}$, become free and we can make sufficient increment to these parameters so that either scalar medicated ($h_1$, $h_2$) or gauge boson mediated ($Z_\mathrm{BL}$) annihilation processes of $N_i$, $Z_\mathrm{BL}$ or both, can be the dominant contributors in DM production.

Similarly, in the left panel and right panel of Fig. 15, we show two different situations where the DM production is dominated by scalar ($h_1$, $h_2$) mediated diagrams and gauge boson $Z_\mathrm{BL}$ mediated diagrams, respectively. In the left panel, by keeping the $n_\mathrm{BL}$ value low and adjusting the parameters $\lambda _{Dh}$ and $\lambda _{DH}$ one can achieve the correct value DM relic density and on the other hand, in the right panel we keep the values of $\lambda _{Dh}$ and $\lambda _{DH}$ sufficiently low and by suitably adjusting the DM charge $n_\mathrm{BL}$ we achieve the correct value of the DM relic density. Therefore, in this region, a strong correlation exists among the neutrino sector, $\mathrm{U}(1)_{B-L}$ sector and DM sector as the entire DM is now being produced from $N_iN_i$ and $Z_\mathrm{BL}Z_\mathrm{BL}$ annihilations.

Fig. 15

Left (Right) Panel: Variation of the DM relic density $\Omega h^2$ with z when dominant contributions are coming from scalar $h_i$ (gauge boson $Z_\mathrm{BL}$) mediated annihilation channels. The other relevant parameter values have been kept fixed at $\lambda _{Dh} = 7.017\times 10^{-12}$ ($7.212\times 10^{-13}$), $\lambda _{DH} = 6.307\times 10^{-11}$ ($8.316\times 10^{-12}$), $n_\mathrm{BL} = 1.0 \times 10^{-10}$ ($1.34 \times 10^{-8}$), $M_\mathrm{DM} = 1600$ GeV, $M_{Z_\mathrm{BL}}= 30004$ GeV, $g_\mathrm{BL}= 0.07$, $M_{h_{1}} = 125.5$ GeV, $M_{h_{2}} = 500$ GeV, $\alpha = 10^{-5}$, $M_{N_2} \approx M_{N_1} = 2000$ GeV and $M_{N_3} = 2500$ GeV

Fig. 16

Allowed region in the $M_\mathrm{DM}$–$M_{N_1}$ plane which mimics the observed DM relic density. The blue coloured star represents our benchmark point ($M_\mathrm{DM}=1600$ GeV, $M_{N_1}=2000$ GeV)

In Fig. 16, we show the allowed parameter space in the $M_\mathrm{DM}$–$M_{N_1}$ plane by DM relic density. In order to generate this plot we vary the DM mass in the range $1500\,\mathrm{GeV}\le M_\mathrm{DM}\le 3000\,\mathrm{GeV}$, the RH neutrino masses $1500\,\mathrm{GeV}\le M_{N_i} \le 10000\,\mathrm{GeV}$ ($i=1,\,2$), $M_{N_1}<M_{N_3}\le M_{N_1} + 5000$ GeV and $10^{-10}\le n_\mathrm{BL}\le 10^{-8}$. The other relevant parameters have been kept fixed at $\lambda _{Dh} = 7.212\times 10^{-13}$, $\lambda _{DH} = 8.316\times 10^{-12}$, $M_{Z_\mathrm{BL}}$ = 3000 GeV, $g_\mathrm{BL}= 0.07$, $M_{h_{2}} = 500$ GeV, $\alpha = 10^{-5}$ As discussed above, in this regime ($M_\mathrm{DM}>\dfrac{M_{h_1}}{2},\, \dfrac{M_{h_2}}{2},\,\dfrac{M_{Z_\mathrm{BL}}}{2}$) $\phi _\mathrm{DM}$ is dominantly produced from the annihilations of $Z_\mathrm{BL}$ and RH neutrinos. From this plot one can observe that in this high DM mass range to obtain the observed DM relic density, the mass of the lightest RH neutrino cannot be larger than $\sim 6000$ GeV. Analogous to Fig. 14, here also we indicate the benchmark point for which we compute the baryon asymmetry in Sect. 3.2 by a blue coloured star. Therefore, in this case RH neutrinos are very actively taking part in all three processes we consider in this work, namely DM production processes, tiny neutrino mass generation and the generation of required lepton asymmetry to reproduce the observed baryon asymmetry of the Universe.

From the above four regions, which are based on the mass of our FIMP DM, it is evident that in the first region DM production mainly happens from the decay of $h_1$, $h_2$ and $Z_\mathrm{BL}$ and all annihilations are subdominant. Therefore, in this region only the extra neutral gauge boson ($Z_\mathrm{BL}$), BSM Higgs ($h_2$) and SM-like Higgs ($h_1$) are taking part in the DM relic density estimates and there is no significant role of the RH neutrinos. In the second region, SM-like Higgs decay does not contribute to DM production processes, hence one can safely increase the quartic coupling $\lambda _{Dh}$ and consequently the $h_1 h_1$ annihilation contribution increases. Similar to the previous regime, here also RH neutrinos have less importance in determining the DM relic density. In the third region, the only decay mode that is involved in DM production is $Z_\mathrm{BL}\rightarrow \phi _\mathrm{DM}{\phi _\mathrm{DM}}^\dagger$. Since all other decay modes corresponding to $h_1$ and $h_2$ are kinematically forbidden, we can increase both the quartic couplings $\lambda _{Dh}$ and $\lambda _{DH}$ appropriately, which eventually enhances the annihilation contribution from the BSM Higgs significantly. Moreover, due to the increment of quartic couplings in this region, $Z_\mathrm{BL} Z_{BL}$ and $N_{i} N_{i}$ annihilation channels start contributing in the DM production processes. Lastly in region four, due to the high value of the DM mass no decay process contributes to DM relic density and only the BSM particle annihilation contributes. Therefore, in this region by properly adjusting the extra gauge coupling $g_\mathrm{BL}$, one can get a sizeable fraction of DM production from the annihilation of the RH neutrinos. Apart from the masses of the involved particles, the annihilation of RH neutrinos mediated by $Z_\mathrm{BL}$ depends on the extra (B-L) gauge coupling $g_\mathrm{BL}$ solely. Thus, depending on the mass range of our FIMP DM, we can say that the different model parameters and the additional BSM particles (e.g. $Z_\mathrm{BL}$, $N_i$, $h_2$) are fully associated to the DM production processes in the early Universe.

3.3.5 Analytical estimates

So far, we have solved the full Boltzmann equation (Eq. 34) for a FIMP $\phi _\mathrm{DM}$ numerically. Apart from this, one can estimate the FIMP relic density (or comoving number density) by using the approximate analytical formula. Let us consider a FIMP ($\phi _\mathrm{DM}$) which is produced from the decay of a particle A i.e., $A \rightarrow \phi _\mathrm{DM}\,{\phi _\mathrm{DM}}^{\dagger }$, where A in the present model can be $h_1$, $h_2$ or $Z_\mathrm{BL}$. The contribution of A to the FIMP relic density at the present epoch, considering the effect of both $\phi _\mathrm{DM}$ and ${\phi _\mathrm{DM}}^{\dagger }$, is given by [34]

$$\begin{aligned} \Omega ^\mathrm{FIMP} h^{2} \simeq \frac{2.18 \times 10^{27} g_{A}}{g_\mathrm{s}\sqrt{g_{\rho }}} \frac{M_\mathrm{DM} \Gamma _{A}}{M_{A}^{2}}\,, \end{aligned}$$

(37)

where $M_A$ and $g_A$ are the mass and internal degrees of freedom of the mother particle A, respectively, while $\Gamma _A$ is the decay width of the process $A \rightarrow \phi _\mathrm{DM}\,{\phi _\mathrm{DM}}^{\dagger }$. The analytic expressions for $\Gamma _A$ corresponding to $h_2$, $h_1$ and $Z_\mathrm{BL}$ are given in Eqs. (D4), (D7) and (D9) in the appendices. Moreover, $g_{\rho }$ and $g_\mathrm{s}$, as defined earlier, are the degrees of freedom related to the energy and entropy densities of the Universe, respectively. Let us now compare the analytical result with the numerical value which we obtain by solving the Boltzmann equation Eq. (34). For this purpose, let us consider a situation when a significant fraction of our FIMP candidate ($\phi _\mathrm{DM}$) is produced from the decay mode of the BSM Higgs i.e., $h_{2} \rightarrow \phi _\mathrm{DM} \phi _\mathrm{DM}^{\dagger }$. Substituting the values of the model parameters given in the caption of Fig. 9 to Eq. (37), we get the contribution of $h_2$ to the DM relic density, which is

$$\begin{aligned} \Omega ^\mathrm{FIMP} h^{2} \simeq 0.027, \end{aligned}$$

(38)

where we consider $g_{\rho }=g_\mathrm{s} \approx 100$ and $g_{A} = 1$. This can be compared to the contribution of $h_2$ obtained from the exact numerical estimate shown in the left panel of Fig. 9, which is

$$\begin{aligned} \Omega _{h_{2}\rightarrow \phi _\mathrm{DM} \phi _\mathrm{DM}^{\dagger }} h^{2} = 0.0276. \end{aligned}$$

(39)

Therefore, from the above two estimates it is clearly evident that the analytical result agrees well with the full numerical result. Similarly, for the other decay modes also (i.e. $h_1$, $Z_\mathrm{BL}$) one can match the analytical and numerical results.

4 Conclusion

In this work we considered a local $\mathrm{U}(1)_{B-L}$ extension of the SM and, to cancel the additional anomalies associated with this gauge symmetry, we introduced three RH neutrinos ($N_{i}$, $i = 1, 2, 3$). Besides the three RH neutrinos, we also introduced two SM gauge singlet scalars, $\phi _{H}$ and $\phi _\mathrm{DM}$. The scalar field $\phi _{H}$, being charged under $\mathrm{U}(1)_{B-L}$, takes a non-zero VEV and breaks the proposed ${B-L}$ symmetry spontaneously. Moreover, as the scalar field $\phi _\mathrm{DM}$ has also a non-zero ${B-L}$ charge, one can adjust this charge suitably so that after symmetry breaking we are left with a model with a residual $\mathbb {Z}_2$ symmetry and only $\phi _\mathrm{DM}$ behaves as an odd particle under this leftover symmetry. This makes $\phi _\mathrm{DM}$ absolutely stable over the cosmological time scale and hence acts as a DM candidate. After spontaneous breaking of $\mathrm{U}(1)_{B-L}$ gauge symmetry, all RH neutrinos and the extra neutral gauge boson $Z_\mathrm{BL}$, acquired mass. Due to the presence of the three RH neutrinos in the model, we easily generated Majorana masses for the three light neutrinos by the Type-I seesaw mechanism. This model is also able to explain baryogenesis via leptogenesis, where we generated the lepton asymmetry in the Universe from out of equilibrium, CP violating decays of two degenerate RH neutrinos and converted this lepton asymmetry to the observed baryon asymmetry through the sphaleron transitions.

In explaining the neutrino masses by Type-I seesaw mechanism, we considered a complex Dirac mass matrix $\mathcal {M_{D}}$ and a diagonal Majorana mass matrix $\mathcal {M_{R}}$ for the RH neutrinos. In determining the allowed model parameter space, we used the measured values of the neutrino oscillation parameters, namely three mixing angles ($\theta _{12}$, $\theta _{13}$ and $\theta _{23}$) and two mass square differences ($\Delta m_{21}^{2}$, $\Delta m_\mathrm{atm}^{2}$) in their current $3\sigma$ range. In particular, in the current model we could reproduce the whole allowed $3 \sigma$ range of the neutrino oscillation parameters by different combinations of the relevant model parameters. The Dirac CP phase was constrained to lie within two distinct regions. One is the entire first quadrant ($0^\circ$–$90^\circ$), while the other one spans the entire fourth quadrant ($270^\circ$–$360^\circ$). However, if we considered the T2K result on the Dirac CP phase then the values of $\delta$ lying in the fourth quadrant are more favourable compared to those in the first quadrant. We also computed the magnitudes of the Jarlskog invariant $J_\mathrm{CP}$ and found that the values of $J_\mathrm{CP}$, for the model parameters which satisfy the neutrino oscillation data, always lie below 0.039. Finally, we calculated the values of $m_{\beta \beta }$, the quantity relevant to neutrino-less double $\beta$ decay, for the allowed model parameter space.

Since we allowed complex Yukawa couplings in the Dirac mass matrix $\mathcal {M_{D}}$, the decays of the RH neutrinos were CP violating. We took the masses of the RH neutrinos in the TeV range and worked in the parameter space where the lightest two RH neutrino states were nearly degenerate, with their masses separated by their tree level decay width. This scenario led to resonant leptogenesis (or TeV scale leptogenesis) for the production of observed baryon asymmetry in the Universe from the out of equilibrium decays of the RH neutrinos. We generated the observed baryon asymmetry for three different values of the RH neutrino masses namely $M_{N_1}=1600$ GeV, 1800 GeV and 2000 GeV, respectively, where the required values of the CP asymmetry parameter ($\varepsilon _1$) were $4.4\times 10^{-4}$, $2.25\times 10^{-4}$ and $1.8\times 10^{-4}$, respectively. These values of $M_{N_1}$ and $\epsilon _1$ were also seen to be allowed by the neutrino oscillation data.

Lastly, we studied the DM phenomenology by considering a FIMP type DM candidate $\phi _\mathrm{DM}$. We took into account all the production modes of $\phi _\mathrm{DM}$ (both before and after EWSB) arising from the annihilations and decays of the SM as well as BSM particles. We found that depending on the mass of $\phi _\mathrm{DM}$, the production processes of $\phi _\mathrm{DM}$ can be classified into four distinct categories. These are: (1) SM and BSM particles decay dominated region, (2) BSM particles decay and SM particles annihilation dominated region, (3) BSM particles annihilation and $Z_\mathrm{BL}$ decay dominated region, and finally (4) BSM particles annihilation dominated region. The first region is characterised by $M_\mathrm{DM} < \dfrac{M_{h_1}}{2}, \,\dfrac{M_{h_2}}{2},\,\dfrac{M_{Z_\mathrm{BL}}}{2}$ and here DM is mainly produced from the decays of $h_1$, $h_2$ and $Z_\mathrm{BL}$. In the second region, DM mass is concentrated between $\dfrac{M_{h_1}}{2}$ and min$\left[ \dfrac{M_{h_2}}{2}, \dfrac{M_{Z_\mathrm{BL}}}{2}\right]$ i.e. $\dfrac{M_{h_1}}{2}< M_\mathrm{DM} < \dfrac{M_{h_2}}{2},\,\dfrac{M_{Z_\mathrm{BL}}}{2}$. In this case, $h_2$, $Z_\mathrm{BL}$ decays and $h_1h_1$, $W^+W^-$, ZZ annihilations act as the dominant production modes of FIMP DM. In the third region where $\dfrac{M_{h_1}}{2},\,\dfrac{M_{h_2}}{2}< M_\mathrm{DM} < \dfrac{M_{Z_\mathrm{BL}}}{2}$, DM has mainly been produced from $Z_\mathrm{BL}$ decay and from the annihilation of the BSM Higgs $h_2$ (for $M_\mathrm{DM}<M_{h_2}$). Finally, in the last region all three decay modes become kinematically forbidden as $M_\mathrm{DM} > \dfrac{M_{h_1}}{2},\,\dfrac{M_{h_2}}{2},\,\dfrac{M_{Z_\mathrm{BL}}}{2}$ and hence entire DM is produced from the self annihilations of $Z_\mathrm{BL}$ and RH neutrinos ($N_i$). Therefore in all four regions the $\mathrm{U}(1)_{B-L}$ gauge boson has played a significant role in DM production, while the effects of the RH neutrinos are important in the last two regions only. We also found that, since for a FIMP candidate $\phi _\mathrm{DM}$ the observed DM relic density ($0.1172\le \Omega _{h^2}\le 0.1226$) is generated via the freeze-in mechanism; this puts upper bounds on the scalar and gauge portal couplings of $\phi _\mathrm{DM}$ to restrict its over-production i.e. $\lambda _\mathrm{Dh}\lesssim 10^{-11}$, $\lambda _\mathrm{DH}\lesssim 10^{-10}$ and $n_\mathrm{BL}\lesssim 10^{-8}$. Hence, due to such extremely feeble couplings $\phi _\mathrm{DM}$ can easily evade all the constraints coming from any terrestrial DM direct detection experiment.

In conclusion, our spontaneously broken local $\mathrm{U}(1)_{B-L}$ extension of the SM with three additional RH and two additional scalars can explain the three main pieces of evidence for physics beyond the SM, viz., small neutrino masses, matter–antimatter asymmetry of the Universe and DM. Tiny neutrino masses and all mixing angles can be obtained via the Type-I seesaw mechanism where we chose a certain pattern for the real and complex Yukawa couplings. The model gave a definite prediction for the CP violating phase to be measured in the next generation long baseline experiments. The DM candidate is a scalar which is neutral under the SM gauge group and has a non-zero ${B-L}$ charge. DM is made stable by virtue of a remnant $\mathbb {Z}_2$ symmetry arising after the spontaneous breaking of the $\mathrm{U}(1)_{B-L}$ gauge symmetry. This can be achieved by imposing a suitable ${B-L}$ charge on $\phi _\mathrm{DM}$ so that the Lagrangian does not contain any odd term of $\phi _\mathrm{DM}$. This scalar DM can easily be taken as a FIMP candidate which is produced from the decays and annihilations of the SM and BSM particles. Therefore, even if the WIMP type DM is ruled out in the near future from direct detection experiments, the present variant of the $\mathrm{U}(1)_{B-L}$ scenario with FIMP DM will still survive. Further, since $g_\mathrm{BL}$ is of the order of the SM gauge couplings, this model has the potential to be tested in the LHC or in other future collider experiments by detecting ${B-L}$ gauge boson $Z_\mathrm{BL}$ from its SM decay products. Moreover, considering the masses of the RH neutrinos in the TeV scale allows us to simultaneously explain the baryon asymmetry of the Universe from resonant leptogenesis, FIMP DM production via a freeze-in mechanism and neutrino masses and mixing from the TeV scale Type-I seesaw mechanism. Thus, all three phenomena addressed in this article are interconnected.

Appendices

Appendix A: Expression for the Majorana mass matrix of light neutrinos

Here we give the expression of all the elements of the light neutrino mass matrix $m_{\nu }$ in terms of the Yukawa couplings and the RH neutrino masses:

$$\begin{aligned} (m_{\nu })_{11}= & {} -\frac{y_{ee}^{2}}{M_{N_1}} -\frac{y_{e\mu }^{2}}{M_{N_2}} -\frac{y_{e\tau }^{2}}{M_{N_3}}, \nonumber \\ (m_{\nu })_{12}= & {} -\frac{y_{e\mu }\,y_{\mu \mu }}{M_{N_2}} -\frac{y_{e\tau }\,y_{\mu \tau }}{M_{N_3}} -\frac{y_{ee}\,y_{\mu e}}{M_{N_1}}- i\,\frac{y_{ee}\,\tilde{y}_{\mu e}}{M_{N_1}}, \nonumber \\ (m_{\nu })_{13}= & {} -\frac{y_{e\tau }\,y_{\tau \tau }}{M_{N_3}} -\frac{y_{e e}\,y_{\tau e}}{M_{N_1}} -\frac{y_{e\mu }\,y_{\tau \mu }}{M_{N_2}} \nonumber \\&-i\,\left( \frac{y_{e e}\,\tilde{y}_{\tau e}}{M_{N_1}} +\frac{y_{e\mu }\,\tilde{y}_{\tau \mu }}{M_{N_2}}\right) , \nonumber \\ (m_{\nu })_{21}= & {} (m_{\nu })_{12}, \nonumber \\ (m_{\nu })_{22}= & {} -\frac{y_{\mu \mu }^{2}}{M_{N_2}} -\frac{y_{\mu \tau }^{2}}{M_{N_3}} -\frac{y^2_{\mu e}}{M_{N_1}} +\frac{\tilde{y}^2_{\mu e}}{M_{N_1}} -i\,\frac{2\,y_{\mu e}\,\tilde{y}_{\mu e}}{M_{N_1}}, \nonumber \\ (m_{\nu })_{23}= & {} -\frac{y_{\mu \tau }\,y_{\tau \tau }}{M_{N_3}} - \frac{y_{\mu e}\,y_{\tau e}}{M_{N_1}} -\frac{y_{\mu \mu }\,y_{\tau \mu }}{M_{N_2}} +\frac{\tilde{y}_{\mu e}\,\tilde{y}_{\tau e}}{M_{N_1}} \nonumber \\&-i\,\left( \frac{y_{\tau e}\,\tilde{y}_{\mu e}}{M_{N_1}} +\frac{y_{\mu e}\,\tilde{y}_{\tau e}}{M_{N_1}} +\frac{y_{\mu \mu }\,\tilde{y}_{\tau \mu }}{M_{N_2}}\right) , \nonumber \\ (m_{\nu })_{31}= & {} (m_{\nu })_{13}, \nonumber \\ (m_{\nu })_{32}= & {} (m_{\nu })_{23}, \nonumber \\ (m_{\nu })_{33}= & {} -\frac{y_{\tau \tau }^{2}}{M_{N_3}} -\frac{y_{\tau e}^{2}}{M_{N_1}} -\frac{y_{\tau \mu }^{2}}{M_{N_2}} +\frac{\tilde{y}_{\tau e}^{2}}{M_{N_1}} +\frac{\tilde{y}_{\tau \mu }^{2}}{M_{N_2}} \nonumber \\&-i\,2\left( \frac{y_{\tau e}\,\tilde{y}_{\tau e}}{M_{N_1}} +\frac{y_{\tau \mu }\,\tilde{y}_{\tau \mu }}{M_{N_2}} \right) , \nonumber \\ \end{aligned}$$

(A1)

$$\begin{aligned} m_{\nu }= & {} \left( \begin{array}{ccc} (m_{\nu })_{11} &{} (m_{\nu })_{12} &{}(m_{\nu })_{13}\\ (m_{\nu })_{21} &{} (m_{\nu })_{22} &{}(m_{\nu })_{23}\\ (m_{\nu })_{31} &{} (m_{\nu })_{32} &{} (m_{\nu })_{33}\\ \end{array}\right) \,. \end{aligned}$$

(A2)

Appendix B: Neutrino-less double $\beta$ decay parameter $m_{\beta \beta }$

Since the light neutrino mass matrix is Majorana in nature, it is a complex symmetric matrix. A complex symmetric matrix $m_{\nu }$ can be diagonalised by a unitary matrix $U_\mathrm{PMNS}$ (defined in Eq. (9)) in the following way:

$$\begin{aligned} m_\mathrm{diag}= & {} U_\mathrm{PMNS}^{\dagger } \,m_{\nu }\, U_\mathrm{PMNS}^{*}, \nonumber \\ \Rightarrow m_{\nu }= & {} U_\mathrm{PMNS}\, m_\mathrm{diag}\, U_\mathrm{PMNS}^{T}. \end{aligned}$$

Now equating the $(i,\,j)$th element from both sides of the above equation, we get

$$\begin{aligned} (m_{\nu })_{ij} = (U_\mathrm{PMNS})_{ik} \, (m_\mathrm{diag})_{k k^{\prime }} \, (U_\mathrm{PMNS}^{T})_{k^{\prime } j}. \end{aligned}$$

Since $m_\mathrm{dia}$ is a diagonal matrix, we can further simplify $({m_{\nu }})_{ij}$ by using $m_\mathrm{diag} = m_{k}\,\delta _{k k^{\prime }}$, where $m_k$ is the mass of kth light neutrino. Therefore $(m_{\nu })_{ij}$ takes the following form:

$$\begin{aligned} (m_{\nu })_{ij} = \sum _{k = 1}^{3} m_{k}\,(U_\mathrm{PMNS})_{ik}\, (U_\mathrm{PMNS})_{jk}\,. \end{aligned}$$

The above equation expresses the elements of the light neutrino mass matrix (Eq. (A1)) in terms of the light neutrino masses, the intergenerational mixing angles and the phases. Taking $i=j=1$, we get the expression of the (1,1) element of $m_{\nu }$ i.e.

$$\begin{aligned} (m_{\nu })_{11} = \sum _{k=1}^{3} m_{k}\,(U_\mathrm{PMNS})^2_{\,1\,k}, \end{aligned}$$

which is related to the important parameter $m_{\beta \beta }$ of the neutrino-less double $\beta$ decay [81] by

$$\begin{aligned} m_{\beta \beta } = \left| \sum _{k=1}^{3} m_{k}\,(U_\mathrm{PMNS})^2_{1\,k}\right| =\left| (m_{\nu })_{11}\right| \,. \end{aligned}$$

(B1)

Appendix C: CP asymmetric parameter calculation for leptogenesis

The amount of lepton asymmetry generated in the out of equilibrium decay of the RH neutrino $N_i$ is parametrised by the CP asymmetry parameter ($\varepsilon _i$), which is defined as

$$\begin{aligned} \varepsilon _{i} = \frac{\sum _{j} \left[ \Gamma (N_{i} \rightarrow L_j\,\phi _h) - \Gamma (N_{i} \rightarrow \bar{L}_j\,{\phi _h}^{\star })\right] }{\sum _{j} \left[ \Gamma (N_{i} \rightarrow L_j\,\phi _h) + \Gamma (N_{i} \rightarrow \bar{L}_j\,{\phi _h}^{\star })\right] }\,. \end{aligned}$$

(C1)

If we consider only the tree level decay process of $N_i$ (first diagram in Fig.  2), there will not be any CP violation. The non-zero CP asymmetry is generated only by the interference between the tree level and the one loop level diagrams. The expression of the CP asymmetry parameter ($\varepsilon _i$) is given by [85, 86, 98].

$$\begin{aligned} \varepsilon _{i}= & {} -\sum _{j\ne i} \frac{M_{N_i}}{M_{N_j}} \frac{\Gamma _{j}}{M_{N_j}} \left( \frac{V_{j}}{2} + S_{j} \right) \nonumber \\&\times \frac{\mathrm{Im} \left[ (\mathcal {M_{D}} \mathcal {M_{D}}^{\dagger })^{2}_{ij}\right] }{(\mathcal {M_{D}} \mathcal {M_{D}}^{\dagger })_{ii} \,(\mathcal {M_{D}} \mathcal {M_{D}}^{\dagger })_{jj}}, \end{aligned}$$

(C2)

where $V_{j}$ and $S_{j}$ are the contributions coming from the vertex correction and the self energy correction diagrams, respectively (second and third diagrams in Fig. 2). The expressions of $V_{j}$ and $S_{j}$ have the following forms [85, 86, 98]:

$$\begin{aligned} V_{j}= & {} 2 \frac{M_{N_j}^{2}}{M_{N_i}^{2}} \left[ \left( 1 + \frac{M_{N_j}^{2}}{M_{N_i}^{2}}\right) \log \left( 1 + \frac{M_{N_i}^{2}}{M_{N_j}^{2}}\right) - 1\right] , \nonumber \\ S_{j}= & {} \frac{M_{N_j}^{2} \Delta M_{ij}^{2}}{(\Delta M_{ij}^{2})^{2} + M_{N_i}^{2} \Gamma _{j}^{2}}\,, \end{aligned}$$

(C3)

with

$$\begin{aligned} \Delta M_{ij}^{2} = M_{N_j}^{2} - M_{N_i}^{2}, \end{aligned}$$

(C4)

and $\Gamma _{j}$ denotes the tree level decay width of the RH neutrino $N_j$ (neglecting subdominant one loop corrections), which is given by

$$\begin{aligned} \Gamma _{j} = \frac{M_{N_j}}{4 \pi v^{2}} (\mathcal {M_{D}} \mathcal {M_{D}}^{\dagger })_{jj}\,\,. \end{aligned}$$

(C5)

Now, as mentioned in the beginning of this section, the enhancement in the CP asymmetry factor (Eq. (C1)) occurs when two RH neutrinos are almost degenerate i.e. $M_{N_2}-M_{N_1}\simeq \dfrac{\Gamma _1}{2}$. This is known as the resonance condition. In the present scenario, we consider $M_{N_3}> M_{N_2}\simeq M_{N_1}$. Therefore, the resonance condition is satisfied only for the two lightest RH neutrinos $N_2$ and $N_1$. Hence we can neglect the contribution of $N_3$ in the CP asymmetry parameter (Eq. (C2)) by considering the summation over only $N_1$ and $N_2$ (i.e. $j=1,\,2$). Using the resonance condition in Eq. (C3), one can easily notice that $S_j\sim \mathcal {O}\left( \frac{M_{N_j}}{\Gamma _j}\right)>>1$ ($j=1,\,2)$ and

$$\begin{aligned} \varepsilon _i \!\simeq \!-\!\sum ^2_{j\ne i,\,\,j=1} \frac{M_{N_i}}{M_{N_j}} \frac{\Gamma _{j}}{M_{N_j}}\,S_{j}\, \dfrac{\mathrm{Im}\left[ (\mathcal {M_{D}} \mathcal {M_{D}}^{\dagger })^{2}_{ij}\right] }{(\mathcal {M_{D}} \mathcal {M_{D}}^{\dagger })_{ii} \,(\mathcal {M_{D}} \mathcal {M_{D}}^{\dagger })_{jj}}\,\,, \nonumber \\ \end{aligned}$$

(C6)

where we neglect the quantity $V_j$, which is, under the present condition ($M_{N_2}-M_{N_1}\simeq \dfrac{\Gamma _1}{2}$), much smaller compared to $S_j$. The resonance condition leads to

$$\begin{aligned} \Delta M^2_{21}= & {} M^2_{N_2} -M^2_{N_1} \,,\nonumber \\= & {} \dfrac{\Gamma _1}{2} \left( 2\,M_{N_1}+\dfrac{\Gamma _1}{2}\right) \,,\nonumber \\\simeq & {} M_{N_1}\,\Gamma _1 + \mathcal {O}\left( \Gamma ^2_1\right) \,. \end{aligned}$$

(C7)

Using Eq. (C7) in Eq. (C3) we get

$$\begin{aligned} S_1\simeq & {} -\dfrac{M^2_{N_1}}{2\,M_{N_2}\,\Gamma _1}\,,\nonumber \\ S_2\simeq & {} \dfrac{M^2_{N_2}}{M_{N_1}} \dfrac{\Gamma _1}{\Gamma ^2_1+\Gamma ^2_2}\,. \end{aligned}$$

(C8)

Now, substituting the expressions of $S_1$ and $S_2$ in Eq. (C6) and using $\mathrm{Im}\left[ (\mathcal {M_{D}} \mathcal {M_{D}}^{\dagger })^{2}_{12}\right] = -\,\mathrm{Im}\left[ (\mathcal {M_{D}} \mathcal {M_{D}}^{\dagger })^{2}_{21}\right]$, one obtains

$$\begin{aligned} \varepsilon _2\simeq & {} -\dfrac{1}{2} \frac{\mathrm{Im} \left[ (\mathcal {M_{D}} \mathcal {M_{D}}^{\dagger })^{2}_{12}\right] }{(\mathcal {M_{D}} \mathcal {M_{D}}^{\dagger })_{11}\,(\mathcal {M_{D}} \mathcal {M_{D}}^{\dagger })_{22}} \,, \end{aligned}$$

(C9)

$$\begin{aligned} \varepsilon _1\simeq & {} -\dfrac{\Gamma _1\,\Gamma _2}{\Gamma ^2_1+\Gamma ^2_2}\, \frac{\mathrm{Im} \left[ (\mathcal {M_{D}} \mathcal {M_{D}}^{\dagger })^{2}_{12}\right] }{(\mathcal {M_{D}} \mathcal {M_{D}}^{\dagger })_{11}\,(\mathcal {M_{D}} \mathcal {M_{D}}^{\dagger })_{22}} \,, \end{aligned}$$

(C10)

$$\begin{aligned}\simeq & {} \dfrac{2\,\Gamma _1\,\Gamma _2}{\Gamma ^2_1+\Gamma ^2_2}\,\varepsilon _2\,. \end{aligned}$$

(C11)

Appendix D: Expressions of decay widths of $h_2$, $h_1$ and $Z_\mathrm{BL}$

In the present work, we consider the effect of electroweak symmetry breaking on DM production. After EWSB the SM particles become massive and affect DM production, while before EWSB, those particles have no effect. To take this effect into account we define an extra constant, $C_\mathrm{ASB}$. In all the equations, the value of the constant $C_\mathrm{ASB} = 0$ before the EWSB and it is equal to unity i.e. $C_\mathrm{ASB} = 1$ after the EWSB. Also before the EWSB, there is no mixing between the SM and BSM Higgs bosons, i.e. $\alpha =0$. The two vertices which are common to all Higgs mediated diagrams are as follows:

$$\begin{aligned} g_{h_{1} \phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}= & {} - \left( v\lambda _{Dh}\cos \alpha + v_\mathrm{BL}\lambda _{DH}\sin \alpha \right) \,, \nonumber \\ g_{h_{2} \phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}= & {} \left( v\lambda _{Dh}\sin \alpha - v_\mathrm{BL}\lambda _{DH}\cos \alpha \right) \,. \end{aligned}$$

(D1)

${\mathbf{Total~decay~width~of}~h_2}$:

• $\underline{h_2\rightarrow VV}$ ($V= W^\pm , Z$):

  $$\begin{aligned} g_{h_{2}VV}= & {} -\dfrac{2M_{V}^{2}}{v}\,\sin \alpha \,,\nonumber \\ \Gamma (h_2 \rightarrow VV)= & {} \dfrac{C_\mathrm{ASB}\,M_{h_2}^{3}\,g_{h_{2}VV}^{2}}{64\,\pi M_{V}^{4}\,S_{V}} \sqrt{1 - \dfrac{4 M_{V}^{2}}{M_{h_2}^{2}}}\nonumber \\&\times \left( 1 - \dfrac{4 M_{V}^{2}}{M_{h_2}^{2}} + \dfrac{12M_{V}^{4}}{M_{h_2}^{4}}\right) \,, \end{aligned}$$

  (D2)

  where $S_V=2\,(1)$ for the ZZ ($W^+W^-$) final state.

• $\underline{h_{2}\rightarrow h_1\,h_1}$:

  $$\begin{aligned}&\Gamma ({h_{2}} \rightarrow {h_1}{h_1}) = \dfrac{g_{h_{1}h_{1}h_{2}}^{2}}{32\,\pi \,M_{h_2}} \,\sqrt{1 - \dfrac{4M_{h_1}^{2}}{M_{h_2}^{2}}}\,. \end{aligned}$$

  (D3)

• $\underline{h_{2}\rightarrow \phi _\mathrm{DM}^\dagger \phi _\mathrm{DM}}$:

  $$\begin{aligned} \Gamma ({h_{2}} \rightarrow \phi _\mathrm{DM}^\dagger \phi _\mathrm{DM})= & {} \dfrac{g_{h_{2}\phi _\mathrm{DM}^\dagger \phi _\mathrm{DM}}^{2}}{16\,\pi \,M_{h_2}} \,\sqrt{1 - \dfrac{4 M_\mathrm{DM}^{2}}{M_{h_2}^{2}}}\,. \end{aligned}$$

  (D4)

• $\underline{h_{2}\rightarrow f\bar{f}}$:

  $$\begin{aligned} g_{h_{2}ff}= & {} \dfrac{M_{f}}{v}\,\sin \alpha \,,\nonumber \\ \Gamma (h_{2} \rightarrow \mathrm{f} \,\bar{\mathrm{f}})= & {} \dfrac{C_\mathrm{ASB}\,\,n_{c}\, M_{h_{2}}\, g_{h_{2}ff}}{8\pi } \,\left( 1 - \dfrac{4 M_{f}^{2}}{M_{h_2}^{2}}\right) ^{{3}/{2}},\nonumber \\ \end{aligned}$$

  (D5)

  $n_c$ is the colour charge, for leptons it is 1 and for quarks it is 3.

  The total decay width of the extra Higgs, $h_2$, in the present case is

  $$\begin{aligned} \Gamma _{h_2}= & {} \sum _{V=W,Z}\Gamma (h_2 \rightarrow VV) + \Gamma ({h_{2}} \rightarrow {h_1}{h_1}) \nonumber \\&+ \Gamma ({h_{2}} \rightarrow \phi _\mathrm{DM} \phi _\mathrm{DM}) + \sum _{f}\Gamma (h_{2} \rightarrow {f} \,\bar{f})\,. \nonumber \\ \end{aligned}$$

  (D6)

  ${\mathbf{Total\,decay\,width\,of\,} h_1}$:

  $$\begin{aligned} \Gamma ({h_{1}} \rightarrow \phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM})= & {} \dfrac{C_\mathrm{ASB}\,\,g_{h_{1}\phi _\mathrm{DM}^{\dagger }\phi _\mathrm{DM}}^{2}}{16\,\pi \,M_{h_1}} \,\sqrt{1 - \dfrac{4 M_\mathrm{DM}^{2}}{M_{h_1}^{2}}}.\nonumber \\ \end{aligned}$$

  (D7)

  The total decay width of the SM-like Higgs boson is

  $$\begin{aligned} \Gamma _{h_1} = \cos ^{2}\alpha \,\Gamma _\mathrm{SM} + \Gamma ({h_{1}} \rightarrow \phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM})\,\,, \end{aligned}$$

  (D8)

  where $\Gamma _\mathrm{SM}$ is the total decay width of the SM Higgs boson.

  ${\mathbf{\,Total\,decay\,width\,of\,} Z_\mathrm{BL}}$:

  $$\begin{aligned} \Gamma (Z_\mathrm{BL} \rightarrow f \bar{f})= & {} \frac{M_{Z_\mathrm{BL}}}{12 \pi } n_{c} (q_{f}\,g_\mathrm{BL})^{2} \nonumber \\&\times \left( 1 + \frac{2 M_{f}^{2}}{M_{Z_\mathrm{BL}}^{2}} \right) \sqrt{1 - \frac{4 M_{f}^{2}}{M_{Z_\mathrm{BL}}^{2}}}\,,\nonumber \\ \Gamma (Z_\mathrm{BL} \rightarrow \nu _{x} \bar{\nu _{x}})= & {} \frac{M_{Z_\mathrm{BL}}}{24 \pi } g_\mathrm{BL}^{2} \left( 1 - \frac{4 M_{\nu _{x}}^{2}}{M_{Z_\mathrm{BL}}^{2}} \right) ^{{3}/{2}}\,,\nonumber \\ \Gamma (Z_\mathrm{BL} \rightarrow N_{x} \bar{N_{x}})= & {} \frac{M_{Z_\mathrm{BL}}}{24 \pi } g_\mathrm{BL}^{2} \left( 1 - \frac{4 M_{N_{x}}^{2}}{M_{Z_\mathrm{BL}}^{2}} \right) ^{{3}/{2}}\,,\nonumber \\ \Gamma (Z_\mathrm{BL}\rightarrow {\phi _\mathrm{DM}}^\dagger \phi _\mathrm{DM})= & {} \dfrac{g_\mathrm{BL}^2 n_\mathrm{BL}^2 M_{Z_\mathrm{BL}}}{48\,\pi }\left( 1-\dfrac{4\,M^2_\mathrm{DM}}{M_{Z_\mathrm{BL}}}\right) ^{3/2}. \nonumber \\ \end{aligned}$$

  (D9)

  The total decay width of the extra neutral gauge boson $Z_\mathrm{BL}$ is

  $$\begin{aligned} \Gamma _{Z_\mathrm{BL}}= & {} \sum _{f} \Gamma (Z_\mathrm{BL} \rightarrow f \bar{f}) + \Gamma (Z_\mathrm{BL} \rightarrow \nu _{x} \bar{\nu _{x}}) \nonumber \\&+ \Gamma (Z_\mathrm{BL} \rightarrow N_{x} \bar{N_{x}})+ \Gamma (Z_\mathrm{BL}\rightarrow {\phi _\mathrm{DM}}^\dagger \phi _\mathrm{DM})\,.\nonumber \\ \end{aligned}$$

  (D10)

Appendix E: Analytical expression of relevant cross sections

Here we will give the expressions of the cross sections for all relevant processes which take part in the FIMP DM production.

• $\underline{h_{1}h_{1}\rightarrow \phi _\mathrm{DM}^{\dagger } \,\phi _\mathrm{DM}}$:

  $$\begin{aligned} g_{h_{1}h_{1}h_{1}}= & {} -3\,[2\,v\lambda _{h}\cos ^{3}\alpha + 2\,v_\mathrm{BL}\,\lambda _{H}\sin ^{3}\alpha \nonumber \\&+\lambda _{hH}\sin \alpha \,\cos \alpha \, (v\sin \alpha + v_\mathrm{BL}\cos \alpha )],\nonumber \\ g_{h_{1}h_{1}h_{2}}= & {} [6\,v\lambda _{h}\cos ^{2}\alpha \sin \alpha - 6\,v_\mathrm{BL}\lambda _{H}\sin ^{2}\alpha \,\cos \alpha \nonumber \\&-(2-3\,\sin ^{2}\alpha )\,v\,\lambda _{hH}\,\sin \alpha \nonumber \\&-(1-3\sin ^{2}\alpha )v_\mathrm{BL}\, \lambda _{hH}\cos \alpha ] \,, \end{aligned}$$

  (E1)
  $$\begin{aligned} g_{h_{1}h_{1}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}= & {} - (\lambda _{Dh} \cos ^{2}\alpha + \lambda _{DH} \sin ^{2}\alpha ) \,,\nonumber \\ M_{h_{1} h_{1}}= & {} \left( \dfrac{C_\mathrm{ASB}\,g_{h_{1}h_{1}h_{1}}\, \,g_{h_{1}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}}{(s-M_{h_1}^{2}) + i M_{h_1} \Gamma _{h_1}} \right. \nonumber \\&\left. + \dfrac{g_{h_{1}h_{1}h_{2}} \,\,g_{h_{2}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}}{(s-M_{h_2}^{2}) + i M_{h_2} \Gamma _{h_2}}\right) \nonumber \\&- g_{h_{1}h_{1}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}\,, \sigma _{h_{1}h_{1} \rightarrow \phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}} \nonumber \\= & {} \dfrac{1}{16 \pi s}\,\, \sqrt{\dfrac{s - 4M_\mathrm{DM}^{2}}{s - 4M_{h_1}^{2}}} \,\,\,|M_{h_{1}h_{1}}|^{2}\,. \end{aligned}$$

  (E2)

• $\underline{h_{2}h_{2}\rightarrow \phi _\mathrm{DM}^{\dagger }\,\phi _\mathrm{DM}}$:

  $$\begin{aligned} g_{h_{2}h_{2}h_{2}}= & {} 3\,[2\,v\lambda _{h}\sin ^{3} \alpha - 2\,v_\mathrm{BL}\lambda _{H}\cos ^{3}\alpha \nonumber \\&+ \lambda _{hH}\sin \alpha \cos \alpha \, (v\cos \alpha - v_\mathrm{BL}\sin \alpha )],\nonumber \\ g_{h_{2}h_{2}h_{1}}= & {} -[6\,v\lambda _{h}\sin ^{2} \alpha \cos \alpha + 6\,v_\mathrm{BL}\lambda _{H}\cos ^{2}\alpha \sin \alpha \nonumber \\&-(2-3\,\sin ^{2}\alpha )v_\mathrm{BL}\lambda _{hH}\sin \alpha \,\,\nonumber \\&+(1-3\sin ^{2}\alpha )v\lambda _{hH}\cos \alpha ]\,, \nonumber \\&g_{h_{2}h_{2}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}} = -\,(\lambda _{Dh} \sin ^{2}\alpha \nonumber \\&+ \lambda _{DH} \cos ^{2}\alpha ) \,,\nonumber \\ M_{h_{2}h_{2}}= & {} \left( C_\mathrm{ASB}\,\,\dfrac{g_{h_{2}h_{2}h_{1}}\, \,g_{h_{1}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}}{(s-M_{h_1}^{2}) + i M_{h_1} \Gamma _{h_1}}\right. \nonumber \\&\left. + \dfrac{g_{h_{2}h_{2}h_{2}} \,\,g_{h_{2}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}}{(s-M_{h_2}^{2}) + i M_{h_2} \Gamma _{h_2}}\right) \nonumber \\&- g_{h_{2}h_{2}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}\,, \sigma _{h_{2}h_{2} \rightarrow \phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}} \nonumber \\= & {} \dfrac{1}{16 \pi s}\sqrt{\dfrac{s - 4M_\mathrm{DM}^{2}}{s - 4M_{h_2}^{2}}} \,\,\,|M_{h_{2}h_{2}}|^{2}\,. \end{aligned}$$

  (E3)

• $\underline{h_{1}h_{2}\rightarrow \phi _\mathrm{DM}^{\dagger }\,\phi _\mathrm{DM}}$:

  $$\begin{aligned} g_{h_{1}h_{1}h_{2}}= & {} [6\,v\lambda _{h}\cos ^{2}\alpha \,\sin \alpha \nonumber \\&- 6\,v_\mathrm{BL}\,\lambda _{H}\sin ^{2}\alpha \,\cos \alpha \\&-(2-3\,\sin ^{2}\alpha )\,v\,\lambda _{hH}\sin \alpha \\&-(1-3\sin ^{2}\alpha )v_\mathrm{BL}\,\lambda _{hH}\cos \alpha ] \\ g_{h_{2}h_{2}h_{1}}= & {} -[6\,v\lambda _{h}\sin ^{2}\alpha \,\cos \alpha \nonumber \\&+ 6\,v_\mathrm{BL}\lambda _{H}\cos ^{2}\alpha \sin \alpha \\&-(2-3\,\sin ^{2}\alpha )\,v_\mathrm{BL}\,\lambda _{hH}\sin \alpha \nonumber \\&+(1-3\sin ^{2}\alpha )v\lambda _{hH}\cos \alpha ]\,, \\ g_{h_{1}h_{2}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}= & {} \,\sin \alpha \cos \alpha (\lambda _{Dh} -\lambda _{DH}) \,,\\ M_{h_{1}h_{2}}= & {} -C_\mathrm{ASB}\left( g_{h_{1}h_{2}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}} \right. \\&\left. -\dfrac{g_{h_{2}h_{2}h_{1}} \,\,g_{h_{2}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}}{(s-M_{h_2}^{2}) + i M_{h_2} \Gamma _{h_2}}\right) \\&+ \dfrac{g_{h_{1}h_{1}h_{2}}\, \,g_{h_{1}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}}{(s-M_{h_1}^{2}) + i M_{h_1} \Gamma _{h_1}}, \end{aligned}$$
  $$\begin{aligned}&\sigma _{h_{1}h_{2} \rightarrow \phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}} = \dfrac{1}{16 \pi s}\nonumber \\&\quad \sqrt{\dfrac{s(s - 4M_\mathrm{DM}^{2})}{(s-(M_{h_1}+M_{h_2})^{2})(s - (M_{h_2} - M_{h_1})^{2})}} \,\,\,|M_{h_{1}h_{2}}|^{2}.\nonumber \\ \end{aligned}$$

  (E4)

• $\underline{W^{+}W^{-}\rightarrow \phi _\mathrm{DM}^{\dagger }\,\phi _\mathrm{DM}}$:

  $$\begin{aligned} g_{h_{1}WW}= & {} \dfrac{2M_{W}^{2} \cos \alpha }{v}\,,\nonumber \\ g_{h_{2}WW}= & {} -\dfrac{2M_{W}^{2} \sin \alpha }{v}, \nonumber \\ A_{WW}= & {} C_\mathrm{ASB}\left( \dfrac{g_{h_{1}WW}\,\,g_{h_{1}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}}{(s-M_{h_1}^{2}) + i M_{h_1} \Gamma _{h_1}} \right. \nonumber \\&\left. + \dfrac{g_{h_{2}WW}\,g_{h_{2}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}}{(s-M_{h_2}^{2}) + i M_{h_2} \Gamma _{h_2}}\right) , \nonumber \\ M_{WW}= & {} \dfrac{2}{9}\,\left( 1 + \dfrac{(s - 2M_{W}^{2})^{2}}{8M_{W}^{4}}\right) \,A_{WW}, \nonumber \\ \sigma _{WW \rightarrow \phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}= & {} \dfrac{1}{16 \pi s}\,\, \sqrt{\dfrac{s - 4M_\mathrm{DM}^{2}}{s - 4M_{W}^{2}}} \,\,\,|M_{WW}|^{2}\,. \end{aligned}$$

  (E5)

• $\underline{Z\,Z \rightarrow \phi _\mathrm{DM}^{\dagger }\,\phi _\mathrm{DM}}$:

  $$\begin{aligned} g_{h_{1}ZZ}= & {} \dfrac{2M_{Z}^{2} \cos \alpha }{v}\,,\nonumber \\ g_{h_{2}ZZ}= & {} -\dfrac{2M_{Z}^{2} \sin \alpha }{v}, \nonumber \\ A_{ZZ}= & {} C_\mathrm{ASB}\left( \dfrac{g_{h_{1}ZZ}\,g_{h_{1}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}}{(s-M_{h_1}^{2}) + i M_{h_1} \Gamma _{h_1}} \right. \nonumber \\&\left. + \dfrac{g_{h_{2}ZZ}\,g_{h_{2}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}}{(s-M_{h_2}^{2}) + i M_{h_2} \Gamma _{h_2}}\right) , \nonumber \\ M_{ZZ}= & {} \dfrac{2}{9}\,\,\left( 1 + \dfrac{(s - 2M_{Z}^{2})^{2}}{8M_{Z}^{4}}\right) \,A_{ZZ}, \nonumber \\ \sigma _{ZZ \rightarrow \phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}= & {} \dfrac{1}{16 \pi s}\,\,\sqrt{\dfrac{s - 4M_\mathrm{DM}^{2}}{s - 4M_{Z}^{2}}} \,\,\,|M_{ZZ}|^{2}\,. \end{aligned}$$

  (E6)

• $\underline{t\bar{t}\rightarrow \phi _\mathrm{DM}^\dagger \,\phi _\mathrm{DM}}$:

  $$\begin{aligned} g_{h_{1}tt}= & {} -\dfrac{M_{t}}{v} \cos \alpha \,, \nonumber \\ g_{h_{2}tt}= & {} \dfrac{M_{t}}{v} \sin \alpha \,, \nonumber \\ g_{Z_\mathrm{BL}tt}= & {} \dfrac{g_\mathrm{BL}}{3} \,, \nonumber \\ M_{tt}= & {} C_\mathrm{ASB}\left( \dfrac{g_{h_{1}tt}\, \,g_{h_{1}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}}{(s-M_{h_1}^{2}) + i M_{h_1} \Gamma _{h_1}} \right. \nonumber \\&\left. + \dfrac{g_{h_{2}tt} \,\,g_{h_{2}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}}{(s-M_{h_2}^{2}) + i M_{h_2} \Gamma _{h_2}}\right) , \nonumber \\ \sigma _{{t}{\bar{t}} \rightarrow \phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}^{h_{1} h_{2}}= & {} \dfrac{1}{32 \pi s\,n_{c}}\,\,(s - 4M_{t}^{2})\,\, \nonumber \\&\times \sqrt{\dfrac{s - 4M_\mathrm{DM}^{2}}{s - 4M_{t}^{2}}} \,\,\,|M_{tt}|^{2}\,, \nonumber \\ \sigma _{{t}{\bar{t}} \rightarrow \phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}^{Z_\mathrm{BL}}= & {} \dfrac{g_\mathrm{BL}^{2}\, n_\mathrm{BL}^{2}}{64 \pi s\,n_{c}}\,\, \sqrt{\dfrac{s - 4M_\mathrm{DM}^{2}}{s - 4M_{t}^{2}}}\nonumber \\&\times \frac{s\, (s - 4M_\mathrm{DM}^{2})\, g_{Z_\mathrm{BL}t t}^{2}}{(s - M^{2}_{Z_\mathrm{BL}})^{2} + \Gamma ^{2}_{Z_\mathrm{BL}} M^{2}_{Z_\mathrm{BL}}}\,,\nonumber \\ \sigma _{{t}{\bar{t}} \rightarrow \phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}= & {} \sigma _{{t}{\bar{t}} \rightarrow \phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}^{h_1 h_2} + \sigma _{{t}{\bar{t}} \rightarrow \phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}^{Z_\mathrm{BL}}\,. \end{aligned}$$

  (E7)

• $\underline{N_{i}N_{i}\rightarrow \phi _\mathrm{DM}^\dagger \,\phi _\mathrm{DM}\,\,(i=1,\, 2,\,3)}$:

  $$\begin{aligned} g_{h_{1}N_{i}N_{i}}= & {} \frac{y_{N_i}\sin \alpha }{\sqrt{2}} \,, \nonumber \\ g_{h_{2}N_{i}N_{i}}= & {} \frac{y_{N_i}\cos \alpha }{\sqrt{2}} \,, \nonumber \\ M_{N_{i}N_{i}}= & {} \dfrac{C_\mathrm{ASB}\,\,g_{h_{1}N_{i}N_{i}}\, \,g_{h_{1}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}}{(s-M_{h_1}^{2}) + i M_{h_1} \Gamma _{h_1}} \\&+ \dfrac{g_{h_{2}N_{i}N_{i}} \,\,g_{h_{2}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}}{(s-M_{h_2}^{2}) + i M_{h_2} \Gamma _{h_2}}\,, \nonumber \\ \sigma _{N_{i}N_{i} \rightarrow \phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}^{h_1 h_2}= & {} \dfrac{(s \!-\! 4\,M_{N_j}^{2})}{32 \pi s}\,\\&\times \sqrt{\dfrac{(s \!-\! 4M_\mathrm{DM}^{2})}{(s\!-\!4 M_{N_i}^{2})}} \,\,\,|M_{N_{i}N_{i}}|^{2},\nonumber \\ \end{aligned}$$
  $$\begin{aligned}&\sigma _{N_{i}N_{i} \rightarrow \phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}^{Z_\mathrm{BL}} = \dfrac{g_{\mu \tau }^{4}n_{\mu \tau }^{2}}{192 \pi s} \,\nonumber \\&\quad \times \sqrt{\dfrac{s-4M_\mathrm{DM}^{2}}{s-4M_{N_i}^{2}}} \dfrac{(s-4M_\mathrm{DM}^{2})(s-4M_{N_i}^{2})}{(s - M_{Z_\mathrm{BL}}^{2})^{2} + \Gamma _{Z_\mathrm{BL}}^{2}M_{Z_\mathrm{BL}}^{2}}\,, \nonumber \\&\sigma _{N_{i}N_{i} \rightarrow \phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}} = \sigma _{N_{i}N_{i} \rightarrow \phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}^{h_1 h_2} \!+\!\sigma _{N_{i}N_{i} \rightarrow \phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}^{Z_\mathrm{BL}}.\nonumber \\ \end{aligned}$$

  (E8)

• $\underline{Z_\mathrm{BL}\,Z_\mathrm{BL}\rightarrow \phi _\mathrm{DM}^{\dagger }\,\phi _\mathrm{DM}}$ :

  $$\begin{aligned} g_{h_{1} Z_\mathrm{BL}Z_\mathrm{BL}}= & {} \dfrac{2M_{Z_\mathrm{BL}}^{2} \sin \alpha }{v}\,,\\ g_{h_{2}Z_\mathrm{BL}Z_\mathrm{BL}}= & {} -\dfrac{2M_{Z_\mathrm{BL}}^{2} \cos \alpha }{v}, \\ g_{Z_\mathrm{BL}Z_\mathrm{BL}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}= & {} 2\, g_\mathrm{BL}^{2} n_\mathrm{BL}^{2}\,,\\ \end{aligned}$$
  $$\begin{aligned}&A_{Z_\mathrm{BL}Z_\mathrm{BL}} = C_\mathrm{ASB}\left( \dfrac{g_{h_{1}Z_\mathrm{BL}Z_\mathrm{BL}}\,g_{h_{1} \phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}}{(s-M_{h_1}^{2}) + i M_{h_1} \Gamma _{h_1}}\right. \nonumber \\&\quad \left. + \dfrac{g_{h_{2}Z_\mathrm{BL}Z_\mathrm{BL}}\,g_{h_{2}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}}}{(s-M_{h_2}^{2}) + i M_{h_2} \Gamma _{h_2}} - g_{Z_\mathrm{BL}Z_\mathrm{BL}\phi _\mathrm{DM}^{\dagger } \phi _\mathrm{DM}} \right) , \nonumber \\&M_{Z_\mathrm{BL}Z_\mathrm{BL}} = \dfrac{2}{9}\,\,\left( 1 + \dfrac{(s - 2M_{Z_\mathrm{BL}}^{2})^{2}}{8M_{Z_\mathrm{BL}}^{4}}\right) \,A_{Z_\mathrm{BL}Z_\mathrm{BL}}, \nonumber \\&\sigma _{Z_\mathrm{BL}Z_\mathrm{BL}\rightarrow \phi _\mathrm{DM}^{\dagger }\phi _\mathrm{DM}} = \dfrac{1}{16 \pi s}\,\sqrt{\dfrac{s - 4M_\mathrm{DM}^{2}}{s - 4M_{Z_\mathrm{BL}}^{2}}} \,\,|M_{Z_\mathrm{BL}Z_\mathrm{BL}}|^{2}.\nonumber \\ \end{aligned}$$

  (E9)