1 Introduction

White dwarfs (WDs) are the final evolution state of main sequence stars with initial masses up to 8.5–10.6 M\(_{\odot }\). They correspond to 95–97% of all observed stars in the Universe [1]. The main sequence progenitors can reach sufficiently high core temperatures (8–12\(\times 10^{8}\) K), to proceed to carbon burning and produce either oxygen-neon (ONe) core WDs or undergo a core-collapse supernova (SNII) via electron capture on the products of carbon burning.

Chandrasekhar has shown that a WD cannot sustain a mass over \(1.44M_{\odot }\), establishing the so-called Chandrasekhar mass limit [2]. If a WD grows over this limit, as in binary systems in which a WD is receiving mass from a nearby star, a type Ia supernova (SNIa) explosion may occur. SNIa progenitors are expected to be similar, with nearly equal luminosity, therefore being considered standard candles [3]. In fact, in the late 1990s, the use of SNIa led to the discovery that the expansion of the Universe is accelerating [4, 5].

Nevertheless, some super luminous SNIas were found recently [6, 7]. It has been suggested that their progenitors are WDs that exceed the Chandrasekhar mass limit (2.1–2.8 M\(_{\cdot }\)) [6,7,8,9,10,11], being termed “super-Chandrasekhar WDs”.

WDs usually are not considered as a “laboratory” for strong field regimes. However, general relativistic effects have shown to be non-negligible in the massive and very magnetic WD regime [12,13,14,15,16]. Particularly, it has been shown in [13] and [17] that the inclusion of general relativistic effects tends to reduce the maximum mass of WDs with strong magnetic fields. Chandrasekhar and Tooper showed that instability criteria for WDs under radial oscillations in a general relativistic framework has its consequences for critical central density depending on the composition of the star [18, 19]. Moreover, in [20,21,22] it was shown that this critical central density yields a larger minimum radius in comparison with Newtonian gravity outcomes.

On this regard, despite the detection of gravitational waves [23] and innumerable other positive results, as one can check, for instance, in [24], there are two cosmological phenomena, namely dark energy and dark matter, not well understood within the General Relativity (GR) framework. Such a dark sector of the universe composition is a possible indication that GR is not the ultimate theory of gravity, but a particular case of a fundamental theory.

Also, the discovery of a very massive pulsar (PSR J1614-2230) [25], with mass \(M=1.97\pm 0.04M_{\odot }\), has led to interpretative problems either on the neutron star physics or on the background theory of gravity.

In fact, compact astrophysical objects, such as black holes and neutron stars, are often used as a tool to constrain extended gravity theories. For instance, in [26, 27] the bounds that could be placed on different gravitational theories using gravitational wave detection from spiraling compact binaries were investigated.

In particular, WD properties have been recently verified from extended theories of gravity, as it can be checked, for instance, in [28, 29].

The authors of Ref. [29] have explored WD properties from an extension of GR, named f(R) gravity, with R being the Ricci scalar. They have shown that extended theories of gravity effects are significant in high density WDs and that the Chandrasekhar limit is not unique. By assuming \(f(R)=R+\alpha R^2\), with constant \(\alpha \), they have obtained super and sub-Chandrasekhar limiting mass WDs, depending on the magnitude and sign of \(\alpha \), getting in touch with observations hardly explained within GR framework.

WD properties also proved to be useful to constrain modified theories of gravity. For instance, in [30] the free parameters of a scalar-tensor theory of gravity was widely restricted by WD observational data.

In the present work, we are interested in analyzing WDs within the f(R, T) gravity [31], with T being the trace of the energy-momentum tensor. More precisely, we will investigate the hydrostatic equilibrium [32, 33] of WDs in such a theory.

The f(R, T) gravity has as its starting point a gravitational action which depends generally on R and T. In this way, after the application of the variational principle, the field equations of the model are expected to present correction terms on both geometrical and material sides.

The f(R, T) gravity application is motivated by its recent outcomes in different areas. It has been shown that from a minimal coupling between matter and geometry, predicted in f(R, T) theories, it is possible to obtain a flat rotation curve in the halo of galaxies [34]. f(R, T) models passed through solar system tests in [35]. A complete cosmological scenario was constructed from the f(R, T) gravity in [36]. In [37], a cosmological model in accordance with observations was obtained from the simplest non-minimal matter-geometry coupling within the f(R, T) formalism. The validity of first and second laws of thermodynamics was discussed in [38].

Furthermore, the hydrostatic equilibrium equation in the f(R, T) gravity was originally derived in [39] and further studied in [40]. In [41], the stability of collapsing spherical body coupled with isotropic matter was investigated. In [42], the collapse equation in f(R, T) gravity was derived from the perturbation scheme application. In [43], the instability range of the f(R, T) gravity for an anisotropic background constrained by zero expansions has been developed. Moreover, the evolution of a spherical star by employing a perturbation scheme was explored in [44, 45].

As it shall be outlined below, the f(R, T) gravity may be an important tool to study WD macroscopical properties. It also can present some advantages when compared to f(R) gravity predictions for such objects, as we will show.

2 A brief review of the f(R, T) gravity formalism

Proposed by Harko et al. [31], the f(R, T) gravity is a generalization of the f(R) theories (check, for instance, [46]). Its gravitational action depends on an arbitrary function of both the Ricci scalar R and the trace of the energy-momentum tensor T. The dependence on T is inspired by the consideration of quantum effects.

The f(R, T) action reads [31]

$$\begin{aligned} {\mathscr {S}}=\int \mathrm{d}^{4}x\sqrt{-g}\left[ \frac{f(R,T)}{16\pi }+{\mathscr {L}}_{m}\right] . \end{aligned}$$
(1)

In (1), f(R, T) is the general function of R and T, \({\mathscr {L}}_{m}\) is the matter Lagrangian density and g is the determinant of the metric tensor \(g_{\mu \nu }\). Throughout this work, it will be considered the metric signature \(-2\) and \(c=1=G\).

The field equations of the theory are obtained by varying the action with respect to the metric \(g_{\mu \nu }\), yielding [31]

$$\begin{aligned}&f_{R}(R,T)R_{\mu \nu }-\frac{1}{2}f(R,T)g_{\mu \nu }+(g_{\mu \nu }\Box -\nabla _{\mu }\nabla _{\nu })f_{R}(R,T)\nonumber \\&\quad =8\pi T_{\mu \nu }-f_{T}(R,T)(T_{\mu \nu }+\varTheta _{\mu \nu }), \end{aligned}$$
(2)

where

$$\begin{aligned} f_{R}(R,T)\equiv & {} \frac{\partial f(R,T)}{\partial R},\quad f_{T}(R,T)\equiv \frac{\partial f(R,T)}{\partial T}, \end{aligned}$$
(3)
$$\begin{aligned} \varTheta _{\mu \nu }\equiv & {} g^{\alpha \beta }\frac{\delta T_{\alpha \beta }}{\delta g^{\mu \nu }},\quad T_{\mu \nu }=g_{\mu \nu }{\mathscr {L}}_{m}-2\frac{\partial {\mathscr {L}}_{m}}{\partial g^{\mu \nu }}. \end{aligned}$$
(4)

Still in Equation (2) above, \(R_{\mu \nu }\) represents the Ricci tensor, \(\Box =\nabla ^{\mu }\nabla _{\mu }\) is the D’Alembertian and \(\nabla _{\mu }\) is the covariant derivative.

From the covariant derivative of the field equation (2), one obtains [39, 47, 48]

$$\begin{aligned} \nabla ^{\mu }T_{\mu \nu }= & {} \frac{f_{T}(R,T)}{8\pi -f_{T}(R,T)} \nonumber \\&\times \bigg [(T_{\mu \nu }+\varTheta _{\mu \nu })\nabla ^{\mu }\ln f_{T}(R,T)\nonumber \\&-\frac{1}{2}g_{\mu \nu }\nabla ^{\mu }T+\nabla ^{\mu }\varTheta _{\mu \nu }\bigg ]. \end{aligned}$$
(5)

We will consider the energy-momentum tensor of a perfect fluid, such that

$$\begin{aligned} T_{\mu \nu }=(p+\rho )u_{\mu }u_{\nu }-pg_{\mu \nu }, \end{aligned}$$
(6)

where p and \(\rho \) represent the pressure and the energy density of the fluid, respectively, and \(u_{\mu }\) is the four velocity of the fluid, with \(u_{\mu }u^{\mu }=1\) and \(u^{\mu }\nabla _{\nu }u_{\mu }=0\). The energy-momentum tensor and the conditions aforementioned imply that

$$\begin{aligned} {\mathscr {L}}_{m}= & {} -p, \end{aligned}$$
(7)
$$\begin{aligned} \varTheta _{\mu \nu }= & {} -pg_{\mu \nu }-2T_{\mu \nu }. \end{aligned}$$
(8)

In order to obtain exact solutions in the f(R, T) theory, it is necessary to consider a specific form for the function f(R, T). Following a previous work [39], we will consider the functional form \(f(R,T)=R+2\,f(T)\) with \(f(T)=\lambda T\) and \(\lambda \) a constant. Such a functional form has been broadly applied in f(R, T) models [49,50,51,52,53] and allows the recovering of GR by simply taking \(\lambda =0\).

By considering \(f(R,T)=R+2\lambda T\) in Eqs. (2) and (5), it follows that

$$\begin{aligned}&G_{\mu \nu }=8\pi T_{\mu \nu }+\lambda [Tg_{\mu \nu } +2(T_{\mu \nu }+pg_{\mu \nu })], \end{aligned}$$
(9)
$$\begin{aligned}&\nabla ^{\mu }T_{\mu \nu }=-\frac{2\lambda }{8\pi +2\lambda } \left[ \nabla ^{\mu }(pg_{\mu \nu })+\frac{1}{2}g_{\mu \nu }\nabla ^{\mu }T\right] , \end{aligned}$$
(10)

with \(G_{\mu \nu }\) in Eq. (9) representing the usual Einstein tensor.

3 Stellar structure equations in f(R, T) gravity

The line element used to describe spherical objects follows the form:

$$\begin{aligned} ds^2=e^{a(r)}dt^2-e^{b(r)}dr^2-r^2(d\theta ^2+\sin ^2\theta d\phi ^2), \end{aligned}$$
(11)

where \((t,r,\theta ,\phi )\) are the Schwarzschild-like coordinates and the exponents a(r) and b(r) are functions of the radial coordinate r.

Considering the space-time metric (11) in the field equation (9) we obtain:

$$\begin{aligned} G_{0}^{0}= & {} \frac{e^{-b}}{r^2}\left( b'r+e^{b}-1\right) = 8\pi \rho + \lambda (3\rho - p), \end{aligned}$$
(12)
$$\begin{aligned} G_{1}^{1}= & {} -\frac{e^{-b}}{r^2}\left( a'r-e^{b}+1\right) = -8\pi p + \lambda (\rho - 3p), \end{aligned}$$
(13)
$$\begin{aligned} G_{2}^{2}= & {} G_{3}^{3} = \frac{e^{-b}}{4r}\left( \left( a'b'-2a''-a'^2 \right) r + 2(b' - a') \right) \nonumber \\= & {} -8\pi p + \lambda (\rho - 3p), \end{aligned}$$
(14)

in which primes (\('\)) indicate derivatives with respect to r.

Now, we introduce a new function m(r) which depends on the radial coordinate only, in such a form that

$$\begin{aligned} \mathrm{e}^{-b}=1-\frac{2m}{r}. \end{aligned}$$
(15)

By replacing it in Eq. (12) yields

$$\begin{aligned} \frac{\mathrm{d}m}{\mathrm{d}r}= 4\pi \rho r^2 +\frac{\lambda }{2}(3\rho -p)r^2, \end{aligned}$$
(16)

for which the function \(m=m(r)\) represents the gravitational mass enclosed in a surface of radius r according to the f(R, T) gravity.

An additional equation is derived from (10) and reads

$$\begin{aligned} \frac{\mathrm{d}p}{\mathrm{d}r}+\left( \rho +p\right) \frac{a'}{2} = -\frac{\lambda }{8\pi +2\lambda }(p'-\rho '). \end{aligned}$$
(17)

Considering the relation \(\rho =\rho (p)\) and Eqs. (13) and (15) in (17), the hydrostatic equilibrium equation for the \(f(R,T)=R+2\lambda T\) gravity is obtained as

$$\begin{aligned} \frac{dp}{dr}= & {} -(p+\rho ) \left[ 4\pi pr+\frac{m}{r^2} -\frac{\lambda (\rho -3p)r}{2}\right] \nonumber \\&\times \left( 1-\frac{2m}{r}\right) ^{-1}\left[ 1+\frac{\lambda }{8\pi +2\lambda }\left( 1-\frac{\mathrm{d}\rho }{\mathrm{d}p} \right) \right] ^{-1}.\nonumber \\ \end{aligned}$$
(18)

It is quite simple to recover the usual TOV equation [32, 33] in (18) by making \(\lambda =0\).

We remark that stellar equilibrium configurations are found only for:

$$\begin{aligned} \frac{\lambda }{8\pi +2\lambda }\left( 1-\frac{\mathrm{d}\rho }{\mathrm{d}p}\right) >-1. \end{aligned}$$
(19)

If Eq.(19) is not satisfied, the sign of the pressure gradient is changed, what makes the pressure to grow up from the center of the star to its surface, instead of decreasing, which is necessary for the star hydrostatic equilibrium. Since the sound velocity \(v_s^2=\mathrm{d}p/\mathrm{d}\rho \) is in the interval \(0<\mathrm{d}p/\mathrm{d}\rho <1\) and for the WD equation of state (EoS), where the electron degeneracy pressure is very small compared to the energy density, due to the very large ion contribution, \(\mathrm{d}\rho /\mathrm{d}p\) becomes very large, and we can rewrite (19) as

$$\begin{aligned} \frac{\lambda }{8\pi +2\lambda }<\frac{\mathrm{d}p}{\mathrm{d}\rho }. \end{aligned}$$
(20)

Considering that \(\mathrm{d}p/\mathrm{d}\rho \) tends to zero at the surface of the WD, we have from (20) that only negative values for \(\lambda \) are allowed.

4 Numerical procedure, boundary conditions and equation of state

By using the set of Eqs. (22) and (23), the equilibrium Eqs. (16) and (18) will be solved numerically through the Runge-Kutta 4th-order method for diverse values of central density \(\rho _c\) and \(\lambda \).

The boundary conditions in f(R, T) gravity will be the same as in GR, i.e., at the center \((r=0)\) we have

$$\begin{aligned} m(0)=0, \quad p(0)=p_c \quad \mathrm{and} \quad \rho (0)=\rho _c. \end{aligned}$$
(21)

The surface of the star \(r=R\) is reached when the pressure vanishes, i.e., \(p(R)=0\).

The EoS which describes the fluid properties inside WDs follows the model used for complete ionized atoms embedded in a relativistic Fermi gas of electrons [2, 54]:

$$\begin{aligned} p(k_F)= & {} \frac{1}{3\pi ^2\hbar ^3}\int _0^{k_F}\frac{k^4}{\sqrt{k^2+m_e^2}}\mathrm{d}k, \end{aligned}$$
(22)
$$\begin{aligned} \rho (k_F)= & {} \frac{1}{\pi ^2\hbar ^3}\int _0^{k_F}\sqrt{k^2+m_e^2}k^2\mathrm{d}k +\frac{m_N\mu _e}{3\pi ^2 \hbar ^3}k_F^3, \end{aligned}$$
(23)

where the last term of the right hand side of Eq. (23) is the ions energy contribution, and \(m_N\) represents the nucleon mass, \(m_e\) the electron mass, \(k_F\) is the Fermi momentum, \(\hbar \) is the reduced Planck constant and \(\mu _e=A/Z\) is the ratio between the nucleon number A and the atomic number Z for ions, such that in the present work we use \(\mu _e=2\), valid for He, Ca, and O WDs. We neglected the lattice ion energy contribution that is small and responsible for a small reduction of the WD radius [12].

5 Results

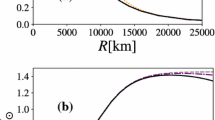
The mass of the WDs as a function of their total radii is shown in Fig. 1 for six different values of \(\lambda \). \(\lambda =0\) recovers the GR case.

Fig. 1
figure 1

Total mass as a function of the total radius for different values of \(\lambda \). The full magenta circles indicate the maximum mass points

Full size image

From Fig. 1, we note that the masses of the stars grow and their total radii increase until attain the maximum mass point, which will be represented by full magenta circles. After that, the masses decrease with the total radii. It is important to remark that the total maximum mass grows with the decrement of \(\lambda \) and the radius increases much more when we consider a fixed star mass. We also mention that the curves above tend to a plateau when \(\lambda \) is \(\approx -4\times 10^{-4}\). For smaller values of the parameter \(\lambda \), all stars are unstable, what can be seen in Figs. 1 and 4 for \(\lambda =-1\times 10^{-3}\), where \(\partial M/\partial R<0\) and the necessary stability criterion \(\partial M/\partial \rho _c>0\) are not satisfied. So, from the equilibrium configurations, the minimum value allowed for \(\lambda \) is \(\sim -4\times 10^{-4}\), which defines a limit for the maximum mass of the WD in the f(R, T) gravity to be \(\sim 1.467M_{\odot }\).

Fig. 2
figure 2

Mass as a function of the radius for massive WDs with different values of \(\lambda \). The blue circles with error bars represent the observational data of a sample of massive WDs taken from the catalogs [55, 56]

Full size image
Fig. 3
figure 3

On the top panel it is presented the star energy density as a function of the radial coordinate, on the central panel we show the star pressure fluid against the radial coordinate and on the bottom panel we display the mass (in solar masses, \(M_{\odot }\)) inside the star versus the radial coordinate. We consider \(\rho _c=10^9\ [{\mathrm{g/cm}}^3]\) and the displayed values of \(\lambda \)

Full size image
Fig. 4
figure 4

The dependence of the total mass of the white dwarfs on central density for different values of \(\lambda \)

Full size image

In addition, in Fig. 2 we highlight the massive WDs region of Fig. 1, in which we have also inserted some observational data taken from the catalogs of Refs. [55, 56]. It can be clearly seen from Fig. 2 that some of the data can hardly be described purely from General Relativity, while some values of \(\lambda \) can, indeed, predict the existence of massive WDs with larger radii.

Thus, according to observations of some massive WDs, in particular the most massive, WD (1659+440J), found in [55], the inferior limit for \(\lambda \) is \(\lambda _{\min }\approx -3\times 10^{-4}\). We regard that this restriction is obtained by neglecting the WD data (0003+436J) with the largest error bar in Fig. 2. Such a constraint is more restrictive than the one obtained from Fig. 1, with no observational data.

In Fig. 3 the energy density, fluid pressure and mass profile in the interior of the star are plotted on the top, central and bottom panels, respectively, as functions of the radial coordinate. We take into account \(\rho _c=10^9\ [{\mathrm{g/cm}}^3]\) and different values of \(\lambda \). On the top and central panels, we can observe that the energy density and the fluid pressure decrease monotonically towards the surface of the object.

On the other hand, concerning the bottom panel, it can be noted that the mass profile \(m/M_{\odot }\), with \(M_{\odot }\) representing the Sun’s mass, grows until it reaches the surface of the star. It can also be seen that the total mass of the star increases with \(\lambda \). This is due to the effect caused by the term \(2\lambda T\).

Figure 4 shows the behavior of the total mass against the central energy density of the stars. The values considered for the central energy density are between \(1.3\times 10^8\) and \(4.2\times 10^{11}\ [{\mathrm{g/cm}}^3]\). The upper limit is the neutron drip limit, i.e., the point where the WD turn into a neutron star. We can note that the total mass grows monotonically with central energy density until it attains a maximum value, except for \(\lambda =-1\times 10^{-3}\). After that point, the stellar mass decreases with the increment of \(\rho _c\) and becomes unstable.

Additionally, in Fig. 4, we observe an increment of the maximum mass with \(\lambda \) (see also Table 1). For example, the maximum mass value found in GR case (\(\lambda =0\)) is \(1.417M_{\odot }\), while for \(\lambda =-4\times 10^{-4}\), it is \(1.467M_{\odot }\). A similar effect for \(\lambda \) in the structure of the stars has been found for neutron stars and strange stars [39, 57]. Moreover, it is remarkable that for lower values of \(\lambda \), the maximum mass point is reached for lower values of \(\rho _c\), which can be considered an advantage of this approach when compared with f(R) theory of gravity or GR outcomes, as we will argue in the next section.

In Fig. 5 the dependence of the total radius with the central energy density is shown. In all cases presented, we can note that the total radius decreases when the central energy density is incremented. Larger radii are found for smaller central energy densities when \(\lambda \) is decreased. This is the most important effect of f(R, T) theory for massive WDs, that is, the increase of the radius, and as a consequence, the decrease of the central density, in comparison with GR and also f(R) results. This is mainly due to the fact that the sound velocity becomes very small near the surface of the star, so that the term (19) weakens the gradient of pressure, yielding to the predicted larger radii.

Table 1 The maximum masses of the white dwarfs found for each value of \(\lambda \) with their respective total radii and central energy densities
Full size table
Fig. 5
figure 5

The total star radius versus central density for different values of \(\lambda \)

Full size image

In Table 1 the maximum masses are presented, with their total radii and central energy densities, for each value of \(\lambda \). We can see that more massive and larger WDs are found with the decrement of \(\lambda \). The values of maximum masses are obtained for lower central densities (range of \(\rho _c \sim 10^9-10^{10} [{\mathrm{g/cm}}^3]\)) when compared with those predicted in the f(R) gravity or GR scope (\(\rho _c \sim 10^{11} [{\mathrm{g/cm}}^3]\)) [29].

6 Discussion and conclusions

In this paper we investigated the effects of an extended theory of gravity, namely f(R, T) gravity, in WDs, by developing the hydrostatic equilibrium analysis for such a theory. Our main goal was to check the imprints of the extra material terms - coming from the \(T-\)dependence of the theory - on WD properties.

One can argue that the hydrostatic equilibrium of compact objects was already performed, originally in [39] and posteriorly in [40], which is true, however those analysis have not considered the WDs EoS (22)-(23) to close the system of equilibrium equations to be solved, which characterizes the path to obtain the new information content of the present paper when compared to [39, 40]. In this way, since recently it was shown that alternative gravity theories may contribute also to the macroscopical features of WDs (check, for instance, [28, 29]), the present analysis is worthed.

The hydrostatic equilibrium configurations of WDs in alternative gravity theories others than f(R, T) gravity can be seen in the recent literature. In [28] the consequences of modifications in GR were deeply analyzed in the WDs perspective. A similar approach can be seen in [29]. In [30] it was shown that WDs provide a unique setup to constrain Horndeski theories of gravity. In [58], it was explored the effects that WDs suffers when described in various modified gravity models, such as scalar-tensor-vector, Eddington inspired Born-Infeld and f(R) theories of gravity. Furthermore, WDs have been used to constrain hypothetical variations on the gravitational constant [59,60,61].

The equilibrium configurations of WDs were analyzed for \(f(R,T)=R+2\lambda T\) with different values of \(\lambda \) and central energy densities. We showed that the extended theory of gravity affects the maximum mass and radius of WDs depending on the value of \(\lambda \).

Since gravitational fields are smaller for WDs than for neutron stars or quarks stars, the scale parameter \(\lambda \) used here is small when compared to the values used in Ref. [39]. In this way, WDs data can be used as a tool to constrain an inferior limit on \(\lambda \), which is \(\lambda _{min}\approx -3 \times 10^{-4}\).

The values of the parameter \(\lambda \) used in the present article are clearly small when compared to those of Ref. [39], in which the hydrostatic equilibrium configurations of neutron and quark stars were calculated in f(R, T) gravity. This may be due to the fact that the compactness M / R of WDs is small when compared to those of neutron and quark stars. In fact, it can be seen in [39] that the values of \(\lambda \) needed to get stable quark stars are greater than the values used for neutron stars, as a probable consequence of the higher compactness of quarks stars in relation to neutron stars. In this way, these analysis indicate that higher compactness objects would need higher deviations from GR.

We found that for \(\lambda =-4\times 10^{-4}\), the maximum mass of the WD is \(1.47M_{\odot }\). This value is determined in a central energy density \(\sim 85\)% lower and radius \(\sim 110\)% greater than those values used to find the maximum mass value in the GR case (\(\lambda =0\)). The outcomes for the central energy density are also smaller than those obtained in \(f(R)=R+\alpha R^2\) gravity, for different values of \(\alpha \) [29].

We argue about the advantages of having WDs with lower central energy densities in the following. In [62] some constraints on the central density of a WD were obtained. The authors have derived a system of equations and inequalities that allows one to determine constraints on \(\rho _c\). They have found that \(\rho _c\le 10^9\,{\mathrm{g/cm}}^3\). Moreover, in a seminal paper by Hamada and Salpeter [63], it was found that for the maximum masses of WDs, \(\rho _c\sim 10^9-10^{10}\,{\mathrm{g/cm}}^3\). Recently, WD calculations in GR also showed that central energy densities are limited by nuclear fusion reactions [12, 16, 64]. It is worth quoting that the values of the central energy densities that we have obtained for the f(R, T) gravity respect these constraints. In contrast, what has been found for the central energy density of WDs in f(R) gravity is \(\rho _c\sim 10^{11}\,{\mathrm{g/cm}}^3\) [29].

As a direct extension of the present work, one can also consider quadratic terms on T for the functional form of f(R, T), that is, \(f(R,T)=R+2\lambda T+\xi T^2\), with \(\xi \) being a free parameter. Since the extra material terms seem to yield an increment on the mass of WDs, one may expect the presence of the quadratic term \(T^2\) to significantly elevate the Chandrasekhar limit and predict the existence of super-Chandrasekhar WDs [6, 7], which still require convincing physical explanation.

Also, in a further work, the analysis presented here can be performed in models of nonminimal torsion-matter coupling, like those in References [65, 66]. While the hydrostatic equilibrium of quark stars has already been performed in such models [67], the application for neutron stars and WDs still lacks.