1 Introduction

Recently, the possibility of some white dwarfs (WD) surpassing the Chandrasekhar mass limit was raised [1,2,3,4,5,6]. The possible progenitor of such massive stars (\(M>2 M_\odot \)) are being termed super-Chandrasekhar white dwarfs. In this context, plenty of works have been done to model these very massive white dwarfs (MWD). The properties of MWDs have been studied in different contexts: rotation [7,8,9,10]; high electric and magnetic fields [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]; temperature [27, 28] and modified gravity [29,30,31,32,33,34,35,36,37,38,39,40]. It has been shown that general relativistic effects are essential for massive white dwarfs and cannot be disregarded [41,42,43,44,45]. The main contribution of the general relativistic effects is in the radius of the stars, which, as pointed out in Ref. [42] can be up to 37% for some cases. General relativistic effects are also important for the stellar structure, since they can lead to global instabilities, limiting the maximum mass. Modified gravity is also per se a topic of great current interest due to the unknown entity (dark energy) which accelerates [46] the Universe. Therefore, through the modified theory of gravity, many strategies were developed to explain the rapid expansion [47].

White dwarfs have been useful to constrain parameters in modified theories [30, 48, 49]. That is possible due to the well-known equation of state (EoS) that describes the white dwarfs, as well as the huge amount of observational data for these stars. This makes white dwarfs also a good “laboratory” to test the strong gravity regime.

In the present work, we are continuing to investigate compact objects in \(f(\mathtt {R,L_m})\) gravity, which we have applied in previous works to neutron stars [50, 51]. In those works, we showed that this theory can account for the enhancement of the maximum mass in neutron stars, in better agreement with the observational data from GW170817 and NICER as compared to General Relativity [51]. This theory is a generalization of the so-called \(f(\mathtt {R})\) theories and was proposed by Harko and Lobo [52]. The \(f(\mathtt {R,L_m})\) theory considers an explicit coupling between matter and geometry, described by a general function that depends on the Ricci scalar \(\mathtt {R}\) and the matter Lagrangian density, \(\mathtt {L_m}\) i.e., there is a term such as \(\sigma \mathtt {R}\mathtt {L_m}\) in the Lagrangian, where \(\sigma \) is a coupling constant. Models with non-minimal curvature-matter coupling have been extensive objects of investigation [53]. As stated in Ref. [52], as a result of the coupling, the motion of particles is non-geodesic, there is an extra force orthogonal to the four-velocity and so on. The study and viability of the theory already started in different contexts [54,55,56] and the results are promising.

In the next section, we shall discuss the possible progenitor candidates for supermassive white dwarfs, showing the present and future observations that lead to them. In Sect. 4 we shall briefly present the resulting hydrostatic equilibrium equation for the \(f(\mathtt {R,L_m})\) theory of gravity. In Sect. 5, we will present the numerical procedure, boundary conditions, the equation of state and threshold due to the composition used in this work. Results are presented in Sect. 6, followed by the discussion and conclusions in the last section (Sect. 7).

2 Super-Chandrasekhar candidates

Though the origin of the supernovas of type Ia (SN Ia) is understood as the thermonuclear detonation of a white dwarf (WD) which is triggered either by the merger of two WDs in a binary or a single WD accreting mass from a companion, the experimental evidence for the progenitors of SN Ia is scarce. Observation of progenitors near and above the Chandrasekhar limit is challenging. In particular, some observed SN Ia, such as SN 2009dc, have spectral observations similar to normal SN Ia, however they are overluminous and ejecta velocities are slower compared to normal ones [1,2,3,4]. The ejecta masses are estimated to be highly super-Chandrasekhar (2.2–2.8 \(M_\odot \)) [5]; while double degenerate merger, off-center explosion and differential rotation models still struggle to explain these large values [57,58,59].

Besides the highly super-Chandrasekhar SN Ia progenitors, spectra of the pulsating subdwarf-B (sdB) star KPD 1930+2752 confirmed that this star is a binary [60]. The amplitude of the orbital motion (349.3 \(\pm 2.7 \mathrm{km s^{-1}}\)) combined with the canonical mass for sdB stars (0.5 M\(_{\odot }\)) implied a total mass for the binary of 1.47 ± 0.01 M\(_{\odot }\), thus making it the first possible candidate for a super-Chandrasekhar progenitor. Another discovery of the shortest period binary comprising a hot subdwarf star (CD-30 11223, GALEX J1411-3053) and a massive unseen companion was reported in [61]. The measured parameters of the sdB CD-30 11223 were found to favor a canonical mass close to 0.48 M\(_{\odot }\) that would correspond to a minimum mass of 0.77 M\(_{\odot }\) for the companion. Constraining the radius of the primary using a measurement of its rotation velocity and fitting the amplitude of the ellipsoidal variations, the authors set an upper limit of 0.87 M\(_{\odot }\) for the secondary mass at an orbital inclination of 68\(^{\circ }\) and hence obtained a total mass of 1.35 M\(_{\odot }\) for the system. However, the authors mention that systematic effects in the measurement of the rotation velocity and the possibility that the primary mass may exceed 0.48 M\(_{\odot }\) imply that the total mass of the system may exceed the Chandrasekhar mass limit.

More recently, HD265435, a binary system with an orbital period of less than a hundred minutes, consisting of a white dwarf and a hot subdwarf was discovered [62]. This system was observed by the Transiting Exoplanet Survey Satellite (TESS). Combining the spectra obtained at the Palomar 200-inch telescope with the radius estimate from fitting the spectral energy distribution (SED), the visible star was characterized to be a hot subdwarf of spectral type OB. The orbital inclination of the system allowed the authors to estimate the mass of the unseen companion, which is probably a white dwarf with a carbon-oxygen core. The total mass of the system was estimated to be 1.65 ± 0.25 solar masses, thus exceeding the maximum allowed value of the mass of a stable white dwarf to make it a super-Chandrasekhar candidate progenitor.

3 Massive white dwarfs on the grounds of modified gravity

As we mentioned above, the Chandrasekhar limit may not be unique. Some early studies considered a high magnetic field to violate it. However, it was soon shown that one can have a maximum limit for extreme magnetic fields in these highly magnetized WDs, i.e., huge magnetic fields bring instabilities to the hydrostatic equilibrium equations. For details and discussions see Ref. [12] and references therein. Soon after the stability of these magnetic white dwarfs was explored in solid grounds, and a maximum magnetic field was established, depending on the core composition of the star [63]. Considering all sorts of instabilities, the maximum limit was established around \(2.0\ M_{\odot }\) [16, 23, 26, 64]. Above this limit the star changes its geometry too much, becoming a torus due to anisotropic pressures. Simulations of mergers of WDs leading to magnetic super-Chandrasekhar WDs have been performed [65] leading to a maximum mass of \(1.45\ M_{\odot }\). For the case of isolated sources, it would be \(1.46\ M_{\odot }\) [10]. This is in accordance with new observations such as the one in Ref. [66], where a WD has a mass around \(1.32\ M_{\odot }\), radius around 2140 km and a possible magnetic field of 600-900 megagauss. Although magnetic fields could enhance the mass, strongly magnetic white dwarfs are still absent among detached white dwarf binaries that are younger than one billion years. This is in contrast with semi-detached binaries, such as Cataclysmic Variables [67], i.e., according to these data, super-Chandrasekhar due to magnetic field would likely be formed by Cataclysmic Variables as progenitors.

As one can see, the highly expected breaking of spherical symmetry and the absence of strong magnetic fields in isolated white dwarfs, leads to an open window for other mechanisms that could also violate the Chandrasekhar limit. One such mechanism would be modified gravity [29,30,31,32,33,34,35,36,37,38,39,40, 68]. In Ref. [29], the well-known \(f(\mathtt {R})\) gravity which is one of the most studied modified theory of gravity was used. The maximum masses found in this work were between \(1.772-2.701\ M_{\odot }\). This theory was also explored in the Palatini formalism [69] and for this formalism the WDs could have mass beyond \(2\ M_{\odot }\) for high values of the theory’s parameter. Such works used perturbative approaches to find the equilibrium configurations of WDs in \(f(\mathtt {R})\) gravity, but recently Ref. [70] showed that perturbative results for neutron stars differ from non-perturbative ones, which means that those perturbative WD approaches can be misleading. The authors of Ref. [32] also considered the \(f(\mathtt {R})\) gravity as well as: fourth order gravity theories (FOG), Eddington inspired Born–Infeld gravity (EiBI) and Scalar–Tensor–Vector gravity (STVG). They used WD as a tool to constraint these alternative theories. For STVG, there was no significant enhancement of the mass for any value of the theory’s parameter. For the case of the EiBI, for different positive values of the parameter of the theory, one could have a significant enhancement of the mass, however for some value that could lead to huge (unrealistic) mass-radius. For the case of FOG, one can have the same behavior, i.e., a large enhancement of the mass-radius. Finally, for the case of \(f(\mathtt {R})\) gravity, where the model was characterized by two parameters, the maximum mass of white dwarfs was near the Chandrasekhar limit. Unlike FOG and EiBI, one could have the mass near \(3.0\ M_{\odot }\) for a pair of parameter combinations. Massive gravity theory also could count for enhancement of the maximum mass of white dwarfs. In Ref. [36], the authors using the Rham–Gabadadze–Tolley like massive gravity have found WDs with maximum mass of 1.41 to 3.41 \(M_{\odot }\) with radius of 871 to 1168 km, respectively. As we can see the massive white dwarfs have been heavily studied under modified gravity in an attempt to have white dwarfs above the Chandrasekhar limit, nevertheless, WDs also have been used as tools to test these modified gravity theories [30, 32, 39], which in general, are used broadly in neutron star astrophysics. The aim is to have bounds in the theories’ coupling constant and its behavior in the Newtonian limit. The EoS of WDs is well-defined, as well as the nuclear instabilities present in these systems and the mass-radius in the Newtonian limit.

4 Hydrostatic equilibrium equation in \(f(\mathtt {R,L_m})\) theory

The \(f(\mathtt {R,L_m})\) gravity action reads [52] as,

$$\begin{aligned} S=\int d^{4}x\sqrt{-g}\, f(\mathtt {R,L_m}), \end{aligned}$$
(1)

where \(f(\mathtt {R,L_m})\) is a general function of the Ricci scalar \(\mathtt {R}\) and of the matter Lagrangian density \(\mathtt {L_m}\), g is the metric determinant. When the function takes the form \(f(\mathtt {R,L_m})= \mathtt {R}/2 + \mathtt {L_m}\), the principle of least action leads to the Einstein’s field equations \(G_{\mu \nu }=T_{\mu \nu }\), where \(G_{\mu \nu }\) is the Einstein tensor and \(T_{\mu \nu }\) represents the energy–momentum tensor. We have been considering \(c = 8\pi G =1\).

For the case where the function is \(f(\mathtt {R,L_m})= \mathtt {R}/2 + \mathtt {L_m}+ \sigma \mathtt {R}\mathtt {L_m}\) as considered in references [71, 72]; where \(\sigma \) is the coupling constant, and \(\mathtt {L_m}= -p\); the variation of the action leads to the following field equations,

$$\begin{aligned}&(1-2\sigma p)G_{\mu \nu }+\frac{1}{3} \mathtt {R}g_{\mu \nu }-\frac{\sigma p}{3} \mathtt {R}g_{\mu \nu }\nonumber \\- & {} (1+\sigma \mathtt {R})\left( T_{\mu \nu }-\frac{1}{3}Tg_{\mu \nu }\right) + 2\sigma \nabla _\mu \nabla _\nu p = 0. \end{aligned}$$
(2)

which for the static spherically symmetric spacetime and taking the energy–momentum tensor for a perfect fluid, leads to the Tolman–Oppenheimer–Volkov (T.O.V.) – like equations, i.e., the hydrostatic equilibrium equations,

$$\begin{aligned}&\alpha '(p+\rho ) + 2z = 0, \end{aligned}$$
(3a)
$$\begin{aligned}&p' - z = 0, \end{aligned}$$
(3b)
$$\begin{aligned}&\Bigg [\bigg (2 r^{2} \rho e^{\beta } + \big (2 \mathtt {R}r^{2} \rho e^{\beta } + 3 r^{2} z \alpha '+ 6 p r \beta ' \nonumber \\&\quad + 2 \big (2 \mathtt {R}p r^{2} + 3 p\big ) e^{\beta } - 6 p\big ) \sigma - \left( {\left( \mathtt {R}- 3 p\right) } r^{2} + 3\right) e^{\beta } \nonumber \\&\quad - 3 r \beta ' + 3\bigg ) e^{-\beta }\Bigg ]({3r^{2}})^{-1} = 0, \end{aligned}$$
(3c)
$$\begin{aligned}&\Bigg [\bigg (r^{2} \rho e^{\beta } + (\mathtt {R}r^{2} \rho e^{\beta } + 3 \, r^{2} z \beta ' + 6 \, p r \alpha ' - 6 \, r^{2} z' \nonumber \\&\quad - (\mathtt {R}p r^{2} + 6 \, p) e^{\beta } + 6 \, p) \sigma + {\left( \mathtt {R}r^{2} + 3\right) } e^{\beta } \nonumber \\&\quad - 3 \, r \alpha ' - 3\bigg ) e^{-\beta }\Bigg ]({3 \, r^{2}})^{-1} = 0. \end{aligned}$$
(3d)

Here, \(\alpha \) and \(\beta \) are the metric potentials depending on the radial coordinate r and primes denote their derivatives. Finally, p and \(\rho \) are the pressure and energy density, respectively, and z is an auxiliary variable which is the derivative of the pressure. For complete details, see Ref. [51]. It is worth pointing out that the trace of Eq. (2) will provide \( \mathtt {R}= -T\) for \(\sigma =0\), and using this result one can recover the field equations of General Relativity for this particular case. Furthermore, one can note from (3), that the four-divergence of the energy–momentum tensor is conserved, which is a remarkable feature of the \(f(\mathtt {R,L_m})\) theory for stars with spherical symmetry. The four-divergence conservation of \(T_{\mu \nu }\) is a consequence of our choice for the matter Lagrangian [50, 51], \(\mathtt {L_m}=-p\), which is consistent with the on-shell Lagrangian for relativistic perfect fluids [73]. Finally we mention that for \(\mathtt {L_m}=0\), i.e., the vacuum case in which we also have \(T_{\mu \nu }=0\) and \(p=0\), the new Einstein equations reduce to \(G_{\mu \nu }+ \mathtt {R}g_{\mu \nu }/3=0\). This implies \(\mathtt {R}= 0\) and hence \(G_{\mu \nu }=0\). We are then back to vacuum Einstein equations and as a result the tests of the theory under discussion are in stars, compact objects and cosmology.

5 Numerical procedure, boundary conditions and equation of state

To solve the system of equations (3) numerically, we need to set an equation of state and the boundary conditions: the latter reads, \(p(0) = p_c\) and \(\rho (0) = \rho _c\) at the center of the star \((r=0)\), where \(p_c\) and \(\rho _c\) are the central pressure and central energy density. The stellar surface is the point at the radial coordinate \(r=R\), where the pressure vanishes, \(p(R)=0\). For the metric potentials, we use \(\beta (0)=0\) and \(\alpha (0)=1\). For the auxiliary variable z, we use \(z(0)=0\), once p(0) is a global maximum point. The total mass is contained inside the radius R, as measured by the gravitational field felt by a distant observer. As the boundary condition is at \(r=R\) (the Ricci scalar vanishes at the surface). The continuity of the metric, i.e., the connection conditions with the exterior Schwarzschild solution, requires that [48, 74, 75]

$$\begin{aligned} M = m(R) = \int _0^R4\pi r^2\rho (r)dr. \end{aligned}$$
(4)

5.1 Equation of state

The simplest EoS which describes the fluid properties of WDs follows the model used for the relativistic Fermi gas of electrons [76, 77], which is called the Chandrasekhar EoS. There are other equations of state for WDs that insert some corrections into the Chandrasekhar EoS, but essentially, they are all based on the Fermi gas of electrons. Because of this, there is little uncertainty in the EoS for WDs, which is not the case for neutron stars. Some studies, considering massive white dwarfs, generalized the Chandrasekhar model to account for the mass threshold in the ultra-relativistic limit. Here, we point out the work of Chamel and Fantina [78], where the threshold for density and pressure are found to be increased due to electron-ion interactions.

Table 1 Pressure and density threshold for which matter becomes unstable for four elements. The pressure values are taken from Ref. [78]. Considering the threshold pressure within the Hamada–Salpeter EoS, we have the corresponding density threshold
Full size table

We use the Hamada–Salpeter (HS) EoS, which accounts for corrections due to electrostatic energy, Thomas–Fermi deviations, exchange energy and spin-spin interactions [79, 80]. However, only electrostatic corrections are found to be non-negligible. This EoS changes the way that the critical mass depends on the nuclear composition, i.e., now depends on A/Z and Z, while for Chandrasekhar it only has A/Z dependence. The extended HS EoS slightly decreases the Chandrasekhar limit. Using the limit due to electron capture instability, we constrain the massive white dwarfs in \(f(\mathtt {R,L_m})\) gravity and the parameter of the theory. We use four elements: \(^4\)He, \(^{12}\)C, \(^{16}\)O and \(^{20}\)Ne. The maximum values for pressure are described in the Table 1, taken from Ref. [78]. Using the HS EoS and the pressure thresholds of Table 1, we obtain the maximum allowed densities.

The Hamada–Salpeter equation of state can be written as [80],

$$\begin{aligned}&p = p_{\mathrm{e}} + p_{\mathrm{l}}, \end{aligned}$$
(5)
$$\begin{aligned}&\rho = \rho _{\mathrm{e}} + \rho _{\mathrm{l}} + \rho _{\mathrm{i}}, \end{aligned}$$
(6)

where,

$$\begin{aligned}&p_{\mathrm{e}} = \frac{m_e^4c^5}{24\pi ^2\hbar ^3}f(x) \end{aligned}$$
(7a)
$$\begin{aligned}&f(x) = x(2x^2 - 3)(x^2 + 1)^{1/2} + 3\sinh ^{-1}x, \end{aligned}$$
(7b)
$$\begin{aligned}&p_{\mathrm{l}} = -\frac{3}{10}\left( \frac{4\pi }{3}\right) ^{1/3}Z^{2/3}e^2\frac{m_e^4c^4}{(3\pi ^2)^{4/3}\hbar ^4}x^4, \end{aligned}$$
(7c)

and

$$\begin{aligned}&\rho _{\mathrm{e}} = \frac{m_e^4c^5}{8\pi ^2\hbar ^3}g(x), \end{aligned}$$
(8a)
$$\begin{aligned}&g(x) = x(2x^2 + x)(x^2 + 1)^{1/2} - \sinh ^{-1}x, \end{aligned}$$
(8b)
$$\begin{aligned}&\rho _{\mathrm{l}} = -\frac{9}{10}\left( \frac{4\pi }{3}\right) ^{1/3}Z^{2/3}e^2\frac{m_e^4c^4}{(3\pi ^2)^{4/3}\hbar ^4}x^4, \end{aligned}$$
(8c)
$$\begin{aligned}&\rho _{\mathrm{i}} = m_Nc^2\frac{A}{Z}\frac{m_e^3c^3}{3\pi ^2\hbar ^3}x^3. \end{aligned}$$
(8d)

The subscripts e, l and i denote the degenerate electrons (Chandrasekhar EoS) term, the Coulomb interactions in the lattice and the rest-mass energy of the ions terms, respectively. x is the relativity parameter defined in terms of the Fermi momentum \(\mathrm{k_f}\) as \(x \equiv \mathrm{k_f}/mc\).

6 Results

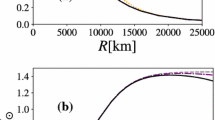
In Fig. 1, we present the mass-radius relationship for white dwarfs. We generated the mass-radius within the \(f(\mathtt {R,L_m})\) gravity framework, considering four values for the coupling constant \(\sigma \). For \(\sigma =0\), the theory recovers the General Relativity outcomes. For the other cases, \(\sigma \) is assumed to have positive values, going from 0.05 to \(0.5\ \mathrm{km^2}\). The constant presents different values from previous works, where it was larger for neutron stars [50, 51], and smaller for weak-field limit [54, 55]. As we pointed in our previous works, \(\sigma \) has a dependence on the energy–matter density, i.e., depending on the astrophysical system, the parameter will have a different value. We expect that for black holes, the absolute values of the parameters will be the largest ones, while for the weak regime the smallest ones. In Fig. 1, we have considered the threshold for \(^4\)He. We have the maximum pressure and central density: \(p_c = 3.59\times 10^{29}\ \mathrm{dyn\ cm^{-2}}\) and \(\rho _c = 1.44\times 10^{11}\ \mathrm{g\ cm^{-3}}\). As one can see, the theory increases the mass in the diagram. The effects start to be more accentuated for stars with radii \(R< 2000\) km, i.e., for more massive stars the modified gravity effects start to be non-negligible and the curves deviate from the GR regime. Considering the effects from the theory, it is possible to surpass the Chandrasekhar limit of \(1.4M_{\odot }\). For the value of \(\sigma =0.5\ \mathrm{km^2}\), the contribution of the theory becomes so relevant, that it is possible to have white dwarfs with more than two solar masses, if one considers the \(^4\)He density threshold. These stars made of Helium and considering \(f(\mathtt {R,L_m})\) gravity with \(\sigma =0.5\ \mathrm{km^2}\), would be within the super-Chandrasekhar limit (2.1–2.8\(M_{\odot }\)), giving a possible explanation for the superluminous supernovae SNIa, since they will be near instability. In the figure we have a black-shaded square region which corresponds to the mass-radius observations of the white dwarf ZTFJ1901+1458 [66]. We also highlight massive WD observations in Fig. 1; the blue dots with error bars, which are between 2500 and 4000 km [81, 82]. For the region \(R>2500\) km, one can see that the contribution from the theory is almost negligible, even for the highest values of the coupling parameter \(\sigma \). This behavior is entirely different from a previous work, where we applied the \(f(\mathtt {R},T)\) theory of gravity to white dwarfs, e.g., see figure 2 of our work [31]. In this figure, we also have two systems: the white dwarf in the system HD 49799 the RX J0648.0-4418 [83] with a mass of \(1.28\pm 0.05\ M_{\odot }\) (black line and shaded region) and the compact object in the AR Scorpii system [84], with an upper limit of \(1.29\ M_{\odot }\) (red line). The former is a new system that has attracted attention in the last years with its being a possible white dwarf pulsar. We also include two binary systems that could be possible super-Chandrasekhar progenitors, i.e., two possible candidates for super-Chandrasekhar WDs in the future. The first system is the J1411-3053 in black dot-dashed line with shaded region. This system has a total mass of \(1.47\pm 0.01\ M_{\odot }\); the second one in black dotted-line is the system HD265435 with a total mass of \(1.65\pm 0.25\ M_{\odot }\). In this system we have not considered the error bar in the figure. For the curve \(\sigma = 0\) we have a dot indicating the GR instability, i.e., one has \(dM/dR>0\), defining a maximum mass before the nuclear instabilities. When one has the effects of the theory, this behavior changes. We have more massive stars with a decrement of the central density, as in the case of the \(f(\mathtt {R},T)\) gravity [31]. This is the same when magnetic white dwarfs are considered. Due to this feature, the limiting factor always will be the nuclear instabilities and that should be treated carefully when one wants to constrain extended gravity theories’ parameters and find the WD’s maximum mass in such a theory.

Fig. 1
figure 1

Mass radius relationship for white dwarfs with different \(\sigma \) parameters and considering a star made of Helium. Four values of \(\sigma \) were considered. For \(\sigma =0.0\), the theory represents General Relativity. The black-shaded region indicates the observed mass-radius of ZTFJ1901+1458, this region and mass-radius are taken from Ref. [66]. The black line and shaded region are \(1.28\pm 0.05\ M_{\odot }\) corresponding to RX J0648.0-4418 [83]. The red line represents the upper limit of the compact object in AR Scorpii [84]. The black dot-dashed line with shaded region is the binary system with total mass of \(1.47\pm 0.01\ M_{\odot }\) from Ref. [60] and the black dotted line is the binary system with a total mass of \(1.65\pm 0.25\ M_{\odot }\) from Ref. [62]. The blue circles with error bars represent the observational data of a sample of massive WDs taken from Refs. [81, 82]

Full size image

In Fig. 2, we have the mass-radius relation for white dwarfs. The threshold for carbon-12 was considered. In this case, the maximum pressure and central density are: \(p_c = 6.99\times 10^{28}\ \mathrm{dyn\ cm^{-2}}\) and \(\rho _c = 4.20\times 10^{10}\ \mathrm{g\ cm^{-3}}\). Now, the influence of the theory on the maximum mass is slightly smaller (the coupling term has dependence on the energy–mass density), but still strong. It is possible to see, for the highest value of the coupling constant, \(\sigma =0.5\ \mathrm{km^2}\), that the maximum mass reaches near \(1.8M_{\odot }\). We can also observe that the white dwarfs are more compact in comparison with the previous case. One can see that the curves cross the shaded region of RX J0648.0-4418 more to the left side. This is due to the change in the EoS. For the carbon threshold, the maximum mass limit may be increased if one uses even higher values of \(\sigma \).

Fig. 2
figure 2

Same as Fig. 1, but considering the \(^{12}\)C threshold for equation of state

Full size image

In Fig. 3, we present the mass-radius relationship for white dwarfs considering the threshold for \(^{16}\)O, the maximum central pressure is \(2.73\times 10^{28}\ \mathrm{dyn\ cm^{-2}}\), corresponding to a maximum central density of \(2.07\times 10^{10}\ \mathrm{g\ cm^{-3}}\). This third case follows the same line as the previous one. For the highest coupling constant value, the maximum mass reached is near \(1.6\ M_{\odot }\), which means that smaller density thresholds requires higher values of \(\sigma \) to enhance maximum masses up to 2.2–2.4 \(M_\odot \). The minimum radii reached are a little more than 1000 km.

Fig. 3
figure 3

Same as Fig. 1, but considering the \(^{16}\)O threshold for equation of state

Full size image

Finally, we present the mass-radius relation for white dwarfs, considering the threshold for \(^{20}\)Ne in Fig. 4. In this last case, the maximum pressure and central density are: \(p_c = 6.21\times 10^{27}\ \mathrm{dyn\ cm^{-2}}\) and \(\rho _c = 6.89\times 10^{9}\ \mathrm{g\ cm^{-3}}\). It has a maximum mass of just a few percents above the Chandrasekhar limit for the highest value of the parameter of the theory considered. As we can see, for this composition, one cannot have white dwarfs that would have a mass around \(1.47\ M_{\odot }\). The nuclear instabilities limit a lot the enhancement of the mass for WDs. Considering elements heavier than oxygen, the nuclear instabilities will largely affect the maximum mass and limit it before gravitational effects.

Fig. 4
figure 4

Same as Fig. 1, but considering the \(^{20}\)Ne threshold for equation of state

Full size image

7 Discussion and conclusions

In this work, we have studied for the first time the mass-radius relationship of massive white dwarfs in the context of \(f(\mathtt {R,L_m})\) gravity. We have considered the specific case \(f(\mathtt {R,L_m})= \mathtt {R}+ \mathtt {L_m}+ \sigma \mathtt {R}\mathtt {L_m}\), where the term \(\sigma \mathtt {R}\mathtt {L_m}\) represents a non-minimal coupling between the matter and gravitational field. We solved the hydrostatic equilibrium equation for the Hamada–Salpeter EoS and used electron capture instability as threshold for the central mass density and consequently for the central pressure. We have found that the effects of the theory are more important for stars with radius less than 2500 km, i.e., for more massive stars. This is because the coupling term is dependent on the energy–mass density. Hence, the effects of the theory are noticeable for larger central densities. We see that curves start to deviate from the General Relativity case. We found here that the coupling parameter is at least one order of magnitude smaller than it is for neutron stars. This is expected since WDs have a central density smaller than the central densities of neutron stars, and \(\sigma \) has a dependence on the energy–matter density. This behavior is the same as the non-minimal model \(f(\mathtt {R},T)\) of gravity, e.g., see figures in Ref. [85]. As one can see, the parameters in the theory have different values depending on the astrophysical system.

Furthermore, it is remarkable that the effects of the theory are negligible for stars with \(M< 1.3M_{\odot }; R < 3000\) km, which means that the theory recovers General Relativity and Newtonian results for small densities independent of the value of the coupling constant, i.e., the curves are indistinguishable at low densities. This means that the theory can accommodate the observational data of WDs with \(< 3000\) km, without any problem. This behavior is different from other theories of gravity, which in general do not recover this limit on this region. e.g., see figures of Ref. [32]. \(f(\mathtt {R,L_m})\) gravity has a similarity with the \(f(\mathtt {R})\) in the Palatini formalism [69], where the effects of the alternative theory are negligible in this regime. As one goes to higher densities, the curves deviates from the GR limit, showing the contribution of the modified gravity on the mass-radius relation. This is completely in agreement with the data, which shows that for less massive WDs (\(M<1.3M_\odot \)), the Newtonian theory can describe very well the data. With new data showing more massive WDs [82, 86,87,88], the relativistic effects, i.e., gravity corrections, are necessary to explain the mass-radius.

For stars near the threshold due to the electron-ion interactions, the effects of the theory lead to stars well above the Chandrasekhar mass limit. For a star made of oxygen, the increment could be at least \(0.18\ M_{\odot }\), for Ne it is \(0.06\ M_{\odot }\). The increment would reduce a lot or be negligible for white dwarfs made of heavier elements, such as \(^{40}\)Ca or \(^{56}\)Fe due to nuclear instabilities. For lighter elements the increment in the mass can be very significant, reaching a limit more than \(2.0\ M_{\odot }\), thus explaining the superluminous supernovae type SNIas. The enhancement in the mass can be comparable to the ones coming from magnetic field effects [23, 26, 63, 78], without the anisotropic instabilities of the huge magnetic field. However, it is worth considering other nuclear instabilities besides the electron capture.

In Fig. 5 we compare our results of Fig. 2 with the maximum mass of strongly magnetized \(^{12}\)C WDs from Ref. [64]. They are represented by the green, red, and black solid lines where the masses correspond to the magnetic moments \(10^{33}, 10^{34}\) and \(2\times 10^{34}\ \mathrm {A m^2}\) respectively. The magnetic moment of \(10^{33}\ \mathrm {A m^2}\) corresponds to a magnetized \(^{12}\)C WD of \(1.41\ M_{\odot }\), the \(10^{34}\ \mathrm {A m^2}\) corresponds to \(1.86\ M_{\odot }\) and \(2\times 10^{34}\ \mathrm {A m^2}\) corresponds to \(1.99\ M_{\odot }\). For the purpose of comparison, when considering \(f(\mathtt {R,L_m})\) gravity effects with \(\sigma =0.5\ \mathrm{km^2}\), we could come close to \(1.8\ M_{\odot }\) for carbon-12 WDs. We also compare with two samples of mass-radius: one from Ref. [29], which considers the \(f(\mathtt {R})\) gravity and another one from Ref. [36], which considers the Vegh’s massive gravity. They are represented by the blue and red dots, respectively. As one can see for this case, the modified theories of \(f(\mathtt {R})\) and massive gravity can reach more massive stars, however, if one considers nuclear instabilities the scenario can be thoroughly changed. As we mentioned, the nuclear instabilities limit the maximum mass significantly, so the WD EoS should always consider the threshold. Some results for massive gravity are similar to ours.

Fig. 5
figure 5

Mass radius relationship for white dwarfs with different \(\sigma \) parameters and considering a star made of \(^{12}\)C. Four values of \(\sigma \) were considered. For \(\sigma =0.0\), the theory represents General Relativity. The black-shaded region indicates the observed mass-radius of ZTFJ1901+1458, this region, i.e., the mass-radius are taken from Ref. [66]. The black dotted-line and shaded region are \(1.28\pm 0.05\ M_{\odot }\) corresponding to RX J0648.0-4418 [83]. The pink line represents the upper limit of the compact object in AR Scorpii [84]. The blue circles with error bars represent the observational data of a sample of massive WDs taken from Refs. [81, 82]. In this figure we have included the maximum mass of strongly magnetized \(^{12}\)C WDs from Ref. [64]. They are represented by the green, red, and black solid lines. These masses correspond to the following magnetic moments: \(10^{33}, 10^{34}\) and \(2\times 10^{34}\ \mathrm {A m^2}\). We also included two samples of mass-radius: from Ref. [29], which considers the \(f(\mathtt {R})\) gravity and from Ref. [36], which considers the Vegh’s massive gravity. They are represented by the blue and red dots, respectively

Full size image

In Fig. 6 we repeat the methodology for WDs made of oxygen-16, in comparison with the Fig. 3. As one can see the maximum mass that considers magnetic field decreases. As we have also used electron-capture as threshold, our results also decreased, i.e., they are consistent for these \(^{16}\)O WDs and present a very similar behavior for the maximum mass. As one can see, this modified gravity, \(f(\mathtt {R,L_m})\) model, can be as good as highly magnetized models.

Fig. 6
figure 6

Same as Fig. 5, but considering the \(^{16}\)O threshold for equation of state

Full size image

In conclusion, we show that the \(f(\mathtt {R,L_m})\) modified theory of gravity can explain super-Chandrasekhar white dwarfs, i.e., a non-minimal coupling between the particle fields and the gravitational field could enhance the maximum mass for white dwarfs above the Chandrasekhar limit. More aspects of the theory must be addressed, such as the bounds for the coupling parameter from statistical analyses, to establish a new maximum mass limit. The electron capture limits the maximum central density for different WD compositions [78, 89]. One could enhance the \(\sigma \) parameter, since it reduces the central density for the same star. However, there are other instabilities that need to be considered such as those due to pycnonuclear reactions. The theory allows the mass of WDs to be higher without surpassing the threshold for nuclear instabilities. Another valid consideration would be to have the theory coupled to the electromagnetic field and have magnetic WDs within the theory.

Presently, we can say that electron capture instabilities and estimated masses of superluminous SNIas constrain the coupling parameter within the interval \(0< \sigma <1\ \mathrm{km^2}\) for white dwarfs systems.