Determinations of $|V_{cb}|$ and $|V_{ub}|$ from baryonic $\Lambda _b$ decays

Abstract

We present the first attempt to extract $|V_{cb}|$ from the $\Lambda _b\rightarrow \Lambda _c^+\ell \bar{\nu }_\ell$ decay without relying on $|V_{ub}|$ inputs from the B meson decays. Meanwhile, the hadronic $\Lambda _b\rightarrow \Lambda _c M_{(c)}$ decays with $M=(\pi ^-,K^-)$ and $M_c=(D^-,D^-_s)$ measured with high precisions are involved in the extraction. Explicitly, we find that $|V_{cb}|=(44.6\pm 3.2)\times 10^{-3}$, agreeing with the value of $(42.11\pm 0.74)\times 10^{-3}$ from the inclusive $B\rightarrow X_c\ell \bar{\nu }_\ell$ decays. Furthermore, based on the most recent ratio of $|V_{ub}|/|V_{cb}|$ from the exclusive modes, we obtain $|V_{ub}|=(4.3\pm 0.4)\times 10^{-3}$, which is close to the value of $(4.49\pm 0.24)\times 10^{-3}$ from the inclusive $B\rightarrow X_u\ell \bar{\nu }_\ell$ decays. We conclude that our determinations of $|V_{cb}|$ and $|V_{ub}|$ favor the corresponding inclusive extractions in the B decays.

1 Introduction

In the standard model (SM), the unitary $3\times 3$ Cabibbo–Kobayashi–Maskawa (CKM) matrix elements present the coupling strengths of quark decays, with the unique physical weak phase for CP violation. Being unpredictable by the theory, the matrix elements as the free parameters need the extractions from the experimental data. Nonetheless, there exists a long-standing discrepancy between the determinations of $|V_{cb}|$ based on the exclusive $B\rightarrow D^{(*)}\ell \bar{\nu }_\ell$ and inclusive $B\rightarrow X_c \ell \bar{\nu }_\ell$ decays, given by [1,2,3]

$$\begin{aligned} |V_{cb}|= & {} (39.18\pm 0.99)\times 10^{-3},\quad ({B\rightarrow D\ell \bar{\nu }_\ell })\nonumber \\ |V_{cb}|= & {} (38.71\pm 0.75)\times 10^{-3},\quad ({B\rightarrow D^*\ell \bar{\nu }_\ell })\nonumber \\ |V_{cb}|= & {} (42.11\pm 0.74)\times 10^{-3}.\quad ({B\rightarrow X_c\ell \bar{\nu }_\ell }) \end{aligned}$$

(1)

From the data in Eq. (1), we see that the deviations between the central values of the inclusive and exclusive decays are around (2–3)$\sigma$. For the resolution, the analysis in Ref. [4] suggests that the $B\rightarrow D^*$ transition form factors developed by Caprini, Lellouch and Neubert (CLN) [5] may underestimate the uncertainty that is associated with the extraction of $|V_{cb}|$. Moreover, it has been recently pointed out that the theoretical parameterizations of the $B\rightarrow D^{(*)}$ transitions given by Boyd, Grinstein and Lebed (BGL) [6] are more flexible in reconciling the difference [7, 8]. Similar to the data for $|V_{cb}|$ in Eq. (1), there also exists a tension as regards the determination of $|V_{ub}|$ between the exclusive and inclusive B decays, which has drawn a lot of theoretical attentions to search for the solutions in the SM and beyond [9,10,11,12,13,14].

Fig. 1

Feynman diagrams depicted for a $\Lambda _b\rightarrow \Lambda _c\ell \bar{\nu }_\ell$ and b $\Lambda _b\rightarrow \Lambda _c M_{(c)}$

On the other hand, the baryonic $\Lambda _b$ decays could provide some different theoretical inputs for the CKM matrix elements, which are able to ease the tensions between the exclusive and inclusive determinations. Indeed, to have an accurate determination of $|V_{ub}|/|V_{cb}|$ the LHCb Collaboration has carefully analyzed the ratio of [15],

$$\begin{aligned} \mathcal{R}_{ub}\equiv \frac{ \mathcal{B}(\Lambda _b\rightarrow p \mu \bar{\nu })_{q^2>15\,{\text {GeV}^2}}}{\mathcal{B}\left( \Lambda _b\rightarrow \Lambda _c^+\mu \bar{\nu }_\mu \right) _{q^2>7\,{\text {GeV}^2}}} =\frac{|V_{ub}|^2/|V_{cb}|^2}{R_{FF}}, \end{aligned}$$

(2)

where $\mathcal{B}$ denotes the branching fraction and q is the certain range of the integrated energies for the data collection. In Eq. (2), $\mathcal{R}_{ub}$ by relating $\mathcal{B}(\Lambda _b\rightarrow p\mu \bar{\nu }_\mu )$ to $\mathcal{B}(\Lambda _b\rightarrow \Lambda _c\mu \bar{\nu }_\mu )$ reduces the experimental uncertainties, while $R_{FF}$ is the ratio of the $\Lambda _b\rightarrow \Lambda _c$ and $\Lambda _b\rightarrow p$ transition form factors, calculated by the lattice QCD (LQCD) model [16] with a smaller theoretical uncertainty.

In this work, we would like to first explore the possibility to determine $|V_{cb}|$ from the baryonic decays. In particular, we use the observed branching ratios of $\Lambda _b\rightarrow \Lambda _c\ell \bar{\nu }_\ell$ and $\Lambda _b\rightarrow \Lambda _c M_{(c)}$ with $\ell =e^-$ or $\mu ^-$, $M=(\pi ^-,K^-)$ and $M_c=(D^-,D^-_s)$, which have never been used in the previous studies. The full energy-range measurement of the semileptonic $\Lambda _b\rightarrow \Lambda _c\ell \bar{\nu }_\ell$ decay is given by [17]

$$\begin{aligned} \mathcal{B}(\Lambda _b\rightarrow \Lambda _c\ell \bar{\nu }_\ell )= & {} \left( 6.2^{+1.4}_{-1.3}\right) \times 10^{-2}, \end{aligned}$$

(3)

and the decay branching ratios of $\Lambda _b\rightarrow \Lambda _c^+ M_{(c)}$ are observed as [17]

$$\begin{aligned} \mathcal{B}\left( \Lambda _b\rightarrow \Lambda _c^+\pi ^-\right)= & {} (4.9\pm 0.4) \times 10^{-3},\nonumber \\ \mathcal{B}\left( \Lambda _b\rightarrow \Lambda _c^+ K^-\right)= & {} (3.59\pm 0.30) \times 10^{-4},\nonumber \\ \mathcal{B}\left( \Lambda _b\rightarrow \Lambda _c^+ D^-\right)= & {} (4.6\pm 0.6) \times 10^{-4},\nonumber \\ \mathcal{B}\left( \Lambda _b\rightarrow \Lambda _c^+D_s^-\right)= & {} (1.10\pm 0.10)\times 10^{-2}\,. \end{aligned}$$

(4)

The above modes in Eq. (4) can be regarded to proceed through the $\Lambda _b\rightarrow \Lambda _c$ transition together with the recoiled mesons, such that the theoretical estimations give

$$\begin{aligned} \frac{\mathcal{B}(\Lambda _b\rightarrow \Lambda _c^+\pi ^-)}{\mathcal{B} \left( \Lambda _b\rightarrow \Lambda _c^+ K^-\right) }\simeq & {} R(M)(\frac{V_{ud}}{V_{us}})^2 \bigg (\frac{f_\pi }{f_K}\bigg )^2=13.2,\nonumber \\ \frac{\mathcal{B}(\Lambda _b\rightarrow \Lambda _c^+ D_s^-)}{\mathcal{B}(\Lambda _b\rightarrow \Lambda _c^+ D^-)}\simeq & {} R(M_c)\bigg (\frac{V_{cs}}{V_{cd}}\bigg )^2 \bigg (\frac{f_{D_s}}{f_D}\bigg )^2=25.1,\nonumber \\ \end{aligned}$$

(5)

where $f_{M_{(c)}}$ are the meson decay constants and $R(M_{(c)})$ are the rates to account for the mass differences from the phase spaces. Note that the ratios in Eq. (5) remarkably agree with $(13.6\pm 1.6,24.0\pm 3.8)$ from the data in Eq. (4), respectively. This implies that the theoretical calculations of $\mathcal{B}(\Lambda _b\rightarrow \Lambda _c M_{(c)})$ can be reliable to be involved in the fitting of $|V_{cb}|$. Moreover, it is proposed in the soft-collinear effective theory (SCE) [18] that the non-leptonic $\Lambda _b\rightarrow \Lambda _c\pi ^-$ decay can be related to the semileptonic $\Lambda _b\rightarrow \Lambda _c\ell \bar{\nu }_\ell$ decays if the factorization works. This leads to the predictions of $\mathcal{B}(\Lambda _b\rightarrow \Lambda _c\ell ^-\bar{\nu }_\ell )\approx 6\times 10^{-2}$ and $\mathcal{B}(\Lambda _b\rightarrow \Lambda _c\pi ^-)=4.6\times 10^{-3}$, which agree well with the data in Eqs. (3) and (4), respectively. Particularly, the data in Eq. (4) have the significances of (8–12)$\sigma$, which apparently benefit the precise determination of $|V_{cb}|$. As a result, the extraction of $|V_{cb}|$ from the data in Eqs. (3) and (4) can be an independent one besides those from the $B\rightarrow D^{(*)}\ell \bar{\nu }_\ell$ and $B\rightarrow X_c\ell \bar{\nu }_\ell$ decays. With the newly extracted $|V_{cb}|$ value, we will then be able to determine $|V_{ub}|$.

2 Formalism

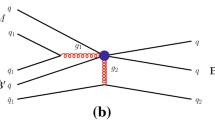
As seen in Fig. 1, in terms of the effective Hamiltonian at quark level for the semileptonic $b\rightarrow c\ell \bar{\nu }_\ell$ and non-leptonic $b\rightarrow c \bar{\alpha }\beta$ ($\bar{\alpha }=\bar{u}(\bar{c})$ and $\beta =q=d,s$) transitions by the W-boson external emissions, the amplitudes of the $\Lambda _b\rightarrow \Lambda _c\ell \bar{\nu }_\ell$ and $\Lambda _b\rightarrow \Lambda _c M_{(c)}$ decays are found to be [16, 19]

$$\begin{aligned}&\mathcal{A}\left( \Lambda _b\rightarrow \Lambda _c^+\ell \bar{\nu }_\ell \right) \nonumber \\&=\frac{G_\mathrm{F}}{\sqrt{2}}V_{cb} \left\langle \Lambda _c^+|\bar{c}\gamma _\mu (1-\gamma _5)b|\Lambda _b\right\rangle \bar{\ell }\gamma ^\mu (1-\gamma _5)\nu _\ell ,\nonumber \\&\mathcal{A}\left( \Lambda _b\rightarrow \Lambda _c^+ M_{(c)}\right) \nonumber \\&= \frac{G_\mathrm{F}}{\sqrt{2}}V_{cb}V_{\alpha \beta }^* a_1^{M_{(c)}} if_{M_{(c)}} q^\mu \left\langle \Lambda _c^+|\bar{c}\gamma _\mu (1-\gamma _5)b|\Lambda _b\right\rangle , \end{aligned}$$

(6)

where $G_\mathrm{F}$ is the Fermi constant, $V_{\alpha \beta }=V_{u(c)q}$ ($q=d,s$) for $M_{(c)}=\pi ^-(D^-),K^-(D^-_s)$, and the matrix elements of $\langle M_{(c)}|\bar{\beta }\gamma ^\mu (1-\gamma _5)\alpha |0\rangle =if_{M_{(c)}} q^\mu$ have been used for the meson productions. The parameters $a_1^{M_{(c)}}=c_1^{\mathrm{eff}}+c_2^{\mathrm{eff}}/N_c^{\mathrm{eff}}$ are derived by the generalized factorization approach with the effective Wilson coefficients $(c_1^{\mathrm{eff}},c_2^{\mathrm{eff}})=(1.168,-0.365)$ and color number $N_c^{eff}$ [20].

In the helicity-based definition, the matrix elements of the $\Lambda _b\rightarrow \Lambda _c$ transition are given by [21]

$$\begin{aligned}&\langle \Lambda _c|\bar{c} \gamma _\mu b|\Lambda _b\rangle \nonumber \\&\quad = \bar{u}_{\Lambda _c}(p^\prime ,s^\prime )\bigg [ f_0(q^2)(m_{\Lambda _b}-m_{\Lambda _c})\frac{q^\mu }{q^2} \nonumber \\&\qquad +f_+(q^2)\frac{m_{\Lambda _b}+m_{\Lambda _c}}{s_+}\nonumber \\&\qquad \times \bigg (p^\mu +p^{\prime \mu }- \bigg (m_{\Lambda _b}^2-m_{\Lambda _c}^2\bigg )\frac{q^\mu }{q^2}\bigg )+f_\perp (q^2)\nonumber \\&\qquad \times \bigg (\gamma ^\mu -\frac{2m_{\Lambda _c}}{s_+}p^\mu - \frac{2m_{\Lambda _b}}{s_+}p^{\prime \mu }\bigg ) \bigg ]u_{\Lambda _b}(p,s),\nonumber \\&\langle \Lambda _c|\bar{c} \gamma _\mu \gamma _5 b|\Lambda _b\rangle \nonumber \\&\quad = -\bar{u}_{\Lambda _c}(p^\prime ,s^\prime )\gamma _5\bigg [ g_0(q^2)(m_{\Lambda _b}+m_{\Lambda _c})\frac{q^\mu }{q^2}\nonumber \\&\qquad +g_+(q^2)\frac{m_{\Lambda _b}-m_{\Lambda _c}}{s_-}\nonumber \\&\qquad \times \bigg (p^\mu +p^{\prime \mu }- \bigg (m_{\Lambda _b}^2-m_{\Lambda _c}^2\bigg )\frac{q^\mu }{q^2}\bigg )+g_\perp (q^2)\nonumber \\&\qquad \times \bigg (\gamma ^\mu +\frac{2m_{\Lambda _c}}{s_-}p^\mu -\frac{2m_{\Lambda _b}}{s_-}p^{\prime \mu }\bigg ) \bigg ]u_{\Lambda _b}(p,s), \end{aligned}$$

(7)

where $q=p-p'$, $s_\pm =(m_{\Lambda _b}\pm m_{\Lambda _c})^2-q^2$, and $(f_0,f_+,f_\perp )$ and $(g_0,g_+,g_\perp )$ are form factors. The momentum dependences of $f=f_j$ and $g_j$ ($j=0,+,\perp$) are written as [16]

$$\begin{aligned} f(t)=\frac{1}{1-t/\bigg (m^f_{\mathrm{pole}}\bigg )^2}\sum _{n=0}^{n_{\mathrm{max}}} a_n^f \bigg [\frac{\sqrt{t_+ -t_0}-\sqrt{t_+ -t_0}}{\sqrt{t_+ -t}+\sqrt{t_+ -t_0}}\bigg ]^n,\nonumber \\ \end{aligned}$$

(8)

where $(n_{\mathrm{max}},t_+,t_0)=(1,(m^f_{\mathrm{pole}})^2,$ $(m_{\Lambda _b}-m_{\Lambda _c})^2)$ with $m^f_{\mathrm{pole}}$ representing the corresponding pole masses. In terms of the equations in Ref. [17], one is able to integrate over the variables of the phase spaces in the two-body and three-body decays for the decay widths.

The inclusions of $\mathcal{B}(\Lambda _b\rightarrow \Lambda _c M_{(c)})$ can refrain the theoretical uncertainties for the fit of $|V_{cb}|$ as the $\Lambda _b\rightarrow \Lambda _c$ transition form factors in Eq. (7) are associated with both decays of $\Lambda _b\rightarrow \Lambda _c M_{(c)}$ and $\Lambda _b\rightarrow \Lambda _c\ell \bar{\nu }_\ell$. For the demonstration, we define

$$\begin{aligned}&\mathcal{F}(\Lambda _b\rightarrow \Lambda _c)=\frac{1}{|V_{cb}|^2} \nonumber \\&\times \int _{q^2}\, \frac{\hat{\tau }_{\Lambda _b}}{(2\pi )^3\,32\,m_{\Lambda _b}^3} \frac{\mathrm{d}\Gamma (\Lambda _b\rightarrow \Lambda _c\ell \bar{\nu }_\ell )}{\mathrm{d}q^2} \mathrm{d}q^2, \end{aligned}$$

(9)

where $\hat{\tau }_{\Lambda _b}\equiv \tau _{\Lambda _b}/(6.582\times 10^{-25})$, which leads to the total branching fraction of $\mathcal{B}(\Lambda _b\rightarrow \Lambda _c\ell \bar{\nu }_\ell ) =|V_{cb}|^2 \mathcal{F}(\Lambda _b\rightarrow \Lambda _c)$ with $q^2>(m_\ell +m_{\bar{\nu }})^2$.

Table 1 Inputs of the experimental data

3 Numerical results and discussions

For the numerical analysis, we perform the minimum $\chi ^2$ fit with $|V_{cb}|$ being a free parameter to be determined. The theoretical inputs for the CKM matrix elements, decay constants and $a_1^{M_{(c)}}$ are given by [17, 20]

$$\begin{aligned} (|V_{cd}|,|V_{cs}|)= & {} (0.220\pm 0.005,0.995\pm 0.016),\nonumber \\ (|V_{ud}|,|V_{us}|)= & {} (0.97417\pm 0.00021,0.2248\pm 0.0006),\nonumber \\ (f_\pi ,f_K)= & {} (130.2\pm 1.7,155.6\pm 0.4)\,\text {MeV},\nonumber \\ (f_D,f_{D_s})= & {} (203.7\pm 4.7,257.8\pm 4.1)\,\text {MeV},\nonumber \\ a_1^{M_{(c)}}= & {} 1.05\pm 0.12\,. \end{aligned}$$

(10)

The experimental values in Eqs. (3) and (4) are accounted to be five data points, summarized in Table 1. Note that the $\Lambda _b\rightarrow \Lambda _c$ form factors in Eq. (8) are adopted from Ref. [16]. For the minimum $\chi ^2$ fit, we have

$$\begin{aligned} \chi ^2=\sum _{i=1}^{6} \bigg (\frac{\mathcal{B}^i_{\mathrm{th}}-\mathcal{B}^i_{\mathrm{ex}}}{\sigma _{\mathrm{ex}}^i}\bigg )^2+ \sum _{j} \bigg (\frac{\mathcal{F}^j_{\mathrm{fit}}-\mathcal{F}^j_{\mathrm{th}}}{\sigma _{\mathcal{F}_{\mathrm{th}}}^j}\bigg )^2, \end{aligned}$$

(11)

where $\mathcal{B}_{\mathrm{th}}^i$ and $\mathcal{B}_{\mathrm{ex}}^i$ stand for the branching ratios from the amplitudes in Eq. (6) and experimental data inputs in Table 1, $\sigma ^i_{ex}$ illustrate the experimental errors, $i=1, 2, \ldots , 5$ correspond to the five observed decay modes involved in the fit, and $\mathcal{F}^j_{\mathrm{th}(\mathrm{fit})}$ and $\sigma _{\mathcal{F}_{\mathrm{th}}}^j$ denote the central (best fit) value and error for the jth theoretical input in Eq. (10) along with the $\Lambda _b\rightarrow \Lambda _{(c)}$ transition form factors in Eq. (8), respectively. Subsequently, we obtain

$$\begin{aligned} |V_{cb}|= & {} (44.6\pm 3.2)\times 10^{-3},\nonumber \\ \left( a_1^M,a_1^{M_c}\right)= & {} (1.19\pm 0.08,0.87\pm 0.06),\nonumber \\ \mathcal{F}(\Lambda _b\rightarrow \Lambda _c)= & {} 31.18\pm 0.64,\nonumber \\ \chi ^2/\mathrm{d.o.f}= & {} 7.3/4\simeq 1.8, \end{aligned}$$

(12)

where d.o.f. represents the degrees of freedom. In Eq. (12), our fit with $\chi ^2/\mathrm{d.o.f}\sim 1.8$ indicates a good one, and the value of $|V_{cb}|$ clearly agrees with the inclusive result in Eq. (1) from $B\rightarrow X_c\ell \bar{\nu }_\ell$. Note that this is the first attempt to extract $|V_{cb}|$ from the $\Lambda _b\rightarrow \Lambda _c^+\ell \bar{\nu }_\ell$ decay without relying on $|V_{ub}|$ inputs from the B meson decays. Clearly, it leaves the room for the more future accurate measurements of $\Lambda _b\rightarrow \Lambda _c \ell \bar{\nu }_\ell$ to improve the fit. On the other hand, like the $|V_{ub}|$ extraction from $\mathcal{R}_{ub}$ in Eq. (2) using the input of $|V_{cb}|$ from the B decays, one can inversely use the value of $|V_{ub}|$ from the $B\rightarrow \pi \ell \bar{\nu }$ decay to extract that $|V_{cb}|=(44\pm 3)\times 10^{-3}$ [22], where the central value and error are in agreement with our results in Eq. (12).

Table 2 The fitting results for the different scenarios in comparison with the experimental data

For the initial input of $a_1^{M_{(c)}}$ in Eq. (10), the central value with $N_c^{\mathrm{eff}}=3$ corresponds to the factorizable contributions, and the error with $N_c^{\mathrm{eff}}$ ranging from 2 to $\infty$ is to accommodate the non-factorizable effects. In the two-body B meson decays, this empirical estimation has been demonstrated to agree with the sub-leading calculations like the QCD factorization [23,24,25], where the similar $a_1$ is modified by the detailed calculation for the non-factorizable effects but with the number to fall into the allowed range with $N_c^{\mathrm{eff}}$ from 2 to $\infty$ in the generalized version of the factorization [20]. While the theory depends on the data to test its validity, in the $\Lambda _b$ decays the generalized factorization has been used to explain the data well [19, 26,27,28,29]. However, it is clear that the sub-leading calculations for the non-factorizable effects have not been well developed in $\Lambda _b\rightarrow \Lambda _c M_{(c)}$ yet. Nonetheless, in the soft-collinear effective theory [18], the tree-level diagram as in Fig. 1b is estimated to dominate over the non-factorizable ones, where the predictions of $\mathcal{B}(\Lambda _b\rightarrow \Lambda _c\pi ^-)=4.6\times 10^{-3}$ and $\mathcal{B}(\Lambda _b\rightarrow \Lambda _c\ell ^-\bar{\nu }_\ell )\approx 6\times 10^{-2}$ are consistent with the values of $4.66\times 10^{-3}$ and $6.43\times 10^{-2}$ from our fit, respectively. The determinations of $a_1^{M_{(c)}}$ in Eq. (12) that give around $\mathcal{O}(10\%)$ deviations from the initial inputs in Eq. (10) implies that the decay is insensitive to the non-factorizable effects. Note that, with $a_1=1$ as the input, together with the form factors computed by the light-front quark model, one obtains that $\mathcal{B}(\Lambda _b\rightarrow \Lambda _c\pi ^-,\Lambda _c K^-)=(4.22,3.41)\times 10^{-3}$ in the heavy quark limit [30], which are close to our results of $(4.66,3.63)\times 10^{-3}$, respectively. We remark that based on the QCD factorization and the same $\Lambda _b\rightarrow \Lambda _c$ transition form factors as our inputs [16], the next-next-leading-order calculations result in [31] $\mathcal{B}(\Lambda _b\rightarrow \Lambda _c\pi ^-)=2.85\pm 0.54\times 10^{-3}$ and $\mathcal{B}(\Lambda _b\rightarrow \Lambda _c K^-)=2.21\pm 0.40 \times 10^{-4}$, which are all lower than the data in Eq. (4).

By bringing the newly extracted $|V_{cb}|$ into $|V_{ub}|/|V_{cb}|=0.095\pm 0.005$ as the most recent ratio from the exclusive B and $\Lambda _b$ decays [17], we get

$$\begin{aligned} |V_{ub}|=(4.3\pm 0.4)\times 10^{-3}, \end{aligned}$$

(13)

which is consistent with the inclusive result of $(4.49\pm 0.24)\times 10^{-3}$ from $B\rightarrow X_u\ell \bar{\nu }_\ell$ [17] but different from the exclusive one of $(3.72\pm 0.19)\times 10^{-3}$ from $B\rightarrow \pi \ell \bar{\nu }_\ell$ [17]. To compare our fitting results with different data inputs, we set two scenarios:

$$\begin{aligned}&(S1)\quad \mathcal{B}(\Lambda _b\rightarrow \Lambda _c\ell \bar{\nu }_\ell )+\mathcal{B}(\Lambda _b\rightarrow \Lambda _c M_{(c)}), \nonumber \\&(S2)\quad \mathcal{B}(\Lambda _b\rightarrow \Lambda _c M_{(c)}), \end{aligned}$$

(14)

where S1 corresponds to the fitting shown in Eqs. (12) and (13), which gives the lowest uncertainty for $|V_{cb}|$ along with the best value of $\chi ^2/\mathrm{d.o.f}$. In Table 2, we summarize our results as well as the data from the B decays. In Eq. (12) and Table 2, the result of $\mathcal{F}(\Lambda _b\rightarrow \Lambda _c)=31.18\pm 0.64$ compared to the value of $31.19\pm 1.33$ as the initial theoretical input in the LQCD models presents that the fit with $\mathcal{B}(\Lambda _b\rightarrow \Lambda _c M_{(c)})$ is indeed able to reduce the theoretical error from 1.33 to 0.64 for the extraction of $|V_{cb}|$. Besides, the nearly identical central values of $\mathcal{F}(\Lambda _b\rightarrow \Lambda _c)$ hints that the form factors claimed to be less uncertain at $q^2>7$ GeV$^2$ [16] are also suitable for $\Lambda _b\rightarrow \Lambda _c M_{(c)}$ at a small $q^2$. Note that $a_1^{M_{(c)}}$ slightly deviated from the initial value by the fitting.

Finally, we remark that if we take the $\Lambda _b\rightarrow \Lambda _c$ transition form factors in the forms of $f(q^2)=f(0)/[1-a (q^2/m_{\Lambda _{b}})+b(q^2/m_{\Lambda _{b}})^2]$, adopted from Refs. [32], we obtain a lower value of $|V_{cb}|=(35.7\pm 4.0)\times 10^{-3}$ with $\chi ^2/\mathrm{d.o.f}=0.8$ by keeping the five data points in Table 1 in the fitting. In this case, less flexible inputs for the form factors with only central values for (f(0), a, b) are used, leading to the result similar to the extraction from the exclusive $B\rightarrow D^{(*)}\ell \bar{\nu }_\ell$ decays with the CLN parameterization for the $B\rightarrow D^{(*)}$ transitions [5].

4 Conclusions

In sum, since the extractions of $|V_{cb}|$ showed the $(2-3)\sigma$ deviations between the exclusive $B\rightarrow D^{(*)}\ell \bar{\nu }_\ell$ and inclusive $B\rightarrow X_c\ell \bar{\nu }_\ell$ decays, we have performed an independent determination from the exclusive $\Lambda _b\rightarrow \Lambda _c\ell \bar{\nu }_\ell$ and $\Lambda _b\rightarrow \Lambda _c M_{(c)}$ decays. We have obtained $|V_{cb}|=(44.6\pm 3.2)\times 10^{-3}$ to agree with the extraction in $B\rightarrow X_c\ell \bar{\nu }_\ell$. With the improved ratio of $|V_{ub}|/|V_{cb}|$ from the LHCb and PDG, we have derived that $|V_{ub}|=(4.3\pm 0.4)\times 10^{-3}$, which is close to the result from the inclusive decays of $B\rightarrow X_u\ell \bar{\nu }_\ell$. Consequently, we have demonstrated that our extractions of $|V_{cb}|$ and $|V_{ub}|$ support those from the inclusive B decays. Clearly, the reliabilities for the determinations of $|V_{cb,ub}|$ from the exclusive B decays should be reexamined.