LHC phenomenology of composite 2-Higgs doublet models

Abstract

We investigate the phenomenology of Composite 2-Higgs doublet models (C2HDMs) of various Yukawa types based on the global symmetry breaking $SO(6)\rightarrow SO(4)\times SO(2)$. The kinetic part and the Yukawa Lagrangian are constructed in terms of the pseudo Nambu–Goldstone Boson (pNGB) matrix and a 6-plet of fermions under SO(6). The scalar potential is assumed to be the same as that of the Elementary 2-Higgs doublet model (E2HDM) with a softly broken discrete $Z_2$ symmetry. We then discuss the phenomenological differences between the E2HDM and C2HDM by focusing on the deviations from standard model (SM) couplings of the discovered Higgs state (h) as well as on the production cross sections and branching ratios (BRs) at the large Hadron collider (LHC) of extra Higgs bosons. We find that, even if the same deviation in the hVV ($V=W,Z$) coupling is assumed in the two scenarios, there appear significant differences between the E2HDM and C2HDM from the structure of the Yukawa couplings, so that production and decay features of extra Higgs bosons can be used to distinguish between the two scenarios.

1 Introduction

After the discovery of a Higgs boson in July 2012 [1, 2], an intense period of analysis of its properties has begun and is bearing fruits. We now know that this object is very consistent with the spinless scalar state embedded in the SM. Following the precision measurement of its mass, around 125 GeV, its couplings to all other states of the SM can be derived and compared with experimental data. Agreement between the SM and experimental results is presently within a few tens of percent at worse, thus leaving some scope for a beyond the SM (BSM) Higgs sector.

By bearing in mind that the discovered Higgs state has a doublet nature, in the class of the many new physics scenarios available embedding such a structure those among the easiest to deal with are clearly the 2-Higgs doublet models (2HDMs). Furthermore, these scenarios always include a neutral scalar Higgs state that can play the role of the discovered one, which—as intimated—is very SM-like. Furthermore, they are also easily compliant with past collider data (from LEP/SLC and Tevatron) as well as present ones (from the LHC), while still offering a wealth of new Higgs states and corresponding signals that can be searched for by the ATLAS and CMS collaborations. In fact, a significant experimental effort at the LHC is presently being spared on direct searches for new Higgs bosons, in parallel with the one of extracting their possible presence indirectly from the aforementioned precision measurements.

However, 2HDMs per se do not have the ability to solve the so-called hierarchy problem of the SM. An elegant way to do so, though, is to presume that the Higgs boson discovered in 2012 and its possible 2HDM companions are not fundamental particles. This approach is not unreasonable as any other (pseudo)scalar state found in Nature eventually revealed itself to be a (fermion) composite state, i.e., a mesonic state of the now standard theory of strong interactions (QCD). Specifically, one can construct 2HDMs in which all Higgs bosons, both neutral and charged, both scalar or pseudoscalar, are not fundamental, rather composite. A phenomenologically viable possibility, wherein the mass of the lightest Higgs state is kept naturally lighter than a new strong scale (of compositeness, f, in the $\sim$ TeV region) is, in particular, the one of assigning to them a pNGB nature. In essence, we have in mind those composite Higgs models (CHMs) arising from the spontaneous symmetry breaking around the TeV scale, of the global symmetry of the strong sector [3]. The resisual symmetry is explicitly broken by the SM interactions through the partial compositeness paradigm [4, 5].

In the minimal CHM [6, 7], the composite version of the SM Higgs doublet, the only light scalar in the spectrum is indeed a pNGB (surrounded by various composite resonances, both spin-1/2 and spin-1, generally heavier). Hence, it is natural to assume that the new (pseudo)scalar Higgs states of a C2HDM are also pNGBs. In fact, even in the case in which they are eventually found to be heavier than the SM-like Higgs state, compositeness could provide a mechanism to explain their mass differences with respect to the latter. Finally, in the case of extra Higgs doublets with no vacuum expectation value (VEV) nor couplings to quark and leptons, one could also have neutral light states as possible composite dark matter candidates [8,9,10]. Another example for a composite scalar dark matter candidate emerging as a pNGB is given in [11].

C2HDMs embedding pNGBs arising from a new strong dynamics at the TeV scale, ultimately driving electro-weak symmetry breaking (EWSB), can be constructed by either adopting an effective Lagrangian description (see example [12]) invariant under the SM symmetries for light composite SU(2) Higgses or explicitly imposing a specific symmetry breaking structure containing multiple pNGBs. We take here the second approach. In detail, we will analyse 2HDMs based on the spontaneous global symmetry breaking of an $SO(6)\rightarrow SO(4)\times SO(2)$ symmetry [13]. Within this construct, which we have tackled in Ref. [14], one can then study the deviations of C2HDM couplings from those of a generic renormalisable E2HDM [15] as well as pursue searches for new non-SM-like Higgs signals different from the elementary case. In the $f\rightarrow \infty$ limit the pNGB states are in fact identified with the physical Higgs states of doublet scalar fields of the E2HDM and deviations from the E2HDM are parametrised by $\xi =v_\mathrm{SM}^2/f^2$, with $v_\mathrm{SM}$ the SM Higgs VEV.

Once the new strong sector is integrated out, the pNGB Higgses, independently of their microscopic origin, are described by a non-linear $\sigma$-model associated to the coset. In Ref. [14], we have constructed their effective low-energy Lagrangian according to the prescription developed by Callan, Coleman, Wess and Zumino (CCWZ) [16, 17], which makes only few specific assumptions as regards the strong sector, namely, the global symmetries, their pattern of spontaneous breaking and the sources of explicit breaking (in our case they come from the couplings of the new strong sector with the SM fields). The scalar potential is in the end generated by loop effects and, at the lowest order, is mainly determined by the free parameters associated to the top sector [13].

However, as in Ref. [14], we will not calculate the ensuing Higgs potential à la Coleman–Weinberg (CW) [18] generated by such radiative corrections, instead, we will assume the same general form as in the E2HDM with a $Z_2$ symmetry, the latter imposed in order to avoid flavour changing neutral currents (FCNCs) at the tree level [19]. We do so in order to study the phenomenology of C2HDMs in a rather model independent way, as this approach in fact allows for the most general 2HDM Higgs potential¹ It is our intention to eventually construct the true version of the latter through the proper CW mechanism [20]. However, first we intend to infer guidance in approaching this task from the study of theoretical (i.e., perturbativity, unitarity, vacuum stability, etc.—the subject of Ref. [14]) and experimental (one of the subjects of the present paper) constraints, specifically, by highlighting the parameter space regions where differences can be found between the E2HDM and C2HDM. This will inform the choice of how to construct a phenomenologically viable and different (from the E2HDM) realisation of a C2HDM in terms of underlying gauge symmetries, their breaking patterns and the ensuing new bosonic and fermionic spectrum, that is, indeed, to settle on a specific model dependence.

The paper is organised as follows. In Sect. 2 we describe the C2HDM based on $SO(6)/SO(4)\times SO(2)$. In Sect. 3, the LHC phenomenology is discussed in the presence of both the theoretical and the experimental constraints. Conclusions are drawn in Sect. IV. In Appendix A, relevant Feynman rules for the phenomenological study are presented.

2 The composite two Higgs doublet model

We construct the Lagrangian of the C2HDM based on the spontaneous breaking of the global symmetry $SO(6)\rightarrow SO(4)\times SO(2)$ at a scale f. In this model, eight (pseudo)scalar fields emerge as pNGBs from such a breaking pattern, which constructs two isospin doublet fields. In our approach, we do not specify the physics at any scale above a (large) cutoff $\Lambda$, which is expected to be $\sim 4\pi f$ from a naïve dimensional analysis [21, 22], i.e., we do not fix the concrete structure of the gauge and matter contents. Even in this setup, the kinetic term of the pNGBs is uniquely determined by the structure of the global symmetry breaking. For the Yukawa sector though, we need to assume an embedding scheme for the SM fermions into SO(6) multiplets to build the Lagrangian at low energy. Although in this framework the scalar potential is generated via the CW mechanism at loop level [18], as intimated, we assume here its renormalisable form of the E2HDM. This gives a sort of more general approach to the potential, namely, once the CW potential is calculated in a fixed configuration, all the potential terms can be translated into the strong sector parameters. We therefore adopt the same setup of [14], to which we refer the reader for further details of the model construction.

2.1 Two Higgs doublets as pseudo Nambu–Goldstone bosons

We construct the $6\times 6$ pNGB matrix U using the eight broken generators² of SO(6) $T_\alpha ^{\hat{a}}$ ($\alpha =1,2$ and $\hat{a}=1$-4) as

$$\begin{aligned}&U=\exp \left( i\frac{\Pi }{f}\right) ,\nonumber \\&\text {with}~~ \Pi \equiv \sqrt{2}\pi _{\alpha }^{\hat{a}}T^{\hat{a}}_{\alpha }=-i \begin{pmatrix} 0_{4\times 4} &{} (\pi _1^{\hat{a}},\pi _2^{\hat{a}}) \\ -(\pi _1^{\hat{a}},\pi _2^{\hat{a}})^T &{} 0_{2\times 2} \end{pmatrix}. \end{aligned}$$

(1)

The eight real spinless fields $\pi _\alpha ^{\hat{a}}$ associated with the broken generators can be expressed through two complex doublets as

$$\begin{aligned} \Phi _\alpha = \frac{1}{\sqrt{2}}\begin{pmatrix} \pi _\alpha ^2 + i\pi _\alpha ^1 \\ \pi _\alpha ^4 - i\pi _\alpha ^3 \end{pmatrix}, \end{aligned}$$

(2)

where the $\pi _\alpha ^4$’s acquire the non-zero VEVs: $\langle \pi _\alpha ^4 \rangle =v_\alpha$. Their ratio is expressed as $\tan \beta = v_2/v_1$ and we define $v \equiv \sqrt{v_1^2 + v_2^2}$. The EW scale, $v_{\text {SM}}^{}$, related to the Fermi constant $G_F$, is expressed by f and v as follows:

$$\begin{aligned} v_{\text {SM}}^{}\equiv f\sin (v/f) = (\sqrt{2}G_F)^{-1/2} \simeq 246~\text {GeV}. \end{aligned}$$

(3)

We here introduce the Higgs basis in which the physical Higgs states are separated from the NG boson states $G^\pm$ and $G^0$, which are absorbed into the longitudinal components of the $W^\pm$ and Z bosons, as

$$\begin{aligned} \begin{pmatrix} \Phi _1 \\ \Phi _2 \end{pmatrix} = \begin{pmatrix} \cos \beta &{} -\sin \beta \\ \sin \beta &{} \cos \beta \end{pmatrix} \begin{pmatrix} \Phi \\ \Psi \end{pmatrix} , \end{aligned}$$

(4)

where

$$\begin{aligned} \Phi = \begin{pmatrix} G^+ \\ \frac{v+h_1' + iG^0}{\sqrt{2}} \end{pmatrix}, \quad \Psi = \begin{pmatrix} H^+ \\ \frac{h_2' + iA}{\sqrt{2}} \end{pmatrix}. \end{aligned}$$

(5)

The doublet $\Psi$ contains the physical CP-odd Higgs boson (A) and a pair of charged Higgs bosons $(H^\pm )$. As noted in Ref. [14], in the Higgs basis the $G^0$, $G^\pm$ and $h_2'$ fields do not yield the kinetic terms in canonical form, hence we shift these fields so as to render them to canonical up to $\mathcal{O}(1/f^2)$ by

$$\begin{aligned} G^+&\rightarrow \left( 1-\frac{\xi }{3}\right) ^{-1/2}G^+,\quad G^0 \rightarrow \left( 1-\frac{\xi }{3}\right) ^{-1/2}G^0,\nonumber \\ h_2'&\rightarrow \left( 1-\frac{\xi }{3}\right) ^{-1/2}h_2'. \end{aligned}$$

(6)

In general, the two CP-even scalar states $h_1'$ and $h_2'$ can mix with each other. Their mass eigenstates can be defined by

$$\begin{aligned} \begin{pmatrix} h_1' \\ h_2' \end{pmatrix}= \begin{pmatrix} \cos \theta &{} -\sin \theta \\ \sin \theta &{} \cos \theta \end{pmatrix} \begin{pmatrix} h \\ H \end{pmatrix}, \end{aligned}$$

(7)

where $-\pi /2 < \theta \le \pi /2$. We identify the mass eigenstate h as the Higgs boson with a mass of 125 GeV discovered at the LHC.

The matrix U is transformed under SO(6) non-linearly, i.e., $U \rightarrow gUh^{-1}$ with g and h being the transformation matrices for SO(6) and $SO(4)\times SO(2)$, respectively. It is useful to define the linear representation of the pNGB fields from U to construct the SO(6) invariant Lagrangian. In the following, we use the SO(6) adjoint representation $\Sigma$, i.e., 15-plet, which is reducible under the $SO(4)\times SO(2)$ subgroup as $\mathbf{15} = (\mathbf{6},\mathbf{1})\oplus (\mathbf{4},\mathbf{2}) \oplus (\mathbf{1},\mathbf{1})$. Namely,

$$\begin{aligned} \Sigma = U\Sigma _0U^T, \end{aligned}$$

(8)

where $\Sigma _0$ is the $SO(4)\times SO(2)$ invariant VEV parametrised as

$$\begin{aligned} \Sigma _0 = \begin{pmatrix} 0_{4\times 4} &{} 0_{4\times 2} \\ 0_{2\times 4} &{} i\sigma _2 \end{pmatrix}. \end{aligned}$$

(9)

Then the field $\Sigma$ is transformed linearly under SO(6), i.e., $\Sigma \rightarrow g\Sigma g^T$.

The kinetic terms of the eight pNGB fields can then be written in terms of $\Sigma$ as follows:

$$\begin{aligned} \mathcal {L}_{\text {kin}}=\frac{f^2}{4}\text {tr}[D_\mu \Sigma \, (D^\mu \Sigma )^T]. \end{aligned}$$

(10)

The covariant derivative $D_\mu$ is given by

$$\begin{aligned} D_\mu \Sigma = \partial _\mu \Sigma -i[V_\mu ,\Sigma ], \end{aligned}$$

(11)

where

$$\begin{aligned} V_\mu&\equiv g(T_L^+ W_\mu ^++T_L^- W_\mu ^-) +\frac{g}{\cos \theta _W}(T_L^3-\sin ^2\theta _W Q)Z_\mu \nonumber \\&\quad +\;g\sin \theta _W QA_\mu , \end{aligned}$$

(12)

with $T_L^\pm =(T_L^1\pm i T_L^2)/\sqrt{2}$, $Q=T_L^3+T_R^3$ and $\theta _W$ being the Weinberg mixing angle.

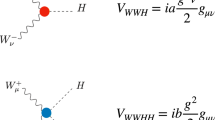
In Appendix A, we give all the Feynman rules relevant to the discussion of the Higgs phenomenology, which are derived from the kinetic term given in Eq. (10)

2.2 Yukawa Lagrangian

In this subsection, we construct the low-energy (below the scale f) Yukawa Lagrangian. In order to do this, we need to determine the embedding scheme of the SM fermions into SO(6) multiplets. This embedding can be justified via the mechanism based on the partial compositeness assumption [4], where elementary SM fermions mix with composite fermions in the invariant form under the SM $SU(2)_L\times U(1)_Y$ gauge symmetry but not under the global SO(6) symmetry. Through the mixing, the SO(6) invariant Yukawa Lagrangian given in terms of $\Sigma$ and composite fermions turns out to be the SM-like Yukawa Lagrangian after integrating out the (heavy) composite fermions.

2.2.1 Fermion embeddings

We discuss the embeddings of the SM quarks and leptons using 6-plet representations of SO(6). In order to reproduce the correct electric charge of the SM fermions, we introduce an additional $U(1)_X$ symmetry and assign its appropriate charge to 6-plets. The electric charge Q is thus given by³ $Q=T_3^L+T_3^R+X$. In the SO(6) basis, the 6-plet fermion $\Psi _X$, with the $U(1)_X$ charge X expressed as a mixture of the states in the $SU(2)_L\times SU(2)_R$ basis, is obtained as follows:

$$\begin{aligned} \Psi _X&= \left[ -i\frac{\psi _{++}+\psi _{--}}{\sqrt{2}}, \frac{\psi _{++}-\psi _{--}}{\sqrt{{2}}}, i\frac{\psi _{-+}-\psi _{+-}}{\sqrt{2}}, \right. \nonumber \\&\quad \left. \times \,\frac{\psi _{-+}+\psi _{+-}}{\sqrt{2}}, \psi _{00}, \psi _{00}' \right] _X^T, \end{aligned}$$

(13)

where $\psi _{++}$, $\psi _{+-}$, $\psi _{-+}$ and $\psi _{--}$ denote the ($+1/2,+1/2$), ($+1/2,-1/2$), ($-1/2,+1/2$) and ($-1/2,-1/2$) state for ($T_L^3$, $T_R^3$), while $\psi _{00}$ and $\psi _{00}'$ are singlets under $SU(2)_L$ and $SU(2)_R$, respectively. From this relation, we can embed the SM quarks and leptons into the 6-plet representation $\Psi _X$ as follows:

$$\begin{aligned}&(\Psi _{2/3})_L \equiv Q_L^u = ( -id_L^{} , -d_L^{} , -iu_L^{}, u_L^{} , 0 , 0 )^T, \end{aligned}$$

(14)

$$\begin{aligned}&(\Psi _{-1/3})_L \equiv Q_L^d = (-iu_L^{}, u_L^{} , id_L^{} , d_L^{} , 0 , 0 )^T, \end{aligned}$$

(15)

$$\begin{aligned}&(\Psi _{2/3})_R \equiv U_R^{} = (0 , 0 , 0, 0, 0, u_R )^T, \end{aligned}$$

(16)

$$\begin{aligned}&(\Psi _{-1/3})_R \equiv D_R = (0, 0, 0, 0, 0, d_R)^T, \end{aligned}$$

(17)

$$\begin{aligned}&(\Psi _{-1})_L \equiv L_L = (-i\nu _L^{} , \nu _L^{} , ie_L^{} , e_L^{} , 0 , 0 )^T, \end{aligned}$$

(18)

$$\begin{aligned}&(\Psi _{-1})_R \equiv E_R^{} = (0, 0, 0, 0, 0, e_R)^T. \end{aligned}$$

(19)

2.2.2 Yukawa Lagrangian

Table 1 Charge assignment for right-handed fermions under the $C_2$ symmetry in the C2HDM. All the left-handed fermions $Q_L^u$, $Q_L^d$ and $L_L$ are transformed as even under $C_2$. In the third column, the symbol $\surd$ means non-zero $a_f$ or $b_f$

The Yukawa Lagrangian at low energy is given in terms of the 15-plet of pNGB fields $\Sigma$ and the 6-plet of fermions defined in the previous subsection:

$$\begin{aligned} \mathcal{L}_Y&= f\Big [\overline{Q}_L^u (a_u \Sigma - b_u \Sigma ^2) U_{R} +\overline{Q}_L^d (a_d \Sigma - b_d \Sigma ^2) D_{R}\nonumber \\&\quad +\overline{L}_L (a_e \Sigma - b_e \Sigma ^2) E_{R}\Big ] + \text {h.c.} \end{aligned}$$

(20)

We note that the $\Sigma ^3$ term is equivalent to the $-\Sigma$ term, thus the terms with the cubic and more than cubic power of $\Sigma$ do not give any additional independent contributions to the Yukawa Lagrangian. The parameters $a_f$ and $b_f$ should be understood as $3\times 3$ complex matrices in flavour space. This Lagrangian is rewritten, up to the order $1/f^2$, using the complex doublet form of the Higgs fields defined in Eq. (2), as

$$\begin{aligned} \mathcal{L}_Y&= \sqrt{2}a_u\overline{Q}_L \left[ \tilde{\Phi }_1 -\frac{1}{f^2}\tilde{\Phi }_1\left( \frac{1}{3}\Phi _1^\dagger \Phi _1 +\Phi _2^\dagger \Phi _2 \right) \right. \nonumber \\&\left. \quad +\;\frac{1}{3f^2}\tilde{\Phi }_2(\Phi _1^\dagger \Phi _2 +\text {h.c.}) \right] u_R^{} +\sqrt{2}b_u\overline{Q}_L \nonumber \\&\quad \times \,\left[ \tilde{\Phi }_2-\frac{2}{3f^2}\left( \tilde{\Phi }_1(\Phi _1^\dagger \Phi _2 + \text {h.c.})+2\tilde{\Phi }_2(\Phi _2^\dagger \Phi _2) \right) \right] u_R^{} \nonumber \\&\quad +\sqrt{2}a_d\overline{Q}_L \left[ \Phi _1 -\frac{1}{f^2}\Phi _1\left( \frac{1}{3}\Phi _1^\dagger \Phi _1 +\Phi _2^\dagger \Phi _2 \right) \right. \nonumber \\&\left. \quad +\;\frac{1}{3f^2}\Phi _2(\Phi _1^\dagger \Phi _2 +\text {h.c.}) \right] d_R^{} +\sqrt{2}b_d\overline{Q}_L \nonumber \\&\quad \times \;\left[ \Phi _2-\frac{2}{3f^2}\left( \Phi _1(\Phi _1^\dagger \Phi _2 + \text {h.c.})+2\Phi _2(\Phi _2^\dagger \Phi _2) \right) \right] d_R^{} \nonumber \\&\quad +\sqrt{2}a_e\overline{L}_L\left[ \Phi _1 -\frac{1}{f^2}\Phi _1\left( \frac{1}{3}\Phi _1^\dagger \Phi _1 +\Phi _2^\dagger \Phi _2 \right) \right. \nonumber \\&\quad \left. +\;\frac{1}{3f^2}\Phi _2(\Phi _1^\dagger \Phi _2 +\text {h.c.}) \right] e_R^{} +\sqrt{2}b_e\overline{L}_L \nonumber \\&\quad \times \;\left[ \Phi _2-\frac{2}{3f^2}\left( \Phi _1(\Phi _1^\dagger \Phi _2 + \text {h.c.})+2\Phi _2(\Phi _2^\dagger \Phi _2) \right) \right] e_R^{}, \end{aligned}$$

(21)

where $\tilde{\Phi }_\alpha = i\sigma _2 \Phi _\alpha ^*$. The fermion mass terms, at the same order, are then extracted to be

$$\begin{aligned} m_f=v_\mathrm{SM}\left[ a_f c_\beta +b_f s_\beta \left( 1-\frac{\xi }{ 2} \right) \right] . \end{aligned}$$

(22)

Clearly, the existence of two independent Yukawa matrices, $a_f$ and $b_f$, for $f=u,d,e$, introduces FCNCs at the tree level. As it is well known, they are induced by the fact that both doublets $\Phi _1$ and $\Phi _2$ couple to each fermion types. This property is common to the E2HDM. In fact, the Yukawa Lagrangian in Eq. (21), in the limit $f\rightarrow \infty$, reproduces to so-called Type-III E2HDM.

In order to avoid FCNCs at the tree level, we impose a discrete $C_2$ symmetry [13] as follows:

$$\begin{aligned}&U(\pi _1^{\hat{a}},\pi _2^{\hat{a}}) \rightarrow C_2U(\pi _1^{\hat{a}},\pi _2^{\hat{a}})C_2 = U(\pi _1^{\hat{a}},-\pi _2^{\hat{a}}), \end{aligned}$$

(23)

where $C_2 = \text {diag}(1,1,1,1,1,-1)$. By this definition, $\pi _1^{\hat{a}}$ and $\pi _2^{\hat{a}}$ have a $C_2$-even and $C_2$-odd charge, respectively. Depending on the $C_2$ charge assignment of the right-handed fermions, we can define four independent types of Yukawa interactions, just like the softly broken $Z_2$ symmetric version of the E2HDM [23,24,25], as shown in Table. 1. For example, the Type-I Yukawa interaction is obtained by taking $a_f=0$.

In the $C_2$ symmetric case, we obtain the following interaction terms in the mass eigenbasis of the fermions:

$$\begin{aligned} \mathcal{L}_Y&=\sum _{f=u,d,e}\frac{m_f}{v_{\text {SM}}}\bar{f}\Big (X_f^h h +X_f^H H - 2iI_f X_f^A \gamma _5 A \Big )f\nonumber \\&\quad + \frac{\sqrt{2}}{v_{\text {SM}}}\bar{u}V_{ud}(m_dX_d^A\,P_R-m_uX_u^A\,P_L )d\,H^+ \nonumber \\&\quad + \frac{\sqrt{2}}{v_{\text {SM}}}\bar{\nu }m_eX_e^AP_R\, e \, H^+ +\text {h.c.}, \end{aligned}$$

(24)

where $I_f=+1/2~(-1/2)$ for $f=u~(d,e)$, $V_{ud}$ are the CKM matrix elements and $P_{L,R}$ are the projection operators for left and right-handed fermions. The coefficients $X_f^{h,H,A}$ can be either $\zeta _{h,H,A}$ or $\xi _{h,H,A}$ as shown in Table 1, and their expressions, at the first order in $\xi$, are given by

$$\begin{aligned} \zeta _h&= \left( 1-\frac{3}{2}\xi \right) c_\theta + s_\theta \cot \beta , \nonumber \\ \xi _h&= \left( 1-\frac{\xi }{2} \right) c_\theta -s_\theta \tan \beta , \end{aligned}$$

(25)

$$\begin{aligned} \zeta _H&= -\left( 1-\frac{3}{2}\xi \right) s_\theta + c_\theta \cot \beta , \nonumber \\ \xi _H&= -\left( 1-\frac{\xi }{2} \right) s_\theta - c_\theta \tan \beta , \end{aligned}$$

(26)

$$\begin{aligned} \zeta _A&= \left( 1+\frac{\xi }{2} \right) \cot \beta , \nonumber \\ \xi _A&= -\left( 1-\frac{\xi }{2} \right) \tan \beta . \end{aligned}$$

(27)

In the limit of $\xi \rightarrow 0$, these coefficients get the same form as the corresponding ones in a softly broken $Z_2$ symmetric version of the E2HDM [25].

2.3 Potential

We adopt the same form of the potential as in the E2HDM. We have in total eight parameters, which can be translated into eight physical inputs, as explicitly done in Ref. [14]:

$$\begin{aligned} m_h, \quad m_H^{}, \quad m_A^{}, \quad m_{H^\pm }^{}, \quad M^2, \quad v_{\text {SM}}^{}, \quad \tan \beta \quad \text {and} \quad s_\theta , \end{aligned}$$

(28)

where $m_h,~~m_H^{},~~m_A^{}$ and $m_{H^\pm }^{}$ are, respectively, the mass of h, H, A and $H^\pm$, among which $m_h$ should be fixed to be 125 GeV. The parameter M describes the soft breaking scale of the $C_2$ symmetry.

3 Phenomenology

In this section, we discuss how we can discriminate the C2HDM from the E2HDM. Firstly, we discuss the constraints on the parameter space in the C2HDM from various (null) searches of extra Higgs bosons at collider experiments (Sect. 3.1). Secondly, we focus on deviations in the SM-like Higgs boson (h) couplings from the SM predictions (Sect. 3.2). Thirdly, we discuss the difference in the properties of the decay (Sect. 3.3) and production mechanisms at the LHC (Sect. 3.4) of the extra Higgs bosons.

Before proceeding further though, we ought to note now that CHMs usually also predict heavy spin-1 and spin-1/2 states via the partial compositeness mechanism. These extra particles can potentially enter the ensuing phenomenological analysis through loop-induced couplings of the composite Higgs bosons to Z, photons and gluons. Contributions from these particles to loop-induced Higgs production and/or decay modes were studied in detail in Ref. [26] (albeit for a single doublet realisation of a CHM). It was found therein that the individual extra gauge boson contributions to the loop-induced couplings of the SM-like h state are always negligible while this is not the case for the extra fermion ones. However, the extra fermion effects are not dramatically large, i.e., at the $\mathcal {O}$(1%) level in the $h\rightarrow \gamma \gamma ,\gamma Z$ cases and $\mathcal {O}$(10%) in the $h\rightarrow gg$ case. Thus, Ref. [26] indicates that all such contributions to h phenomenology at the LHC are not crucial for our purposes. Similarly, we expect that these extra resonances (both bosons and fermions) will not affect significantly the $H, A \rightarrow gg,\gamma \gamma$ and $Z\gamma$ partial widths either. Hence, in our forthcoming C2HDM analysis at the LHC, we will not include all such effects.

3.1 Constraints from collider experiments

We start discussing constraints on the parameter space of the E2HDM and C2HDM from data collected at LEP, Tevatron and LHC by using the HiggsBounds [27,28,29,30] (v4.3.1) package. This tells us if a given set of model parameters is allowed at 95% confidence level (CL) by various (null) searches of Higgs bosons.

Fig. 1

Regions allowed at 95% CL from LEP, Tevatron and LHC experiments in the Type-I, -II, -X and -Y C2HDMs (green shaded). The black, red and blue curves display the contours for $\Delta \chi ^{2}= 2.30$ (68.27% CL), 6.18 (95.45% CL) and 11.83 (99.73% CL), respectively. As for the reference input values, we take $m_h = 125$ GeV, $m_H = m_{H^{\pm }} = m_A = 500$ GeV and $M = 0.8\,m_A$. The first, second, and third column of panels show the results with $\xi = 0,~ 0.04,~0.08$, respectively

Table 2 Higgs search channels most responsible for excluding parameter points in Fig. 1

In Fig. 1, we show the allowed regions (green shaded) in the $(\sin \theta ,\tan \beta )$ plane using HiggsBounds. We can see that larger values of $\xi$ give more excluded regions in the Type-I C2HDM, but in the other three models the $\xi$ dependence is not so significant. In particular, in the Type-I C2HDM with $\xi =0.08$ negative values of $\sin \theta$ are mostly ruled out, mainly because of the positive deviation of the signal strength for the vector-boson fusion production of h (the SM-like state) decaying into $W^+W^-$ [34] as compared to the Type-I E2HDM (corresponding to $\xi =0$ and shown in the first column of Fig. 1). In the Type-X C2HDM, additional exclusion parameter regions appear for larger $\xi$, which is mostly due to the same reason as in the Type-I C2DHM. In the Type-II and -Y C2HDMs, the excluded regions almost do not depend upon the $\xi$ value. In Table 2 we list the Higgs search channels most responsible for the exclusions.

In Fig. 1 we also present the compatibility of the signal strengths of the SM-like Higgs boson h based on a $\Delta \chi ^2$ analysis by using the HiggsSignals [31] (v1.4.0) package. In this figure, the black, red and blue contours, respectively, show the compatibility with 68.27, 95.45 and 99.73% CL from the minimum value of $\chi ^2$ in the $(\sin \theta ,\tan \beta )$ plane. Apart from the Type-I case, which reveals a better compliance with the LHC data (this is after all the scenario which more closely resembles the SM), the other three types respond similarly to the LHC Higgs data. Overall, the $\xi$ dependence is only marginally evident, being more pronounced for Type-I.

3.2 Deviation in the Higgs boson couplings

In both the E2HDM and the C2HDM, the Higgs boson couplings can deviate from the SM predictions. However, the pattern of deviations can be different between these two scenarios. In order to discuss these, it is convenient to define the scaling factor $\kappa _X^{}$ for the hXX couplings by $\kappa _X^{} = g_{hXX}^{\text {NP}}/g_{hXX}^{\text {SM}}$ and $\Delta \kappa _X=\kappa _X-1$. In the C2HDM, these deviations are given at the tree level by

$$\begin{aligned} \kappa _V^{}&= \left( 1-\frac{\xi }{2} \right) c_\theta ~~(V=W,Z), \nonumber \\ \kappa _f^{}&= X_f^h = \zeta _h \quad \text { or }\;\xi _h~~(f=u,d,e). \end{aligned}$$

(29)

Those for the E2HDM can easily be obtained by taking $\xi \rightarrow 0$ corresponding to $f\rightarrow \infty$. We can see that there are two sources giving $\kappa _X^{} \ne 1$ in the C2HDM, i.e., non-zero values of $\xi$ and $\theta$. Conversely, only $\theta \ne 0$ gives $\kappa _X^{}\ne 1$ in the E2HDM.⁴ Therefore, for a given measured value of $\kappa _X^{}$, the value of $\theta$ is determined in the E2HDM while only the combination $(\theta ,\xi )$ is determined in the C2HDM.

In Fig. 2, we plot the contour for $\Delta \kappa _V^{}$ as a function of $\xi$ and $\sin \theta$. We note that there is no sign dependence of $\sin \theta$ in this plot. From this figure, it is clear that a fixed value of the deviation $\Delta \kappa _V^{}$ at $\xi =0$, which corresponds to the E2HDM can be reproduced in the C2HDM by different parameter with non-zero $\theta$ and/or $\xi$. For example, the deviation $|\Delta \kappa _V^{}|=2\%$ can be reproduced by e.g., $(\xi ,\theta )=(0.04,0)$, (0.03, 0.1) and (0, 0.2). This result suggests an interesting consequence, namely, even if there is no mixing between the CP-even Higgs bosons h and H, in the C2HDM, we can have a non-zero deviation in the hVV couplings. As a result, we will find a significant difference in the two scenarios for the decay branching ratios (BRs) of the extra Higgs bosons for a given value of $\Delta \kappa _V^{}$, which will be discussed in the succeeding subsections.

As has been discussed in Ref. [42], the type of Yukawa interactions can be determined by looking at the correlation between $\Delta \kappa _E$ and $\Delta \kappa _D$ in the E2HDM, where E and D represent a charged lepton and a down-type quark, respectively. Now, let us discuss the correlation between $\Delta \kappa _E$ and $\Delta \kappa _D$ in the C2HDM.

In Fig. 3, we plot the prediction in the four types of the Yukawa interaction on the $\Delta \kappa _E^{}$ and $\Delta \kappa _D^{}$ plane with the fixed value of $\Delta \kappa _V^{}$ being $-1\%$ (left panel) and $-2\%$ (right panel). The range of $\tan \beta$ is taken from 1 to 10. In these plots, the value of $\theta$ is determined by fixing $\Delta \kappa _V^{}$ and f (or equivalently $\xi$). For each type of Yukawa interaction, we take $f=1780$ GeV (dotted curve), 2200 GeV (dashed curve) and $\infty$ (solid curve) for the left panel, while $f=1250$ GeV (dotted curve), 1500 GeV (dashed curve) and $\infty$ (solid curve) for the right panel. From this figure, we can extract two important aspects: (i) the models with a different type of Yukawa interaction can be separated by looking at $\Delta \kappa _E$ and $\Delta \kappa _D$ and (ii) for a fixed value of $\Delta \kappa _V^{}$ and the type of Yukawa interaction, predicted regions on the $\Delta \kappa _E$-$\Delta \kappa _D$ plane can be different depending on the value of f. It is also shown that the magnitude of $\Delta \kappa _{E,D}^{}$ with a smaller value of f tends to be small for a given value of $\tan \beta$ as compared to that with a larger f. As an extreme case $f=1740\,(1230)$ GeV, where the deviation $\Delta \kappa _V^{}=-1\%\,(-2\%)$ comes only via the non-zero $\xi$ (or equivalently the case with $s_\theta =0$), the prediction is given as a point indicated by the triangle, because the $\tan \beta$ dependence vanishes in this case. In addition, the predicted region with a fixed range of $\tan \beta$ shrinks when the value of f is getting small, because the $\tan \beta$ dependent part of $\kappa _f^{}$ is proportional to $s_\theta$ as seen in Eq. (25).

Therefore, if a non-zero value of $\Delta \kappa _V^{}$ is measured at collider experiments, we have an indirect evidence for a non-minimal Higgs sector, possibly belonging to a E2HDM or C2HDM. Furthermore, by looking at the pattern of the deviations in $\Delta \kappa _E$ and $\Delta \kappa _D$, we can discriminate between the four types of Yukawa interactions. In particular, if the Type-X or Type-Y Yukawa interaction is realised, the composite dynamics can also be extracted from the different allowed regions of the predictions on the $\Delta \kappa _E$–$\Delta \kappa _D$ plane. For the Type-I and Type-II cases, a prediction with a non-zero value of $\xi$ corresponds to the case with a different value of $\tan \beta$ in the E2HDM, so that we need to use other information, such as the decay properties of the extra Higgs bosons as we will discuss below. We note that making use of information from $\Delta \kappa _U^{}$ with U being an up-type quark is also helpful to extract the sign of $s_\theta$ as long as $\tan \beta$ and/or $\xi$ are not very large.

3.3 Decays of extra Higgs bosons

Next, we discuss the decay properties of the extra Higgs bosons H, A and $H^\pm$ in both the E2HDM and the C2HDM with the four types of Yukawa interaction. In particular, we compare the BRs of the extra Higgs bosons in the two models with the same value of $\Delta \kappa _V^{}$. As examples, we consider the following three benchmark points giving $\Delta \kappa _V^{} = -2\%$:

$$\begin{aligned}&\text {BP1}: (s_\theta ,\xi ) = (-0.2,0), \quad \text {BP2}: (s_\theta ,\xi ) = (-0.1,0.03),\nonumber \\&\text {BP3}: (s_\theta ,\xi ) = (0,0.04). \end{aligned}$$

(30)

BP1 corresponds to the E2HDM case, while BP2 and BP3 are two possible C2HDM cases, the latter corresponding to the zero-mixing angle.

Fig. 2

Contour plot for the deviation in the hVV couplings $\Delta \kappa _V^{}=\kappa _V^{}-1$ from the SM prediction

Fig. 3

Deviations in the Yukawa couplings on the $\Delta \kappa _E^{}$ (E stands for a charged lepton) and $\Delta \kappa _D^{}$ (D stands for a down-type quark) plane in the C2HDMs with $s_\theta < 0$. The left (right) panel shows the case for $\Delta \kappa _V^{}=-1(-2)\%$. The black, red, green and blue curves show the results in the Type-I, -II, -X and -Y C2HDM, respectively, while the solid, dashed and dotted curves show the case for $f=\infty$, 2200 (1500) GeV and 1780 (1250) GeV, respectively, for the left (right) panel. Each dot on the curve denotes the prediction with $\tan \beta = 1{-}10$ with its interval of 1, and the dot at the left edge on each curve corresponds to $\tan \beta = 1$. The triangles represent the prediction with $\theta = 0$

Fig. 4

Upper limit on the mass parameter $m_\Phi ^{}(=m_{H^\pm }^{}=m_A^{}=m_H^{})$ from the perturbative unitarity (indicated by the dashed curves) and the vacuum stability bounds (indicated by the solid curves) as a function of $\tan \beta$ in BP1 (left), BP2 (center) and BP3 (right). We take several fixed values of the ratio $M/m_\Phi ^{}$ and $\sqrt{s}=1$ TeV for the unitarity bound

Before studying the BRs, we survey the allowed parameter regions by bounds from the perturbative unitarity and the vacuum stability. Details of these bounds have been discussed in Ref. [14]. Concerning to the unitarity bound, we take into account all the elastic scatterings of 2 body to 2 body scalar boson processes up to $\mathcal{O}(s^0)$ dependences, where $\sqrt{s}$ is the scattering energy. Differently from E2HDMs, the s-wave amplitude matrix has terms proportional to $s \, \xi$, thus indicating that an UV completion of the theory is needed at high energy. Here we fix $\sqrt{s}=1$ TeV.

In Fig. 4, we show the allowed parameter region on the ($\tan \beta$, $m_{\Phi }^{})$ plane for the three benchmark points, where $m_\Phi = m_{H^\pm } = m_A = m_H$. The region above each curve is excluded by perturbative unitarity or vacuum stability, so that this figure shows the absolute theoretical upper limit on $m_{\Phi }^{}$. Different colours of each curve show different choices of the ratio $M/m_\Phi ^{}$, being 1, 0.8. 0.6 and 0.4. We can see that, typically, the unitarity and/or the vacuum stability bounds become stronger as the value of $\tan \beta$ increases. In addition, the case with $M/m_\Phi ^{}\lesssim 1$ tends to have a larger allowed value of $m_{\Phi }^{}$ as compared to the case with $M/m_\Phi ^{}=1$. Following this result, we take $\tan \beta = 2$, $m_{\Phi }^{}\le 500$ GeV and $M/m_{\Phi }^{}=0.8$ for the following analysis.

In Figs. 5, 6 and 7, we respectively show the $m_\Phi ^{}$ dependence of the BRs for H, A and $H^\pm$ for BP1 (left), BP2 (center) and BP3 (right) in the Type-I, -II, -X and -Y configurations, respectively.

When we look at the left and center panels of Fig. 5, we can observe the two thresholds at $m_H^{}\simeq 250$ and 350 GeV which correspond to the $H\rightarrow hh$ and $H \rightarrow t\bar{t}$ channel, respectively. If we compare them and the right panels of Fig. 5, we find significant differences in the H decay modes. Namely, the $H\rightarrow VV$ ($V=W^+W^-,\,ZZ$) and $H \rightarrow hh$ modes are absent in the right panels, because they are proportional to $s_\theta ^2$. In addition, in the BP3 case, the difference among the four types of Yukawa interactions becomes more clear, because only the fermionic final states of the H decay mode are dominant.

Fig. 5

BRs of H as a function of $m_\Phi ^{}(=m_H^{}=m_A^{}=m_{H^\pm })$ with $\tan \beta = 2$ and $M = 0.8\times m_\Phi ^{}$ in the four types of Yukawa interaction. The left, center and right panels show the case for BP1, BP2 and BP3, respectively

Fig. 6

Same as Fig. 5, but for the BRs of A

Fig. 7

Same as Fig. 5, but for the BRs of$H^\pm$

Concerning the BRs of A (Fig. 6), it is seen that their behaviour is drastically changed at $m_A^{}\simeq 350$ GeV. Namely, below $m_A^{}\simeq 350$ GeV, the $A\rightarrow Z^{(*)}h$ channel can be dominant in BP1 and BP2 depending on $m_\Phi ^{}$, while the $A\rightarrow b\bar{b}$, $\tau ^+\tau ^-$ and/or gg modes are dominant in BP3 depending on the type of Yukawa interactions. Notice that we have taken into account the three body decay process $A \rightarrow Z^*h \rightarrow f\bar{f}h$, which becomes important when $m_A^{}< m_Z^{}+m_h\simeq 215$ GeV. Conversely, above $m_A^{}\simeq 350$ GeV, $A\rightarrow t\bar{t}$ becomes dominant in all four type models and all three benchmark points. In BP1 (BP2) with $m_A^{}\simeq 350$ GeV, $A \rightarrow Z^{(*)}h$ can be 10–20% (a few %) level depending on $m_\Phi ^{}$ and the type of Yukawa interactions. Regarding the results for BP3, the behaviour of the BRs of A is almost the same as those of H, where the $A\rightarrow Z^{(*)}h$ mode does not appear, because its decay rate is proportional to $s_\theta ^2$. Only for the BR of the $A\rightarrow gg$ mode, it is slightly larger than that of the $H\rightarrow gg$ mode when we compare them with the same configuration, because of the difference in the loop function.

Fig. 8

Cross section of the gluon-fusion process for H (left) and A (right) as a function of the extra neutral Higgs boson mass at $\sqrt{s}=13$ TeV in BP1, BP2 and BP3 with $\tan \beta = 2$

The mass dependence on the BRs of $H^\pm$ is shown in Fig. 7. We see that the $H^+\rightarrow t\bar{b}$ mode is dominant in all the four types of Yukawa interactions and all the three benchmark points. In BP1 (BP2), the $H^+\rightarrow W^{+(*)}h$ mode can be about 20% (5%) at $m_{\Phi }^{}\simeq 500$ GeV.

3.4 Productions of extra Higgs bosons at the LHC

Finally, we discuss the production cross sections of the extra Higgs bosons at the LHC. We here consider the gluon-fusion process $gg\rightarrow H/A$, the bottom quark associated process $gg \rightarrow b\bar{b}H/A$ and the gluon–bottom fusion process $g\bar{b} \rightarrow H^+ \bar{t}$. In fact the cross sections for the vector-boson fusion ($qq' \rightarrow qq'H$) and vector boson associated ($q\bar{q}\rightarrow ZH$ and $q\bar{q}'\rightarrow W^\pm H^\mp$) processes are negligibly small, because of the suppressed gauge–gauge–Higgs couplings (by $s_\theta$).

For the calculation of the gluon-fusion cross section, we use the following equation:

$$\begin{aligned} \sigma (gg\rightarrow \phi ^0)&= \frac{\Gamma (\phi ^0 \rightarrow gg)}{\Gamma (h_{\text {SM}}\rightarrow gg)}\times \sigma (gg \rightarrow h_{\text {SM}}) \nonumber \\&\quad \times \,(\phi ^0=H~\text {or}~A), \end{aligned}$$

(31)

where $h_{\text {SM}}$ is the SM Higgs boson with the mass artificially set at $m_{\phi ^0}$. We adopt the value of the gluon fusion cross section $\sigma (gg \rightarrow h_{\text {SM}})$ in the SM from Ref. [43]. For the other calculations of the production cross sections, we use CalcHEP [44] and adopt the CTEQ6L [45] for the parton distribution functions with factorisation/renormalisation scale set at $Q=\sqrt{\hat{s}}$. We note that the lepton Yukawa coupling is not relevant for the calculation of the production cross sections, so that the results in the Type-I (Type-II) and Type-X (Type-Y) models are the same. As in the previous subsection, we take BP1, BP2 and BP3 given in Eq. (30) and $\tan \beta = 2$ for the numerical analysis.

In Fig. 8, we show the gluon-fusion production cross section as a function of the mass of the produced Higgs boson. In this process, the dependence of the type of Yukawa interactions is almost negligible, because only the top Yukawa coupling is important to determine the size of the cross section. The results for BP1, BP2 and BP3 are, respectively, shown as the solid, dashed, and dotted curves. We find differences in the cross section of $gg \rightarrow H$ among the three benchmark points, which comes from the $s_\theta$ term in $\zeta _H$ or $\xi _H$ given in Eq. (26). In contrast, the cross section for A is essentially the same for the three benchmark points.

Fig. 9

Cross section for the bottom quark associated production process for H (left) and A (right) as a function of the extra neutral Higgs boson mass at $\sqrt{s}=13$ TeV in BP1, BP2 and BP3 with $\tan \beta = 2$

In Fig. 9, we show the cross section of the bottom quark associated production as a function of the mass of the produced Higgs boson. Typically, the cross section is more than one order of magnitude smaller than the gluon-fusion production process because of the smallness of the bottom Yukawa coupling and the three body phase space. Differently from the gluon fusion, the dependence of the type is important, because the bottom Yukawa coupling determines the size of the cross section. In fact, the cross section in Type-II and Type-Y is almost one order of magnitude greater than that in Type-I and Type-X. Similar to the case for the gluon fusion, a larger discrepancy of the cross section among BP1, BP2 and BP3 is seen for the production of H state, as for the A one differences are marginal.

Fig. 10

Cross section of the gluon–bottom fusion process of $H^\pm$ as a function of the extra neutral Higgs boson mass at $\sqrt{s}=13$ TeV in BP1, BP2 and BP3 with $\tan \beta = 2$

In Fig. 10, we show the gluon–bottom fusion production cross section for the $H^\pm$ state. Similar to the gluon-fusion process, the dependence of the type of Yukawa interactions is almost negligible, because of involving the top Yukawa coupling. The differences among the three benchmark points are negligibly small.

To summarise, in this section, we have discussed the differences between the E2HDM and C2HDM by focusing on the deviations in the SM-like Higgs boson couplings from the SM predictions as well as the decay BRs and production cross sections at the LHC. We have shown that, even if E2HDM and C2HDM give the same value of the deviation in the hVV coupling, we can find significant differences in the correlation of $\Delta \kappa _E^{}$-$\Delta \kappa _D^{}$ in the two scenarios (elementary and composite). In addition, through the combination of the differences in the decay BRs and production cross sections for the extra Higgs bosons, we may be able to distinguish these two hypotheses on the nature of the Higgs bosons responsible for EWSB.

4 Conclusions

In this paper, we have continued our exploration of C2HDM scenarios, started with Ref. [14], assuming four different types of Yukawa interactions, wherein the nature of all Higgs states is such that they are composite objects. Specifically, they are the pNGBs from the global symmetry breaking $SO(6)\rightarrow SO(4)\times SO(2)$, induced explicitly by interactions between a new strong sector and the SM fields at the compositeness scale f. Such pNGBs, for which we adopt the same scalar potential as in the E2HDM, then trigger EWSB governed by the SM gauge group. Under the assumption of partial compositeness, it is rather natural that one of the emerging physical Higgs fields, the lightest one, is the 125 GeV state, h, discovered at CERN.

Within this construct, we then proceed to carry out a phenomenological study aiming at establishing the potential of the LHC in disentangling the two hypotheses, E2HDM versus C2HDM, by exploiting the fact that drastically different production and decay patterns for the four heavy Higgs states (H, A and $H^\pm$) may onset in the composite scenario with respect to the elementary one, even when the properties of SM-like Higgs state are the same (within experimental accuracy) in the two scenarios. This has been done after imposing both theoretical (already derived in Ref. [14]) and experimental (obtained here by suitably modifying numerical toolboxes used in E2HDM analysis to also embed the C2HDM option) constraints, the latter revealing a marked dependence upon $\xi$ only for the case of Type-I Yukawa interactions. Specifically, the most dramatic situation could occur when, e.g., in the presence of an established deviation of a few percents from the SM prediction for the hVV ($V=W^\pm ,Z$) coupling (in fact, possibly the most precisely determined one at the LHC), the E2HDM would require the mixing between the h and H states to be non-zero whereas in the C2HDM compliance with such a measurement could be achieved also for the zero-mixing case. Hence, in this situation, the $H\rightarrow W^+W^-$ and ZZ decays would be forbidden in the composite case, while still being allowed in the elementary one. (Similarly, Higgs-strahlung and vector-boson fusion would be nullified in the C2DHM scenario, unlike in the E2HDM, while potentially large differences also appear in the case of gluon–gluon fusion and associated production with $b\bar{b}$ pairs.) Clearly, also intermediate situations can be realised. Therefore, a close scrutiny of the possible signatures of a heavy CP-even Higgs boson, H, would be a key to assess the viability of either model. Regarding the CP-odd Higgs state, A, in the extreme case of non-zero (zero) mixing in the E2HDM(C2HDM), again, it is the absence of a decay, i.e., $A\rightarrow Zh$, in the C2HDM that would distinguish it from the E2HDM. In the case of the $H^\pm$ state, a similar role is played by the $H^\pm \rightarrow W^\pm h$ decay. Obviously, for both these states too, intermediate situations are also possible, so that a precise study of these two channels would be a further strong handle to use in order to disentangle the two hypotheses. As far as A and $H^\pm$ production modes which are accessible at the LHC, i.e., gluon–gluon fusion and associate production with $b\bar{b}$ pairs (for the A) and associated production with $b\bar{t}$ pairs (for the $H^+$), are concerned though, practically no difference appears. The actual size of all these differences between the E2HDM and C2HDM is governed by the value of the $\xi = v_\mathrm{SM}^2/f^2$ parameter, the larger the latter the more significant the former. Finally, although there are quantitative differences between the usual four Yukawa types (I, II, X and Y, in our notation) when predicting the yield of both the E2HDM and the C2HDM, the qualitative pattern we described would generally persist. In fact, a similar phenomenology would emerge if deviations were instead (or in addition) established in the Yukawa couplings of the h state to b-quarks and/or $\tau$-lepton.

In short, if deviations will be established during Run 2 of the LHC in the couplings of the discovered Higgs state with either SM gauge bosons or matter fermions, then not only a thorough investigation of the 2HDM hypothesis is called for (as one of the simplest non-minimal version of EWSB induced by the Higgs mechanism via doublet states, like the one already discovered) but a dedicated scrutiny of the decay patters of all potentially accessible heavy Higgs states could enable one to separate the E2HDM from the C2HDM.

Appendix: Feynman rules

Table 3 Coefficients of the Scalar–Scalar–Gauge type vertices

We present the trilinear couplings of the Higgs bosons which are relevant to the discussion of the phenomenology given in Sect. 3. First, the gauge–gauge–scalar type interactions are given by

$$\begin{aligned} \mathcal{L}_{\text {kin}}&= \left( 1-\frac{\xi }{2}\right) (h\cos \theta -H\sin \theta ) \nonumber \\&\quad \times \;\left( gm_W W_\mu ^+W^{-\mu } + \frac{g_Z^{}}{2}m_ZZ_\mu Z^\mu \right) . \end{aligned}$$

(A1)

Second, the coefficients of the scalar–scalar–gauge type interactions are extracted as given in Table 3, where we introduce

$$\begin{aligned} X\overleftrightarrow {\partial }_\mu Y = X(\partial _\mu Y) - (\partial _\mu X) Y. \end{aligned}$$

(A2)

Finally, the scalar trilinear Hhh and $H^+H^-h$ couplings defined by

$$\begin{aligned} \mathcal{L} = +\lambda _{Hhh}Hhh + \lambda _{H^+H^-h}H^+H^-h + \cdots \end{aligned}$$

(A3)

are extracted by

$$\begin{aligned} \lambda _{Hhh}&= \frac{s_\theta }{v_{\text {SM}}s_{2\beta }}\left[ -\frac{s_{2(\beta +\theta )}}{2}(2m_h^2 + m_H^2)\right. \nonumber \\&\left. \quad +\;\frac{1}{2}(s_{2\beta }+3s_{2(\beta +\theta )})M^2\right] +\frac{\xi }{12v_{\text {SM}}}s_\theta \nonumber \\&\quad \times \;\left[ m_H^2-2m_h^2 + (1+3c_{2\theta }+6\cot 2\beta s_{2\theta })M^2\right] , \end{aligned}$$

(A4)

$$\begin{aligned} \lambda _{H^+H^-h}&= \frac{c_\theta }{v_{\text {SM}}}\left[ -(1+2\cot 2\beta \tan \theta )m_h^2-2m_{H^\pm }^2\right. \nonumber \\&\left. \quad +\;\frac{2}{s_{2\beta }c_\theta }s_{2\beta +\theta }M^2\right] +\frac{\xi }{6v_{\text {SM}}}c_{\theta }\nonumber \\&\quad \times \;\left[ (1+4\cot 2\beta \tan \theta )m_h^2+2(m_{H^\pm }^2-M^2) \right] . \end{aligned}$$

(A5)