1 Introduction

At present, type 1a supernova [1], cosmic microwave background (CMB) radiation [2] and large scale structure [3, 4] analyses have shown that our universe is currently in an accelerating expansion period. Dark energy is responsible for this acceleration and it has the strange property of violating the null energy condition (NEC) and the weak energy condition (WEC) [5, 6] and it produces strong repulsive gravitational effects. Recent observations suggest that approximately 74% of our universe is occupied by dark energy and the rest, 22 and 4% is for dark matter and ordinary matter, respectively. Nowadays dark energy is the most challenging problem in astrophysics. Many theories have been proposed to handle this important problem in last two decade.

With the discovery of cosmic acceleration, black hole (BH) phenomena have become most fascinating in illustrating the significant physical properties. There exist two major types of vacuum BH solutions in general relativity, i.e., uncharged (for example Schwarzschild BH) and charged (for example Reissner–Nordstrom BH). These BHs have been thoroughly investigated by many authors over the years. For example, there exists a well-known phenomenon in which a body experiences compression in the angular direction and stretching in radial direction when it falls toward the event horizon of uncharged static BHs [7,8,9,10,11]. However, for a Reissner–Nordstrom BH, a body may experience stretching in the radial direction and compression in the angular direction, depending upon two phenomena: (1) the location of the body, and (2) the charge to mass ratio of the BH [12]. Tidal forces change sign in the radial or the angular direction at certain points of the Reissner–Nordstrom BH, unlike the Schwarzschild BH. Geodesic deviations of Schwarzschild and Reissner–Nordstrom space-times were studied in detail by [7, 12,13,14,15].

However, several BHs of Einstein general relativity in the non-vacuum case have also been presented [16,17,18,19,20,21], which need more physical examination. One of them is the Kiselev BH, which shows a new set of phenomena unlike the Schwarzschild BH because of the important complex properties [21] and this BH has been surrounded by various types of matter depending on the state parameter \(\omega \). The Kiselev BH has been investigated through various phenomena, i.e., accretion [22], strong gravitational lensing [23], thermodynamics and phase transitions [24]. In this work, we apply the technique of [25] to the solution of a Kiselev BH surrounded by energy matter; i.e. we consider a Kiselev BH surrounded by dust and radiation using a parameter derived by Kiselev [21], in which we consider non-zero electric charge, dust and radiation but no angular momentum. They are exact solutions of the Einstein–Maxwell equation [13]; in the case of vanishing dust and radiation parameter it reduces to RN space-time and in the case of vanishing electric charge it reduces to SH space-time.

In this paper we discuss the tidal forces in Kiselev space-time and consider its two cases, which leads to a Kiselev space-time surrounded by dust \((\omega = 0)\) and radiation \((\omega = 1/3)\). We solve the geodesic deviation equations to observe the variation of a test body in-falling radially toward the Kiselev BH for specific choices of the dust and radiation parameter. This paper is organized as follows: In Sect. 2, we discuss Kiselev BHs, its two special cases and radial geodesics. In Sect. 3, we derive the tidal forces in a Kiselev space-time on a neutral body in radial free fall. In Sect. 4, we find the solutions of the geodesic equations in Kiselev space-time. In the end, we conclude our results. In this paper, we use the metric signature (+, −, −, −) and set the speed of light c and the Newtonian gravitational constant G to 1.

2 Kiselev black holes and its two special cases

The line element of a static charged BH surrounded by energy–matter is given by

$$\begin{aligned} \mathrm{d}s^{2}=f(r)\mathrm{d}t^{2}-f(r)^{-1}\mathrm{d}r^{2}- r^2({\mathrm{d}\theta }^{2}+\sin \theta {\mathrm{d}\phi }^{2}), \end{aligned}$$
(1)

with

$$\begin{aligned} f(r)= 1-\frac{2M}{r}+\frac{q^2}{r^2}-\frac{\sigma }{r^{3\omega +1}}, \end{aligned}$$
(2)

where M and q are the mass and electric charge, and \(\sigma \) and \(\omega \) are the normalization parameter and state parameter of matter around BH, respectively [21]. We assume \(\omega =1/3\), which becomes a Kiselev BH surrounded by radiation and \(\omega =0\), for a Kiselev BH surrounded by dust. For a Kiselev BH surrounded by radiation, the radial coordinated of horizons are obtained by taking \(f(r)=0\), i.e.

$$\begin{aligned} r_{\pm }= & {} M+\sqrt{M^2-q^2+\sigma _{r}}, \end{aligned}$$
(3)

where \(\sigma _{r}\) is parameter of radiation. We will assume only the cases in which \(M^2-q^2+\sigma _{r}\ge 0\) because naked singularities (\(M^2-q^2+\sigma _{r}< 0\)) do not occur in nature if the cosmic conjecture is true. Equation (3) gives the location of the event as well as Cauchy horizon of the BH, respectively.

Similarly, for a Kiselev BH surrounded by dust (\(\omega =0\)), the radial coordinates of the horizons are

$$\begin{aligned} r_{\pm }= & {} \frac{2M+\sigma _{d}\pm \sqrt{(2M+\sigma _{d})^2-4q^2}}{2}, \end{aligned}$$
(4)

where \(\sigma _{d}\) is the parameter of dust. We choose the case in which \((2M+\sigma _{d})^2\ge 4q^2\) because naked singularities (\((2M+\sigma _{d})^2 < 4q^2\)) do not occur in nature if the cosmic conjecture is true [26]. Equation (4) gives the location of the event as well as Cauchy horizon of the BH, respectively [21].

2.1 Radial geodesics

The radial geodesic motion for line element (1) in spherically symmetric space-times is obtained by considering \(\mathrm{d}s=\mathrm{d}\tau \) in Eq. (1), which is [27]

$$\begin{aligned} f(r) \dot{t}^2-f(r)^{-1} \dot{r}^2=1, \end{aligned}$$
(5)

where a dot represents the derivative with respect to proper time \(\tau \). Because of the assumption of radial motion, we have \(\dot{\theta }=\dot{\phi }=0\). \(E = f(r)\dot{t}\) is well known to be the conserved energy. By putting this in Eq. (4), we have

$$\begin{aligned} \frac{\dot{r}^2}{2}=\frac{E^2-f(r)}{2}. \end{aligned}$$
(6)

For the radial in-fall of a test particle from rest at position b, we get \(E=\sqrt{f(r=b)}\) from Eq. (6) [28]. Newtonian radial acceleration is defined by [29]

$$\begin{aligned} A^{R} = \ddot{r}. \end{aligned}$$
(7)

Using Eqs. (6) and (7), we obtain

$$\begin{aligned} A^{R} = -\frac{f'(r)}{2}, \end{aligned}$$
(8)

where a prime represents the derivative with respect to r (radial coordinate). For a Kiselev BH surrounded by radiation and dust, we obtain

$$\begin{aligned} A_r^{R} =-\frac{M}{r^2}+\frac{q^2}{r^3}-\frac{\sigma _{r}}{r^3}, \quad A_d^{R} =-\frac{M}{r^2}+\frac{q^2}{r^3}-\frac{\sigma _{d}}{r^2}. \end{aligned}$$
(9)

The terms \(\frac{q^2}{r^3}-\frac{\sigma _{r}}{r^3}\) and \(\frac{q^2}{r^3}-\frac{\sigma _{d}}{r^2}\) in Eq. (9) represent the purely relativistic effect. Equation (9) explains the “exertion” of Kiselev space-time surrounded by radiation and dust on a neutral free-falling massive test body. Interestingly, in a free fall test of a particle from rest at \(r=b\) (for \(q,\sigma _{r},\sigma _{d}\ne 0\)) we would see a bounce back at radius \(R^\mathrm{stop}\). The radius \(R^\mathrm{stop}\) for the Kiselev space-time surrounded by radiation (\(R_r^\mathrm{stop}\)) and dust (\(R_d^\mathrm{stop}\)) could be found to be

$$\begin{aligned} R_r^\mathrm{stop}= & {} \frac{b(q^2-\sigma _{r})}{2Mb-q^2+\sigma _{r}},\end{aligned}$$
(10)
$$\begin{aligned} R_d^\mathrm{stop}= & {} \frac{b~q^2}{(2Mb+b\sigma _{d}-q^2)}, \end{aligned}$$
(11)

where b is the initial position starting from rest of the test particle. \(R^\mathrm{stop}\) is located inside the Cauchy (internal) horizon. One can find in the limit \(b\rightarrow \infty \), \(R_r^\mathrm{stop}\rightarrow (q^2-\sigma _{r})/2M\) for radiation and \(R_d^\mathrm{stop}\rightarrow q^2/(2M-\sigma _{d})\) for dust. The particle in the Kiselev BH surrounded by radiation and dust would emerge in different asymptotically flat regions in a maximal analytic extension. Thus, the particle is physically unstable in maximal analytic extension beyond the internal (Cauchy) horizons of the Kiselev space-time surrounded by radiation and dust.

3 Tidal forces in Kiselev space-time on a neutral body in radial free fall

The equation for the space-like components of the geodesic deviation vector \(\zeta ^{\alpha }\) that describes the distance between two infinitesimally close particles in free fall is given by [7, 8]

$$\begin{aligned} \frac{D^2\zeta ^{\alpha }}{D \tau ^2}-R^{\alpha }_{\beta \gamma \delta } v^{\beta } v^{\gamma } \zeta ^{\delta } = 0, \end{aligned}$$
(12)

where \(v^{\gamma }\) is the unit vector tangent to the geodesic. We use the tetrad basis for radial free-fall reference frames [25],

$$\begin{aligned} \hat{e}^{\alpha }_{\hat{0}}= & {} \left( \frac{E}{f(r)}, -\sqrt{E^2-f(r)},0,0\right) , \end{aligned}$$
(13)
$$\begin{aligned} \hat{e}^{\alpha }_{\hat{1}}= & {} \left( \frac{-\sqrt{E^2-f(r)}}{f(r)},E,0,0\right) , \end{aligned}$$
(14)
$$\begin{aligned} \hat{e}^{\alpha }_{\hat{2}}= & {} r^{-1}(0,0,1,0), \end{aligned}$$
(15)
$$\begin{aligned} \hat{e}^{\alpha }_{\hat{3}}= & {} (r \sin (\theta )^{-1}(0,0,0,1), \end{aligned}$$
(16)

where \((x^0,x^1,x^2,x^3)=(t,r,\theta ,\phi )\). These unit vectors satisfy the following orthonomality condition:

$$\begin{aligned} \hat{e}^{\mu }_{\hat{\alpha }} \hat{e}_{\hat{\gamma }\mu }=\zeta _{\hat{\alpha } \hat{\gamma }}, \end{aligned}$$
(17)

where \(\zeta _{\hat{\alpha } \hat{\gamma }}\) is the Minkowski metric [7]. We have \(\hat{e}^{\alpha }_{\hat{0}}=v^{\alpha }\). The geodesic deviation vector, also called the Jacobi vector, can be written as

$$\begin{aligned} \zeta ^{\alpha }=\hat{e}^{\alpha }_{\hat{\gamma }}\zeta ^{\hat{\gamma }}. \end{aligned}$$
(18)

Here we note that \(\zeta ^{\hat{0}}=0\) [7] and \(\hat{e}^{\alpha }_{\hat{\gamma }}\) are all parallel-transported vectors along the geodesic.

The non-zero independent components of the Riemann tensor in spherically symmetric space-times are

$$\begin{aligned} R^{1}_{010}= & {} \frac{f(r) f''(r)}{2}, \quad R^{1}_{212} = -\frac{r f'(r)}{2}, \\ R^{1}_{313}= & {} -\frac{r f'(r)}{2}\sin ^2\theta \\ R^{2}_{020}= & {} \frac{f(r) f'(r)}{2r}, \quad R^{2}_{323} = \left( 1-f(r)\right) \sin ^2\theta ,\\ R^{3}_{030}= & {} \frac{f(r) f'(r)}{2r}. \end{aligned}$$

Using the above equations in Eq. (12), we find the following equations for radial free-fall tidal forces [12]:

$$\begin{aligned} \ddot{\zeta }^{\hat{1}}= & {} -\frac{f''}{2}\zeta ^{\hat{1}}, \end{aligned}$$
(19)
$$\begin{aligned} \ddot{\zeta }^{\hat{i}}= & {} -\frac{f'}{2r}\zeta ^{\hat{i}}, \end{aligned}$$
(20)

where \(i = 2, 3\). For the aforementioned cases of the Kiselev BH, Eqs. (19) and (20) provided that the tidal forces depend on the mass and electric charge of a BH as well as radiation and dust fluid. Tidal forces are identical to Newtonian tidal forces with the force \(-\frac{f'}{2}\) in the radial direction which can be observed in Eqs. (19) and (20). Further, we will explore Eqs. (19) and (20) for the Kiselev space-time in detail.

3.1 Radial tidal forces

Radial tidal forces vanish at \(r=R^{rtf}_0\) (for radiation) and \(r=R^{rtf}_1\) (for dust) by using Eqs. (19) and (20),

$$\begin{aligned} R^{rtf}_0= & {} \frac{3(q^2-\sigma _{r})}{2M}, \end{aligned}$$
(21)
$$\begin{aligned} R^{rtf}_1= & {} \frac{3q^2}{2M+\sigma _{d}}. \end{aligned}$$
(22)

The maximum value of radial tidal force is at \(R^{rtf}_{0max}\) for radiation and \(R^{rtf}_{1max}\) for dust such that

$$\begin{aligned} R^{rtf}_{0max}= & {} \frac{2(q^2-\sigma _{r})}{M}, \end{aligned}$$
(23)
$$\begin{aligned} R^{rtf}_{1max}= & {} \frac{2q^2}{M+\sigma _{d}}. \end{aligned}$$
(24)

The maximum radial stretching for the above equations is

$$\begin{aligned} \ddot{\zeta }^{1}|_{max}= & {} \frac{M^4}{16(q^2-\sigma _{r})^4}, \end{aligned}$$
(25)
$$\begin{aligned} \ddot{\zeta }^{1}|_{max}= & {} \frac{(M+\sigma _{d})^4}{16q^6}. \end{aligned}$$
(26)

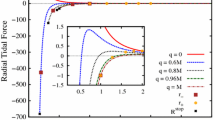
The radial tidal force using Eqs. (21) and (22) for the Kiselev BH surrounded by radiation and dust for their different choices are shown in Figs. 1 and 2. The local maximum of the radial tidal force for radiation is greater than for dust near the singularity.

Fig. 1
figure 1

Radial tidal force for a Kiselev BH surrounded by radiation for chosen values of the radiation parameter, also we have \(q=0.6\) and \(b = 100\)

Full size image
Fig. 2
figure 2

Radial tidal force for a Kiselev BH surrounded by dust for chosen values of the dust parameter, also we have \(q=0.6\), \(M=1\) and \(b = 100\)

Full size image

3.2 Angular tidal forces

The angular tidal forces vanish at

$$\begin{aligned} R^{atf}_0= & {} \frac{q^2-\sigma _r}{M}, \end{aligned}$$
(27)
$$\begin{aligned} R^{atf}_1= & {} \frac{2q^2}{(2M+\sigma _d)}, \end{aligned}$$
(28)

by using Eqs. (2) and (20) for the Kiselev space-time surrounded by radiation and dust, respectively. Also one can find the following conditions from Eqs. (3), (4), (27) and (28):

$$\begin{aligned} r_{-}\le & {} R^{atf}_0 \le r_{+}, \end{aligned}$$
(29)
$$\begin{aligned} r_{-}\le & {} R^{atf}_1 \le r_{+}. \end{aligned}$$
(30)
Fig. 3
figure 3

Angular tidal force for a Kiselev BH surrounded by radiation for chosen values of the radiation parameter, also we have \(q=0.6\), \(M=1\) and \(b = 100\)

Full size image
Fig. 4
figure 4

Angular tidal force for a Kiselev BH surrounded by dust for chosen values of the dust parameter, also we have \(q=0.6\) and \(b = 100\)

Full size image

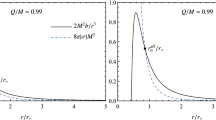
On the basis of these relations, it is pointed out here that the angular tidal forces become zero at some points between the event horizon and the Cauchy horizon. The angular tidal forces for different choices of \(\sigma _r\) and \(\sigma _d\) for a Kiselev BH surrounded by radiation and dust are given in Figs. 3 and 4. The local minimum of the radial tidal force for radiation is greater than for dust near the singularity.

4 Solutions of the geodesic equations for a Kiselev BH

We solve the geodesic deviation Eqs. (19) and (20) and find the geodesic deviation vectors as functions of r for radially free-falling geodesics. Equations (19) and (20) along with \(\frac{\mathrm{d}r}{\mathrm{d}\tau } = -\sqrt{E^2-f(r)}\) lead to the following differential equations:

$$\begin{aligned} (E^2-f(r))\zeta ^{\hat{1}\prime \prime }-\frac{f^{\prime }(r)}{2} \zeta ^{\hat{1}\prime } + \frac{f^{\prime \prime }(r)}{2} \zeta ^{\hat{1}}= & {} 0, \end{aligned}$$
(31)
$$\begin{aligned} (E^2-f(r))\zeta ^{\hat{i}\prime \prime }-\frac{f^{\prime }(r)}{2} \zeta ^{\hat{i}\prime } + \frac{f^{\prime \prime }(r)}{2} \zeta ^{\hat{i}}= & {} 0. \end{aligned}$$
(32)

The general solution of radial component using Eqs. (19) and (20) is given by

$$\begin{aligned} \zeta ^{\hat{1}}(r)=\sqrt{E^2-f(r)}\left( C_1+C_2\int \frac{\mathrm{d}r}{(E^2-f(r))^{3/2}}\right) , \end{aligned}$$
(33)

and similarly for the angular component

$$\begin{aligned} \zeta ^{\hat{i}}(r)=r\left( C_3+C_4\int \frac{\mathrm{d}r}{r^2(E^2-f(r))^{1/2}}\right) , \end{aligned}$$
(34)

where \(C_1\), \(C_2\), \(C_3\) and \(C_4\) are integration constants [25]. Since we are considering two cases of Kiselev space-time i.e. surrounded by radiation and dust. We consider the geodesic corresponding to a body released from rest at \(r=b\). Then the solution to the geodesic deviation equations about the geodesic for the case of radiation is given by

$$\begin{aligned}&\zeta ^{\hat{1}}(r)=\frac{b^3}{M b-q^2+\sigma _{r}}\dot{\zeta }^{\hat{1}}(b)\nonumber \\&\quad \times \sqrt{-\frac{2M}{b}+\frac{q^2}{b^2} -\frac{\sigma _{r}}{b^2}+\frac{2M}{r}-\frac{q^2}{r^2}+\frac{\sigma _{r}}{r^2}}\nonumber \\&\quad +\,\zeta ^{\hat{1}}(b)\left[ \left( \frac{3Mb^2 \sqrt{2Mrb(b-r)-(q^2-\sigma _{r})(b^2-r^2)}(M b-q^2+\sigma _{r}) }{(2Mb-q^2+\sigma _{r})^{5/2}b r}\right) \right. \nonumber \\&\quad \times \left. \arctan \left( \frac{(-2Mb+q^2-\sigma _{r})r+Mb^2}{\sqrt{2Mrb(b-r)-(q^2-\sigma _{r})(b^2-r^2)}\sqrt{2Mb-q^2+\sigma _{r}}}\right) \right. \nonumber \\&\quad + \frac{1}{(2Mb-q^2+\sigma _{r})^{2}(M b-q^2+\sigma _{r})b r} \nonumber \\&\quad \times (M^2(6Mr-3q^2+3\sigma _{r})b^4 \nonumber \\&\quad - 2M^3r^2b^3+10M^2rb^3(q^2-\sigma _{r}) \nonumber \\&\quad -4Mb^3(q^2-\sigma _{r})^2+ (5M^2r^2 \nonumber \\&\quad + 5r(q^2-\sigma _{r})M-2(q^2-\sigma _{r})^2)(q^2-\sigma _{r})b^2\nonumber \\&\quad -4Mr^2(q^2-\sigma _{r})^2b + r^2(q^2-\sigma _{r})^3)]. \end{aligned}$$
(35)

The angular component turns out to be

$$\begin{aligned} \zeta ^{\hat{i}}(r)= & {} \left( \frac{\zeta ^{\hat{i}}(b)}{b}+\frac{2b}{\sqrt{q^2-\sigma _{r}}}\dot{\zeta }^{\hat{i}}(b)\tan ^{-1}\right. \nonumber \\&\left. \times \,\sqrt{\frac{(q^2-\sigma _{r})(b-r)}{2Mbr-(q^2-\sigma _{r})(b+r)}}\right) r. \end{aligned}$$
(36)

Similarly, the solution to the geodesic deviation equations about the geodesic for the case of dust is given by

$$\begin{aligned}&\zeta ^{\hat{1}}(r)=\frac{2b^3}{2M b-2q^2+b\sigma _{d}}\dot{\zeta }^{\hat{1}}(b)\nonumber \\&\quad \times \sqrt{-\frac{2M}{b}+\frac{q^2}{b^2} -\frac{\sigma _{d}}{b}+\frac{2M}{r}-\frac{q^2}{r^2}+\frac{\sigma _{d}}{r}}\nonumber \\&\quad +\,\zeta ^{\hat{1}}(b)\left[ \left( \frac{3b \sqrt{(b-r) ((2M+\sigma _{d})b r-q^2b-q^2r }\left( \left( M+\frac{\sigma _{d}}{2}\right) b-q^2\right) }{\left( M+\frac{\sigma _{d}}{2}\right) ^{-1} (2(M b+\sigma _{d})-q^2 )^{5/2} r}\right) \right. \nonumber \\&\quad \times \left. \tan ^{-1}\left( \frac{\left( M+\frac{\sigma _{d}}{2}\right) (b^2-2br)+rq^2}{\sqrt{(b-r) (((2M+\sigma _{d})r-q^2)b-q^2r ) (((2M+\sigma _{d})b-q^2)}}\right) \right. \nonumber \\&\quad + \left. \frac{1}{\left( 2(M b+\sigma _{d})-q^2\right) ^{2} b r \left( \left( M+\frac{\sigma _{d}}{2}\right) b-q^2\right) }\left( 3\left( M+\frac{\sigma _{d}}{2}\right) ^2b^4\right. \right. \nonumber \\&\quad \times \left. \left. \left( 2(M b+\sigma _{d})-q^2\right) +4q^4 b^3\left( M+\frac{\sigma _{d}}{2}\right) -10q^2 r b^3\left( M+\frac{\sigma _{d}}{2}\right) ^2 \right. \right. \nonumber \\&\quad - \left. 2 r^2 b^3\left( M+\frac{\sigma _{d}}{2}\right) ^3-\left. 2q^4+5rq^2 b^2\left( M+\frac{\sigma _{d}}{2}\right) \right. \right. \nonumber \\&\quad +5r^2q^2 b^2\left( M+\frac{\sigma _{d}}{2}\right) ^2- \left. \left. 4r^2q^4 b\left( M+\frac{\sigma _{d}}{2}\right) +q^6 r^2\right) \right] . \end{aligned}$$
(37)

For a Kiselev BH dust case, the angular component becomes

$$\begin{aligned} \zeta ^{\hat{i}}(r)&=\left( \frac{\zeta ^{\hat{i}}(b)}{b}+\frac{2b^2}{q}\dot{\zeta }^{\hat{i}}(b) \tan ^{-1}\right. \nonumber \\&\times \left. \sqrt{\frac{q^2(b-r)}{2Mbr-bq^2-b r \sigma _{d}-q^2 r}}\right) r. \end{aligned}$$
(38)
Fig. 5
figure 5

Radial components of geodesic deviation for a Kiselev BH surrounded by radiation with IC1 for different values of the radiation parameter with \(M=1\), \(q=0.6\) and \(b = 100\)

Full size image
Fig. 6
figure 6

Radial components of geodesic deviation for a Kiselev BH surrounded by dust with IC1 for different values of the dust parameter with \(M=1\), \(q=0.6\) and \(b = 100\)

Full size image
Fig. 7
figure 7

Radial components of geodesic deviation for a Kiselev BH surrounded by radiation with IC2 for different values of the radiation parameter with \(M=1\), \(q=0.6\) and \(b = 100\)

Full size image
Fig. 8
figure 8

Radial components of geodesic deviation for a Kiselev BH surrounded by dust with IC2 for different values of the dust parameter with \(M=1\), \(q=0.6\) and \(b = 100\)

Full size image

Here, \(\zeta ^{\hat{1}}(b)\) and \(\zeta ^{\hat{i}}(b)\) are the radial and angular components of the initial geodesic deviation vector at \(r=b\) and \(\dot{\zeta }^{\hat{1}}(b)\) and \(\dot{\zeta }^{\hat{i}}(b)\) are the corresponding derivatives with respect to the proper time \(\tau \). Figures 5, 6, 7, 8, 9 and 10 represent the radial and angular components of the geodesic deviation vector of a body in-falling from rest at \(r =b\) towards the BH for different choices of the radiation and dust parameters. We choose the initial condition (IC1) \(\zeta ^{\hat{1}}(b) > 0\), \(\dot{\zeta }^{\hat{1}}(b)=0\) and \(\zeta ^{\hat{i}}(b) > 0\), \(\dot{\zeta }^{\hat{i}}(b)=0\). It represents releasing of a body at rest consisting of dust with no internal motion. On the other hand, we choose the initial condition (IC2) \(\zeta ^{\hat{1}}(b) = 0\), \(\dot{\zeta }^{\hat{1}}(b)>0\) and \(\zeta ^{\hat{i}}(b) = 0\), \(\dot{\zeta }^{\hat{i}}(b)>0\). It corresponds to letting such a body explode from a point at \(r=b\). The behavior of the geodesic deviation vector is almost identical for different values of the radiation and dust parameters until r becomes of the same order as the horizon radius.

Fig. 9
figure 9

Angular components of geodesic deviation for Kiselev BH surrounded by radiation with IC2 for different values of the radiation parameter with \(M=1\), \(q=0.6\) and \(b = 100\)

Full size image
Fig. 10
figure 10

Angular components of geodesic deviation for Kiselev BH surrounded by dust with IC2 for different values of the dust parameter with \(M=1\), \(q=0.6\) and \(b = 100\)

Full size image

In Fig. 5, the radial tidal force for a Kiselev BH surrounded by radiation depends upon the radiation parameter with IC1 i.e. it attains the highest maximum value at \(\sigma _r = 0.3\), while as the radiation parameter decreases the maximum value of radial tidal force also decreases. Also the maximum value is shifting towards BH as the radiation parameter increases. For \(\sigma _r > 0.3\), it becomes unphysical. Figure 6 represents the radial tidal force for a Kiselev BH surrounded by dust for different choices of dust parameter with IC1. It is clear from the figure that the maximum value of the radial tidal force is increasing as the value of the dust parameter increases as well as it shifts towards the BH. It is concluded that the maxima of radial tidal force depend upon the radiation and the dust parameters; they increase for large values of \(\sigma _r\) and \(\sigma _d\). Figures 7 and 8 represent the radial tidal forces for a Kiselev BH surrounded by radiation and dust for different choices of the parameters with IC2. In Fig. 7, maxima of radial tidal force increase for higher values of the radiation parameter and one attains the maximum value at \(\sigma _r=0.3\), and also it is shifted towards the BH as the radiation parameter increases. But in Fig. 8, the maximum value of radial tidal force is the same for all chosen values of the dust parameter. However, the radial tidal force is shifting towards the BH as the dust parameter increases.

Table 1 Location of event horizon for chosen values of the dust parameter
Full size table

The angular tidal force for a Kiselev BH surrounded by radiation and dust with IC1 is similar; as explained in [25], it does not depend upon the radiation and the dust parameters. However, the angular tidal forces with IC2 are discussed in Figs. 9 and 10 for a Kiselev BH surrounded by radiation and dust, respectively. It can be seen in Fig. 9 that the angular tidal force is increasing from \(r=100\) and attains a maximum value at \(r=50\); then it starts to decrease, reflecting the compressing nature of angular component. At some point near the BH, the angular tidal force starts increasing as shown in Fig. 9. Also, it is shifting towards the singularity as the radiation parameter increases. In Fig. 10, the angular tidal forces have the maximum values for \(\sigma _d = 0\), while they decrease for large values of the dust parameter.

Table 2 Location of Cauchy horizon for chosen values of the dust parameter
Full size table
Table 3 Location of event horizon for chosen values of the radiation parameter
Full size table
Table 4 Location of Cauchy horizon for chosen values of the radiation parameter.
Full size table

Tables 1, 2, 3 and 4 represent the location of event horizon and Cauchy horizon for chosen values of the radiation and the dust parameters. Here, we find the location of the event and Cauchy horizons of rtf (Figs. 1, 2), atf (Figs. 3, 4), the radial tidal force with IC1 (Figs. 5, 6) and IC2 (Figs. 7, 8), respectively, and the angular tidal force with IC2 (Figs. 9, 10) for chosen values of the radiation and dust parameter, respectively. It is noted that the radial tidal force (in Figs. 1, 2) and angular tidal force (in Figs. 3, 4) change sign between the event and Cauchy horizons. The event horizon is increasing (away from the singularity) and the Cauchy horizon is decreasing (shifting towards singularity) as the radiation and the dust parameters increase.

5 Conclusion

We investigated the tidal forces of the Kiselev BHs by assuming two special cases, i.e. Kiselev BHs surrounded by radiation and dust. We have observed that the radial tidal forces can change behavior from stretching to compressing for specific choices of the radiation and the dust parameters and the angular tidal forces can only be zero between the event and Cauchy horizons of the BH. It is also mentioned here that the radial and angular tidal forces possess the ability to change sign between the event and Cauchy horizons. The event horizon is increasing (away from the singularity) and the Cauchy horizon is decreasing (shifting towards singularity) as the radiation and the dust parameters increase. Furthermore, the geodesic deviation equations can be solved analytically about a radially free-falling geodesic for a Kiselev BH [25]. The behavior of the geodesic deviation vector for such a geodesic under the influence of the tidal forces is examined. We choose the initial condition IC1, which represents releasing a body at rest consisting of dust with no internal motion and IC2 corresponds to letting such a body explode from a point at \(r=b\). It is pointed out here that the radial tidal forces for a Kiselev BH surrounded by radiation attains the maximum value at \(\sigma _r = 0.3\), as shown in Fig. 5, and it becomes unphysical for \(\sigma _r > 0.3\). Moreover, the maxima of the radial tidal forces for a Kiselev BH surrounded by dust is increasing as well as shifting towards the BH as the dust parameter increases. These results are the agreement with [25]. Hence it is concluded that the radial component of the geodesic deviation vector becomes zero, while the angular component remains finite for certain initial conditions.