Stable exponential cosmological solutions with zero variation of G in the Einstein–Gauss–Bonnet model with a $\Lambda$-term

Abstract

A D-dimensional gravitational model with a Gauss–Bonnet term and the cosmological term $\Lambda$ is considered. By assuming diagonal cosmological metrics, we find, for a certain fine-tuned $\Lambda$, a class of solutions with exponential time dependence of two scale factors, governed by two Hubble-like parameters $H >0$ and $h < 0$, corresponding to factor spaces of dimensions $m > 3$ and $l > 1$, respectively, with $(m,l) \ne (6,6), (7,4), (9,3)$ and $D = 1 + m + l$. Any of these solutions describes an exponential expansion of three-dimensional subspace with Hubble parameter H and zero variation of the effective gravitational constant G. We prove the stability of these solutions in a class of cosmological solutions with diagonal metrics.

1 Introduction

In this paper we consider a D-dimensional gravitational model with Gauss–Bonnet term and the cosmological term $\Lambda$. The so-called Gauss–Bonnet term appeared in string theory as a correction to the (Fradkin–Tseytlin) effective action [1,2,3,4,5].

We note that at present the Einstein–Gauss–Bonnet (EGB) gravitational model and its modifications, see [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27] and the references therein, are intensively studied in cosmology, e.g. for possible explanation of the accelerating expansion of the Universe which follows from supernovae (type Ia) observational data [28,29,30].

Here we deal with the cosmological solutions with diagonal metrics governed by $n >3$ scale factors depending upon one variable, which is the synchronous time variable. We restrict ourselves by the solutions with exponential dependence of scale factors and present a class of such solutions with two scale factors, governed by two Hubble-like parameters $H >0$ and $h < 0$, which correspond to factor spaces of dimensions $m > 3$ and $l > 1$, respectively, with $D = 1 + m + l$ and $(m,l) \ne (6,6), (7,4), (9,3)$. Any of these solutions describes an exponential expansion of 3d subspace with Hubble parameters $H > 0$ [31] and has a constant volume factor of $(m - 3 + l)$-dimensional internal space, which implies zero variation of the effective gravitational constant G either in a Jordan or an Einstein frame [32, 33]; see also [34,35,36] and the references therein. These solutions satisfy the most severe restrictions on variation of G [37].

We study the stability of these solutions in a class of cosmological solutions with diagonal metrics by using results of Refs. [25, 26] (see also approach of Ref. [23]) and show that all solutions, presented here, are stable. It should be noted that two special solutions for $D = 22, 28$ and $\Lambda = 0$ were found earlier in Ref. [22]. In Ref. [25] it was proved that these solutions are stable. Another set of six stable exponential solutions, five in dimensions $D = 7, 8, 9, 13$ and two for $D = 14$, were considered recently in [27].

2 The cosmological model

The action of the model reads

$$\begin{aligned} S = \int _{M} d^{D}z \sqrt{|g|} \{ \alpha _1 (R[g] - 2 \Lambda ) + \alpha _2 \mathcal{L}_2[g] \}, \end{aligned}$$

(2.1)

where $g = g_{MN} dz^{M} \otimes dz^{N}$ is the metric defined on the manifold M, ${\dim M} = D$, $|g| = |\det (g_{MN})|$, $\Lambda$ is the cosmological term, R[g] is the curvature scalar,

$$\begin{aligned} \mathcal{L}_2[g] = R_{MNPQ} R^{MNPQ} - 4 R_{MN} R^{MN} +R^2 \end{aligned}$$

is the standard Gauss–Bonnet term, and $\alpha _1$, $\alpha _2$ are nonzero constants.

We consider the manifold

$$\begin{aligned} M = {\mathbb {R}}\times M_1 \times \cdots \times M_n \end{aligned}$$

(2.2)

with the metric

$$\begin{aligned} g= - \mathrm{d} t \otimes \mathrm{d} t + \sum _{i=1}^{n} B_i e^{2v^i t} \mathrm{d}y^i \otimes \mathrm{d}y^i, \end{aligned}$$

(2.3)

where $B_i > 0$ are arbitrary constants, $i = 1, \ldots , n$, and $M_1, \ldots , M_n$ are one-dimensional manifolds (either ${\mathbb {R}}$ or $S^1$) and $n > 3$.

The equations of motion for the action (2.1) give us the set of polynomial equations [25]

$$\begin{aligned}&G_{ij} v^i v^j + 2 \Lambda - \alpha G_{ijkl} v^i v^j v^k v^l = 0,\nonumber \\&\left[ 2 G_{ij} v^j - \frac{4}{3} \alpha G_{ijkl} v^j v^k v^l \right] \sum _{i=1}^n v^i- \frac{2}{3} G_{ij} v^i v^j + \frac{8}{3} \Lambda = 0,\nonumber \\ \end{aligned}$$

(2.4)

$i = 1,\ldots , n$, where $\alpha = \alpha _2/\alpha _1$. Here

$$\begin{aligned} G_{ij} = \delta _{ij} -1, \quad G_{ijkl} = G_{ij} G_{ik} G_{il} G_{jk} G_{jl} G_{kl} \end{aligned}$$

(2.5)

are, respectively, the components of two metrics on ${\mathbb {R}}^{n}$ [17, 18]. The first one is a 2-metric and the second one is a Finslerian 4-metric. For $n > 3$ we get a set of fourth-order polynomial equations.

We note that for $\Lambda =0$ and $n > 3$ the set of equations (2.4) and (2.5) has an isotropic solution $v^1 = \cdots = v^n = H$ only if $\alpha < 0$ [17, 18]. This solution was generalized in [20] to the case $\Lambda \ne 0$.

It was shown in [17, 18] that there are no more than three different numbers among $v^1,\ldots ,v^n$ when $\Lambda =0$. This is valid also for $\Lambda \ne 0$ if $\sum _{i = 1}^{n} v^i \ne 0$ [26].

3 Solutions with constant G

In this section we present a class of solutions to the set of Eqs. (2.4), (2.5) of the following form:

$$\begin{aligned} v =(\underbrace{H,H,H}_{``our'' \ space},\underbrace{\overbrace{H, \ldots , H}^{m-3}, \overbrace{h, \ldots , h}^{l}}_{internal \ space}). \end{aligned}$$

(3.1)

Here H is the Hubble-like parameter corresponding to an m-dimensional factor space with $m > 3$ and h is the Hubble-like parameter corresponding to an l-dimensional factor space, $l>1$. We split the m-dimensional factor space into a product of two subspaces of dimensions 3 and $m-3$, respectively. The first one is identified with “our” 3d space, while the second one is considered as a subspace of $(m-3 +l)$-dimensional internal space.

We set

$$\begin{aligned} H > 0 \end{aligned}$$

(3.2)

for a description of an accelerated expansion of a three-dimensional subspace (which may describe our Universe) and also put

$$\begin{aligned} (m-3) H + lh = 0 \end{aligned}$$

(3.3)

for a description of a zero variation of the effective gravitational constant G.

We remind the reader that the effective gravitational constant $G = G_{\mathrm{eff}}$ in the Brans–Dicke–Jordan (or simply Jordan) frame [32] (see also [33]) is proportional to the inverse volume scale factor of the internal space; see [34, 36] and the references therein.

Remark

Due to the ansatz (3.1) “our” 3d space expands (isotropically) with Hubble parameter H and the $(m -3)$-dimensional part of internal space expands (isotropically) with the same Hubble parameter H too. To avoid possible puzzles with the separation of these two subspaces, we consider for physical applications (in our epoch) the internal space to be compact, i.e. we put in (2.2) $M_4 = \cdots = M_n = S^1$. We also set the internal scale factors corresponding to the present time $t_0$: $a_j (t_0) = B_j^{1/2} \exp (v^j t_0)$, $j =4, \ldots , n$, [see (2.3)] to be small enough in comparison with the scale factor of “our” space for $t = t_0$: $a (t_0) = B^{1/2} \exp (H t_0)$, where $B_1 = B_2 = B_3 = B$.

According to the ansatz (3.1), the m-dimensional factor space is expanding with the Hubble parameter $H >0$, while the l-dimensional factor space is contracting with the Hubble-like parameter $h < 0$.

It was shown in [26] (for a more general prescription see also [21]) that if we consider the ansatz (3.1) with two Hubble-like parameters H and h with two restrictions imposed,

$$\begin{aligned} m H + lh \ne 0, \quad H \ne h, \end{aligned}$$

(3.4)

then equations (2.4) and (2.5) may be reduced to the following set of equations:

$$\begin{aligned} E= & {} m H^2 + l h^2 - (mH + lh)^2 + 2 \Lambda \nonumber \\&-\, \alpha [m (m-1) (m-2) (m - 3) H^4 \nonumber \\&+\, 4 m (m-1) (m-2) l H^3 h {+} 6 m (m-1) l (l - 1) H^2 h^2 \nonumber \\&+\, 4 m l (l - 1) (l - 2) H h^3 + l (l - 1) (l - 2) (l - 3) h^4]\nonumber \\&= 0, \end{aligned}$$

(3.5)

$$\begin{aligned} Q= & {} (m - 1)(m - 2)H^2 + 2 (m - 1)(l - 1) H h \nonumber \\&+ (l - 1)(l - 2)h^2 = - \frac{1}{2 \alpha }. \end{aligned}$$

(3.6)

The restrictions (3.4) are satisfied for our ansatz (3.2) and (3.3).

Using Eqs. (3.3) and (3.6) we get for $m > 3$ and $l > 1$

$$\begin{aligned} H = l (- 2 \alpha P)^{-1/2}, \quad h = - (m-3) H/l < 0, \end{aligned}$$

(3.7)

where

$$\begin{aligned} P = P(m,l) = (l + m - 3) ( (5 - m) l + 2m - 6) \ne 0 \end{aligned}$$

(3.8)

and

$$\begin{aligned} \alpha P < 0. \end{aligned}$$

(3.9)

The substitution of equation (3.7) into (3.5) gives us

$$\begin{aligned} \Lambda = \Lambda (m,l) = l ( -4 \alpha P)^{-1} ( M - (1/2) P^{-1} R) \end{aligned}$$

(3.10)

where

$$\begin{aligned} M = M(m,l) = (9 - m) l - (m - 3)^2 \end{aligned}$$

(3.11)

and

$$\begin{aligned} R= & {} R(m,l) = - 3 m (m - 1) (m - 2) (m - 3) l^3 \nonumber \\&+ 6 m (m -1) (m - 3)^2 l^2 (l - 1) \nonumber \\&- 4 m (m - 3)^3 l (l-1)(l - 2)\nonumber \\&+ (m - 3)^4 (l - 1) (l - 2)(l - 3). \end{aligned}$$

(3.12)

It may be verified that the equality $P(m,l) = 0$ occurs for $(m,l) = (9,3), (7,4), (6,6)$.

The domains with different signs of $P =P(m,l)$ and $\alpha$ are depicted in Fig. 1, where we enlarged our setup by adding the case $m = 3$, which gives a solution with $h =0$. For a more general solution with $m \ge 3$ and $h =0$ see also [26].

Fig. 1

The domains with different signs of $P =P(m,l)$ and $\alpha$. Red points correspond to $P > 0$ and $\alpha < 0$, while blue points correspond to $P < 0$ and $\alpha > 0$

The equation $P(m,l) > 0$, or $\alpha < 0$, holds in the following cases:

$$\begin{aligned} (m \ge 3; l =2), \quad (m = 3, 4, 5 ; l \ge 3), \nonumber \\ (m = 6,7, 8; l = 3), \quad ( m = 6 ; l = 4, 5). \end{aligned}$$

(3.13)

The equation $P(m,l) < 0$, or $\alpha > 0$, is valid in the following cases:

$$\begin{aligned} (m \ge 10; l \ge 3), \quad (m = 8, 9; l \ge 4), \nonumber \\ (m = 7; l \ge 5), \quad (m = 6 ; l \ge 7). \end{aligned}$$

(3.14)

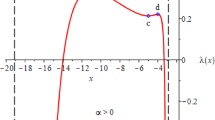
The domains with different signs of $\Lambda = \Lambda (m,l)$ are depicted in Fig. 2.

For fixed $l > 2$ we get the asymptotic relation

$$\begin{aligned} \Lambda (m,l) \sim \frac{l}{8 \alpha (l - 2)} \end{aligned}$$

(3.15)

as $m \rightarrow + \infty$.

For fixed $m \ge 3$, $m \ne 5$, and $m \ne 9$, we obtain

$$\begin{aligned} \Lambda (m,l) \sim \frac{(m - 9) (m+1)}{8 \alpha (m - 5)^2} \end{aligned}$$

(3.16)

as $l \rightarrow + \infty$, while

$$\begin{aligned} \Lambda (5,l) \sim - \frac{3 l^2}{16 \alpha } \rightarrow + \infty \end{aligned}$$

(3.17)

and

$$\begin{aligned} \Lambda (9,l) \sim - \frac{9}{4 \alpha l} \rightarrow 0, \end{aligned}$$

(3.18)

as $l \rightarrow + \infty$.

Fig. 2

The domains with different signs of $\Lambda = \Lambda (m,l)$. Green points correspond to $\Lambda >0$ and brown points indicate $\Lambda < 0$

For $m=11$, $l=16$, and $\alpha = 1$ we get $\Lambda =0$, $H= \frac{1}{\sqrt{15}}$ and $h= -\frac{1}{2 \sqrt{15}}$. This solution was found in [25]. For $m=15$, $l=6$, and $\alpha = 1$ we are led to another solution from [22] with $\Lambda =0$, $H=\frac{1}{6}$ and $h=-\frac{1}{3}$. It was proved in [25] that these two solutions are stable.

4 Stability analysis

Here, as in [25, 26], we deal with exponential solutions (2.3) with a non-static volume factor, which is proportional to $\exp (\sum _{i = 1}^{n} v^i t)$, i.e. we put

$$\begin{aligned} K = K(v) = \sum _{i = 1}^{n} v^i \ne 0. \end{aligned}$$

(4.1)

We set the following restriction:

$$\begin{aligned} (\mathrm{R }) \quad \det (L_{ij}(v)) \ne 0 \end{aligned}$$

(4.2)

on the matrix

$$\begin{aligned} L =(L_{ij}(v)) = (2 G_{ij} - 4 \alpha G_{ijks} v^k v^s). \end{aligned}$$

(4.3)

For a general cosmological setup with the metric

$$\begin{aligned} g= - \mathrm{d}t \otimes \mathrm{d}t + \sum _{i=1}^{n} e^{2\beta ^i(t)} \mathrm{d}y^i \otimes \mathrm{d}y^i, \end{aligned}$$

(4.4)

we have the (mixed) set of algebraic and differential equations [17, 18]

$$\begin{aligned} E= & {} G_{ij} h^i h^j + 2 \Lambda - \alpha G_{ijkl} h^i h^j h^k h^l = 0, \end{aligned}$$

(4.5)

$$\begin{aligned} Y_i= & {} \frac{\mathrm{d} L_i}{\mathrm{d}t} + \left( \sum _{j=1}^n h^j\right) L_i - \frac{2}{3} (G_{sj} h^s h^j - 4 \Lambda ) = 0, \end{aligned}$$

(4.6)

where $h^i = \dot{\beta }^i$,

$$\begin{aligned} L_i = L_i(h) = 2 G_{ij} h^j - \frac{4}{3} \alpha G_{ijkl} h^j h^k h^l , \end{aligned}$$

(4.7)

$i = 1,\ldots , n$.

It was proved in [26] that a fixed point solution $(h^i(t)) = (v^i)$ ($i = 1, \ldots , n$; $n >3$) to Eqs. (4.5) and (4.6) obeying the restrictions (4.1) and (4.2) is stable under perturbations

$$\begin{aligned} h^i(t) = v^i + \delta h^i(t), \end{aligned}$$

(4.8)

$i = 1,\ldots , n$ (as $t \rightarrow + \infty$), if

$$\begin{aligned} K(v) = \sum _{k = 1}^{n} v^k > 0, \end{aligned}$$

(4.9)

and it is unstable (as $t \rightarrow + \infty$) if $K(v) = \sum _{k = 1}^{n} v^k < 0$.

We remind the reader that the perturbations $\delta h^i$ obey (in linear approximation) the following set of equations [25, 26]:

$$\begin{aligned} C_i(v) \delta h^i= & {} 0, \end{aligned}$$

(4.10)

$$\begin{aligned} L_{ij}(v) \delta \dot{h}^j= & {} B_{ij}(v) \delta h^j, \end{aligned}$$

(4.11)

where

$$\begin{aligned} C_i(v)= & {} 2 v_{i} - 4 \alpha G_{ijks} v^j v^k v^s, \end{aligned}$$

(4.12)

$$\begin{aligned} L_{ij}(v)= & {} 2 G_{ij} - 4 \alpha G_{ijks} v^k v^s, \end{aligned}$$

(4.13)

$$\begin{aligned} B_{ij}(v)= & {} - \left( \sum _{k = 1}^n v^k\right) L_{ij}(v) - L_i(v) + \frac{4}{3} v_{j}, \end{aligned}$$

(4.14)

$v_i = G_{ij} v^j$, $L_i(v) = 2 v_{i} - \frac{4}{3} \alpha G_{ijks} v^j v^k v^s$ and $i,j,k,s = 1, \ldots , n$.

It was proved in Ref. [26] that the set of linear equations on perturbations (4.10) and (4.11) has the following solution:

$$\begin{aligned}&\delta h^i = A^i \exp ( - K(v) t ), \end{aligned}$$

(4.15)

$$\begin{aligned}&\sum _{i =1}^{n} C_i(v) A^i =0, \end{aligned}$$

(4.16)

$i = 1, \ldots , n$, when the restrictions (4.1) and (4.2) are imposed.

It was shown in [26] that for the vector v from (3.1), obeying Eq. (3.4), the matrix L has a block-diagonal form,

$$\begin{aligned} (L_{ij}) = \mathrm{diag}(L_{\mu \nu }, L_{\alpha \beta } ), \end{aligned}$$

(4.17)

where

$$\begin{aligned} L_{\mu \nu }= & {} G_{\mu \nu } (2 + 4 \alpha S_{HH}), \end{aligned}$$

(4.18)

$$\begin{aligned} L_{\alpha \beta }= & {} G_{\alpha \beta } (2 + 4 \alpha S_{hh}), \end{aligned}$$

(4.19)

and

$$\begin{aligned} S_{HH}= & {} (m-2)(m -3) H^2 + 2(m-2)lHh + l(l - 1)h^2 , \nonumber \\ \end{aligned}$$

(4.20)

$$\begin{aligned} S_{hh}= & {} m(m-1)H^2 + 2m(l - 2)Hh+ (l- 2)(l- 3)h^2. \nonumber \\ \end{aligned}$$

(4.21)

The matrix (4.17) is invertible if and only if $m > 1$, $l > 1$, and

$$\begin{aligned} S_{HH}\ne & {} - \frac{1}{2 \alpha }, \end{aligned}$$

(4.22)

$$\begin{aligned} S_{hh}\ne & {} - \frac{1}{2 \alpha }, \end{aligned}$$

(4.23)

since the matrices $(G_{\mu \nu }) = (\delta _{\mu \nu } -1 )$ and $(G_{\alpha \beta }) = (\delta _{\alpha \beta } - 1)$ are invertible only if $m > 1$ and $l > 1$.

The first condition (4.9) is obeyed for the solutions under consideration since due to (3.3) we get $K(v) = 3H > 0$ [26].

Now, let us prove that inequalities (4.22) and (4.23) are satisfied.

Let us suppose that (4.22) is not satisfied, i.e. $S_{HH} = - \frac{1}{2 \alpha }$. Then using (3.6) we get

$$\begin{aligned} S_{HH} - Q = - 2 (H - h) ((m-2) H + (l -1) h ) = 0,\nonumber \\ \end{aligned}$$

(4.24)

which implies, due to $H - h \ne 0$ [see (3.7)],

$$\begin{aligned} (m-2) H + (l -1) h = 0. \end{aligned}$$

(4.25)

The substitution of $h = - (m - 3)H/l$ into (4.25) gives us $(l + m - 3) H = 0$, which is in contradiction with the inequalities $m > 3$, $l > 1$ and $H > 0$. This contradiction proves the inequality (4.22).

Now we suppose that (4.23) is not valid, i.e. $S_{hh} = - \frac{1}{2 \alpha }$. Then using (3.6) we get

$$\begin{aligned} S_{hh} - Q = - 2 (h - H) ((l - 2) h + (m -1) H ) = 0, \end{aligned}$$

(4.26)

which implies due to $H - h \ne 0$

$$\begin{aligned} (l - 2) h + (m -1) H = 0. \end{aligned}$$

(4.27)

Substituting $h = - (m - 3)H/l$ into (4.27) implies the equation $2 ( l + m - 3) H = 0$, which contradicts the equations $m > 3$, $l > 1$, and $H > 0$. The contradiction proves the inequality (4.23).

Thus, we proved that Eqs. (4.22) and (4.23) are valid, hence the restrictions (4.2) are satisfied for our solutions. This completes the proof of the stability of the solutions under consideration.

5 Conclusions

We have considered the D-dimensional Einstein–Gauss–Bonnet (EGB) model with the $\Lambda$-term and two constants $\alpha _1$ and $\alpha _2$. By using the ansatz with diagonal cosmological metrics, we have found, for certain $\Lambda = \Lambda (m,l)$ and $\alpha = \alpha _2 / \alpha _1$, a class of solutions with exponential time dependence of two scale factors, governed by two Hubble-like parameters $H >0$ and $h < 0$, corresponding to submanifolds of dimensions $m > 3$ and $l > 1$, respectively, with $(m,l) \ne (6,6), (7,4), (9,3)$ and $D = 1 + m + l$. Here $m > 3$ is the dimension of the expanding subspace and $l > 1$ is the dimension of the contracting one.

Any of these solutions describes an exponential expansion of “our” three-dimensional subspace with the Hubble parameter $H > 0$ and anisotropic behavior of $(m-3+ l)$-dimensional internal space: expanding in $(m-3)$ dimensions (with Hubble-like parameter H) and contracting in l dimensions (with Hubble-like parameter $h < 0$). Each solution has a constant volume factor of internal space and hence it describes a zero variation of the effective gravitational constant G. By using the results of Ref. [26] we have proved that all these solutions are stable as $t \rightarrow + \infty$.