1 Introduction

Increasing attention has recently been devoted to black hole physics and the connection with both string theory and thermodynamical models. Particularly, many studies focus on the relationship between the gravity theories and the thermodynamical physics using Anti-de Sitter geometries. In this context, the laws of thermodynamics have been translated into laws of black holes [2–6]. Hence, the phase transitions along with various critical phenomena for AdS black holes have been extensively analyzed in the framework of different approaches [7–11]. Also, the equations of state describing rotating black holes have been interpreted by confronting them to some known thermodynamical ones, like the van der Waals gas [12–19]. Emphasis has also been put on the free energy and its behavior in the fixed charge ensemble. These studies shed some light on the thermodynamical criticality, free energy, first order phase transition, and on understanding of the behaviors near the critical points with respect to the liquid–gas systems.

In this context, very recently the thermodynamics and thermodynamical geometry for five-dimensional AdS black holes in a type IIB superstring background known as \(AdS_5\times S^5\) [20–22] have been scrutinized. This geometry has been studied in many places in connection with the AdS/CFT correspondence providing a very useful framework to investigate such a geometry via the equivalence between gravitational theories in d-dimensional AdS space and conformal field theories (CFT) in a \((d-1)\)-dimensional boundary of such AdS spaces [23–27]. The number of colors has been interpreted as a thermodynamical variable in these works. In this respect, various thermodynamical quantities have been computed and the stability problem of \(AdS_5\times S^5\) black holes was analyzed by identifying the cosmological constant in the bulk with the number of colors.

All these recent inspiring works on asymptotically Ad\(S_4\) black holes in M-theory [28–32] motivate us to study the thermodynamics and thermodynamical geometry of \(AdS_{4}\times S^{7}\), from the physics of M2-branes, where we interpret the number of M2-branes as a thermodynamical variable as in [1]. We then discuss the stability of such solutions and examine the corresponding first phase transition by analyzing various relevant quantities including the chemical potential, free energy, and heat capacities. Besides, we also evaluate the thermodynamical curvatures from the Weinhold, Ruppeiner, and Quevedo metrics for M2-branes geometry and study the corresponding stability problems via their singularities.

The paper is arranged as follows: In Sect. 2 we discuss the thermodynamical properties and stability of the charged black holes in \(AdS_{4}\times S^{7}\), by assuming the number of M2-branes as a thermodynamical variable. Sections 3 and 4 are devoted to showing that similar results are recovered through thermodynamical curvature calculations associated with the Weinhold, Ruppeiner, and Quevedo metrics. Our conclusion is drawn in Sect. 5.

2 Thermodynamics of black holes in \(AdS_4\times S^7\) space

In this section, we investigate the phase transition of the Reissner–Nordstrom-AdS black holes in M-theory in the presence of solitonic objects. Here we recall that, at low energy, M-theory describes an eleven-dimensional supergravity. This theory, as proposed by Witten, can produce some nonperturbative limits of superstring models after its compactification on particular geometries [33].

First, let us consider the case of M2-brane. The corresponding geometry is \(AdS_4\times S^7\). In such a geometric background, the line element of the black M2-brane metric is given by [34, 36]

$$\begin{aligned} \mathrm{d}s^2= \frac{r^4}{L^4}\left( -f \mathrm{d}t^2+\sum _{i=1}^2 \mathrm{d}x_i^2 \right) +\frac{L^2}{r^2}f^{-1}\mathrm{d}r^2+ L^2 \mathrm{d}\varOmega _7^2,\nonumber \\ \end{aligned}$$
(1)

where \(\mathrm{d}\varOmega _7^2\) is the metric of seven-dimensional sphere with unit radius. In this solution, the metric function reads as follows:

$$\begin{aligned} f=1-\frac{m}{r}+\frac{q^2}{r^2}+\frac{r^2}{L^2}, \end{aligned}$$
(2)

where L is the AdS radius and m and q are integration constants. The cosmological constant is \(\varLambda = -6/L^2\). Form M-theory point of view, the eleven-dimensional spacetime in Eq. (1) can be interpreted as the near horizon geometry of N coincident configurations of M2-branes. In this background, the AdS radius L is linked to the M2-brane number N via the relation [1, 34, 37, 38]

$$\begin{aligned} L^9={N^3/2} \frac{\kappa _{11}^2 \sqrt{2}}{\pi ^5}. \end{aligned}$$
(3)

According to the proposition reported in [1, 20–22], we consider the cosmological constant as the number of M2-branes in the M-theory background and its conjugate quantity as the associated chemical potential.

The event horizon \(r_h\) of the corresponding black hole is determined by solving the equation \(f = 0\). From Eq. (2), the mass of the black hole can be written asFootnote 1

$$\begin{aligned} M=\frac{m \omega _2}{8 \pi G_4}=\frac{r \omega _2 (L^2+r^2)}{8 \pi G_4 L^2}+\frac{2 \pi G_4 Q^2}{r \omega _2}, \end{aligned}$$
(4)

where the charge of the black hole Q is related to the constant q through the formula

$$\begin{aligned} Q=\frac{\omega _2}{4\pi G_4}q. \end{aligned}$$
(5)

The Bekenstein–Hawking entropy formula of the black hole reads

$$\begin{aligned} S=\left. \frac{A}{4 G_4}\right. =\frac{\omega _2 r^2}{4 G_4}. \end{aligned}$$
(6)

Here we recall that the four-dimensional Newton gravitational constant is related to the eleven-dimensional one by

$$\begin{aligned} G_4=\frac{3 G_{11} }{2 \pi \omega _{2}L^{4}}.\, \end{aligned}$$
(7)

For simplicity reasons, we use \(G_{11}=\kappa _{11}=1\) in the remainder of the paper. In this way, the black hole mass can be expressed as a function of N and S,

$$\begin{aligned} M(S,N,Q)=\frac{3 \root 9 \of {2} \pi ^{11/9} \root 3 \of {N} Q^2+3 \root 3 \of {\pi } S^2+8 \root 3 \of {2} N S}{4\ 2^{13/18} \sqrt{3} \pi ^{11/18} N^{2/3} \sqrt{S}}.\nonumber \\ \end{aligned}$$
(8)

Using the standard thermodynamic relation \(\mathrm{d}M = T\mathrm{d}S + \mu \, \mathrm{d}N+ \varPhi \, \mathrm{d}Q\), the corresponding temperature takes the following form:

$$\begin{aligned} T= & {} \left. \frac{\partial M(S,N,Q)}{\partial S}\right| _N \nonumber \\= & {} \frac{-3 \root 9 \of {2}\pi ^{11/9} \root 3 \of {N} Q^2+9 \root 3 \of {\pi } S^2+8 \root 3 \of {2} N S}{8\ 2^{13/18} \sqrt{3} \pi ^{11/18} N^{2/3} S^{3/2}}. \end{aligned}$$
(9)

This quantity can be identified with the Hawking temperature of the black hole. Using Eq. (8) the chemical potential \(\mu \) conjugate to the number of M2-branes is given by

$$\begin{aligned} \mu= & {} \left. \frac{\partial M_4(S,N,Q)}{\partial N}\right| _S \nonumber \\= & {} \frac{-3 \root 9 \of {2} \pi ^{11/9} \root 3 \of {N} Q^2-6 \root 3 \of {\pi } S^2+8 \root 3 \of {2} N S}{12\ 2^{13/18} \sqrt{3} \pi ^{11/18} N^{5/3} \sqrt{S}}. \end{aligned}$$
(10)

It defines the measure of the energy cost to the system when one increases the variable N.

The electric potential reads

$$\begin{aligned} \varPhi =\left. \frac{\partial M(S,N,Q)}{\partial Q}\right| _S=\frac{\sqrt{3} \pi ^{11/18} Q}{2\ 2^{11/18} \root 3 \of {N} \sqrt{S}}. \end{aligned}$$
(11)

In terms of these quantities, the Helmholtz free energy is expressed by

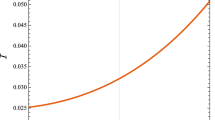
$$\begin{aligned} {\mathscr {F}}(S,N,Q)= & {} M(S,N,Q)-T\ S\nonumber \\= & {} \frac{9 \root 9 \of {2} \pi ^{11/9} \root 3 \of {N} Q^2-3 \root 3 \of {\pi } S^2+8 \root 3 \of {2} N S}{8\ 2^{13/18} \sqrt{3}\pi ^{11/18} N^{2/3} \sqrt{S}}.\nonumber \\ \end{aligned}$$
(12)

Having calculated the relevant thermodynamical quantities, we turn now to the analysis of the corresponding phase transition. For this purpose, we study the variation of the Hawking temperature as a function of the entropy.

Fig. 1
figure 1

The temperature as a function of the entropy S, with \(N=3\)

Full size image

This variation plotted in Fig. 1 shows that the Hawking temperature is a monotonic function if \(Q>Q_c\), but when \(Q\le Q_c\), it represents a critical point to be determined by solving the system

$$\begin{aligned} \left( \frac{\partial T}{\partial S}\right) _{Q_c}=\left( \frac{\partial ^2 T}{\partial S^2}\right) _{Q_c}=0. \end{aligned}$$
(13)

The solution of this equation is easily derived,

$$\begin{aligned} Q_c=\frac{4\ 2^{5/18} N^{5/6}}{9 \pi ^{7/9}},\quad S_c=\frac{4 }{9}\root 3 \of {\frac{2}{\pi }} N. \end{aligned}$$
(14)

In Fig. 2, we illustrate the Helmholtz free energy as a function of the Hawking temperature T for some fixed values of N.

Fig. 2
figure 2

The free energy as a function of the temperature T

Full size image

The sign change of the free energy indicates the Hawking–Page phase transition, which occurs at

$$\begin{aligned} S_{\mathrm{HP}}=\frac{\root 18 \of {2} \left( 4\ 2^{5/18} N+\sqrt{16\ 2^{5/9} N^2+27 \pi ^{14/9} \root 3 \of {N} Q^2}\right) }{3 \root 3 \of {\pi }}.\nonumber \\ \end{aligned}$$
(15)

It can be seen that we have the “wallow tail” a type signal for the first phase transition, between a small black hole and a large one.

To study the phase transition, we vary the chemical potential in terms of the entropy, and we plot in Fig. 3 such a variation for a fixed value of N.

Fig. 3
figure 3

The chemical potential \(\mu \) as a function of the entropy for \(N=3\)

Full size image

From the figure we can see that he chemical potential becomes positive when the entropy lies within the interval \(S_-\le S\le S_+\) with

$$\begin{aligned} S_{\pm }=\frac{4 \root 3 \of {2} N\pm 2^{5/9} \sqrt{8\ 2^{5/9} N^2-9 \pi ^{14/9} \root 3 \of {N} Q^2}}{6 \root 3 \of {\pi }}. \end{aligned}$$
(16)

Furthermore, we also plot, in Fig. 4, the behavior of the chemical potential as a function of temperature T for a fixed N.

Fig. 4
figure 4

The chemical potential \(\mu \) as a function of the temperature T, with \(N=3\)

Full size image

From Fig. 4 we can see that there exists a multivalued region, which just corresponds to the unstable region of the black hole with a negative heat capacity (red line in Fig. 1).

To illustrate the effect of the number of the M2-branes, we discuss the behavior of the chemical potential \(\mu \) in terms of such a variable as shown in Fig. 5.

Fig. 5
figure 5

The chemical potential \(\mu \) as a function of N; we have set \(S_4=4\)

Full size image

We clearly see that the chemical potential \(\mu \) presents a maximum at

$$\begin{aligned} N_{\mathrm{max}}= & {} \frac{3 \root 3 \of {\pi }}{16 S^{3/2}}\left[ \frac{2 \pi ^2 Q^6}{\root 3 \of {15 Q^6 S^{5/2}+\sqrt{225 Q^{12} S^5-4 \pi ^3 Q^{18}}}}\right. \nonumber \\&+\,\root 3 \of {2} \pi \root 3 \of {15 Q^6 S^{5/2}+\sqrt{225 Q^{12} S^5-4 \pi ^3 Q^{18}}}\nonumber \\&\left. +\,5\ 2^{2/3} S^{5/2}\right] . \end{aligned}$$
(17)

We remark that this is quite different from the classical gas having a negative chemical potential. In the case where the chemical potential approaches zero and becomes positive, quantum effects should be considered and become relevant in the discussion [22].

In the subsequent sections, we consider thermodynamical geometry of the M2-branes black holes in the extended phase space and study the stability problem when either N or the charge is held fixed.

3 Geothermodynamics and phase transition of charged AdS black holes with fixed N case

There are several approaches to probe the critical behavior and obtain phase transition points of black holes: a standard method is based on the study of the heat capacity. It was pointed out that roots and divergences of the heat capacity represent phase transition points. In other words, roots and divergences of the heat capacity signal that the system may undergo a phase transition. Another important property of the heat capacity appears in the investigation of the thermal stability. Systems with positive heat capacity are described by thermally stable states. Consequently, the stability conditions occur when the sign of heat capacity changes.

Recently another method, dubbed geothermodynamics, has received increasing interest. This approach relies on differential geometry tools for studying the critical behavior. More specifically, by employing the thermodynamical potential and its corresponding extensive parameters, one can construct the phase space. The phase transition occurs at points where the Ricci scalar in the constructed metric is singular.

Here we discuss the geothermodynamics (GDM) of the charged AdS black holes in \(AdS_{4}\times S^{7}\): Our analysis will focus on the singular limits of certain thermodynamical quantities, including the heat capacities and scalar curvatures, which are relevant in the study of the stability of such black hole solutions.

To do this, the number of branes N should be held fixed to consider the thermodynamics in the canonical ensemble. For a fixed N, the heat capacities for M2-branes AdS black holes are given, respectively, by

$$\begin{aligned}&C_{Q,N}=T\left( \frac{\partial S}{\partial T}\right) _{Q,N},\nonumber \\&\quad = T_4\left( \frac{8 \root 3 \of {2} N+18 \root 3 \of {\pi } S}{-3 \root 9 \of {2} \pi ^{11/9} \root 3 \of {N} Q^2+9 \root 3 \of {\pi } S^2+8 \root 3 \of {2} N S}-\frac{3}{2 S}\right) ^{-1},\nonumber \\ \end{aligned}$$
(18)
$$\begin{aligned} C_{\varPhi ,N}= & {} T\left( \frac{\partial S}{\partial T}\right) _{\varPhi ,N}, \nonumber \\= & {} \left( \frac{9 S}{-3 \root 9 \of {2} \pi ^{8/9} \root 3 \of {N} Q^2+9 S^2+8 \root 3 \of {\frac{2}{\pi }} N S}-\frac{1}{2 S}\right) ^{-1}.\nonumber \\ \end{aligned}$$
(19)

In the canonical ensemble with fixed N, a critical point exists and is given by Eq. (14). The behavior of \(C_{\varPhi ,N}\) as a function of the entropy is plotted in Fig. 6.

Fig. 6
figure 6

The heat capacity in the case with a fixed \(N = 3\) as a function of the entropy S for \(Q=0.5\ Q_c\)

Full size image

From the figure we can see that \(C_{\varPhi ,N }\) presents two singularities at

$$\begin{aligned} \nonumber S_{\varPhi ,\pm }=\frac{1}{9} \left( 4 \root 3 \of {\frac{2}{\pi }} N\pm \sqrt{16 \left( \frac{2}{\pi }\right) ^{2/3} N^2-27 \root 9 \of {2} \pi ^{8/9} \root 3 \of {N} Q^2}\right) .\\ \end{aligned}$$
(20)

The heat capacity \(C_{Q,N}\) is plotted in Fig. 7.

Fig. 7
figure 7

The heat capacity in the case with a fixed \(N = 3\) as a function of the entropy S

Full size image

We see that it is consistent with the temperature shown in Fig. 1 (red line). For small and large black hole the heat capacity is always positive, while for the intermediate black holes it is negative when Q is less than the critical value, whereas it is always positive in the case when the charge is larger than the critical point.

The heat capacity \(C_{Q,N}\) in the critical case has two singularities at

$$\begin{aligned} S_{Q.\pm }=\frac{8 \root 3 \of {2} N\pm 2 \sqrt{16\ 2^{2/3} N^2-81 \root 9 \of {2} \pi ^{14/9} \root 3 \of {N} Q^2}}{18 \root 3 \of {\pi }}. \end{aligned}$$
(21)

These two singularities coincide for \(Q=Q_c\), hence (21) reduces to

$$\begin{aligned} S_Q=\frac{4}{9} \root 3 \of {\frac{2}{\pi }} \left( \sqrt{N^2-3\ 3^{2/3} \root 3 \of {N}}+N\right) . \end{aligned}$$
(22)

We turn now our attention to the thermodynamical geometry of the black hole to see whether the thermodynamical curvature can reveal the singularities of these two specific heats. Since the GDM approach fails to explain the correspondence between phase transitions and singularities of the scalar curvature for phantom Reissner–Nordstrom AdS black holes, as reported in [39–42], it is legitimate and well justified hereafter to check the thermodynamic geometry of black holes metric by metric and to see the divergent points of the specific heat correspond exactly to the singularities derived by GTD method.

The Weinhold metric [43] is defined as the second derivative of the internal energy with respect to the entropy and other extensive quantities in the energy representation, while the Ruppeiner metric [44] is related to the Weinhold metric by a conformal factor of the temperature [45]; we have

$$\begin{aligned} \mathrm{d}s_R^2=\frac{1}{T} \mathrm{d}s_W^2 \end{aligned}$$
(23)

Notice that the Weinhold and Ruppeiner metrics, which depend on the choice of thermodynamic potentials, are not Legendre invariant. The Quevedo metric defined as [46–49]

$$\begin{aligned} g= & {} \left( E^c\frac{\partial \phi }{\partial E^c}\right) \left( \eta _{ab}\delta _{bc}\frac{\partial ^2 \phi }{\partial E^c \partial E^d}\right) ,\nonumber \\ \eta _{cd}= & {} \hbox {diag}(-1,1,\ldots ,1). \end{aligned}$$
(24)

It is Legendre invariant. \(\phi \) denotes the thermodynamic potential, \(E^a\) and \(I^a\) represent, respectively, the set of extensive variables and the set of the intensive variables, while \(a=1,2,\ldots ,n\).

In this context we can evaluate the thermodynamical curvature of the black hole. For the Weinhold metric,

$$\begin{aligned} g^W=\left( \begin{array}{cc}M_{SS} &{}\quad M_{S Q} \\ M_{Q S} &{}\quad M_{Q Q}\end{array}\right) , \end{aligned}$$
(25)

where \(M_{ij}\) stands for \(\partial ^2 M/ \partial x^i\partial x^j\), and \(x^1=S\), \(x^2=Q\); we can see that its scalar curvature is derived via a direct calculation, simply by substituting Eq. (8) into Eq. (25),

$$\begin{aligned} R_1^W=-\frac{64 \root 18 \of {2} \sqrt{3} \pi ^{11/18} N^{5/3} S^{3/2}}{\left( 3 \root 9 \of {2} \pi ^{11/9} \root 3 \of {N} Q^2+9 \root 3 \of {\pi } S^2-8 \root 3 \of {2} N S\right) ^2}. \end{aligned}$$
(26)

The Ruppeiner metric, deduced from Eq. (23), is given by

$$\begin{aligned} g^R=\frac{1}{T}\left( \begin{array}{ll} M_{SS} &{}\quad M_{SQ} \\ M_{Q S} &{}\quad M_{QQ} \end{array}\right) , \end{aligned}$$
(27)

with the following curvature:

$$\begin{aligned} R_1^R=\frac{A_1}{B_2} \end{aligned}$$
(28)

where

$$\begin{aligned} A_1= & {} 162 \pi ^{2/3}S[-486\ 2^{4/9} \pi ^7 N^2 Q^{12}\nonumber \\&+\,6480\ 2^{2/3} \pi ^{52/9} N^{8/3} Q^{10}S+1296\ 2^{2/9} \pi ^{2/3} N^{4/3} S^9\nonumber \\&\times \,(896\ 2^{5/9} N^{5/3}-351 \pi ^{14/9} Q^2)\nonumber \\&-\, 432 \root 3 \of {2} \pi ^{41/9} N^{5/3} Q^8 S^2(80\ 2^{5/9} N^{5/3}-9 \pi ^{14/9}Q^2)\nonumber \\&+\, 144 \root 9 \of {2} \pi ^{10/3} N^{7/3} Q^6 S^3 (1280 N^{5/3}-261\ 2^{4/9} \pi ^{14/9} Q^2)\nonumber \\&+\, 18 \root 3 \of {\pi } N^{2/3} S^8 (90112 \root 9 \of {2} N^{10/3}+5103 \pi ^{28/9}Q^4\nonumber \\&-\,62208\ 2^{5/9}\pi ^{14/9} N^{5/3} Q^2)-96 \root 3 \of {2} N^{5/3} S^7\nonumber \\&\times \,(-4096 \root 9 \of {2} N^{10/3}-3645 \pi ^{28/9} Q^4\nonumber \\&+\,8640\ 2^{5/9} \pi ^{14/9} N^{5/3} Q^2)+48 \root 9 \of {2} \pi ^{11/9} N Q^2 S^6\nonumber \\&\times \,(-4096 \root 9 \of {2} N^{10/3}-729 \pi ^{28/9} Q^4 +5184\ 2^{5/9} \pi ^{14/9} N^{5/3} Q^2)\nonumber \\&- 32 \pi ^{8/9} N^2 Q^2 S^5 (-4096\ 2^{5/9} N^{10/3} +243\ 2^{4/9} \pi ^{28/9} Q^4\nonumber \\&+\,8064 \pi ^{14/9} N^{5/3} Q^2)+6\ 2^{2/9} \pi ^{19/9} N^{4/3} Q^4 S^4\nonumber \\&\times \,(-40960 \root 9 \of {2} N^{10/3}-729 \pi ^{28/9} Q^4\nonumber \\&+\,20736\ 2^{5/9} \pi ^{14/9} N^{5/3} Q^2)\nonumber \\&-\, 59049\ 2^{7/9} \pi ^{5/3} S^{12}-104976 \root 9 \of {2} \pi ^{4/3} N S^{11}\nonumber \\&+\,559872\ 2^{4/9} \pi N^2 S^{10}],\end{aligned}$$
(29)
$$\begin{aligned} B_1= & {} (3 \root 9 \of {2} \pi ^{11/9} \root 3 \of {N} Q^2-9 \root 3 \of {\pi } S^2-8 \root 3 \of {2} N S)^3 \nonumber \\&\times (-18 \root 9 \of {2} \pi ^{22/9} N^{2/3} Q^4 +96 \root 3 \of {2} \pi ^{11/9} N^{4/3} Q^2 S\nonumber \\&+81\ 2^{8/9} \pi ^{2/3} S^4128\ 2^{5/9} N^2 S^2)^2. \end{aligned}$$
(30)

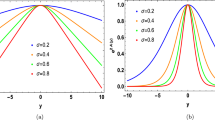
In Fig. 8 we plot the scalar curvatures of the Weinhold and Ruppeiner metrics where the charge is less than the critical one.

Fig. 8
figure 8

The scalar curvatures of Weinhold and Ruppeiner metrics vs. entropy with \(N = 3\) and \(Q=0.5\ Q_c\)

Full size image

From Fig. 8 we see that the scalar curvatures of the Weinhold and the Ruppeiner metrics reveal both the same singularities \(S_{\phi ,\pm }\) as those of the heat capacity \(C_{\varPhi ,N}\). Also, the Ruppeiner metric presents an additional singularity in \(S_0\) where the black hole is extremal, \(T=0\). Hence both Weinhold and Ruppeiner metrics are able to show a phase transition of the black hole in the fixed \(\varPhi \) ensemble.

As to the Quevedo metric, it is defined by

$$\begin{aligned} g^Q=(S\, T+ Q\, \varPhi )\left( \begin{array}{cc}-M_{SS} &{}\quad 0 \\ 0 &{}\quad M_{Q Q}\end{array}\right) . \end{aligned}$$
(31)

Using Eqs. (8), (9) and Eq. (31) we show that the scalar curvature reads

$$\begin{aligned} R_1^Q=\frac{A_2}{B_2} \end{aligned}$$
(32)

with

$$\begin{aligned} \nonumber A_2= & {} -768 \root 9 \of {2} \pi ^{11/9} N^{4/3} S \left[ 4374 \root 9 \of {2} \pi ^{44/9} N^{4/3} Q^8\right. \\ \nonumber&+\left. 131220 \pi ^4 N Q^6 S^2+19440 \root 3 \of {2} \pi ^{11/3} N^2 Q^6 S\right. \\ \nonumber&+\, 104976\ 2^{8/9} \pi ^{28/9} N^{2/3} Q^4 S^4\\&+\,85536\ 2^{2/9} \pi ^{25/9} N^{5/3} Q^4 S^3\nonumber \\ \nonumber&+\, 17280\ 2^{5/9} \pi ^{22/9} N^{8/3} Q^4 S^2\\&+\, 21870\ 2^{7/9} \pi ^{20/9} \root 3 \of {N} Q^2 S^6\nonumber \\ \nonumber&+\, 19440 \root 9 \of {2} \pi ^{17/9} N^{4/3} Q^2 S^5\\&-\,34560\ 2^{4/9} \pi ^{14/9}N^{7/3} Q^2 S^4\nonumber \\ \nonumber&+ \left. 21504\ 2^{7/9} \pi ^{11/9} N^{10/3} Q^2 S^3 - 19683\ 2^{2/3} \pi ^{4/3} S^8\right. \\ \nonumber&- \left. 46656 \pi N S^7-10368 \root 3 \of {2} \pi ^{2/3} N^2 S^6 \right. \\&+\left. 18432\ 2^{2/3} \root 3 \of {\pi } N^3 S^5+32768 N^4 S^4\right] ,\end{aligned}$$
(33)
$$\begin{aligned} B_2= & {} \left( 9\ 2^{7/9} \pi ^{11/9} \root 3 \of {N} Q^2+9\ 2^{2/3} \root 3 \of {\pi } S^2+16 N S\right) ^2\nonumber \\&\times \left( 9 \root 9 \of {2} \pi ^{11/9} \root 3 \of {N} Q^2+9 \root 3 \of {\pi } S^2-8 \root 3 \of {2} N S\right) ^2\nonumber \\&\times \left( 9 \root 9 \of {2} \pi ^{11/9} \root 3 \of {N} Q^2+9 \root 3 \of {\pi } S^2+8 \root 3 \of {2} N S\right) ^2. \end{aligned}$$
(34)

In the next figure, we plot \(R_1^Q\) in terms of the entropy for a fixed N (here \(N=3\)) (Fig. 9).

Fig. 9
figure 9

The scalar curvature vs. entropy for the Quevedo metric case with \(N = 3\). Top \(Q<Q_c\), bottom \(Q=Q_c\)

Full size image

In the critical scheme \(Q<Q_c\), the scalar curvature of the Quevedo metric presents two singularities at \(S_{Q,\pm }\), which are the same as those of the heat capacity \(C_{Q,N}\) shown in Fig. 7 (red line). When \(Q=Q_c\), the two singularities \(S_{Q,\pm }\) coincide and become one \(S_Q\) (represented by a dashed black line). This means that the Quevedo metric can reveal the phase transition in the fixed charge ensemble.

To close this section as in [1], we learn that one can associate the singularities of the \(C_{\phi ,N}\) with the poles of the Weinhold and Ruppeiner scalar curvatures metrics, while the divergences of \(C_{Q,N}\) correspond exactly to the singular points of the curvature of Quevedo metric.

4 Geothermodynamics and phase transition of charged AdS black holes with fixed charge Q

In this section we study the thermodynamics geometry of the M2-branes black holes in the canonical ensemble (fixed charge). This means that the charge of the black hole is not treated as a thermodynamical variable but as a fixed external parameter. The critical number of M2-branes reads

$$\begin{aligned} N_c=\frac{9\ 3^{2/5} \pi ^{14/15} Q^{6/5}}{4\ 2^{11/15}}. \end{aligned}$$
(35)

The heat capacity \(C_{\mu ,Q}\) with a fixed chemical potential is given by

$$\begin{aligned} C_{\mu ,Q}=T\left( \frac{\partial T }{\partial S}\right) _{\mu , Q}^{-1}. \end{aligned}$$
(36)

The full expression of the \(C_{\mu ,Q}\), being quite lengthy, is not given here. Instead we plot, in Fig. 10, \(C_{\mu ,Q}\) in terms of the entropy in the critical sector.

Fig. 10
figure 10

The specific heat \(C_{\mu ,Q}\) vs. entropy with \(Q=.55\), for \(N>N_c\) and \(N=N_c\)

Full size image

From the top panel, we see that the heat capacity \({{C}_{\mu ,Q}}\) presents two divergences up to the critical regime, given numerically by \({{S}_{\mu ,-}}\simeq 0.5\) and \({{S}_{\mu ,+}}\simeq 1.27\) for \({{Q}}=0.55\). When \({{N}}={{N}_{c}}\), these two singularities coincide, as shown in the bottom panel, leading to only one singularity.

In the fixed charge case the Weinhold metric can be expressed as

$$\begin{aligned} g^W=\left( \begin{array}{cc}M_{SS} &{}\quad M_{S N} \\ M_{N S} &{}\quad M_{N N}\end{array}\right) . \end{aligned}$$
(37)

From a treatment similar to the calculation performed in the previous section, one can derive the full expression of the scalar curvatures of both the Weinhold and the Ruppeiner metrics, respectively. For the former one finds

$$\begin{aligned} R_2^W= \frac{A_3}{B_3} \end{aligned}$$
(38)

with

$$\begin{aligned} A_3= & {} 120\ 2^{5/6} \sqrt{3} \pi ^{11/6} N Q^2 S^{3/2} \Big [-408\ 2^{4/9} \pi ^{11/9} N^{4/3} Q^2\nonumber \\&+837 \root 9 \of {2} \pi ^{14/9} \root 3 \of {N} Q^2 S+1404 \pi ^{2/3} S^3+64 \root 3 \of {2} N S \nonumber \\&\times \Big (7 \root 3 \of {2} N-27 \root 3 \of {\pi } S\Big )\Big ],\end{aligned}$$
(39)
$$\begin{aligned} B_3= & {} \Big (-99\ 2^{2/9} \pi ^{22/9} N^{2/3} Q^4-486 \root 9 \of {2} \pi ^{14/9} \root 3 \of {N} Q^2 S^2\nonumber \\&+288\ 2^{4/9} \pi ^{11/9} N^{4/3} Q^2 S+54 \pi ^{2/3} S^4+96 \root 3 \of {2 \pi } N S^3\nonumber \\&-64\ 2^{2/3} N^2 S^2\Big )^2, \end{aligned}$$
(40)

while the result of the latter metric is

$$\begin{aligned} R_2^R=\frac{A_4}{B_4} \end{aligned}$$
(41)

with

$$\begin{aligned} A_4= & {} 15 \root 3 \of {\pi } \root 3 \of {N} \left[ 768 \root 3 \of {\pi } N^{8/3} S (27 \pi ^3 Q^6-16 S^5)\right. \nonumber \\&+\left. 99144 \root 3 \of {2} \pi ^4 N^{2/3} Q^6 S^3-432 (2 \pi )^{2/3} N^{5/3} S^2 \right. \nonumber \\&\times \left. (261 \pi ^3 Q^6+8 S^5)+111537\ 2^{2/9} \pi ^{28/9} \root 3 \of {N} Q^4 S^5\right. \nonumber \\&-\left. 126360\ 2^{5/9} \pi ^{25/9} N^{4/3} Q^4 S^4+123264\ 2^{8/9} \pi ^{22/9} N^{7/3} Q^4 S^3\right. \nonumber \\&-\left. 55296\ 2^{2/9} \pi ^{19/9} N^{10/3} Q^4 S^2+99144 \root 9 \of {2} \pi ^{20/9} Q^2 S^7\right. \nonumber \\&-\left. 153600 \root 9 \of {2} \pi ^{11/9} N^3 Q^2 S^4+49152\ 2^{4/9} \pi ^{8/9} N^4 Q^2 S^3\right. \nonumber \\&-\left. 432\ 2^{7/9} \pi ^{14/9} N^2 Q^2 (3 \pi ^3 Q^6+100 S^5)\right. \nonumber \\&+\left. 81\ 2^{4/9} \pi ^{17/9} N Q^2 S (357 \pi ^3 Q^6+640 S^5)\right. \nonumber \\&+\left. 8192 \root 3 \of {2} N^{11/3} S^5\right] ,\end{aligned}$$
(42)
$$\begin{aligned} B_4= & {} \left( -3 \root 9 \of {2} \pi ^{11/9} \root 3 \of {N} Q^2+9 \root 3 \of {\pi } S^2+8 \root 3 \of {2} N S\right) \nonumber \\&\times \Big (-99\ 2^{2/9} \pi ^{22/9} N^{2/3} Q^4-486 \root 9 \of {2} \pi ^{14/9} \root 3 \of {N} Q^2 S^2\nonumber \\&+288\ 2^{4/9} \pi ^{11/9} N^{4/3} Q^2 S+54 \pi ^{2/3} S^4+96 \root 3 \of {2 \pi } N S^3\nonumber \\&-64\ 2^{2/3} N^2 S^2\Big )^2. \end{aligned}$$
(43)
Fig. 11
figure 11

The scalar curvature of the Weinhold and Ruppeiner metrics vs. entropy for \(N>N_c\), with \(Q=0.55\)

Full size image

These two scalar curvatures are plotted as functions of the entropy in Fig. 11, which shows that the two metrics reproduce the results obtained in the previous section regarding the singularities of the heat capacity \({{C}_{\mu ,Q}}\). Furthermore, this figure also illustrates the divergence of the scalar curvatures of the Weinhold metric (top) and Ruppeiner (bottom) metric when the entropy tends to the value \({{S}_0}\) for which the black hole becomes extremal \(T=0\).

In addition to these singularities, the Ruppeiner metric exhibits an additional singularity \(S_\star \), corresponding to an entropy less than the extremal case with a negative Hawking temperature. This situation is non-physical and will not be treated in this manuscript.

Next, we revisit the Quevedo metric in the fixed charge case,

$$\begin{aligned} g^Q=(S\, T+ N\, \mu )\left( \begin{array}{cc}-M_{SS} &{}\quad 0 \\ 0 &{}\quad M_{N N}\end{array}\right) , \end{aligned}$$
(44)

and compute its corresponding scalar curvature, which is given by

$$\begin{aligned} R_2^Q=\frac{A_5}{B_5}. \end{aligned}$$
(45)

The expressions of \(A_5\) and \(B_5\) are found to be

$$\begin{aligned} A_5= & {} 864 \pi ^{14/9} N^{5/3} S^2 \left[ 768\ 2^{4/9} \root 3 \of {\pi } N^{8/3} S (123 \pi ^3 Q^6-88 S^5)\right. \nonumber \\&-243\ 2^{7/9} \pi N^{2/3} S^3 (953 \pi ^3 Q^6-48 S^5)\nonumber \\&-\,144 \root 9 \of {2} \pi ^{2/3} N^{5/3} S^2 \times (5817 \pi ^3 Q^6+2176 S^5)\nonumber \\&-\,522450\ 2^{2/3} \pi ^{28/9} \root 3 \of {N} Q^4 S^5\nonumber \\&+\left. 490320 \pi ^{25/9} N^{4/3} Q^4 S^4+2116224 \root 3 \of {2} \pi ^{22/9} N^{7/3} Q^4 S^3\right. \nonumber \\&-\left. 190464\ 2^{2/3} \pi ^{19/9} N^{10/3} Q^4 S^2-24786\ 2^{5/9} \pi ^{20/9} Q^2 S^7\right. \nonumber \\&-\left. 1588224\ 2^{5/9} \pi ^{11/9} N^3 Q^2 S^4+114688 (2 \pi )^{8/9} N^4 Q^2 S^3\right. \nonumber \\&-\left. 864\ 2^{2/9} \pi ^{14/9} N^2 Q^2 (17 \pi ^3 Q^6-792 S^5)\right. \nonumber \\&+\left. 81\ 2^{8/9} \pi ^{17/9} N Q^2 S (459 \pi ^3 Q^6+12520 S^5)\right. \nonumber \\&+\left. 131072\ 2^{7/9} N^{11/3} S^5\right] ,\end{aligned}$$
(46)
$$\begin{aligned} B_5= & {} 5 \left( 3 \root 9 \of {2} \pi ^{11/9} \root 3 \of {N} Q^2-3 \root 3 \of {\pi } S^2-8 \root 3 \of {2} N S\right) ^3\nonumber \\&\times \left( 6 \root 9 \of {2} \pi ^{11/9} \root 3 \of {N} Q^2+15 \root 3 \of {\pi } S^2-8 \root 3 \of {2} N S\right) ^2\nonumber \\&\times \left( 9 \root 9 \of {2} \pi ^{11/9} \root 3 \of {N} Q^2+9 \root 3 \of {\pi } S^2-8 \root 3 \of {2} N S\right) ^2. \end{aligned}$$
(47)

An illustration of the \(R_2^Q\) behavior as a function of the entropy is given in the next figure for \(N>N_c\).

Fig. 12
figure 12

The heat capacity as a function of the entropy S for the two backgrounds in the case with a fixed \(Q = 0.55\)

Full size image

From Fig. 12 we can see that the Quevedo metric presents singularity points, here denoted by \(S_{Q,\pm }\), similar to those obtained previously in the analysis of the \(C_{Q,N}\) for fixed N as shown in Eq. 18. Besides we note that at \(S=S_{\mu ,+}\), \(C_{\mu ,Q}\) becomes also singular, while at \(S=S_0\) an additional singularity shows up, signaling the extremal case.

At this stage, it is worth to notice that the singularities of the heat capacity \(C_{\mu ,N}\) correspond exactly to the poles of the Weinhold and Ruppeiner metric curvatures. Unfortunately this is not the case for the Quevedo metric. The latter develop singular points reproducing all the poles occurring in the heat capacities. Hence the association of the singularities of \(C_{Q,N}\) alone and the poles of the Quevedo metric fails.

Therefore, as in several previous works [51–53], the Weinhold, Ruppeiner, and Quevedo metrics can exhibit extra divergences, which are not related to any phase transition point of the heat capacities. In order to cure the shortcoming of the GTD approach, Hendi et al. [51–53] proposed an efficient new formalism dubbed HPEM and showed that all divergences of the Ricci scalar and phase transition points of the heat capacity coincide.

5 Conclusion

In this paper, we have explored the thermodynamics and thermodynamical geometry of charged AdS black holes from M2-branes. More concretely, by assuming the number of M2-branes to be a thermodynamical variable, we have considered AdS black holes in \(AdS_{4}\times S^{7}\). Then we have discussed the corresponding phase transition by computing the relevant quantities. In particular, we have computed the chemical potential and discussed the corresponding stabilities, the critical coordinates, and the Helmholtz free energy. In addition, we have also studied the thermodynamical geometry associated with such AdS black holes. More precisely, we have derived the scalar curvatures from the Weinhold, Ruppeiner, and Quevedo metrics and demonstrated that these thermodynamical properties are similar to those which show up in the phase transition diagram. In the limit of vanishing charge, we recover all results of [1]. We aim to extend this work to other geometries and black hole configurations.

As mentioned in [38], the variations of N, which can be seen as a sort of RG flow in the dual quantum field theory, can only be probed if one considers higher-order curvature corrections to AdS geometries. We aim to extend this work to other geometries considering higher-order corrections in future work.