Abstract
We study the experimental DK invariant mass spectra of the reactions  , \(B^{0} \rightarrow D^{-} D^{0} K^{+}\) (measured by the BaBar collaboration) and \(B_s \rightarrow \pi ^{+} \bar{D}^{0} K^{-}\) (measured by the LHCb collaboration), where an enhancement right above the threshold is seen. We show that this enhancement is due to the presence of \(D^*_{s0}(2317)\), which is a DK bound state in the \(I(J^P) = 0(0^{+})\) sector. We employ a unitarized amplitude with an interaction potential fixed by heavy meson chiral perturbation theory. We obtain a mass \(M_{D^*_{s0}} = 2315^{+12}_{-17}\ ^{+10}_{-5}\ \text {MeV}\), and we also show, by means of the Weinberg compositeness condition, that the DK component in the wave function of this state is \(P_{DK} = 70^{+4}_{-6}\ ^{+4}_{-8} \,\%\), where the first (second) error is statistical (systematic).
, \(B^{0} \rightarrow D^{-} D^{0} K^{+}\) (measured by the BaBar collaboration) and \(B_s \rightarrow \pi ^{+} \bar{D}^{0} K^{-}\) (measured by the LHCb collaboration), where an enhancement right above the threshold is seen. We show that this enhancement is due to the presence of \(D^*_{s0}(2317)\), which is a DK bound state in the \(I(J^P) = 0(0^{+})\) sector. We employ a unitarized amplitude with an interaction potential fixed by heavy meson chiral perturbation theory. We obtain a mass \(M_{D^*_{s0}} = 2315^{+12}_{-17}\ ^{+10}_{-5}\ \text {MeV}\), and we also show, by means of the Weinberg compositeness condition, that the DK component in the wave function of this state is \(P_{DK} = 70^{+4}_{-6}\ ^{+4}_{-8} \,\%\), where the first (second) error is statistical (systematic).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The charmed and strange meson \(D^*_{s0}(2317)\), with quantum numbers \(I(J^P) = 0(0^{+})\), was first observed in the isospin violating \(D_s^{+}\pi ^{0}\) decay channel by the BABAR collaboration [1, 2] and its existence was confirmed by CLEO [3], BELLE [4], and FOCUS [5] collaborations. Its mass, \(M_{D^*_{s0}} \simeq 2317\ \text {MeV}\), is approximately \(160\ \text {MeV}\) below the prediction of the successful constituent quark model for the charmed mesons of Refs. [6, 7] (see, however, Refs. [8–10]). Because of its low mass, the structure of this meson has been extensively discussed. The suggested interpretations cover a wide range: \(c\bar{s}\) state [11–16], two-meson molecular state [17–27], K–D mixing [28], four-quark states [29–33] or a mixture between two-meson and four-quark states [34].
Some recent results from lattice QCD simulations [35–38] have given additional support to the DK molecular picture for the \(D^*_{s0}(2317)\) state. In previous lattice studies it was studied with conventional quark–antiquark correlators, but no state with a mass below the DK threshold was found (see e.g. [39]). In Refs. [35, 37], introducing DK operators and using the effective range formula, a bound state (below the DK threshold) with a binding energy around \(40\ \text {MeV}\) was obtained. A similar result is obtained in other lattice simulations [40]. Since the bound state appears when the DK interpolators are included, a large DK molecular component can be ascribed to this state, but more precise statements cannot be done. In Ref. [36] lattice QCD results for the DK scattering length are obtained, and through the Weinberg compositeness condition [41, 42] the amount of DK content in \(D^*_{s0}(2317)\) is determined, with the result of a large fraction (around 70 %). Yet, this is done using an approximate formula for the scattering length. An improved version of this work is presented in Ref. [43], but the DK probability is not mentioned there. Work along these lines is also done in Refs. [44, 45], using covariant chiral unitary approach. Reference [46] investigates methods to study the nature of \(D^*_{s0}(2317)\) (as a specific case) from lattice QCD simulations. A reanalysis of the lattice spectra of Refs. [35, 37] has recently been done in Ref. [38], considering the three lattice energy levels of Refs. [35, 37] and going beyond the effective range expansion. Therefore, more quantitative analysis about the nature of the \(D^*_{s0}(2317)\) could be performed, with the common result of a DK component around \(70\ \%\).
Beyond these lattice results it is of foremost importance to have experimental data to test the internal structure of this enigmatic state. Weak decays of heavy hadrons into lighter states (which strongly interact thereafter, possibly generating resonant or bound states) offer an excellent opportunity for such a purpose [47]. In the specific case of \(D^*_{s0}(2317)\), in Ref. [48] it was proposed to use the DK invariant mass distribution of the (so far unmeasured) decay \(\bar{B}_s \rightarrow D_s^{-} DK\) to investigate the mass and the nature of this state.Footnote 1 There are at least three reactions that have been actually measured that give access to the DK invariant mass spectrum and which are relevant for the study of the \(D^*_{s0}(2317)\) state. The Belle collaboration [50] measured the decay  , observing an enhancement right above the DK threshold. The BaBar collaboration [51] has observed the same enhancement in the two decays \(B^{+} \rightarrow \bar{D}^{0} D^0 K^{+}\) and \(B^{0} \rightarrow D^{-} D^{0} K^{+}\). Since the reaction measured by the Belle collaboration is included in the two ones measured by the BaBar collaboration, we shall focus in this work on the latter. Finally, the LHCb collaboration [52] has measured another decay, \(B_s \rightarrow \pi ^{+} \bar{D}^{0} K^{-}\), where an enhancement is also seen. The Belle collaboration shapes this enhancement with an exponential background, and so does the BaBar collaboration, not drawing definitive conclusions about the possible contribution of a scalar meson to this effect. On the other hand, the enhancement is partly attributed to the \(D^*_{s0}(2317)\) state by the LHCb collaboration. In the present work, an attempt is made to explain the excess in the event distributions right above threshold as a consequence of the \(D^*_{s0}(2317)\) state, which is associated to a bound state in the \(0(0^{+})\)
DK amplitude. We also try to quantify the DK component of this state, \(P_{DK}\), by means of the Weinberg compositeness condition.
, observing an enhancement right above the DK threshold. The BaBar collaboration [51] has observed the same enhancement in the two decays \(B^{+} \rightarrow \bar{D}^{0} D^0 K^{+}\) and \(B^{0} \rightarrow D^{-} D^{0} K^{+}\). Since the reaction measured by the Belle collaboration is included in the two ones measured by the BaBar collaboration, we shall focus in this work on the latter. Finally, the LHCb collaboration [52] has measured another decay, \(B_s \rightarrow \pi ^{+} \bar{D}^{0} K^{-}\), where an enhancement is also seen. The Belle collaboration shapes this enhancement with an exponential background, and so does the BaBar collaboration, not drawing definitive conclusions about the possible contribution of a scalar meson to this effect. On the other hand, the enhancement is partly attributed to the \(D^*_{s0}(2317)\) state by the LHCb collaboration. In the present work, an attempt is made to explain the excess in the event distributions right above threshold as a consequence of the \(D^*_{s0}(2317)\) state, which is associated to a bound state in the \(0(0^{+})\)
DK amplitude. We also try to quantify the DK component of this state, \(P_{DK}\), by means of the Weinberg compositeness condition.
On the other hand, the D0 collaboration has recently reported on the possible existence of a new \(1(0^{+})\) state, X(5568), in the \(B_s\pi \) spectrum [53]. However, the LHCb collaboration has not found any signature of this state in the same spectrum [54]. If this state actually exists, heavy quark flavor symmetry will predict a partner of it around \(2.2\ \text {GeV}\) in the \(D_s\pi \) channel [55, 56], where the \(D^*_{s0}(2317)\) has been observed. Therefore, to further constrain the analysis of the \(D_s\pi \) spectrum, it is important to determine the properties of \(D^*_{s0}(2317)\) from other sources.
The manuscript is organized as follows. After this Introduction, we set up in Sect. 2 the formalism for the construction of the DK scattering amplitude (Sect. 2.1) and for the study of the aforementioned decays (Sect. 2.2). Our results are presented in Sect. 3, while conclusions are presented in Sect. 4.
2 Formalism
2.1 DK scattering amplitude
The \(D^*_{s0}(2317)\) is an \(I(J^P)=0(0^{+})\) state, and it will arise in our formalism as a DK bound state. The BaBar and LHCb experiments actually measure the \(D^{0} K^{+}\) spectrum, so we need to consider the \(D^{0} K^{+} \rightarrow D^{0} K^{+}\) (direct, \(T_d\)) and \(D^{+} K^{0} \rightarrow D^{0} K^{+}\) (crossed, \(T_c\)) transition amplitudes and its relation to those with definite isospin I (\(I=0,1\)), \(T_I\). We first set our convention for isospin states,
which fixes the isospin eigenstates \(\left| DK \right\rangle _I\),
Assuming isospin conservation, and neglecting the \(I=1\) interaction (as seen below), the amplitudes \(T_{d,c}\) are given by
The elastic DK \(0(0^{+})\) unitary amplitude, \(T_0(s)\) (where s is the center of mass energy squared), can be written as (see e.g. Refs. [20, 27])
where \(G_{DK}(s)\) is a loop function computed from a once-subtracted dispersion relation,
The subtraction constant \(a(\mu )\) is an unknown parameter (we set the scale \(\mu \) to the value \(1.5\ \text {GeV}\)). The DK S-wave interaction potentials in the isospin I channel, \(V_I(s)\), are computed from the Heavy Meson Chiral Perturbation Theory (HMChPT) lagrangian [57, 58]. Their expressions are (see e.g. Refs. [20, 27])
It is worth noticing that the potentials are completely fixed at leading order in the combined heavy quark and chiral expansions, and hence the unitary amplitude \(T_0(s)\) depends on a single parameter, \(a(\mu )\).
If the amplitude has a pole at \(s = M_{D^*_{s0}}^2\),
then the coupling \(g^2\) can be computed as
where the derivatives are to be evaluated at \(s = M_{D^*_{s0}}^2\). Whence the following sum rule can be written:
It was shown in Ref. [59] (see also Ref. [60] for detailed discussions), as a generalization of the Weinberg compositeness condition [41, 42], that the last term represents the probability \(P_{DK}\) of finding the molecular DK component in the \(D^*_{s0}(2317)\) wave function,
Since the amplitude depends only on the parameter \(a(\mu )\), \(M_{D^*_{s0}}\) and \(P_{DK}\) are also uniquely determined by this parameter.
Finally, the \(I=0\) DK scattering length is defined by
where \(s_\text {th} = (m_D+m_K)^2\). In Ref. [38], this scattering length was determined, with the result
This value will be used in our fits as an additional experimental input.
2.2 Weak decays \(B \rightarrow \bar{D} D^{0} K^{+}\) and \(B_s \rightarrow \pi ^{+} \bar{D}^{0} K^{-}\)
We want to study the two processes  , where B (
, where B ( ) can refer to \(B^{+}\) (
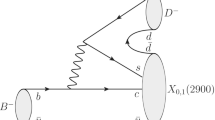
) can refer to \(B^{+}\) ( ) or \(B^{0}\) (\(D^{-}\)). The process is mediated by the weak decays \(\bar{b} \rightarrow W^{+} \bar{c} \rightarrow (c\bar{s})\bar{c}\). In order to have a three-meson final state, an extra \(q\bar{q}\) pair must be created ex vacuo. Since a \(D^{0} K^{+}\) state must be present in the final state, it can be produced either directly or through the transition \(D^{+} K^{0} \rightarrow D^{0} K^{+}\) after a \(D^{+} K^{0}\) pair appears in the hadronization. There are two diagrams that contribute to each of the decays (\(B^{+}\) or \(B^{0}\)), as depicted in Fig. 1. In diagram (c1) the \(\bar{s}c\) pair produced by the W decay hadronizes together with a \(\bar{q}q\) pair into a two-meson final state, and the remaining \(\bar{c}u\) produces a
) or \(B^{0}\) (\(D^{-}\)). The process is mediated by the weak decays \(\bar{b} \rightarrow W^{+} \bar{c} \rightarrow (c\bar{s})\bar{c}\). In order to have a three-meson final state, an extra \(q\bar{q}\) pair must be created ex vacuo. Since a \(D^{0} K^{+}\) state must be present in the final state, it can be produced either directly or through the transition \(D^{+} K^{0} \rightarrow D^{0} K^{+}\) after a \(D^{+} K^{0}\) pair appears in the hadronization. There are two diagrams that contribute to each of the decays (\(B^{+}\) or \(B^{0}\)), as depicted in Fig. 1. In diagram (c1) the \(\bar{s}c\) pair produced by the W decay hadronizes together with a \(\bar{q}q\) pair into a two-meson final state, and the remaining \(\bar{c}u\) produces a  . In diagram (c2), with the topology of internal emission [61], the \(\bar{q}q\) is inserted between the \(\bar{c}c\) pair, and the \(\bar{s}u\) one gives rise to a \(K^{+}\). An analogous discussion can be applied to diagrams (n1) and (n2) for the case of \(B^{0}\) decay. The \(\bar{c}d\) pair in (n1) gives now a \(D^{-}\) and the \(\bar{s}d\) pair in (n2) gives a \(K^{0}\). To see the specific two-meson states that arise in the hadronization of a given quark–antiquark pair plus an extra \(\bar{q}q\) pair, we introduce the following quark–antiquark matrix M:
. In diagram (c2), with the topology of internal emission [61], the \(\bar{q}q\) is inserted between the \(\bar{c}c\) pair, and the \(\bar{s}u\) one gives rise to a \(K^{+}\). An analogous discussion can be applied to diagrams (n1) and (n2) for the case of \(B^{0}\) decay. The \(\bar{c}d\) pair in (n1) gives now a \(D^{-}\) and the \(\bar{s}d\) pair in (n2) gives a \(K^{0}\). To see the specific two-meson states that arise in the hadronization of a given quark–antiquark pair plus an extra \(\bar{q}q\) pair, we introduce the following quark–antiquark matrix M:
which fulfills
The first factor in the last equality represents the \(\bar{q}q\) creation. This matrix M is in correspondence with the meson matrix \(\phi \):
The hadronization of the \(\bar{s}c\) and the \(\bar{c}c\) proceed through the matrix elements \((M^2)_{43}\) and \((M^2)_{44}\), respectively, of the \(M^2\) matrix. The resulting two-meson states are then given by the same matrix elements of the \(\phi ^2\) matrix, namely:

We have retained only the terms that are relevant for the processes under consideration. Thus, in a primary step, we have in (c1) \(\bar{D}^{0} (D^0 K^{+} + D^{+} K^{0})\), in (c2) \(K^{+} (D^{0} \bar{D}^{0} + D^{+} D^{-})\), in (n1) \(D^{-} (D^{0} K^{+} + D^{+} K^{0})\), and in (n2) \(K^{0} (D^0 \bar{D}^{0} + D^{+} D^{-})\). These configurations can also be obtained by regarding \(\bar{q}q\) in Fig. 1 as \(\bar{u}u\) and \(\bar{d}d\) with the same weight.
The mechanisms in Fig. 1 give the bare vertices for the weak decays \(B \rightarrow \bar{D} D^{0} K^{+}\) and \(B \rightarrow \bar{D} D^{+} K^{0}\), and these bare vertices should be renormalized by the strong interactions among quarks. However, neither the weight of diagram (c1), equal to (n1), nor that of the diagram (c2), equal to (n2), are known, and hence we assign them a (constant) value \(\gamma _1\) and \(\gamma _2\), respectively. After this bare interaction takes place, the DK pairs are allowed to interact, as shown in Fig. 2. Let us denote by \(\Gamma _{B \rightarrow \bar{D} D^{0} K^{+}}\) the full amplitudes. Performing the summation shown in Fig. 2, these are expressed as
Now, taking into account that \(T_d = T_c = T_0/2\) and the relation between \(T_0\), \(V_0\), and \(G_{DK}\), these relations are written simply as
with \(K = \gamma _2 / 2\) and \(\beta = 1 + 2\gamma _1/\gamma _2\). The parameter K is irrelevant, since it will be absorbed in a global normalization constant, and we are thus left with a single relevant parameter, \(\beta \). Furthermore, our fits to the experimental data, to be discussed in more detail below, will prefer solutions with \(\beta \gg 1\), which, in turn, makes the parameter \(\beta \) also irrelevant, since it is again absorbed in a global normalization constant.Footnote 2 This means that the diagrams (c1) and (n1) in Fig. 1 are dominant. This is an interesting empirical support for the general rule that the diagrams of external emission are color favored and dominate the processes [61].
A completely analogous procedure can be taken over the reaction  (with the obvious replacements), for which the relevant diagrams are depicted in Fig. 3. The amplitude is written also as Eqs. (22) and (23),
(with the obvious replacements), for which the relevant diagrams are depicted in Fig. 3. The amplitude is written also as Eqs. (22) and (23),
and, also here, the parameters \(K'\) and \(\beta '\) will turn out to be irrelevant.
The experimental DK invariant mass spectra in the reactions under study certainly contain contributions other than the one stemming from DK with \(0(0^{+})\) quantum numbers, such as non-resonant background and other resonances. The full spectra, denoted here with \(N_{B^{+}}\), \(N_{B^{0}}\) and \(N_{B_s}\) for the \(B^{+} \rightarrow D^{-} D^{0} K^{+}\),  ,
,  decays, respectively, are thus parameterized as follows:
decays, respectively, are thus parameterized as follows:
where the different momenta involved are defined as
The background contributions are parameterized by means of smooth energy functions,
where the parameters \(a,b,a'\), and \(b'\) are free. The contributions from resonances other than the \(D^*_{s0}(2317)\) are included in \(\Gamma _{D^*_{sJ}}\). These functions are parameterized with energy dependent width Breit–Wigner functions, as done in the experimental analyses [51, 52]. To avoid the proliferation of free parameters, the masses of the resonances included in our analysis are fixed to those given by the experimental collaborations, namely (all values in MeV) \(M_{D^*_{s1}(2700)} = 2699 \pm 10\), \(\Gamma _{D^*_{s1}(2700)} = 127 \pm 22\), \(M_{D^*_{s2}(2573)} = 2568.39 \pm 0.39\), and \(\Gamma _{D^*_{s2}(2573)} = 16.9 \pm 0.75\), where we have added in quadratures the statistical and systematic errors given by the collaborations. The normalization constants \(\mathcal {N}_X^{(i)}\) are in principle free parameters.
3 Results
The experimental information at our disposal comprises the three event distributions for the decays \(B^{+} \rightarrow D^{-} D^{0} K^{+}\) and  , from the BaBar collaboration [51], and
, from the BaBar collaboration [51], and  , from the LHCb collaboration [52], together with the result for the \(0(0^{+})\)
DK scattering length calculated in lattice simulations [38], shown in Eq. (15).Footnote 3 For the \(B_s \rightarrow \pi ^{+} \bar{D}^{0} K^{-}\) spectrum, we fit the data up to \(\sqrt{s} = 2.8\ \text {GeV}\), since at that energy starts the contribution from another resonance, \(D^*_{sJ}(2860)\). In the \(B \rightarrow \bar{D} D^{0} K^{+}\) spectra, to have a more constrained fit, our background contributions are fitted to the background given in the experimental analysis of the BaBar collaboration [51], by including an additional appropriate piece in the \(\chi ^2\) function to be minimized. The background is fitted in the whole range available for \(\sqrt{s}\), while the signal data are fitted only up to \(\sqrt{s} = 3\ \text {GeV}\), where the contribution of the \(D^*_{s1}(2700)\) resonance is already small. Furthermore, in these two decays the contribution from the \(D^*_{s2}\) is quite small, so we fix the value of the normalization constants \(\mathcal {N}^{(0)}_{D^*_{s2}}\) and \(\mathcal {N}^{(+)}_{D^*_{s2}}\) so as to reproduce the result given by the BaBar collaboration.
, from the LHCb collaboration [52], together with the result for the \(0(0^{+})\)
DK scattering length calculated in lattice simulations [38], shown in Eq. (15).Footnote 3 For the \(B_s \rightarrow \pi ^{+} \bar{D}^{0} K^{-}\) spectrum, we fit the data up to \(\sqrt{s} = 2.8\ \text {GeV}\), since at that energy starts the contribution from another resonance, \(D^*_{sJ}(2860)\). In the \(B \rightarrow \bar{D} D^{0} K^{+}\) spectra, to have a more constrained fit, our background contributions are fitted to the background given in the experimental analysis of the BaBar collaboration [51], by including an additional appropriate piece in the \(\chi ^2\) function to be minimized. The background is fitted in the whole range available for \(\sqrt{s}\), while the signal data are fitted only up to \(\sqrt{s} = 3\ \text {GeV}\), where the contribution of the \(D^*_{s1}(2700)\) resonance is already small. Furthermore, in these two decays the contribution from the \(D^*_{s2}\) is quite small, so we fix the value of the normalization constants \(\mathcal {N}^{(0)}_{D^*_{s2}}\) and \(\mathcal {N}^{(+)}_{D^*_{s2}}\) so as to reproduce the result given by the BaBar collaboration.
Before presenting our results, we first discuss the error estimation performed in this work. For each quantity displayed in this manuscript, the first (second) error shown is statistical (systematic). Statistical errors represent \(1\sigma \) confidence intervals, and they are estimated by Monte Carlo resampling of the experimental data [62]. They also take into account the uncertainties in the masses of the \(D^*_{sJ}\) resonances included in the spectra. The systematic errors are estimated by performing two variations in our theoretical approach. First, we consider the influence of higher orders in the potential (Eq. (8)),
where the parameter h is free. In principle, there could also be an additional term independent of s, but it can be absorbed, as we have checked, by a renormalization of the subtraction constant, \(a(\mu )\), in the loop function (Eq. (7)). By the same token, we can take, for convenience, \(s_0 = M_{D^*_{s0}}^2\). A potential of the type of Eq. (33) can account for some missing channels, which demand an energy dependent effective potential [63]. Actually, in general, and as we shall see in our results, \(P_{DK} \leqslant 1\), indicating missing channels. This also means that the \(D^*_{s0}(2317)\) state can be formed directly (and not through the DK rescattering) in the B decay reactions. For this reason, as done in Ref. [49] we consider in Eqs. (22), (23) and (24) the modification
and analogously for the other two amplitudes. Both modifications (Eqs. (33), (34)) are considered separately, and the new parameters (h, \(C_{B^{+}}\), ...) are allowed to vary together with the original ones. The contributions stemming from these new parameters are relatively small. For each quantity quoted in this work, the difference between the value obtained with the new fit and the central fit gives the systematic error.
The \(D^{0}K^{+}\) invariant mass distributions for the reactions \(B_s \rightarrow \pi ^{+} \bar{D}^{0} K^{-}\) (top panels), \(B^{0} \rightarrow D^{-} D^{0} K^{+}\) (middle panels) and  (lower panels). In the left panels, our fitted theoretical distributions (blue lines) together with their error (blue bands), and confronted with the experimental distributions (data taken from the LHCb [52] and the BaBar [51] collaborations). In the right panels we show the different contributions to each decay. The fit shown here is the one called “combined” in Table 1
(lower panels). In the left panels, our fitted theoretical distributions (blue lines) together with their error (blue bands), and confronted with the experimental distributions (data taken from the LHCb [52] and the BaBar [51] collaborations). In the right panels we show the different contributions to each decay. The fit shown here is the one called “combined” in Table 1
We start by performing two different fits to the LHCb and BaBar data separately. Among all the free parameters, we only show in Table 1 the value of the one that is directly relevant for the DK
T-matrix, namely the subtraction constant \(a(\mu )\). Alongside this value we also show the computed quantities stemming from each fit, \(M_{D^*_{s0}}\), \(P_{DK}\), \(a_0\), and also the value \(\chi ^2/\text {d.o.f.}\). It can be seen that both fits have a good and similar quality, with \(\chi ^2/\text {d.o.f.} \simeq 1.3-1.4\), and that the values of the aforementioned quantities are compatible already at the \(1\sigma \) level. The difference in the \(D^*_{s0}(2317)\) mass in both fits is around \(20\ \text {MeV}\), and the PDG [64] average value, \(2318 \pm 1\ \text {MeV}\), is comprised in the ranges obtained from both fits. Hence we perform a combined fit, also shown in Table 1, and the resulting mass, \(M_{D^*_{s0}} = 2315^{+12}_{-17}\ ^{+10}_{-5}\ \text {MeV}\), is closer to the central value given by the PDG [64] (albeit our errors are larger). For this combined fit, we show the mass spectra for the three reactions in Fig. 4. The enhancement at threshold is due to the \(0(0^{+})\)
DK amplitude, where the \(D^*_{s0}(2317)\) appears as a pole, and the enhancement is then clearly explained by the presence of this bound state. The threshold enhancement is more clearly seen in the LHCb data (since it has a smaller bin size), where the \(0(0^{+})\)
DK amplitude dominates at threshold. In our analysis, the contribution of the latter amplitude is larger than that attributed to the \(D^*_{s0}(2317)\) state by the LHCb analysis [52] in the \(B_s \rightarrow \pi ^{-} \bar{D}^{0} K^{-}\) amplitude. On the contrary, it can be seen that the contributions of this amplitude to the distributions in the two BaBar reactions, \(B^{0} \rightarrow D^{-} D^{0} K^{+}\) and  , are similar to those reported in the BaBar experimental analysis [51], although they are attributed there to an exponential background, similar to the Belle collaboration [50].
, are similar to those reported in the BaBar experimental analysis [51], although they are attributed there to an exponential background, similar to the Belle collaboration [50].
Surprisingly enough, from these experiments we can learn not only about the mass of the \(D^*_{s0}(2317)\), but also about its nature, namely, about its DK component \(P_{DK}\), computed by means of Eq. (13). For the separate fits to the LHCb and BaBar data we get \(P_{DK} = 74^{+7}_{-6}\ ^{+9}_{-1}\%\) and \(67^{+5}_{-7}\ ^{+6}_{-10}\%\), respectively, whereas the combined fit gives \(P_{DK} = 70^{+4}_{-6}\ ^{+4}_{-8}\%\). This result is similar to that obtained in Ref. [38]. This large DK component implies a mostly DK molecular nature of \(D^*_{s0}(2317)\).
4 Conclusions
We have performed a study of the \(D^{0} K^{+}\) invariant mass distributions for the weak decays  ,
,  and \(B^{0} \rightarrow D^{-} D^{0} K^{+}\), recently measured by the BaBar and LHCb collaborations [51, 52]. In the three reactions, a clear enhancement at the DK threshold is seen, which is difficult to interpret. The LHCb partly attributes this enhancement to the \(D^*_{s0}(2317)\) resonance, but it is not a significant signal in their analysis. The BaBar collaboration models this enhancement through an exponential background, since they cannot draw definitive conclusions about its nature. In this work, we have shown that these enhancements are naturally explained by means of the \(0(0^{+})\)
DK elastic unitary amplitude, built from general principles (unitarity and HMChPT). This amplitude depends on a single parameter (a subtraction constant) fitted so as to reproduce the experimental distributions. A pole is found in this amplitude at a mass \(M_{D^*_{s0}} = 2315^{+12}_{-17}\ ^{+10}_{-5}\ \text {MeV}\), which agrees with the PDG average value, although our errors are larger. Finally, by means of the Weinberg compositeness condition, we are also able to determine its DK molecular nature, finding a DK component \(P_{DK} = 70^{+4}_{-6}\ ^{+4}_{-8}\ \%\).
and \(B^{0} \rightarrow D^{-} D^{0} K^{+}\), recently measured by the BaBar and LHCb collaborations [51, 52]. In the three reactions, a clear enhancement at the DK threshold is seen, which is difficult to interpret. The LHCb partly attributes this enhancement to the \(D^*_{s0}(2317)\) resonance, but it is not a significant signal in their analysis. The BaBar collaboration models this enhancement through an exponential background, since they cannot draw definitive conclusions about its nature. In this work, we have shown that these enhancements are naturally explained by means of the \(0(0^{+})\)
DK elastic unitary amplitude, built from general principles (unitarity and HMChPT). This amplitude depends on a single parameter (a subtraction constant) fitted so as to reproduce the experimental distributions. A pole is found in this amplitude at a mass \(M_{D^*_{s0}} = 2315^{+12}_{-17}\ ^{+10}_{-5}\ \text {MeV}\), which agrees with the PDG average value, although our errors are larger. Finally, by means of the Weinberg compositeness condition, we are also able to determine its DK molecular nature, finding a DK component \(P_{DK} = 70^{+4}_{-6}\ ^{+4}_{-8}\ \%\).
Notes
A different decay has also been proposed in Ref. [49].
Since the amplitude is of the form \(1 + \beta T_0/V_0\), the last term dominates for \(\beta \gg 1\) unless \(T_0/V_0\) has a zero, which is not the case here.
The scattering length is computed by means of Eq. (14), and the value in Eq. (15) is included as an extra experimental point in our \(\chi ^2\) function. However, no significant differences are found if the scattering length is not fitted, although its inclusion in the fits improves the error estimation of the parameters and derived quantities.
References
B. Auber et al., BABAR Coll., Phys. Rev. Lett. 90, 242001 (2003)
B. Auber et al., BABAR Coll., Phys. Rev. D 69, 031101 (2004)
D. Besson et al., CLEO Coll., Phys. Rev. D 68, 032002 (2003)
P. Krokovny et al., BELLE Coll., Phys. Rev. Lett. 91, 262002 (2003)
E.W. Vaandering, FOCUS Coll., arXiv:hep-ex/0406044
S. Godfrey, N. Isgur, Phys. Rev. D 32, 189 (1985)
S. Godfrey, R. Kokoshi, Phys. Rev. D 43, 1679 (1991)
O. Lakhina, E.S. Swanson, Phys. Lett. B 650, 159 (2007)
J. Segovia, D.R. Entem, F. Fernandez, E. Hernandez, Int. J. Mod. Phys. E 22, 1330026 (2013)
P.G. Ortega, J. Segovia, D.R. Entem, F. Fernandez, arXiv:1603.07000 [hep-ph]
Y.-B. Dai, C.-S. Huang, C. Liu, S.-L. Zhu, Phys. Rev. D 68, 114011 (2003)
G.S. Bali, Phys. Rev. D 68, 071501(R) (2003)
A. Dougall, R.D. Kenway, C.M. Maynard, C. Mc-Neile, Phys. Lett. B 569, 41 (2003)
A. Hayashigaki, K. Terasaki, arXiv:hep-ph/0411285
S. Narison, Phys. Lett. B 605, 319 (2005)
Z.G. Wang, S.L. Wan, Phys. Rev. D 73, 094020 (2006)
T. Barnes, F.E. Close, H.J. Lipkin, Phys. Rev. D 68, 054006 (2003)
A.P. Szczepaniak, Phys. Lett. B 567, 23 (2003)
E.E. Kolomeitsev, M.F.M. Lutz, Phys. Lett. B 582, 39 (2004)
F.K. Guo, P.N. Shen, H.C. Chiang, R.G. Ping, B.S. Zou, Phys. Lett. B 641, 278 (2006)
D. Gamermann, E. Oset, D. Strottman, M.J. Vicente Vacas, Phys. Rev. D 76, 074016 (2007)
F.K. Guo, C. Hanhart, U.G. Meißner, Eur. Phys. J. A 40, 171 (2009)
M. Cleven, F.K. Guo, C. Hanhart, U.G. Meißner, Eur. Phys. J. A 47, 19 (2011)
M. Cleven, H.W. Griesshammer, F.K. Guo, C. Hanhart, U.G. Meißner, Eur. Phys. J. A 50, 149 (2014)
A. Faessler, T. Gutsche, S. Kovalenko, V.E. Lyubovitskij, Phys. Rev. D 76, 014003 (2007)
A. Faessler, T. Gutsche, V.E. Lyubovitskij, Y.L. Ma, Phys. Rev. D 76, 014005 (2007)
J.M. Flynn, J. Nieves, Phys. Rev. D 75, 074024 (2007)
E. van Beveren, G. Rupp, Phys. Rev. Lett. 91, 012003 (2003)
H.-Y. Cheng, W.-S. Hou, Phys. Lett. B 566, 193 (2003)
K. Terasaki, Phys. Rev. D 68, 011501(R) (2003)
L. Maiani, F. Piccinini, A.D. Polosa, V. Riquer, Phys. Rev. D 71, 014028 (2005)
M.E. Bracco, A. Lozea, R.D. Matheus, F.S. Navarra, M. Nielsen, Phys. Lett. B 624, 217 (2005)
Z.G. Wang, S.L. Wan, Nucl. Phys. A 778, 22 (2006)
T. Browder, S. Pakvasa, A.A. Petrov, Phys. Lett. B 578, 365 (2004)
D. Mohler, C.B. Lang, L. Leskovec, S. Prelovsek, R.M. Woloshyn, Phys. Rev. Lett. 111, 222001 (2013)
L. Liu, K. Orginos, F.K. Guo, C. Hanhart, U.G. Meißner, Phys. Rev. D 87, 014508 (2013)
C.B. Lang, L. Leskovec, D. Mohler, S. Prelovsek, R.M. Woloshyn, Phys. Rev. D 90, 034510 (2014)
A.M. Torres, E. Oset, S. Prelovsek, A. Ramos, JHEP 1505, 153 (2015)
G. Moir, M. Peardon, S.M. Ryan, C.E. Thomas, L. Liu, JHEP 1305, 021 (2013)
C.E. Thomas, in Proceedings of the XVI International Conference on Hadron Spectroscopy (Hadron 2015), to appear in AIP Conference Proceedings
S. Weinberg, Phys. Rev. 137, B672 (1965)
V. Baru, J. Haidenbauer, C. Hanhart, Y. Kalashnikova, A.E. Kudryavtsev, Phys. Lett. B 586, 53 (2004)
D.L. Yao, M.L. Du, F.K. Guo, U.G. Meißner, JHEP 1511, 058 (2015)
M. Altenbuchinger, L.-S. Geng, W. Weise, Phys. Rev. D 89, 014026 (2014)
M. Altenbuchinger, L.S. Geng, Phys. Rev. D 89, 054008 (2014)
D. Agadjanov, F.-K. Guo, G. Ros, A. Rusetsky, JHEP 1501, 118 (2015)
E. Oset et al., Int. J. Mod. Phys. E 25, 1630001 (2015). arXiv:1601.03972 [hep-ph]
M. Albaladejo, M. Nielsen, E. Oset, Phys. Lett. B 746, 305 (2015)
Z.F. Sun, M. Bayar, P. Fernandez-Soler, E. Oset, arXiv:1510.06316 [hep-ph]
J. Brodzicka et al., [Belle Collaboration], Phys. Rev. Lett. 100, 092001 (2008)
J.P. Lees et al., [BaBar Collaboration], Phys. Rev. D 91, 052002 (2015)
R. Aaij et al., [LHCb Collaboration], Phys. Rev. D 90, 072003 (2014)
V.M. Abazov et al., [D0 Collaboration], arXiv:1602.07588 [hep-ex]
The LHCb Collaboration [LHCb Collaboration], LHCb-CONF-2016-004, CERN-LHCb-CONF-2016-004
F.K. Guo, U.G. Meiner, B.S. Zou, arXiv:1603.06316 [hep-ph]
M. Albaladejo, J. Nieves, E. Oset, Z.F. Sun, X. Liu, arXiv:1603.09230 [hep-ph]
M.B. Wise, Phys. Rev. D 45, 2188 (1992)
A.V. Manohar, M.B. Wise, Camb. Monogr. Part Phys. Nucl. Phys. Cosmol. 10, 1 (2000)
D. Gamermann, J. Nieves, E. Oset, E. Ruiz Arriola, Phys. Rev. D 81, 014029 (2010)
T. Sekihara, T. Hyodo, D. Jido, PTEP 2015, 063D04 (2015)
L.L. Chau, Phys. Rep. 95, 1 (1983)
W.H. Press, S.A. Teukolsky, W.T. Vetterling, B.P. Flannery, Numerical Recipes in FORTRAN: The Art of Scientific Computing. (1992) ISBN-9780521430647
F. Aceti, L.R. Dai, L.S. Geng, E. Oset, Y. Zhang, Eur. Phys. J. A 50, 57 (2014)
K.A. Olive et al., [Particle Data Group Collaboration], Chin. Phys. C 38, 090001 (2014)
Acknowledgments
M. A. acknowledges financial support from the “Juan de la Cierva” program (27-13-463B-731) from the Spanish MINECO. This work is supported in part by the Spanish MINECO and European FEDER funds under the contracts FIS2014-51948-C2-1-P, FIS2014-51948-C2-2-P, FIS2014-57026-REDT and SEV-2014-0398, and by Generalitat Valenciana under contract PROMETEOII/2014/0068. This work was partially supported by Open Partnership with Spain of JSPS Bilateral Joint Research Projects, and the work of DJ was supported by Grants-in-Aid for Scientific Research (No. 25400254).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Albaladejo, M., Nieves, J., Oset, E. et al. \(D^*_{s0}(2317)\) and \(\textit{DK}\) scattering in B decays from BaBar and LHCb data. Eur. Phys. J. C 76, 300 (2016). https://doi.org/10.1140/epjc/s10052-016-4144-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-016-4144-3





 decays
decays
 decays taking into account the
decays taking into account the 
 decays
decays