1 Introduction

The study of the asymptotic behavior of scattering amplitudes in the limit of high center-of-mass energy is an active area of research for particle phenomenology. The Large Hadron Collider (LHC) is producing an abundance of data allowing for the study of very exclusive observables with stringent cuts in the final state. One of the key points for understanding multi-jet production at high energies is the multi-Regge kinematics (MRK). MRK is the kinematics that, by presupposing a strong ordering in rapidity for the final state jets, allows for large logarithms in the colliding energy to be present in all orders of the perturbative expansion. This fact alone calls for a resummation framework of the large logarithms in energy.

In the high energy (Regge) limit, the common basis for the perturbative description of a hard process in QCD is the Balitsky–Fadin–Kuraev–Lipatov (BFKL) approach, at leading (LL) [1–12] and next-to-leading (NLL) [13, 14] accuracy. This approach offers a resummation of those enhanced terms in MRK in regions of phase space where a fixed-order calculation might not be enough. This formalism has been successfully applied to lepton–hadron deep inelastic scattering at HERA (see, e.g. [15, 16]) to describe quite inclusive processes, which are not that suitable though, if one is interested in discriminating between BFKL dynamics and other resummation programs. At the LHC, however, it is possible to investigate processes with much more exclusive final states which could, in principle, be only described by the BFKL framework. This would allow us to precisely determine the applicability window of the framework.

With this idea in mind there has been a lot of recent activity in the study of the so-called Mueller–Navelet jets [17], i.e. the inclusive hadro-production of two forward jets with large and similar transverse momenta and a big relative separation in rapidity Y, proportional to \(\sqrt{s}\), and with associated inclusive mini-jet radiation. Interesting observables associated to this process are the azimuthal angle (\(\theta \)) correlations \(\langle \cos {(n \, \theta )} \rangle \) of the two tagged jets, and it has been shown [18–21] that the further gluon radiation manifests as a fast decrease of these functions with Y. However, these observables are strongly affected by collinear effects [22, 23] due to their dependence on the \(n=0\) Fourier component in \(\theta \) of the BFKL kernel, which is strongly dependent on collinear radiation. In order to remove this problem, new observables were proposed [22, 23] which are independent from the \(n=0\) contribution: the ratios \(\mathcal{R}^{M}_{N} = \langle \cos {(M \, \theta )} \rangle / \langle \cos {(N \, \theta )} \rangle \). They have been calculated at NLL [24–28] and show a very good agreement with the experimental data at the LHC.

Nevertheless, Mueller–Navelet configurations are still too inclusive to study MRK with precision. A step toward other observables capable to pin down the MRK dynamics in much more detail has been taken in [29], where a new study was proposed that demands the tagging of a third, central in rapidity, jet within the usual Mueller–Navelet configuration. It is important to remain within the general Mueller–Navelet setup because having two forward/backward jets allows the use of collinear factorization which is in a better theoretical control than \(k_t\)-factorization. Since a unique footprint of BFKL physics is its azimuthal angle dependence, the main new observables studied in [29] are the ratios

$$\begin{aligned} \mathcal{R}^{M N}_{P Q} =\frac{ \langle \cos {(M \, \phi _1)} \cos {(N \, \phi _2)} \rangle }{ \langle \cos {(P \, \phi _1)} \cos {(Q \, \phi _2)} \rangle } \, , \end{aligned}$$

with \(\phi _1\) and \(\phi _2\) being the azimuthal angle difference, respectively, between the first and the second (central) jet and between this one and the third jet. These observables depend strongly on the \(p_t\) and less strongly on the rapidity of the central jet, and this information can be used to probe the characteristic properties of the BFKL ladder in a very precise way.

The present work, original results of which are presented in the next Section, is a natural continuation of [29], by allowing the production of a second central jet, thus making it possible to define more differential distributions in the transverse momenta, azimuthal angles and rapidities of the two central jets, for fixed values of the four momenta of the forward jets.

2 Inclusive four-jet production

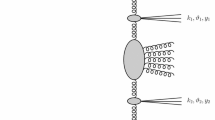
We now present the analysis of events with two forward/backward jets together with two more central jets, all of them well separated in rapidity from each other, making use of the BFKL formalism to describe the associated inclusive multi-jet emission. The two tagged forward/backward jets A and B have transverse momentum \(\vec {k}_{A,B}\), azimuthal angle \(\vartheta _{A,B}\), and rapidity \(Y_{A,B}\), while the pair of tagged more central jets are characterized, respectively, by \(\vec {k}_{1,2}\), \(\vartheta _{1,2}\) and \(y_{1,2}\). The differential cross section on the latter variables can be written in the form

$$\begin{aligned}&\frac{d^6\sigma ^\mathrm{4-jet} \left( \vec {k_A},\vec {k_B},Y_A-Y_B\right) }{d^2\vec {k_1} dy_1 d^2\vec {k_2} dy_2} \nonumber \\&\quad = \frac{\bar{\alpha }_s^2}{\pi ^2 k_1^2 k_2^2} \int d^2\vec {p_A} \int d^2\vec {p_B} \int d^2\vec {p_1} \int d^2\vec {p_2}\nonumber \\&\qquad \times \delta ^{(2)}\left( \vec {p_A}+\vec {k_1}-\vec {p_1}\right) \delta ^{(2)}\left( \vec {p_B}-\vec {k_2}-\vec {p_2}\right) \nonumber \\&\qquad \times \varphi \left( \vec {k_A},\vec {p_A},Y_A-y_1\right) \varphi \left( \vec {p_1},\vec {p_2},y_1-y_2\right) \nonumber \\&\qquad \times \varphi \left( \vec {p_B},\vec {k_B},y_2-Y_B\right) . \end{aligned}$$
(1)

Here we have introduced the rapidity ordering characteristic of MRK: \(Y_A > y_1 > y_2 > Y_B\); and \(k_1^2\), \(k_2^2\) lie above the experimental resolution scale. \(\varphi \) are BFKL gluon Green functions normalized to \( \varphi \left( \vec {p},\vec {q},0\right) = \delta ^{(2)} \left( \vec {p} - \vec {q}\right) /(2 \pi )\) and \(\bar{\alpha }_s = \alpha _s N_c/\pi \).

Following the course taken in Ref. [29], our goal is to define and study the behavior of observables for which the BFKL approach will show distinct features with respect to other formalisms and, if possible, are also quite insensitive to higher-order corrections. We start with the study of a quantity similar to the usual Mueller–Navelet case such that we integrate over the azimuthal angles of the two central jets and over the difference in azimuthal angle between the two forward jets, \(\Delta \theta = \vartheta _A - \vartheta _B - \pi \), to define

$$\begin{aligned}&\int _0^{2\pi } \mathrm{d}\Delta \theta \cos \left( M\Delta \phi \right) \int _0^{2\pi } \mathrm{d}\vartheta _1\nonumber \\&\qquad \times \int _0^{2\pi } \mathrm{d}\vartheta _2 \frac{\mathrm{d}^6\sigma ^\mathrm{4-jet}\left( \vec {k_A},\vec {k_B},Y_A-Y_B\right) }{\mathrm{d}k_1 \mathrm{d}y_1 \mathrm{d}\vartheta _1 \mathrm{d}k_2 \mathrm{d}\vartheta _2 \mathrm{d}y_2}\nonumber \\&\quad = \frac{4 \bar{\alpha }_s^2}{k_1 k_2}\nonumber \\&\qquad \times \left( e^{iM\pi } \, \tilde{\Omega }_{M}(\vec {k_A},\vec {k_B},Y_A,Y_B,\vec {k_1},\vec {k_2}, y_1,y_2) + c.c. \right) \end{aligned}$$
(2)

where

$$\begin{aligned}&\tilde{\Omega }_{n}(\vec {k_A},\vec {k_B},Y_A,Y_B,\vec {k_1},\vec {k_2}, y_1,y_2)\nonumber \\&\quad = \int _0^{+\infty } \mathrm{d}p_A \, p_A \int _0^{+\infty } \mathrm{d}p_B \, p_B \int _0^{2\pi } \mathrm{d}\phi _A \int _0^{2\pi } \mathrm{d}\phi _B\nonumber \\&\qquad \times \frac{\left( p_A+k_1 e^{-i\phi _A}\right) ^n \, \left( p_B-k_2 e^{i\phi _B}\right) ^n}{ \sqrt{\left( p_A^2+k_1^2+2 p_A k_1 \cos \phi _A\right) ^n} \ \sqrt{\left( p_B^2+k_2^2-2 p_B k_2 \cos \phi _B\right) ^n} } \nonumber \\&\qquad \times \varphi _n\left( |\vec {k_A}|,|\vec {p_A}|,Y_A-y_1\right) \varphi _n\left( |\vec {p_B}|,|\vec {k_B}|,y_2-Y_B\right) \nonumber \\&\qquad \times \varphi _n\left( \sqrt{p_A^2+k_1^2+2 p_A k_1 \cos \phi _A} ,\right. \nonumber \\ {}&\qquad \quad \left. \sqrt{p_B^2+k_2^2-2 p_B k_2 \cos \phi _B} ,y_1-y_2\right) \end{aligned}$$
(3)

and

$$\begin{aligned}&\varphi _{n} \left( |p|,|q|,Y\right) = \int _0^\infty \mathrm{d} \nu \cos {\left( \nu \ln {\frac{p^2}{q^2}}\right) } \frac{e^{\bar{\alpha }_s \chi _{|n|} \left( \nu \right) Y}}{\pi ^2 \sqrt{p^2 q^2} }, \end{aligned}$$
(4)
$$\begin{aligned}&\chi _{n} \left( \nu \right) \; = \; 2\, \psi (1) - \psi \left( \frac{1+n}{2} + i \nu \right) - \psi \left( \frac{1+n}{2} - i \nu \right) \end{aligned}$$
(5)

(\(\psi \) is the logarithmic derivative of Euler’s gamma function). The associated experimental observable corresponds to the mean value of the cosine of \(\Delta \theta = \vartheta _A - \vartheta _B - \pi \) in the recorded events:

$$\begin{aligned}&\left\langle \cos (M(\vartheta _A - \vartheta _B - \pi ))\right\rangle \nonumber \\&\quad = \frac{\int _0^{2\pi } \mathrm{d}\Delta \theta \cos (M\Delta \theta ) \int _0^{2\pi } \mathrm{d}\vartheta _1 \int _0^{2\pi } \mathrm{d}\vartheta _2 \frac{\mathrm{d}^6\sigma ^\mathrm{4-jet}}{\mathrm{d}k_1 \mathrm{d}y_1 \mathrm{d}\vartheta _1 \mathrm{d}k_2 \mathrm{d}\vartheta _2 \mathrm{d}y_2}}{\int _0^{2\pi } \mathrm{d}\Delta \theta \int _0^{2\pi } \mathrm{d}\vartheta _1 \int _0^{2\pi } \mathrm{d}\vartheta _2 \frac{\mathrm{d}^6\sigma ^\mathrm{4-jet}}{\mathrm{d}k_1 \mathrm{d}y_1 \mathrm{d}\vartheta _1 \mathrm{d}k_2 \mathrm{d}\vartheta _2 \mathrm{d}y_2}}. \end{aligned}$$
(6)

In order to improve the perturbative stability of our predictions (see [30] for a related discussion) it is convenient to remove the contribution from the zero conformal spin [which corresponds to the index \(n=0\) in Eq. (4)] by defining the ratios

$$\begin{aligned} \mathcal {R}^M_N = \frac{\left\langle \cos (M(\vartheta _A - \vartheta _B - \pi ))\right\rangle }{\left\langle \cos (N(\vartheta _A - \vartheta _B - \pi ))\right\rangle } \end{aligned}$$
(7)

where we consider M, N as positive integers.

Our next step now is to propose new observables, different from those characteristic of the Mueller–Navelet case though still related to azimuthal angle projections. We thus define

$$\begin{aligned} \mathcal {C}_{MNL}&= \int _0^{2\pi } \mathrm{d}\vartheta _A \int _0^{2\pi } \mathrm{d}\vartheta _B \int _0^{2\pi } \mathrm{d}\vartheta _1 \int _0^{2\pi } \mathrm{d}\vartheta _2\nonumber \\&\quad \times \cos \left( M\left( \vartheta _A-\vartheta _1-\pi \right) \right) \cos \left( N\left( \vartheta _1-\vartheta _2-\pi \right) \right) \nonumber \\&\quad \times \cos \left( L\left( \vartheta _2-\vartheta _B-\pi \right) \right) \nonumber \\&\quad \times \frac{\mathrm{d}^6\sigma ^\mathrm{4-jet}\left( \vec {k_A},\vec {k_B},Y_A-Y_B\right) }{\mathrm{d}k_1 \mathrm{d}y_1 \mathrm{d}\vartheta _1 \mathrm{d}k_2 \mathrm{d}\vartheta _2 \mathrm{d}y_2}, \end{aligned}$$
(8)

where we consider M, N, and \(L > 0\), and integer. After a bit of algebra we have

$$\begin{aligned} \mathcal {C}_{MNL}&= \frac{2\pi ^2 \bar{\alpha }_s^2}{k_1 k_2} \, (-1)^{M + N + L} \,\nonumber \\&\quad \times ( \tilde{\Omega }_{M,N,L} + \tilde{\Omega }_{M,N,-L} + \tilde{\Omega }_{M,-N,L}\nonumber \\&\quad + \tilde{\Omega }_{M,-N,-L}+ \tilde{\Omega }_{-M,N,L} + \tilde{\Omega }_{-M,N,-L}\nonumber \\&\quad + \tilde{\Omega }_{-M,-N,L} + \tilde{\Omega }_{-M,-N,-L}) \end{aligned}$$
(9)

with

$$\begin{aligned} \tilde{\Omega }_{m,n,l}&= \int _0^{+\infty } \mathrm{d}p_A \, p_A \int _0^{+\infty } \mathrm{d}p_B \, p_B \int _0^{2\pi } \mathrm{d}\phi _A \int _0^{2\pi } \mathrm{d}\phi _B \nonumber \\&\quad \times \, \frac{e^{-im\phi _A} \, e^{il\phi _B} \, \left( p_A e^{i\phi _A}+k_1\right) ^n \, \left( p_B e^{-i\phi _B}-k_2\right) ^n}{ \sqrt{\left( p_A^2+k_1^2+2 p_A k_1 \cos \phi _A\right) ^n} \ \sqrt{\left( p_B^2+k_2^2-2 p_B k_2 \cos \phi _B\right) ^n} }\nonumber \\&\quad \times \varphi _m\left( |\vec {k_A}|,|\vec {p_A}|,Y_A-y_1\right) \varphi _l\left( |\vec {p_B}|,|\vec {k_B}|,y_2-Y_B\right) \nonumber \\&\quad \times \varphi _n\left( \sqrt{p_A^2+k_1^2+2 p_A k_1 \cos \phi _A} ,\right. \nonumber \\ {}&\qquad \left. \sqrt{p_B^2+k_2^2-2 p_B k_2 \cos \phi _B} ,y_1-y_2\right) . \end{aligned}$$
(10)

In order to drastically reduce the dependence on collinear configurations we can remove the zero conformal spin contribution by defining the following ratios:

$$\begin{aligned}&\mathcal {R}^{MNL}_{PQR}\nonumber \\&\ \ = \frac{\left\langle \cos (M(\vartheta _A \,{-}\, \vartheta _1 \,{-}\, \pi )) \cos (N(\vartheta _1 \,{-}\, \vartheta _2 \,{-}\, \pi )) \cos (L(\vartheta _2 \,{-}\, \vartheta _B \,{-}\, \pi ))\right\rangle }{\left\langle \cos (P(\vartheta _A \,{-}\, \vartheta _1 \,{-}\, \pi )) \cos (Q(\vartheta _1 \,{-}\, \vartheta _2 \,{-}\, \pi )) \cos (R(\vartheta _2 \,{-}\, \vartheta _B \,{-}\, \pi ))\right\rangle } \end{aligned}$$
(11)

with integer \(M,N,L,P,Q,R > 0\).

It is now possible to numerically investigate many different momenta configurations. In order to cover two characteristic cases, namely \( k_A \sim k_B \) and \( k_A < k_B \) (or equivalently \(k_A > k_B\)) we choose the following two fixed configurations for the transverse momenta of the forward jets: \(\left( k_A, k_B \right) \) = (40, 50) and \(\left( k_A, k_B \right) \) = (30, 60) GeV. We also fix the rapidities of the four tagged jets to the values \(Y_A = 9\), \(y_1 = 6\), \(Y_2 = 3\), and \(Y_B = 0\) whereas the two inner jets can have transverse momenta in the range \(20 < k_{1,2} < 80\) GeV.

In Fig. 1 we present our results for the normalized coefficients \(\mathcal{C}_{111}\), \(\mathcal{C}_{112}\), \(\mathcal{C}_{121}\) and \(\mathcal{C}_{122}\) after they are divided by their respective maximum. We find that the distributions are quite similar for the two configurations here chosen (\(\left( k_A, k_B \right) \) = (40, 50), (30, 60) GeV) apart from the coefficient \(\mathcal{C}_{121}\), which is quite more negative for the latter configuration when the transverse momentum of the first central jet, \(k_1\), is low. Further coefficients, normalized as above, are calculated in Fig. 2 for the cases \(\mathcal{C}_{211}\), \(\mathcal{C}_{212}\), \(\mathcal{C}_{221}\), and \(\mathcal{C}_{222}\). Again they are rather similar with the exception of \(\mathcal{C}_{221}\) at low \(p_t\) of one of the centrals jets with largest rapidity.

Fig. 1
figure 1

\(k_{1,2}\)-dependence of the normalized \(\mathcal{C}_{111}\), \(\mathcal{C}_{112}\), \(\mathcal{C}_{121}\) and \(\mathcal{C}_{122}\) for the two selected cases of forward jet transverse momenta \(k_A\) and \(k_B\)

Full size image
Fig. 2
figure 2

\(k_{1,2}\)-dependence of the normalized \(\mathcal{C}_{211}\), \(\mathcal{C}_{212}\), \(\mathcal{C}_{221}\) and \(\mathcal{C}_{222}\) for the two selected cases of forward jet transverse momenta \(k_A\) and \(k_B\)

Full size image

Since these coefficients change sign on the parameter space here studied, it is clear that for the associated ratios \(\mathcal {R}^{MNL}_{PQR}\) there will be some lines of singularities. We have investigated \(\mathcal {R}^{121}_{212}\), \(\mathcal {R}^{212}_{211}\) and \(\mathcal {R}^{221}_{222}\) in Fig. 3.

Fig. 3
figure 3

\(k_{1,2}\)-dependence of \(\mathcal {R}^{121}_{212}\), \(\mathcal {R}^{212}_{211}\) and \(\mathcal {R}^{221}_{222}\) for the two selected cases of forward/backward jets transverse momenta \(k_A\) and \(k_B\)

Full size image

In this case the configurations \(\left( k_A, k_B \right) = (40, 50), (30, 60)\) GeV behave quite differently. This is due to the variation of the position of the zeros of those coefficients \(\mathcal{C}_{MNP}\) chosen as denominators in these quantities. It would be very interesting to test if these singularity lines are present in any form in the LHC experimental data. A further set of ratios, \(\mathcal {R}^{111}_{112}\), \(\mathcal {R}^{111}_{122}\), \(\mathcal {R}^{112}_{122}\), and \(\mathcal {R}^{222}_{211}\), with their characteristic singular lines, is presented in Fig. 4. In general, we have found a very weak dependence on variations of the rapidity of the more central jets \(y_{1,2}\) for all the observables here presented.

Fig. 4
figure 4

\(k_{1,2}\)-dependence of \(\mathcal {R}^{111}_{112}\), \(\mathcal {R}^{111}_{122}\), \(\mathcal {R}^{112}_{122}\) and \(\mathcal {R}^{222}_{211}\) for the two selected cases of forward/backward jets transverse momenta \(k_A\) and \(k_B\)

Full size image

We have used both Fortran and Mathematica for the numerical computation of the ratios \(\mathcal {R}^{MNL}_{PQR}\). We made extensive use of the integration routine Vegas [31] as implemented in the Cuba library [32, 33]. Furthermore, we used the Quadpack library [34] and a slightly modified version of the Psi [35] routine.

We conclude here our numerical analysis. We have offered several interesting observables where BFKL effects could have sizable effects. More detailed calculations are needed, including the introduction of parton distribution functions effects and higher-order terms in jet vertices and Green functions. However, we argue that the bulk of the relevant contributions are already contained in the calculations here discussed, in particular, for the ratios \(\mathcal {R}^{MNL}_{PQR}\). It will be very important to compare against the BFKL Monte Carlo code BFKLex [36–42] as well as to calculate the same quantities with other, more conventional, approaches [43–45] in order to gauge if they differ from our results. This includes those analysis where the four-jet predictions stem from two independent gluon ladders [46, 47].

3 Summary and outlook

We have presented new observables to study four-jet production at hadron colliders in terms of its azimuthal angle dependences. These correspond to the ratios of correlation functions of products of cosines of azimuthal angle differences among the tagged jets. We used a single BFKL ladder approach, with inclusive production of two forward/backward and two further, more central, tagged jets. The dependence on the transverse momenta and rapidities of the two central jets is a distinct signal of BFKL dynamics. For future work, more accurate analyses are needed: the introduction of parton distribution functions, higher-order effects, and realistic experimental cuts. It is also pressing to calculate our proposed observables using other approaches not based on the BFKL approach and to test how they can differ from our predictions. Last but not least, we encourage our experimental colleagues to analyze these observables in recent and future LHC data.