Double vector meson production in $\gamma \gamma$ interactions at hadronic colliders

Abstract

In this paper we revisit the double vector meson production in $\gamma \gamma$ interactions at heavy ion collisions and present, by the first time, predictions for the $\rho \rho$ and $J/\Psi J/\Psi$ production in proton–nucleus and proton–proton collisions. In order to obtain realistic predictions for rapidity distributions and total cross sections for the double vector production in ultra peripheral hadronic collisions we take into account the description of $\gamma \gamma \rightarrow VV$ cross section at low energies as well as its behavior at large energies, associated to the gluonic interaction between the color dipoles. Our results demonstrate that the double $\rho$ production is dominated by the low energy behavior of the $\gamma \gamma \rightarrow VV$ cross section. In contrast, for the double $J/\Psi$ production, the contribution associated to the description of the QCD dynamics at high energies contributes significantly, mainly in pp collisions. Predictions for the RHIC, LHC, FCC, and CEPC–SPPC energies are shown.

In recent years a series of experimental results from RHIC [1, 2], Tevatron [3] and LHC [4–12] demonstrated that the study of photon-induced interactions in hadronic colliders is feasible and that it can be used to, among other things, improve our knowledge on the nuclear gluon distribution [13–19], on details of QCD dynamics [20–30], on the mechanism of quarkonium production [29–36], on the Odderon [37, 38] and on the photon flux of the proton [39, 40]. These data have stimulated the development of the theoretical description of these processes as well as the proposal of new forward detectors to be installed in the LHC [41, 42].

The basic idea in the photon-induced processes is that an ultra relativistic charged hadron (proton or nucleus) creates strong electromagnetic fields. A photon stemming from the electromagnetic field of one of the two colliding hadrons can interact with one photon coming from the other hadron (photon–photon process) or it can interact directly with the other hadron (photon–hadron process) [43–48]. In these processes the total cross section can be factorized in terms of the flux of equivalent photons from the hadron projectile and the photon–photon or photon–target production cross section. In this paper we will focus on two-photon interactions in hadronic collisions. Experimental results on exclusive two-photon production of $W^+W^-$ and $\ell ^+\ell ^-$ pairs in $\gamma \gamma$ interactions reported by the CMS and ATLAS Collaborations [9–12] have demonstrated that it is possible to measure such events with the experimental apparatus already available at the LHC, allowing for novel studies of QCD at very high energies and searches for Beyond Standard Model Physics (see, e.g., Ref. [49–59]). This motivates us to revisit the analysis of double vector meson production in ultra peripheral heavy ion collisions performed some time ago in Refs. [60–62], taking into account recent improvements in the description of the $\gamma \gamma \rightarrow VV$ ($V = \rho , J/\Psi$) cross section at low [63, 64] and at high [65] energies. In this work we will derive, for the first time, realistic predictions for double meson production in $\gamma \gamma$ interactions at pp and pA collisions at RHIC and LHC energies as well as for the proposed energies for the Future Circular Collider (FCC) at CERN [66] and in the Circular Electron Positron Collider with a subsequent Super proton–proton Collider (CEPC–SPPC) in China [67]. Our goal is to determine if this process, after the inclusion of the recent theoretical improvements, can be used to study the QCD dynamics at high energies, as originally proposed in Ref. [60]. As we will show, this remains true for double $J/\Psi$ production, mainly in pp collisions.

Let us start our analysis presenting a brief review of the main formulas to describe double vector meson production in $\gamma \gamma$ interactions at hadronic colliders. In the Equivalent Photon Approximation (EPA) [43–48] the total cross section for this process can be written as

$$\begin{aligned}&\sigma \left( h_1 h_2 \rightarrow h_1 \otimes V_1V_2 \otimes h_2 ;s \right) \nonumber \\&\quad = \int \hat{\sigma }\left( \gamma \gamma \rightarrow V_1V_2 ; W \right) \nonumber \\&\qquad \times N\left( \omega _{1},{\mathbf b_{1}} \right) N\left( \omega _{2},{\mathbf b_{2}} \right) S^2_{abs}({\mathbf b}) \text{ d }^{2} {\mathbf b_{1}} \text{ d }^{2} {\mathbf b_{2}} \text{ d } \omega _{1} \text{ d } \omega _{2} , \end{aligned}$$

(1)

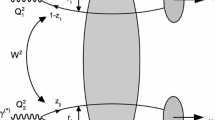
where $\sqrt{s}$ is center-of-mass energy of the $h_1 h_2$ collision ($h_i = p, A$), $\otimes$ characterizes a rapidity gap in the final state and $W = \sqrt{4 \omega _1 \omega _2}$ is the invariant mass of the $\gamma \gamma$ system. Moreover, $N(\omega , {\mathbf b})$ is the equivalent photon spectrum of photons with energy $\omega$ at a distance ${\mathbf b}$ from the hadron trajectory, defined in the plane transverse to the trajectory. The spectrum can be expressed in terms of the charge form factor F as follows:

$$\begin{aligned}&N(\omega ,b) = \frac{Z^{2}\alpha _{em}}{\pi ^2}\frac{1}{b^{2}\omega } \nonumber \\&\quad \times \left[ \int u^{2} J_{1}(u) F\left( \sqrt{\frac{\left( \frac{b\omega }{\gamma _\mathrm{L}}\right) ^{2} + u^{2}}{b^{2}}} \right) \frac{1}{\left( \frac{b\omega }{\gamma _\mathrm{L}}\right) ^{2} + u^{2}} \text{ d }u \right] ^{2}, \end{aligned}$$

(2)

where $\gamma _\mathrm{L}$ is the Lorentz factor. The factor $S^2_{\mathrm{abs}}({\mathbf b})$ is the absorption factor, given in what follows by

$$\begin{aligned}&S^2_{abs}({\mathbf b}) = \Theta \left( \left| {\mathbf b}\right| - R_{h_1} - R_{h_2} \right) \nonumber \\&\quad = \Theta \left( \left| {\mathbf b_{1}} - {\mathbf b_{2}} \right| - R_{h_1} - R_{h_2} \right) , \end{aligned}$$

(3)

where $R_{h_i}$ is the radius of the hadron $h_i$ ($i = 1,2$). The presence of this factor in Eq. (1) excludes the overlap between the colliding hadrons and allows one to take into account only ultra peripheral collisions. Remembering that the photon energies $\omega _1$ and $\omega _2$ are related to W and the rapidity ($Y = \frac{1}{2}(y_{V_1} + y_{V_2})$) of the outgoing double meson system by

$$\begin{aligned} \omega _1 = \frac{W}{2} e^Y \,\,\,\,\text{ and }\,\,\,\,\omega _2 = \frac{W}{2} e^{-Y}, \,\,\, \end{aligned}$$

(4)

the total cross section can be expressed by (for details see e.g. Ref. [68])

$$\begin{aligned}&\sigma \left( h_1 h_2 \rightarrow h_1 \otimes V_1V_2 \otimes h_2 ;s \right) = \int \hat{\sigma }\left( \gamma \gamma \rightarrow V_1V_2 ; W \right) \nonumber \\&\qquad \times N\left( \omega _{1},{\mathbf b_{1}} \right) N\left( \omega _{2},{\mathbf b_{2}} \right) S^2_{\mathrm{abs}}({\mathbf b}) \frac{W}{2} \text{ d }^{2} {\mathbf b_{1}} \text{ d }^{2} {\mathbf b_{2}} \text{ d }W \text{ d }Y. \end{aligned}$$

(5)

It is important to emphasize that in EPA we disregard the photon virtualities, which is a good approximation, mainly for ions, since the typical virtualities are ${<}1/R_h$. Moreover, the highest energy of the photons is of the order of the inverse Lorentz contracted radius of the hadron $\approx \gamma _\mathrm{L}/R_h$, with the spectra decreasing exponentially at larger energies. Consequently, for the same Lorentz factor, we have $W_{\mathrm{max}}^{pp} > W_{\mathrm{max}}^{pA} > W_{\mathrm{max}}^{AA}$. Finally, due to the $Z^2$ dependence of the photon spectra, for a fixed W the following hierarchy is valid for processes induced by $\gamma \gamma$ interactions: $\sigma _{AA} \sim Z^2 \cdot \sigma _{pA} \sim Z^4 \cdot \sigma _{pp}$.

In order to estimate this cross section we must describe the $\gamma \gamma \rightarrow V_1V_2$ interaction in a large energy range. In the following we will assume that

$$\begin{aligned} \hat{\sigma }\left( \gamma \gamma \rightarrow V_1V_2 ; W \right) = \hat{\sigma }^{\mathrm{LE}}\left( W \right) + \hat{\sigma }^{\mathrm{HE}}\left( W \right) \end{aligned}$$

(6)

where the LE term is associated to the description of the cross section at low energies $W \lesssim 10$ GeV, while the HE term describes the region of larger values of W. Double vector meson production at low energies has been discussed and improved in Refs. [63, 64]. As in Ref. [63], we will evaluate double $\rho$ production in $\gamma \gamma$ interactions directly from the experimental measurements using a fit to the world data, which describes the experimental data in the region of few GeV. In particular, we will take into account the huge enhancement close to the threshold observed in the data, which is not yet well understood. As demonstrated in Ref. [63] this contribution determines the behavior of double $\rho$ production in AA collisions. In the case of double $J/\Psi$ production, as in Ref. [64], we will consider the contribution associated to the box diagrams, calculated in the heavy quark non-relativistic approximation. In Ref. [64] the authors have also estimated the contribution associated to the two-gluon exchange, which implies a $\gamma \gamma \rightarrow J/\Psi J/\Psi$ cross section independent of the energy. In our analysis, we will not include this contribution in the low energy term, since it is the leading order term in the dipole–dipole interaction present in our formalism to treat the high energy term discussed in the following. Finally, it is important to emphasize that one of the main conclusions from Ref. [64] is that in PbPb collisions the box mechanism significantly dominates over the two-gluon exchange one.

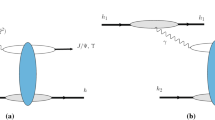
The description of double vector meson production in $\gamma \gamma$ interactions at high energies has attracted the attention of several theoretical groups in the last years, with the cross section being estimated in different theoretical frameworks [60, 61, 63–65, 69–80], as, for instance, the solution of the BFKL equation and impact factors at leading and next-to-leading orders. In particular, in Ref. [65] we have estimated the total $\gamma (Q_1^2) + \gamma (Q_2^2) \rightarrow V_1 + V_2$ cross sections for $V_i = \rho$, $\phi$, $J/\psi$, and $\Upsilon$ in the color dipole formalism considering the improved treatment of the dipole–dipole cross section proposed in Ref. [81]. We have also taken advantage of the progress in the knowledge of vector meson wave functions. Moreover, in Ref. [65] we have taken into account the non-linear effects in the QCD dynamics, which are expected to be present at large energies. An important aspect of the analysis presented in Ref. [65] is that the main ingredients are constrained by LEP and HERA data. In particular, assuming the values for the slope parameter $B_{V_1V_2}$ proposed in Ref. [78], it is possible to obtain parameter-free predictions for the $\rho \rho$ and $J/\Psi J/\Psi$ production cross sections at high energies. In the case of ultra peripheral hadronic collisions, double meson production is induced by the interaction of real photons and can be represented by the diagram in Fig. 1 in the color dipole formalism. In this approach the $\gamma \gamma \rightarrow V_1 V_2$ interaction at hadronic colliders can be seen as a succession in time of four factorizable subprocesses (see Fig. 1): (1) the photons are emitted by the incident hadrons, (2) the photons fluctuate into quark–antiquark pairs (the dipoles), (3) these color dipoles interact and, (4) the pairs convert into the vector meson final states. In particular, the $\gamma \gamma \rightarrow V_1 V_2$ cross section can be expressed as follows:

$$\begin{aligned} \sigma \, (\gamma \gamma \rightarrow V_1 \, V_2)&= \int \mathrm{d}t \, \frac{\mathrm{d}\sigma (\gamma \gamma \rightarrow V_1 \, V_2)}{\mathrm{d}t}\,\nonumber \\&= \frac{1}{B_{V_1 \,V_2}} \left. \frac{\mathrm{d}\sigma (\gamma \gamma \rightarrow V_1 \, V_2)}{\mathrm{d}t}\,\right| _{t_{\mathrm{min}}=0}\nonumber \\ {}&= \frac{[\mathcal{I}m \, \mathcal{A}(W^2,\,t=0)]^2}{16\pi \,B_{V_1 \,V_2}}, \end{aligned}$$

(7)

Fig. 1

Double vector meson production in $\gamma \gamma$ interactions at hadronic colliders in the color dipole picture

where we have approximated the t-dependence of the differential cross section by an exponential with $B_{V_1 \, V_2}$ being the slope parameter. The imaginary part of the amplitude at zero momentum transfer $\mathcal{A}(W^2,\,t=0)$ reads

$$\begin{aligned}&\mathcal{I}m \, \mathcal{A}\, (\gamma \gamma \rightarrow V_1 \, V_2) \nonumber \\&\quad =\int \mathrm{d}z_1\, \mathrm{d}^2\varvec{r}_1 \,[\Psi ^\gamma (z_1,\,\varvec{r}_1)\,\, \Psi ^{V_1*}(z_1,\,\varvec{r}_1)]_T \nonumber \\&\qquad \times \int \mathrm{d}z_2\, \mathrm{d}^2\varvec{r}_2 \,[\Psi ^\gamma (z_2,\,\varvec{r}_2)\,\, \Psi ^{V_2 *}(z_2,\,\varvec{r}_2)]_T \, \sigma _{d d}(\varvec{r}_1, \varvec{r}_2,Y), \end{aligned}$$

(8)

where $\Psi ^{\gamma }$ and $\Psi ^{V_i}$ are the light-cone wave functions of the photon and vector meson, respectively, and T the transverse polarization. The variable $\varvec{r}_1$ defines the relative transverse separation of the pair (dipole) and $z_1$ $(1-z_1)$ is the longitudinal momentum fraction of the quark (antiquark). Similar definitions hold for $\varvec{r}_2$ and $z_2$. The variable Y is the rapidity and will be defined later. The basic blocks are the photon wave function, $\Psi ^{\gamma }$, the meson wave function, $\Psi ^{V}$, and the dipole–dipole cross section, $\sigma _{d\,d}$. In contrast to the photon wave function, which is well known in the literature (see e.g. [82]), the description of the vector meson wave functions is still a subject of debate. The simplest approach is to assume that the vector meson is predominantly a quark–antiquark state and that the spin and polarization structure is the same as in the photon [82–86]. As in Ref. [65] we will assume that the overlap between the photon and the vector meson wave function, for the transversely polarized case, is given by (for details see Ref. [82])

$$\begin{aligned} (\Psi _{V}^* \Psi )_T&= \hat{e}_f e \frac{N_c}{\pi z (1-z)}\left\{ m_f^2K_0(\epsilon r)\phi _T(r,z)\right. \nonumber \\&\quad \left. -\,[z^2+(1-z)^2]\epsilon K_1(\epsilon r) \partial _r \phi _T(r,z)\right\} , \end{aligned}$$

(9)

where $\hat{e}_f$ is the effective charge of the vector meson, $m_f$ is the quark mass, $N_c = 3$, $\epsilon ^2 = z(1-z)Q^2 + m_f^2$ and $\phi _T(r,z)$ defines the scalar part of the vector meson wave function. In the following we will consider the Gauss-LC model for $\phi _T(r,z)$, which is then given by

$$\begin{aligned} \phi _T(r,z) = N_T [z(1-z)]^2 \exp \left( -\frac{r^2}{2R_T^2}\right) . \end{aligned}$$

(10)

The parameters $N_T$ and $R_T$ are determined by the normalization condition of the wave function and by the decay width (see Ref. [65] for details). The other main input to calculate the $\gamma \gamma \rightarrow V_1 V_2$ cross section is the dipole–dipole cross section, $\sigma _{d\,d}$. At lowest order, the dipole–dipole interaction can be described by the two-gluon exchange between the dipoles, with the resulting cross section being energy independent (see, e.g., Ref. [87]). The inclusion of the leading corrections associated to terms $\propto \log (1/x)$ (as described by the BFKL equation) leads to a power-law energy behavior of the cross section, which violates the unitarity at high energies. Unitarity corrections were introduced in Ref. [88], considering the color dipole picture and independent multiple scatterings between the dipoles. These corrections were also addressed in Refs. [89, 90] in the context of the Color Glass Condensate (CGC) formalism [91–95].

In the eikonal approximation the dipole–dipole cross section can be expressed as follows:

$$\begin{aligned} \sigma ^{dd} (\varvec{r}_1,\varvec{r}_2,Y) = 2 \int \mathrm{d}^2\varvec{b}\,\mathcal{{N}}(\varvec{r}_1,\varvec{r}_2,\varvec{b},Y) \end{aligned}$$

(11)

where $\mathcal{{N}}(\varvec{r}_1,\varvec{r}_2,\varvec{b},Y)$ is the scattering amplitude of the two dipoles with transverse sizes $\varvec{r}_1$ and $\varvec{r}_2$, relative impact parameter $\varvec{b}$ and rapidity separation Y. The interaction of two dipoles of similar sizes is still an open question (see, e.g., Ref. [96]). In a first approximation, it is useful to express $\mathcal{{N}}$ in terms of the solution of the Balitsky–Kovchegov (BK) equation (obtained disregarding the $\varvec{b}$ dependence), which has been derived considering an asymmetric frame where the projectile has a simple structure and the evolution occurs in the target wave function [97–99]. A shortcoming of this approach is that, although the unitarity of the S-matrix ($\mathcal{{N}} \le 1$) is respected by the solution of the BK equation, the associated dipole–dipole cross section can still rise indefinitely with the energy, even after the black disk limit ($\mathcal{{N}} = 1$) has been reached at central impact parameters, due to the non-locality of the evolution. In Ref. [81] we have proposed a more elaborated model for the impact parameter dependence in order to obtain more realistic predictions for the dipole–dipole cross section. Basically, we assumed that only the range $b < R$, where $R =$ Max$(r_1,r_2)$, contributes to the dipole–dipole cross section, i.e. we assumed that $\mathcal{{N}}$ is negligibly small when the dipoles have no overlap with each other ($b>R$). Therefore the dipole–dipole cross section can be expressed as follows [81]:

$$\begin{aligned} \sigma ^{dd} (\varvec{r}_1,\varvec{r}_2,Y) \!=\! 2 \, {{N}}(\varvec{r},Y) \int _0^R \mathrm{d}^2\varvec{b}\!=\! 2 \pi R^2 {{N}}(\varvec{r},Y), \end{aligned}$$

(12)

where ${{N}}(\varvec{r},Y)$ is the forward scattering amplitude, which can be obtained as a solution of the BK equation disregarding the impact parameter dependence or from phenomenological models that describe the HERA data. The explicit form of $\sigma ^{dd}$ reads

$$\begin{aligned} \sigma ^{dd} (\varvec{r}_1,\varvec{r}_2,Y)&= 2 \pi r_1^2 N(r_2,Y_2) \, \Theta (r_1 - r_2)\nonumber \\&\quad + 2 \pi r_2^2 N(r_1,Y_1) \, \Theta (r_2 - r_1), \end{aligned}$$

(13)

where $Y_i = \ln (1/x_i)$ and

$$\begin{aligned} x_i = \frac{Q_i^2 + 4 m_f^2}{W^2 + Q_i^2}. \end{aligned}$$

(14)

As in Refs. [65, 81] we will consider in our calculations the IIM-S model [100, 101] for the forward scattering amplitude, which is based on the solutions of the BK equation at small and large dipoles, and is given by

$$\begin{aligned} {{N}}(\varvec{r},Y) \!=\! \left\{ \begin{array}{l@{\quad }l} {\mathcal N}_0\, \left( \frac{r\, Q_s}{2}\right) ^{2\left( \gamma _s \!+\! \frac{\ln (2/r Q_s)}{\kappa \,\lambda \,Y}\right) }\,, &{} \text{ for } r Q_s(x) \le 2,\\ 1 - \exp ^{-a\,\ln ^2\,(b\,r\, Q_s)}\,, &{} \text{ for } r Q_s(x) > 2, \end{array} \right. \nonumber \\ \end{aligned}$$

(15)

where a and b are determined by continuity conditions at $\varvec{r}Q_s(x)=2$, $\gamma _s= 0.6194$, $\kappa = 9.9$, $\lambda =0.2545$, $Q_0^2 = 1.0$ GeV$^2$, $x_{0}=0.2131\times 10^{-4}$ and ${\mathcal N}_0=0.7$. As demonstrated in Ref. [81], using this model we can describe the LEP data for the total $\gamma \gamma$ cross sections and photon structure functions.

Fig. 2

Rapidity distribution in double vector meson production in $\gamma \gamma$ interactions at PbPb collisions considering different values of $\sqrt{s}$

Fig. 3

Rapidity distribution in double vector meson production in $\gamma \gamma$ interactions at $p\mathrm{Pb}$ collisions considering different values of $\sqrt{s}$

Fig. 4

Rapidity distribution for double vector meson production in $\gamma \gamma$ interactions at pp collisions considering different values of $\sqrt{s}$

Fig. 5

Energy dependence of the total cross section of double vector meson production in $\gamma \gamma$ interactions at pp, $p\mathrm{Pb}$, and PbPb collisions

In the following we present our predictions for the rapidity distributions and total cross sections for $\rho$–$\rho$ and $J/\Psi$–$J/\Psi$ production through $\gamma \gamma$ interactions in pp, $p\mathrm{Pb}$, and PbPb collisions. In order to estimate the contribution of the gluonic part associated with the dipole–dipole interaction, we will compare the full predictions, obtained considering the low and high energy contributions (denoted Low Energy + IIM-S hereafter) with those without the high energy contribution (Low Energy hereafter). In order to estimate the equivalent photon spectra for $A = \mathrm{Pb}$, we will consider the a monopole form factor $F(q^2) = \Lambda ^2/(\Lambda ^2 + q^2)$, with $\Lambda = 0.088$ GeV adjusted to reproduce the root mean square (rms) radius of the nucleus. Moreover, we will assume that $R_A = 1.2 \, A^{\frac{1}{3}}$ fm. In the proton case, we will consider that $F(q^2) = 1/[1 + q^2/(0.71\,\, \text{ GeV }^2)]^2$ and $R_p = 0.7$ fm. Finally, as in [78] we will assume $B_{\rho \rho } = 10$ GeV$^{-2}$ and $B_{\psi \psi } = 0.44$ GeV$^{-2}$. Our results for the rapidity distributions are presented in Figs. 2, 3 and 4. In the case of PbPb collisions, presented in Fig. 2, we see that the Low Energy and Low Energy + IIM-S predictions are almost identical for double $\rho$ production for all considered energies, which indicates that the gluonic contribution for this process is very small, in agreement with the conclusion obtained in Ref. [63]. This result is can be related to the energy behavior of the $\gamma \gamma \rightarrow \rho \rho$ cross section at high energies, which presents a mild growth with W, expected in a process dominated by large dipoles, and to the fact that in AA collisions we are probing values of $W \le 160$ GeV for $\sqrt{s} = 5.5$ TeV. In contrast, for double $J/\Psi$ production, we observe that the gluonic contribution increases with the energy, which is associated to the steep energy behavior of the $\gamma \gamma \rightarrow J/\Psi J/\Psi$ cross section. For $\sqrt{s} = 0.5$ TeV the analysis of this process can be useful to probe the box mechanism. On the other hand, for $\sqrt{s} = 5.5$ TeV the gluonic contribution implies an enhancement by a factor 2 of the rapidity distribution at $Y = 0$. When $p\mathrm{Pb}$ collisions are considered, we obtain the asymmetric rapidity distributions presented in Fig. 3, which is expected since the nuclear equivalent photon spectra is enhanced by a factor $Z^2$. Moreover, in this case the energy range probed in the $\gamma \gamma$ interactions increases for $W \le 160$ GeV for $\sqrt{s} = 8.8$ TeV. As a consequence, we observe that the difference between the Low Energy and Low Energy + IIM-S predictions starts to occur in the case of double $\rho$ production and becomes appreciable for double $J/\Psi$ production. Finally, in Fig. 4 we present our results for pp collisions for different values of $\sqrt{s}$. In this case the double vector meson production is induced by $\gamma \gamma$ interactions with $W \le 4500$ GeV for $\sqrt{s} = 14$ TeV. This large range of energies probed in the interaction implies that the gluonic contribution becomes very important for the description of double vector production, increasing the rapidity distributions at $Y = 0$ by a factor 2 in the case of $\rho \rho$ production and by a factor 40 for double $J/\Psi$ production in pp collisions at 14 TeV. The importance of the gluonic contribution can also be estimated by the analysis of the energy dependence of the total cross section for double vector meson production in $\gamma \gamma$ interactions at pp, $p\mathrm{Pb}$, and PbPb collisions. Our results are presented in Fig. 5. In agreement with our previous discussion, we can see that this contribution is small for double $\rho$ production and appreciable for double $J/\Psi$ production, mainly in pp collisions. This result indicates that the analysis of double $J/\Psi$ production in ultra peripheral hadronic collisions can be useful to study the QCD dynamics at high energies, as originally suggested in Ref. [60]. In Tables 1 and 2 we present our predictions for total cross sections for double vector meson production in pp, $p\mathrm{Pb}$, and PbPb collisions for the energies of RHIC and LHC as well as for the conceptual design energies of the FCC [66] and CEPC–SPPC [67]. It is important to emphasize that our Low Energy + IIM-S predictions can be considered as a lower bound for the gluonic contribution, since other models for the dipole–dipole cross section or for the description of the QCD dynamics imply larger values for the $\gamma \gamma \rightarrow J/\Psi J/\Psi$ cross section (for a detailed discussion see Ref. [65]). Consequently, we believe that the analysis of this process is feasible in hadronic colliders. Additionally, considering the results from Ref. [65], which indicate that $\gamma \gamma \rightarrow V_1 V_2$ cross sections for the $\rho J/\Psi$, $\phi J/\Psi$, $\rho \Upsilon$, $J\Psi \Upsilon$, and $\Upsilon \Upsilon$ production increase strongly with the energy, we can also expect that these final states could be analyzed in the future. As discussed in detail in Refs. [60–62, 65], the study of these different final states is important to understand the transition between the soft and hard regimes of the QCD dynamics, since different dipole sizes are probed in each process.

Table 1 Total cross sections for double $\rho$ production in $\gamma \gamma$ interactions at pp, $p\mathrm{Pb}$, and PbPb collisions for RHIC, LHC, FCC, and CEPC–SPPC energies. Values in nb

Table 2 Total cross sections for double $J/\psi$ production in $\gamma \gamma$ interactions at pp, $p\mathrm{Pb}$, and PbPb collisions for RHIC, LHC, FCC, and CEPC–SPPC energies. Values em pb

Finally, let us summarize our main conclusions. In recent years, a series of studies have discussed in detail the computation of the total cross section and the exclusive production of different final states in $\gamma \gamma$ interactions considering very distinct theoretical approaches. One of the basic motivations for these efforts is the possibility to study the behavior of QCD dynamics at high energies. The ideal laboratory for these studies is the scattering of two off-shell photons at high energy in $e^+\,e^-$ colliders, which could be performed in the International Linear Collider (ILC). However, as the schedule for the construction and operation of this collider is still an open question, the analysis of alternative ways to study the $\gamma \gamma$ interactions is an important theme. The study of double vector meson production in $\gamma \gamma$ interactions in ultra peripheral heavy ion collisions as a probe of the QCD dynamics was proposed in Ref. [60] and developed in Refs. [61, 62]. However, these studies focused only on the high energy regime and disregarded the low energy mechanisms for double vector production. As emphasized in Refs. [63, 64], the contribution of these mechanisms is important in AA collisions, since the maximum center of mass energies probed in the $\gamma \gamma$ interactions is not large and the main contribution of the equivalent photon spectrum comes from photons with low energy. However, these studies have disregarded the effects of the QCD dynamics discussed in Refs. [61, 62] and recently updated in Ref. [65]. In this paper we have combined these two approaches and derived predictions for the $\gamma \gamma \rightarrow VV$ cross section which are valid in the full kinematical range. We have obtained realistic predictions for the total cross sections in hadronic collisions and estimated the relative contribution of the low and high energy regimes. In particular, the results for pp and $p\mathrm{Pb}$ have been derived by the first time. Our results demonstrated that double $\rho$ production is dominated by low energy mechanisms. On the other hand, the gluonic contribution for double $J/\Psi$ production strongly increases with the energy, the study of this process becomes feasible in hadronic collisions (mainly in pp collisions) and it may be useful to constrain the QCD dynamics at high energies, as proposed originally in Ref. [60].