Light stop decays: implications for LHC searches

Abstract

We investigate the flavour-changing neutral current decay of the lightest stop into a charm quark and the lightest neutralino and its four-body decay into the lightest neutralino, a down-type quark and a fermion pair. These are the relevant stop search channels in the low-mass region. The SUSY-QCD corrections to the two-body decay have been calculated for the first time and turn out to be sizeable. In the four-body decay both the contributions from diagrams with flavour-changing neutral current couplings and the mass effects of final state bottom quarks and $\tau$ leptons have been taken into account, which are not available in the literature so far. The resulting branching ratios are investigated in detail. We find that in either of the decay channels the branching ratios can deviate significantly from 1 in large parts of the allowed parameter range. Taking this into account, the experimental exclusion limits on the stop, which are based on the assumption of branching ratios equal to 1, are considerably weakened. This should be taken into account in future searches for light stops at the next run of the LHC, where the probed low stop mass region will be extended.

1 Introduction

With the discovery of a new scalar particle by the LHC experiments ATLAS and CMS [1–4] we have entered a new era of particle physics. The investigation of its properties, like spin and CP quantum numbers and couplings to other standard model (SM) particles, have identified it as the long-sought Higgs particle predicted by the Higgs mechanism [5–9]. The absence of any discovery of new particles beyond the SM, however, leaves the question of the underlying dynamics of the mechanism of electroweak symmetry breaking open. Models with the Higgs boson emerging as composite bound state from a strongly coupled sector [10–17] are compatible with the LHC data, as well as extensions like supersymmetry (SUSY) [18–32] based on a weakly interacting theory. One of the main goals of the LHC is therefore the search for new particles and the subsequent investigation of their properties in order to pin down the true nature of the discovered Higgs boson.

Among the plethora of beyond the SM extensions, SUSY is one of the most extensively studied models. It requires the introduction of at least two complex Higgs doublets, leading in its most economic version, the minimal supersymmetric extension of the SM (MSSM) [33–38], to five Higgs bosons, among which the lightest CP-even state h can be identified with the recently discovered SM-like boson. Within SUSY models the hierarchy problem can be solved by the symmetry between bosonic and fermionic degrees of freedom. Assuming SUSY to be softly broken, the Higgs mass corrections grow logarithmically with the square of the SUSY scale $m_S$. The loop corrections from the top loops and their SUSY partners, the stops, are crucial in order to shift the mass of the lightest SUSY Higgs boson above the upper tree-level bound set by the Z boson mass $M_Z$. With the SUSY scale given by the average stop mass, $m_S^2=m_{\tilde{t}_1} m_{\tilde{t}_2}$, and the stop mixing parameter $X_t$, the mass squared of the lightest Higgs boson including the leading corrections in the SM limit, is given by

$$\begin{aligned}&M_h^2 = M_Z^2 \cos ^2 2\beta + \frac{3 m_t^4}{2 \pi ^2 v^2}\left( \log \left( \frac{m_S^2}{m_t^2} \right) + X_t^2 \left( 1 - \frac{X_t^2}{12} \right) \right) ,\!\!\!\nonumber \\ \end{aligned}$$

(1)

with $m_t$ denoting the top-quark mass, v the vacuum expectation value (VEV) with $v \approx 246$ GeV and

$$\begin{aligned} X_t = \frac{A_t - \mu \cot \beta }{m_S}. \end{aligned}$$

(2)

The ratio of the two VEVs of the neutral components of the MSSM Higgs doublets is given by $\tan \beta$ and $A_t$ denotes the soft SUSY breaking trilinear coupling in the stop sector. A large Higgs boson mass of around 125 GeV can hence be obtained either through a large stop mixing $X_t$ or through heavy stops. Naturalness arguments suggest at least one of the two stop mass eigenstates to be light, since the amount of fine-tuning of the electroweak scale is significantly driven by the stop sector [39]. The maximal mixing scenario, with $X_t^2 \approx 6$ and $m_S \approx 500$ GeV leading to the observed Higgs mass value, therefore optimally reduces the amount of fine-tuning [40]. In most SUSY models a light stop arises naturally due to the mixing being proportional to the large Yukawa coupling, which leads to a large mass splitting between the stop mass eigenstates.

Light stops not only play a special role in view of the Higgs mass and naturalness arguments. A light stop can also lead to the correct relic density through co-annihilation, in particular for mass differences between the stop and the lightest neutralino $\tilde{\chi }_1^0$ of 15–30 GeV [41–46]. Moreover, light stops allow for successful baryogenesis within the MSSM [47–59].¹

Despite the LHC searches pushing the limits on the coloured sparticles above the 1–1.5 TeV range for the first two generations [65, 66], the lightest stop can still be rather light, with masses below the respective kinematical thresholds for the decay into a top and a lightest neutralino $\tilde{\chi }_1^0$, $\tilde{t}_1 \rightarrow t \tilde{\chi }_1^0$, and for the decay $\tilde{t}_1 \rightarrow \tilde{\chi }_1^0 W b$ into a neutralino, a W boson and a bottom quark b. Assuming the lightest stop to be the next-to-lightest supersymmetric particle and the $\tilde{\chi }_1^0$ to be the lightest SUSY particle (LSP), the light stop can then decay into the LSP and a charm quark c or an up quark u, $\tilde{t}_1 \rightarrow (u/c) \tilde{\chi }_1^0$ [67, 68]. Another possible decay channel is the four-body decay $\tilde{t}_1 \rightarrow \tilde{\chi }_1^0 b f \bar{f}'$ [69], with f and $f'$ denoting generic light fermions. The two-body decay into charm/up and neutralino is flavour-violating (FV). The MSSM in general exhibits many sources of flavour violation, so that the decay can already occur at tree level. High precision tests in the sector of quark flavour violation and limits on flavour-changing neutral currents from K, D and B meson studies put stringent constraints on the amount of possible flavour violation [70–72]. In order to solve this new physics flavour puzzle the framework of minimal flavour violation (MFV) has been proposed [73–77], which requires all sources of flavour and CP violation to be given by the SM structure of the Yukawa couplings. The hypothesis of MFV is not renormalisation group invariant [76], however, inducing flavour off-diagonal squark mass terms through the Yukawa couplings, which results in tree-level FCNC couplings. If the FV stop-neutralino-up/charm quark coupling is very small, the four-body decay can become important and has to be taken into account for a reliable prediction of the $\tilde{t}_1$ branching ratios.

Bounds on the stop masses have been set by LEP [78, 79] and tevatron [80, 81], and more recently by the ATLAS [60] and the CMS [82] collaborations. The strongest limits come from the ATLAS analyses Refs. [61, 62]. All these analyses assume a branching ratio of 1 for the analysed decay channel of the $\tilde{t}_1$, either the FV two-body or the four-body decay. However, in Ref. [68] it was already pointed out that the competing FV two-body and four-body stop decays can lead to substantial deviations from branching ratios of 1 in either of the decay channels. This has a significant impact on the stop mass bounds set by the experiments. The calculation in Ref. [68] improved the existing approximate result for the $\tilde{t}_1 \rightarrow (u/c) \tilde{\chi }_1^0$ decay of Ref. [67] by computing the exact one-loop decay width in the framework of MFV. Resummation effects, which can become important, have not been taken into account in that approach. In this work, we therefore include resummation effects through renormalisation group running induced FCNC couplings already at tree level and calculate the one-loop SUSY-QCD corrections to the two-body decay. In order to correctly determine the $\tilde{t}_1$ branching ratios, also the four-body decay is computed by consistently including FCNC couplings. Moreover, non-vanishing masses for the third generation final state fermions have been taken into account. These decay widths have been implemented into the SDECAY [83, 84] routine of SUSY-HIT [85] for the calculation of the decay widths and branching ratios of SUSY particles in the MSSM. With the thus obtained $\tilde{t}_1$ branching ratios we discuss the implications for the LHC stop searches and the bounds obtained on the mass of the lightest stop $m_{\tilde{t}_1}$. The program with the newly implemented stop decays is available at [86].

The outline of the paper is as follows. In Sect. 2 we present the calculation of the SUSY-QCD corrections to the FCNC two-body decay. The computation of the four-body decay is deferred to Sect. 3. In Sect. 4 the details of our parameter scan are given as well as the applied constraints. We discuss our results in the numerical analysis in Sect. 5. Section 6 summarises our findings.

2 The flavour-violating two-body stop decay

The two-body decay of the lightest stop into a charm or an up quark and the lightest neutralino is mediated at tree level by a FCNC coupling. In the MSSM with flavour violation the squark and quark mass matrices cannot be diagonalised simultaneously any more. The squarks are no longer flavour eigenstates and the SUSY partners of the left- and right-chiral up-type quarks mix to form a six-component vector $\tilde{u}_s$ ($s=1,\ldots ,6$). Analogously, the down-type squarks are described by the six-component vector $\tilde{d}_s$. We assume the entries to be ordered in mass, with $\tilde{u}_1$ ($\tilde{d}_1$) denoting the lightest up-type (down-type) squark. The MFV approach naturally accounts for small flavour violation, with the only source of flavour violation being the CKM matrix. A way to implement it, is by assuming that the squark and quark mass matrices can be diagonalised simultaneously at a scale $\mu = \mu _{\text {MFV}}$, so that there are no FCNC couplings at tree level. Flavour mixing is induced through renormalisation group equation (RGE) running at any scale $\mu \ne \mu _{\text {MFV}}$. Due to the large mixing in the stop sector, the lightest up-type squark $\tilde{u}_1$ is hence mostly stop-like. In the following, we will refer to $\tilde{u}_1$ as the lightest stop where appropriate, although it is understood that it has a small flavour admixture from the charm- and up-flavours. Considering a light stop with a mass close to the one of the lightest neutralino, it mainly decays through the FV two-body decays,

$$\begin{aligned} \tilde{u}_1 \rightarrow (u/c) + \tilde{\chi }_1^0. \end{aligned}$$

(3)

Due to the smallness of the up-flavour admixture (because of the small CKM matrix elements, which are responsible for flavour mixing through RGE running) the decay into the up quark final state is suppressed by about two orders of magnitude compared to the charm quark final state. We have performed our calculations for both final states, but will discuss here the one with the charm quark in the final state.

2.1 The squark sector

In order to set up our notation we start with the introduction of the squark sector. Denoting by $\tilde{q}_L^\prime$ and $\tilde{q}_R^\prime$, respectively, a three-component vector in generation space, we define the six-component vector $\tilde{q}^\prime$ describing the squark interaction eigenstates,

$$\begin{aligned} \tilde{q}^\prime = \left( \begin{array}{c} \tilde{q}_L^\prime \\ \tilde{q}_R^\prime \end{array} \right) . \end{aligned}$$

(4)

The squark mass matrix, written as a $2\times 2$ Hermitian matrix of $3\times 3$ blocks,

$$\begin{aligned} \mathcal{M}_{\tilde{q}^\prime }^2 = \left( \begin{array}{cc} \mathcal{M}_{\tilde{q}^\prime _{LL}}^2 &{} \mathcal{M}_{\tilde{q}^\prime _{LR}}^2 \\ \mathcal{M}_{\tilde{q}^\prime _{RL}}^2 &{} \mathcal{M}_{\tilde{q}^\prime _{RR}}^2 \end{array} \right) , \end{aligned}$$

(5)

is diagonalised by a $6 \times 6$ unitary matrix $\widetilde{W}$, rotating the squark interaction eigenstates to the mass eigenstates $\tilde{q}^m$,

$$\begin{aligned} \tilde{q}^m = \widetilde{W} \tilde{q}^\prime , \end{aligned}$$

(6)

where the $\tilde{q}^m$ are ordered in mass. We can decompose the squark mass eigenstate field into left- and right-chiral interaction eigenstates through ($s=1,\ldots ,6, \,i=1,2,3$)

$$\begin{aligned} \tilde{q}^m_s = \widetilde{W}_{si} \tilde{q}^\prime _{iL} + \widetilde{W}_{s \, i+3} \tilde{q}^\prime _{iR} \equiv (\widetilde{W}_L \tilde{q}^\prime _L + \widetilde{W}_R \tilde{q}^\prime _R)_s, \end{aligned}$$

(7)

where i is the generation index. The matrices $U^{u_{L,R}}$ and $U^{d_{L,R}}$ are the $3\times 3$ unitary matrices that rotate the left- and right-handed up- and down-type current eigenstates $u_{L,R}$ and $d_{L,R}$ to their corresponding mass eigenstates, $u^m_{L,R}$ and $d^m_{L,R}$,

$$\begin{aligned} u_{L,R}^m = U^{u_{L,R}} u_{L,R} \quad \text{ and } \quad d_{L,R}^m = U^{d_{L,R}} d_{L,R} \; . \end{aligned}$$

(8)

They define the CKM matrix $V^{\text {CKM}}$ as

$$\begin{aligned} V^{\text {CKM}} = U^{u_L} U^{d_L\dagger }. \end{aligned}$$

(9)

In the super-CKM basis the squarks are rotated by the same unitary matrices as the quarks, implying that at scales $\mu \ne \mu _{\text {MFV}}$ or in non-minimal flavour violation models, the squark mass matrix is flavour-mixed, contrary to the quark mass matrix. Otherwise, the squarks are flavour eigenstates after rotation by $U^{q_{L,R}}$, and we have

$$\begin{aligned} \tilde{q}_L = U^{q_L} \tilde{q}_L^\prime \quad \text{ and } \quad \tilde{q}_R = U^{q_R} \tilde{q}_R^\prime , \end{aligned}$$

(10)

with the squared mass matrix in the flavour eigenstate basis $(\tilde{q}_L,\tilde{q}_R)^T$ given by

$$\begin{aligned} \mathcal{M}_{\tilde{q}}^2 = \left( \begin{array}{cc} (\tilde{M}_{\tilde{q}_L}^2 +m_q^2) \mathbf{1}_3 &{} m_q (A_q -\mu r_q) \mathbf{1}_3 \\ m_q (A_q -\mu r_q) \mathbf{1}_3 &{} (\tilde{M}_{\tilde{q}_R}^2 +m_q^2) \mathbf{1}_3 \end{array} \right) , \end{aligned}$$

(11)

where $\mathbf{1}_3$ denotes a $3\times 3$ unit matrix.² Here $\tilde{M}_{\tilde{q}_{L,R}}$ are given by the left- and right-handed scalar soft SUSY breaking masses $M_{\tilde{q}_{L,R}}$ and the D-terms

$$\begin{aligned} \tilde{M}_{\tilde{q}_{L,R}}^2= & {} M_{\tilde{q}_{L,R}}^2 + D_{\tilde{q}_{L,R}} ,\end{aligned}$$

(12)

$$\begin{aligned} D_{\tilde{q}_L}= & {} M_Z^2 \cos 2\beta (I^3_q - Q_q \sin ^2 \theta _W) ,\end{aligned}$$

(13)

$$\begin{aligned} D_{\tilde{q}_R}= & {} M_Z^2 \cos 2\beta Q_q \sin ^2 \theta _W, \end{aligned}$$

(14)

with the third component $I^3_q$ of the weak isospin of the quark q, $Q_q$ its electric charge and $\theta _W$ denoting the Weinberg angle. The soft SUSY breaking trilinear coupling is given by $A_q$, and $\mu$ stands for the higgsino mass parameter. In addition, we have used the abbreviations $r_d= 1/r_u = \tan \beta$ for down- and up-type quarks. The flavour eigenstates are rotated to their mass eigenstates by the $6\times 6$ unitary matrix W, $(s,t=1,\ldots ,6$, $i=1,2,3)$,

$$\begin{aligned} \tilde{q}^m_s= & {} W_{st} \left( \begin{array}{c} \tilde{q}_L \\ \tilde{q}_R \end{array} \right) _t = W_{si} \, \tilde{q}_{Li} + W_{s \, i+3} \, \tilde{q}_{Ri}\nonumber \\\equiv & {} (W_L \tilde{q}_L + W_R \tilde{q}_R)_s. \end{aligned}$$

(15)

The $6\times 3$ matrices $\widetilde{W}_{L,R}$ can hence be factorised into the $6\times 3$ matrices $W_{L,R}$, which are flavour-diagonal at $\mu _{\text {MFV}}$, and the $3\times 3$ quark rotation matrices,

$$\begin{aligned} \widetilde{W}_L = W_L U^{q_L} \quad \text{ and } \quad \widetilde{W}_R = W_R U^{q_R}, \quad q=u,d, \end{aligned}$$

(16)

as can be inferred from comparing Eq. (15) with Eq. (7) and using Eq. (10).

2.2 The loop-corrected stop two-body decay

Defining the $4\times 4$ neutralino mixing matrix Z diagonalising the neutralino mass matrix in the bino, wino, down- and up-type higgsino basis $(-i\tilde{B},-i\widetilde{W}_3, \tilde{H}_1^0, \tilde{H}_2^0)$, we can write the coupling between an up-type quark $u_i$ ($i=1,2,3$), an up-type squark $\tilde{u}_s$ ($s=1,\ldots ,6$) and a neutralino $\tilde{\chi }^0_l$ ($l=1,\ldots ,4$) in terms of the left- and right-chiral couplings as

$$\begin{aligned} g^L_{isl}= & {} -ge^{u_i}_{Rl} W^\dagger _{i+3 \,s} - \frac{gZ_{l4} m_{u_i} \delta _{ij}}{\sqrt{2} M_W \sin \beta } W^\dagger _{js} \end{aligned}$$

(17)

$$\begin{aligned} g^R_{isl}= & {} -ge^{u_i}_{Ll} W^\dagger _{is} - \frac{g Z_{l4} m_{u_i} \delta _{ij}}{\sqrt{2} M_W \sin \beta } W^\dagger _{j+3 \, s}. \end{aligned}$$

(18)

Here $M_W$ and $m_{u_i}$ denote, respectively, the mass of the W boson and of the quark and g the SU(2) gauge coupling. Furthermore, we have introduced the abbreviations

$$\begin{aligned} e^q_{Ll}= & {} \sqrt{2} [Z_{l1} t_W (Q_q-I^3_q)+Z_{l2} I_q^3] ,\end{aligned}$$

(19)

$$\begin{aligned} e^q_{Rl}= & {} -\sqrt{2} Q_q t_W Z_{l1}, \end{aligned}$$

(20)

where $t_W$ is a short-hand notation for $\tan \theta _W$. We can then write the leading order tree-level two-body decay width for the decay of the lightest up-type squark into a charm quark and the lightest neutralino as

(21)

with the two-body phase space function

$$\begin{aligned} \lambda (x,y;z) = \sqrt{(1-x/z-y/z)^2 - 4xy/z^2} \end{aligned}$$

(22)

and the lightest up-type squark and neutralino masses, $m_{\tilde{u}_1}$ and $m_{\tilde{\chi }_1^0}$. Note that for a non-vanishing decay width the flavour off-diagonal matrix elements of the squark mixing matrix W have to be non-vanishing. For simplicity, in the following we set the charm quark mass to zero, which does not have any significant effects unless the mass difference between the decaying squark and the neutralino becomes comparable with the charm quark mass or the lightest neutralino becomes mostly higgsino-like. For a mass difference of 5 GeV e.g. the difference between the leading order (LO) decay width with $m_c=0$ and the one with non-vanishing charm quark mass is about 3 % and less than 1 % for 10 GeV mass difference. In mSUGRA models the lightest neutralino for a top-quark mass of 173 GeV never becomes higgsino-like [87]. The lightest neutralino can only be higgsino-like for mass values close to the mass of the lightest chargino. While the limits on the chargino masses are model-dependent, the parameter space for light charginos gets more and more constrained by the LHC experiments [88, 89]. In scenarios with the lightest neutralino mass much lighter than the chargino masses, the neutralino is mainly bino-like.

The decay width $\Gamma ^{\text {NLO}}$ including the next-to-leading order (NLO) SUSY-QCD corrections is composed of the LO width $\Gamma ^{\text {LO}}$, of the contributions $\Gamma ^{\text {virt}}$ from the virtual corrections, $\Gamma ^{\text {real}}$ from the real corrections and the one arising from the counterterms, $\Gamma ^{\text {CT}}$,

$$\begin{aligned} \Gamma ^{\text {NLO}} = \Gamma ^{\text {LO}} + \Gamma ^{\text {virt}} + \Gamma ^{\text {real}} + \Gamma ^{\text {CT}}. \end{aligned}$$

(23)

2.2.1 The NLO SUSY-QCD corrections

The virtual corrections arise from the vertex diagrams shown in Fig. 1 (upper) and the squark and quark self-energies, depicted in Fig. 1 (middle) and (lower), respectively. The vertex corrections involve gluons and gluinos. The gluinos can in general couple to two different flavours of quarks and squarks, which is taken into account by the quark and squark indices i and s ($i=1,2,3$, $s=1,\ldots ,6$) in the corresponding second Feynman diagram.

Fig. 1

Generic diagrams of the vertex corrections (upper) and of the squark (middle) and quark self-energies (lower) contributing to the SUSY-QCD corrections of the decay $\tilde{u}_1 \rightarrow c \tilde{\chi }_1^0$, with the quark indices $i,j=1,2,3$ and the squark indices $r,s,t=1,\ldots ,6$

The counterterm diagrams in Fig. 2 cancel the ultraviolet (UV) divergences of the virtual corrections in the renormalisation procedure.

Fig. 2

Counterterm diagrams

After renormalisation the virtual corrections still exhibit infrared (IR) and collinear divergences. The real corrections, shown in Fig. 3, arise from the radiation of a gluon off the squark and off the charm quark line. In accordance with the Kinoshita–Lee–Nauenberg theorem [90, 91] the IR divergences emerging from the real corrections cancel those of the virtual corrections. As there are no massless particles in the initial state, in our case also the collinear divergences of the virtual and real corrections cancel. The computation of the decay width is performed in $D=4-2\epsilon$ dimensions. The UV and IR divergences arise then as poles in $\epsilon$. We distinguish between the UV and IR divergences by denoting the corresponding poles as $1/\epsilon _{\text {UV}}$ and $1/\epsilon _{\text {IR}}$. The loop integrals are evaluated in the framework of dimensional reduction [92, 93] in order to ensure the conservation of the SUSY relations.

The virtual corrections have been calculated with FeynArts/FormCalc [94–97]. The results for the gluon contribution are the same as for the squark decay into a quark and a neutralino, $\tilde{q}_{1,2} \rightarrow q \tilde{\chi }_1^0$, given in Refs. [98–101]. In order to regularise the UV divergences we adopt an on-shell renormalisation scheme. The bare quark and squark fields with superscript (0) are replaced by the corresponding renormalised fields according to

$$\begin{aligned} \tilde{q}^{(0)} = \left( 1 + \frac{1}{2} \delta Z^{\tilde{q}} \right) \tilde{q},\quad q_{L,R}^{(0)} = \left( 1 + \frac{1}{2} \delta Z^{L/R} \right) q_{L/R}.\nonumber \\ \end{aligned}$$

(24)

In terms of the real parts of the squark self-energy $\tilde{\Sigma }$, the squark wave function renormalisation constants $\delta Z^{\tilde{q}}$ are given by ($s,t=1,\ldots ,6$)

$$\begin{aligned} \delta Z^{\tilde{q}}_{st} = \left\{ \begin{array}{ll} - \text{ Re } \left. \frac{\partial \tilde{\Sigma }_{ss} (p^2)}{\partial p^2}\right| _{p^2=m_{\tilde{q}_s}^2} &{} \quad \text{ if } s=t \\ \frac{2}{m_{\tilde{q}_s}^2-m_{\tilde{q}_t}^2} \text{ Re } \tilde{\Sigma }_{st} (p^2=m_{\tilde{q}_t^2}) &{} \quad \text{ if } s\ne t. \end{array} \right. \end{aligned}$$

(25)

The self-energies $\tilde{\Sigma }$ are obtained from the Feynman diagrams in Fig. 1 (middle). Here, the third diagram comprises the quartic squark coupling. As we calculate only the $\mathcal{O}(\alpha _s)$ corrections, in the quartic squark coupling consistently only the terms proportional to $\alpha _s$ are taken into account. Another diagram, not shown in Fig. 1 (middle), involving a quartic coupling between up- and down-type squarks, vanishes due to the flavour structure.

Fig. 3

Diagrams contributing to the real corrections

Defining the following structure for the quark self-energies ($i,j=1,2,3$),

(26)

with $\mathcal{P}_{L/R} = (1\mp \gamma _5)/2$, the off-diagonal chiral components of the wave function renormalisation constants for the quarks read

$$\begin{aligned} \delta Z^L_{ij}= & {} \frac{2}{m_{q_i}^2-m_{q_j}^2} \left[ m_{q_i} \, \text{ Re } \Sigma _{ij}^{Ls} (m_{q_j}^2) + m_{q_j} \, \text{ Re } \Sigma _{ij}^{Rs} (m_{q_j}^2)\right. \nonumber \\&+\left. m_{q_j}^2 \, \text{ Re } \Sigma _{ij}^{L} (m_{q_j}^2) + m_{q_i} m_{q_j} \, \text{ Re } \Sigma _{ij}^{R} (m_{q_j}^2) \right] ,\nonumber \\ \delta Z^R_{ij}= & {} \frac{2}{m_{q_i}^2-m_{q_j}^2} \left[ m_{q_j} \, \text{ Re } \Sigma _{ij}^{Ls} (m_{q_j}^2) + m_{q_i} \, \text{ Re } \Sigma _{ij}^{Rs} (m_{q_j}^2)\right. \nonumber \\&+ \left. m_{q_i} m_{q_j} \, \text{ Re } \Sigma _{ij}^{L} (m_{q_j}^2) + m_{q_j}^2 \, \text{ Re } \Sigma _{ij}^{R} (m_{q_j}^2) \right] \nonumber \\&\quad \text{ for } i\ne j. \end{aligned}$$

(27)

The diagonal components read ($i=j$)

$$\begin{aligned} \delta Z_{ii}^{L/R}= & {} - \text{ Re } \Sigma _{ii}^{L/R} (m_{q_i}^2) \nonumber \\&- m_{q_i} \frac{\partial }{\partial p^2} \text{ Re } \left( m_{q_i} \Sigma _{ii}^{L/R} (p^2) + m_{q_i} \Sigma _{ii}^{R/L} (p^2)\right. \nonumber \\&+ \left. \Sigma _{ii}^{L/Rs} (p^2) + \Sigma _{ii}^{R/Ls} (p^2) \right) \left| _{p^2=m_{q_i^2}}{.}\right. \end{aligned}$$

(28)

The self-energies $\Sigma$ appearing in the wave function renormalisation constants are obtained from the diagrams in Fig. 1 (lower). The gluon diagram does not contain any scale and naively would be expected to be zero. However, it exhibits UV and IR divergences. The diagram is proportional to $1/\epsilon _{\text {UV}} - 1/\epsilon _{\text {IR}}$ and has to be taken into account, in order to ensure the separate cancellation of the UV and IR divergences.

After the on-shell renormalisation of the quark and squark wave functions we are only left with the one-loop vertex diagrams and the FCNC vertex counterterm. It is given by the wave function renormalisation, the renormalisation of the quark and squark mixing matrices [102–109] and the renormalisation of the quark masses. The mixing matrix counterterms $\delta u$ and $\delta \tilde{w}$ relate the bare mixing matrices $U^{(0)}$ and $\widetilde{W}^{(0)}$ with the renormalised ones,

$$\begin{aligned} \begin{array}{l@{\quad }l} U_{ij}^{(0)L/R} = (\delta _{ik}+\delta u_{ik}^{L/R}) U_{kj}^{L/R} \; &{} i,j,k=1,2,3,\\ \widetilde{W}^{(0)}_{st} = (\delta _{sr}+\delta \tilde{w}_{sr}) \widetilde{W}_{rt} \; &{} r,s,t=1,\ldots ,6. \end{array} \end{aligned}$$

(29)

Both the bare and the renormalised mixing matrices are required to be unitary leading to antihermitian counterterms. We determine the UV divergent part of each counterterm such that it cancels the divergent part of the antihermitian part of the corresponding wave function renormalisation matrix [105–109],

$$\begin{aligned} \delta u^{L/R}= & {} \frac{1}{4} \left( \delta Z^{L/R} - \delta Z^{L/R\dagger } \right) ,\end{aligned}$$

(30)

$$\begin{aligned} \delta \tilde{w}= & {} \frac{1}{4} (\delta Z^{\tilde{q}} - \delta Z^{\tilde{q}\dagger }). \end{aligned}$$

(31)

The counterterms are defined on-shell. This definition of the counterterms is known to be gauge dependent [107, 108, 110, 111]. In [108] it was stated, however, that the Feynman’t Hooft gauge, which we adopt here, leads to a result which coincides with the gauge independent result. In the Yukawa part of the squark-quark-neutralino coupling given in terms of the left- and right-chiral couplings in Eqs. (17) and (18), the bare quark mass $m^{(0)}_{u_i}$ needs to be renormalised ($i=1,2,3$),

$$\begin{aligned} m^{(0)}_{u_i} = m_{u_i} + \delta m_{u_i}, \end{aligned}$$

(32)

with the counterterm $\delta m_{u_i}$ given by

$$\begin{aligned} \delta m_{u_i}= & {} \frac{1}{2} \text{ Re } \left[ m_{u_i} \left( \Sigma ^L_{ii} \left( m_{u_i}^2\right) + \Sigma ^R_{ii} \left( m_{u_i}^2\right) \right) \right. \nonumber \\&+ \left. \Sigma _{ii}^{Ls} \left( m_{u_i}^2\right) + \Sigma ^{Rs}_{ii} \left( m_{u_i}^2\right) \right] . \end{aligned}$$

(33)

Even in case of a vanishing fermion mass, a mass counterterm is generated due to the $\Sigma ^{Ls/Rs}$ contributions from the gluino diagram in Fig. 1 (lower); see e.g. also [112]. In the basis of the mass eigenstates of the squark, quark and neutralino the Lagrangian $\mathcal{L}_{\bar{u} \tilde{u} \tilde{\chi }_1^0}$ containing the vertex counterterm is then given by

$$\begin{aligned} \mathcal{L}_{\bar{u} \tilde{u} \tilde{\chi }_1^0}= & {} \bar{u}_i (g^L_{isl} + \delta g^L_{isl} ) \mathcal{P}_L \tilde{u}_s \tilde{\chi }_l^0\nonumber \\&+ \,\bar{u}_i (g^R_{isl} + \delta g^R_{isl} ) \mathcal{P}_R \tilde{u}_s \tilde{\chi }_l^0, \end{aligned}$$

(34)

with the left- and right-chiral coupling counterterms ($i,j,k=1,2,3,\,s,t=1,\ldots ,6,\, l=1,\ldots ,4$)³

$$\begin{aligned}&\delta g^L_{isl}\nonumber \\&\quad = -g e_{Rl}^{u_i} \left[ \!\frac{\delta Z^{R\dagger }_{ij}}{2} W^{\dagger }_{j+3 \, s} + \delta u^R_{ij} W^\dagger _{j+3 \, s} + W^\dagger _{i+3 \, t} \delta \tilde{w}^\dagger _{ts} + W_{i+3 \, t}^\dagger \frac{\delta Z^{\tilde{u}}_{ts}}{2}\!\right] \nonumber \\&\qquad -\frac{g Z_{l4}}{\sqrt{2} M_W \sin \beta } \left[ \delta m_{u_i} \delta _{ij} W^\dagger _{js} + \frac{\delta Z_{ij}^{R\dagger }}{2} m_{u_j} \delta _{jk} W^\dagger _{ks} + m_{u_i} \delta u^L_{ij} W^\dagger _{js} \right. \nonumber \\&\qquad \left. +\, m_{u_i} \delta _{ij} W^\dagger _{jt} \delta \tilde{w}^\dagger _{ts} + m_{u_i} \delta _{ij} W^\dagger _{jt} \frac{\delta Z^{\tilde{u}}_{ts}}{2}\right] ,\end{aligned}$$

(35)

$$\begin{aligned}&\delta g^{R}_{isl}\nonumber \\&\quad = - ge_{Ll}^{u_i} \left[ \frac{\delta Z^{L \dagger }_{ij}}{2} W^\dagger _{js} + \delta u^L_{ij} W^\dagger _{js} + W^\dagger _{it} \delta \tilde{w}^\dagger _{ts} + W^\dagger _{it} \frac{\delta Z^{\tilde{u}}_{ts}}{2} \right] \nonumber \\&\qquad - \frac{g Z_{l4}}{\sqrt{2} M_W \sin \beta } \left[ \delta m_{u_i} \delta _{ij} W^\dagger _{j+3 \, s} + \frac{\delta Z^{L \dagger }_{ij}}{2} m_{u_j} \delta _{jk} W^\dagger _{k+3 \, s}\right. \nonumber \\&\qquad \left. +\, m_{u_i} \delta u^R_{ik} W^\dagger _{k+3 \, s} + m_{u_i} \delta _{ij} W^\dagger _{j+3 \, t} \delta \tilde{w}^\dagger _{ts} + m_{u_i} \delta _{ij} W^\dagger _{j+3 \, t} \frac{\delta Z^{\tilde{u}}_{ts}}{2} \right] . \end{aligned}$$

(36)

Note that the wave function renormalisation constants $\delta Z^{\tilde{u}}_{st}$ in Eq. (25), and $\delta Z^{L/R}_{ij}$ in Eq. (27) have a vanishing denominator in case of equal masses for quarks i and j and squarks s and t. This in particular turns out to be a problem when the first and second generation quark masses are set to zero. If both the fields and the mixing matrices are renormalised on-shell, however, this problem does not occur, as the combination of the renormalisation constants is non-singular; see e.g. Ref. [113]. For degenerate fermions we hence make the replacement ($i,j=1,2,3$)

$$\begin{aligned}&\frac{\delta Z_{ij}^{L/R \dagger }}{2} + \delta u_{ij}^{L/R}\nonumber \\&=\frac{1}{4} \left( \delta Z_{ij}^{L/R} + \delta Z_{ij}^{L/R\dagger } \right) \mathop {\longrightarrow }\limits ^{m_{u_i}= m_{u_j}} - \frac{1}{2} \left[ \text{ Re } \Sigma ^{L/R}_{ij} \left( m_{u_i}^2\right) \right. \nonumber \\&\quad - m_{u_i} \frac{\partial }{\partial p^2} \text{ Re } \left( m_{u_i} \left( \Sigma ^{L/R}_{ij} (p^2) + \Sigma ^{R/L}_{ij} (p^2) \right) \right. \nonumber \\&\quad \left. \left. \left. + \Sigma ^{L/Rs}_{ij} (p^2) + \Sigma ^{R/Ls}_{ij} (p^2) \right) \right] \right| _{p^2=m_{u_i}^2} \end{aligned}$$

(37)

and

$$\begin{aligned}&\frac{1}{2} \delta Z_{ij}^{L/R\dagger } m_{u_j} + \delta u_{ij}^{R/L} m_{u_i} = \frac{1}{2} \delta Z_{ij}^{L/R\dagger } m_{u_j}\nonumber \\&\quad + \frac{1}{4} (\delta Z^{R/L}_{ij} - \delta Z_{ij}^{R/L\dagger }) m_{u_i} \nonumber \\&\quad \mathop {\longrightarrow }\limits ^{m_{u_i}= m_{u_j}} \frac{1}{2} \text{ Re } \left[ m_{u_i} \Sigma ^{R/L}_{ij} (m_{u_i}^2) + 2 \Sigma _{ij}^{R/Ls} (m_{u_i}^2) \right] \nonumber \\&\quad - \frac{1}{2} \frac{\partial }{\partial p^2} \text{ Re } \left[ m_{u_i}^3 \Sigma _{ij}^{L/R} +m_{u_i}^3 \Sigma _{ij}^{R/L} (p^2) \right. \nonumber \\&\quad \left. \left. + m_{u_i}^2 \Sigma ^{L/Rs}_{ij} (p^2) + m_{u_i}^2 \Sigma ^{R/Ls}_{ij} (p^2) \right] \right| _{p^2=m_{u_i}^2}.\nonumber \\ \end{aligned}$$

(38)

In Eqs. (37) and (38) we do not sum over common indices. In the derivation of these equations we have used

$$\begin{aligned} \delta Z_{ij}^\dagger = \delta Z_{ij} (m_{u_i}^2 \leftrightarrow m_{u_j}^2) \end{aligned}$$

(39)

in Eq. (27). This relation follows from the hermiticity of the Lagrangian, implying that the self-energies obey $\Sigma _{ij} = \gamma _0 \Sigma _{ij}^\dagger \gamma _0$. For degenerate squark masses we use ($s,t=1,\ldots ,6$)

$$\begin{aligned}&\frac{1}{2} \delta Z^{\tilde{u}}_{st} + \delta \tilde{w}_{st}^\dagger = \frac{1}{4} \left( \delta Z^{\tilde{u}}_{st} + \delta Z^{\tilde{u}\dagger }_{st} \right) \nonumber \\&\quad \mathop {\longrightarrow }\limits ^{m_{\tilde{u}_s}= m_{\tilde{u}_t}}-\left. \frac{1}{2} \text{ Re } \frac{\partial }{\partial p^2} \tilde{\Sigma }_{st} (p^2)\right| _{p^2=m_{\tilde{u}_s^2}}. \end{aligned}$$

(40)

Note finally that in our calculation we have chosen the quark mass in the Yukawa terms of the squark–quark–neutralino couplings given in Eqs. (17) and (18) to be the on-shell mass, in consistency with our renormalisation scheme.

The real corrections have been evaluated in $D=4-2\epsilon$ dimensions with $\epsilon \equiv \epsilon _{\text {IR}}$. As we are only interested in the total decay width, the D-dimensional phase space integration can be performed analytically. We checked explicitly that the IR and collinear divergences of the real corrections cancel those of the virtual corrections. Analogously we have performed the computation of the decay width $\Gamma (\tilde{u}_1 \rightarrow u \tilde{\chi }_1^0)$ at NLO SUSY-QCD. All computations presented here have been performed in two independent calculations and have been cross-checked against each other. In the Appendix we give the explicit formulae for the full result of the partial decay width at NLO SUSY-QCD.

3 The four-body decay

In the parameter region where the FV two-body decay of the lightest squark plays a role, the four-body decay into the lightest neutralino, a down-type quark and a fermion pair can become competitive and even dominate. The latter is in particular the case for a small FV coupling $\tilde{u}_1-c-\tilde{\chi }_1^0$, as the four-body decay contains flavour-conserving subprocesses. We revisit this decay, which has been first calculated in [69], by allowing for FV couplings at tree level and by taking into account the full dependence on the masses of third generation fermions. Because of possible flavour violation the four-body decay that we consider is given by

$$\begin{aligned} \tilde{u}_1 \rightarrow \tilde{\chi }_1^0 d_i f\bar{f}', \end{aligned}$$

(41)

where $d_i$ denotes a down-type quark of any of the three flavours, $i=1,2,3$. The final state fermions are $f,f'=u,d,c,s,b,e,\mu ,\tau ,\nu _e, \nu _\mu , \nu _\tau$. Figure 4 shows the Feynman graphs contributing to the process. They are mediated by charged Higgs $H^\pm$, W, chargino $\tilde{\chi }_{1,2}^\pm$, quark and sfermion exchanges. With the exchanged particles being far off-shell we do not take into account total widths in the propagators, except for the one of the W boson. Additionally, there are diagrams in which neutral particles as e.g. neutralinos or gluinos are exchanged and which can only proceed via FV couplings.

Fig. 4

Generic Feynman diagrams contributing to the four-body decay $\tilde{u}_1 \rightarrow \tilde{\chi }_1^0 d_i f\bar{f}'$ ($i,j=1,2,3$, $s=1,\ldots ,6$, $k=1,2$)

These will not be considered in the numerical analysis. They are negligibly small, as we checked explicitly. The diagrams displayed in Fig. 4 contain fermion number flow violating interactions, which were treated following the recipe given in Ref. [114]. The calculation of the process has been performed in two independent approaches. One calculation was done automatically by using FeynArts/FormCalc [94–97]. The second calculation only used FeynCalc [115] to evaluate the traces. Both results were cross-checked against each other.

We computed the analytic formula for the decay width in the general $R_\xi$ gauge and explicitly verified that the dependence on the gauge parameter $\xi$ drops out so that gauge invariance is manifest. In the result thus obtained we plugged in the mass values of the various particles as obtained from a spectrum calculator. The formulae of the final result are quite cumbersome and lengthy, so that they are not displayed explicitly here.

The FV two-body and four-body decays have been implemented in SDECAY [83, 84], which is part of the program package SUSY-HIT [85]. Together with some follow-up routines, for the former a new routine called SD_lightstop2bod and for the latter a routine named SD_lightstop4bod have been implemented. The original version of SUSY-HIT features the SUSY Les Houches Accord (SLHA) format [116]. As in the case of flavour violation the SUSY Les Houches Accord 2 (SLHA2) format [117] needs to be read in, the read-in subroutine has been modified accordingly.

4 The parameter scan

For the numerical analysis a scan was performed in the MSSM parameter space. The value of $\tan \beta$ and the mass of the pseudoscalar Higgs boson $M_A$ have been varied in the ranges

$$\begin{aligned} 1 \le \tan \beta \le 15 \quad \text{ and } \quad 150 \text{ GeV } \le M_A \le 1 \text{ TeV } . \end{aligned}$$

(42)

In our scenarios, larger values of $\tan \beta$ are disfavoured due to B-physics observables. At tree level, $M_A$ and $\tan \beta$ determine the MSSM Higgs sector, consisting of two neutral CP-even Higgs bosons h and H, the pseudoscalar A and two charged Higgs bosons $H^\pm$. In order to shift the SM-like neutral Higgs boson mass, given in our scenarios by the lighter scalar h, to about 125 GeV, as reported by the LHC experiments [118, 119], radiative corrections have to be taken into account, which are dominated by the contributions from the (s)top sector. This and the determination of the entire SUSY spectrum requires the definition of the soft SUSY breaking masses and trilinear couplings. The Higgs and SUSY spectra have been obtained from the spectrum calculator SPheno [120, 121], which allows for flavour violation.⁴ The program package SPheno reads in the parameters in the SLHA2 format. In the SLHA format all input parameters listed here below are understood as $\overline{\text{ DR }}$ parameters given at the scale $M_{\text {input}}$.⁵ After the application of renormalisation group running the parameters, masses and mixing values are given out in the SLHA format at a user defined output scale $M_{\text {output}}$. We chose the input scale $M_{\text {input}}$ to be the GUT scale and the output scale as

$$\begin{aligned} M_{\text {output}} = 300 \text{ GeV }. \end{aligned}$$

(43)

This is within the mass range of the lightest stop resulting from our parameter scan. The input soft SUSY breaking gaugino mass parameters have been chosen as

$$\begin{aligned}&75 \text{ GeV } \le M_1 \le 500 \text{ GeV }, \quad M_2 = 650 \text{ GeV } \quad \text{ and } \nonumber \\&\quad M_3 = 1530 \text{ GeV }. \end{aligned}$$

(44)

The lower bound on $M_1$ restricts the neutralino masses to values in accordance with the bounds from the relic density and the ones resulting from light stop mass searches. The chosen value for $M_3$ leads to heavy enough gluino masses to avoid the LHC exclusion bounds. The higgsino mass parameter has been set to

$$\begin{aligned} \mu = 900 \text{ GeV }. \end{aligned}$$

(45)

The chargino masses obtained are of the order of several hundred GeV and not in conflict with any exclusion bounds. The soft SUSY breaking trilinear couplings and mass parameters of the slepton sector, the right-handed up-type squark mass parameters and trilinear couplings of the first and second generations, and the right-handed down-type mass parameters and trilinear couplings of all three generations have been chosen as ($E \equiv e, \mu , \tau$, $U \equiv u,c$, $D \equiv d,s,b$)

$$\begin{aligned} M_{\tilde{E}_R}= & {} M_{\tilde{L}_{1,2,3}} = 1 \text{ TeV }, \quad A_E = 0 \text{ TeV },\nonumber \\ M_{\tilde{U}_R}= & {} M_{\tilde{D}_R} = 1.5 \text{ TeV }, \quad A_U = A_D = 0 \text{ TeV }. \end{aligned}$$

(46)

We do not apply strict MFV, but allow the right-handed stop mass parameter and the top trilinear coupling to vary in the range

$$\begin{aligned} 300 \text{ GeV } \le M_{\tilde{t}_R} \le 600 \text{ GeV } \quad \text{ and } \quad 1 \text{ TeV } \le A_t \le 2 \text{ TeV }.\nonumber \\ \end{aligned}$$

(47)

Furthermore, in the input file of the spectrum generator SPheno we chose two different flavour symmetries for the squark sector, a $U(2)_{Q_L}\times U(2)_{u_R} \times U(3)_{d_R}$ symmetry, to which we refer as U(2)-inspired or simply U(2) in the following, and a $U(3)_{Q_L}\times U(2)_{u_R} \times U(3)_{d_R}$ symmetry, to which we refer as U(3)-inspired, respectively U(3), i.e.⁶

(48)

One remark is here in order. In SPheno the flavour off-diagonal mixing matrix elements are induced through renormalisation group running. We regard the masses and mixing matrix elements thus generated as pure input values measured by the experiments, once SUSY will have been discovered. This allows us to treat them independently of the scheme that has been adopted in SPheno upon their calculation, and exempts us from the necessity to adapt them to our renormalisation scheme. The reason behind this is the fact that SPheno is regularly updated, which may also entail a change in the, for us, relevant renormalisation procedure and would require again an adaption of the input values. Furthermore, the user might choose to use a different spectrum generator with yet another procedure in order to obtain the masses and mixings, which then in turn would require to transform these input values to our renormalisation scheme. With our pragmatic approach such problems can be circumvented.

With these parameter values the squarks of the first two generations are heavy enough not to be excluded by the experiments. The choice of the soft SUSY breaking parameters in the stop sector guarantees rather low lightest stop mass values, which we are interested in here. The SM input parameters as required by the SLHA format are set to the particle data group (PDG) [123] values

$$\begin{aligned} G_F&= 1.166379 \cdot 10^{-5} \text{ GeV }^{-2},\nonumber \\ \alpha _s (M_Z)_{\overline{\text {MS}}}&= 0.1185, \nonumber \\ m_b (m_b)_{\overline{\text {MS}}}&= 4.18 \text{ GeV },\nonumber \\ m_t (\text {pole})&= 173.07 \text{ GeV }, \nonumber \\ m_{\tau } (\text {pole})&= 1.77682 \text{ GeV },\nonumber \\ M_Z (\text {pole})&= 91.1876 \text{ GeV }. \end{aligned}$$

(49)

Finally, according to the SLHA2 format we need the CKM matrix elements in the Wolfenstein parametrisation. The values given by the PDG are

$$\begin{aligned} \lambda = 0.22535, \; A= 0.811, \; \bar{\rho } = 0.131, \; \bar{\eta } = 0.345. \end{aligned}$$

(50)

From the scan only those points are retained that lead to a mass difference $\Delta m$ between the lightest squark $\tilde{u}_1$ and the lightest neutralino $\tilde{\chi }_1^0$ of

$$\begin{aligned} 5 \text{ GeV } \le \Delta m = m_{\tilde{u}_1} - m_{\tilde{\chi }_1^0} \le 75 \text{ GeV }, \end{aligned}$$

(51)

and that in addition fulfill the constraints we apply. The constraints arise from the searches for Higgs boson(s) and SUSY particles, from the relic density measurements and from flavour observables.

In the following, these constraints will be explained in detail.

Constraints from Higgs data The compatibility with the experimental Higgs data is checked with the programs HiggsBounds [124–126] and HiggsSignals [127]. The program HiggsBounds needs as inputs the effective couplings of the Higgs bosons of the model under consideration, normalised to the corresponding SM values, as well as the masses, the widths and the branching ratios of the Higgs bosons. It then checks for the compatibility with the non-observation of the SUSY Higgs bosons, in particular whether the Higgs spectrum is excluded at the 95 % confidence level (CL) with respect to the Tevatron and LHC measurements or not. The package HiggsSignals on the other hand takes the same input and validates the compatibility of the SM-like Higgs boson with the data from the observation of a Higgs boson. As result a p-value is given out, which we demanded to be at least 0.05, corresponding to a non-exclusion at 95 % CL. For the computation of the effective couplings and decay widths of the SM and MSSM Higgs bosons, the Fortran code HDECAY [128–132] is used, which provides the SM and MSSM decay widths and branching ratios including the state-of-the-art higher order corrections. As HDECAY does not support flavour violation, the dominant flavour-diagonal entries of the mass and mixing matrices provided by SPheno have been extracted before passing them on to HDECAY. Since FV effects in the Higgs decays are tiny and far beyond the experimental precision, the effect of this procedure on the final results is negligible.

Constraints from SUSY searches In order not to be in conflict with the SUSY mass bounds reported by the LHC experiments for the gluino and squark masses of the first two generations [65, 66] we required these SUSY particles to have masses of

$$\begin{aligned}&m_{\tilde{g}} > 1450 \text{ GeV } \quad \text{ and } \nonumber \\&m_{\tilde{q}_{1,2}}> 900 \text{ GeV } \quad (q=u,c,d,s). \end{aligned}$$

(52)

At the LHC, searches have been performed for the lightest stop with mass close to the LSP assumed to be $\tilde{\chi }_1^0$ in the two decay channels we are interested in here, the flavour-changing two-body decay Eq. (3) and the four-body decay Eq. (41). Based on monojet-like [60, 61, 82] and charm-tagged event selections [60, 61] and on searches for final states with one isolated lepton, jets and missing transverse momentum [62], limits are given on the lightest stop mass as a function of the neutralino mass, assuming, respectively, a branching ratio of 1, depending on the final state under investigation. At present, the most stringent bounds have been reported in [61, 62] for $\tilde{t}_1$ masses down to $\sim 100$ GeV. Giving up the assumption of maximum branching ratios, we re-interpreted these limits for arbitrary stop branching ratios below 1. The results are shown in Fig. 5 in the $m_{\tilde{\chi }_1^0}$–$m_{\tilde{t}_1}$ plane.⁷ The grey dashed lines limit the region in which

$$\begin{aligned} m_{\tilde{\chi }_1^0} + m_c \le m_{\tilde{t}_1} \le m_{\tilde{\chi }_1^0} + m_b + m_W. \end{aligned}$$

(53)

In this region the stop can be searched for in the FV two-body decay Eq. (3) and the four-body decay Eq. (41). Neglecting the two-body decay $\tilde{t}_1 \rightarrow u \tilde{\chi }_1^0$, which is usually suppressed by two orders of magnitude compared to the two-body decay with the charm quark final state, the $\tilde{t}_1$ branching ratios in this mass region are given by

$$\begin{aligned} \text{ BR } (\tilde{t}_1 \rightarrow c \tilde{\chi }_1^0)= & {} \frac{\Gamma (\tilde{t}_1 \rightarrow c \tilde{\chi }_1^0)}{\Gamma _{\text {tot}}} ,\end{aligned}$$

(54)

$$\begin{aligned} \text{ BR } (\tilde{t}_1 \rightarrow \tilde{\chi }_1^0 b f \bar{f}')= & {} \frac{\Gamma (\tilde{t}_1 \rightarrow \tilde{\chi }_1^0 b f \bar{f}')}{\Gamma _{\text {tot}}}, \quad \text{ with } \end{aligned}$$

(55)

$$\begin{aligned} \Gamma _{\text {tot}}= & {} \Gamma (\tilde{t}_1 \rightarrow c \tilde{\chi }_1^0) + \Gamma (\tilde{t}_1 \rightarrow \tilde{\chi }_1^0 b f \bar{f}').\nonumber \\ \end{aligned}$$

(56)

Fig. 5

Exclusion limits in the $m_{\tilde{\chi }_1^0}$–$m_{\tilde{t}_1}$ plane at 95 % CL, based on the results for the $\tilde{t}_1 \rightarrow c \tilde{\chi }_1^0$ signature from [61] (upper) and on the results for the $\tilde{t}_1 \rightarrow \tilde{\chi }_1^0 b f\bar{f}'$ signature from [61, 62] (lower). The colour code indicates the branching ratio down to which the exclusion limits are valid

The full pink line in the upper plot shows the 95 % CL exclusion limit based on combined charm-tagged and monojet ATLAS searches⁸ in the $\tilde{t}_1 \rightarrow c\tilde{\chi }_1^0$ decay [61], assuming 100 % branching ratio. For a $\tilde{t}_1$ decaying exclusively into the four-body final state ATLAS derived from the monojet analysis [61] the exclusion given by the pink line (close to the upper dashed line) in Fig. 5 (lower) and from the final states with one isolated lepton the exclusion region delineated by the green line (close to the lower dashed line) [62]. With the information given in [61, 62] we derived the exclusion limits for the two- and the four-body final state as a function of the branching ratio, which is given by the colour code. In order to do so, we used the tabulated acceptance times efficiency $A\times \epsilon$ of Refs. [61, 62] and the production cross section $\sigma _\mathrm{prod}$ for stop-pair production, but checked the cross section explicitly with Prospino [133]. The $\sigma _\mathrm{prod}\times A\times \epsilon$ are scaled by the respective branching ratios. The two decay channels are then combined under the assumption that $\text{ BR }(\tilde{t}_1 \rightarrow \tilde{\chi }_1^0 b f\bar{f}')+\text{ BR }(\tilde{t}_1 \rightarrow c\tilde{\chi }_1^0)=1$.⁹ For the exclusion limits of Ref. [61] we derived the limits with the CL$_s$ method [134]. Uncertainties on both background and signal were taken into account by Gaussian probability distribution functions. In the derivation of the limits in the four-body final state we assumed that the branching ratio with jet final states, $\text{ BR } (\tilde{t}_1 \rightarrow \tilde{\chi }_1^0 b jj)$, makes up 66 %, and the branching ratios $\text{ BR } (\tilde{t}_1 \rightarrow \tilde{\chi }_1^0 b \bar{l} \nu _l)$ ($l=e,\mu ,\tau$) each account for 11 % of the four-body decay branching ratio, see also the discussion on the four-body decay branching ratio in Sect. 5.2.

From the plots it can be read off that stop masses with a branching ratio above the one associated with a specific colour are excluded. It is immediately evident that for smaller branching ratios the exclusion limits become weaker. The two plots can be combined to extract the exclusion limits for stops of a given mass as a function of the neutralino mass and the stop branching ratio. Thus it can be read off from Fig. 5 (upper) that $\tilde{t}_1$ masses of 150 GeV can be excluded for $m_{\tilde{\chi }_1^0}=80$ GeV if their branching ratio into $c + \tilde{\chi }_1^0$ exceeds 0.43. This in turn implies that the stop four-body branching ratio is below 0.57. On the other hand the lower plot shows that in the same region stops can be excluded if their branching ratio into the four-body final state is larger than 0.88, which implies that the two-body decay branching ratio is below 0.12 then. This means that $m_{\tilde{t}_1} = 150$ GeV can be excluded for $m_{\tilde{\chi }_1^0}=80$ GeV for scenarios in which $\text{ BR } (\tilde{t}_1 \rightarrow c \tilde{\chi }_1^0) < 0.12$ and $\text{ BR } (\tilde{t}_1 \rightarrow c \tilde{\chi }_1^0) > 0.43$, respectively, $\text{ BR } (\tilde{t}_1 \rightarrow \tilde{\chi }_1^0 b f \bar{f}') > 0.88$ and $\text{ BR } (\tilde{t}_1 \rightarrow \tilde{\chi }_1^0 b f \bar{f}') < 0.57$. The dark-blue region corresponds to stop branching ratios that are zero, so that all stop mass values associated with this region are excluded.¹⁰ In Fig. 5 (upper) there is no smooth transition between the dark-blue and its neighbouring regions, as the exclusion limits in the two-body final state are related to the ones in the four-body final state which here apply for branching ratios ${\gtrsim }$0.46, so that of course also in Fig. 5 (lower) there is no continuous colour gradient here.

Our exclusion limits given by the border of the coloured region at 100 % two-, respectively, four-body decay branching ratio, do not exactly match the ones derived by ATLAS. The reason is that ATLAS provided information on the values of the excluded production cross section times branching ratio only for a few points in the $m_{\tilde{\chi }_1^0}$–$m_{\tilde{t}_1}$ plane and we had to interpolate linearly between these points in order to cover the whole region. Nevertheless, the agreement of our results with the given exclusion limits is reasonably good. We take the thus derived exclusion limits as a function of the stop branching ratio in order to restrain our parameter points to the experimentally allowed values. The advantage of our approach is to take fully into account the information on the actual stop branching ratios which can considerably weaken the stop exclusion limits as is evident from Fig. 5. As our plots can only be an approximation of what can be done much more accurately by the experiments, they should be taken as an encouragement to provide results also as a function of the stop branching ratios.

Constraints from relic density and B-physics measurements The space telescope PLANCK [135] has measured the relic density of dark matter (DM) to be

$$\begin{aligned} \Omega _c h^2 = 0.1199 \pm 0.0027. \end{aligned}$$

(57)

In our set-up we assume the lightest neutralino to be the LSP and hence the DM candidate. We have used the program SuperIso Relic [136, 137] to calculate the relic density for neutralino DM and have compared the outcome to the experimental value. SuperIso Relic does not take into account FV effects in the calculaton of the relic density but these effects are expected to be highly CKM-suppressed. We require the relic density resulting from neutralinos to be

$$\begin{aligned} \Omega _c h^2 (\tilde{\chi }_1^0) < 0.12, \end{aligned}$$

(58)

which means that neutralinos are assumed not to be the only source contributing to the measured relic density.

Further constraints arise from flavour observables. In particular, in models with FCNC couplings at tree level, new particles can have a significant impact on rare meson decays mediated by loops. We use the program SuperIso [138, 139] to calculate the relevant B meson branching ratios and require them to be compatible within two standard deviations with the experimentally measured values. With the errors denoting the 1-sigma bounds, they are given by

$$\begin{aligned} \mathcal{B} (B_s^0 \rightarrow \mu ^+ \mu ^-)&= (2.9\pm 0.7) \times 10^{-9}&\quad [140] \nonumber \\ \mathcal{B} (B^0 \rightarrow \mu ^+ \mu ^-)&< 8.1 \times 10^{-10} \; \text{ at } 95\,\% \text{ CL }&\quad [141] \nonumber \\ \mathcal{B} (B^+ \rightarrow \tau ^+ \nu _\tau )&= (1.05 \pm 0.25) \times 10^{-4}&\quad [123] \nonumber \\ \mathcal{B} (B\rightarrow X_s \gamma )&= (355 \pm 24 \pm 9) \times 10^{-6}&\quad [142]. \end{aligned}$$

(59)

We do not use the measured value of the anomalous magnetic moment $a_\mu$ as constraint, as the SUSY contribution resulting from our parameter scan cannot explain the discrepancy between the SM prediction and the experimental value.

For completeness we give the $\tilde{u}_1$ masses that we obtain as a result of our scan and after application of all constraints. For the two flavour scenarios they are

$$\begin{aligned} U(2)&: 246 \text{ GeV } \lesssim m_{\tilde{u}_1} \lesssim 556 \text{ GeV } ,\nonumber \\ U(3)&: 197 \text{ GeV } \lesssim m_{\tilde{u}_1} \lesssim 555 \text{ GeV }. \end{aligned}$$

(60)

The charged Higgs boson masses range between about 392 and 1003 GeV, the chargino masses between approximately 652 and 661 GeV.

5 Numerical results

In the following we present results for the parameter points of our scan that pass the constraints discussed in Sect. 4. Two scenarios of flavour violation are investigated in the left-handed squark sector, one with a flavour symmetry U(2) and a second where the flavour symmetry is enhanced to U(3), cf. Eq. (48). Furthermore, the decay $\tilde{u}_1 \rightarrow u \tilde{\chi }_1^0$ has been included in the total width everywhere where applicable. When we talk about the FCNC decay in the following, we implicitly refer to the $\tilde{u}_1 \rightarrow c \tilde{\chi }_1^0$ decay, however, as the decay with the up quark final state is negligible compared to the one with the charm quark in the final state.

5.1 SUSY-QCD corrections to the FCNC two-body decay

We first analyse the effect of the SUSY-QCD corrections on the two-body decay $\tilde{u}_1 \rightarrow c \tilde{\chi }_1^0$. Figure 6 shows the K-factor, i.e. the ratio of the NLO decay width with respect to the LO decay width, as a function of the mass difference $\Delta m = m_{\tilde{u}_1}- m_{\tilde{\chi }_1^0}$. The strong coupling constant has been evaluated in the $\overline{\text{ DR }}$ scheme at the scale $m_{\tilde{u}_1}$. As stated in Eq. (51) we vary $\Delta m$ between 5 and 75 GeV, which on the lower and upper bounds corresponds to the lightest squark mass interval Eq. (53), in which the two-body (and also the four-body) decay is relevant, modulo an off-set of a few GeV. The lower off-set of 5 GeV accounts for the fact that we have not taken into account the finite charm quark mass in the two-body decay. With 5 GeV we are far enough away from the threshold so that finite charm quark mass effects are negligible. Note also that for a stop mass too close to the neutralino mass its lifetime becomes larger than the flight time within the detector. The upper bound takes into account that for a meaningful prediction in the mass region where the three-body off-shell decay becomes important a smooth interpolation between the two- (also the four-) and the three-body decays is required, which is not available at present.

Fig. 6

The SUSY-QCD K-factor for the FCNC decay $\tilde{u}_1 \rightarrow c \tilde{\chi }_1^0$ as a function of the squark-neutralino mass difference assuming a U(2) (left) and a U(3) (right) symmetry in the left-handed squark sector

As can be inferred from the right plot in Fig. 6, the SUSY-QCD corrections are significant and vary between at most $\sim$27 % to about 6 % for U(3) when going from $\Delta m= 5$ GeV to 75 GeV. The K-factor increases for small mass differences, where the real corrections become more important and increase the partial width. The virtual corrections on the other hand decrease the partial width, but less strongly, so that the net effect is a $\sim$27 % increase of the loop-corrected width for U(3). For large mass differences the K-factors for the real and the virtual corrections approach 1 from above and below, respectively, resulting in a residual 7 % correction for the overall K-factor.¹¹ Similar results hold for the majority of the scenarios found in the U(2) case in Fig. 6 (left). For some scenarios, however, the K-factor can become significantly larger, reaching values of up to $\sim$2.1. The reason is in the specific flavour mixings of the heavier squarks that contribute to the gluino loop in the virtual corrections. These are such that they lead to an enhancement of the K-factor. In the parameter points passing all constraints this occurred only when the charm- and top-flavour contributions to $\tilde{u}_4$ and $\tilde{u}_6$ were roughly equal. The tree-level decay, the real corrections and the gluon loop, which only depend on the flavour composition of $\tilde{u}_1$, are not affected by this behaviour. Furthermore, such flavour mixing only appears for a small region of the parameter space and therefore only very few points passing the constraints led to such a high K-factor in our random scan. We did not find flavour mixings of that kind in the U(3) case.

5.2 The four-body decay

The new element in our calculation of the four-body decay $\tilde{u}_1 \rightarrow \tilde{\chi }_1^0 d_i f \bar{f}'$ compared to the literature [69] is the inclusion of FCNC couplings at tree level and the inclusion of the full mass dependence of the final state bottom quarks and $\tau$ leptons.

The effect of taking into account non-vanishing $m_b$ and $m_\tau$ is shown in the plots of Fig. 7 (upper), which show the ratio of the partial four-body decay width with non-vanishing masses and the corresponding width, where $m_b = m_\tau =0$, as a function of $\Delta m$. As expected, as soon as $\Delta m$ crosses the threshold of $m_b$ the ratio steeply increases to reach an almost constant value of 0.92 for large $\Delta m$, both for the U(2) and the U(3) symmetry. Below the threshold the ratio does not become zero due to the diagrams contributing to the four-body decay which proceed via FCNC couplings leading to massless final states, e.g. $\tilde{u}_1 \rightarrow \tilde{\chi }_1^0 d_{1} \bar{e} \nu _e$. The ratio scatters over a wider range for U(2), cf. Fig. 7 (upper left), than for U(3), cf. Fig. 7 (upper right), due to the lower flavour symmetry in the former case. While the mass effect in the partial width with up to 8 % even in the region far above threshold is non-negligible, in the branching ratio it gets more and more washed out with increasing importance of the four-body decay width, cf. Fig.7 (lower). As in case of the U(3) symmetry for large $\Delta m$ the four-body decay dominates over the two-body decay, cf. next subsection, the mass effect becomes almost zero in the branching ratio then. For the U(2) symmetry it can still be up to 8 % for $\Delta m=75$ GeV. In the threshold region, the mass effect in the branching ratios is important and has to be taken into account as it is phenomenologically relevant; see also the discussion of the comparison between two- and four-body $\tilde{u}_1$ decays below.

Fig. 7

Upper Ratio of the partial width for the $\tilde{u}_1 \rightarrow \tilde{\chi }_1^0 d_i f \bar{f}'$ ($i=1,2,3$) decay with non-zero $m_b$ and $m_\tau$ and of the corresponding decay width with zero masses. Lower Same as upper, but for the branching ratios. In the left-handed squark sector a U(2) (left) or a U(3) (right) symmetry is assumed

In Fig. 8 the branching ratios of the dominant final state signatures to the four-body decay are shown, i.e. $\tilde{u}_1 \rightarrow \tilde{\chi }_1^0 b q\bar{q}'$ and $\tilde{\chi }_1^0 b \bar{l} \nu _l$ ($l=e,\mu ,\tau$), as a function of $\Delta m$. Among the various Feynman diagrams contributing to the decay, the dominant contribution arises from the first diagram in Fig. 4, with the virtual top-quark and W exchange. This is because the squark mixing matrix elements, entering the $\tilde{u}_1-u_j-\tilde{\chi }_1^0$ coupling, have larger values in the diagonal entries (i.e. here for $j=3$), and because of the smaller top-quark mass compared to the chargino and charged Higgs boson masses, which amount to several hundred GeV in our scenarios.¹² The branching ratios for the final states involving $\bar{e} \nu _e$ and $\bar{\mu } \nu _\mu$, marked by the green points, lie on top of each other. The only difference in these final states arises from the diagrams with virtual sleptons (last row in Fig. 4), which are negligibly small. In Fig. 8 (left) we see that for most parameter points the four-body decay is not important and we again observe widespread results in the investigated parameter space as a consequence of the smaller flavour symmetry. For the U(3) symmetry this is not the case, cf. Fig. 8 (right), and a clear hierarchy of the final states can be read off in the large $\Delta m$ region. The $\tilde{\chi }_1^0 b q\bar{q}'$ final state makes up $\sim$66 % of the four-body decay branching ratio, the $\tilde{\chi }_1^0 b \bar{l} \nu _l$ ($l=e,\mu ,\tau$) final states each contribute $\sim$11 % which corresponds to the branching ratios of an on-shell W boson into quark and lepton final states, respectively. In the threshold region due to the non-vanishing $\tau$ mass, which is taken into account in our calculation, the rise for the final state involving $\bar{\tau } \nu _\tau$ sets in later than for the decays with $\bar{e} \nu _e$ and $\bar{\mu } \nu _\mu$ final states.

Fig. 8

The dominant final state branching ratios of the four-body decay, assuming in the left-handed squark sector a U(2) (left) or a U(3) (right) symmetry

5.3 The stop total width and branching ratios and phenomenological implications

In Fig. 9 (upper) the partial two-body and four-body decay widths are displayed for the two chosen flavour symmetries. As can be inferred from the figures the results for the two-body decay width scatter much more than for the four-body decay, and even more in case of the smaller flavour symmetry U(2), Fig. 9 (upper left). This is a consequence of the former being mediated exclusively by FCNC couplings while the latter also contains flavour-conserving diagrams. In case of the U(3) symmetry, the off-diagonal squark mixing matrix elements $W_{12}$ and $W_{15}$ for the charm admixture to the top-flavour state, entering the $\tilde{u}_1-c-\tilde{\chi }_1^0$ coupling, are much smaller, typically by four orders of magnitude, than if U(2) is the applied symmetry. This leads to a corresponding two-body FCNC decay width which is about six orders of magnitudes smaller, cf. Fig. 9 (upper right). This is also illustrated in Fig. 10, which shows the possible values of $W_{12}$ and $W_{15}$ for the U(2) and the U(3) symmetry and the corresponding value of the FCNC decay branching ratio, given by the colour code. As expected, in both cases the right-chiral scharm admixture to the right-chiral stop-like squark (given by $W_{15}$) is much smaller than the left-chiral scharm admixture ($W_{12}$). Overall due to the larger flavour symmetry, for the case of U(3) shown in Fig. 10 (right) the mixing matrix elements $W_{12}$ and $W_{15}$ are $\mathcal{O} (10^4)$ smaller than for an assumed U(2) symmetry, leading to a much smaller two-body decay branching ratio compared to Fig. 10 (left), where we have branching ratios close to one for the major part of the parameter points.

Fig. 9

The two- and four-body decays widths (upper), the total widths (middle) and the branching ratios (lower) as a function of $\Delta m = m_{\tilde{u}_1}-m_{\tilde{\chi }_1^0}$, applying a U(2) (left) and a U(3) (right) symmetry in the left-handed squark sector

Fig. 10

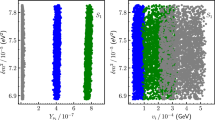
Values of the squark mixing matrix elements $W_{12}$ and $W_{15}$ for the points of the parameter scan passing all applied constraints. The colour code indicates the corresponding values of the branching ratios of the FCNC two-body decay assuming U(2) (left) and U(3) (right) symmetry in the left-handed squark sector

The four-body decay width is dominated by the diagrams mediated by flavour-conserving couplings, so that it hardly depends on the details of the assumed flavour symmetries and both for U(2) and U(3) yields values of $\mathcal{O}(10^{-8})$ GeV for $\Delta m =75$ GeV. Due to the smallness of the two-body decay, it becomes the dominating decay channel already for mass differences $\Delta m \gtrsim 18$ GeV for the enhanced flavour symmetry, while for U(2) the dominating decay for most parameter points is the FCNC two-body decay over large parts of $\Delta m$. The decay widths become comparable for $\Delta m \gtrsim 60$ GeV. The determination of the relative size of the two decay channels to each other could hence be used to reveal information on the underlying flavour symmetry.

The total widths given by the sum of the two- and four-body decays in the investigated $\Delta m$ range are depicted in Fig. 9 (middle). Dominated by the FCNC decay, for the U(2) symmetry it reaches almost $10^{-6}$ GeV for $\Delta m =75$ GeV and the values are widely spread in the investigated mass range. Applying the U(3) symmetry, the values are spread for $\Delta m \lesssim 18$ GeV where the total width is dominated by the FCNC decay and reaches maximum values of $10^{-8}$ GeV given by the four-body decay width at $\Delta m =75$ GeV, see Fig. 9 (middle right). The black line at $\Gamma _{\text {tot}}= 10^{-12}$ GeV corresponds to the value of the total width where displaced vertices can be observed. It corresponds to a $\tilde{u}_1$ lifetime of the order of pico-seconds, which is a flight time for the squark, which is long enough to lead to displaced vertices in the detector.¹³ Obviously, the more the FCNC couplings are suppressed, the smaller is the total width, so that the observation of displaced vertices allows for conclusions on the flavour symmetry of the model as has been pointed out in [146, 147]. In the case the total decay width is below $10^{-12}$ GeV even two displaced vertices could be possible, one from the $\tilde{u}_1$ decay and the second from the b-quark final state.

The branching ratios finally, are displayed in Fig. 9 (lower). In case of the smaller flavour symmetry, the branching ratio into $c \tilde{\chi }_1^0$ is close to 1 for $\Delta m \lesssim 15$ GeV. Beyond this value, however, the four-body decay becomes important and both branching ratios can significantly deviate from 1, as can be inferred from Fig. 9 (lower left).¹⁴ For the U(3) symmetry there is a transition region $10 \text{ GeV } \lesssim \Delta m \lesssim 30 \text{ GeV }$, where the two-body and four-body decay branching ratios cross, leading to a branching close to 1 for the four-body decay above this $\Delta m$ range. In this transition region, however, again the branching ratios for the two final state signatures can deviate significantly from 1. This demonstrates that over large parts of the parameter space the assumption of 100 % decay probability in either of the final states is not valid. This therefore has to be taken into account by the experiments by allowing also for deviations from 1 in the branching ratios in the interpretation of their data. As evident from Fig. 5 this has an important phenomenological impact, as smaller branching ratios lead to considerably weakened exclusion bounds on the lightest squark mass, i.e. the lightest stop mass. In order to further illustrate this, we show in Fig. 11 the values of the two-body decay branching ratios for our investigated scenarios in the $m_{\tilde{\chi }_1^0}$–$m_{\tilde{u}_1}$ plane in the region where the two- and four-body decays are relevant.

Fig. 11

Parameter points of the scan, surviving all applied constraints, in the $m_{\tilde{\chi }_1^0}$–$m_{\tilde{u}_1}$ plane. The colour code indicates the corresponding values of the FCNC two-body decay branching ratios. The upper grey line shows the threshold for the two-body decay, the lower grey line the threshold for the $\tilde{u}_1$ three-body decay into $\tilde{\chi }_1^0 W b$. Upper U(2), lower U(3) flavour symmetry applied in the left-handed squark sector

Displayed are the points that result from our parameter scan and that survive the constraints, described in detail in Sect. 4. In particular, the stop mass exclusion limits from the LHC experiments have been applied in our refined approach, where deviations of the branching ratios from 1 are taken into account, cf. Fig. 5. In case of the U(2) symmetry (upper plot) there are barely any viable parameter points for $m_{\tilde{u}_1} \lesssim 270$ GeV. In the scenarios, where the two-body decay dominates this is due to the stop mass exclusion bounds. In the case the four-body decay is important (corresponding to the blue points in the plot) it is either the mass bounds or the constraints from the relic density, which exclude the points. As the mass exclusions based on the four-body decay are weaker, there are points that survive the constraints. This is also why in case of the U(3) symmetry (lower plot), where the four-body decay dominates in large parts of the parameter space, there is a considerable amount of points down to $\sim$220 GeV. However, close to the two-body decay threshold, i.e. the upper grey line, the two-body decay becomes more important and the more stringent mass exclusions based on this decay apply, so that there are fewer allowed points. In this region of the mass plane, our constraint on the relic density is fulfilled due to stop co-annihilation. Close to the three-body decay threshold, however, points are excluded due to the restrictions from the relic density. In this range near the lower grey line above $\sim$300 GeV, neutralino annihilation via Higgs boson exchange becomes effective, so that the constraint on the relic density can be fulfilled and there are somewhat more points. This also applies in the U(2) case. The plots show in particular that, contrary to the naive application of the LHC exclusion limits, given by the full lines in the plots of Fig. 5, there are viable parameter points for masses below these lines both in the U(2) and even more in the U(3) scenario. Thus, in the U(2) scenario, where the two-body decay dominates, there are points below 290 GeV (given by the limits from the searches in the $c \tilde{\chi }_1^0$ final state) down to about 246 GeV. In the U(3) scenario, where $\tilde{u}_1$ mostly decays into the four-body final state, masses below the limit given from the four-body final state searches, i.e. $\sim$270 GeV, down to approximately 197 GeV are allowed. This is because the assumption of a two- or four-body decay branching ratio close to 1, as applied by the experiments, is not valid.

Overall the picture for the branching ratios is as follows. For the smaller flavour symmetry U(2) the dominating decay is the two-body FCNC decay with branching ratios close to 1, implying strongly suppressed branching ratios into the four-body final state. However, for larger mass differences between $m_{\tilde{u}_1}$ and $m_{\tilde{\chi }_1^0}$, close to the lower grey line, the four-body decay becomes increasingly important and the displayed branching ratio differs from 1 for a considerable amount of parameter points, cf. in Fig. 11 (upper) the dark-pink to dark-blue points. For the enhanced flavour symmetry U(3) the situation evidently is reversed. In large parts of the $\Delta m$ region the four-body decay dominates implying suppressed branching ratios for the FCNC decay. For small $\Delta m$ values, i.e. close to the upper grey line, the FCNC decay, however, takes over, and branching ratios close to 1 are possible, as can be inferred from Fig. 11 (lower). From the plots for both flavour symmetries it is evident that the assumption of branching ratios of 1 for either the two- or four-body decay is not justified over large parts of the parameter space. Taking this into account and re-interpreting the exclusion limits given by the experiments accordingly, the exclusion bounds on the lightest squark, i.e. the light stop, are significantly weakened. This should therefore be taken into account in order to properly interpret the experimental data, in particular at the next run of the LHC where a more extended part of the low stop mass range will be probed. For realistic, non-fine-tuned scenarios, there is hence still plenty of room in the SUSY world for a light stop.

6 Conclusions

The supersymmetric partners of the top quark, the stops, play an important role in the phenomenology of SUSY extensions. Taking into account constraints from Higgs physics, B-physics and relic density measurements, light stops are still allowed by the LHC experiments. The direct searches for the lightest stop-like squark $\tilde{u}_1$ in the low-mass range are based on signatures from the two-body decay $\tilde{u}_1 \rightarrow c \tilde{\chi }_1^0$ and from the four-body decay $\tilde{u}_1 \rightarrow \tilde{\chi }_1^0 b f \bar{f}'$, which are the relevant decay channels in the low stop mass region $m_{\tilde{\chi }_1^0} + m_c \lesssim m_{\tilde{u}_1} \lesssim m_{\tilde{\chi }_1^0}+m_W + m_b$. We have revisited these two decay channels with the aim of providing precise theoretical predictions and subsequently investigating the implications for the exclusion limits on the stop mass.

Allowing for FCNC couplings already at tree level, we have calculated for the first time the SUSY-QCD corrections to the two-body decay of the lightest stop-like $\tilde{u}_1$ into charm and neutralino. They turn out to be important, increasing the partial decay width by close to 27 % near the kinematic threshold and approaching a constant value of about 6 % far above. Additionally we found that for special flavour mixings of the heavy up-type squarks the K-factor can reach values of up to about 2. In the calculation of the four-body decay we have taken into account the contributions from the additional diagrams due to FCNC couplings and the finite masses of the final state bottom quark and $\tau$ lepton. Both effects have not been available in the literature so far. Evidently, in the threshold region the mass effects play an important role, but also far above they are still significant, changing the partial width by up to 8 %. Above the bottom and $\tau$ mass threshold the four-body decay is mainly given by the flavour-conserving diagrams and hence much less sensitive to the details of the flavour symmetry of the squark sector than the two-body decay. In the input of the spectrum generator we have assumed two different flavour patterns in the left-handed squark sector, based on a U(2) and a U(3) symmetry. Accordingly, in the more symmetric U(3) case the flavour off-diagonal mixing in the squark sector is smaller, leading to smaller FCNC two-body decay widths, while the four-body decay is mostly insensitive to the flavour pattern. Depending on the flavour symmetry the relative importance of the two- and four-body branching ratios to each other changes, so that the knowledge on the branching ratios gives information on the underlying flavour symmetry. In particular, for the U(3) case the total $\tilde{u}_1$ width can be very small leading to displaced vertices in the detector, and even the observation of two displaced vertices may be possible, from the $\tilde{u}_1$ decay and from the b-quark final state.

The detailed investigation of the size of the two- and four-body decay branching ratios in our extensive parameter scan, which takes into account all relevant constraints, reveals that the assumption of branching ratios of 1 for either of the decay channels, which the experiments make in their exclusion plots for the lightest stop quark, is not justified for large parts of the parameter space. Taking into account information given by the experiments we have re-examined the exclusions as a function of the exact value of the $\tilde{u}_1$ branching ratio. As expected, the bounds on the excluded lightest stop masses are considerably weakened. Applying this information on the scenarios of our parameter scan we find that there is still a sizeable amount of scenarios with allowed stop mass values below the presently given experimental exclusion limits. This is in particular the case for scenarios where the four-body decay dominates, i.e. for the U(3) symmetry assumption, as here the exclusions given by the experiment are weaker.

In summary, the precise prediction for the FCNC two-body and the four-body decay of the lightest stop-like squark in the low stop mass region, taking into account SUSY-QCD corrections, mass effects and flavour violation at tree level, as done here for the first time, is indispensable for the correct interpretation of the experimental exclusion limits. Deviations of either of the branching ratios from 1 in large parts of the parameter space considerably weaken the stop exclusion limits. This should be taken into account at the next run of the LHC with higher centre-of-mass energy and luminosity where a bigger part of the stop mass region dominated by these two decay channels will be probed. Contrary to the present naive picture, in the SUSY world there is actually a larger range of light stop masses that is still allowed by the LHC experiments.

Appendix: The NLO decay width \(\tilde{u}_1\rightarrow c\tilde{\chi }_1^0\)

In this appendix we give the result for the SUSY-QCD corrected NLO decay width of the FCNC decay. We give the finite part of the result that remains after the application of the renormalisation procedure and performing the sum of the virtual and real corrections. Furthermore, we assume $m_c$ to be zero. The decay width at NLO is composed of, cf. also Eq. (23),

$$\begin{aligned} \Gamma ^{\text {NLO}} = \Gamma ^{\text {LO}} + \Gamma ^{\text {virt}} + \Gamma ^{\text {real}} + \Gamma ^{\text {CT}}, \end{aligned}$$

(61)

with $\Gamma ^{\text {LO}}$ as given in Eq. (21). The scalar integrals appearing in the virtual and counterterm contributions, $\Gamma ^{\text {virt}}$ and $\Gamma ^{\text {CT}}$, are defined as

$$\begin{aligned}&A(m_1^2) = \frac{(2\pi \mu )^{4-D}}{i\pi ^2}\int \mathrm {d}^D q\frac{1}{ (q^2-m_1^2)},\end{aligned}$$

(62)

$$\begin{aligned}&B_{i}(m_1^2, m_2^2) =\frac{(2\pi \mu )^{4-D}}{i\pi ^2}\nonumber \\&\quad \times \int \mathrm {d}^D q\frac{1}{(q^2-m_1^2)(\left( q+p_i\right) ^2-m_2^2)},\end{aligned}$$

(63)

$$\begin{aligned}&p_{\mu } B_1(p^2,m_1^2, m_2^2)=\frac{(2\pi \mu )^{4-D}}{i\pi ^2}\nonumber \\&\quad \times \int \mathrm {d}^D q\frac{q_{\mu }}{(q^2-m_1^2)(\left( q+p\right) ^2-m_2^2)},\end{aligned}$$

(64)

$$\begin{aligned}&C_{ij}(m_1^2, m_2^2, m_3^2)=\frac{(2\pi \mu )^{4-D}}{i\pi ^2}\nonumber \\&\quad \times \!\!\int \mathrm {d}^Dq\frac{1}{ (q^2-m_1^2)((q+p_i)^2-m_2^2)((q+p_i+p_j)^2-m_3^ 2)}. \end{aligned}$$

(65)

The indices i, j of the four-momenta refer to either c, $\tilde{u}_1$ or $\tilde{\chi }_1^0$ and will be specified later. Applying on-shell renormalisation the virtual corrections $\Gamma ^{\text {virt}}$ only receive contributions from the gluon and gluino vertex corrections, $\Gamma ^{\text {virt}}_g$ and $\Gamma ^{\text {virt}}_{\tilde{g}}$, depicted in Fig. 1 (upper),

$$\begin{aligned} \Gamma ^{\text {virt}}= \Gamma ^{\text {virt}}_g + \Gamma ^{\text {virt}}_{\tilde{g}}, \end{aligned}$$

(66)

with the specific contributions given by

(67)

and

$$\begin{aligned} \Gamma ^{\text {virt}}_{\tilde{g}}&=\frac{\alpha _s(\mu )}{12 \pi ^2\,m_{\tilde{u}_1}}\left( 1-\frac{m_{\tilde{\chi }_1^0}^2}{m_{\tilde{u}_1}^2} \right) \sum _{i=1}^3\sum _{s=1}^6 \text {Re} \left[ m_{\tilde{\chi }_1^0} B_{\tilde{ \chi }_0 }( m_{u_i}^2, m_{\tilde{u}_s}^2) \right. \nonumber \\&\quad \times \left[ - W^*_{1i} W^*_{s5}\left( g^L_{211} g^L_{is1}m_{u_i} +g^L_{211}g^R_{is1}m_{\tilde{\chi }_1^0} \right) \right. \nonumber \\&\quad - W^*_{1\,i+3}W^*_{s2} \left( g^R_{211} g^R_{is1}m_{u_i} + g^R_{211}g^L_{is1}m_{\tilde{\chi }_1^0} \right) \nonumber \\&\quad + \left. W^*_{1i} W^*_{s2} \, g^R_{211}g^R_{is1}m_{\tilde{g}}+ W^*_{1\,i+3} W^*_{s5} \, g^L_{211}g^L_{is1}m_{\tilde{g}}\right] \nonumber \\&\quad + B_{\tilde{u}}(m_{u_i}^2, m_{\tilde{g}}^2)\left[ W^*_{1i}W^*_{s5} \left( g^L_{211}g^L_{is1}m_{\tilde{\chi }_1^0} m_{u_i} + g^L_{211}g^R_{is1}m_{\tilde{u}_1}^2\right) \right. \nonumber \\&\quad + W^*_{1\,i+3} W^*_{s2} \left( g^R_{211}g^R_{is1}m_{\tilde{\chi }_1^0} m_{u_i}+g^R_{211}g^L_{is1}m_{\tilde{u}_1}^2 \right) \nonumber \\&\quad - \left. W^*_{1\,i+3} W^*_{s5}\, g^L_{211}g^L_{is1}m_{\tilde{\chi }_1^0} m_{\tilde{g}} - W^*_{1i} W^*_{s2} \,g^R_{211}g^R_{is1}m_{\tilde{\chi }_1^0} m_{\tilde{g}}\right] \nonumber \\&\quad + C_{c,\tilde{\chi }_1^0}(m_{\tilde{g}}^2,m_{\tilde{u}_s}^2,m_{u_i}^2)\left[ - W^*_{1i}W^*_{s5} \left( g^L_{211}g^L_{is1}m_{u_i}m_{\tilde{\chi }_1^0} \right. \right. \nonumber \\&\quad (m_{\tilde{g}}^2- m_{\tilde{u}_s}^2)+\left. g^L_{211}g^R_{is1}\left( m_{\tilde{ \chi } _0 } ^2 m_{\tilde{g}}^2 - m_{\tilde{u}_1}^2 m_{\tilde{u}_s}^2\right) \right. \nonumber \\&\quad -W^*_{1\,i+3}W^*_{s2} \left( g^R_{211}g^R_{is1}m_{u_i}m_{\tilde{\chi }_1^0} \left( m_{\tilde{g}}^2 - m_{\tilde{u}_s}^2\right) \right. \nonumber \\&\quad \left. + g^R_{211}g^L_{is1}\left( m_{\tilde{ \chi } _0 } ^2 m_{\tilde{g}}^2 - m_{\tilde{u}_1}^2 m_{\tilde{u}_s}^2\right) \right) \nonumber \\&\quad +W^*_{s5} W^*_{1\,i+3}\left( g^L_{211}g^L_{is1}m_{\tilde{\chi }_1^0} m_{\tilde{g}} \left( m_{\tilde{\chi }_1^0}^2+ m_{\tilde{g}}^2 \right. \right. \nonumber \\&\quad -\left. \left. m_{\tilde{u}_1}^2 - m_{\tilde{u}_s}^2\right) +g^L_{211}g^R_{is1}m_{\tilde{g}}m_{u_i} \left( m_{\tilde{\chi }_1^0}^2-m_{\tilde{u}_1} ^2\right) \right) \nonumber \\&\quad +W^*_{s2} W^*_{1i} \left( g^R_{211}g^R_{is1}m_{\tilde{\chi }_1^0} m_{\tilde{g}}\left( m_{\tilde{\chi }_1^0}^2+ m_{\tilde{g}}^2- m_{\tilde{u}_1}^2 - m_{\tilde{u}_s}^2\right) \right. \nonumber \\&\quad \left. \left. \left. +g^R_{211}g^L_{is1}m_{\tilde{g}}m_{u_i} \left( m_{\tilde{\chi }_1^0}^2-m_{\tilde{u}_1}^2\right) \right) \right] \right] , \end{aligned}$$

(68)

where here and in the following the A, B and C functions are understood not to contain any divergent poles in $\epsilon _{\text {UV}}$ or $\epsilon _{\text {IR}}$ any more. The gluino mass is denoted by $m_{\tilde{g}}$ and $\mu$ denotes the renormalisation scale. The decay width stemming from the counterterms, $\Gamma ^{\text {CT}}$, reads

$$\begin{aligned} \Gamma ^{\text {CT}}=\frac{1}{8\pi } m_{\tilde{u}_1}\left( 1-\frac{m^2_{\tilde{\chi }_1^0}}{m_{\tilde{u}_1}^2} \right) ^2(\delta g^L_{211} g^L_{211}+\delta g^R_{211} g^R_{211}), \end{aligned}$$

(69)

with $\delta g^{L/R}$ as defined in Eqs. (35) and (36). For the computation of the counterterms the quark and squark self-energies are needed. The squark self-energy can be cast into the form ($s,t=1,\ldots ,6$)

(70)

The symbol $B_{p^2}$ is defined in analogy to Eq. (64), with unspecified momentum $p^2$. The quark self-energies read

$$\begin{aligned} \Sigma ^L_{ij}&=-\frac{2\alpha _s(\mu )}{3\pi }\sum _{s=1}^6 B_1\left( p^2,m_{\tilde{g}}^2, m_{\tilde{u}_s}^2\right) W_{si}W^*_{sj},\end{aligned}$$

(71)

$$\begin{aligned} \Sigma ^R_{ij}&=-\frac{2\alpha _s(\mu )}{3\pi }\sum _{s=1}^6 B_1\left( p^2,m_{\tilde{g}}^2, m_{\tilde{u}_s}^2\right) W_{s\,i+3}W^*_{s\,j+3},\end{aligned}$$

(72)

$$\begin{aligned} \Sigma ^{Ls}_{ij}&=-\frac{2\alpha _s(\mu )}{3\pi }\sum _{s=1}^6 m_{\tilde{g}} B_{p^2}\left( m_{\tilde{g}}^2, m_{\tilde{u}_s}^2\right) W^*_{s\,i+3}W_{s\,j},\end{aligned}$$

(73)

$$\begin{aligned} \Sigma ^{Rs}_{ij}&=-\frac{2\alpha _s(\mu )}{3\pi }\sum _{s=1}^6 m_{\tilde{g}} B_{p^2}\left( m_{\tilde{g}}^2, m_{\tilde{u}_s}^2\right) W_{s\,j+3}W^*_{s\,i}. \end{aligned}$$

(74)

For the computation of the real corrections we use the parametrisation as in [151],

$$\begin{aligned} r^2\equiv & {} \frac{(p_{\tilde{u}_1}-p_c-p_g)^2}{m_{\tilde{u}_1}^2} = \frac{m_{\tilde{\chi }_1^0}^2}{m_{\tilde{u}_1}^2} ,\end{aligned}$$

(75)

$$\begin{aligned} p_c p_g= & {} \frac{m_{\tilde{u}_1}^2}{2} (1-r)^2 y ,\end{aligned}$$

(76)

$$\begin{aligned} p_{\tilde{u}_1} p_g= & {} \frac{m_{\tilde{u}_1}^2}{2} (1-r^2) (1-z), \end{aligned}$$

(77)

in terms of the four-momenta of the squark, charm quark and gluon, $p_{\tilde{u}_1}$, $p_c$ and $p_g$, respectively. The squared matrix element evaluated from the Feynman diagrams of the real corrections, depicted in Fig. 3, is integrated over the three-particle phase space in $D=4-2\epsilon$ dimensions, with $\epsilon \equiv \epsilon _{\text {IR}}$. The D-dimensional differential three-particle phase space $\mathrm{d}\Phi ^{(3)}$ reads

$$\begin{aligned}&\mathrm{d}\Phi ^{(3)} (p_c,p_{\tilde{\chi }_1^0},p_g;p_{\tilde{u}_1})\nonumber \\&\quad = \mathrm{d} \Phi ^{(2)} (p_c,p_{\tilde{\chi }_1^0}; p_{\tilde{u}_1}) \frac{(1-r)^2}{16 \pi ^2} \frac{(m_{\tilde{u}_1}^2)^{1-\epsilon } (4 \pi )^\epsilon }{\Gamma (1-\epsilon )} \left( \frac{1+r}{1-r}\right) ^{2 \epsilon } \nonumber \\&\qquad \times \int _0^1 \mathrm{d}z (r^2 + (1-r^2) z )^{-\epsilon } \int _0^{y_{max}} \mathrm{d}y \, y^{-\epsilon } (y_{max} - y)^{-\epsilon },\nonumber \\ \end{aligned}$$

(78)

where $\mathrm{d}\Phi ^{(2)}$ denotes the differential two-particle phase space, $p_{\tilde{\chi }_1^0}$ the four-momentum of the neutralino and $\Gamma$ the Gamma function. The upper integration limit $y_\mathrm{max}$ is given by

$$\begin{aligned} y_\mathrm{max} = \frac{(1+r)^2 z (1-z)}{(z-r^2 z+r^2)}. \end{aligned}$$

(79)

Neglecting the factor $(4 \pi )^\epsilon /\Gamma (1-\epsilon )$ in compliance with the virtual corrections this leads to the following result for the finite part of the real corrections:

$$\begin{aligned} \Gamma ^{\text {real}}&=-\frac{\alpha _s(\mu )}{288\pi ^2} m_{\tilde{u}_1}((g^L_{211})^2 + (g^R_{211})^2)\nonumber \\&\times \, \left[ 10\pi ^2-99+204 r^2-20\pi ^2 r^2 \right. \nonumber \\&\quad -105 r^4 + 10 \pi ^2 r^4 - 6(-1 + r^2)^2 \log ^2\left( \frac{m_{\tilde{u}_1}^2}{\mu ^2}\right) \nonumber \\&\quad + 24 r^2 \log (r^2) - 18 r^4 \log (r^2) \nonumber \\&\quad + 60 \log (1 - r^2) - 120 r^2 \log (1 - r^2)\nonumber \\&\quad + 60 r^4 \log (1 - r^2) - 24 \log ^2(1 - r^2) \nonumber \\&\quad + 48 r^2 \log ^2(1 - r^2) - 24 r^4 \log ^2(1 - r^2)\nonumber \\&\quad - 6(-1 + r^2)^2 \log \left( \frac{m_{\tilde{u}_1}^2}{\mu ^2}\right) (-5 + 4 \log (1 - r^2)) \nonumber \\&\left. \quad - 24 (-1 + r^2)^2 Li_2(1-r^2) \right] , \end{aligned}$$

(80)

with the Spence function

$$\begin{aligned} Li_2(z)=-\int _0^z \mathrm{d}u\frac{\log (1-u)}{u},\quad z\in \mathbb C \setminus [1,\infty ). \end{aligned}$$

(81)