1 Introduction

In the present article, we are going to reconsider the issue of cosmological distances measurement in cosmology. Methods commonly used by astronomers are collected in the review [1], a good introduction to this topic.

The angular diameter distance and the luminosity distance are known for being of much practical use. These two distances are connected by the following relation [2]:

$$\begin{aligned} d_\mathrm{l} = (1+f)^2d_\mathrm{a} \end{aligned}$$
(1)

where \(d_\mathrm{l}\) is the luminosity distance, \(d_\mathrm{a}\) the angular diameter distance, and f the redshift. This relation shows the feasibility to concentrate our study on the angular diameter distance.

As a rule, the derivation of the angular diameter distance [1] is undertaken for the homogeneous Universe [3], i.e. all matter of the Universe is distributed homogeneously according to the assumption.

This assumption is valid for volumes of the order of about 500 Mps as the side of a cube, and it does not reflect the real situation in the case of the distance measurement when the beam of light is propagating through a generally small volume.

Let us briefly define the problem of the cosmological angular diameter distance (ADD) measurement. The definition of ADD, which is valid in Euclidean space, is usually extended to a curved space [4] with the formula

$$\begin{aligned} d_\mathrm{a} = \frac{z}{\phi }. \end{aligned}$$
(2)

Here, z is the linear size of the object and \(\phi \) is its angular size (Fig. 1). In the Friedmann–Lemaitre–Robertson–Walker (FLRW) geometry we can find the linear size of a distant object using the metric

$$\begin{aligned} \mathrm{d}s^2=\mathrm{d}t^2-a(t)^2\left( \frac{\mathrm{d}r^2}{1-kr^2}+ r^2(\mathrm{d}\theta ^2 + \sin ^2\theta \mathrm{d}\phi ^2)\right) . \end{aligned}$$
(3)

For example, in the spatially flat universe, where \( k=0\), one can obtain

$$\begin{aligned} z = a_\mathrm{e} r\phi \end{aligned}$$
(4)

where \(a_\mathrm{e}\) is the scale factor at the time of emission. Combining the expressions above, it is easy to obtain (as commonly used by astronomers) the equation for the angular diameter distance:

$$\begin{aligned} d_\mathrm{a} = a_\mathrm{e}r. \end{aligned}$$
(5)

To obtain the result (5) we used the FLRW metric (3) corresponding to the homogeneous universe. Therefore, if we suggested that our universe were not homogeneous in the cone of light rays (CLR)Footnote 1 of an ADD measurement, then we must take into account local inhomogeneities inside or close to the CLR.

Fig. 1
figure 1

The angular diameter distance setup. Field and empty cone of light rays schemes

Full size image

What will the ADD measurement be if we take into account a local inhomogeneity? As far as we know, the first who dealt with this question was Zeldovich. He presented the solution for “the homogeneous in the mean Universe” in [5]. It is interesting to mention that in the monograph [4] Novikov and Zeldovich noted that during the Symposium in Burokan (1966), American astronomers reported that familiar ideas were declared by Feynman. Recently in Ref. [6] it was also confirmed that Feynman pondered over the same problem, and he also suggested that one should consider a zero stress-energy tensor inside a light cone.

Considering a congruence of null geodesics, we will use the following terminology proposed by Penrose [7]:

  • The Ricci focusing is the focusing due to the gravitational effect of intrinsic mass inside the light cone;

  • the Weyl focusing is the focusing due to inhomogeneous clumps of matter along the null geodesics path.

Let us review the main stream of Zeldovich’s original ideas represented in the papers [5, 8]. In the article [5] Zeldovich introduced “a homogeneous in the mean universe“ and he analyzed the effect of the local non-uniformity of the matter-dominated spatially flat Friedmann Universe on the angular and luminosity distances measurement. It was found for the ADD under suggestion that there was a negligible amount of matter inside the light cone and it was possible to neglect the gravitational effect of that matter. The method applied is the integration of numerous lensing deflections due to the intrinsic mass of a light cone.

The solutions of an ADD measurement for a nonhomogeneous nonflat universe were found in the paper by Dashevskii and Zeldovich [8]. In this paper they also presented the method for describing Ricci focusing through the photon momenta. Later on we will explain this approach in detail where we make use of this method in our study. In the work by Dashevskii and Slysh [9] the analytical solution for a closed matter-dominated Universe for a partly filled light cone was found. They also derived the differential equation on the linear distance between the two rays emitted by the outer points of the object. Let us mention here that this equation does not contain the dark energy component and it may not be applied for ADD measurement now from the current observational data.

Let us note that Zeldovich’s original ideas were used afterwards in a series of papers by Dyer and Roeder [10–12]. Their papers are much cited and we comment on them briefly.

In the first paper [10] they used Sachs’ equations [13] and obtained the result which was found in [5]. In the second paper [12] they obtained a differential equation similar to the equation from [9] which was valid only for the Universe without dark energy, because the energy-momentum tensor was set up as \(T_{\mu \nu }=\hbox {diag}(\rho , 0,0,0)\). The solution of this equation proves to be a result from [9]. In the third paper [11] the result was found for the Swiss Cheese Universe.

In 1976, Weinberg [14] showed that the summation of gravitational deflection caused by individual clumps of matter is equal to the effect caused by the homogeneous distribution of the same mass. This paper narrowed the interest of the community to the effects of inhomogeneity to the distance measurement and it provides a strong criticism of the Swiss Cheese Universe model. Nonetheless, Weinberg’s results are in agreement with Zeldovich’s ideas. Indeed, the matter enclosed inside a light cone for the homogeneous in the mean Universe may be considered as a homogeneous distribution (of a small density). What is the problem with the direct application of the original solutions of Zeldovich for calculating cosmological distances? The problem is the fact that these solutions were obtained in the absence of dark energy and dark matter, i.e. for the Universe which contains only baryonic matter. This is controversial in our current understanding of the Universe. Therefore in the present paper we are going to extend Zeldovich’s original ideas for solving this problem in a general form.

Let us mention the series of papers by Alcock and Anderson where they discuss the problem of the distance measurement. In the first paper [15] they emphasized the importance of a correct cosmological distance measurement for calculating the Hubble constant through gravitational lensing. In the second paper [16] they presented an original method for the distance measurement; the so called “effective distance”. The problem with their approach is that all our cosmological and astronomical theories were developed for the angular diameter (luminosity) distance. This is why we are not ready to apply “effective distance” methods and we are going to keep commonly accepted definitions of fundamental concepts.

The ideas of Dyer and Roeder were developed by Kantowski [17], who constructed an analysis of differential equations and their solutions for the Swiss Cheese Universe. In Ref. [18] the solutions for various inhomogeneous cosmological models were found. We would like to mention the impact of the work by Schneider and Weiss [19], and Seitz et al.[20] in the development of Dyer and Roeder’s ideas.

Why should we reconsider previous results in the distance measurements? From our point of view, the main problem in these results is that they were obtained for an inhomogeneous Universe.

Our understanding is that this assumption is too strong, because it is already proven that the global Universe mass distribution is homogeneous. Thus we assume that the Universe evolves like a homogeneous universe, but if we measure the distance to an object in the space, the effect of Ricci focusing becomes weaker. The reason is in fact that the density inside the light cone is smaller than the critical density of the Universe. Summing up the discussion above we can state that the Zeldovich model of the Universe (the homogeneous in the mean Universe) is very suitable for describing observations in the present Universe.

Let us explain our last thesis in detail by firstly discussing the method of Dyer and Roeder. They start from Sachs’ equations [13], which are a version of the Raychaudhuri equation for null geodesics [21]. It should be noted that the Raychaudhuri equation is more general than the Friedmann equation [22] and it already includes the effects of gravitational lensing.

Starting from these mentioned works by Dyer and Roeder, physicists are using (as proposed by Penrose [7]) the Weyl and Ricci focusing for calculating the ADD.

For the Friedmann Universe, the Weyl tensor is equal to zero (\(W_{iklm} = 0\)) [22]. In the case of small clumps of the Swiss Cheese Universe, Dyer and Roeder showed [23] that effects of the Weyl focusing on every clump can be approximated by the Ricci focusing. This proposition proves Weinberg’s results [14]. If we follow Zeldovich’s ideas for the ADD measurement, then our universe remains a Friedmann Universe and there are no concentrated clumps of matter on the line of sight. Thus the effect of the Weyl focusing can be neglected. To take into account the concentrated clumps of matter, we suggest that one should use the well-developed gravitational lensing theory. How will we take the value of the Ricci focusing in the cases of the ADD measurement? We will follow the Zeldovich and Dashevskii ideas, which were published in [8], i.e. we use the fraction of perpendicular and longitudinal components of the photon.

It should be noted that the interest of the scientific community with regards to the problem of a distance measurement in an inhomogeneous Universe does not end. For example, in the paper by Bolejko and Ferreira [24], the authors once again emphasize the importance of the effects of inhomogeneities in cosmology. We should also mention that our idea of developing Zeldovich’s original ideas for cosmological distance measurements is not new. In the paper by Kayser et al.[25] the differential equation presented in Ref. [9] was used with the aim of finding the cosmological distance in the Universe filled with dark energy. Unfortunately, as mentioned before, the differential equation obtained by Dashevskii and Slysh for the matter-dominated Universe did not account for dark energy and could not be applied to the \(\Lambda CDM\) model. It is easy to check, by using standard cosmological parameters and assuming a filled light cone, that the equations obtained by Kayser et al. [25] give wrong results in this case.

The investigation of inhomogeneities and its connection to a luminosity distance (LD) has been performed within the framework of Lemaitre–Tolman–Bondy (LTB) solutions in the work by Romano et al. [26]. It was shown there that an inhomogeneous isotropic universe described by an LTB solution admits a positive, averaged acceleration. Thus, this model may be considered as an alternative to standard FLRW cosmology with dark energy (DE). Also, the effect of inhomogeneities in the presence of a cosmological constant has been considered for LTB solutions which were only locally inhomogeneous. Finally, as regards LD, it was found that the luminosity distance as a function of the redshift, \(D_\mathrm{L}(z)\), is not significantly affected by small inhomogeneities, but the apparent cosmological observables, derived from \(D_\mathrm{L}(z)\) under the assumption of homogeneity, are significantly affected because they are sensitive to its derivatives. Further investigation of the effects of primordial curvature perturbations on the apparent value of a cosmological constant, using the LTB solution, was performed in the work by Romano et al. [27].

A series of works [28–33] are devoted to the investigation of the luminosity–redshift relation up to second order in perturbation theory using a very promising geodesic light-cone (GLC) gauge, first proposed in the work by Gaspirini et al. [28]. The LCG approach is based on null geodesics as well and is present in our work. The key differences in the methods are a consideration of a perturbed FLRW metric in LCG and the analysis of homogeneous in the mean universe used in our approach. The luminosity distance was computed to first order in the longitudinal gauge in the works by Sasaki [34] and Kasai and Sasaki [35]. For example, in the recent work by Marozzi [36] the expressions for the redshift and the luminosity distance–redshift relation in a generic homogeneous FLRW universe with anisotropic stress have been computed with perturbations up to second order.

Umeh et al. [37] noted that precision cosmology from the next generation of telescopes should be complemented with theoretical models of the same level of precision. To this end, the distance–redshift relation in [37] was extended from first order to second order in cosmological perturbation theory for a general dark energy model. In Ref. [38] the derivation of the distance–redshift relation was presented in detail and the observed redshift and the lensing magnification to second order in perturbation theory was found. Let us note that in [37, 38] the ADD and luminosity distance of a source are considered to be the same, i.e. they are connected with the Etherington identity [2].

We should stress here that in the present work we are considering the angle diameter distance in cosmology. It is well known that for ADD measurements a very small angle (of a few arc seconds) should be considered. For this reason, we cannot say anything about a homogeneous and isotropic universe in this thin cone of light rays and thus the use of the FLRW metric is questionable in this case. When the luminosity distance measurement is under consideration, we use the total celestial sphere, which includes the properties of homogeneity and isotropy so that the application of the FLRW metric is justified. From this position, we can tell that the Etherington identity may have small deviations for large redshifts [39].

The paper is organized as follows: in Sect. 2 we present the general approach for the ADD measurement in the Friedmann Universe and we derive the equation for the evolution of the cross-section diameter z of a light beam from a distant object. We show that the derived equation is valid for any type of Friedmann Universe, for any forms of energy-momentum tensor and the equation includes a separate term, which is responsible for Ricci focusing. In Sect. 3, we apply the general formula obtained in Sect. 2 for z for ADD calculation in the Friedmann Universe of any type, filled by dark energy and radiation. We demonstrate also that the formula for the ADD calculation is valid for a wide range of modified gravity theories. We present the numerical solution for a partly filled light cone in Sect. 4.

2 ADD in the Friedmann Universe: general approach

Let us start from the definition of the angular diameter distance (2), which is generally exploited in astronomy. As mentioned before, it is the fraction of linear and angular sizes of the object. In astronomy we generally deal with spherical bodies and therefore we can simplify our task by considering the diameter of the object (z in (2)) instead of its area. As we are discussing a congruence from a distance object of radial null geodesics which are crossed at a point of observation (center of our spherical coordinate system), the angle \(\phi \) between the boundary points of a diameter z remains constant by its definition (2).

Let us choose a spherical coordinate system \([t,r,\theta ,\phi ]\) with an observer placed in the center of it. To calculate the changing of the linear size z during the travel of the light beams, we have to account for the following effects:

  1. 1.

    Expansion of the universe.

  2. 2.

    The Ricci focusing.

Let us remind ourselves that in the Friedmann Universe all matter is involved with the Hubble current and in the comoving coordinates (with the Earth observer in the center), the spatial coordinates of all particles are not changing \(\dot{x}_i = 0\) [40]. Therefore we have to consider not the object itself, but the photons which are moving along null radial geodesics. In this context z will be the distance between two light rays from the end points of the object at the time of emission. Evidently z will be variable.

Our next task is to derive the differential equation involving z, which allows us to take into account the effects arising when measuring distances in a Friedmann Universe.

For the Friedmann–Lemaitre–Robertson–Walker (FLRW) metric, we will use the two forms

$$\begin{aligned} \mathrm{d}s^2= & {} \mathrm{d}t^2 - a^2[\mathrm{d}r^2 + f^2(r)(\mathrm{d}\theta ^2 + \sin ^2\theta \mathrm{d}\phi ^2)] \end{aligned}$$
(6)
$$\begin{aligned}= & {} \mathrm{d}t^2-a(t)^2\left( \frac{\mathrm{d}r^2}{1-kr^2}+ r^2(\mathrm{d}\theta ^2 + \sin ^2\theta \mathrm{d}\phi ^2)\right) \end{aligned}$$
(7)

where \(f(r)= \sin r, r , \sinh r \) or \(k=1,0,-1\) for a closed, spatially flat, open universe, respectively. For the sake of simplicity we choose \(\theta = \frac{\pi }{2}\). Let us in the analysis use radial null geodesics \(d\phi =0\), then the metric (7) is reduced to

$$\begin{aligned} \mathrm{d}s^2 = a^2\left( \frac{\mathrm{d}t}{a} - \mathrm{d}r\right) \left( \frac{\mathrm{d}t}{a} + \mathrm{d}r\right) . \end{aligned}$$
(8)

We now define new coordinates

$$\begin{aligned} u= \eta - r,\quad v= \eta + r \end{aligned}$$
(9)

where \(\eta = \int \frac{\mathrm{d}t}{a}\) is a conformal time. Then we have \(u=\hbox {const}\) for ongoing geodesics (in relation to the observer), and \(v=\hbox {const}\) for ingoing ones. Since we are interested in ingoing geodesics, we choose \(v=\hbox {const}\) or in terms of cosmic time t

$$\begin{aligned} \mathrm{d}r=-\frac{\mathrm{d}t}{a}. \end{aligned}$$
(10)

The co-vector field

$$\begin{aligned} k^\mathrm{in}_\alpha = - \partial _\alpha v \end{aligned}$$
(11)

should be a null one and has to satisfy the geodesics equation. From the metric (7) it is easy to find

$$\begin{aligned} k^\mathrm{in}_\alpha = \left( -\frac{1}{a},-1,0,0\right) ,\quad k^\alpha _\mathrm{in} = \left( -\frac{1}{a}, \frac{1}{a^2},0,0\right) . \end{aligned}$$
(12)

It is easy to check that \(k^\alpha k_\alpha =0\).

Now we will find the affine parameter for \(k^\alpha _\mathrm{in}\) from the geodesic equation,

$$\begin{aligned} k^\alpha _{;\beta }k^\beta = \frac{\partial k^\alpha }{\partial \lambda } + \Gamma ^{\alpha }_{\gamma \beta }k^\gamma k^\beta = 0. \end{aligned}$$
(13)

By substituting (12) into (13) we obtain

$$\begin{aligned} \frac{\partial a}{\partial \lambda } + \frac{\dot{a}}{a} = 0. \end{aligned}$$
(14)

From Eq. (14) we can find the relation for the affine parameter,

$$\begin{aligned} \mathrm{d} \lambda = - a\mathrm{d}t. \end{aligned}$$
(15)

Using the Eq. (15) we can calculate the expansion of \(\Theta \) [21]:

$$\begin{aligned} \Theta \equiv k^\alpha _{;\alpha } = - \frac{2}{a^2}\left( \dot{a} - \frac{f'(r)}{f(r)}\right) . \end{aligned}$$
(16)

We can also use the geometrical interpretation of the expansion \(\Theta \):

$$\begin{aligned} \Theta = \frac{1}{S}\frac{\partial S}{\partial \lambda }. \end{aligned}$$
(17)

It is easy to see that a congruence’s cross-sectional area S in the chosen metric (7) is

$$\begin{aligned} S = \frac{\pi z^2}{4} \end{aligned}$$
(18)

where z is the diameter of the cross section.

Our task now is to represent \(\Theta \) through z, the distance between two neighbor rays (one from the beginning of the object and another from the end of the object). Further, we will interpret z as the diameter of the cross section if we assume rotational symmetry in the FLRW metric. For the sake of simplicity, let the first light ray propagate along the axis \(\phi =0\). As we noted at the beginning of this section, we first want to find a differential equation for z in the Friedmann Universe. From the definition of the ADD in the curved space-time (for the FLRW metric (7) \(d_\mathrm{a}= a f(r)\)) we have the distance between the two rays,

$$\begin{aligned} z = a\phi f(r). \end{aligned}$$
(19)

Substituting (19) and (18) into (17) one can find \(\Theta = -\frac{2\dot{z}}{az}\) and using (16) we obtain

$$\begin{aligned} \dot{z} = \frac{z}{a}\left( \dot{a} - \frac{f'(r)}{f(r)}\right) . \end{aligned}$$
(20)

For the derivative along the path, using (10), we find

$$\begin{aligned} \ddot{z} = \frac{z}{a}\left( \ddot{a}-\frac{\dot{a}}{a}\frac{f'(r)}{f(r)} + \frac{f''(r)}{f(r)a}\right) . \end{aligned}$$
(21)

We can express \(\frac{f'(r)}{f(r)}\) from (20) and insert it into (21). Then taking into account that \(\frac{f''(r)}{f(r)}=k\), we obtain the equation for an arbitrary curvature,

$$\begin{aligned} \ddot{z} - \frac{\dot{a}}{a}\dot{z} - \left( \frac{\ddot{a}}{a}-\frac{\dot{a}^2}{a^2} - \frac{k}{a^2}\right) z = 0. \end{aligned}$$
(22)

The initial conditions are

$$\begin{aligned} z(t_0) = 0,\quad \dot{z}|_{t_0} = \phi . \end{aligned}$$
(23)

The initial conditions are derived from the fact that the distance at the point of observation between two rays from the object is equal to zero, and the change in the velocity of this distance equals the angle of observation by definition, and the fact that \(c=1\).

Our next task is to derive the expression for Ricci focusing in the Friedmann Universe. To this end let us approach the work in [8] and restore the result for the sake of completeness without essential changes.

Let us define the angle \(\psi \) between the rays by the formula

$$\begin{aligned} \tan \psi \cong \psi = -\frac{\mathrm{d} z}{\mathrm{d}t} = -\phi f(r)\dot{a} + \phi f'(r) \end{aligned}$$
(24)

where (19) and (10) were used. The first ray propagates along the axis of the coordinates. Let us write the angle \(\psi \) as the ratio of the perpendicular component of the momentum of the second photon q to its longitudinal component h,

$$\begin{aligned} \psi = -\frac{q}{h}. \end{aligned}$$
(25)

Since \(|q|\le h \) the total momentum P is proportional to the frequency of the quantum, and it is equal to h. From the redshift formula, the total momentum P is given by

$$\begin{aligned} P = h = \hbar \omega = \frac{K}{a(t)} \end{aligned}$$
(26)

where \(K= \hbar \omega (t_0)a(t_0)\) is a constant. From (26) we obtain the expression for the transverse component q in the case of propagation in the homogeneous universe,

$$\begin{aligned} q = -\psi h = \frac{K\phi }{a}\left( \dot{a}f(r)- f'(r)\right) , \end{aligned}$$

while for the derivative of this component along the path, using (10), we find for arbitrary curvature \(k=\{-1,0,1\}\)

$$\begin{aligned} \frac{\mathrm{d} q}{\mathrm{d}t} = hz\left[ \frac{\ddot{a}}{a} - \frac{\dot{a}^2}{a^2} - \frac{k}{a^2}\right] . \end{aligned}$$
(27)

Thus we can rewrite (22) using (27)

$$\begin{aligned} \ddot{z} - \frac{\dot{a}}{a}\dot{z} - \frac{\dot{q}}{h} = 0. \end{aligned}$$
(28)

Let us reaffirm for ourselves that we derived the general differential equation for the Friedmann Universe where the part responsible for Ricci focusing is represented by the separate term. We want to focus attention on the difference between the resulting differential equation and that obtained by Dashevsky and Slysh [9]. The result obtained by them is valid for the special case—a Friedmann Universe with \(\Omega _0=\Omega _M=1\). Equation (28) is valid for any type of Friedmann Universe: an open, spatially flat or closed model, and for any expression and form of the energy-momentum tensor. Thus our equation is valid even for modified theories of gravitation if a Friedmann Universe is involved.

3 Method of ADD calculation

Let us investigate “homogeneous” and “homogeneous in the mean universe” cases. We will study a Friedmann Universe filled by a perfect fluid (matter, radiation) with vacuum energy. We will consider the method of the ADD calculation for such a universe.

Let us start with the homogeneous universe. The dynamics of the universe can be described by the Einstein–Friedmann equations,

$$\begin{aligned}&\frac{\dot{a}^2}{a^2}+\frac{k}{a^2} = \frac{8\pi G}{3}\rho ,\end{aligned}$$
(29)
$$\begin{aligned}&\frac{\ddot{a}}{a} = -\frac{4\pi G}{3} (3p+\rho ). \end{aligned}$$
(30)

Using these equations in (27) we can obtain the important relation

$$\begin{aligned} \frac{\dot{q}}{h} = -4\pi G z(p+\rho ). \end{aligned}$$
(31)

Thus Eq. (28) transforms to

$$\begin{aligned} \ddot{z} - \frac{\dot{a}}{a}\dot{z} + 4\pi G z(p+\rho )= 0. \end{aligned}$$
(32)

We can find the solutions for (32) independent of the form of the scale factor a(t) and compatible with the initial conditions (23),

$$\begin{aligned} z = \left\{ \begin{array}{l} \phi a \sin \int _t^{t_0}\frac{dt}{a} : k=1, \\ \phi a \int _t^{t_0}\frac{dt}{a} : k=0 ,\\ \phi a \sinh \int _t^{t_0}\frac{dt}{a} : k=-1. \end{array}\right. \end{aligned}$$
(33)
Fig. 2
figure 2

The angular diameter distance with respect to the redshift for empty, half-filled, and filled cones

Full size image

One can easily check these solutions by direct substitution of the solutions (33) into (32). Thus (33) is the solution for the homogeneous universe, and the angular diameter distance can be calculated with the formulas

$$\begin{aligned} d_\mathrm{a} = \left\{ \begin{array}{l} a \sin \int _t^{t_0}\frac{\mathrm{d}t}{a} : k=1 ,\\ a \int _t^{t_0}\frac{\mathrm{d}t}{a} : k=0 ,\\ a \sinh \int _t^{t_0}\frac{\mathrm{d}t}{a} : k=-1. \end{array}\right. \end{aligned}$$
(34)

To obtain the dependence \(d_\mathrm{a}\) on the redshift f Footnote 2, an expression of the form \(d_\mathrm{a} = \psi (f)\) for the most general cosmological model (for a mixture of vacuum energy and relativistic and non-relativistic matter) should involve the equation of state [3]

$$\begin{aligned} -\frac{\mathrm{d}\rho }{\rho + p} = 3d\ln a. \end{aligned}$$
(35)

This equation can be solved for matter (\(p=0\)), radiation (\(p=\rho /3\)), and vacuum energy (\(p_\Lambda =-\rho _\Lambda =\hbox {const}\)). The expression for a mixture of them is

$$\begin{aligned} \rho = \frac{3H_0^2}{8\pi G}\left[ \Omega _\Lambda + \Omega _M\left( \frac{a_0}{a}\right) ^3 + \Omega _R\left( \frac{a_0}{a}\right) ^4\right] \end{aligned}$$
(36)

where the present energy densities in the vacuum, non-relativistic matter, and relativistic matter are, respectively,

$$\begin{aligned} \rho _\Lambda = \frac{3H_0^2\Omega _\Lambda }{8\pi G},\quad \rho _M = \frac{3H_0^2\Omega _M}{8\pi G},\quad \rho _R = \frac{3H_0^2\Omega _R}{8\pi G}. \end{aligned}$$
(37)

Using (37), the Friedmann equation (30) can be represented in the form

$$\begin{aligned} \mathrm{d}t = \frac{\mathrm{d}x}{H_0x\sqrt{\Omega _S}} \end{aligned}$$
(38)

where \(x=\frac{a}{a_0} = \frac{1}{1+f}\) (\(t=t_0 \Rightarrow x = 1\)), \(\Omega _k=-\frac{k}{a_0^2H_0^2}\), the redshift f, and

$$\begin{aligned} \Omega _S = \Omega _\Lambda + \Omega _kx^{-2} + \Omega _M x^{-3} + \Omega _Rx^{-4}. \end{aligned}$$

Thus following (34) we can present the resulting formulas for ADD in the form

$$\begin{aligned} d_\mathrm{a} = \left\{ \begin{array}{l} \frac{1}{1+f}\frac{1}{H_0\sqrt{\Omega _k}} \sin \int _\frac{1}{1+f}^1\sqrt{\Omega _k}\frac{\mathrm{d}x}{x^2\sqrt{\Omega _S}} : k=1, \\ \frac{1}{1+f} \int _\frac{1}{1+f}^1\frac{dx}{H_0x^2\sqrt{\Omega _S}} : k=0 ,\\ \frac{1}{1+f} \frac{1}{H_0\sqrt{\Omega _k}}\sinh \int _\frac{1}{1+f}^1\sqrt{\Omega _k}\frac{\mathrm{d}x}{x^2\sqrt{\Omega _S}} : k=-1 .\\ \end{array}\right. \end{aligned}$$
(39)

Let us mention that the result (39) is in agreement with the widely used formulas represented in [1].

We should mention that (34) is valid for any modified gravitational theory where the “Einstein–Friedmann” equations can be written in the form

$$\begin{aligned} \frac{\dot{a}^2}{a^2}+\frac{k}{a^2} = \psi (t), \end{aligned}$$
(40)
$$\begin{aligned} \frac{\ddot{a}}{a} = \xi (t). \end{aligned}$$
(41)

Here \(\xi (t)\) and \(\psi (t)\) are arbitrary functions.

Let us turn our attention to the investigation of the “homogeneous in the mean universe” case.

The description of such a universe contains two propositions: (1) we have a homogeneous distribution of matter over the whole universe; (2) the interaction between matter and light rays is negligible under standard observations.

The proposition (2) means that for this type of universe, we have \(\dot{q}=0\) and Eq. (28) takes the form

$$\begin{aligned} \ddot{z} - \frac{\dot{a}}{a}\dot{z} = 0. \end{aligned}$$
(42)

The solution of (42) can be presented in a form compatible with the initial conditions (23),

$$\begin{aligned} z = \frac{\phi }{a_0}\int a \mathrm{d}t. \end{aligned}$$
(43)

Thus, the expression for the angular diameter distance for any curvature in the case of the “homogeneous in the mean universe” is

$$\begin{aligned} d_\mathrm{a} = \frac{1}{a_0}\int _t^{t_0} a \mathrm{d}t. \end{aligned}$$
(44)

Note that the result is valid for any modified gravity theory when the Friedmann Universe is under consideration.

If we consider the \(\Lambda \)CDM model, the ADD formula (44), with the help of (38), transforms to

$$\begin{aligned} d_\mathrm{a} = \int _\frac{1}{1+f}^1\frac{\mathrm{d}x}{H_0\sqrt{\Omega _\Lambda + \Omega _kx^{-2} + \Omega _M x^{-3} + \Omega _Rx^{-4}}}. \end{aligned}$$
(45)

The obtained expression for ADD coincides with the solution found by Dashevskii and Zeldovich [5, 8], when \(\Omega _\Lambda = \Omega _R =0\).

4 Numerical solutions

We now present numerical solutions to Eq. (28) for the partly filled cone for the present day Universe: \(k=0\), \(\Omega _R = 0\), \(\Omega _M + \Omega _\Lambda = 1\).

As a first step, we may rewrite the Einstein–Friedmann equations (29) and (30) for the spatially flat universe,

$$\begin{aligned}&\frac{\ddot{a}}{a} = -\frac{4\pi G}{3}(\rho + 3p) ,\end{aligned}$$
(46)
$$\begin{aligned}&\frac{\dot{a}^2}{a^2} = \frac{8\pi G \rho }{3}. \end{aligned}$$
(47)

Let us write the solution for the equation of state (35) of a mixture of matter and vacuum energy

$$\begin{aligned} \rho = \frac{3H_0^2}{8\pi G}\left[ \Omega _\Lambda + \Omega _M\left( \frac{a_0}{a}\right) ^3\right] . \end{aligned}$$
(48)

Now we make the substitution of (48) into (46),

$$\begin{aligned} \frac{\dot{a}^2}{a^2}=H_0^2\left[ \Omega _\Lambda + \Omega _M\left( \frac{a_0}{a}\right) ^3\right] . \end{aligned}$$
(49)

The solution (it is also presented in [41], as an exercise) is

$$\begin{aligned} a =a_0\left[ \sqrt{\frac{\Omega _M}{\Omega _\Lambda }}\sinh \frac{3}{2}H_0\sqrt{\Omega _\Lambda }t\right] ^\frac{2}{3}. \end{aligned}$$
(50)

We introduce \(\alpha \) as the coefficient of the light cone “fillness”, i.e. \(\alpha = 1\) for the filled cone (with the critical density) and \(\alpha = 0\) for the empty cone (with null density inside). Thus we can rewrite Eq. (22) in the form

$$\begin{aligned} \ddot{z} - \frac{\dot{a}}{a}\dot{z} - \alpha \frac{\dot{q}}{h} = 0. \end{aligned}$$
(51)

Using (50) we can transform (51) into

$$\begin{aligned} \ddot{z} - k\coth \left( \frac{3}{2}kt\right) \dot{z} + \frac{3}{2}\alpha k^2\left( \sinh \frac{3}{2}kt\right) ^{-2}z = 0, \end{aligned}$$
(52)

with initial conditions \(z(t_0) = 0\) and \(\dot{z}|_{t_0}=\phi \). We know that \(d_a =\frac{z}{\phi }\); thus we can rewrite (52),

$$\begin{aligned} \ddot{d_\mathrm{a}} - k\coth \left( \frac{3}{2}kt\right) \dot{d_\mathrm{a}} + \frac{3}{2}\alpha k^2\left( \sinh \frac{3}{2}kt\right) ^{-2}d_\mathrm{a} = 0, \end{aligned}$$
(53)

with initial conditions \(d_\mathrm{a}(t_0) = 0\) and \(\dot{d_a}|_{t_0}=1\). In terms of the redshift f we may calculate \(t_e\), the time of emission, and \(t_0\), the time of observation, with the relation

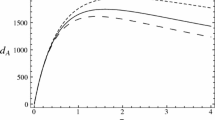
$$\begin{aligned} t = \frac{1}{h_0}\int _0^\frac{1}{1+f}\frac{\mathrm{d}x}{x\sqrt{\Omega _\Lambda + \Omega _M x^{-3}}} \end{aligned}$$
(54)

for \(t_\mathrm{e}\). For \(t_0\) we should select \(f=0\). The results are shown in Fig. 2. It is clear from the plots in Fig. 2 that the difference in the ADD measurement may lead to 600–700 Mps at \(f \simeq 3\).

The GNU Octave codeFootnote 3 for solving (53) may be found on the web-page http://lgca.ulspu.ru/nikolaev.

5 Conclusions

We extended Zeldovich’s ideas for ADD measurements in two directions. First, we have a generalization of the ADD formula from a closed to spatially flat and open Friedmann Universes. Second, we proposed not only empty and filled cone of light rays (CLR), but also the partly filled CLR.

These main results are represented by the differential equation (28) which allows us to separate the effects of the expansion of an homogeneous universe and Ricci focusing for congruence of radial null geodesics. It was shown that this equation consists of a classical solution for the homogeneous Friedmann Universe and, as a special case, it reduces to the equations obtained by Zeldovich et al. The solution of (28) was presented in quadratures in a form suitable for further numerical analysis.

The numerical solution for the partly filled CLR was obtained. From this solution (Fig. 2) it became evident that the standard ADD measurement (in a universe filled by (dark and baryonic) matter and dark energy) may be applied for an object with redshift f of not more than 0.5. For objects with \(f>0.5\), the influence of CLR filling became crucial. For example, for a redshift of \(f \simeq 3\), the ADD may have a difference of about 600–700 Mps for an empty and a totally filled CLR.

These results can help astronomers to improve their calculations where ADD is involved. We plan to present an extension of this method to gravitational lensing and a supernova data analysis in the next publication.