1 Introduction

Despite the fact that the glueball state has not been confirmed experimentally, its existence is an unavoidable and yet uncanny prediction of QCD. Glueball states may have different Lorentz structures in general, such as a scalar, a pseudoscalar or even a tensor with either normal or exotic \(J^\mathrm{PC}\) assignment. The prediction for the glueball masses is, however, a difficult task. Theoretical calculations indicate that the lowest lying glueball state is a scalar \(0^{++}\) state with a mass in the range of 1.6–2 GeV. A previous quenched lattice QCD calculation gave such a glueball mass \(m_G\) a value equal to \(1.71\pm 0.05 \pm 0.08\) GeV [1]. A recent result from an unquenched lattice QCD calculation [2] gives a result of \(1.795\pm 0.060\) GeV for this state. These results support that the scalar meson \(f_0(1710)\) is a glueball. Phenomenologically, \(f_0(1710)\) could be an impure glueball since it may be contaminated by possible mixings with the colorless quark–antiquark states that have total isospin zero [3–9]. These mixing effects can be either small [5–8] or large [3–5, 9], depending largely on the mixing schemes one chose to do the fits in and these may complicate the analysis.

A quenched lattice calculation also showed that the lowest lying \(0^{-+}\) state for a pure pseudoscalar glueball may have a higher mass: around \(2.560 \pm 0.035 \pm 0.120\) GeV [1]. A QCD sum-rule approach [10–13] also predicted a value higher than 1.8 GeV for the pseudoscalar glueball mass. All these results do not favor the earlier speculation of the \(\eta (1405)\) being a pseudoscalar glueball. \(\eta (1405)\) is indeed a perfect candidate for a \(0^{-+}\) glueball, since it is copiously produced from the radiative decay of \(J/\psi \) and not seen in the \(\gamma \gamma \) mode. Recently it has been shown that when mixing effects and related data for the transition matrix elements of the anomalous axial-vector current between vacuum and the three states \(\vert \eta \rangle \), \(\vert \eta ^\prime \rangle \), and \(\vert \eta \left( 1405 \right) \rangle \) are taken into account, the physical pseudoscalar glueball might be as light as \(1.4 \pm 0.1\) GeV [14]. Clearly, a full unquenched lattice calculation with the fermion determinant included must be performed in order to settle this issue satisfactorily. Indeed, it has been argued some time ago [13] that due to the dynamical fermion effects the full QCD prediction for the pseudoscalar glueball mass will substantially depart from its quenched approximation. However, the mass for the lowest lying \(0^{-+}\) state is still missing in the latest unquenched lattice results [2].

Understanding glueball dynamics is therefore important, though very challenging. In this work we will study scalar or pseudoscalar glueball production from rare semi-inclusive \(B\) meson decay. The main purpose of this paper is to refocus the attention of experimentalists for undertaking the proposed searches. From the experimental findings we can learn a lot. The quantitative numerical predictions are bound to have significant theoretical uncertainties; nevertheless experimental efforts will be useful.

For a recent review of the phenomenology of scalar and pseudoscalar glueballs, we refer to Refs. [15, 16], and for a recent summary of glueballs on the lattice, see Ref. [17].

We organize this paper as follows. In Sect. 2, we discuss the effective vertex of \(b \rightarrow s g^*\) induced by the gluonic penguin and the effective couplings between scalar and pseudoscalar glueballs with the gluons. In Sect. 3, we discuss the interaction of a scalar glueball with the light pseudoscalar meson octet using the chiral Lagrangian technique. The pseudoscalar glueball case will be briefly mentioned as well. In Sect. 4, the rates of the semi-inclusive \(B\) meson decay into scalar and pseudoscalar glueballs are presented. In Sect. 5, mixing effects for both scalar and pseudoscalar glueballs will be considered. We summarize our results in Sect. 6.

2 Effective couplings

Since the leading Fock space of a glueball \(G\) is made up of two gluons, the production of glueballs is most efficient at a gluonic rich environment like \(J/\psi \) or \(\Upsilon \) \(\rightarrow (gg)\gamma \rightarrow G\gamma \) [18, 19]. Direct glueball production is also possible at the \(e^+e^-\) [20] and hadron colliders. In this work, we show that \(B\rightarrow G + X_s\) decay also provides an interesting mechanism to produce and to detect a glueball. The leading contribution for this process is shown in Fig. 1, where the squared vertex refers to the gluonic penguin interaction and the round vertex stands for an effective coupling between a glueball and the gluons. The gluonic penguin \(b\rightarrow s g^*\) has been studied extensively in the literature and was used in the context for inclusive decay \(b \rightarrow s g \eta '\) [21, 22]. The effective interaction for \(b\rightarrow s g^*\) with next-to-leading QCD correction can be written as [23]

(1)

where \(\Delta F_1 = 4\pi (C_4(q, \mu ) + C_6(q, \mu ))/\alpha _s(\mu )\) and \(F_2 = -2 C_8(\mu )\) with \(C_i(q,\mu )\) \((i=4,6, \, \mathrm{and} \, 8\)) the Wilson coefficients of the corresponding operators in the \(\Delta B = 1\) effective weak Hamiltonian, \(q = p - p'=k+k'\), and \(T^a\) is the generator for the color group. We will use the next-to-leading order numerical values of \(\Delta F_1\) and \(F_2\) [23]. The top quark contribution gives \(\Delta F^\mathrm{top}_1 = -4.86\) and \(F^\mathrm{top}_2 = +0.288\) at \(\mu = 5\) GeV; whereas the charm quark contribution involves a \(q^2\) dependence through \(C_4^\mathrm{charm}(q,\mu ) = C^\mathrm{charm}_6(q,\mu ) = P^\mathrm{charm}_s(q,\mu )\) with

$$\begin{aligned} P^\mathrm{charm}_s(q,\mu )= & {} {\alpha _s(\mu ) \over 8 \pi } C_2(\mu ) \left( {10\over 9} + Q(q,m_c,\mu ) \right) \end{aligned}$$
(2)

and

$$\begin{aligned} Q(q,m,\mu )= & {} 4\int ^1_0 dx \, x\,(1-x) \ln \left[ m^2 - x(1-x)q^2\over \mu ^2 \right] \; \, \nonumber \\= & {} \frac{2\left[ 3q^2\ln (m^2/\mu ^2)-12m^2-5q^2 \right] }{9q^2}\nonumber \\&+ \frac{4(2m^2{+}q^2)\sqrt{4m^2{-}q^2}}{3\root 3 \of {q^2}}\mathrm{arctan}\sqrt{\frac{q^2}{4m^2{-}q^2}}.\nonumber \\ \end{aligned}$$
(3)

Here \(m_c = \) 1.4 GeV is the charm quark mass and \(C_2(\mu = 5\,\text{ GeV }) = 1.150\).

Fig. 1
figure 1

The leading diagram for \(B\rightarrow \text{ glueball } + X_s\)

Full size image

The effective coupling between a scalar glueball and two gluons can be parametrized as [24–27]

$$\begin{aligned} \mathcal{L}_0 = f \mathcal{G} G^a_{\mu \nu }G^{a\mu \nu }, \end{aligned}$$
(4)

where \(\mathcal{G}\) is the interpolating field for the glueball \(G\), \(G^a_{\mu \nu }\) is the gluon field strength, and \(f\) is an unknown coupling constant. When combined with the interaction vertex in Eq. (1), a scalar glueball can be produced in rare \(b\) quark decay, \(b \rightarrow s g G\) (Fig. 1). At the hadronic level, this leads to the rare semi-inclusive decay \(B \rightarrow G + X_s\). The above effective coupling has also been used for the study of exclusive decays of \(B^\pm \rightarrow f_0(1710) + K^{(*)\pm }\) [28].

Analogously one can also study inclusive \(B\) decays into a pseudoscalar glueball \(\tilde{G}\), whose leading effective coupling to the gluon can be parameterized as [24–27],

$$\begin{aligned} \mathcal{L}_0^\prime = \tilde{f} \tilde{\mathcal{G}} \tilde{G}^a_{\mu \nu } G^{a\mu \nu } \quad \mathrm{with} \; \tilde{G}^a_{\mu \nu } = {1 \over 2}\epsilon _{\mu \nu \alpha \beta } G^{a\alpha \beta } , \end{aligned}$$
(5)

\(\tilde{\mathcal{G}}\) denoting the interpolating field for the pseudoscalar glueball and \(\tilde{f}\) being an unknown coupling. When combined with the interaction vertex in Eq. (1), a pseudoscalar glueball can be produced in rare \(b\) quark decay, \(b \rightarrow s g \tilde{G}\) (Fig. 1). At the hadronic level, this leads to the rare semi-inclusive decay \(B \rightarrow \tilde{G} + X_s\).

3 Decay rates

If glueballs are composed of only gluons, one can easily obtain the branching ratios for \(B\rightarrow G + X_s\). With the two effective couplings given in Eqs. (1) and (4), the following decay rate for \(b(p) \rightarrow s(p') g (k) G (k')\) (Fig. 1) can be obtained readily:

$$\begin{aligned} \Gamma _{b \rightarrow sgG}= & {} \left( {N_c^2 - 1 \over 4 N_c} \right) {G_F^2 m_b^5 \vert V^*_{ts} V_{tb} \vert ^2 \over 2^5 \pi ^3} \left( {g_s \over 4 \pi ^2} \right) ^2 (m_b f)^2 \nonumber \\&\times \int _0^{(1-\sqrt{r})^2} dx \int _{y_-}^{y_+} dy \left\{ |\Delta F_1|^2 c_0 \right. \nonumber \\&+\left. \mathrm{\mathbf Re}(\Delta F_1 F^*_2) {c_1\over y} + |F_2|^2 {c_2\over y^2} \right\} , \end{aligned}$$
(6)

with

$$\begin{aligned} y_{\pm } = {1 \over 2} \left[ (1-x+r) \pm \sqrt{(1-x+r)^2 - 4 r} \right] . \end{aligned}$$
(7)

In Eq. (6), \(N_c\) is the number of colors and the \(c_{0,1,2}\) are given by

$$\begin{aligned} \begin{aligned} c_0&= \frac{1}{2} \left[ -2x^2 y + (1-y)(y-r)(2x+y-r)\right] ,\\ c_1&= (1-y)(y-r)^2,\\ c_2&= \frac{1}{2} \left[ 2x^2y^2 -(1-y)(y-r)(2xy-y+r)\right] , \end{aligned} \end{aligned}$$
(8)

with \(x = (p' + k)^2/m^2_b\), \(y=(k+k')^2/m^2_b\), and \(r=m^2_G/m^2_b\).

The decay rate for pseudoscalar glueball case \(B\rightarrow \tilde{G} + X_s\) can be deduced from the scalar glueball one by replacing the coupling \(f\) with \(\tilde{f} \) and the mass \(m_G\) with the pseudoscalar glueball mass \(m_{\tilde{G}}\) in Eq. (6). This also reproduces the previous result for the \(x\)–\(y\) distribution obtained in Refs. [21, 22] for a similar process \(b \rightarrow sg\eta ^\prime \). Thus it is not possible to differentiate the produced glueball to be a scalar or apseudoscalar from the \(x\)–\(y\) distribution of this semi-inclusive \(B\) decay.

4 Interaction of glueballs with light mesons

The production rate of a scalar or a pseudoscalar glueball from \(B\) decays depends on the strength of the couplings \(f\) or \(\tilde{f}\) respectively. We first discuss how to use the chiral Lagrangian methods to incorporate the interaction for a scalar glueball with the other light mesons and then employ experimental data to determine \(f\).

The form of the effective coupling of a scalar glueball with two gluons, \(\mathcal{L}_0 = f \mathcal{G} G^a_{\mu \nu }G^{a\mu \nu }\), suggests that the glueball couples to the QCD trace anomaly. As briefly mentioned in [29, 30], the interaction of a scalar glueball with light hadrons through the trace anomaly can be formulated systematically by using the techniques of chiral Lagrangians. The kinetic energy and the symmetry breaking mass terms for the light pseudoscalar mesons are given by [31]

$$\begin{aligned} \mathcal{L}_\chi = {f^2_\pi \over 8} \left[ \mathrm{Tr}(\partial ^\mu \Sigma \partial _\mu \Sigma ^\dagger ) + \mathrm{Tr}(\xi ^\dagger \chi \xi ^\dagger + \xi \chi \xi )\right] , \end{aligned}$$
(9)

\(f_\pi = 132\) MeV being the pion decay constant, \(\xi ^2 =\Sigma = \exp (2i\Pi /f_\pi )\) with \(\Pi \) the \(SU(3)\) pseudoscalar meson octet,

$$\begin{aligned} \Pi = \left( \begin{array}{cccc} {1 \over \sqrt{2}}\pi ^0+{1 \over \sqrt{6}}\eta &{}\pi ^+ &{}K^+\\ \pi ^-&{}- {1 \over \sqrt{2}}\pi ^0 +{1 \over \sqrt{6}}\eta &{}K^0\\ K^-&{}{\overline{K}}^0 &{}-{2 \over \sqrt{6}} \eta \end{array}\right) , \end{aligned}$$
(10)

and

$$\begin{aligned} \chi = 2B_0 \, \mathrm{diag}(\hat{m}, \hat{m}, m_s) = \mathrm{diag}\left( m^2_\pi , m^2_\pi , 2m^2_K - m^2_\pi \right) \nonumber \\ \end{aligned}$$
(11)

with \(B_0 = 2031\) MeV. Here we have neglected the isospin breaking effects due to the small mass difference between the light \(u\) and \(d\) quarks and used \(\hat{m} = m_u = m_d\). The QCD trace anomaly is well known and is given by [31]

$$\begin{aligned} \Theta ^\mu _\mu= & {} - \frac{b\alpha _s}{8\pi } G^a_{\mu \nu }G^{a\mu \nu } + \sum _q m_q \bar{q} q , \end{aligned}$$
(12)

where \(b = 11 - 2 n_f / 3\) is the QCD one-loop beta function with \(n_f = 3\) being the number of light quarks. Treating the effective interaction (4) as a perturbation to the energy-momentum stress tensor, one would then modify \(\Theta ^{\mu }_{\mu }\) to be

$$\begin{aligned} -\frac{b\alpha _s}{8\pi } G^a_{\mu \nu }G^{a\mu \nu } \left( 1+ f \frac{8\pi }{ b \alpha _s} \mathcal{G} \right) + \sum _q \left( m_q +f_q \mathcal{G} \right) \bar{q} q ,\nonumber \\ \end{aligned}$$
(13)

\(f_q = f\alpha _s m_q(16\pi \sqrt{2}/3\beta )\ln \left[ (1+\beta )/(1-\beta )\right] \) being the one-loop induced \(G q \bar{q}\) coupling [27] with \(\beta = (1-4m^2_q/m_G^2)^{1/2}\). Note that \(f_q\) is proportional to \(f\). The corresponding chiral Lagrangian is thus modified accordingly,

$$\begin{aligned} \mathcal{L}_\chi= & {} {1\over 8} f^2_\pi \left( 1+ f {8\pi \over b \alpha _s} \mathcal{G} \right) \mathrm{Tr} \left[ \partial ^\mu \Sigma \partial _\mu \Sigma ^\dagger \right] \nonumber \\&{+}{1\over 8} f^2_\pi \, \mathrm{Tr} \left[ \xi ^\dagger (\chi {+}2B_0 f_\chi \mathcal{G})\xi ^\dagger {+} \xi (\chi {+} 2 B_0 f_\chi \mathcal{G}) \xi \right] , \nonumber \\ \end{aligned}$$
(14)

where \(f_\chi = \mathrm{diag}(f_u, f_d, f_s)\).

Using the above chiral Lagrangian, one can calculate the decay rates for \(G \rightarrow \pi ^+\pi ^-, \pi ^0\pi ^0\), \(K^+K^-, K^0{\overline{K}}^0\), and \(\eta ^0\eta ^0\). At present there are some data on the ratios of decay width, \(\Gamma (\pi \pi )/\Gamma (K\bar{K}) \sim 0.41^{+0.11}_{-0.17}\) and \(\Gamma (\eta \eta )/\Gamma (K\bar{K}) \sim 0.48 \,\pm \,0.15\) [32]. Theoretically, we obtain \(\Gamma (\pi \pi )/\Gamma (K\!\bar{K}) \sim 0.36\) and \(\Gamma (\eta \eta )/\Gamma (K\bar{K}) \sim 0.30\), which agrees with the data at about \(1 \sigma \) level. With the above chiral Lagragian, Eq. (14), one can also obtain information as regards the size of the coupling \(f\) if combined with the branching ratio \(\mathrm{Br}(f_0(1710) \rightarrow K \overline{K}) = 0.36 \,\pm \, 0.12\) [33] and the total width \(\Gamma _{f_0(1710)} = 137\pm 8\) MeV for \(f_0(1710)\) [32]. Using a value of the strong coupling constant \(\alpha _s = 0.35\) extracted from the experimental data of \(\tau \) decay, we estimate the central value of the unknown coupling \(f =0.07\) \(\mathrm{GeV}^{-1}\).

In our estimation of \(f\) given above, we have extrapolated low energy theorems to the glueball mass scale which is higher than \(\Lambda _\mathrm{QCD}\). The use of a chiral Lagrangian is quite questionable. One might overestimate the hadronic matrix elements in due course. This implies that the extracted value of \(f\) would be too small.

An alternative approach is to use perturbative QCD. Indeed, this calculation was carried out some time ago for the decay \(G \rightarrow K\overline{K}\) in [29, 30]. This approach can also give an estimate of the amplitude. The problem this approach faces is that the energy scale may not be high enough to have the perturbative QCD contribution dominating. Using the asymptotic light-cone wave functions, we find that the branching ratios for \(G \rightarrow K\overline{K}\) and \(G \rightarrow \pi \pi \) decays are proportional to \(f_K^2\) and \(f_\pi ^2\), respectively. This leads to the ratio of \(\Gamma (\pi \pi )/\Gamma (K\bar{K})\) to be about 0.48, in agreement with the data within the error bar. Fitting the branching ratio for \(G\rightarrow K\overline{K}\), we find that the value of \(f\) would be about 20 times larger than that obtained above using the chiral approach. Incidentally, the value of \(f\) derived from the chiral Lagrangian is within a factor of 2 compared with that estimated just by using the free quark decay rate of \(G \rightarrow s \bar{s}\).

In our later calculations, we will use the conservative value \(f=0.07\) \(\mathrm{GeV}^{-1}\), determined using the chiral Lagrangian given in Eq. (14). This will give the most conservative estimate for the branching ratio, since the chiral approach gives the smallest \(f\). Clearly, a rigorous determination of \(f\) is on the lattice. But we do not anticipate to have a lattice evaluation of its value any time soon. We have to contend with its rough estimation from all the theoretical tools that are available so far. Despite the fact one cannot have a precise determination of the effective coupling \(f\), we believe that glueball production from the proposed rare semi-inclusive \(B\) decay is a very interesting mechanism, which is worth searching for experimentally.

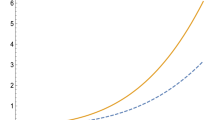
Using the value of \(f\) determined above from the chiral Lagrangian, we find the branching ratio for \(b\rightarrow s g G\) to be \(4.5\times 10^{-5}(f \cdot \text{ GeV }/0.07)^2\) with just the leading top penguin contribution to \(\Delta F_1\) being taken into account. The correction from the charm penguin is nevertheless substantial and should not be neglected. The inclusion of both top and charm penguins gives rise to an enhancement about a factor of 3 in the branching ratio \(\mathrm{Br}(b \rightarrow s gG) \approx 1.3\times 10^{-4}(f \,\cdot \, \text{ GeV }/0.07)^2\). Since \(f_0(1710)\) has a large branching ratio into \(K\overline{K}\), the signal of the scalar glueball can be identified by looking at the secondary \(K \overline{K}\) invariant mass. The recoil mass spectrum of \(X_s\) can also be used to extract information. The distribution of \(d\mathrm{Br}(b \rightarrow s g G)/dM_{X_s}\) as a function of the recoil mass of \(X_s\) is plotted in Fig. 2, where \(M_{X_s}^2 = (p' + k)^2 = m_b^2 x \).

Fig. 2
figure 2

\(d\mathrm{Br}(B\rightarrow G + X_s)/dM_{X_s}\) in unit of \(10^{-5}\). In the figure the \(b\) quark mass \(m_b\) is taken to be 4.248 GeV, \(\alpha _s = 0.21\) at the \(b\) quark scale, \(\tau _B = 1.674 \times 10^{-12}\) s, and \(f = 0.07\) GeV\(^{-1}\)

Full size image

Due to parity conservation, a pseudoscalar glueball will not decay into two pseudoscalar mesons. Instead it will decay into one scalar and one pseudoscalar meson or three pseudoscalar mesons. If \(\eta (1405)\) is indeed the lowest lying pseudoscalar glueball, kinematics allows it to decay into \(f_0(980) \eta \), \(K \overline{K} \pi \), \(\eta \pi \pi \), and so on, as these modes were indeed reported as seen by Particle Data Group [32]. The interaction of the pseudoscalar glueball with the light scalar and pseudoscalar meson octets has been studied in Ref. [34] using the chiral Lagrangian techniques for the resonance \(X(2370)\) identified as a pseudoscalar glueball. One could apply the chiral Lagrangian given in Ref. [34] to the lighter state \(\eta (1405)\). However, the available phase space for \(\eta (1405)\) to decay is much smaller than \(X(2370)\). We will not pursuit this further here.

5 Mixing effects

As is well known, glueballs can mix with other pure \(q \bar{q}\) states with the same quantum numbers, which had complicated the identification of glueballs experimentally. For these mixing effects, we will adopt the mixing models of Ref. [9] for the scalar glueballs and Ref. [14] for the pseudoscalar glueballs. For the scalar case, we have [9]

$$\begin{aligned} \left( \begin{array}{c} \vert f_0(1370) \rangle \\ \vert f_0(1500) \rangle \\ \vert f_0(1710) \rangle \end{array} \right) = \left( \begin{array}{l@{\quad }l@{\quad }l} 0.78 &{} 0.51 &{} -0.36 \\ -0.54 &{} 0.84 &{} 0.03 \\ 0.32 &{} 0.18 &{} 0.93 \end{array} \right) \cdot \left( \begin{array}{c} \vert N \rangle \\ \vert S \rangle \\ \vert G \rangle \end{array} \right) .\nonumber \\ \end{aligned}$$
(15)

Inverting the above relation, we obtain

$$\begin{aligned} \vert G \rangle = -0.36 \vert f_0(1370) \rangle + 0.03 \vert f_0(1500) \rangle + 0.93 \vert f_0(1710) \rangle . \end{aligned}$$
(16)

Thus the above mixing induces \(B\rightarrow f_0(1710)X_s\), \(B\rightarrow f_0(1370)X_s\), and \(B\rightarrow f_0(1500) X_s\) with the following relative branching ratios:

$$\begin{aligned}&\mathrm{Br}(f_0(1710)){:}\mathrm{Br}(f_0(1370)) {:}\mathrm{Br}(f_0(1500))\nonumber \\&\quad = (0.93)^2{:} (-0.36)^2 {:} (0.03)^2 = 1 {:} 0.15 {:} 0.001, \end{aligned}$$
(17)

up to the corrections from the mass differences among the three states.

Similarly, for the pseudoscalar case, we have [14]

$$\begin{aligned} \left( \begin{array}{c} \vert \eta \rangle \\ \vert \eta ' \rangle \\ \vert \eta (1405) \rangle \end{array} \right) = \left( \begin{array}{l@{\quad }l@{\quad }l} 0.749 &{} -0.657 &{} 0.085 \\ 0.600 &{} 0.728 &{} 0.331 \\ -0.279 &{} -0.197 &{} 0.940 \end{array} \right) \cdot \left( \begin{array}{c} \vert \eta _8 \rangle \\ \vert \eta _1 \rangle \\ \vert {\tilde{G}} \rangle \end{array} \right) , \end{aligned}$$
(18)

with

$$\begin{aligned} \vert \tilde{G} \rangle = 0.085 \vert \eta \rangle + 0.331 \vert \eta ' \rangle + 0.94 \vert \eta (1405) \rangle . \end{aligned}$$
(19)

Hence one deduces \(B\rightarrow \eta (1405) X_s \), \(B\rightarrow \eta ' X_s \), and \(B\rightarrow \eta X_s\) with the following relative branching ratios:

$$\begin{aligned}&\!\!\!\mathrm{Br}(\eta (1405)){:}\mathrm{Br}(\eta '){:}\mathrm{Br}(\eta )\nonumber \\&\!\!\!\quad = (0.94)^2 {:} (0.331)^2 {:} (0.085)^2 = 1 {:} 0.12 {:} 0.008, \end{aligned}$$
(20)

up to the corrections from the mass differences among the three states.

We note that the above relative branching ratios were derived under the assumption that \(B \rightarrow \left( G/\tilde{G}\right) + X_s\) arises purely from the three-body process \(b \rightarrow s g \left( G/\tilde{G} \right) \) with the glueball mixing effects taken into account. There may be a two-body process \(B \rightarrow \left( G / \tilde{G} \right) + X_s\) via \(b\rightarrow s \left( G / \tilde{G}\right) \) from four-quark operators in the effective Hamiltonian for the \(G /\tilde{G}\) production from \(B\) decay. These contributions will modify the above predictions of the relative branching ratios. Being of two-body decay type, the energy of \(G/\tilde{G}\) is high, given by \(E^\mathrm{2-body}_{G /\tilde{G}} = (m^2_B + m^2_{G / \tilde{G}} - m_{X_s}^2)/2m_B\) with \(m_B = 5279.50 \pm 0.30\) MeV and \(m_{X_s}\) typically equaling 1 GeV or so. On the other hand, for the \(G/\tilde{G}\) production induced by \(b\rightarrow s g \left( G/\tilde{G} \right) \), the energy of \(G/\tilde{G}\) is more spread out. One therefore expects that with a suitable cut on the glueball energy the two-body contributions can be removed, leaving the softer \(G/\tilde{G}\) production presumably coming from the mechanism that we suggested in this paper to satisfy the relative branching ratios given in this section.

To implement the cut, recall that the energy of the glueball \(E_{G/\tilde{G}}\) is related to the rescaled variable \(x = (p'+k)^2/m_b^2\) according to \(x = 1+r-2 E_{G/\tilde{G}}/m_b\) where \(r = m_{G / \tilde{G}}^2 / m_b^2\). With \(E_{G/\tilde{G}}^\mathrm{max} = m_b (1 + r)/2\), \(x_\mathrm{min} = 0\). Thus to make a cut on the maximum of \(E_{G/\tilde{G}}\) corresponds to a cut on the minimum (lower limit in the integration) of \(x\). In the two-body decay, the energy of the glueball is fixed at \(E^\mathrm{2-body}_{G/\tilde{G}} = m_b (1 + r - \tilde{r})/2\) with \(\tilde{r} = m_{X_s}^2 /m_b^2\). Since \(m_{X_s}\) is of order 1 GeV, we will impose a cut on the minimum of \(x\) in the form \(x^\mathrm{min} = \delta \cdot \tilde{r}\) by varying \(\delta \) in the range from 1 to 3. The effects of these cuts on the branching ratios of Br(\(B \rightarrow f_0(1710)X_s\)) and Br(\(B \rightarrow \eta (1405)X_s\)) are shown in Table 1. The impact of these cuts reduce the branching ratios by at most a factor of 3.

Table 1 Branching ratios Br(\(B \rightarrow f_0(1710)X_s\)) and Br(\(B \rightarrow \eta (1405)X_s\)) as a function of the maximum energy (or minimum \(x\)) cut of the glueballs. We take the nominal value of \(f = \tilde{f} = 0.07\) GeV\(^{-1}\)
Full size table

6 Discussion

Before closing, we would like to make the following comments:

  1. (1)

    In 2005, the BESII experiment [35] has observed an enhanced decay in \(J/\psi \rightarrow \gamma \eta ' \pi \pi \) with a peak around the invariant mass of \(\eta '\pi \pi \) at 1835 MeV. A proposal has been made to interpret this state \(X(1835)\) to be due to a pseudoscalar glueball [36]. The later BESIII experiment [37] has further confirmed the observation of \(X(1835)\), and its spin is consistent with the expectation for a pseudoscalar. Taking \(X(1835)\) to be a pseudoscalar glueball, we would obtain a branching ratio of \(3.7\times 10^{-5}(\tilde{f} \cdot \text{ GeV } / 0.07)^2\) with a top penguin contribution only, and it is enhanced to \(1.1 \times 10^{-4}(\tilde{f} \cdot \text{ GeV }/0.07)^2\) if the charm penguin is also included. If the coupling \(\tilde{f}\) is of the same order of magnitude as \(f\), the branching ratio for \(B\rightarrow X(1835) + X_s\) is also sizable.

  2. (2)

    Lattice QCD calculations also predicted lowest lying spin 2 tensor states: the \(2^{++}\) and \(2^{-+}\) masses are \(2390 \pm 30 \pm 120\) MeV and \(3040 \pm 40 \pm 150\) MeV, respectively, from the earlier quenched calculations [1], and \(2620 \,\pm \, 50\) MeV and \(3460 \,\pm \, 320\) MeV, respectively, from recent unquenched results [2]. These heavier tensor states can also be produced from the semi-inclusive \(B\) decay but with much smaller available kinematic phase space compared with the scalar and pseudoscalar states. The leading operators describing the couplings between these tensor glueballs with the gluons are

    $$\begin{aligned} \quad \mathcal{G}^{\mu \nu } G^a_{\mu \alpha } G^{a \alpha }_ {\nu } \; \;\;\; \mathrm{and} \;\;\; \; \tilde{\mathcal{G}}^{\mu \nu } G^a_{\mu \alpha } {\tilde{G}}^{a \alpha }_ {\nu } , \end{aligned}$$
    (21)

    where \(\mathcal{G}^{\mu \nu }\) and \(\tilde{\mathcal{G}}^{\mu \nu }\) are interpolating fields for the \(2^{++}\) and \(2^{-+}\) glueball states, respectively. Note that \(\tilde{\mathcal{G}}^{\mu \nu }\) is not the dual of \(\mathcal{G}^{\mu \nu }\) despite the \(\tilde{}\). It is straightforward to extend the present analysis to these tensor states.

  3. (3)

    Lattice calculations [2] also predicted lowest lying spin 1 vector glueball states which would necessarily decay into three gluons. We can also use effective operators describing the interactions between the vector glueballs and gluons. We will leave them as exercises for our readers.

To conclude, we have studied semi-inclusive production of a scalar/pseudoscalar glueball in rare \(B\) decays through the gluonic penguin and effective glueball–gluon interactions. The branching ratio for the scalar glueball case is found to be of the order \(10^{-4}\). \(B\) decays into a pseudoscalar glueball through gluonic penguin are also expected to be sizable. Note that for the scalar glueball case, we have used a conservative estimate of the effective coupling \(f\). The observation of \(B \rightarrow X_s f_0(1710)\) at a branching ratio of order \(10^{-4}\) or larger will provide a strong indication that \(f_0(1710)\) is mainly a scalar glueball.

Recall that we have now more than 600 millions of \(B\overline{B}\) accumulated at Belle and more than 300 millions at BABAR. An enhancement by a factor of 50 is expected at the Super B Factory with a designed luminosity of \(8 \times 10^{35}\) cm\(^{-2}\) s\(^{-1}\) [38]. Moreover, at the 14 TeV LHCb, the \(b \bar{b}\) cross section can be as large as 500 \(\mu \)b. One would expect about \(50 \times 10^{12}\) \(b \bar{b}\) pairs with an integrated luminosity of 100 fb\(^{-1}\) at the LHCb. Probing the branching ratio \(\mathrm{Br}(b \rightarrow s g G/\tilde{G})\) at the level of \(10^{-4}\) is quite feasible. One should emphasize that both chiral Lagrangian and perturbative QCD approaches used to extract the value of the effective coupling \(f\) are not precise. Despite this shortcoming, the glueball production mechanism suggested in this work is an interesting one. Measurement of this type may also help to pin down the energy scale where the chiral Lagrangian is valid for hadronic matrix element calculations. We strongly urge our experimental colleagues to rekindle their interests in the search for the various glueball states; in particular those produced by the semi-inclusive decays of the \(B\) mesons proposed in this work.