1 Introduction

A scalar with mass around 125 GeV has been discovered at the LHC [1, 2]. According to the analysis of the ATLAS and CMS collaborations, the measured properties of this scalar, albeit with large experimental uncertainties, agree well with those of the Higgs boson in the Standard Model (SM), which means that it plays a role in the electroweak (EW) symmetry breaking and also in the mass generation for the fermions in the SM [3–5]. Even so, due to the deficiencies of the SM itself in describing the symmetry breaking, it is well motivated to interpret this scalar in various frameworks of new physics. Obviously, in order to ambiguously decipher the nature of the scalar, it is mandatory to scrutinize both experimentally and theoretically the couplings of the scalar, including its self-interactions. In this direction, the couplings of the scalar with the yet known heaviest particle, top quark, are of fundamental importance since, as suggested by the LHC Higgs data, the \(h\bar{t}t\) coupling is strong, and meanwhile it is widely conjectured to be sensitive to new physics. In fact, great efforts have been made recently to investigate the top-Higgs associated production processes like \(pp \rightarrow t\bar{t}h\) [6–11] and \(p p \rightarrow q t h\) [12–17] at the LHC to extract the size and sign of the \(h\bar{t}t\) Yukawa coupling, and also the top quark flavor-changing decay \(t \rightarrow \mathrm{c h}\) to prob anomalous top-Higgs interaction [18–24].

Among the new physics models, the supersymmetric theory (SUSY) is a promising one due to its capability to solve the hierarchy problem of the SM, unify the gauge coupling as well as provide a viable Dark Matter candidate [25–27]. In SUSY, a SM-like Higgs boson \(h\) around 125 GeV usually implies third generation squarks at or heavier than \(1\, \mathrm{TeV}\), and the preference of the heavy squarks is further corroborated by the absence of any signal in the search for SUSY at the LHC. If the SUSY scale is really high, which was focused on in many recent theoretical works [28–36], the only way to detect SUSY is through its possibly large remanent effects in EW processes. Such effects may exist in the Higgs process because the dominant part of the Higgs couplings to squarks is proportional to soft SUSY-breaking parameters [25, 26], and consequently, the suppression induced by the squark propagators in SUSY radiative correction to the process may be compensated under certain conditions. This feature has been demonstrated in the SUSY correction to the \(h\bar{b}b\) vertex [37], the Higgs pair production process at the LHC [38], and also the Higgs rare decay \(h \rightarrow \tau \bar{\mu }\) [39]. Here we emphasize that the existence of the remanent effect in the asymptotic large SUSY mass limit does not contradict the Appelquist–Carazzone theorem [40], which is valid only for supersymmetric theories with an exact gauge symmetry. Previous studies on such remanent effects in SUSY, also see [41–47].

In this work, we focus on the top quark flavor-changing decay \(t \rightarrow c h\) in SUSY. The reasons that we are interested in it mainly come from three considerations. Firstly, the LHC as a top factory has great capability to scrutinize the properties of top quark, including its rare decay modes. As far as the flavor-changing decay \(t \rightarrow \mathrm{c h}\) is concerned, its branching ratio in the SM is only at the order of \(10^{-14}\) [48–50], while in SUSY it may be greatly enhanced to \(10^{-4}\) according to previous studies [51, 52]. Since any observation of the decay in future will be a robust evidence of new physics, this decay should be paid attention to in the LHC era, especially noting the fact that the Higgs boson has been recently discovered. Secondly, as introduced before, the LHC experiment has measured Higgs mass and pushed SUSY to a rather high scale. These results have great impacts on the SUSY prediction about \(t\rightarrow \mathrm{c h}\), so it is necessary to update previous studies on \(t \rightarrow \mathrm{c h}\) in light of the experimental progress. Thirdly, unlike the other top FCNC processes in SUSY [53–56], the decay \(t \rightarrow \mathrm{c h}\) may have a remanent effect in the heavy SUSY limit. From theoretical point of view, it is worthwhile to investigate such a feature in detail. Besides, we recall that, if the flavor mixings between scharm and stop are present, which may push up the rate of \(t \rightarrow \mathrm{c h}\) greatly, the LHC constraint on the stop masses can be relaxed. This in turn may alleviate the fine tuning problem of the SUSY [57].

This paper is organized as follows. In Sect. 2, we parameterize the flavor mixings in squark sector and define our conventions. We also list various constraints on SUSY. In Sect. 3, we study the decay \(t \rightarrow \mathrm{c h}\) in both low energy SUSY and heavy SUSY, and present some benchmark points at which the predictions on \(t \rightarrow c h\) are optimized. We also exhibit the features of the remanent effect on \(t \rightarrow \mathrm{c h}\). Finally, we present our conclusions in Sect. 4.

2 FCNC interactions in SUSY

In the supersymmetric theories such as the Minimal Supersymmetric Standard Model (MSSM) [25, 26] and the Next-to-Minimal Supersymmetric Standard Model (NMSSM) [27], the squark sector consists of six up-type squarks (\(\tilde{u}_\mathrm{L}\), \(\tilde{c}_\mathrm{L}\), \(\tilde{t}_\mathrm{L}\), \(\tilde{u}_\mathrm{R}\), \(\tilde{c}_\mathrm{R}\), \(\tilde{t}_\mathrm{R}\)) and six down-type squarks (\(\tilde{d}_\mathrm{L}\), \(\tilde{s}_\mathrm{L}\), \(\tilde{b}_\mathrm{L}\), \(\tilde{d}_\mathrm{R}\), \(\tilde{s}_\mathrm{R}\), \(\tilde{b}_\mathrm{R}\)). In general, the states with different chiral and flavor quantum numbers in each type of squarks will mix to form mass eigenstates, and consequently potentially large flavor-changing interactions arise from the misalignment between the rotations that diagonalize quark and squark sectors. In the super-CKM basis, the \(6\times 6\) squark mass matrix \(\mathcal{M}^2_{\tilde{q}}\) (\(\tilde{q}=\tilde{u}, \tilde{d}\)) takes the form [58–60]

$$\begin{aligned} \mathcal{M}^2_{\tilde{q}}=\left( \begin{array}{ll} \left( M^2_{\tilde{q}}\right) _{\mathrm{LL}}+ C_{\tilde{q}}^{\mathrm{LL}} &{} \left( M^2_{\tilde{q}}\right) _{\mathrm{LR}}-C_{\tilde{q}}^{\mathrm{LR}} \\ \left( \left( M^2_{\tilde{q}}\right) _{\mathrm{LR}}-C_{\tilde{q}}^{\mathrm{LR}}\right) ^\dag &{} \left( M^2_{\tilde{q}}\right) _{\mathrm{RR}}+C_{\tilde{q}}^{\mathrm{RR}} \end{array} \right) , \end{aligned}$$
(1)

where \(C_{\tilde{q}}^{\mathrm{LL}} = m_q^2 + \cos 2\beta M_Z^2 ( T_3^q - Q_q s_W^2) {\hat{1}}\), \(C_{\tilde{q}}^{\mathrm{RR}} = m_q^2 + \cos 2\beta M_Z^2 Q_q s_W^2 {\hat{1}}\) and \(C_{\tilde{q}}^{\mathrm{LR}}=m_q \mu (\tan \beta )^{- 2 T_3^q}\) are \(3\times 3\) diagonal matrices with \({\hat{1}}\) standing for the unit matrix in flavor space, \(m_q\) being the diagonal quark mass matrix and \(T_3^q=\frac{1}{2},-\frac{1}{2}\) for \(q=u,d,\) respectively, and \(\tan \beta =\frac{v_2}{v_1}\) is the ratio of the vacuum expectation values of the \(\mathrm{SU}(2)\) doublet Higgs fields. If one only considers the flavor mixings between the second and the third generation squarks, the soft breaking squared masses \((M^2_{\tilde{q}})_{\mathrm{LL}}\), \((M^2_{\tilde{q}})_{\mathrm{LR}}\) and \((M^2_{\tilde{q}})_{\mathrm{RR}}\) can be parameterized as

$$\begin{aligned} \left( M^2_{\tilde{u}}\right) _{\mathrm{LL}}&= \left( \begin{array}{ccc} M_{Q_1}^2 &{} 0 &{} 0 \\ 0 &{} M_{Q_2}^2 &{} \delta _{\mathrm{LL}} M_{Q_2} M_{Q_3} \\ 0 &{} \delta _{\mathrm{LL}} M_{Q_2} M_{Q_3} &{} M_{Q_3}^2 \end{array} \right) , \nonumber \\ \left( M^2_{\tilde{u}}\right) _{\mathrm{LR}}&= \left( \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} \delta _{\mathrm{LR}} v_2 M^{U}_{\mathrm{LR}}\\ 0 &{} \delta _{\mathrm{RL}} v_2 M^{U}_{\mathrm{RL}} &{} m_t A_t \end{array} \right) , \nonumber \\ \left( M^2_{\tilde{u}}\right) _{\mathrm{RR}}&= (M^2_{\tilde{u}})_{\mathrm{LL}}|_{M_{Q_i}^2 \rightarrow M_{U_i}^2,~ \delta _{\mathrm{LL}} \rightarrow \delta _{\mathrm{RR}}}, \end{aligned}$$
(2)

where \(M_{Q_i}\) and \(M_{U_i}\) (\(i=1,2,3\) denotes generation index) are soft breaking parameters with mass dimension, \(M^{U}_{\mathrm{LR}}\) and \(M^{U}_{\mathrm{RL}}\) represent the SUSY scale defined as \(M^{U}_{\mathrm{LR}} = (M_{U_3} + M_{Q_2})/2\) and \(M^{U}_{\mathrm{RL}} = (M_{U_2} + M_{Q_3})/2\), and \(\delta _{\mathrm{LL}}\), \(\delta _{\mathrm{LR}}\), \(\delta _{\mathrm{RL}}\), and \(\delta _{\mathrm{RR}}\) reflect the extent of the flavor violation. Similarly, for down-squarks we have

$$\begin{aligned} \left( M^2_{\tilde{d}}\right) _{\mathrm{LR}}&= \left( \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} \delta _{\mathrm{LR}}^d v_1 M^{D}_{\mathrm{LR}}\\ 0 &{} \delta _{\mathrm{RL}}^d v_1 M^D_{\mathrm{RL}} &{} m_b A_b \end{array} \right) , \nonumber \\ \left( M^2_{\tilde{d}}\right) _{\mathrm{RR}}&= \left( M^2_{\tilde{u}}\right) _{\mathrm{LL}}|_{M_{Q_i}^2 \rightarrow M_{D_i}^2,~ \delta _{\mathrm{LL}} \rightarrow \delta _{\mathrm{RR}}^d}, \end{aligned}$$
(3)

and due to \(\mathrm{SU}(2)\) gauge symmetry, \((M^2_{\tilde{d} })_{\mathrm{LL}}\) is determined by [58–60]

$$\begin{aligned} \left( M^2_{\tilde{d}}\right) _{\mathrm{LL}} = V_{\mathrm{CKM}}^\dag (M_{\tilde{u}}^2)_{\mathrm{LL}} V_{\mathrm{CKM}} \end{aligned}$$
(4)

with \(V_{\mathrm{CKM}}\) denoting the Cabibbo–Kobayashi–Maskawa matrix in the SM. Note that in Eqs. (2) and (3) we only keep the chiral-flipping terms for third-family squarks because these terms are usually assumed to be proportional to the corresponding quark masses, and they cannot be neglected only for third-family squarks.

The squark mass eigenstates can be obtained by diagonalizing the mass matrix presented above with a unitary rotation \(U_{\tilde{q}}\), which is performed numerically in our analysis. The interaction of the field \(X\) with a pair of squark mass eigenstates is then obtained by

$$\begin{aligned} V(X \tilde{q}_{\alpha }^*\tilde{q}_{\beta }^\prime ) \; = \; U^{\dag \tilde{q}}_{\alpha ,i} \; U^{\tilde{q}^\prime }_{j, \beta } \; V\left( X \tilde{q}_i^*\tilde{q}^\prime _j\right) , \end{aligned}$$
(5)

where \(V(X\tilde{q}_i^*\tilde{q}^\prime _j)\) denotes a generic vertex in the interaction basis and \(V(X\tilde{q}_{\alpha }^*\tilde{q}_{\beta }^\prime )\) is the vertex in the mass-eigenstate basis. It is clear that both the squark masses and their interactions depend on the mixing parameters \(\delta _is\).

In some fundamental supersymmetric theories like the mSUGRA and gauge-mediated SUSY-breaking models, the mixing parameters are functions of the soft breaking masses and usually exhibit a certain hierarchy structure [61–63]. In this work, in order to make our discussion as general as possible, we treat all \({\delta _i}s\) as free parameters, and we limit them by some physical observables. The constraints we consider include:

  1. (I)

    The recently measured SM-like Higgs boson mass \(m_h\). In the MSSM, this mass is determined by the renormalized self-energies of the doublet CP-even Higgs fields, \(h_u\) and \(h_d\), and the transition between them. Squarks contribute to these quantities through the \(\tilde{q}^*\tilde{q} S\) and \(\tilde{q}^*\tilde{q} S S\) interactions with \(S\) denoting either \(h_u\) or \(h_d\) [51, 64]. In the presence of the flavor mixings, both the interactions and the squark masses may be quite different from those in the case of \(\delta _is=0\), and so is the SM-like Higgs boson mass. Among the flavor mixing parameters \(\delta _i\), the Higgs mass is more sensitive to the chiral-flipping ones \(\delta _{\mathrm{LR}}\) and \(\delta _{\mathrm{RL}}\). In this work, we get \(m_h\) in the MSSM by the code FeynHiggs [65–68]. In our scan over the parameter space of the low energy MSSM, we require the mass to be about 2 GeV around its measured central value, i.e. \(123 \,\mathrm{GeV} \le m_h \le 127\, \mathrm{GeV}\). While for the MSSM in heavy SUSY case (see below), noting that the mass obtained by FeynHiggs suffers from potentially large theoretical uncertainties, we require a moderately wider range, i.e. \(121\, \mathrm{GeV} \le m_h \le 129\, \mathrm{GeV}\).

  2. (II)

    The LHC search for SUSY. By now both the ATLAS and the CMS collaborations have made great efforts in searching for the signals of gluino, squarks as well as charginos and neutralinos, and, based on certain assumptions, they exclude some SUSY particles up to about 1 TeV [69–77]. These obtained results, however, cannot be applied directly to the general SUSY case, and, in order to implement the LHC constraints, one has to perform detailed Monte Carlo simulations for each SUSY parameter point with the same strategies as those of the collaborations, and then compare the simulated results with the LHC data [78, 79]. In practice, such a process is rather time consuming and cannot be applied to an extensive scan over the SUSY parameter space, where a large number of samples are involved. In order to simplify our analysis, we note that by now the gluino is preferred to be at the TeV scale without considering special cases such as compressed SUSY spectra [69–77], while the second and third generation squark may still be as light as several 100 GeV [78–80], especially in the presence of the flavor mixing when the limitation on the squark spectrum can be further relaxed [57]. So we make the following assumption in our discussion:

    $$\begin{aligned}&m_{\tilde{q}_\alpha }, m_{U_3} \ge 200\, \mathrm{GeV}, \quad m_{\tilde{g}} \ge 1\, \mathrm{TeV}, \nonumber \\&\quad m_{Q_{2}}, m_{U_2}, m_{Q_3} \ge 500\, \mathrm{GeV}. \end{aligned}$$
    (6)

    As will be shown below, our conclusions are not sensitive to such a assumption.

  3. (III)

    The metastability of the vacuum state. This constraint reflects the fact that squarks as scalar fields contribute to SUSY potential, and consequently their soft breaking parameters should be limited by the stability (or more general metastability) of the vacuum state [81, 82]. Assuming only \(\delta _{\mathrm{LR}}\) or \(\delta _{\mathrm{RL}}\) contributes to the potential, the metastability requires [81, 82]

    $$\begin{aligned} |\delta _{\mathrm{LR}}^u| \!&\lesssim \! 1.2\times \frac{m_t}{v_2} \frac{\sqrt{M_{Q_2}^2 + M_{U_3}^2 + M_A^2 \cos ^2 \beta }}{M^{U}_{\mathrm{LR}}}, \nonumber \\ |\delta _{\mathrm{RL}}^u|&\lesssim 1.2\times \frac{m_t}{v_2} \frac{\sqrt{M_{U_2}^2 + M_{Q_3}^2 + M_A^2 \cos ^2 \beta }}{M^{U}_{\mathrm{RL}}}, \nonumber \\ |A_t|&\lesssim 2.67 \sqrt{M_{Q_3}^2 + M_{U_3}^2 + M_A^2 \cos ^2 \beta }. \end{aligned}$$
    (7)

    Note that in the previous study of the top quark flavor-changing neutral current process, this constraint was usually missing.

  4. (IV)

    The EW precision observables \(M_W\) and \(\sin ^2 \theta _{\mathrm{eff}}\). In SUSY, the corrections to \(M_W\) and \(\sin ^2 \theta _{\mathrm{eff}}\) are dominated by squark loops, and their sizes reflect the mass disparity of left-handed SU(2) doublet squarks. To a good approximation, these two quantities are related with the \(\delta \rho \) parameter by

    $$\begin{aligned} \delta M_W \simeq \frac{M_W}{2} \frac{c_W^2}{c_W^2 -s_W^2} \delta \rho , \quad \delta \sin ^2 \theta _{\mathrm{eff}} \simeq -\!\frac{c_W^2 s_W^2}{c_W^2 -s_W^2} \delta \rho ,\nonumber \\ \end{aligned}$$
    (8)

    where

    $$\begin{aligned} \delta \rho =\frac{\Sigma _Z(0)}{M_Z^2} - \frac{\Sigma _W(0)}{M_W^2}. \end{aligned}$$
    (9)

    In this work, we repeat our previous calculation of \(\delta M_W\) and \(\delta \sin ^2 \theta _{\mathrm{eff}}\) in [51] where three generation squarks are considered to implement the \(\mathrm{SU}(2)\) relation between \((M_{\tilde{U}}^2)_{\mathrm{LL}}\) and \((M_{\tilde{D}}^2)_{\mathrm{LL}}\), and require

    $$\begin{aligned} \delta M_W \le 21 \,\mathrm{MeV}, \quad \delta \sin ^2 \theta _{\mathrm{eff}} \le 19.6\times 10^{-5}, \end{aligned}$$
    (10)

    which are their allowed ranges at \(2\sigma \) level after considering experimental and theoretical uncertainties [83].

  5. (V)

    Constraint from \(B \rightarrow X_s \gamma \). In the MSSM, the SUSY contributions to \(B\rightarrow X_s \gamma \) come from four kinds of loops mediated by charged Higgs bosons, charginos, neutralinos, and gluinos, respectively. We calculate these contributions by the code FeynHiggs [65–68], and we require \(3.04\times 10^{-4} \le \mathrm{Br}(B \rightarrow X_s \gamma ) \le 4.02\times 10^{-4} \) in our parameter scan, which corresponds to the experimentally allowed range of \(\mathrm{Br}(B \rightarrow X_s \gamma )\) at \(2\sigma \) level [84]. Since the neutralino contribution is usually small, the expression of \(B \rightarrow X_s \gamma \) in the NMSSM is roughly identical to that of the MSSM.

As regards the above constraints, it should be noted that constraints (I), (III), and (IV) do not diminish as the SUSY scale becomes higher, that is, they are not decoupled in the heavy SUSY limit, while the process \( B\rightarrow X_s \gamma \) does not possess such a property.

3 SUSY prediction on the rate of \(t \rightarrow { ch}\)

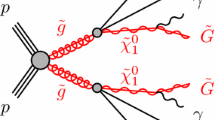
In the MSSM, the dominant contribution to the process \(t \rightarrow \mathrm{ch}\) arises from the SUSY-QCD diagrams shown in Fig. 1. The relevant Lagrangian is given by [85]

$$\begin{aligned} \mathcal{{L}}&= \sqrt{2}g_{s} \left[ \bar{\tilde{g}}_{a} \left( -U^{*}_{2 \alpha }P_{\mathrm{L}} + U^{*}_{5 \alpha }P_{\mathrm{R}}\right) \tilde{q}_{\alpha i}^{*} T_{i j}^{a} c_{j}\right. \nonumber \\&\left. + \bar{\tilde{g}}_{a}\left( -U^{*}_{3 \alpha }P_{\mathrm{L}} + U^{*}_{6 \alpha }P_{\mathrm{R}}\right) \tilde{q}_{\alpha i}^{*} T_{i j}^{a} t_{j}\right] + h.c. \nonumber \\&+ \sum _{\alpha ,\beta =1}^6 C_{\alpha \beta } \tilde{q}^*_{\alpha } \tilde{q}_\beta h + Y_t \bar{t} t h, \end{aligned}$$
(11)

where \(\tilde{g}\) and \(\tilde{q}_\alpha \) denote the gluino and the squark in the mass eigenstate, respectively, \(T^{a}\) is the Gell-Mann matrix with \(i\) and \(j\) representing color indices, \(U_{\tilde{q}}\) is the \(6\times 6\) rotation matrix to diagonalize the mass matrix for up-type squarks, \(C_{\alpha \beta }\) parameterizes the coupling of the Higgs boson with squark mass eigenstates \(\tilde{q}_\alpha \) and \(\tilde{q}_\beta \), and \(Y_t = \frac{m_t}{v}\frac{\cos \alpha }{\sin \beta }\) with \(\alpha \) being the rotation angle to diagonalize the CP-even Higgs mass matrix. The amplitude of \(t \rightarrow c h \) can then be expressed by

$$\begin{aligned} i \mathcal {M}(\rightarrow c h) \!=\! \bar{u}(p_{c})[(F_{1\mathrm{L}}+F_{2\mathrm{L}})P_{\mathrm{L}} + (F_{1\mathrm{R}}+F_{2\mathrm{R}})P_{\mathrm{R}}]u(p_{t}), \end{aligned}$$
(12)

where, after neglecting the charm quark mass, the \({F_i}s\) are given by

$$\begin{aligned} F_{1\mathrm{L}}&= \frac{i g^{2}_{s}}{6{\pi }^{2}}\left\{ C_{\alpha \beta }U^{*}_{3 \alpha }U_{5 \beta }m_{\tilde{g}} C_0\left( p_c^2,p_h^2,p_t^2,m_{\tilde{g}}^2,m^{2}_{{\tilde{q}}_{\alpha }},m^{2}_{{\tilde{q}}_{\beta }}\right) \right. \nonumber \\&\left. - C_{\alpha \beta }U^{*}_{6 \alpha }U_{5 \beta }m_t C_{12}\left( p_c^2,p_h^2,p_t^2,m_{\tilde{g}}^2,m^{2}_{{\tilde{q}}_{\alpha }},m^{2}_{{\tilde{q}}_{\beta }}\right) \right\} , \nonumber \\ F_{1\mathrm{R}}&= \frac{i g^{2}_{s}}{6{\pi }^{2}}\left\{ C_{\alpha \beta }U^{*}_{6 \alpha }U_{2 \beta }m_{\tilde{g}} C_0\left( p_c^2,p_h^2,p_t^2,m_{\tilde{g}}^2,m^{2}_{{\tilde{q}}_{\alpha }},m^{2}_{{\tilde{q}}_{\beta }}\right) \right. \nonumber \\&\left. - C_{\alpha \beta }U^{*}_{3 \alpha }U_{2 \beta }m_t C_{12}\left( p_c^2,p_h^2,p_t^2,m_{\tilde{g}}^2,m^{2}_{{\tilde{q}}_{\alpha }},m^{2}_{{\tilde{q}}_{\beta }}\right) \right\} , \nonumber \\ F_{2\mathrm{L}}&= -\frac{i g^{2}_{s}m_{\tilde{g}}}{6{\pi }^{2}m_{t}}Y_{t}U^{*}_{3 \alpha }U_{5 \alpha } B_0\left( p_c^2,m_{\tilde{g}}^2,m^{2}_{{\tilde{q}}_{\alpha }}\right) , \nonumber \\ F_{2\mathrm{R}}&= -\frac{i g^{2}_{s}m_{\tilde{g}}}{6{\pi }^{2}m_{t}}Y_{t}U^{*}_{6 \alpha }U_{2 \alpha } B_0\left( p_c^2,M_{\tilde{g}}^2,m^{2}_{{\tilde{q}}_{\alpha }}\right) . \end{aligned}$$
(13)

In the above expressions, \(p_t\), \(p_c\), and \(p_h\) denote the momenta of the top quark, charm quark, and Higgs boson, respectively, \(m_{\tilde{g}}\) and \(m_{{\tilde{q}}_{\alpha }}\) represent the masses of the gluino and squark, respectively, and \(B_0\), \(C_0\), and \(C_{12}\) are the standard two-point and three-point loop functions, respectively [86, 87]. In the heavy SUSY case discussed below, since the involved sparticle masses are much larger than \(m_t\), the contribution from \(C_{12}\) can be safely ignored, and \(B_0\), \(C_0\) can be approximated by

$$\begin{aligned}&C_0\left( p_c^2,p_h^2,p_t^2,m_{\tilde{g}}^2, m^{2}_{{\tilde{q}}_{\alpha }}, m^{2}_{{\tilde{q}}_{\beta }} \right) \nonumber \\&\quad = \frac{1}{m_{\tilde{g}}^2} \frac{1}{1-{\delta }_{\beta }}\left[ \frac{{\delta }_{\beta }}{{\delta }_{\alpha }-{\delta }_{\beta }}\ln \left( \frac{{\delta }_{\alpha }}{{\delta }_{\beta }}\right) -\frac{1}{{\delta }_{\alpha }-1}\ln {\delta }_{\alpha } \right] \nonumber \\&\quad \quad + \mathcal{{O}}\left( \frac{p_t^2}{m_{\tilde{g}}^2}\right) , B_0\left( p_c^2,m_{\tilde{g}}^2,m^{2}_{{\tilde{q}}_{\alpha }}\right) \nonumber \\&\quad = \Delta + 1 + \frac{{\delta }_{\alpha }}{1-{\delta }_{\alpha }} \ln {\delta }_{\alpha }+\mathcal{{O}}\left( \frac{p_c^2}{m_{\tilde{g}}^2}\right) , \end{aligned}$$
(14)

where \( {\delta }_{\alpha }\) is defined as \({\delta }_{\alpha }= m^{2}_{{\tilde{q}}_{\alpha }}/m^{2}_{\tilde{g}}\).

Fig. 1
figure 1

Feynman diagrams of the SUSY-QCD contribution to \(t \rightarrow \mathrm{ch}\). If the charm quark mass is neglected, the contribution from diagram (c) vanishes

Full size image

3.1 \(t \rightarrow { ch}\) in low energy SUSY

As shown in [52], the SUSY-QCD contribution to \(t \rightarrow c h\) in low energy MSSM has the following features:

  • In the case that only one flavor mixing parameter \(\delta _i\) is non-zero, the rate of \(t \rightarrow \mathrm{c h}\) increases monotonously as the \(\delta _i\) becomes larger, while if several non-vanishing \(\delta _i\) coexist, their effects may cancel each other out.

  • Since the effective \(h\bar{c}t\) vertex involves both chiral flipping and flavor changing, the chiral-conserving parameter \(\delta _{\mathrm{LL}}\)/\(\delta _{\mathrm{RR}}\) must be accompanied with chiral-flipping \(h\tilde{t}_\mathrm{L}^*\tilde{t}_\mathrm{R}\) or \(h\tilde{t}_\mathrm{R}^*\tilde{t}_\mathrm{L}\) interaction in contributing to the vertex, while the chiral-flipping parameter \(\delta _{\mathrm{LR}}\)/\(\delta _{\mathrm{RL}}\) alone is able to lead into the \(h\bar{c}t\) vertex. As a result, the effective vertex is usually more sensitive to \(\delta _{\mathrm{LR}}\) and \(\delta _{\mathrm{RL}}\) if we do not consider the constraints on the mixing parameters.

  • Unlike the other top quark FCNC processes, the Super-GIM mechanism does not apply to the decay \(t\rightarrow \mathrm{c h}\). But since there exists a strong cancelation between diagram (a) and (b) in Fig. 1 (see discussion below), the rate of \(t \rightarrow \mathrm{c h}\) depends on the soft mass parameters in a complex way.

In the following, we do not intend to exhibit these features, but instead, noting that the constraints (I)–(III) introduced above were not considered before, we try to figure out the order of \(\mathrm{Br}(t \rightarrow c h)\) that SUSY can predict after considering these constraints. For this purpose, we perform two independent scans over relevant SUSY parameters by imposing the constraints. Details of our scans are as follows:

  • Scan I: We restrict our discussion in the MSSM, and calculate the Higgs mass with the code FeynHiggs. The parameter region we explore is given by

    $$\begin{aligned}&500\, \mathrm{GeV} \le m_{Q_2}, m_{Q_3},m_{U_2}, m_{D_2}, m_{D_3} \le 2\, \mathrm{TeV}, \nonumber \\&200\, \mathrm{GeV} \le m_{U_3} \le 2 \,\mathrm{TeV}, \nonumber \\&|A_t| \le 6 \sqrt{m_{Q_3} m_{U_3}}, \quad 1\, \mathrm{TeV} \le m_{\tilde{g}} \le 2 \,\mathrm{TeV}, \nonumber \\&1 \le \tan \beta \le 40, \nonumber \\&-1 \le \delta _{\mathrm{LL}},\delta _{\mathrm{RR}} \le 1, \quad -2.0\le \delta _{\mathrm{LR}},\delta _{\mathrm{RL}} \le 2.0, \nonumber \\&-0.5 \le \delta _{\mathrm{LR}}^d,\delta _{\mathrm{RL}}^d \le 0.5, \nonumber \\&400\, \mathrm{GeV} \le m_A \le 2 \,\mathrm{TeV}, -2\, \mathrm{TeV} \le \mu \le 2 \,\mathrm{TeV}. \end{aligned}$$
    (15)

    In drawing up the strategy of this scan, we note that, although the down-type squark parameters like \(\delta _{\mathrm{LR}}^d\) and \(M_{D}\) do not affect the rate of \(t \rightarrow \mathrm{c h}\), they are needed in the calculation of \(\delta \rho \) and \(B \rightarrow X_s \gamma \). So to make our conclusions as general as possible we vary them in reasonable regions. We also note that since too many parameters are involved in the scan, the traditional random scan method is not efficient in searching for maximal value of \(\mathrm{Br}( t \rightarrow \mathrm{c h})\). So we adopt the Markov chain method in doing such a job. During the scan we adjust the optimal value by the results obtained from previous samplings until it reaches some stable values.

  • Scan II: Same as Scan I, but in order to relax the Higgs mass bound, we go beyond the MSSM by considering an extra contribution to the mass. In more detail, we write the Higgs mass as \(m_h^2 = m_{h,\mathrm{MSSM}}^2 + \lambda ^2 v^2 \sin ^2 2\beta \) with \(\tan \beta =1.5\) and \(\lambda \) treated as a free parameter in the range from 0.5 to 0.7. This treatment of the Higgs mass is motivated by the singlet extensions of the MSSM such as the NMSSM, where the interaction between the singlet Higgs field and the doublet Higgs fields in the MSSM provides an additional contribution to the mass at tree level [27]. Our specific choice of \(\tan \beta = 1.5\) is due to the following two considerations. One is that \(\tan \beta \) is not an important parameter in deciding the optimal rate of \(t \rightarrow \mathrm{c h}\) that low energy SUSY can predict. In fact, with less severe constraints than this work we found that both large \(\tan \beta \) and small \(\tan \beta \) are capable to predict the rate at the order of \(10^{-5}\) [52]. The second consideration is that \(\tan \beta \), on the other side, has a great impact on the tree-level mass of \(h\), which affects the ranges of SUSY parameters to predict the \(125\, \mathrm{GeV}\) Higgs boson. Generally speaking, the larger the tree-level mass is, the weaker the Higgs mass constraint becomes on the up-type squark sector. In the NMSSM, such an enlarged tree-level mass can be obtained by choosing \(\lambda > 0.5 \) and a small \(\tan \beta \). Moreover, we also checked that, if we treat \(\tan \beta \) as a free parameter, the optimal value of \(\mathrm{Br}(t\rightarrow \mathrm{c h})\) does not change after a long time scan over the SUSY parameter space.

In Table 1, we show two benchmark points for each scan. These points correspond to very optimal cases in predicting a large rate of \(t \rightarrow \mathrm{c h}\). After analyzing our scan results, we have the following observations:

  • Although we allow \(m_{U_3}\) to be as low as \(200\, \mathrm{GeV}\), it is interesting to see that the optimal points to enhance the rate do not correspond to low \(m_{U_3}\)s. This feature can be understood from the following two aspects. One is that among the mixing parameters \(\delta _{i}\), \(\delta _{\mathrm{RR}}\) is the least constrained one. So in order to enhance the rate of \(t \rightarrow \mathrm{c h}\) in an efficient way, the matrix element \(\delta _{\mathrm{RR}} M_{U_2} M_{U_3}\) in Eq. (2) should be as large as possible. On the other hand, given a relatively low value of \(m_{U_3}\), the element cannot be arbitrarily large since its non-zero value tends to suppress the lightest squark mass, which is now required to be no \(<\) \(200\, \mathrm{GeV}\) in our analysis. An obvious example is if we set \(m_{U_3} = 200\, \mathrm{GeV}\), \(\delta _{i}\) must be 0 to satisfy the requirement, and in this case \(\mathrm{Br}(t \rightarrow \mathrm{c h}) =0\). The other aspect is, as we mentioned before, that the decay \(t \rightarrow \mathrm{c h}\) does not proceed by the Super-GIM mechanism, and meanwhile it has strong cancelations among different contributions in its calculation. Consequently, although a low value of \(m_{U_3}\) will result in large mass splittings between the squarks, such a mass pattern is not necessarily favored to enhance the rate.

    Table 1 Benchmark points in low energy SUSY which correspond to very optimal cases in predicting the rate of \( t \rightarrow \mathrm{c h}\). Points 1 and 2 are obtained from Scan I, and Points 3 and 4 are from Scan II. All these points satisfy the constraints listed in the text
    Full size table

  • In low energy SUSY, the size of \(\mathrm{Br}( t \rightarrow \mathrm{c h})\) for the optimal points in Table 1 is not sensitive to the parameters \(m_A\) and \(\mu \). For example, our results indicate that shifting \(m_A\) from its value in Table 1 by 100 GeV only results in a change of \(\mathrm{Br}( t \rightarrow \mathrm{c h})\) by \(<\) \(1\,\%\). While as will be shown below, these two parameters play an important role in determining the rate of the rare decay in the heavy SUSY limit.

  • Among the considered constraints, the most stringent ones come from the Higgs mass and the LHC search for SUSY. As a result, the branching ratio of \(t \rightarrow \mathrm{c h}\) can only reach \(10^{-6}\) in low energy MSSM, which is about one order smaller than previous predictions obtained before the advent of the LHC [52]. In Scan II, however, since the Higgs mass constraint on squark masses is comparatively relaxed, \(\mathrm{Br}(t \rightarrow \mathrm{c h})\) can reach \(10^{-5}\).

As regards our results on \(t \rightarrow \mathrm{c h}\), we recall that we do not include the SUSY-EW contribution to \(t \rightarrow \mathrm{c h}\). The reason is that the amplitude of the SUSY-EW contribution is roughly determined by \(\alpha m_{\tilde{\chi }^\pm }/\mathrm{Max}(m_{\tilde{q}_{D}}^2\), \(m_{\tilde{\chi }^\pm }^2)\) from naive estimation [88–90], while the SUSY-QCD contribution is determined by \(\alpha _s m_{\tilde{g}}/\mathrm{Max}(m_{\tilde{q}_{U}}^2\), \(m_{\tilde{g}}^2)\), where \(m_{\tilde{q}_{D}}\), \(m_{\tilde{q}_{U}}\), and \(m_{\tilde{\chi }^\pm }\) denote the mass scales for down-type squarks, up-type squarks, and charginos, respectively. Noting that \(m_{\tilde{q}_{D}}\) is not much smaller than \(m_{\tilde{g}}\) as suggested by the LHC search for the second and third generation squarks [69–77, 80], and also that the flavor mixings in the down-type squark sector are more tightly constrained by B-physics than those in up-type squark sector, we conclude that the SUSY-EW contribution should not be comparable with the SUSY-QCD contribution. So our estimates on the magnitude of \(t \rightarrow \mathrm{c h}\) will not change after including the SUSY-EW contribution. Another reason to neglect the EW contribution is that, once considering it, too many parameters will be involved, but meanwhile this does not change our conclusion.

Before we end this subsection, we make two comments. One is that in extensions of the MSSM, the decay chain of a certain sparticle may be quite different from its MSSM prediction, and the analysis of the ATLAS and CMS collaborations in searching for SUSY may become irrelevant [91]. As a result, the constraint on the sparticle mass may be relaxed. This in turn may push up the SUSY prediction on the rate of \( t \rightarrow \mathrm{c h}\). Moreover, in extensions of the MSSM the couplings of the Higgs boson with quarks and squarks may be slightly changed. The influence of such changes on the rate of \( t \rightarrow \mathrm{c h}\) is usually not as significant as the relaxation of the Higgs mass constraint. The other comment is that, given \(\mathrm{Br}(t \rightarrow \mathrm{c h}) \sim 10^{-5}\), it is difficult to detect such a top quark rare decay at the 14-TeV LHC with an integrated luminosity of \(100\, \mathrm{fb}^{-1}\) [92], but at future linear colliders such as TLEP [93], detection of the decay is still possible.

3.2 Remanent effect of \(t \rightarrow { ch}\) in the heavy SUSY limit

As mentioned in Sect. 1, because the \(h\tilde{q}^*\tilde{q}\) coupling strength is mainly determined by soft SUSY-breaking parameters, the SUSY-QCD contribution to the effective \(h\bar{c}t\) interaction may exhibit a remanent effect of SUSY in heavy SUSY limit. In order to investigate such an issue, we in the following assume a common SUSY mass scale, \(m_{Q_2} = m_{Q_3} = m_{U_2} = m_{U_3} = m_{\tilde{g}}=M_{\mathrm{SUSY}}\), and we study the dependence of \(\mathrm{Br}(t \rightarrow \mathrm{c h})\) on \(M_{\mathrm{SUSY}}\) for different choices of \(A_t\) and \(\mu \) in Fig. 2. In Fig. 2, we consider the case that only \(\delta _{\mathrm{LL}}\) is non-vanishing and fix \(\delta _{\mathrm{LL}} = 0.7\), \(\tan \beta = 4, 10\), and \(m_A = 400, 800\, \mathrm{GeV}\). We set \(A_t = M_{\mathrm{SUSY}}\) and \(\mu = 0\) for the left panel, and \(A_t = 0\) and \(\mu = M_{\mathrm{SUSY}}\) for the right panel. These settings are only for exhibiting the decoupling behavior of \(\mathrm{Br}(t \rightarrow \mathrm{c h})\) and we do not consider the constraint from the LEP search for charginos, which requires \(\mu \gtrsim 103\, \mathrm{GeV}\). Figure 2 then indicates that SUSY has remanent effect on the rare decay rate only when \(\mu \) is at SUSY scale and meanwhile \(m_A\) is at weak scale, and the size of the effect depends strongly on \(m_A\) and \(\tan \beta \), e.g. small values of \(m_A\) and \(\tan \beta \) tend to enhance the effect. We also investigate the case that only \(\delta _{\mathrm{LR}}\) and \(\delta _{\mathrm{RL}}\) are non-vanishing, and we do not find such remanent effect in heavy SUSY limit for any choices of \(\mu \) and \(m_A\).

Fig. 2
figure 2

Dependence of \(\mathrm{Br}(t \rightarrow \mathrm{c h})\) on the common squark mass scale \(M_{\mathrm{SUSY}}\). In getting this figure, we assume all soft masses equal to \(M_{\mathrm{SUSY}}\), \(\delta _{\mathrm{LL}}=0.7\), \(\tan \beta = 4,10\) and \(m_A = 400,800\,\mathrm{GeV}\). We set \(A_t = M_{\mathrm{SUSY}}\) and \(\mu = 0\) for the left panel, and \(A_t = 0\) and \(\mu = M_{\mathrm{SUSY}}\) for the right panel. Note the lines corresponding to different choices of \( m_A \) and \(\tan \beta \) overlap in left panel

Full size image

The behaviors shown in Fig. 2 can be understood by the effective Lagrangian that describes the Higgs and quark system. After including loop effects, one can write down the Lagrangian as follows:

$$\begin{aligned} \mathcal{{L}}\!&= \!\! \sum _{i,j=1}^3\left\{ \bar{q}^\prime _i ( m^\prime _{ij} \!+\! \delta m^\prime _{ij}) P_\mathrm{L} q^\prime _j \!+\! h \bar{q}^\prime _i ( Y^\prime _{ij} \!+\! \delta Y^\prime _{ij}) P_\mathrm{L} q^\prime _j \right\} \!+\! h.c. \nonumber \\&= \sum _{i,j=1}^3 \left\{ (\bar{q} V_\mathrm{R}^\dag )_i ( m^\prime _{ij} + \delta m^\prime _{ij}) P_\mathrm{L} ( V_\mathrm{L} q )_j\right. \nonumber \\&\qquad \qquad \left. + h (\bar{q} V_\mathrm{R}^\dag )_i ( Y^\prime _{ij} + \delta Y^\prime _{ij}) P_\mathrm{L} ( V_\mathrm{L} q )_j \right\} + h.c. \nonumber \\&= \sum _{i=1}^3 \left\{ \bar{q}_i m_i P_\mathrm{L} q_i + \frac{h}{v} \bar{q}_i m_i P_\mathrm{L} q_i \right\} \nonumber \\&\quad \!+\! \sum _{i,j=1}^3 h \bar{q}_i \left[ V_\mathrm{R}^+ \left( \delta Y^\prime \!-\! \frac{\delta m^\prime }{v} \right) V_\mathrm{L}\right] _{ij} P_\mathrm{L} q_j \!+\! h.c.,\quad \end{aligned}$$
(16)

where \(q^\prime _i\) and \(m_{ij}^\prime = Y^\prime _{ij} v\) are quark field and its mass matrix at tree level with \(i,j\) denoting flavor indices, and \(\delta m^\prime \) and \(\delta Y^\prime \) represent loop corrections to the mass matrix and the Yukawa coupling, respectively. The second equation reflects the definition of quark mass eigenstate with \(V_\mathrm{L}\) and \(V_\mathrm{R}\) denoting the rotation matrices for left-handed quarks and right-handed quarks, respectively. After such a definition, the loop corrected mass matrix \(m^\prime + \delta m^\prime \) is diagonal with its diagonal element \(m_i\) representing physical quark mass determined by experiments. At this stage, the correction to the \(h\bar{q}_i q_j\) interaction is given by \(h \bar{q}_i [V_\mathrm{R} (\delta Y^\prime - \delta m^\prime /v ) V_\mathrm{L}]_{ij} P_\mathrm{L} q_j + h.c.\). Obviously, if \(\delta Y^\prime = \delta m^\prime /v\), new physics contribution to the \(h\bar{q}_i q_j\) interaction vanishes. In actual calculation, \(\delta m^\prime \) is obtained from \(q_i\)–\(q_j\) transition diagrams like diagram (b) of Fig. 1 without the emission of the Higgs particle, and \(\delta Y^\prime \) comes from the vertex correction like diagram (a) of Fig. 1. The effective Lagrangian then indicates that the two contributions should cancel out each other in contributing to the \(h\bar{q}_i q_j\) interaction.

As far as the SUSY-QCD correction to the \(h\bar{q}_i q_j\) interaction is concerned, its behavior in the heavy SUSY limit can be analysised with the mass insertion approximation. In this method, squark masses are taken to be the diagonal elements of the squark mass matrix, and the non-diagonal elements are treated as interactions. In order to illustrate this method in explaining the remanent effect, we first consider the well-studied SUSY-QCD correction to the \(h\bar{b}b\) vertex [37]. In this example, to get \(\delta m_b\) one needs to insert the \(\tilde{b}_\mathrm{L}\)–\(\tilde{b}_\mathrm{R}\) transition by odd times into the sbottom propagator entered in bottom quark self-energy diagrams, and sum the corresponding contribution to infinite orders of the insertion. One can check that, with one more insertion, the corresponding contribution is suppressed by a factor \(m_b(A_b - \mu \tan \beta )/M_{\mathrm{SUSY}}^2\) compared with that without the insertion, and only for the first order insertion, \(\delta m_b\) is not suppressed by \(M_{\mathrm{SUSY}}\), which means that the corresponding contribution is non-decoupled in the heavy SUSY limit. In a similar way, one can check that even times of the insertion are needed to get the expression of \(\delta Y_b\) in calculating the \(h\bar{b}b\) vertex correction, and only for the zeroth insertion, the contribution is non-decoupled. Putting these two contributions together, one can learn that the non-decoupled terms proportional to \(A_b\) is exactly canceled out, and the remaining contribution is proportional to the well-known form \(\mu m_{\tilde{g}}/M_{\mathrm{SUSY}}^2 (\tan \beta + \cot \alpha ) \simeq (-2 m_Z^2 \mu m_{\tilde{g}})/(M_{\mathrm{SUSY}}^2 m_A^2) \tan \beta \cos 2 \beta \) [37]. This effect, albeit scaling as \(1/m_A^2\), does not diminish as \(\mu \simeq m_{\tilde{g}} \simeq M_{\mathrm{SUSY}}\) approaches infinity for \(m_A\) at weak scale, and is therefore dubbed as the remanent effect of SUSY.

Next we turn to analysis the SUSY-QCD contribution to the \(h\bar{c}t\) vertex. Since such an interaction involves both chiral flipping and flavor changing, appropriate insertions are needed to accomplish both tasks. For the chiral-flipping mixings \(\delta _{\mathrm{LR}}\) and \(\delta _{\mathrm{RL}}\), their role is quite similar to \(A_b\) in the SUSY-QCD correction to the \(h\bar{b}b\) coupling, and their non-decoupling contribution is completely canceled out. While for the chiral-conserving mixings \(\delta _{\mathrm{LL}}\) and \(\delta _{\mathrm{RR}}\), their contribution to the \(h\bar{b}b\) vertex can be split into two parts with one part proportional to \(A_t\) and the other part proportional to \(\mu \). Figure 2 then reflects that the non-decoupling contribution of the former part is exactly canceled out, while that of the latter part is maintained if \(m_A\) is not at the same order as \(M_{\mathrm{SUSY}}\). This situation is actually similar to the SUSY-QCD correction to the \(h\bar{b}b\) vertex with the only difference coming from the fact that such a remanent effect is not enhanced by \(\tan \beta \). In fact, if both \(M_{\mathrm{SUSY}}\) and \(m_A\) approach infinity simultaneously, the genuine SUSY contribution to \(t\rightarrow \mathrm{c h}\) should vanish, since now the Higgs sector of the MSSM is identical to that of the SM, while if only \(M_{\mathrm{SUSY}}\) approaches infinity, the Higgs sector is described by a two-Higgs-doublet model, and SUSY may leave its imprint in Higgs sector [94, 95]. Our results in Fig. 2 actually reflect such a possibility.

We finally discuss how large SUSY can predict the rate of \(t \rightarrow c h\) in heavy SUSY case. For this purpose, we require all squarks to be heavier than \(3\, \mathrm{TeV}\) and perform two independence scans over relevant SUSY parameter space by considering the constraints listed in Sect. 2. These scans are as follows:

  • Scan III: Similar to Scan I except that we fix \(m_A = 800 \,\mathrm{GeV}\) and consider the following parameter space:

    $$\begin{aligned}&4 \,\mathrm{TeV} \le m_{Q_2},m_{Q_3},m_{U_2}, m_{U_3}, m_{D_2}, m_{D_3} \le 7 \,\mathrm{TeV}, \nonumber \\&|A_t| \le 6 \sqrt{m_{Q_3} m_{U_3}}, \nonumber \\&4\,\mathrm{TeV} \le m_{\tilde{g}} \le 10\,\mathrm{TeV}, \quad |\mu | \le 20 \,\mathrm{TeV},\nonumber \\&1 \le \tan \beta \le 40, \nonumber \\&-1 \le \delta _{\mathrm{LL}},\delta _{\mathrm{RR}} \le 1, \quad -2.0\le \delta _{\mathrm{LR}},\delta _{\mathrm{RL}} \le 2.0, \nonumber \\&-0.5 \le \delta _{\mathrm{LR}}^d,\delta _{\mathrm{RL}}^d \le 0.5. \end{aligned}$$
    (17)

    In our scan, we do not consider very large squark soft breaking parameters, because, in such a case, the Higgs mass calculated by FeynHiggs suffers from large theoretical uncertainties.

  • Scan IV: Similar to Scan II except that the scan regions are now given by Eq. (17).

For both scans, we find that the rate of \(t \rightarrow \mathrm{c h}\) may reach \(10^{-8}\) in the optimal case, and a smaller value of \(m_A\) can lead to a larger branching ratio. In Table 2, we provide two benchmark points for future study with Point 5 obtained from Scan III, and Point 6 from Scan IV. One can learn that, comparing the prediction in heavy SUSY with that in low energy SUSY, although the optimal values of \(\mathrm{Br}(t \rightarrow \mathrm{c h})\) are suppressed by at least two orders, they are still \(10^6\) times larger than the corresponding SM prediction.

Table 2 Same as Table 1, but for the heavy SUSY case. Point 5 and Point 6 are taken from Scan III and Scan IV, respectively
Full size table

Before we end this section, we would like to clarify one point. From Tables 1 and 2, it seems that a gluino as light as possible seems to be favored to maximize the rate of \(t \rightarrow \mathrm{c h}\). This is actually incorrect. From our calculation formula presented in Eq. (12), one can infer that the dependence of \(\mathcal {M}\) on \(m_{\tilde{g}}\) should roughly take the form \(\frac{(\mu , A_t) m_{\tilde{g}}}{\mathrm{Max}(m_{\tilde{q}}^2, m_{\tilde{g}}^2)}\). This form indicates that neither a light gluino nor a heavy gluino is favored to maximize the rate. As a verification of this conclusion, we vary the value of \(m_{\tilde{g}}\) for the benchmark Point 6 in Table 2 and meanwhile keep the other parameters unchanged; we find \(\mathrm{Br}(t \rightarrow \mathrm{c h}) \times 10^8 = 0.97, 1.65, 1.78, 1.66, 1.47 \) for \(m_{\tilde{g}} = 1, 2, 3, 4, 5\, \mathrm {TeV}\), respectively.

4 Conclusion

In this work, we studied the top quark FCNC decay \(t \rightarrow \mathrm{ch}\) in the MSSM under the constraints from the Higgs mass measurement, the LHC searches for sparticles, the vacuum stability, the precision electroweak observables, and \(B \rightarrow X_s \gamma \). From a scan over the relevant parameter space, we found the following:

  • Due to the strong constraints from the measured Higgs mass and the results of SUSY searches at the LHC, the branching ratio of \( t \rightarrow \mathrm{c h}\) can only reach \(O(10^{-6})\) in the MSSM, which is about one order smaller than the old results.

  • In the singlet extension of the MSSM, which can lift the Higgs mass at tree level, \(\mathrm{Br}(t \rightarrow \mathrm{c h})\) can reach \(O(10^{-5})\) in the allowed parameter space.

  • The chiral-conserving mixings \(\delta _{\mathrm{LL}}\) and \(\delta _{\mathrm{RR}}\) can induce a SUSY remanent effect on the rate of \(t \rightarrow \mathrm{c h}\). For heavy squarks above 3 TeV and a gluino above 4 TeV, \(\mathrm{Br}(t\rightarrow \mathrm{c h})\) can still reach \(10^{-8}\).