1 Introduction

The apparent mismatch between the fundamental scales of particle physics and gravity is resolved in recent years by changing the behavior of gravity at short distance. One of the most promising candidates for resolving this is the introduction of a large extra dimension and reducing the scale of quantum gravity all way down to the weak scale, which was shown first by Arkani-Hamed et al. [1–9]. This possibility might imply the existence of large extra dimensions and this opens up a new cosmological scenario for the early universe [10–17]. Though it is an interesting concept, the existence of a large hierarchy between the weak and the Planck scale leads to new hierarchy through the length scale of the large extra dimension where the radius of the extra dimension is much larger than the natural value.

We could have a different setup where the extra dimensions are small but the background metric is not flat along the extra coordinate. This possibility was first analyzed by Randall and Sundrum (RS) [18, 19]. The metric along the extra dimension was a slice of anti-de Sitter (AdS\(_{5}\)) space due to the negative cosmological constant being balanced by two brane tensions. This non-flat geometry causes the physical scales on two branes to be different and exponentially suppressed on the negative tension brane. Some generalizations of the RS models are discussed in works by Goldberger and Wise [20–24], and embedding this into supergravity has been discussed by Hawking et al. [25, 26].

The cosmology of this model can be very different from the ordinary inflationary cosmology in four dimensions. The study of early cosmology in the RS brane world appears to be hindered by one obstacle i.e. the late time cosmology differs widely from the usual Friedman–Robertson–Walker (FRW) universe in the 4D theory on the brane. This conclusion has been reached by Binetruy et al. [27] by examining the solutions to the Einstein equation in five dimensions on an \(S^{1}/Z_{2}\) orbifold, with matter on two branes and no cosmological constant on the bulk or brane. This issue was resolved by Csáki et al. [28] using a time independent stabilized radion field.

The RS model consists of a space-time with an \(S^{1}/Z_{2}\) orbifold symmetry, two branes with opposite tension reside on the orbifold fixed point such that the space-time metric has a redshift factor depending exponentially on the radius of the compactified dimension. The lowering of the Planck scale on the negative tension brane also depends exponentially on this compactified radius. For \(kr_{c}=12\), where \(r_{c}\) is the compactification radius and \(k\) is the parameter of same order as Planck scale \(M\), the weak scale is dynamically generated from this fundamental scale. The Kaluza–Klein excitations have a TeV mass splitting and couplings [19]. In this scenario (as presented in [18]), \(r_{c}\) is associated with the vacuum expectation value of a massless four-dimensional scalar field. Since the modulus field has zero potential, the stabilization of \(r_{c}\) cannot be determined from the dynamics of the model. Subsequently Goldberger and Wise (GW) [29] provided a stabilization mechanism by introducing a bulk scalar field to generate a potential for the modulus. However, it does not address the dynamics of this stabilization mechanism. Recently many other variants of the stabilization mechanisms have been presented [30–34]. The stabilization mechanism has also been discussed from the point of view of gauge theories, string-inspired models in many other works [35–39].

In this work we shall first consider the Einstein equation with a metric ansatz having the FRW structure in 4D sector and a time dependent radion field with energy density on both branes. From the Einstein equations we first determine the averaged Einstein equations and then the equation for the radion field to find the dynamics of the radion field in the early universe. In this context we have shown the equivalence of our result with the covariant curvature approach adopted in Refs. [40, 41]. It turns out that this evolution of the radion field depends on the energy density on the visible brane. We have then obtained the evolution of the scale factor which depends on the time evolution of the radion field. It has been shown that the scale factor has an inflationary solution, which comes from the compactification of the extra dimension to a small value. Finally, we generalize the GW stabilization mechanism to the time dependent radion field and find the stabilized value of the radion field, which coincides with the Goldberger–Wise solution. The paper ends with a short discussion of our results.

2 Einstein equations and solution

In this section we shall discuss the Einstein equation in the RS model with time dependent radion field along with matter on the brane and a bulk cosmological constant. Using the Einstein equation and following the procedure used in the work of Csáki et al. [28] we find four-dimensional Friedman-like equations induced on both branes and try to find the radion time dependence. The action for our system is given by

$$\begin{aligned} S&= \int d^{5}x \sqrt{-\tilde{g}}\left( 2M^{3}R-\Lambda \right) \nonumber \\&+\int d^{4}x \sqrt{-g_\mathrm{hid}}~\left\{ \mathcal {L}_\mathrm{hid}-V_\mathrm{hid}\right\} \nonumber \\&+\int d^{4}x \sqrt{-g_\mathrm{vis}}~\left\{ \mathcal {L}_\mathrm{vis}-V_\mathrm{vis}\right\} \end{aligned}$$
(1)

where the first term corresponds to the bulk part of the action with a bulk cosmological constant. The second part represents the action on the hidden or Planck brane with \(V_\mathrm{hid}\) as the brane tension and \(\mathcal {L}_\mathrm{hid}\) as the matter Lagrangian on the hidden 3-brane. Similar considerations hold for the third term as well for the visible or TeV brane. The quantity \(M\) corresponds to the five-dimensional Planck scale.

The metric ansatz for the five-dimensional space-time is taken as

$$\begin{aligned} ds^{2}&= e^{-2A(\phi ,t)}\left[ -dt^{2}+a^{2}(\phi ,t)\left( dx^{2}+dy^{2}+dz^{2}\right) \right] \nonumber \\&+r^{2}(\phi ,t)d\phi ^{2} \nonumber \\&\equiv \tilde{g}_{AB}(x,\phi )dx^{A}dx^{B}. \end{aligned}$$
(2)

The two branes are being located at \(\phi =0\) and \(\phi =\pi \). The Einstein tensor for this metric is component-wise given by

$$\begin{aligned} G_{00}&= 3\left( \dot{A}^{2}-\dot{A}\frac{\dot{r}}{r} \right) + 3\left( \frac{\dot{a}^{2}}{a^{2}}+\frac{\dot{a}}{a} \frac{\dot{r}}{r}- 2 \dot{A} \frac{\dot{a}}{a} \right) \nonumber \\&+\,3\frac{e^{-2A}}{r^{2}}\left( A^{''}-2(A^{'})^{2}-A^{'} \frac{r^{'}}{r}+ 4A^{'} \frac{a^{'}}{a}\right. \nonumber \\&\left. -\frac{a^{''}}{a}- (\frac{a^{'}}{a})^{2}+\frac{a^{'}}{a}\frac{r^{'}}{r} \right) ;\nonumber \\ G_{ii}&= a^{2}\left( 2\ddot{A}-\dot{A}^{2}+\dot{A}\frac{\dot{r}}{r} \right) \nonumber \\&+\, a^{2}\left( -2\frac{\ddot{a}}{a}-\frac{\dot{a}^{2}}{a^{2}}+ 4\dot{A}\frac{\dot{a}}{a}-\frac{\ddot{r}}{r}-2\frac{\dot{a}}{a}\frac{\dot{r}}{r}\right) \nonumber \\&+\,a^{2} \frac{e^{-2A}}{r^{2}}\left[ 3\left( -A^{''}+2(A^{'})^{2}+ A^{'}\frac{r^{'}}{r}\right) \right. \nonumber \\&\left. +\left( 2\frac{a^{''}}{a}-8A^{'}\frac{a^{'}}{a}+ (\frac{a^{'}}{a})^{2}-2\frac{a^{'}}{a}\frac{r^{'}}{r} \right) \right] ;\nonumber \\ G_{04}&= 3\dot{A}^{'}-3A^{'}\frac{\dot{r}}{r}+3 \frac{a^{'}}{a}(\dot{A}+\frac{\dot{r}}{r})-3 \frac{\dot{a}^{'}}{a};\nonumber \\ G_{44}&= 6(A^{'})^{2}+3\left[ \left( \frac{a^{'}}{a}\right) ^{2}-3\frac{a^{'}}{a}A^{'}\right] \nonumber \\&+\, r^{2}e^{2A}\left( 3\ddot{A}-3\dot{A}^{2}-3\frac{\ddot{a}}{a}-3\frac{\dot{a}^{2}}{a^{2}}+9\dot{A}\frac{\dot{a}}{a}\right) . \end{aligned}$$
(3)

Here primes (overdots) denote derivatives with respect to \(\phi (t)\). The contribution to the energy momentum tensor from the bulk cosmological constant has the form

$$\begin{aligned} T_{ab}^\mathrm{bulk}=\tilde{g}_{ab}\Lambda \end{aligned}$$
(4)

and for the branes we readily obtain

$$\begin{aligned} T_{a}^{b,~\mathrm{brane}}&= \frac{\delta (\phi )}{r}\mathrm{diag}\left( V_\mathrm{hid}+\rho _\mathrm{hid},V_\mathrm{hid}\right. \nonumber \\&\left. -p_\mathrm{hid},V_\mathrm{hid}-p_\mathrm{hid},V_\mathrm{hid}-p_\mathrm{hid},0\right) \nonumber \\&+\frac{\delta (\phi -\pi )}{r}diag\left( V_\mathrm{vis}+\rho _\mathrm{vis},V_\mathrm{vis}\right. \nonumber \\&\left. -p_\mathrm{vis},V_\mathrm{vis}-p_\mathrm{vis},V_\mathrm{vis}-p_\mathrm{vis},0\right) \end{aligned}$$
(5)

where \('\) denotes the derivative with respect to \(\phi \) and the overdot denotes the derivative with respect to \(t\). Here \(\Lambda \) is the bulk cosmological constant and \(V_\mathrm{vis}\) and \(V_\mathrm{hid}\) are the constant “vacuum energies” on the 3-branes, which act as the gravitational source even in the absence of particle excitations. The parameters \(V_\mathrm{hid}\), \(V_\mathrm{vis}\), and \(\lambda \) are related to a single scale k such that

$$\begin{aligned} \left. \begin{array}{c} V_\mathrm{hid}=-V_\mathrm{vis}=24M^{3}k\\ \Lambda =-24M^{3}k^{2} \end{array} \right\} . \end{aligned}$$
(6)

Now the quantities \(\rho _\mathrm{hid}\) and \(p_\mathrm{hid}\) are the density and pressure of matter on the positive tension brane. Also the quantities \(\rho _\mathrm{vis}\) and \(p_\mathrm{vis}\) are the respective quantities in the TeV brane. In the limit \(\rho _\mathrm{hid},p_\mathrm{hid},\rho _\mathrm{vis},p_\mathrm{vis}\rightarrow 0\) we should recover the static Randall–Sundrum solution. However, an initial investigation of the cosmology of brane world models shows some inconsistency, since there appears a constraint on the bare matter density in Planck and TeV brane. Also, from the Hubble parameter it appears that \(\rho _\mathrm{hid}>0\), which in turn implies that the energy density on the TeV brane is negative. These results were discussed in [28], and physical interpretations were given in a quiet general sense. From the above Einstein equations it is quite clear that if we assume that the warp factor \(A\) depends only on the extra space-time coordinate \(\phi \), the scale factor and the radion field depend on \(t\). Then from the \(G_{04}\) equation one finds \(\dot{r}=0\). Hence the radion field cannot have a time dependence and therefore cannot evolve dynamically. Also from the other equations we see that the scale factor becomes time independent, leading to the static Randall–Sundrum solution.

2.1 Averaged Einstein equations

In this subsection we present the averaged Einstein equations over the bulk to demonstrate that without a stabilizing potential the system would become over-constrained if we require the modulus to be static. We apply the following expansion around a RS solution:

$$\begin{aligned} a(\phi ,t)&= a(t)\left[ 1+\delta a(\phi ,t)\right] ,\nonumber \\ r(\phi ,t)&= r(t)\left[ 1+\delta r(\phi ,t)\right] ,\nonumber \\ A(\phi ,t)&= kr(t)\mid \phi \mid \left[ 1+\delta A(\phi ,t)\right] . \end{aligned}$$
(7)

The warp factor can be given by introducing the \(A(\phi ,t)\) as

$$\begin{aligned} \Omega \equiv \Omega (\phi ,r(t))=e^{-kr(t)\mid \phi \mid }; ~~~\Omega _{r}\equiv e^{-kr(t)\pi }. \end{aligned}$$
(8)

The value of \(\Omega _{r}\), when \(r=r_{c}=\mathrm constant \) would be given by \(\Omega _{c}\). All the quantities \(\delta a\), \(\delta A\), and \(\delta r\) are perturbations on the RS background along with \(\rho _\mathrm{hid}\) and \(\rho _\mathrm{vis}\). Therefore in the above expansion we can make the assumption that \(\delta a\), \(\delta A\), and \(\delta r\) are linear functions of the energy densities \(\rho _\mathrm{hid}\) and \(\rho _\mathrm{vis}\) only [28]. The linearity assumption is necessary from the requirement that in the limit \(\rho _\mathrm{hid} \rightarrow 0\) and \(\rho _\mathrm{vis} \rightarrow 0\) one should recover RS solution as well as when all the metric perturbations \(\delta a, \delta A\) and \(\delta r\) are set to zero. This implies that an expansion in the brane matter energy density is equivalent to an expansion in the metric perturbations. This amounts to assuming that \(\delta a\), \(\delta A\), and \(\delta r\) are linear in the matter energy density as both are perturbations on the RS background. This has the implication that the time derivatives of the perturbations are of higher order in the energy density, which, then can be neglected. However, we shall work with all possible orders in \(r(t)\) and its time derivative in this subsection.

For completeness we also include a radion potential following the work by Csáki et al. [28]:

$$\begin{aligned} a^{3}V_{r}(r)\equiv -r(t)\int d\phi \Omega ^{4}\mathcal {L_{R}} \end{aligned}$$
(9)

in the following computations and shall set \(V_{r}=0\) whenever desired. Here the quantity \(\mathcal {L_{R}}\), the potential Lagrangian, is generated from some dynamics (maybe a scalar field; see Sect. 3 for a detailed discussion).

For classical electromagnetism on a manifold without any boundary we readily obtain by integrating \(\nabla . E=\rho \) the result that the total charge must vanish. Here, also, to find some topological constraint, we use the analog of Gauss’ law in Einstein theory. For example consider the following integral [28]:

$$\begin{aligned} \int d\phi \Omega ^{4}G_{0}^{0}=\frac{1}{4M^{3}}\int d\phi \Omega ^{4} T_{0}^{0}. \end{aligned}$$
(10)

However, this equation does not imply a topological constraint, rather it is combined with other averaged equations to give the constrained energy densities. This actually follows from requiring a static extra dimension without radion potential. Note that this implies that the radion field could evolve even without any stabilizing potential.

Then substitution of the above expansion, Eq. (7), into Eq. (10) and integrating we arrive at

$$\begin{aligned}&\left( \frac{\dot{a}}{a}\right) ^{2}+2kr_{c}\pi \frac{\Omega _{r}^{2}}{1-\Omega _{r}^{2}} \frac{\dot{a}}{a}\frac{\dot{r}}{r}-k^{2}r^{2}\pi ^{2} \frac{\Omega _{r}^{2}}{1-\Omega _{r}^{2}}\left( \frac{\dot{r}}{r}\right) ^{2}\nonumber \\&\quad = \frac{k}{12M^{3}}\frac{1}{1-\Omega _{r}^{2}} \left[ \rho _\mathrm{hid}+\rho _\mathrm{vis}\Omega _{r}^{4}+V_{r}(r)\right] +\mathcal {O}(\epsilon ^{2})\nonumber \\ \end{aligned}$$
(11)

where \(\epsilon ^{2}= \mathcal {O}(\delta a^{2}, \delta A^{2}, \delta r^{2})\). There are no corrections to the Hubble parameter squared linear in the perturbations. Also the above equation reduces to the conventional FRW solutions when the energy density in the radion is small. In this limit the behavior of the scale factor is determined by the quantity \(\rho _\mathrm{hid}+\rho _\mathrm{vis}\Omega _{r}^{4}\), i.e. it depends on both the energy density in the Planck and in the TeV brane. Hence for a small oscillation of the radion field the expansion of the universe is determined by ordinary FRW cosmology. Hence the bulk averaged \(G_{00}\) equation results in the ordinary Hubble law. We can repeat the above procedure for the spatial \(G_{ij}\) components as well, which results in the following equation:

$$\begin{aligned}&2\left( \frac{\ddot{a}}{a}\right) +\left( \frac{\dot{a}}{a}\right) ^{2}+ 4k\pi r\frac{\Omega _{r}^{2}}{1-\Omega _{r}^{2}} \frac{\dot{a}}{a}\frac{\dot{r}}{r}\nonumber \\&\qquad -k^{2}r^{2}\pi ^{2} \frac{\Omega _{r}^{2}}{1-\Omega _{r}^{2}}\left( \frac{\dot{r}}{r}\right) ^{2}+2kr\pi \frac{\Omega _{r}^{2}}{1-\Omega _{r}^{2}} \frac{\ddot{r}}{r}\nonumber \\&\quad =-\frac{k}{4M^{3}}\frac{1}{1-\Omega _{r}^{2}} \left[ p_\mathrm{hid}+p_\mathrm{vis}\Omega _{r}^{4}-V_{r}(r)\right] +\mathcal {O}(\epsilon ^{2}).\nonumber \\ \end{aligned}$$
(12)

Note that in the limit when the radion field is static and we have no associated radion potential, the above equation reduces to the standard pressure equation in FRW cosmology. This is also in accord with the averaged \(G_{00}\) equation due to the fact that there exists no correction of \(\mathcal {O}(\epsilon )\).

However, for the unaveraged linearized \(G_{44}\) equation the perturbations \(\mathcal {O}(\epsilon )\) appear. Then if we follow the respective jump conditions as given in [27], then at \(\phi =0\), the following equation results [28]:

$$\begin{aligned}&\!\!\!-\frac{k^{2}}{24M^{3}}\left( -\rho _\mathrm{hid}+3p_\mathrm{hid}\right) - \left( \frac{\dot{a}^{2}}{a^{2}}+\frac{\ddot{a}}{a}\right) \nonumber \\&\quad =\frac{1}{12M^{3}}T_{5}^{5}\mid _{0}. \end{aligned}$$
(13)

In the absence of a radion potential, however, the system is over-constrained provided a static radion field solution is imposed. To observe this more closely we can eliminate the scale factor using Eqs. (11) and (12), which ultimately leads to a static solution of r,

$$\begin{aligned} \left( -3p_\mathrm{vis}+\rho _\mathrm{vis} \right) \Omega _{r}^{2}=\left( 3p_\mathrm{hid}-\rho _\mathrm{hid}\right) . \end{aligned}$$
(14)

This along with the conservation of energy leads to a further fine tuning, and the above constraint leads to

$$\begin{aligned} \rho _\mathrm{hid}=-\Omega _{r}^{2}\rho _\mathrm{vis}. \end{aligned}$$
(15)

This constraint arises due to requiring \(r=constant\) without a radion potential. With the above assumptions, the system becomes over-constrained and fine tuning of energy densities is necessary to maintain a static solution in the bulk.

2.2 Equivalence with covariant curvature formalism

The linearized theory in brane world models was discussed in [42, 43]. In Ref. [40] an effective Einstein equation was derived at the low energy scale. However, that derivation was a metric-based approach. Here we will follow the covariant curvature approach illustrated in Ref. [41]. This covariant curvature formalism gives an effective gravitational equation on the branes. We will use the metric ansatz as given by Eq. (2), in the following form:

$$\begin{aligned} ds^{2}=g_{\mu \nu }dx^{\mu }dx^{\nu }+r^{2}d\phi ^{2}. \end{aligned}$$
(16)

Then the proper distance between the branes is given by \(d_{0}=\pi r(t)\) and \(g_{\mu \nu }\) is the induced metric over \(\phi =\) constant hypersurfaces. Then following the procedure as presented in Refs. [41, 44] we obtain the Gauss–Codazzi equations,

$$\begin{aligned} ^{(4)}G_{\mu \nu }&= 3k^{2}\delta _{\nu }^{\mu }+KK^{\mu }_{\nu }-K^{\mu }_{\alpha }K^{\alpha }_{\nu }\nonumber \\&-\frac{1}{2}\delta ^{\mu }_{\nu }\left( K^{2}-K^{\alpha }_{\beta }K^{\beta }_{\alpha }\right) -E^{\mu }_{\nu } \end{aligned}$$
(17)

and

$$\begin{aligned} D_{\mu }K^{\mu }_{\nu }-D_{\mu }K=0 \end{aligned}$$
(18)

with \(D_{\mu }\) being the covariant derivative on the \(\phi =\) constant hypersurfaces. Here \(k\) is the bulk curvature, \(^{(4)}G_{\mu \nu }\) is the four-dimensional Einstein tensor, and \(K_{\mu \nu }\) is the extrinsic curvature of the hypersurfaces defined as

$$\begin{aligned} K_{\mu \nu }=\frac{1}{2}\pounds _{n}q_{\mu \nu }=\nabla _{\mu }n_{\nu }+n_{\mu }a_{\nu } \end{aligned}$$
(19)

where we have \(n=r^{-1}\partial _{\phi }\) and \(a^{\mu }=n^{\nu }\nabla _{\nu }n^{\mu }\). \(E_{\mu \nu }\) is the projected Weyl tensor defined by \(E^{\mu }_{\nu }=^{(5)}C_{\mu \alpha \nu \beta }n^{\alpha }n^{\beta }\), with \(^{(5)}C_{\mu \alpha \nu \beta }\) the five-dimensional Weyl tensor. The respective jump conditions are given by

$$\begin{aligned} \left[ K^{\mu }_{\nu }-\delta ^{\mu }_{\nu }K \right] _{\phi =0}&= -\frac{1}{8M^{3}}\left( -V_\mathrm{hid}\delta ^{\mu } _{\nu }+T_{1~\nu }^{\mu } \right) \end{aligned}$$
(20)
$$\begin{aligned} \left[ K^{\mu }_{\nu }-\delta ^{\mu }_{\nu }K \right] _{\phi =\pi }&= -\frac{1}{8M^{3}}\left( -V_\mathrm{vis}\delta ^{\mu } _{\nu }+T_{2~\nu }^{\mu } \right) \end{aligned}$$
(21)

where \(T_{1~\nu }^{\mu }\) and \(T_{2~\nu }^{\mu }\) are the energy momentum tensors of the hidden and visible brane, respectively. \(V_\mathrm{hid}\) and \(V_\mathrm{vis}\) are the brane tensions of hidden and visible branes, respectively. Then following the procedure adopted in Refs. [40, 41] we arrive at the low-energy effective theory with the effective Einstein equation on the visible brane,

$$\begin{aligned} ^{(4)}G^{\mu }_{\nu }&= \frac{k}{4M^{3}}\frac{1}{\Phi }T_{2~\nu }^{\mu } +\frac{k}{4M^{3}}\frac{(1+\Phi )^{2}}{\Phi }T_{1~\nu }^{\mu } \nonumber \\&+\,\frac{1}{\Phi }\left( D^{\mu }D_{\nu }-\delta ^{\mu }_{\nu }D^{2}\Phi \right) \nonumber \\&+\,\frac{\omega (\Phi )}{\Phi ^{2}}\left( D^{\mu }\Phi D_{\nu }\Phi -\frac{1}{2}\delta ^{\mu }_{\nu }\left( D\Phi \right) ^{2} \right) \end{aligned}$$
(22)

where \(\Phi =e^{2kr(t)\pi }-1=e^{2A}-1\) and \(\omega (\Phi )=-\frac{3}{2}\frac{\Phi }{1+\Phi }\). This is the effective equation in leading order of the brane to bulk curvature ratio. Then using the metric ansatz given by Eq. (2) we readily obtain the time-time component of the above equation to yield

$$\begin{aligned}&\!\!\!\Omega ^{-2}\Big [3\left( \frac{\dot{a}}{a}\right) ^{2}-6k\pi r \frac{\dot{a}}{a}\frac{\dot{r}}{r}+ 3k^{2}\pi ^{2} r^{2}\left( \frac{\dot{r}}{r} \right) ^{2}\Big ]\nonumber \\&\quad =\frac{k}{4M^{3}}\frac{1}{\Omega ^{-2}-1}\left( \rho _\mathrm{vis}+\Omega ^{-4}\rho _\mathrm{hid}\right) \nonumber \\&\qquad +\,6\frac{\Omega ^{-4}}{\Omega ^{-2}-1}k^{2}\pi ^{2}r^{2}\left( \frac{\dot{r}}{r} \right) ^{2}-\,6\frac{\Omega ^{-4}}{\Omega ^{-2}-1}k\pi r \frac{\dot{a}}{a}\frac{\dot{r}}{r}\nonumber \\&\qquad -\,3\frac{\Omega ^{-4}}{\Omega ^{-2}-1}k^{2}\pi ^{2}r^{2}\left( \frac{\dot{r}}{r} \right) ^{2}, \end{aligned}$$
(23)

which can be further simplified to yield

$$\begin{aligned}&\!\!\!\left( \frac{\dot{a}}{a}\right) ^{2}+2k\pi r\left( -1+\frac{1}{1-\Omega ^{2}}\right) \frac{\dot{a}}{a}\frac{\dot{r}}{r}\nonumber \\&\qquad - k^{2}\pi ^{2} r^{2}\left( -1+\frac{1}{1-\Omega ^{2}}\right) \left( \frac{\dot{r}}{r} \right) ^{2} \nonumber \\&\quad = \frac{k}{12M^{3}}\frac{1}{1-\Omega ^{2}}\left( \rho _\mathrm{hid}+\Omega ^{-4}\rho _\mathrm{vis}\right) , \end{aligned}$$
(24)

which is precisely the time-time component of the averaged Einstein equation given by Eq. (11). The quantity \(\Omega \) used in the above equation is given by \(\Omega = e^{-2k\pi r}\). Next we consider the space-space component of the effective equation on the negative tension brane,

$$\begin{aligned}&\!\!\!\Omega ^{-2}\Big [2\left( \frac{\ddot{a}}{a} \right) +\left( \frac{\dot{a}}{a}\right) ^{2} -4k\pi r\frac{\dot{a}}{a}\frac{\dot{r}}{r}\nonumber \\&\qquad - k^{2}r^{2}\pi ^{2}\left( \frac{\dot{r}}{r}\right) ^{2}-2k\pi r \frac{\ddot{r}}{r}\Big ] \nonumber \\&\quad =-\frac{k}{4M^{3}}\frac{1}{\Omega ^{-2}-1}\left( p_\mathrm{vis}+\Omega ^{-4}p_\mathrm{hid}\right) \nonumber \\&\qquad -4k\pi r \frac{\Omega ^{-4}}{\Omega ^{-2}-1} \frac{\dot{a}}{a}\frac{\dot{r}}{r} -k^{2}r^{2}\pi ^{2}\frac{\Omega ^{-4}}{\Omega ^{-2}-1}\left( \frac{\dot{r}}{r}\right) ^{2}\nonumber \\&\qquad - 2k\pi r \frac{\Omega ^{-4}}{\Omega ^{-2}-1} \frac{\ddot{r}}{r}, \end{aligned}$$
(25)

which can be simplified to yield the space-space part of the averaged Einstein equations given by Eq. (12). The same procedure can now be applied for the hidden brane to retrieve the same equations as (11) and (12). This proves the equivalence of the covariant curvature formalism with the averaged Einstein equation procedure. It must be stressed that this equivalence holds only when higher order terms can be neglected. For example, in the case of a strong time dependence the higher order corrections in terms of the brane to bulk curvature ratio cannot be neglected. In that situation the above equivalence may not be valid.

2.3 Dynamics of the radion field

To address the dynamics of compactification we first consider the radion field to be time dependent and subsequently shall provide a stabilization mechanism. We shall use the averaged Einstein equations as given by Eqs. (11) and (12) and obtain averaged equations in terms of the unknown functions \(a(t)\) and \(r(t)\) in terms of the energy densities in the visible and Planck brane. For this purpose we use the equation of state \(\rho _{i}=-p_{i}\). However, in all the bulk Einstein equations the right hand side is canceled by the respective terms on the left hand side; thus, we do not need to bother about the boundary terms anymore. The different components of averaged Einstein equation lead to

$$\begin{aligned}&\!\!\!\left( \frac{\dot{a}}{a}\right) ^{2}+2kr\pi \frac{\Omega _{c}^{2}}{1-\Omega _{c}^{2}} \frac{\dot{a}}{a}\frac{\dot{r}}{r}\nonumber \\&\qquad -\,k^{2}r^{2}\pi ^{2}\frac{\Omega _{c}^{2}}{1-\Omega _{c}^{2}} \left( \frac{\dot{r}}{r}\right) ^{2}=-\frac{k}{12M^{3}}\Omega _{c}^{2}\rho _\mathrm{vis}\end{aligned}$$
(26)
$$\begin{aligned}&\!\!\!2\!\!\left( \frac{\ddot{a}}{a}\right) +\left( \frac{\dot{a}}{a}\right) ^{2} \!+4k\pi r\frac{\Omega _{c}^{2}}{1-\Omega _{c}^{2}} \frac{\dot{a}}{a}\frac{\dot{r}}{r}-k^{2}r^{2}\pi ^{2}\frac{\Omega _{c}^{2}}{1-\Omega _{c}^{2}}\!\!\left( \frac{\dot{r}}{r}\right) ^{2}\nonumber \\&\quad +\,2kr\pi \frac{\Omega _{c}^{2}}{1-\Omega _{c}^{2}} \frac{\ddot{r}}{r} =-\frac{k}{4M^{3}}\Omega _{c}^{2}\rho _\mathrm{vis} \end{aligned}$$
(27)

where we have taken the energy density and pressure such that \(\rho _\mathrm{hid}=-\Omega _{c}^{2}\rho _\mathrm{vis}\) and \(p_\mathrm{hid}=-\rho _\mathrm{hid}\) along with \(p_\mathrm{vis}=-\rho _\mathrm{vis}\). However, for the \(44\) component we readily find that the unaveraged Einstein equation leads to an identity following the work by Csáki et al. [28]. Now Eq. (26) can be solved for \(\dot{a}/a\) such that

$$\begin{aligned} \dot{a}/a&= -k\pi r\frac{\Omega _{c}^{2}}{1-\Omega _{c}^{2}}\dot{r}/r\nonumber \\&\pm \sqrt{k^{2}\pi ^{2}r^{2}\frac{\Omega _{c} ^{2}}{\left( 1-\Omega _{c}^{2}\right) ^{2}} \left( \dot{r}/r\right) ^{2}-k/12M^{3}\Omega _{c}^{2}\rho _\mathrm{vis}}\nonumber \\ \end{aligned}$$
(28)

with the choice of the small time scale such that

$$\begin{aligned} t\ll t_\mathrm{valid}=\frac{90}{\Omega _{c}^{2}}\sqrt{\frac{12M^{3}}{k\rho _\mathrm{vis}}} \frac{\left( 1-\Omega _{c}^{2}\right) }{\left( 1+\Omega _{c}^{2}\right) }; \end{aligned}$$
(29)

we can readily observe that the only physical parameter present in the above expression is \(\left( \rho _\mathrm{vis}\frac{k}{M^{3}} \right) ^{-1}\). Now from Eq. (6) we readily observe that this actually implies that \(\frac{\rho _\mathrm{vis}V_\mathrm{vis}}{M^{6}}\) should be large. Note that the brane tension is of the order of \(M^{3}\); thus, for this to value \(\rho _\mathrm{vis}\) should be greater than \(M^{3}\), which is true only before the Planck time, and that is precisely when the inflation occurs. This justifies our use of the small time approximation and presenting this solution as an inflationary scenario. Also, in the above expression \(t_\mathrm{valid}\) represents the time scale up to which the small time approximation would remain valid. Then under this small time scale we can make a linear choice for the time evolution of the radion field, and that yields the connection between the matter energy density and the radion field,

$$\begin{aligned} \dot{r}=-\sqrt{\frac{\rho _\mathrm{vis}}{12M^{3}k\pi ^{2}}}\left( 1-\Omega _{c}^{2}\right) . \end{aligned}$$
(30)

It is now evident from the above equation that if \(\rho _\mathrm{vis}\) is zero i.e. there is no energy density on the visible brane, the radion field cannot evolve with time. Thus the radion field would have been zero without the Goldberger–Wise stabilization mechanism. The stabilized value \(r=r_{c}\) can be obtained by introducing a bulk scalar field. In the case of a time dependent situation such a stabilization mechanism has been presented in Sect. 3.

However, we should also mention that Eq. (30) only holds if the radion field evolves dynamically with time. After the radion field becomes stabilized the above equation would not be valid. Then we have to resort to the unaveraged Einstein equation and obtain the evolution of the scale factor from those equations directly.

Now we will consider the fact that \(\rho _\mathrm{vis}=\mathrm constant \). The choice \(\rho _\mathrm{vis}=-p_\mathrm{vis}=\mathrm constant \) actually implies the standard dark energy candidate. Then for the differential equation as presented in Eq. (30) we readily obtain

$$\begin{aligned} r(t)=r_{0}-\sqrt{\frac{\rho _\mathrm{vis}}{12M^{3}k\pi ^{2}}} \left( 1-\Omega _{c}^{2}\right) t. \end{aligned}$$
(31)

Now having obtained that solution we proceed to determine the variation of the scale factor with time. For that purpose we use the averaged equation as presented by Eqs. (26) and (28) along with the radion field time evolution equation (30), leading to

$$\begin{aligned} \frac{\dot{a}}{a}=-kr\pi \frac{\Omega _{c}^{2}}{1-\Omega _{c}^{2}}\frac{\dot{r}}{r}. \end{aligned}$$
(32)

Equations (26) and (27) lead finally to the fact that the radion field evolves by the energy density on the brane, which in turn makes the scale factor evolve. Having observed that \(\dot{r}\) is negative, this implies that the radion field depletes with time, explaining the small value of the extra dimension in the present epoch. From the above equations we observe that when the radion field has no time dependence, then the usual Friedman equations are obtained with energy density and pressure. In that limit our result matches with the result of Csáki et al. [28].

Then using the above solution we have the following solution for the scale factor, which we obtain from Eq. (32):

$$\begin{aligned} a(t)=a_{0}e^{H t};\qquad H =\Omega _{c}^{2}\sqrt{\frac{k\rho _\mathrm{vis}}{12M^{3}}}. \end{aligned}$$
(33)

It is generally believed that the universe has undergone an exponential increase of scale factor which resulted in a very smooth universe at large scales solving the flatness–oldness problem, due to quantum fluctuations. The scale factor for that epoch is taken as \(a(t)\propto e^{\kappa t}\), where \(\kappa \) is a constant and denotes the inverse time in which the universe has grown to \(e\) times the previous value. Then the e-folding parameter is given by

$$\begin{aligned} N=\int _{t_{i}}^{t_{f}}Hdt=\Omega _{c}^{2}\sqrt{\frac{k\rho _\mathrm{vis}}{12M^{3}}}\Delta t. \end{aligned}$$
(34)

Thus we have a situation where, as the brane gets inflated, the radion field decreases in magnitude, making it consistent with recent observations. The observations suggest that the e-folding parameter should be \(\simeq 60\). Then by equating \(N=60\) we observe that

$$\begin{aligned} \Delta t \simeq \frac{60}{\Omega _{c}^{2}}\sqrt{\frac{12M^{3}}{k\rho _\mathrm{vis}}} \ll t_\mathrm{valid}. \end{aligned}$$
(35)

Hence the use of a small time approximation is justified and it remains valid during the whole period of inflation [45]. In the above inflationary scenario the radion field plays the role of slow-roll parameter. As the radion field gradually tends to the stabilized value \(r_{c}\), its time dependence is the primary cause of evolution of the scale factor. When the radion field gets stabilized, \(\dot{r}\) vanishes, making the scale factor time independent and implying an exit from the inflationary phase. This time dependent stabilization is addressed in Sect. 3.

Now we try for a solution of the form \(r(t)=r_{0}-\sqrt{\frac{\rho _\mathrm{vis}}{12M^{3}k\pi ^{2}}} \left( 1-\Omega _{c}^{2}\right) t+\beta t^{2}\) in order that it should satisfy Eq. (27). Since we are considering very early times in this discussion we readily see that, while taking the first derivative, the term linear in time does not contribute. Hence using this ansatz in the above equation we readily obtain

$$\begin{aligned} r(t)&= r_{0}-\sqrt{\frac{\rho _\mathrm{vis}}{12M^{3}k\pi ^{2}}} \left( 1-\Omega _{c}^{2}\right) t\nonumber \\&- \left\{ \frac{\left( 1-\Omega _{c}^{2}\right) \left( 2-\Omega _{c}^{2}\right) \rho _\mathrm{vis}}{48 M^{3}\pi }\right\} t^{2}. \end{aligned}$$
(36)

From Eq. (36) it might appear that it is not compatible with Eq. (31), however, we should note that Eq. (30) has been obtained on the ground that all terms that contain \(t\) have been neglected, which is justified for the small time scale we are working with (this is the motivation for introducing small time approximation in this work). Hence the second term in Eq. (36) has no influence on the previous expression.

Further to see that the coefficient of \(t^{2}\) in Eq. (36) should be sub-leading, we use the time derivative of the radion field to get

$$\begin{aligned} \frac{\left( 1-\Omega _{c}^{2}\right) \left( 2-\Omega _{c}^{2}\right) \rho _\mathrm{vis}}{48 M^{3}\pi }\times 2t \ll \sqrt{\frac{\rho _\mathrm{vis}}{12M^{3}k\pi ^{2}}} \left( 1-\Omega _{c}^{2}\right) .\nonumber \\ \end{aligned}$$
(37)

The above inequality can be simplified further using Eq. (35) leading to \(t\ll \Omega _{c}^{2}t_\mathrm{valid}\). Since \(\Omega _{c}^{2}\) is already very small this translates into \(t\ll t_\mathrm{valid}\). Hence the small time approximation makes the \(t^{2}\) term sub-leading.

Thus the radion field decreasing with time triggers the inflation which takes over the brane, in complete agreement with recent theoretical and experimental observations [29]. We should also mention in this context that the inflation can be thought to be driven by the potential generated by the bulk scalar field which stabilizes the radion field as described in the next section. As the radion field runs to its stabilized value, the bulk scalar also goes toward the minima of the potential and thus triggers the inflation. As the radion field gets stabilized the bulk scalar resides at the minima of the potential halting the inflation. Then the evolution of the radion field could be given by Eq. (36).

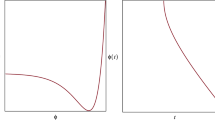
One thing has to be mentioned in this context: in inflation an important parameter is the slow-roll parameter determining the departure from the exponential expansion. In an ideal situation the slow-roll parameter should vanish. In general for all inflationary scenario (with very few exceptions) the slow-roll parameter is negligible. In general the slow-roll parameter is defined by \(\eta _{H}=-\ddot{H}/2H\dot{H}\), which for our case leads to \(\frac{\dddot{r}}{\ddot{r}\dot{r}}\frac{1-\Omega _{c}^{2}}{2k\pi \Omega _{c}^{2}}\). This exactly vanishes for our radion field evolution given by Eq. (36). However, from Fig. 1 it is clear that there is a very tiny difference between the theoretical curve and the numerical curve, suggesting that even if the \(\dddot{r}\) term exists it would be extremely small and hence the slow-roll parameter would satisfy \(\eta _{H}\ll 1\).

Fig. 1
figure 1

The coupled differential equations (26) and (27) have no exact analytical solutions. However, they can be evaluated numerically. In this figure we compare the numerical solution regarding the evolution of the radion field with the theoretical solution as presented in Eq. (36). We have scaled the time unit such that the inflationary time scale becomes equivalent to the range \([0,1]\), which is accomplished by dividing time \(t\) by \(\Delta t\) from Eq. (35). Also the radion field is normalized with respect to \(r_{0}\), which is also in the Planck scale. Along with that, we also present the numerical evolution of the scale factor compared to the theoretical one presented through Eq. (33) with the dotted one being the theoretical solution and the solid line representing the numerical solution. Note that both scale factors show an e-folding of order 60, as desired. The good match between these two curves in respective units shows the validity of our result and the justification of using the small time approximation

Full size image

Thus after the inflationary phase is over, the radion field would have some small value with which it will remain forever. Hence we have considered Einstein’s equation with a specific form for the metric ansatz, which is particularly suitable for examining the scale factor variation with time. We have considered the dynamics of the radion field, showing that the radion field gets evolved by the energy density on the visible brane; this in turn makes the scale factor develop. However, as the radion field gets stabilized and decreases in value at late times, the scale factor variation will be governed by the energy density alone, leading to standard cosmology. In order to get that particular value in terms of the physical parameters of our system we need to find a stabilization mechanism, which we will address next.

3 Dynamics of radion stabilization

For the scenario as depicted in the work of Randall and Sundrum (see [18]), the radion field is associated with the vacuum expectation value (VEV) of a four-dimensional massless scalar field that has zero potential, and its VEV is not determined by the dynamics of the model. Thus it was necessary to determine the mechanism to stabilize the radion field. This work was done by Goldberger and Wise (see [29]) for a time independent radion field, using a bulk scalar field with the interaction term localized on 3-branes. Hence the derivation was completely classical. They have taken the bulk scalar field \(\Phi \) to depend on the extra space dimension \(\phi \) and have obtained \(kr_{c}\sim 12\) without any fine tuning of the parameters.

In the context of string theory where one encounters several moduli, such a stabilization has been addressed by the presence of various antisymmetric tensor fields in the bulk space-time. In particular, the Klebanov–Strassler throat geometry with a \(D_{3}\)–\(D_{7}\) brane configuration has a close resemblance with the warped geometry and can be stabilized by 3-form fluxes [46, 47]. All geometric moduli can thus be classically stabilized by the field strengths of various form fields. In Type IIA theory, AdS4 vacua can be realized in terms of branes, which provides us with solutions between AdS4 and four-dimensional Minkowski space-time, inducing transitions between different vacua. An interesting aspect of the Type II theory is that they are also dynamically unstable in the moduli sector. This represents the fact that the scale of the internal space can be fixed for a quite long time in a region with a large warp factor [48–50]. Here, in an effort to capture the dynamics of moduli stabilization mechanism in a braneworld scenario, we present a simple time dependent generalization of the Goldberger–Wise mechanism with a scalar field in the bulk. Using a time dependent bulk scalar field we have addressed the dynamics of moduli stabilization to determine the evolution of the modulus to its stable value, which also resolves the gauge hierarchy problem. We further relate this dynamical stabilization with the inflationary model of the universe.

The total action for the time dependent scalar field is given by

$$\begin{aligned} S_\mathrm{bulk}=\frac{1}{2}\int d^{4}x \int _{-\pi }^{\pi } d\phi \sqrt{-G} \left[ G^{AB}\partial _{A}\Phi \partial _{B} \Phi + m^{2} \Phi ^{2}\right] \nonumber \\ \end{aligned}$$
(38)

where \(G_{AB}\) with \(A,B=\mu , \phi \) is given by Eq. (2). We also include the interaction terms on the hidden and visible branes (at \(\phi =0\) and \(\phi =\pi \), respectively) as

$$\begin{aligned} S_\mathrm{planck}=\int d^{4}x \int _{-\pi }^{\pi } d\phi \sqrt{-g_{h}}\lambda _{h} \left[ \Phi ^{2}-V_{h}^{2} \right] ^{2}\delta (\phi - 0)\nonumber \\ \end{aligned}$$
(39)

and

$$\begin{aligned} S_\mathrm{visible}=\int d^{4}x \int _{-\pi }^{\pi } d\phi \sqrt{-g_{v}}\lambda _{v} \left[ \Phi ^{2}-V_{v}^{2} \right] ^{2}\delta (\phi - \pi )\nonumber \\ \end{aligned}$$
(40)

where \(g_{h}\) and \(g_{v}\) are the determinants of the induced metric on the hidden and visible branes, respectively. \(\Phi (\phi ,t)\) can be determined by solving the following differential equation:

$$\begin{aligned} 0&= -\frac{\partial }{\partial \phi } \left[ \frac{e^{-4A}a^{3}}{r} \partial _{\phi } \Phi \right] + \frac{\partial }{\partial t} \left[ e^{-2A}a^{3}r \partial _{t}\Phi \right] \nonumber \\&+m^{2}e^{-4A}a^{3}r\Phi +4e^{-4A}a^{3}\lambda _{h}\Phi \left( \Phi ^{2}-V_{h}^{2} \right) \delta (\phi )\nonumber \\&+4e^{-4A}a^{3}\lambda _{v}\Phi \left( \Phi ^{2}-V_{v}^{2} \right) \delta (\phi - \pi ). \end{aligned}$$
(41)

Choosing the solution as

$$\begin{aligned} \Phi (\phi ,t)=T(t)e^{2A\left( \phi ,t\right) }\!\left[ \!X(t)e^{\nu A\left( \phi ,t\right) }+Y(t)e^{-\nu A\left( \phi ,t\right) } \right] \end{aligned}$$
(42)

where \(A\left( \phi ,t\right) =k\mid \phi \mid r(t)\). Then the time dependent part of the differential equation reduces to

$$\begin{aligned}&\!\!\!a^{3}r\left[ e^{\nu A}\left\{ TX_{t}+X\left( T_{t}+(2+\nu )TA_{t}\right) \right\} \right. \nonumber \\&\left. +\,e^{-\nu A}\left\{ TY_{t}+ Y\left( T_{t}+(2-\nu )TA_{t}\right) \right\} \right] =C(\phi ) \end{aligned}$$
(43)

where \(X_{t}\), \(Y_{t}\), \(A_{t}\), and \(T_{t}\) denote time derivatives of the respective functions \(x\), \(Y\), \(A\), and \(T\). \(C(\phi )\) is a \(\phi \) dependent integration constant. The ansatz for the variables \(X(t)\) and \(Y(t)\) is given by

$$\begin{aligned}&\!\!\!X(t)=v_{v}e^{-(2+\nu )k\pi r(t)}-v_{h}e^{-2\nu k\pi r(t)} \nonumber \\&\!\!\!Y(t)=v_{h}\left( 1+e^{-2\nu k\pi r(t)}\right) -v_{v}e^{-(2+\nu )k\pi r(t)}. \end{aligned}$$
(44)

This choice is motivated by the Goldberger–Wise stabilization mechanism, where these two functions \(X\) and \(Y\) were time independent. We have taken this choice so that our solution can be mapped to the GW solution for a time independent radion field scenario quite easily. With this choice we can determine the two quantities \(v_{v}\) and \(v_{h}\) giving the respective boundary conditions,

$$\begin{aligned} \Phi (0,t)=T(t)v_{h},\nonumber \\ \Phi (\pi ,t)=T(t)v_{v}. \end{aligned}$$
(45)

The above expression now brings out the physical meaning of the function \(T(t)\). The function represents the departure of the GW solution due to the inclusion of a time dependence to the radion field. It also determines the scalar field values at the boundary points. Using the forms of \(X(t)\) and \(Y(t)\) from Eq. (44) and the form of \(a(t)\) and \(r(t)\) from Eqs. (33) and (31), the function \(T(t)\) is determined as \(T(t) \propto \left( 1-e^{-2\kappa t}\right) \). Thus we see that at large times our solution reduces to that of the Goldberger and Wise solution. Finally, solving for the potential and then minimizing it, we readily obtain

$$\begin{aligned} r(t)=\left( \frac{4}{\pi }\right) \frac{k^{2}}{m^{2}}\ln \left( \frac{v_{h}}{v_{v}}\right) + \mathcal {O} \left( e^{-2\kappa t}\right) . \end{aligned}$$
(46)

Hence the radion field has the same stabilized value as predicted by Goldberger and Wise [29], with an extra correction factor which decays exponentially with time and decreases to such a small value that the first term only contributes to the stabilized value for the radion field. Hence the time dependent radion field can be stabilized by introducing a time dependent scalar field in the bulk. By minimizing the potential due to the scalar field we readily obtain the stabilized value, which is exactly the GW value at late times. Due to this stabilization, the cosmic evolution exits from inflation and follows standard cosmology at late times.

4 Discussion

In this work we have generalized the RS model for a time dependent radion field and have studied the dynamics of the moduli. The constraint between matter energy density in the visible and the hidden branes appears as a consequence of requiring a static solution without stabilizing it. This constraint never appears in a dynamical theory as considered in this work. We have further considered the evolution of the scale factor as determined from the evolution of the radion field, which in turn is determined by the energy density on the visible brane. The equivalence of this approach with covariant curvature formalism has also been addressed. We have then shown that the inflationary epoch can be connected with the radion field getting compactified and stabilized at a small value. Thus, according to our model this decrease of the moduli can trigger the inflation in the visible brane. This seems a very natural and interesting scenario for inflation on the visible brane in the RS brane world. Also note that the evolution of the scale factor or the radion field is never affected by the bulk cosmological constant, which is due to the reason that in RS model there is a fine tuning between the brane tension and the bulk cosmological constant. This also emerges quite naturally from our calculations. In order to explain the exit from inflation we need to know the stabilization of the dynamical radion field. For this purpose we have discussed how this radion field gets stabilized to the value obtained by Goldberger and Wise by introducing a time dependent bulk scalar field. The dynamics of the moduli can be determined by working out the potential for this time dependent bulk scalar field and then, through the potential, we could determine the stabilized value of bulk scalar field, which coincides with the GW value. This shows that the method of Goldberger and Wise works for the time dependent case as well, which we have generalized from their original time independent scenario. The time dependent part appears to decrease exponentially with time and thus have no relevance in the present epoch. This in turn explains how the issue of the gauge hierarchy problem in connection with the mass of the Higgs boson in the standard model can also be resolved in such a warped geometry model where the radion field needs to be stabilized at a small value, \(\sim \) inverse Planck length, as required by the RS model.