1 Introduction

In the previous studies, the author proposes the payoff-difference-based probabilistic peer-punishment [1, 2] with the characteristic that the greater difference in payoff induces the more punishment on the opponent. The proposed peer-punishment effectively increases the number of cooperators and the average payoff of all players in various ranges of parameters. The mechanism of the proposed peer-punishment prevents antisocial punishment like retaliation of a defector on a cooperator. In addition, when introducing the coevolutionary mechanism that not only the strategy of players but also the connection between players changes according to the preference of players, such mechanism further improves the promotive effect of the proposed peer-punishment on the evolution of cooperation [3]. As a relevant study of the payoff-difference-based probabilistic peer-punishment [1, 2], Chaudhuri [4] shows that conditional cooperators whose contributions to the public good are positively correlated with their beliefs regarding the average group contribution are often able to sustain high contributions to the public good through costly monetary punishment of free-riders.

We can find other punishment-related studies as follows. Perc and Szolnoki [5] propose adaptive punishment that a player is able to change his/her degree to punish another player in relation to the degree of success of cooperation and show that such punishment facilitates the reciprocity based on spatial connections between players and as a result enhances cooperation. Szolnoki and Perc [6] consider the conditional punishment that is proportional to the number of other conditional and unconditional punishers within the group. Perc and Szolnoki [7] introduce the implicated punishment that has a fixed working probability p (0 \(<p<\) 1) and includes the peer-punishment on defectors with a fixed probability q (0 \(<q<\) 1). Szolnoki et al. [8] study the impact of pool-punishment in the spatial public goods game with cooperators, defectors and pool-punishers as the three competing strategies. Chen et al. [9] introduce static class-specific probabilities of punishment that is based on the fixed number of classes. Szolnoki and Perc [10] show that antisocial punishment does not deter public cooperation when the synergistic effects are high, while such punishment is viable when the synergistic effects are low, but only if the cost-to-fine ratio is low. Chen and Szolnoki [11] consider the common resource as a dynamically renewable system that is also influenced by a co-evolutionary system where both strategy and resource are subject to change.

In contrast to the preceding argument, as described in the discussion of the previous study [3], reward as well as punishment is considered to be a mechanism promoting cooperation. Many studies have discussed the effect of reward in the public goods game, a multiplayer version of the prisoner’s dilemma game. There is still room for argument regarding whether reward or punishment is superior in promoting the evolution of cooperation. The seminal study of punishment and reward by Sigmund et al. [12] and the review of punishment and reward by Sigmund [13] show that punishment is more effective than reward. On the other hand, studies related to antisocial punishment [14, 15] and reward [16] show that the effect of punishment on the increase of cooperators and social utility is questionable. In addition, some studies describe that reward is as effective as punishment in maintaining cooperation and realizes higher payoff than punishment without the loss in reputation [17] and the fear of retaliation [18]. Szolnoki and Perc [19] introduce the rewarding cooperators in addition to the traditional cooperators and defectors and show that the reward can promote cooperation, especially if the synergistic effects of cooperation are low. They also mention that moderate reward may promote cooperation better than high reward, which is due to the spontaneous emergence of cyclic dominance between the three strategies.

In addition to those studies, Szolnoki and Perc [20] compare the reward for successful cooperation (adaptive rewarding) with the punishment for successful cooperation (adaptive punishment) and show that the adaptive rewarding can solve the second-order free-rider problem whereas such rewarding hinders network reciprocity. Szolnoki and Perc [21] consider the players of four types, i.e. a defector (D), a cooperator who punishes a defector (P), a cooperator who rewards a cooperator (R), and a cooperator who punishes a defector and rewards a cooperator (B), and show that the combination of reward and punishment does not exceed either reward or punishment alone in the range of realistic parameters. They also show that punishment is basically more effective than reward, however, when reward is given only to those who give reward rather than all cooperators, reward is more effective than punishment. On the other hand, studies introducing the mechanism of switching from reward to punishment based on the evolution of cooperation [22, 23] show that such combination leads to better results. Hilbe and Sigmund [22] regard the reputation of the player that consists of the past history of his/her behaviour as credit, and when every player first gives reward and then switches to punishment depending on the reputation, he/she creates a cooperative society. Chen et al. [23] also describe that the switching mechanism from first reward to punishment realizes the complete cooperation and the recovery to that state at a lower cost than either reward or punishment alone regarding both the well-mixed population where n players are randomly selected to form a group and the spatial population of the \(N\times N\) 2D lattice of periodic boundary conditions.

Regarding probabilistic and conditional rewarding mechanisms, Han and Tran-Thanh [24] have analysed cost-efficient institutional rewarding in the context of finite population setting, and for one-shot prisoner’s dilemma. Han et al. [25] also study cost-efficient institutional rewarding strategies in square-lattice networks, showing that local properties in neighbourhood play an important role to achieve cost-efficient incentivisation. In addition, Cimpeanu et al. [26] study cost-efficient rewarding strategies in the context of heterogenous networks, showing interference in these types of networks is much more difficult than in homogenous networks. Chen et al. [27] show how the cost of peer-punishment can be shared in a probabilistic way to improve cooperation. Moreover, Han and Lenaerts [28] study probabilistic peer-incentive different from this study, i.e. incentive or punishment is not performed alone and is combined with the so-called commitment mechanism, which complements punishment.

Fig.~ 3
figure 1

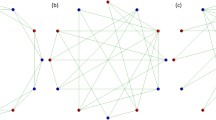
Three panels a, b, and c represent the three types of topology of connections in the case of \(\langle k \rangle =4\): a regular, b random, and c scale-free. Each topology is defined by a one-dimensional lattice of periodic boundary conditions, and each vertex represents each player. Defectors are shown in red, and cooperators are shown in blue. Note that the number of players (N) is not 1000 but 20 to make each topology easy to understand

Full size image

In addition to those studies regarding punishment and reward, we can consider network reciprocity (spatially structured population) [29,30,31,32,33,34,35,36,37,38] as another rule for the evolution of cooperation [39]. For example, Fort and Sicardi [36] show that even if utilizing simple Markovian or one step conditional strategies (like TFT or Pavlov), a system with network reciprocity can escape from Nash equilibrium. Perc and Szolnoki [37] review studies of evolutionary game introducing coevolutionary rules and describe that such rules facilitate the effects of spatial structure or heterogeneity on cooperation. Szabó and Fáth [38] study three prominent classes of game on graphs, i.e. the prisoner’s dilemma, rock–scissors–paper game, and competing associations, and give detailed description of each dynamics from the aspect of non-equilibrium statistical physics.

Based on the discussion of those existing studies, this study newly introduces the payoff-difference-based probabilistic reward. Although the probability of punishing a defector in the proposed peer-punishment [1,2,3] increases as the difference of payoff between a player and a defector becomes large, the probability of rewarding a cooperator in the reward of this study increases as the difference of payoff between a player and a cooperator increases. This study employs the framework of the spatial prisoner’s dilemma game of the previous studies [1, 2] and shows that the reward of this study realizes the evolution of cooperation except some cases.

2 Model

As mentioned in the introduction, the framework of the spatial prisoner’s dilemma game of this study is basically the same as the previous study [1, 2] except the mechanism of punishment. This study employs the three types of topology of connections between players: (a) regular [40], (b) random [40], and (c) scale-free (Barabási-Albert model [41]). Each topology is defined by a one-dimensional lattice of periodic boundary conditions, and each vertex represents each player. The number of players N equals 1000, the degree of player i (the number of connections) is k(i), and the average value of k(i) (\( \langle k \rangle \)) is represented by \(\langle k \rangle =\frac{1}{N}\sum \nolimits _{1\,\,\le i\,\le N} {k\left( i \right) } \). Methods of the previous study [1] detail how to build each topology. Figure 1 illustrates the three types of topology of connections regarding the case of \(\langle k \rangle =4\). Note that N is not 1000 but 20 to make each topology easy to understand in Fig. 1.

The strategy of player i (s(i)) is expressed by (0 1) for a defector and (1 0) for a cooperator utilizing a unit vector. Player i plays the prisoner’s dilemma games with other connected players and gains the total payoff P(i) for all games. When N is the number of players, the opposing player of player i is player j (\(i\ne j\), 1 \(\,\le i\), \(j\,\le N)\), and the strategy and the payoff of player j are s(j) and P(j), respectively, P(i) is expressed by the following Eq. (1) utilizing the payoff matrix A. O(i) is a set of the opposing players that are connected with player i. The payoff matrix of this study follows the one introduced by Nowak and May [29]. In this study, cooperation is difficult to evolve because the temptation of defect (b) equals 1.5, and the payoff of every player is not normalized by him/her number of connections, i.e. a player with many connections will have large payoff.

$$\begin{aligned} \begin{array}{l} P\left( i \right) =\sum \limits _{j\in O\left( i \right) } {s\left( i \right) } As\left( j \right) ^{T} \\ \left( {i\ne j,1\,\le i, j\,\le N} \right) \\ \end{array}, A=\left( {{\begin{array}{*{20}c} 1 &{} 0 \\ b &{} 0 \\ \end{array} }} \right) \left( {1<b\,\le 2} \right) .\nonumber \\ \end{aligned}$$
(1)

Player i compares his/her payoff P(i) with the payoff of his/her opposing player P(j), and when the following conditions of \(s(j)=(1 \,\,0)\) (cooperator), P(i)(1-tn\(_{r}(i))>\) 0, and \(P(j)<P(i)\,\le \)2P(j) hold, player i gives the reward tP(i) to player j at the expense of his/her payoff by tP(i) as shown in the following Eq. (2) with the probability \(u_{i}(j)\) expressed by the following Eq. (3), where t (0\(\,\le t\,\le \)1) is the coefficient of reward, and \(n_{r}(i)\) is the number of players \(j\in O(i)\) satisfying both conditions of \(P(j)<P(i)\) and \(s(j)=(1\,\,0)\). When the following conditions of \(s(j)=(1\,\,0)\) (cooperator), P(i)(1-tn\(_{r}(i))>\) 0, and 2\(P(j)<P(i)\) hold, \(u_{i}(j)\) equals 1. The decrease in the payoff of players due to rewarding the opposing cooperators and the increase in the payoff of cooperators due to being rewarded by the opposing players are calculated independently for each player, and P(i)’ and P(j)’ are never negative values because the payoff of a player is set to 0 when it becomes negative. The reward of this study does not function when t equals 0 and 1 because tP(i) equals 0 in the case of \(t=0\), and P(i)(1-tn\(_{r}(i))>0\) does not hold in the case of \(t=1\).

$$\begin{aligned} \begin{array}{l} P\left( i \right) '=P\left( i \right) -tP\left( i \right) \\ P\left( j \right) '=P\left( j \right) +tP\left( i \right) \\ \end{array} \end{aligned}$$
(2)
$$\begin{aligned} u_{i} \left( j \right) =\frac{P\left( i \right) -P\left( j \right) }{P\left( j \right) }, P\left( j \right) >0. \end{aligned}$$
(3)

The difference of the working mechanism between the coefficient of reward (t) and that of punishment (r) in the previous studies [1,2,3] is as follows. When the coefficient of reward (t) is small, although the reward to every player is a little, all players can reward more players than the case of large t. Conversely, in the case of large t, all players can reward only a few players although the reward to every player is large. On the contrary, when the coefficient of reward (r) is small, although the punishment to every player is weak, all players can punish more players than the case of large r. Conversely, in the case of large r, all players can punish only a few players although the punishment to every player is strong.

After players reward the opposing cooperators, and cooperators are rewarded by the opposing players, as shown in the following Eq. (4), player i adopts the strategy of player \(j_\mathrm{max}\in i\cup O(i)\) for his/her strategy of the matches of the next generation. When there is more than one player with the same maximum payoff, player i randomly chooses his/her strategy of the matches of the next generation from the strategy of those players. This process of adopting new strategy takes place simultaneously for all players. This study defines (1) all matches of the prisoner’s dilemma game, (2) all actions of rewarding the opposing cooperators and being rewarded by the opposing players, and (3) adoption of new strategy by all players as one generation, and each simulation run continues until the number of generations reaches 600 to obtain stable results. The ratio of defectors to cooperators in the initial state is approximately 1:1, and defectors and cooperators are randomly distributed in each simulation run. The results shown below are the average of 20 simulation runs and have error bars indicating the standard deviation if necessary.

$$\begin{aligned} s\left( i \right) ^{'}=s\left( {j_{\max } } \right) j_{\max } \in i\cup O\left( i \right) \nonumber \\ P\left( {j_{\max } } \right) ^{'}=\max \left( {P^{'}\in i\cup O\left( i \right) } \right) . \end{aligned}$$
(4)

3 Results

The author describes the results regarding the regular, random, and scale-free topology of connections of \(\langle k \rangle =\,\,\)4 (left panels of Fig. 2) and \(\langle k \rangle = 8\) (right panels of Fig. 2). Regarding the regular topology of connections, in both cases of \(\langle k \rangle = 4\), 8, the proportion of cooperators and the average payoff of all players stably increase in the range of 0.05\(\,\le t\,\le 0.95\) (Fig. 2a, b). In the case of \(\langle k \rangle = 4\), although the proportion of cooperators increases when t equals 0 and 1 (i.e. the reward of this study does not work), the proportion of cooperators and that of defectors vary widely as indicated by the error ranges. On the other hand, because the error ranges of the proportion of cooperators and that of defectors are quite small in the range of 0.05\(\,\le t\,\le \)0.95 (i.e. when the reward of this study works), it is obvious that the proportion of cooperators and the average payoff of all players stably increase by the reward of this study. The author explains the reason why the proportion of cooperators temporarily decreases in the range of 0.3\(\,\le t\,\le 0.35\) in the regular topology of connections of \(\langle k \rangle = 4\) in the following discussion.

Regarding the random topology of connections, in the case of \(\langle k \rangle = 4\), almost all players become cooperators when t equals 0.1 and 0.15, and approximately 85% (\(t= 0.2\)) and roughly 70% (0.25\(\,\le t\,\le 0.95\)) of players become cooperators (Fig. 2c). Because only around 40–45% of players become cooperators when t equals 0 and 1 (i.e. the reward of this study does not work), the proportion of cooperators and the average payoff of all players obviously increase by the reward of this study. On the other hand, in the case of \(\langle k \rangle = 8\), the proportion of cooperators and the average payoff of all players increase only when t equals 0.1 (Fig. 2d). Approximately 30% of players become cooperators when t equals 0.15, and the proportion of cooperators and that of defectors in the range of 0.2\(\,\le t\,\le 0.95\) are roughly equal to the values when t equals 0 and 1 (i.e. the reward of this study does not work) whereas there are some fluctuations. Therefore, regarding the random topology of connections of \(\langle k \rangle = 8\), the range of t where the proportion of cooperators and the average payoff of all players increase by the reward of this study is limited.

Regarding the scale-free topology of connections, the proportion of cooperators and the average payoff of all players stably increase by the reward of this study except in the ranges of 0.15\(\,\le t\,\le 0.45\) (\(\langle k \rangle = 4\)) and 0.05\(\,\le t\,\le 0.4\) (\(\langle k \rangle = 8\)) (Fig. 2e, f). However, in such ranges of t (where the proportion of cooperators and the average payoff of all players do not increase), because the number of simulation runs that 95% or more players become defectors in the 600 generation (i.e. the number of defector-prevailing simulation runs) never exceeds 9 except in the case of \(\langle k \rangle = 8\) and \(t= 0.05\) (see scale-free results in Fig. 2g, h), the reward of this study effectively suppresses the increase of defectors. Figure 2g and h also shows that in any type of topology of connections, the reward of this study suppresses the number of defector-prevailing simulation runs to 0 in the range of 0.1\(\,\le t\,\le 0.95\). To sum up, the reward of this study stably increases the proportion of cooperators and the average payoff of all players except regarding the random topology of connections of \(\langle k \rangle = 8\) and the scale-free topology of connections in the ranges of 0.15\(\,\le t\,\le \)0.45 (\(\langle k \rangle = 4\)) and 0.05\(\,\le t\,\le 0.4\) (\(\langle k \rangle = 8\)).

Fig.~ 4
figure 2

This figure shows the results regarding the regular a, b, random c, d, and scale-free e, f topology of connections of \(\langle k \rangle = 4\) (left panels) and \(\langle k \rangle = 8\) (right panels). Those panels a–f show the dependence of the proportion of cooperators and that of defectors, and the average payoff of all players in the 600 generation on the coefficient of reward (t) (error bars: SD, standard deviation). Bottom two panels (g: \(\langle k \rangle = 4\), h: \(\langle k \rangle = 8\)) show the dependence of the number of simulation runs that 95% or more players become defectors in the 600 generation (i.e. the number of defector-prevailing simulation runs) on the coefficient of reward (t) regarding each topology of connections. Following the previous study [2], this study also considers that the evolution of cooperation emerges when the number of defector-prevailing simulation runs is 9 or less out of 20 simulation runs, otherwise defectors defeat cooperators

Full size image
Fig.~ 5
figure 3

This figure explains the reason why the lattice of the regular topology of connections of \(\langle k \rangle = 4\) does not achieve the fully cooperative state in the range of 0.3\(\,\le t\,\le \)0.35. In the range of 1/4 (\(= 0.25\)) \(<t<\) 3/8 (\(= 0.375\)), a defector (i) does not reward other cooperators and not become a cooperator from generation to generation because a defector expands into a cluster of five defectors (b), and then shrinks back to a defector (a). Except such range of t, a defector (i) rewards other cooperators and becomes a cooperator (\(t<\) 1/4 (\(= 0.25\))), or becomes a cooperator through a cluster of five defectors because two or more defectors in such cluster will remain defectors and then become cooperators (\(t =\,\) 1/4(\(=\,\)0.25), and 3/8 (\(= 0.375\)) \(\,\le t<\) 1.0)

Full size image

4 Discussion

The author explains the mechanism of the evolution of cooperation induced by the introduction of the reward of this study focusing on the value of t (the coefficient of reward) utilizing the lattice of the regular topology of connections of \(\langle k \rangle = 4\) and \(\langle k \rangle = 8\). When t is small, cooperation evolves because the clusters composed of four cooperators already in the lattice in the initial state are rewarded by adjacent defectors, and those defectors lose the advantage of their high payoff. When t exceeds a certain value, even a single cooperator surrounded by defectors becomes able to survive, and such cooperator generates a large cluster (five cooperators in \(\langle k \rangle = 4\) and nine cooperators in \(\langle k \rangle = 8\)) that leads to the evolution of cooperation. We can find that threshold value of t, 1/5 in \(\langle k \rangle = 4\) and 1/9 in \(\langle k \rangle = 8\), by calculating the expected value of the payoff of such cooperator and other defectors after probabilistically giving and receiving reward. Comparing both cases of \(\langle k \rangle = 4\) and 8, the threshold value of t is smaller, and the effect of facilitating the evolution of cooperation by the reward of this study is higher in the case of \(\langle k \rangle = 8\). In addition, the author also explains the reason why the proportion of cooperators temporarily decreases in the range of 0.3\(\,\le t\,\le \)0.35 in the regular topology of connections of \(\langle k \rangle = 4\). That is because a defector surrounded by cooperators does not eventually change into a cooperator, and therefore a few defectors always remain in the lattice in the range of 1/4 (\(= 0.25\)) \(<t<\) 3/8 (\(= 0.375\)) (see Fig. 3).

In the following, the author summarizes the mechanism of reward of previous studies and makes it clear that the reward of this study is a new mechanism not covered by existing studies, which has the probability of rewarding a cooperator proportional to the difference of payoff between a player and a cooperator. Sigmund [12] considers the rewarding as the strategy in place of punishment in the public goods game, having not dynamical but simple small probabilistic effect. Szolnoki and Perc [19] considers the public goods game on a square lattice with periodic boundary conditions, where initially each player on a site x is designated either as a cooperator, defector, or rewarding cooperator, with equal probability. Cooperators and rewarding cooperators not probabilistically but always receive the reward from every rewarding cooperator that is a member of the focal group, and every rewarding cooperator of that group also bears an additional cost.

The following studies [20,21,22,23,24,25,26,27] have some conditional mechanisms for rewarding cooperators, while such mechanisms are different from the mechanism of this study. In the adaptive rewarding by Szolnoki and Perc [20], players are more inclined to support cooperation by means of additional incentives if defectors are increasing in their group. Szolnoki and Perc [21], as well as Hilbe and Sigmund [22], consider a defector (to do nothing), a cooperator punishing defectors, a cooperator rewarding other cooperators, or a cooperator both punishing defectors and rewarding other cooperators with equal probability. Chen et al. [23] deal with a relative weight that determines the equally shared part among the cooperators and the remainder used for equally punishing the defectors in the group. Han and Tran-Thanh [24] consider the external decision-maker with a budget to reward cooperative population. Han et al. [25] introduce the classes of interference mechanisms based on the number of cooperators and the neighbourhood cooperation level. In addition to such classes, Cimpeanu et al. [26] present the class of interference mechanism based on the connectivity of the node in the network. Chen et al. [27] consider the system that a fraction of cooperators is selected randomly and designated as punishers, and they equally share the associated costs, respectively.

In this study, based on the discussion of existing studies regarding reward, the author introduces the new probabilistic reward based on the difference of payoff. The reward of this study has the mechanism that the greater the difference of payoff between a player and his/her opposing cooperator is, the higher the probability of rewarding his/her opposing cooperator becomes. The introduction of the reward of this study leads to the evolution of cooperation, especially in the regular and scale-free topology of connections. Comparing the reward of this study with the proposed peer-punishment [2], the proposed peer-punishment is superior to the reward of this study particularly in the case of the random topology of connections. On the contrary, in terms of the number of defector-prevailing simulation runs, the reward of this study sometimes shows better results than the proposed peer-punishment especially in the scale-free topology of connections of \(\langle k \rangle = 8\).

In future works, the author would like to consider the other rules (common knowledge of advice [42] and a simple exhortative message [43]) except punishment and reward. Common knowledge of advice [42] generates a process of social learning that leads to high contributions and less free-riding. This behaviour is sustained by advice that is generally exhortative, suggesting high contributions, which in turn creates optimistic beliefs among subjects regarding contributions of others. Chaudhuri et al. [42] suggest that socially connected communities may achieve high contributions to a public good even in the absence of punishment for norm violators. Chaudhuri and Paichayontvijit [43] show that a simple exhortative message appealing to goodwill of participants can achieve high rates of cooperation in social dilemmas played over many rounds, even in the absence of punishments for free-riding. As a further extension, based on the studies introducing the switching mechanism from reward to punishment depending on the evolution of cooperation [22, 23], the author considers the introduction of the combination of the reward of this study and the proposed peer-punishment. In addition, I would like to combine the reward of this study and the proposed peer-punishment with commitments like Han et al. [44] and examine that such combination would ensure even higher levels of cooperation.