Shell-model calculations for two-neutron transfer near the $N=20$ island of inversion

Abstract

We describe connections between shell-model calculation results and predictions for two-nucleon transfer reactions. Measurements of the $^{30}$Mg(t,p)$^{32}$Mg reaction were used to identify a low-lying shape-coexisting 0$^+$ state in $^{32}$Mg. Interpretations of those early, limited data were based on simple empirical models. The cross sections for two-nucleon transfer are, however, extremely sensitive to the details of the nuclear-structure. Motivated by the possibility of new high-resolution two-nucleon transfer measurements around the $N=20$ Island of Inversion, we have performed shell-model calculations wave functions for states in the nuclei $^{30,32}$Mg using the SDPF-M and SDPF-MU interactions, and from those calculations obtain the two-nucleon transfer amplitudes that we use to predict cross sections for the $^{28,30}$Mg(t,p)$^{30,32}$Mg reactions. The combined results show how the nuclear structure properties influence experimental observables for the (t,p) reaction. We compare our results with the existing data.

1 Introduction

Two-neutron transfer reactions have long been used as a probe of nuclear structure. They are particularly effective for studying pairing interactions, and have been key to identifying shape-coexisting $0^+$ states. Due to its selective nature two-neutron transfer is complementary to the single-neutron transfer transfer reactions used to study single-particle states. Simplest in its interpretation is the (t,p) reaction, where the two transferred neutrons from $^3$H are in a relative S = 0 state. The transfer cross sections are very sensitive to the detailed underlying nuclear structure, and have often been compared to the predictions of shell-model calculations either to test shell-model interactions, or to predict the results for experiments not yet carried out [1, 2]. A region of particular interest where two-neutron transfer measurements have ignited considerable interest is near $N=20$, where the diminished gap between the sd and fp shells leads to the well-known $N=20$ “Island of Inversion” (IoI). The importance of intruder configurations, cross-shell excitations and modified magic numbers for very neutron-rich nuclei in this region is by now very robustly understood [3,4,5].

Great interest is focused on the nucleus $^{32}$Mg, where mass measurements provided the first indications of intruder structure around $^{32}$Mg [6]. Later, neutron-knockout studies [7] demonstrated significant fp-shell content in the ground state of $^{32}$Mg, approximately three-times that of the nearby $^{30}$Mg. A combination of Coulomb-excitation [8, 9] and proton-scattering measurements [10] suggested a deformed ground state dominated by fp-shell configurations and the predominance of multi-particle multi-hole neutron excitations, where holes and particles are referred to relative to the sd shell. Very recent measurements of neutron and proton knockout, from $^{33}$Mg and $^{34}$Si [11] extended the spectroscopy of $^{32}$Mg and provided comparisons of knockout spectroscopic factors with shell-model calculations. The positive-parity states interpreted as being built on the ground state were suggested to form a deformed rotational band with large contributions from 2p-2h and 4p-4h configurations.

A particularly impactful measurement was that of the $^{30}$Mg(t,p)$^{32}$Mg reaction at low energy in inverse kinematics [12]. That work reported a new low-lying ($E_X=1.022$ MeV) 0$^+$ state, interpreted in a shape-coexistence picture with an fp-shell dominated ground state, and the excited level being a predominantly sd-shell excitation. The low-lying $E_X=0.882$ MeV $2^+$ state was not observed. While [12] concluded that the results agreed with the conventional view that the ground state of $^{32}$Mg was intruder dominated, other empirical analyses of those data suggested otherwise. Fortune, in a two-state mixing model, found that the relative ground-state and excited state cross sections were consistent with the ground state being sd-shell dominated [13, 14]. A different analysis by Lay et al., using the Distorted-Wave Born Approximation (DWBA) to calculate the (t,p) cross section based on empirical transfer amplitudes came to a similar conclusion [15].

Macchiavelli et al. offered a solution to this puzzle by introducing a third $0^+$ state. Using a three-state mixing analysis, they concluded that the ground- and first-excited states were fp-shell dominated, with mixtures of 2p-2h and 4p-4h configurations. The third 0$^+$ level was suggested to be predominantly 0p-0h  [16, 17]. The analysis suggested that the third $0^+$ state would be weakly populated in (t,p); the low bombarding energy used in [12] may have precluded its observation regardless of the nuclear structure. No other information is available about other excited states in $^{32}$Mg through two-neutron transfer.

Further information about $^{32}$Mg was provided by recent studies of the isomeric decay of the $0^+_2$ state [18], which suggested that this level was as collective as the ground state, perhaps in agreement with the analysis of Macchiavelli et al. Elder et al. raised the question of where exactly was the sd-shell dominated excitation located in $^{32}$Mg. The $0^+_3$ excitation postulated by Macchiavelli et al. remains unobserved, although recent knockout-reaction measurements of Kitamura et al. [11] have provided possible tentative indications of excited $0^+$ states above 2 MeV excitation energy.

An approach that has not yet been applied to $^{30}$Mg(t,p)$^{32}$Mg is one demonstrated by Bayman et al., who used shell-model calculations to predict cross sections for (t,p) and (p,t) reactions with neutron-rich Sn isotopes [2]. They calculated wave functions, two-neutron transfer amplitudes and cross sections. Bayman et al. reported results not only for $0^+$ states, but higher-spin excitations, illustrating how those observables provide important additional points of comparison between theory and experiment. Here, we employ a similar method, using shell-model calculations to calculate wave functions, transfer amplitudes, and cross sections for (t,p) reactions on neutron-rich Mg isotopes.

Also of interest is $^{30}$Mg, in the transitional region leading to the $N=20$ IoI. More is known about $^{30}$Mg, which has been studied with a combination of beta decay [19,20,21], neutron-knockout [7] and fusion-evaporation reactions [22]. While the ground state is not expected to contain as much fp-shell strength as $^{32}$Mg, the neutron-knockout studies [7] indicated that intruder content does exist, approximately a third of that seen in the $^{32}$Mg ground state. Furthermore, the fusion-evaporation measurements of Deacon et al. [22] suggested significant strength for excitations outside the sd shell at higher spin. In $^{30}$Mg, 2p-2h fp-shell strength was also suggested in the first-excited $0^+$ state from a study of the E0 transition to the ground state [21]. Differences between $^{28}$Mg($t,p)^{30}$Mg and $^{30}$Mg($t,p)^{32}$Mg probe changes in nuclear structure in the transition from stability to the IoI. For example, a study of the $^{26}$Mg($t,p)^{28}$Mg two-neutron transfer reaction has identified the intruder-dominated second-excited $0^+$ state of $^{28}$Mg [23].

In this paper, we follow the approach of [2] and use shell-model calculations to calculate wave functions for $^{28,30,32}$Mg and the transfer amplitudes relevant for studies of (t, p) reactions. Those amplitudes inform DWBA calculations of the transfer cross sections. We first present an overview of the theory, then present shell-model results, comparing the nuclear structure of selected states in $^{30,32}$Mg obtained with the two interactions. We then apply the results of those calculations to reaction-model calculations for $^{28}$Mg$(t,p)^{30}$Mg and $^{30}$Mg$(t,p)^{32}$Mg. Our chief aim is to illustrate in detail how differences in nuclear structure in this region lead to differences in the experimental observables, and where possible, compare the results to prior measurements and analyses.

2 Theory

Both nuclear-structure and nuclear-reaction information are necessary to predict cross sections for two-neutron transfer reactions. We performed shell-model calculations using the SDPF-M [24] and SDPF-MU [25] interactions to produce the wave functions for states in $^{28,30,32}$Mg. Other choices of shell-model interaction, for example the SDPF-U-MIX interaction from Caurier et al. [5], the EKK interaction of Tsunoda et al. [26], or modern chiral-based interactions such as that of Coraggio et al. [27] may yield different results.

The two-neutron transfer cross section is obtained using a Distorted-Wave Born Approximation (DWBA) calculation, which requires, in addition to the optical-model parameters, the two-neutron transfer amplitudes (TNA) that describe the overlap between the final and initial states for the different possible two-neutron shell-model configurations. The connection between the nuclear structure and the reaction cross section is described by Glendenning [28] and can be expressed as:

$$\begin{aligned} \sigma (L,S,J,T) \propto \sum _M \left| \sum _N G_{NLSJT}B_{NL}^M(\textbf{k}_1,\textbf{k}_2)\right| ^2. \end{aligned}$$

(1)

The $G_{NLSJT}$ are the nuclear structure factors introduced by Glendenning; these are equivalent to the two-nucleon amplitudes (TNA) that give the magnitude and phase of each configuration N, and the different configurations combine coherently. Here L, S, J and T represent the quantum numbers characterizing the angular-momentum and isospin transfer. For one-step 2n transfer with the (t, p) reaction, T is 1 and S is 0. The quantity $B_{NL}^M$ is the DWBA transfer-reaction amplitude for the configuration NL that includes the form factor for the two neutrons in the appropriate orbitals.

2.1 Shell-model calculations

The shell-model calculations were performed using the code KSHELL [29] run on the University of Connecticut High-Performance Computing Facility. Calculations with the SDPF-MU interaction yielded reasonably good agreement with experiment for $^{28}$Mg and the $^{26}$Mg($t,p)^{28}$Mg reaction [23]. The SDPF-M interaction incorporates the sd shell, and the $0f_{7/2}$ and $1p_{3/2}$ orbitals, whereas SDPF-MU contains all orbitals in the sd and fp shells. For $^{32}$Mg, the full sd–fp model space is very large, with an m-scheme dimension of order 10$^{13}$ for four valence protons and twelve valence neutrons. To make the calculations tractable, we truncated the sd–fp shell model space by restricting the four valence protons to the sd shell, and allowing up to four neutrons in the $0f_{7/2}$ orbital. Preliminary calculations indicated that the $0f_{5/2}$ neutron occupancy was small, so that orbital was omitted from the calculations. For consistency, we truncated the SDPF-M model space in a simlar way, with protons confined to the sd shell, and no more than four neutrons in the $0f_{7/2}$ orbital.

We focused on the specific properties of the four lowest $0^+$ and $2^+$ states, as well as for the lowest $(1,3,5)^-$ excitations. We extracted detailed information on the wave functions, and obtained the TNA necessary for predicting the two-neutron transfer cross sections. In our detailed analysis of the results, we are concerned primarily with the behavior of the neutrons, and sum over the different possible sd-shell proton configurations.

2.2 DWBA calculations

The DWBA calculations were done with the zero-range code DWUCK4 [30]. We assume a direct one-step two-neutron transfer mechanism, neglecting multi-step processes. For spin-zero targets, that assumption restricts the possible final states to those with natural parity. We used a bombarding energy of 6 AMeV, and optical-model parameters for protons and tritons were taken from the global analyses of Refs. [31, 32], respecitvely. Some optical-model parameters, and the neutron binding energy used in the form-factor calculation, depend on the excitation energy. When available, we use the experimental excitation energies, however for states with no clear experimental counterpart we used the excitation energies obtained from the shell-model calculations. The optical-model parameter dependence is small, and the nuclear-structure contribution is more important and has the largest effect on the calculated reaction yields. The total reaction form factor is comprised of interfering form factors for each two-neutron configuration, whose strength and phase are determined by the TNA. The form factors are calculated assuming two neutrons bound in a Woods–Saxon well with the appropriate quantum numbers, and using the usual prescription for the binding energy equal to half the two-neutron separation energy for each neutron.

3 Results: shell-model calculations

In the truncated SDPF-MU (SDPF-M) model spaces there are a total of 5268 (1908) and 5100 (1776) possible proton-neutron configurations for positive-parity, and negative-parity states, respectively. Summing over proton configurations, there remain 439 (159) and 425 (148) different possible neutron configurations for positive-, and negative-parity states, respectively. To present these data, we create a unique index “C” for each possible neutron configuration based on the occupation numbers in the following way. In the sd–fp neutron space, we construct a seven digit number where each digit gives the number of particles in a particular orbital. For example, a configuration in $^{32}$Mg that contains 4 $0d_{5/2}$, 2 $1s_{1/2}$, 0 $0d_{3/2}$, 2 $0f_{7/2}$, 0 $0f_{5/2}$, 2 $1p_{3/2}$, and 2 $1p_{1/2}$ neutrons is represented by $C=2202024$. For presentation we histogram the magnitude of each configuration versus the logarithm of its index Log$_{10}$C. Table 1 lists some of the typical neutron configurations found in positive-parity states in $^{30}$Mg and $^{32}$Mg.

Table 1 Labeling scheme for some typical strong neutron configurations for positive-parity states in $^{30,32}$Mg. The numbers in the seven left columns give the number of neutrons occupying each orbital, and “C” is the configuration label. See text for details

3.1 $^{30}$Mg

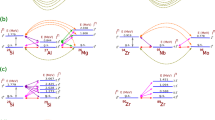
The neutron particle-hole content for the lowest four $0^+$, $2^+$ and $4^+$ states in $^{30}$Mg is shown in Fig. 1, with particles and holes referred to relative to the sd shell. For the $0^+$ states, both interactions produce an sd-shell dominated ground state, with the excited $0^+$ levels predominantly 2p-2h in agreement with the suggestions of [21]. For the $2^+$ and $4^+$ states, both interactions yield a series of alternating 2p-2h and 0p-0h dominated excitations, however the ordering of these differs between SDPF-MU and SDPF-M. Mixing between configurations is greater in the lowest two $2^+$ states with the SDPF-M interaction, and the $4^+$ states from SDPF-M are typically purer. Both interactions suggest very little 4p-4h content for any of these states in $^{30}$Mg, with only the $0^+_2$ state from SDPF-MU having more than a 5% contribution.

Fig. 1

Calculated particle-hole strengths versus excitation energy for positive-parity states in $^{30}$Mg. The black circles, red squares, and green triangles represent the lowest four $0^+$, $2^+$ and $4^+$ states, respectively

3.1.1 $0^+$ and $2^+$ States

Figure 2 shows the strengths of different configurations in the wave functions of the lowest four $0^+$ and $2^+$ states, plotted as a function of Log$_{10}$C. Results from the SDPF-MU interaction are shown as histograms, and the SDPF-M results appear as circles. The binning in these histograms highlights particular aspects of the configurations with very similar Log$_{10}$C values. For example, in Fig. 2a, the bar near Log$_{10}$C=3.3 represents the sum of strength for configurations with two $0f_{7/2}$ neutrons, with the other eight neutrons in different sd-shell orbitals, from the SDPF–MU interaction. In these and all similar figures, configurations with Log$_{10}$C greater than 3.0 contain at least one neutron in the fp shell.

The $0^+$ levels show a distinct evolution from a mainly sd-shell ground state to fp-shell dominated excited states. The strongest configuration in the ground state in both cases is $\nu (1s_{1/2})^2(0d_{3/2})^2(0d_{5/2})^6$ or (226) with more than half of the total strength with each interaction. There exists a non-negligible fp-shell occupancy of 30–40%, consistent with the analysis of [7]. The wave functions for the first-excited $0^+$ state contains are qualitatively similar for the two interactions, with large contributions from configurations containing two $0f_{7/2}$ neutrons, or one $0f_{7/2}$ and one $1p_{3/2}$ neutron. The $0^+_{3,4}$ excitations are rather different with the two interactions, with the $0^+_3$ state being very pure $(0f_{7/2})^2$ in SDPF-M whereas in SDPF-MU it is composed of a mixture of $(0d_{3/2})^2$, $(0f_{7/2})^2$, $(0f_{7/2}1p_{3/2})$ and $(1p_{3/2})^2$ configurations. The results for the $0^+_4$ level are also quite different, with a large $1s^2_{1/2}$ component from SDPF-MU that is absent in the fp-shell dominated SDPF-M state.

Fig. 2

Fraction of configurations C in wave functions of 0$^+$ (a, c, e, g) and 2$^+$ (b, d, f, h) states in $^{30}$Mg. Configurations with Log$_{10}$C greater than 3.0 contain fp-shell neutrons. The bars (circles) represent results from the SDPF-MU (SDPF-M) interactions

The two interactions produce different results for the $2^+$ excitations. With SDPF-MU, the wavefunctions for the $2^+_{1,2}$ states are similar to their $0^+$ counterparts. In contrast, with SDPF-M the $2^+_1$ wave function resembles that of the $0^+_2$ state, and vice-versa for the $2^+_2$ level. The $2^+_3$ excitations are also quite different, with a dominant $(0f_{7/2})^2$ component from SDPF-M that is much weaker in the mostly sd-shell SDPF-MU state. Interestingly, the wave function for the fourth $2^+$ excitation with SDPF-M resembles the third $2^+$ state from SDPF-MU.

3.1.2 Negative-parity states

Negative-parity states can be strongly populated in (t,p), as was seen in the $^{26}$Mg(t, p)$^{28}$Mg reaction. As the negative-parity levels must contain at least one neutron in the fp shell, they provide a complementary probe of the nuclear structure. Figure 3 shows the wave-functions for the lowest 1$^-$, 3$^-$ and 5$^-$ states in $^{30}$Mg. The two interactions produce somewhat different results. With SDPF-MU, the 1$^-_1$ state is mostly $1p_{3/2}$, whereas with SDPF-M it is more mixed between the $0f_{7/2}$ and $1p_{3/2}$ components. For the 3$^-_1$ level, both wave functions are strongly mixed, with SDPF-M having a larger $0f_{7/2}$ component. For the $5^-$ state, both interactions neccessarily give a $0f_{7/2}$ domintated excitation to produce the needed angular momentum.

Fig. 3

Fraction of configurations C in wave functions of the lowest $1^-$ (a), $3^-$ (b) and $5^-$ states in $^{30}$Mg. The bars (circles) represent results from the SDPF-MU (SDPF-M) interactions

3.2 $^{32}$Mg

Figure 4 shows the calculated particle-hole strengths of the $0^+$, $2^+$ and $4^+$ states in $^{32}$Mg. The ground state is predominantly 2p-2h with both interactions, with less 4p-4h content for the yrast states than from the in the analysis of [16, 17] or the SDPF-U-MIX calculations in [9]. For the interesting $0^+_2$ excitation, the SDPF-MU wave function contains nearly even mixing between 0p-0h and 2p-2h configurations with 0p-0h being slightly larger, while the state from SDPF-M is almost completely 4p-4h. Neither of these are consistent with the three-level mixing model, where the $0^+_2$ state is very similar to the ground state. The $0^+_3$ level is the sd-shell dominated excitation with SDPF-M, as in the analysis of Macchiavelli et al., but the SDPF-MU interaction predicts that it is dominated by 2p-2h configurations. The $0^+_4$ state is predominantly 4p-4h with SDPF-MU. Also, with SDPF-MU no other state has appreciable 4p-4h character, but with SDPF-M the $2^+_3$ state is also approximately 80% 4p-4h and the third $4^+$ state also contains a significant 4p-4h component.

Fig. 4

Calculated particle-hole strengths versus excitation energy for positive-parity states in $^{32}$Mg.The circles, squares, and triangles represent the lowest four $0^+$, $2^+$, and $4^+$ states, respectively

3.2.1 $0^+$ and $2^+$ states

Figure 5 shows the wave-function decompositions for the lowest four $0^+$ and $2^+$ levels in $^{32}$Mg. As expected, the character of the ground state with both interactions is much different from that of $^{30}$Mg. The SDPF-MU ground state still contains some sd-shell strength, however the SDPF-M wave function is nearly completely 2p-2 h. Configurations having two $0f_{7/2}$ neutrons carry 41% (62%) of the strength with SDPF-MU (SDPF-M). The largest 4p-4h components have either four $0f_{7/2}$, or two each $0f_{7/2}$ and $1p_{3/2}$ neutrons, and carry approximately 15% of the strength in each interaction.

The interesting first-excited $0^+$ state has dramatically different properties from the two interactions. In SDPF-MU, this level is a relatively pure sd-shell excitation, with more than 50% of the strength in the $(0s_{1/2})^2(0d_{3/2})^4(0d_{5/2})^6$ or (246) configuration. The SDPF-M level, however, is nearly 90% 4p-4h, with strength in the $(1p_{3/2})(0f_{7/2})^3$, $(0f_{7/2})^4$, and $(1p_{3/2})^2(0f_{7/2})^2$ neutron configurations. In Fig. 5, where the SDPF-M 4p-4h configurations are strong and the 4p-4h and 2p-2h configurations have similar Log$_{10}$C values, the SDPF-M 4p-4h configurations are indicated by the star symbols. For the $0^+_4$ state in Fig. 5d, the SDPF-MU 4p-4h configurations are indicated by black text, and SDPF-M 2p-2h in red.

The third and fourth 0$^+$ states are also very different between SDPF-MU and SDPF-M. The SDPF-MU $0^+_3$ 2p-2h strength is split equally between $(0f_{7/2})^2$ and $(1p_{3/2})^2$ components, whereas with SDPF-M the state is dominantly (65%) sd-shell. In SDPF-MU, the $0^+_4$ dominant 4p-4h strength comes from $(1p_{3/2})^2(0f_{7/2})^2$, $(1p_{3/2})(0f_{7/2})^3$, $(0f_{7/2})^4$ and $(1p_{3/2})^3(0f_{7/2})$, configurations and is the only SDPF-MU state with any significant 4p-4h content. With SDPF-M, the 2p-2h strength appears in $(1p_{3/2})(0f_{7/2})$, $(0f_{7/2})^2$ and $(1p_{3/2})^2$ neutron components.

Fig. 5

Fraction of configurations C in wave functions of 0$^+$ (a, c, e, g) and 2$^+$ (b, d, f, h) states in $^{32}$Mg. Configurations with Log$_{10}$C greater than 3.0 contain fp-shell neutrons.The bars(circles) represent results from the SDPF-MU(SDPF-M) interactions, and stars indicate 4p-4h configurations in the SDPF-M interaction. Red text in (b) indicates SDPF-M 4p-4h configurations

The situation for $2^+$ states in $^{32}$Mg also differs from that of $^{30}$Mg, with the calculated structures again quite different between the two interactions. For both calculations, the lowest 2$^+$ states have wave functions similar to the corresponding ground state. As with the 0$^+_1$ excitations, in SDPF-M the 2$^+_1$ level has more $(0f_{7/2})^2$ content than in SDPF-MU, and both are nearly pure 2p-2h states. With the higher levels the situation is more complicated. For SDPF-MU, none of the 2$^+$ states have much sd-shell strength, with the only appreciable contributions in the $2^+_2$ level, and there is very little 4p-4h strength. In contrast, in SDPF-M the 2$^+_2$ state is nearly pure $(0f_{7/2}^2)$ whereas the 2$^+_3$ excitation is dominated by 4p-4h excitations, similar to the SDPF-M 0$^+_2$ level. None of the SDPF-M 2$^+$ states have any significant 0p-0h strength.

Fig. 6

Fraction of configurations C in wave functions of the lowest $1^-$ (a), $3^-$ (b) and $5^-$ states in $^{32}$Mg. Configurations with Log$_{10}$C greater than 3.0 contain fp-shell neutrons. The star symbols indicate 3p-3h configurations

Table 2 Two-nucleon amplitudes (TNA) for the first two 0$^+$ states in $^{30}$Mg and $^{32}$Mg, from the SDPF-M and SDPF-MU interactions

3.2.2 Negative-parity states

Figure 6 shows components for the lowest $(1,3,5)^-$ excitations. The negative-parity states in $^{32}$Mg are more complex that those in $^{30}$Mg, and quite different between SDPF-MU and SDPF-M. While in $^{30}$Mg the negative-parity strength is nearly completely 1p-1h, in $^{32}$Mg, the SDPF-MU interaction reveals 77% of the $1^-$ state, 35% and 32% of the $3^-$ and $5^-$ states, respectively, are from 3p-3h configurations. In the $1^-$ state, this strength comes from the $(1p_{3/2})(0f_{7/2})^2$ configuration, with smaller and roughly equal contributions from $(0f_{7/2})^3$ and $(1p_{3/2})^2(0f_{7/2})$. With SDPF-M the 3p-3h strength is even greater, with more than 90% of the wave functions of the $(1,3,5)^-$ states composed of 3p-3h configurations. The large SDPF-M 3p-3h strength was already suggested to describe the low-lying negative-parity states in the the knockout work of Kitamura et al. [11]. In Fig. 6 the star symbols indicate 3p-3h configurations from the SDPF-M interaction.

4 Results: (t, p) cross-section calculations

As described in Sect. 2.2 the TNA from the shell model calculations are used to calculate angular distributions for the (t,p) reactions. Both SDPF-MU and SDPF-M were used to calculate the ground state of $^{28}$Mg for the $^{28}$Mg(t, p)$^{30}$Mg reaction. These calculations reveal the sensitivity of the cross-section observables to the underlying nuclear structure. For example, Table 2 lists the TNA for transitions to the first two 0$^+$ states in $^{30}$Mg and $^{32}$Mg, calculated with the two interactions. The usual DWBA phase convention applies, with all amplitudes for the ground-state transition having the same phase; the overall phase is arbitrary. For the ground states, the TNA from the two interactions are not very different. More differences are seen for the 0$^+_2$ states, and these could produce differences in the calculated angular distributions. Also, for the excited 0$^+$ transitions, the phases for the fp-shell amplitudes have the opposite sign to those for the ground state. In a simplified description of the states in terms of 0p-0 h and 2p-2 h components, this difference reflects the expected approximate orthogonality between the ground- and excited-0$^+$ excitations.

Those differences are ultimately driven by the DWBA form factors, which are a coherent sum of the two-nucleon form factors for each configuration, each scaled by its corresponding TNA. Those individual form factors are determined by solving the bound-state Schrödinger equation for neutrons bound to the core with the proper quantum numbers. As an example, Fig. 7 shows the form factors for the 0$^+$ transitions discussed above. In most cases the results from the two interactions are similar, however there are some subtle differences. For the $^{30}$Mg $0^+_2$ state, the SDPF-MU form factor has an additional node beyond the nuclear surface from the larger $(1p_{3/2})^2$ amplitude. The effect of the nuclear-structure differences between the ground states of $^{30}$Mg and $^{32}$Mg is seen in Fig. 7a, c, and these differences should be manifested in the angular distributions, as seen below.

Fig. 7

DWBA form factors for transitions to the $0^+_1$ and $0^+_2$ states in $^{30}$Mg and $^{32}$Mg. The solid black (dashed-red) lines correspond to the results from the SDPF-MU (SDPF-M) interactions

4.1 $^{28}$Mg($t,p)^{30}$Mg

Figure 8 shows calculated angular distributions for the $0^+$ and $2^+$ states in $^{30}$Mg, performed using TNA from the two shell-model interactions. The differences in the wave functions between the two interactions produce different angular distributions in many cases, in both magnitude and shape. For the $0^+$ transitions, in both cases the ground-state angular distribtion has a characteristic $\ell =0$ transfer shape, and the size of the cross section is similar for the two interactions as expected, given the similarity of the wave functions, the TNAs, and the DWBA form factors. For the remaining $0^+$ states, fp-shell contributions lead to angular-distribution shapes that are no longer strongly forward-peaked due to the differences in the form factors. This behavior is well known from earlier studies of (t,p) reactions [1, 33]. The difference in shape between the SDPF-MU and SDPF-M angular distributions for the $0^+_2$ state stem from a node in the SDPF-MU form factor that is not present in the SDPF-M curve (see Fig. 7).

For the $0^+_{3,4}$ states, the results differ sharply between the two interactions. With SDPF-MU, the $0^+_3$ excitation, while weaker than the $0^+_2$ state, is markedly stronger than the $0^+_4$ level. For $0^+_3$, the (046) $(0d_{3/2})^4(0d_{5/2})^6$, (2026) $(0f_{7/2})^2(0d_{3/2})^2(0d_{5/2})^6$ and (200206) $(1p_{3/2})^2(1s_{1/2})^2(0d_{5/2})^6$ configurations are the strongest in the wave function and can be reached by the transfer of ($0d_{3/2}^2$), ($0f_{7/2}^2$) and ($1p_{3/2}^2$) pairs, respectively. The SDPF-MU 0$^+_4$ excitation could be reached by strong ($0d_{3/2}^2$) and ($0f_{7/2}^2$) transitions, however this state involves protons excited out of the $0d_{5/2}$ orbital and thus has a small overlap with the $^{28}$Mg ground state. With SDPF-M, a combination of proton excitations, and a large neutron $(0f_{7/2})^2(1s_{1/2})^2(0d_{3/2})(0d_{5/2})^5$ component of the wave function that cannot be easily reached by 2n transfer on the $^{28}$Mg ground state strongly suppress the transition for the 0$^+_3$ state. In contrast, for the SDPF-M $0^+_4$ state, pair transfer to the large $(0f_{7/2})^2$ and $(1p_{3/2})^2$ components enhance the cross section relative to SDPF-MU.

The differences between the angluar distributions from the two interactions for the $2^+$ are also significant. With the exception of the $2^+_1$ state, all of the SDPF-M $\ell =2$ transitions are stronger than those from SDPF-MU. For the $2^+_2$ excitation, the larger sd-shell (226) $(1s_{1/2})^2(0d_{3/2})^2(0d_{5/2})^6$ component enhances the cross section for the SDPF-M state with a stronger ($0d_{3/2}^2$) amplitude. The nearly pure $(0f_{7/2})^2$ wave function for the SDPF-M $2^+_3$ excitation leads to a large transition amplitude and a large cross section in comparison to the sd-shell dominated SDPF-MU state. The fourth $2^+$ state is sd-shell dominated with each interaction, and strongly populated in both cases. The largest component in the SDPF-MU state is (226), that is populated by a $(0d_{3/2})^2$ pair transfer. The SDPF-M state, however, with an additional (136) $(1s_{1/2})(0d_{3/2})^3(0d_{5/2})^6$ configuration in the wave function, is populated by both $(0d_{3/2})^2$ and ($0d_{3/2}1s_{1/2}$) transfers, enhancing the cross section relative to SDPF-MU.

Fig. 8

Angular distributions for (a, b) $0^+$ and $2^+$ (c, d) states in $^{28}$Mg(t, p)$^{30}$Mg, with TNA from the SDPF-MU and SDPF-M interactions. The solid black, dashed red, dot-dashed green and dot-dot-dashed blue curves represent the first, second, third and fourth states of each spin and parity, respectively

Angular distributions for the lowest $(1,3,5)^-$ states appear in Fig. 9. For the odd-parity states, the transfer amplitudes all involve combinations of fp- and sd-shell neutrons. For $^{28}$Mg$(t,p)^{30}$Mg, the results from the two interactions are qualitatively similar, as both predict the same ordering of the strengths for the three transitions. The $1^-$ state is weaker in SDPF-M than SDPF-MU, largely due to the higher purity of the SDPF-MU wave function that is nearly 70% $(1p_{3/2})$, compared to the SDPF-M state, which is equally mixed between $(0f_{7/2})$ and $(1p_{3/2})$ configurations. The $3^-$ transition is weak in both cases, with interference between $(0f_{7/2}0d_{3/2})$, ($0f_{7/2}1s_{1/2}$) and ($1p_{3/2}0d_{3/2}$) transfer amplitudes reducing the cross section. This is in contrast to the case of $^{26}$Mg$(t,p)^{28}$Mg, where the first 3$^-$ state has a very pure $(0f_{7/2})(sd)$ structure and a large cross section [23]. The strongest transition is the $5^-_1$, with a cross section even greater than that of the ground-state, arising from a pure $(0d_{3/2})(0f_{7/2})$) amplitude that is large for both interactions.

Fig. 9

Angular distributions for the first $1^-$ (black solid), $3^-$ (red dashed) and 5$^-$ (green dot-dashed) states in $^{30}$Mg from $^{28}$Mg(t, p)$^{30}$Mg

4.2 $^{30}$Mg(t, p)$^{32}$Mg

Figure 10 shows calculated angular distributions for $0^+$ (a,b) and $2^+$ (c,d) states in $^{32}$Mg. The $\ell =0$ transitions are particularly interesting with their link to shape coexistence in this nucleus. The analysis in Ref. [12] assumed that the identified 0$^+_2$ state was populated in isolation and concluded that the ground state was composed of a combination of $(1p_{3/2})^2$ and $(0f_{7/2})^2$ configurations, with the $(1p_{3/2})^2$ component dominant. The excited 0$^+$ level was identified as predominantly sd, with a possible small $(1p_{3/2})^2$ component, similar to the present SDPF-MU wave function for that state. The angular-distribution shapes for the $\ell =0$ transitions reflect the form factor for the transition arising from the mixture of sd and fp configurations in the wave functions. For the ground state in particular, the difference between $^{32}$Mg and $^{30}$Mg is marked.

The $0^+_2$ state is weaker than the ground state with both interactions, for different reasons. In SDPF-MU, the strongest configuration is $(1s_{1/2})^2(0d_{3/2})^4(0d_{5/2})^6$, which can be populated by the transfer of a $0d_{3/2}$ neutron pair with a reasonably large TNA. The ground-state is stronger due to the stronger pair transfer to the fp shell in comparison to the sd shell. The SDPF-M state is very different. Composed of several 4p-4h configurations, most of which can only be reached through small components of the $^{30}$Mg ground state, the resulting TNAs are small and the cross section is reduced for the transition.

The third and fourth $0^+$ states are also more weakly populated than the ground state, however the two interactions have different predictions for their relative strengths. In SDPF-MU, the $0^+_3$ level is stronger, with roughly equal $(0f_{7/2})^2$ and $(1p_{3/2})^2$ TNA, and a $0^\textrm{o}$ cross section greater than that of the 0$^+_2$ state. In contrast, the SDPF-M $0^+_3$ state is nearly pure sd, with a large TNA for a $0d_{3/2}^2$ neutron pair, but a form factor that is very small at the nuclear surface. The SDPF-M $0^+_4$ excitation is primarily $(0f_{7/2})^2$ and $(1p_{3/2})^2$, with a 0$^\textrm{o}$ cross section as large as that for the $0^+_2$ state.

The strengths of the transitions to the $2^+$ states in $^{32}$Mg are less varied than those for $^{30}$Mg, with both interactions. The ordering of the strengths is again different when comparing SDPF-MU and SDPF-M. Most notably, the $2^+_1$ transition is the strongest for SDPF-MU, but much weaker with SDPF-M. The wave functions are qualitatively similar, however the $(1p_{3/2})^2$ component is twice as large in SDPF-MU, and the $(0f_{7/2})^2$ contribution is smaller in the SDPF-MU wave function. There is also a small but non-negligible $(1p_{1/2}1p_{3/2})$ component in SDPF-MU that does not exist in the SDPF-M model space, with a sizeable $(1p_{1/2})^2$ TNA for that transition. The cumulative effect is that the SDPF-MU state has a larger form factor at large radius, and a correspondingly larger cross section. Population of the $2^+_1$ state in particular plays a role in the interpretation of the data in Ref. [12] as we discuss below.

Fig. 10

Angular distributions for 0$^+$ (a), (b) and $2^+$ (c), (d) states in $^{30}$Mg(t, p)$^{32}$Mg. The solid black, dashed red, dot-dashed green and dot-dot-dashed blue curves represent the first, second, third and fourth states of each spin and parity, respectively

Angular distributions for the lowest (1,3,5)$^-$ transitions appear in Fig. 11. The 1$^-$ state, which, with both interactions, is mostly 3p-3h, is weakly populated in each case. The SDPF-MU 3$^-$ state is strongly (65%) 1p-1h, and the cross section is large, however with SDPF-M the state is nearly all 3p-3h, and also weakly populated. The strong 3p-3h configurations for the SDPF-M 3$^-$ state involve either three $0f_{7/2}$, or one $1p_{3/2}$ and two $0f_{7/2}$ neutrons and can only be reached by transfer to small components of the $^{30}$Mg ground-state wave function. The lowest 5$^-$ state is is purely $(0d_{3/2}0f_{7/2})$ and is strongly excited with both interactions.

Fig. 11

Angular distributions for the first $1^-$ (black solid), $3^-$ (red dashed) and $5^-$ (green dot-dashed) states in $^{32}$Mg from $^{30}$Mg(t, p)$^{32}$Mg

5 Discussion

The present work illustrates how trends in the experimental observables for two-neutron transfer with the (t, p) reaction may be traced to detailed underlying nuclear-structure properties. In cases where the two shell-model interactions predict different nuclear structure, the different shapes and magnitudes of the angular distributions can be traced to aspects of the shell-model wave functions. This approach worked reasonably well for strongly populated states in the $^{26}$Mg(t, p)$^{28}$Mg reaction [23], and could prove useful for future studies of two-neutron transfer in the region around the IoI.

It is interesting to compare the present results for $^{30}$Mg$(t,p)^{32}$Mg with the only existing data from Ref. [12]. Figure 12 shows shows the calculated angular distributions for the two lowest $0^+$ states, the $2^+_1$ state, and the sum of the $0^+_2$ and $2^+_1$ excitations, at the bombarding energy used in Ref. [12], 1.8 AMeV. The energy-dependent paramaters of the optical potential have been adjusted for the change in bombarding energy. Also shown in Fig. 12 are the data from [12], with the ground-state angular-distribution data normalized to the SDPF-MU curve. The shape of the ground-state transition is well-reproduced by the calculation. The measured angular distributions for the ground- and $0^+_2$ states are remarkably similar, in both magnitude and shape. This similarity is notable in view of the calculated $0^+_2$ curves from both interactions, with the excited-$0^+$ cross section weaker by an order of magnitude, and the shapes are very different, lacking the characteristic forward $\ell =0$ rise at forward angles. Clearly the data are not consistent with the predictions of either calculation.

Fig. 12

Angular distributions for the $^{30}$Mg$(t,p)^{32}$Mg reaction, for $0^+_1$ (solid black), $0^+_2$ (dashed red), $2^+_1$ (dot-dashed maroon) and summed $0^+_2$ and $2^+_1$ (dot-dot-dash blue) transitions, calculated at a bombarding energy of 1.8 AMeV, equivalent to that used in Ref. [12]. The data in (a) represent the ground-state (circles) and $0^+_2$ (crosses) transitions from [12]

Reference [12] also reports that the low-lying $2^+_1$ transition was not present, from an analysis of coincident gamma-ray spectra. Compared with the present results, the absence of the $2^+_1$ state is consistent with the SDPF-M calculation where that transition is very weak, but incompatible with the SDPF-MU results where the $2^+_1$ level is as strong as the excited $0^+$ state. Given the resolution of the measurement, absent gamma-ray data it would be impossible to disentangle any yield from the $2^+_1$ transition contaminating that of the $0^+_2$ state. Population of the $2^+_1$ state would require a re-interpretation of the data in  [12].

The empirical analyses of Fortune, Macchiavelli et al., and Lay et al., consider only the quoted cross-section ratio from [12] of 0.65(5) from the presumably measured angle-integrated ground- and excited-state cross-sections of 10.5(7) mb and 6.5(5) mb. From Fig. 12 it seems clear that with the uncertainties in the data the angular distributions are nearly the same and that cross-section ratio could be as large as 1, although that may not change significantly the conclusions of those empirical analyses. While under some assumptions the empirical analyses may be able to reproduce the relative magnitudes of the angular distributions from the two states, it is very difficult, with physically reasonable assumptions about the wave functions of the states, to produce nearly identical angular distributions for the two transitions. Lay et al. do not present a calculated angular distribution for the $0^+_2$ state, so it is difficult to judge their comparison to the data beyond the analysis that only considers the quoted cross-section ratio from  [12].

None of the existing analyses consider the possibility of two-step two-neutron transfers. Wimmer et al. discount them due to the strongly negative Q value of $-$3.9 MeV for the $^{30}$Mg$(t,d)^{31}$Mg reaction. A similar measurement at low bombarding energy, however, of the $^{44}$Ar$(t,p)^{46}$Ar reaction, where the corresponding (t, d) Q value is $-$1.09 MeV, found that two-step processes were necessary to understand the data [34]. The bombarding energy also plays a role in two-step transfer in (t, p) reactions, as noted by Becha et al., in a study of the $^{40}$Ca$(t,p)^{42}$Ca reaction [35]. If these effects are important for $^{32}$Mg, then the various analyses, and the nuclear-structure conclusions derived from them may need to be revisited.

It is important to point out that in a rigorous analysis of these processes, direct and sequential transfer are not distinct amplitudes but rather must be treated coherently. Also, more sophisticated analyses treating all amplitudes together in a theoretically consistent way have been able to make predictions of absolute cross sections for a variety of two-neutron transfer reactions, including $^7$Li$(t,p)^9$Li, $^{11}$Li$(p,t)^9$Li, $^{10}$Be$(t,p)^{12}$Be, $^{48}$Ca$(t,p)^{50}$Ca, and (t, p) and (p, t) reactions for a variety of Sn and Pb isotopes [36, 37]. These methods are beyond the scope of this work, however could provide considerably more insight into the phenomena in this mass region.

New measurements of two-neutron transfer in this mass region, with improved experimental resolution at a higher bombarding energy, should provide important additional information about the physics around the $N=20$ Island of Inversion. High-resolution transfer data for both $^{28}$Mg($t,p)^{30}$Mg and $^{30}$Mg($t,p)^{32}$Mg, for a wider set of excitations, can provide additional tests for nuclear-structure calculations. Although the low-lying $0^+$ states have been the focus of the most interest, transitions to other states are equally sensitive to the underlying nuclear structure, for example as seen in the predictions for the negative-parity states in $^{32}$Mg, which are very different between the two interactions.

6 Summary and conclusions

We have performed shell-model calculations relevant to the study of two-neutron transfer near the $N=20$ Island of Inversion for magnesium isotopes. The aim of this work is to illustrate the connections between the experimental observables with the detailed nuclear structure revealed by the shell-model calculations. The current work, done using the SDPF-MU and SDPF-M interactions, suggests the importance of intruder configurations in the excited states of $^{30}$Mg, and of significant intruder content in the ground state of $^{32}$Mg as in many previous studies. The calculated two-neutron transfer cross sections, obtained using transfer amplitudes provided by the shell-model calculations, display strong sensitivity to the underlying nuclear structure, yielding predictions that can provide guidance for the interpretation of existing data, as well as data from experiments on two-neutron transfer that should be possible at new experimental facilities.