1 Introduction

The elements heavier than iron in the Universe are mainly produced by two distinct nucleosynthesis processes: the slow neutron capture process (s-process) and the rapid neutron capture process (r-process) [1]. Both are characterized by a sequence of neutron capture reactions, interrupted by beta decays. The two processes operate, however, at conditions with drastically different neutron number densities with the result that neutron captures during the s-process are slower than the competing beta decays. As a consequence the s-process path runs close to the valley of stability in the nuclear chart. In contrast, during r-process nucleosynthesis neutron densities are extremely high making the neutron capture reactions much faster than competing beta decays. Thus, the r-process path runs through nuclei with very large neutron excess.

For many decades Franz Käppeler has been one of the leading figures who decisively improved our understanding of the s-process [2, 3]. The authors of this manuscript benefited tremendously from discussions we had with Franz in which he shared his deep understanding of this process, and of other astrophysical and nuclear issues. Sometimes these collaborations could be combined with unforgettable social events (see Fig. 1). We also had the pleasure and the honor to collaborate with Franz on two overview articles [4, 5].

Not the least due to the work of Franz Käppeler, the s-process is generally considered to be the best understood nucleosynthesis process. Its abundance distribution can be reproduced with an uncertainty low enough to determine the r-process solar abundances by subtracting the s-process results from the observed total abundances of heavy elements in the solar system. Understanding how this abundance pattern comes about is one of the main goals of r-process studies. In particular, it is still an open question whether the r-process operates at a single astrophysical site or is the combination of different sites which have operated as distinct events with different frequencies during the age of the galaxy. In addition to neutron star mergers, that so far is the only site for which we have observational evidence, other possible sites considered in the literature include neutrino winds from core-collapse supernova, electron-capture supernovae, quark deconfinement supernovae, magnetorotational supernovae, and collapsars (see [6] for a detailed discussion). For each site reliable predictions of the nucleosynthesis yields are impeded by uncertainties in astrophysical modeling and also by the fact that most nuclides on the r-process path are so neutron rich that they have yet not been produced in the laboratory and their properties are experimentally unknown. Hence they have to be modeled. It is the aim of this manuscript to summarize the current status of nuclear input needed for r-process studies highlighting some of the important progress achieved recently. This has been possible due to improved nuclear models benefiting also from advances in computational facilities and, in particular, from data obtained at modern radioactive ion beam facilities.

Fig. 1
figure 1

Franz Käppeler and the authors enjoying a concert at the Hollywood Bowl together with Marialuisa Aliotta and Almudena Arcones in 2007. The visit happened in connection to the international conference at Caltech celebrating the 50th anniversary of the Burbidge, Burbidge, Fowler, Hoyle paper

Full size image

Our manuscript is organized in the following way. In Sect. 2 we briefly discuss the operation of the r-process in neutron star mergers which we adopt as the site for the r-process in this manuscript. Section 3 then focuses on the nuclear ingredients required for r-process network simulations which are masses, half-lives, neutron capture rates and fission rates and yields of nuclides with large neutron excess. We finish the manuscript with a short outlook in Sect. 4.

2 R-process nucleosynthesis in neutron star mergers

The joint detection and analysis of the gravitational wave and electromagnetic transient signals from GW170817 gave evidence that neutron star mergers are a site of the production of heavy elements by the r-process [8,9,10]. Simulations of neutron star mergers [11,12,13,14] need to describe the different mechanisms of matter ejection during the merger and account for neutrino interactions [15,16,17,18] in the ejected material as they determine its electron-to-nucleon ratio \(Y_e\). During the inspiral period the two merging neutron stars move on nearly circular orbits with successively decreasing orbital separation. Tidal forces deform the stars and accelerate the inspiral. This leaves an imprint on the gravitational wave signal from which the tidal deformability of the neutron stars can be constrained [19]. The strength of this effect depends on the size of the stars and on the nuclear equation of state (EoS). After the merger a central remnant forms surrounded by an accretion disk. Depending on the masses of the neutron stars, the central object collapses promptly to a black hole or produces an hypermassive neutron star whose lifetime depends on the initial mass of the system. For the event GW170817 with a total mass of 2.73 M\(_\odot \) [19] it is generally assumed that it first formed a metastable hypermassive neutron star, temporarily stabilized by differential rotation and temperature, before it collapsed to a black hole.

A neutron star merger sheds off a few percent of the initial gravitational mass. One usually distinguishes between dynamical and secular ejecta [6]. Dynamical ejecta are produced by tidal interactions between the merging neutron stars and shocks at the edges of the forming remnant that push material out [20, 21]. In the postmerger phase, an accretion disk forms around the remnant and matter is ejected by viscous heating associated to angular momentum transport in the disk. Dynamical ejecta move noticeably faster (with about a third of the speed of light) than the secular component (0.1 c). The ejecta become the breeding place of nuclei. The outcome, however, depends sensitively on the electron-to-nucleon ratio \(Y_e\) which is set by the interaction of the nucleons with leptons especially neutrinos. It turns out that the ejected matter covers a rather broad range of \(Y_e\) values where only matter with \(Y_e < 0.2\) is neutron-rich enough to support r-process nucleosynthesis up to the third peak and produce high opacity material that includes lanthanides or actinides [22, 23].

For mergers that involve neutron stars with similar mass, matter in both the dynamical and secular components are ejected at very high temperatures (\(T>10\) GK) where the composition is well described by nuclear statistical equilibrium. As it expands and cools charged-particle reactions freeze out. At this moment, the composition consists of neutrons and nuclei in the mass range \(A \approx \) 80–120 (depending on \(Y_e\)). These nuclei become the seeds of the subsequent r-process. In fact, a neutron-to-seed ratio of 150 or more is required to transform a seed nucleus into actinides like thorium or uranium by neutron captures and beta-decays.

For low \(Y_e\)-matter, which enables a complete r-process, seed nuclei are rapidly transformed by fast neutron captures, followed by beta decays, into heavy extremely neutron-rich nuclides. The process proceeds in \((n,\gamma ) \rightleftarrows (\gamma ,n)\) equilibrium as the energy liberated by beta-decays maintains the high temperatures around 1 GK. The balance of neutron capture and photodissociation reactions ensures that the process proceeds through nuclides with low neutron separation energies. The r-process flow stops at the magic neutron number \(N=184\). The magicity hampers neutron captures and a few beta decays occur, until nuclei are encountered for which neutron induced fission is faster than \((n,\gamma )\) reactions bringing the mass flow back to medium-mass nuclei rather than continuing it beyond \(N=184\). The r-process freezes out once the neutrons are consumed. The neutron-rich short-lived nuclides which existed during the operation of the r-process decay back to stability. For low \(Y_e\), there exists a sizable amount of matter beyond the third r-process peak at \(A \sim 195\). This matter decays partly via different fission channels [24] feeding material into the second r-process peak at \(A \sim 130\), partly by \(\alpha \) and \(\beta \) decays, mainly ending in matter around \(^{208}\)Pb. Fission, \(\alpha \) and \(\beta \) decays are the energy sources which power the kilonova lightcurve. Their relative importance depends on the initial \(Y_e\) value of the ejected material.

Fig. 2
figure 2

Average abundances from outflows of an accretion disk surrounding a black-hole after the merger of two neutron stars, based on the simulations of Ref. [25]. The upper panel illustrates the impact of different nuclear mass models by comparing abundances obtained using neutron-capture rates based on the FRDM-1992 masses [26] and the DZ31 [27] and beta-decay half-lives from the FRDM plus quasi random phase ppproximation (FRDM+QRPA) approach [28]. The lower panel uses neutron-capture rates based on the FRDM-1992 masses [26] combined with two different sets of global calculations of beta-decay rates based on FRDM+QRPA [28] and the covariant density functional D3C* [29] approaches. The calculations reflect the abundances 1 Gy after the merger event, which is shorted than the \(^{232}\)Th and \(^{238}\)U half-lives. (adapted from [25])

Full size image

The r-process abundances produced by neutron star mergers are obtained by calculating the yields for each individual trajectory representing the time evolution of ejected matter and then summing up the various individual abundances properly weighted with the amount of matter ejected in this individual trajectory. An example is given in Fig. 2. The agreement to the solar abundances, which reflects the history of many r-process events in our galaxy, is very satisfying indicating that neutron star mergers likely contribute to the whole inventory of r-process elements.

The r-process abundances are directly and indirectly depending on the nuclear input assumed in the network simulations (see Fig. 2). The direct input comprises the properties of the very neutron-rich nuclei which come temporarily into existence during the operation of the process. The next chapter is devoted to this direct nuclear input. However, the results are also indirectly dependent on the nuclear EoS, which influences the properties of the initial neutron stars and in particular its compactness, the amount of dynamical ejecta and the postmerger evolution when extremely hot and dense matter is produced which can surpass 70 MeV in temperature and noticeably exceeds the nuclear saturation density [13]. Uncertainties in the EoS are introduced by the question which particles contribute at the relevant temperatures and densities and what is their interaction. Experimentally nuclear matter at such extreme densities and temperatures can be studied in relativistic heavy-ion collisions as proven by the HADES experiment [30, 31]. A particularly relevant question is whether nuclear matter undergoes a phase transition to quark matter at the conditions reached in mergers. Simulations have shown that such phase transition might become detectable in the gravitational wave signal [32, 33]. The study of the QCD phase diagram, including potential phase transitions, is the aim of the CBM experiment at the future FAIR facility [34].

3 Nuclear input in r-process network simulations

The nuclear properties needed for r-process calculations are neutron capture and beta decay rates as well as fission rates and yields [6, 35, 36]. The photodissociation rates can be derived from neutron capture by applying detailed balance, see e.g. Eq. (A2) of Ref. [7]. For most of the nuclei involved in r-process nucleosynthesis these data are not known experimentally and have to be modeled. Here the nuclear masses become an important input quantity as they determine the thresholds for neutron captures and fissions as well as the Q value in beta decays. Moreover, in \((n,\gamma ) \rightleftarrows (\gamma ,n)\) equilibrium the r-process proceeds along a path of constant neutron separation energies for given neutron densities and temperatures.

3.1 Mass models

The most commonly used mass tabulations can begrouped in three different approaches: (a) microscopic-macroscopic models like the finite-range droplet model (FRDM) approach [26, 37,38,39], the Extended Thomas-Fermi model with Strutinski Integral (ETFSI) approach [40], the Weizsäcker–Skyrme mass models (WS3) [41, 42]; (b) a microscopically inspired parametrization based on the averaged mean field extracted from the shell model and extended by Coulomb, pairing and symmetry energies [27] (DZ10 and DZ31); and (c) microscopic models based on the non-relativistic [43] (the series of HFB mass models) or relativistic [44] mean-field models.

Table 1 Comparison of the root mean square deviation, in keV, between mass models and experiment; mass models: FRDM-1992 [26], HFB-21 [45], DZ10, DZ31 [27], and WS3 [42], experimental values taken from the 2003 [46] and 2012 evaluations [47, 48]. The recent Brussels-Skyrme-on-a-grid models consider the effects of triaxiality (BSkG1) [49] and the breaking of time-reversal symmetry (BSkG2) [50]. The RMS deviation is calculated compared to the data of the 2020 atomic mass evaluation [51]
Full size table

All mass models have in common that, by fitting a certain set of parameters to known experimental data, they are then used to predict the properties of all nuclei in the nuclear landscape. The models reproduce the experimentally known masses quite well, with mean deviations typically between 350 and 600 keV (see Table 1). It is quite satisfying to see that, when in 2012 a new atomic mass evaluation (AME) [47], including 219 new experimental masses, became available the agreement with data worsened only slightly compared to the comparison with the previous AME. As the new masses typically involve more exotic nuclei than those found in a previous evaluation, they provide a measure of the capabilities of each model to extrapolate to regions far from stability. This is in general one of the most challenging aspects to determine when using a given mass model in r-process calculations. Recent model determinations applied Bayesian machine-learning techniques to assess the predictive power of global mass models towards more unstable neutron-rich nuclei and provide uncertainty quantification of predictions. Nevertheless, deviations between model and data for neutron-rich nuclei are typically related to bulk properties that may not dramatically affect the abundance predictions, e.g. the symmetry energy whose value at saturation density is \(30.8\pm 1.5\) MeV [52]. There have been two recent improvements of the microscopic models including new degrees of freedom. Refs. [49, 50] have performed Skyrme–Hartree–Fock–Bogoliubov calculations on a three-dimensional mesh considering triaxial deformation (BSkG1) and time-reversal symmetry breaking (BSkG2), respectively. The latter is particularly relevant for the description of odd-A and odd-odd nuclei. These microscopic models are computationally quite challenging and were only possible by exploiting machine-learning strategies. They both give a fair account of the experimentally known masses (see Table 1). Here the RMS deviations for the various models have been evaluated for the AME tabulation available at the time the models have been derived. It is worth mentioning that they also describe other nuclear properties like fission barriers or radii quite well.

The upper panel of Fig. 2 shows an example how sensitive r-process abundances are on the nuclear mass model adopted in the r-process simulations [25].

3.2 Beta-decay halflives

Fig. 3
figure 3

Comparison of shell model half lives for \(N=82\) r-process waiting point nuclei with data [53,54,55,56]. The GT strengths underlying the shell model results have been quenched with the standard factor 0.74 [57]. (adapted from [6])

Full size image

R-Process nucleosynthesis proceeds by successive neutron captures and beta decays which increase the mass and charge numbers, respectively. As the r-process occurs in a dynamical environment, the time, needed for the succession of beta-decays to produce thorium and uranium from the seed nuclei available after freeze-out of charged-particle fusion reactions, is competing with the dynamical timescale of the explosion, during which matter is transported to larger radii and lower densities. The latter suppresses the neutron number density required for the mass flow to heavier nuclei by neutron captures. Particularly important are beta-decays of nuclei with magic neutron numbers \(N_\textrm{mag}\), as the matter flow is hindered by the reduced neutron separation energies of the nuclei with \(N_\textrm{mag} +1\). Furthermore, due to the extra binding of the magic nuclei, the Q-value of their beta-decays is relatively reduced, resulting in longer lifetimes. There has been important progress by measuring half lives of some intermediate-mass nuclei on the r-process path [56, 58], including a few \(N=82\) waiting points. However, most half lives still have to be modeled.

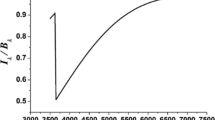
Traditionally, it has been assumed that beta decays of r-process nuclei proceed by Gamow–Teller (GT) transitions. As an important development charged-exchange experiments have shown that the GT strength is strongly fragmented [59, 60]. Such fragmentation is caused by nucleon-nucleon correlations which are included in the interacting shell model [61]. In fact, it has been demonstrated that the measured GT strength functions are well reproduced by shell model calculations if the model space is chosen appropriately large [60, 62, 63]. However, for r-process nuclei such appropriate shell model calculations can only be performed for the waiting points with magic neutron numbers [64,65,66,67], where they reproduce the existing experimental half-lives quite well. Data and shell model results for the \(N=82\) waiting points are compared in Fig. 3. Unfortunately no data exist yet for the \(N=126\) r-process waiting points. For these nuclei two independent shell model calculations have pointed to the importance of forbidden transitions induced by intruder states [66, 67]. These forbidden transitions are predicted to shorten the half lives of the \(N=126\) waiting points noticeably and enhance the mass flow through these waiting points [68]. This implies more r-process material available for fission, thus affecting the abundances of the second r-process peak around \(A=130\) which for very neutron-rich ejecta is built up by fission yields [68]. The enhanced mass flow also increase late-time \(\alpha \)-decays from the decaying r-process matter which influence the kilonova signal [69].

Due to the restrictions of shell model studies to r-process nuclei with magic neutron numbers, global sets of r-process half lives have to rely on less sophisticated models. Such sets have been determined by Quasi Random Phase Approximation (QRPA) calculations on the basis of phenomenological parametrizations [37, 70] and more recently of microscopic HFB or density functional approaches [29, 71,72,73,74,75]. Also the global sets have benefited from experimental half-lives becoming available for nuclei at or near the r-process path serving as constraints for better parametrizations. Modern r-process half-lives also include contributions from forbidden transitions which have important impact on beta delayed neutron emission rates.

Examples how beta-decay half-lives affect the r-process abundances are shown in the lower panel of Fig. 2.

3.3 Neutron captures

Neutron capture rates become relevant for r-process nucleosynthesis once the process drops out of \((n,\gamma ) \rightleftarrows (\gamma ,n)\) equilibrium at temperatures below about 1 GK. An experimental determination of neutron capture rates on the short-lived r-process nuclei is yet not possible. Therefore they are derived within the statistical Hauser–Feshbach model, although this approach might not always be justified for r-process nuclei (see discussion and references in [76]). Important ingredients in the Hauser–Feshbach approach are optical potentials, the nuclear level densities and the \(\gamma \)-strength functions [35]. Rather reliable global proton and neutron potentials exist, while the situation is clearly worse for \(\alpha \) optical potentials (see Ref. [6] and references therein).

Level densities have been traditionally derived on the basis of phenomenological parametrizations like the Fermi gas model, supplemented by data if available, which, however, is rarely the case for r-process nuclei. There has been significant progress in modeling nuclear level densities recently, mainly exploiting the ability of the Shell Model Monte Carlo (SMMC) approach to describe nuclear properties in unprecedentedly large model spaces and at finite temperature while taking correlations among nucleons into account [77, 78]. The method how to derive level densities from SMMC calculations was presented in [79, 80]. In the following years the method has been used to explore the effects of parity, angular-momentum and pairing on the level density [81,82,83]. Alhassid et al. have presented an approach in which a microscopically derived parity-dependence is incorporated into phenomenological level density formulas [84]. This approach has been used to derive a large set of level densities for r-process nuclei, also employing a temperature-dependent parametrization of the pairing parameter, modeled after SMMC calculations [85]. These improved level densities are now part of the statistical model packages NON-SMOKER and SMARAGD, developed by Rauscher [86,87,88]. An alternative microscopic approach to level densities, built on combinatorics and the HFB model, has been derived by Goriely and coworkers and has become part of the BRUSLIB package to calculate nuclear ingredients for astrophysical applications [89,90,91].

It has been questioned whether the level density around the neutron threshold is large enough in the most neutron-rich r-process nuclei to justify the application of a statistical approach [76]. As an alternative neutron capture rates have been calculated in a direct capture model [92,93,94].

Statistical model calculations of the capture rates consider E1, M1 and E2 transitions. The respective \(\gamma \)-strengths of the transitions are usually described by parametrizations to photodissociation and electron scattering data [35]. Recently E1 strength functions calculated within the HFB model [95] or within a relativistic mean-field approach [96] became available. These studies confirm the existence of a low-energy E1 pygmy dipole strength in very neutron-rich nuclei [97] and might significantly increase the neutron capture rate [98]. A similar effect can be expected from the experimentally observed upbend of the dipole strength towards \(E_\gamma =0\) [99, 100] as discussed in [100,101,102,103]. Calculations also show that the M1 scissors mode observed in deformed nuclei [104] can lead to a significant enhancement of the capture rate [105].

3.4 Fission

As mentioned above, fission plays an important role during the r-process in NS mergers, as it determines the region of the nuclear chart at which the flow of neutron captures and beta-decays stops [24, 106,107,108]. Fission has also been suggested to produce a robust r-process pattern [109,110,111], in which the abundances of nuclei with \(A \lesssim 140\) are determined during the r-process freeze-out from the fission yields of nuclei with \(A\lesssim 280\) [68].

Various fission reaction channels can in principle compete during the r-process. However, network simulations have shown that the dominating fission channel during r-process nucleosynthesis is neutron-induced fission [107, 112, 113]. Like the other channels, neutron-induced fission depends sensitively on the fission barriers as the fission process occurs at energies just above the fission barrier. Unfortunately no experimental data exist for barriers in the very neutron-rich nuclei involved in the r-process and they have to be modeled [108, 114,115,116,117,118] to obtain fission reaction rates [24, 108, 112, 116, 119, 120]. In addition to the fission rates, also the corresponding fission yields have to be known for r-process calculations [121,122,123,124]. As discussed above, the fission yields determine the abundance of r-process elements in the second r-process peak and above and can play an important role for abundance distribution of rare-earth elements, e.g. [125,126,127]. Methods based on Density Functional Theory and Generator Coordinate Method have recently been developed to determine potential energy surfaces and fission paths in multidimensional collective spaces [108, 124]. Although these approaches are quite promising, they are very time-consuming which hinders their application to the many neutron-rich nuclei required for r-process studies. This obstacle might be overcome by the use of machine learning techniques [128].

4 Outlook

The observation of the neutron-star merger event GW170817 and its identification as a site of the astrophysical r-process has not only drawn a lot of attention within the science community and beyond, it has also started quite demanding interdisciplinary collaborations. While the studies of the r-process in the past were performed by treating the various astrophysical and nuclear aspects quite distinctly, strong international collaborations have been formed with the aim to tackle the challenges involved in the studies of r-process nucleosynthesis in neutron-star mergers in a combined and consistent way. The chain of models involved starts with sophisticated multidimensional simulations of the merger event including its gravitational wave signal and, importantly, its ejecta at the various stages of the merger. Particular emphasis has to be placed on the effect of neutrinos on the composition of the ejecta and the directionality and time evolution of the ejecta. The ejecta are the cauldrons of element synthesis, but as their composition and evolution varies nucleosynthesis has to be followed individually. While the reproduction of the r-process abundances by itself is of superb interest, a particular challenge is to identify fingerprints which can prove that the mergers are indeed the site of production of heavy elements, perhaps even up to the transactinides. Such fingerprints can be expected from the electromagnetic signal, the kilonova, produced by the r-process nucleosynthesis. However, a consistent description of the kilonova is a superb challenge in the multidimensional description of photon transport and not the least in the description of the associated opacities, in particular requiring knowledge of partially ionized lanthanides and actinides.

While these consistent simulations will certainly improve the modeling of neutron-star mergers, their quality can only be judged by comparison to observations. Although mergers are quite rare events in our galaxy, occurring about once in 10,000 years, novel observational devices will allow to look deeper into space and hence will observe mergers at a significantly improved rate and with much more detailed resolution power. First, these improvements are due to the advanced version of the LIGO detector, and on a mid-term time frame, to the Einstein telescope which will also be able to detect gravitational waves from the postmerger phase hence probing for potential phase transitions in the nuclear Equation of State. Second the James Webb Telescope will be an outstanding tool to observe kilonovae in the infrared which is the preferred wavelength in which the mergers radiate after a few days.

Finally, neutron star merger simulations and their predictions for the r-process and the associated kilonovae cannot be more reliable than the nuclear ingredients which go into the studies. Also here we are at the eve of a new era. The current generation of radioactive ion-beam facilities, like RIKEN, are already capable of producing the neutron-rich nuclei at or close to the r-process path in the mid-mass range. This will drastically improve once FRIB or the intended upgraded RIKEN facility are fully operational. Even the r-process nuclides at the \(N=126\) magic number, which are crucial for the mass flow in the r-process in mergers and for which yet no data exist, will become experimentally available at the FAIR facility currently under construction in Darmstadt. FAIR will also have an extended program to explore the QCD phase diagram for potential phase transitions, including the temperature/density region important for neutron star mergers.

All these progresses are certainly to the delight of Franz Käppeler. But he would probably like most that an idea brought forward recently by him and colleagues [129] how to measure neutron capture rates for short-lived nuclei is now discussed to be utilized at storage rings like those at FAIR.