1 Introduction

Primordial or Big Bang nucleosynthesis (BBN) is a fine laboratory to test our understanding of nuclear and particle physics, for some reviews see Refs. [1,2,3,4]. The light elements generated in BBN can nowadays be calculated from first principles, which offers the possibility to study in a model-independent way the dependence of the element abundances as a function of the fundamental parameters of the Standard Model of particle physics, in particular the light quark masses \(m_u, m_d\) and the QCD \(\theta \)-parameter as well as the electromagnetic fine-structure constant \(\alpha \). This is based on the observation that the strong and the electromagnetic interactions both contribute to the nuclear binding, while the weak interactions makes their presence feel via certain decays, most prominently in the neutron decay into a proton and a lepton pair. In the Standard Model, the quark masses are given in terms of a priori unknown Yukawa couplings to the Higgs boson and the strength (coupling constants) of the various interactions must also be pinned down from experiment. It is therefore obvious that the Standard Model should be an effective field theory, which can eventually be derived from a more fundamental theory, such as string theory or alike. Another possibility is the Multiverse, in which our Universe is simply one particular manifestation with the Yukawa couplings and interaction strengths given as they are measured. Further, anthropic considerations come into play by asking how much these parameters can be modified to still allow for life on Earth (as given by the relative abundances of certain elements like \(^4\)He, \(^{12}\)C and \(^{16}\)O without going into details of galaxy and planet formation and alike). For reviews on these issues, see e.g. Refs. [5,6,7,8,9,10].

Here, we wish to revisit recent works that have derived bounds on the fundamental parameters from element generation in BBN, see e.g. Refs. [11,12,13,14,15]. To really draw conclusions like that the Higgs vacuum expectation value can only be varied by about 1% [13, 14] when keeping the Yukawa couplings constant, requires a full control of the systematic uncertainties in the calculation of BBN nucleosynthesis within our Universe. This is exactly what will be done in the present manuscript which will serve as the basis for future studies of the allowed quark mass and fine-structure constant variations within these uncertainties. In particular, we study the dependence of the element abundances on the nuclear reaction rates and also the temperature dependence of the direct and radiative capture reactions in the BBN network, that is most often neglected. Furthermore, variations in the neutron lifetime, the singlet neutron-proton scattering length as well as the deuteron binding energy are considered, where the latter two enter the leading reaction \(n+p\rightarrow d+\gamma \), which is particular transparent using the effective field theory calculation of Refs. [16, 17]. Most importantly, we utilize four different publicly available codes for BBN [4, 18,19,20,21,22,23] to address the systematic uncertainties related to the modeling of the BBN network. In particular these codes differ in the number of nuclei and reactions taken into account as well as in the specific parametrization of the nuclear rates entering the coupled rate equations for the BBN network. Moreover, in determining the sensitivity of primordial abundances on nuclear parameters, we account for a temperature dependence of the variation of some rates on specific nuclear parameters and found that this leads in general to a reduction of these sensitivities in comparison to previous studies, where this temperature dependence was ignored. To our knowledge, such a comparative study has been not been published, but of course, new cosmological results are always used to update BBN, see e.g. Ref. [24].

The manuscript is organized as follows: In Sect. 2 we collect the basic formalism underlying BBN, which is required in what follows. In this section we also elaborate on the (pionless) Effective Field Theory description of the leading \(n+p \rightarrow d + \gamma \) reaction. The BBN response matrix is introduced in Sect. 3. The numerical results of this study are presented in Sect. 4 and discussed in Sect. 5.

2 Basic formalism

The basic quantities to be determined in BBN are the nuclear abundances \(Y_{n_i}\), where \(n_i\) denotes some nucleus. As pointed out e.g. in Refs. [4, 20, 23], the evolution of nuclear abundances \(Y_{n_i}\) is given generically by

(1)

where the dot denotes the time derivative in a comoving frame, \(N_a\) is the stochiometric coefficient of species a in the reaction and where e.g. for a two-particle reaction \(a + b \rightarrow c + d\), \(\Gamma _{ab \rightarrow cd} = n_B \gamma _{ab\rightarrow cd}\) is the reaction rate with \(n_B\) the baryon volume density. This can readily be generalised to reactions involving more (or less) particles, see [4]. These equations are coupled via corresponding energy densities to the standard Friedmann equation describing the cosmological expansion in the early universe, for details and basic assumptions, see also [4, 20, 23].

2.1 Nuclear reaction rates

The average reaction rate \(\gamma _{ab\rightarrow cd} = N_A\,\langle \sigma _{ab\rightarrow cd}\,v\rangle \) for a two-particle reaction \(a + b \rightarrow c + d\) is obtained by folding the cross section \(\sigma _{ab\rightarrow cd}(E)\) with the Maxwell–Boltzmann velocity distribution in thermal equilibrium

$$\begin{aligned}{} & {} \gamma _{ab\rightarrow cd}(T)\nonumber \\{} & {} \quad = N_A\, \sqrt{\frac{8}{\pi \mu _{ab} (kT)^3}}\, \int _{0}^{\infty }\!\!\!\text {d}{E}\,E\,\sigma _{ab\rightarrow cd}(E)\,\text {e}^{-\frac{E}{kT}}, \end{aligned}$$
(2)

conventionally multiplied by Avogadro’s number \(N_A\), where \(\mu _{ij}\) is the reduced mass of the nuclide pair ij, E is the kinetic energy in the center-of-mass (CMS) system, T is the temperature and k the Boltzmann constant. Defining \(y := {E}/(k T)\) this can be written in the form

$$\begin{aligned} \gamma _{ab\rightarrow cd}(T)= & {} N_A \sqrt{\frac{8\,k T}{\pi \,\mu _{ab}}} \int _{0}^{\infty }\!\!\!\text {d}{y}\,\sigma _{ab\rightarrow cd}\left( k T\,y\right) \,y\,\text {e}^{-y}, \end{aligned}$$
(3)

which is suited for numerical computation e.g. with a Gauss-Laguerre integrator.

With the detailed balance relation

$$\begin{aligned} \sigma _{cd\rightarrow ab}\left( E'\right) = \frac{g_a\,g_b}{g_c\,g_d}\,\frac{p^2}{{p'}^2}\,\sigma _{ab\rightarrow cd}(E), \end{aligned}$$
(4)

where

$$\begin{aligned} E = \frac{p^2}{2\,\mu _{ab}}, ~~~E'=\frac{{p'}^2}{2\,\mu _{cd}}, \end{aligned}$$
(5)

are the kinetic energies in the entrance and exit channels, respectively, and \(g_i\) is the spin multiplicity of particle i. Energy conservation leads to,

$$\begin{aligned} m_a + m_b + E= & {} m_c + m_d + E' \quad \text {or} \quad \nonumber \\ E' = E + Q,&\quad \text {with}\quad&Q = m_a+m_b-m_c-m_d~, \end{aligned}$$
(6)

in terms of the Q-value for the forward reaction. The inverse reaction rate is related to the forward rate as

$$\begin{aligned} \gamma _{cd \rightarrow ab}(T) = \left( \frac{\mu _{ab}}{\mu _{cd}}\right) ^{\frac{3}{2}} \frac{g_a\,g_b}{g_c\,g_d}\, \text {e}^{-\frac{Q}{k T}}\, \gamma _{ab\rightarrow cd}(T). \end{aligned}$$
(7)

2.2 Q-value dependence of the reaction rates

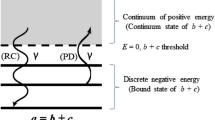
The rates for nuclear reactions of the kind

$$\begin{aligned} a + b \rightarrow c + d \end{aligned}$$
(8)

depend on the Q-value of the reaction, which in turn depends on the nuclear binding energies.

2.2.1 Varying nuclear binding energies

Now, e.g. for a relative change in the binding energy of nucleus \(a: B_a \mapsto B_a\,(1+\delta _a)\) the nuclear mass change is given by

$$\begin{aligned} \Delta m_a = m_a - \delta _a\,B_a \end{aligned}$$

and thus the reduced mass occurring in the expressions above changes as

$$\begin{aligned} \mu _{ab}\mapsto & {} \frac{\left( m_a-\delta _a\,B_a\right) \,m_b}{m_a - \delta _a\,B_a + m_b} = \frac{m_a\,m_b-\delta _a\,B_a\,m_b}{(m_a+m_b) \left( 1-\frac{\delta _a\,B_a}{m_a+m_b}\right) } \nonumber \\\approx & {} \left( \mu _{ab} - \frac{\delta _a\,B_a\,m_b}{m_a+m_b}\right) \left( 1+\frac{\delta _a\,B_a}{m_a+m_b}\right) \nonumber \\\approx & {} \mu _{ab}\left( 1+\frac{\delta _a\,B_a}{m_a+m_b} -\frac{\delta _a\,B_a}{m_a}\right) \nonumber \\= & {} \mu _{ab}\left( 1-\frac{\delta _a\,B_a\,m_b}{(m_a+m_b)\,m_a}\right) \nonumber \\= & {} \mu _{ab}\left( 1-\mu _{ab}\,\frac{\delta _a\,B_a}{m_a^2}\right) . \end{aligned}$$
(9)

Since we shall consider fractional changes in the binding energy \(\delta _a \approx {\mathcal {O}}(10^{-3})\) and \({B_a}/{m_a} \approx {\mathcal {O}}(10^{-2}-10^{-3})\), the change in the reduced masses is very small, \({\mathcal {O}}(10^{-5}\)–\(10^{-6})\) and this change in the reduced masses will therefore be neglected.

Noting that, since the total number of protons and neutrons is conserved in this kind of reaction: \(Z_a+Z_b = Z_c + Z_d, N_a + N_b = N_c + N_d\),

$$\begin{aligned} Q= & {} m_a + m_b - m_c - m_d \nonumber \\= & {} Z_a\,m_p + N_a\,m_n - B_a + Z_b\,m_p + N_b\,m_n - B_b \nonumber \\{} & {} - Z_c\,m_p - N_c\,m_n + B_c - Z_d\,m_p - N_d\,m_n + B_d \nonumber \\= & {} B_c + B_d - B_a - B_b, \end{aligned}$$
(10)

a change in the binding energy will only affect the Q value:

$$\begin{aligned} \Delta Q = -\delta _a\,B_a - \delta _b\,B_b + \delta _c\,B_c + \delta _d\,B_d, \end{aligned}$$
(11)

where \(\delta _i\) is the fractional change in the binding energy \(B_i\) of nuclide i and this will be the major effect to be studied below. We also note that in case of three-particle final states we shall use the same formula, e.g. by taking \({}^{4}\text {He}+{}^{4}\text {He}\) as \({}^{8}\text {Be}\) and \(p+n\) as d etc.

Note that, apart from the reaction \(n + p \rightarrow d + \gamma \), to be discussed in some detail in Sect. 2.2.5, we do not make any assumptions concerning the binding energy dependence of the cross section itself, although, as has been argued in [11], e.g. a \(B_d^{-1}\) dependence for reactions involving deuterons might be considered.

2.2.2 Direct reactions \(a + b \rightarrow c + d\):

Since the cross section is proportional to the final channel momentum \(p'\) and the probability of two charged nuclear particles overcoming their electrostatic barriers is given by the so called Gamow-Sommerfeld-factor [25]

$$\begin{aligned} \text {e}^{-\sqrt{\frac{E'_G}{E'}}}, \quad \text {where}\quad E'_G = 2\pi ^2\,Z_c^2\,Z_d^2\,\alpha ^2\,\mu _{cd}\,c^2 \end{aligned}$$
(12)

is the so called Gamow-energy for the exit channel, \(Z_i\) is the charge number of nuclide i and \(\alpha \simeq 1/137\) is the electromagnetic fine-structure constant, the Q-value dependence is given by

$$\begin{aligned} \sigma (Q;E)_{a b \rightarrow c d} \propto \sqrt{Q+E}\,\text {e}^{-\sqrt{\frac{E'_G}{Q+E}}}. \end{aligned}$$
(13)

One thus finds for a change in the Q-value

$$\begin{aligned} {\widetilde{Q}} = Q_0 + \Delta Q \end{aligned}$$
(14)

with

$$\begin{aligned} \left( \frac{\partial ^{}{\sigma }}{\partial {Q}^{}}\right) (Q_0;E) = \frac{1}{2}\,\sigma (Q_0;E)\left( 1 + \sqrt{\frac{E'_G}{Q+E}}\right) \,\frac{1}{Q+E}\nonumber \\ \end{aligned}$$
(15)

that

$$\begin{aligned}{} & {} \sigma _{ab\rightarrow cd}({\widetilde{Q}};E) \approx \sigma _{ab\rightarrow cd}(Q_0;E) + \left( \frac{\partial ^{}{\sigma }}{\partial {Q}^{}}(Q_0;E)\right) \,\Delta Q \nonumber \\{} & {} \quad = \sigma _{ab\rightarrow cd}(Q_o;E) \left( 1 + \frac{\Delta Q}{2\,(Q_0+E)} \left( 1+\sqrt{\frac{E'_G}{Q_0+E}}\right) \right) .\nonumber \\ \end{aligned}$$
(16)

Thus, in linear approximation we have

$$\begin{aligned}{} & {} \gamma _{ab\rightarrow cd}({\widetilde{Q}};T) \approx \gamma _{ab\rightarrow cd}(Q_0; T) \nonumber \\{} & {} \qquad +\sqrt{\frac{8}{\pi \,\mu _{ab}\,(kT)^3}}\, \int _{0}^{\infty }\!\!\!\text {d}{E}\,E\,\sigma (Q_0;E) \nonumber \\{} & {} \qquad \left( \frac{\Delta Q}{2\,(Q_0+E)} + \frac{\Delta Q\,\sqrt{E'_G}}{2\,(Q_0+E)^\frac{3}{2}} \right) \,\text {e}^{-\frac{E}{kT}} \nonumber \\{} & {} \quad =: \gamma _{ab\rightarrow cd}(Q_0; T) + \Delta \gamma (T)_{ab\rightarrow cd} \end{aligned}$$
(17)

and the determination of the temperature dependent Q-value change requires a separate computation of an integral over the cross section or, equivalently, over the astrophysical S-factor defined as

$$\begin{aligned} S(E) := \sigma (E)\,E\,\text {e}^{\sqrt{\frac{E_G}{E}}}. \end{aligned}$$
(18)

We shall use a numerical integration of Eq. (17) to determine the Q-dependence of the rates for a dozen leading reactions in the BBN network.

If, however, we assume that for the relevant energies in the integrand \(E \ll Q_0\), which might be the case for low temperatures, then this simplifies to

$$\begin{aligned}{} & {} \gamma _{ab\rightarrow cd}({\widetilde{Q}}; T) \approx \gamma _{ab\rightarrow cd}(Q_0; T) \nonumber \\{} & {} \qquad \qquad \qquad \qquad \left( 1 + \frac{\Delta Q}{2\,Q_0} \left( 1 + \sqrt{\frac{E'_G}{Q_0}}\right) \right) \nonumber \\{} & {} = \gamma _{ab\rightarrow cd}(Q_0; T) \left( 1 + \frac{1}{2}\,\delta _Q\, \left( 1 + \sqrt{\frac{E'_G}{Q_0}}\right) \right) \nonumber \\{} & {} =: \gamma _{ab\rightarrow cd}(Q_0; T) + \Delta \gamma _{0;ab\rightarrow cd}, \end{aligned}$$
(19)

where \(\delta _Q = {\Delta Q}/{Q_0}\) is the fractional change in the Q-value. Indeed, Eq. (19) is the approximation that has been used in previous studies, such as e.g. Refs. [11,12,13,14]. Note that with this approximation the Q-value change is temperature independent.

2.2.3 Radiative capture reactions: \(a + b \rightarrow c + \gamma \):

Assuming that the radiation is dominated by electromagnetic dipole transitions,Footnote 1 we have

$$\begin{aligned} \sigma (Q;E)_{ab\rightarrow c\gamma } \propto E_\gamma ^3 \approx (Q+E)^3. \end{aligned}$$
(20)

Accordingly, for a change in the Q-value

$$\begin{aligned} {\widetilde{Q}} = Q_0 + \Delta Q \end{aligned}$$
(21)

with

$$\begin{aligned} \left( \frac{\partial ^{}{\sigma }}{\partial {Q}^{}}\right) (Q_0;E) = 3\,\frac{\sigma (Q_0;E)}{Q_0+E} \end{aligned}$$
(22)

one finds that

$$\begin{aligned} \sigma _{ab\rightarrow c\gamma }({\widetilde{Q}};E)\approx & {} \sigma _{ab\rightarrow c\gamma }(Q_0;E) + \left( \frac{\partial ^{}{\sigma }}{\partial {Q}^{}}(Q_0;E)\right) \,\Delta Q \nonumber \\= & {} \sigma _{ab\rightarrow c\gamma }(Q_o;E) \left( 1+3\,\frac{\Delta Q}{Q_0+E} \right) \end{aligned}$$
(23)

and thus the change in the rate

$$\begin{aligned} \gamma _{ab\rightarrow c\gamma }({\widetilde{Q}}; T)\approx & {} \gamma _{ab\rightarrow c\gamma }(Q_0; T) \nonumber \\{} & {} \quad +\, 3\,\Delta Q\, \sqrt{\frac{2}{\pi \,\mu _{ab}\,c^2\,(kT)^3}}\, \nonumber \\{} & {} \quad \times \int _{0}^{\infty }\!\!\!\text {d}{E}\,\,\sigma (Q_0;E) \frac{E}{Q_0+E} \text {e}^{-\frac{E}{kT}} \nonumber \\=: & {} \gamma _{ab\rightarrow c\gamma }(Q_0; T) + \Delta \gamma (T)_{ab\rightarrow c\gamma }, \end{aligned}$$
(24)

as for the direct reactions before is temperature dependent.

If again, as in Refs. [11,12,13,14], we assume that for the relevant energies in the integrand \(E \ll Q_0\) then this simplifies to

$$\begin{aligned} \gamma _{ab\rightarrow c\gamma }({\widetilde{Q}}; T)= & {} \gamma _{ab\rightarrow c\gamma }(Q_0; T) \left( 1 + \frac{3\,\Delta Q}{Q_0}\right) \nonumber \\= & {} \gamma _{ab\rightarrow cd}(Q_0; T) \left( 1 + 3\,\delta _Q\right) \nonumber \\=: & {} \gamma _{ab\rightarrow c\gamma }(Q_0; T) + \Delta \gamma _{0;ab\rightarrow c\gamma }, \end{aligned}$$
(25)

where \(\delta _Q := {\Delta _Q}/{Q_0}\). In this case:

$$\begin{aligned} Q = m_a + m_b - m_c = B_c - B_a - B_b \end{aligned}$$
(26)

and a fractional change in the binding energy: \(B_i \mapsto ( 1 + \delta _i\,B_i)\) will be assumed, as above, to affect the Q value only:

$$\begin{aligned} \Delta Q = -\delta _a\,B_a - \delta _b\,B_b + \delta _c\,B_c. \end{aligned}$$
(27)

2.2.4 Weak decay rates \(a \rightarrow b + e^{\pm } + {\mathop {\nu }\limits ^{(-)}}\)

Neglecting the nuclear recoil of the daughter nucleus, we have from energy conservation

$$\begin{aligned} M_a = M_b + E_e + E_\nu \end{aligned}$$
(28)

and the maximum \(e^\pm \) energy is given by

$$\begin{aligned} E_e^{\small {max}} = M_a - M_b =: Q\, \end{aligned}$$
(29)

where \(M_a,M_b\) are the nuclear parent and daughter masses. Accordingly, the maximal \(e^\pm \) momentum is given by

$$\begin{aligned} p_e^{\small {max}} = \sqrt{Q^2 - m_e^2} = m_e\,\sqrt{q^2-1}, \quad q := \frac{Q}{m_e}. \end{aligned}$$
(30)

The weak decay rate then reads [26]:

$$\begin{aligned} \lambda = \frac{G^2}{2\pi ^3}\,\frac{m_p\,c^2}{\hbar }|M_{if}|^2\,f(Z,q), \end{aligned}$$
(31)

where G is the weak (Fermi) coupling constant, \(M_{if}\) the nuclear matrix element and (ignoring Coulomb corrections):

$$\begin{aligned} f(q):= & {} \left. f(Z,q)\right| _{Z=0} \nonumber \\= & {} \frac{1}{60}\left[ \sqrt{q^2-1}\,(2\,q^4-9\,q^2-8) \right. \nonumber \\{} & {} \left. \quad + 15\,q\,\log (q+\sqrt{q^2-1}) \right] . \end{aligned}$$
(32)

From this an expression for the fractional change in the rate due to a change in the Q-value,

$$\begin{aligned}{} & {} \frac{\partial ^{}{\log (f(q))}}{\partial {q}^{}} \nonumber \\{} & {} \quad = \frac{ \sqrt{q^2-1}\,\left( 10\,q^3-25\,q\right) + 15\,\log \left( q+\sqrt{q^2-1}\right) }{ \sqrt{q^2-1}\,\left( 2\,q^4-9\,q^2-8\right) + 15\,q\,\log \left( q+\sqrt{q^2-1}\right) }\nonumber \\ \end{aligned}$$
(33)

follows, i.e.

$$\begin{aligned} \frac{\partial ^{}{\log (\lambda )}}{\partial {q}^{}} = \frac{1}{\lambda }\,\frac{\partial ^{}{\lambda }}{\partial {q}^{}} = \frac{\partial ^{}{\log {(f(q))}}}{\partial {q}^{}}. \end{aligned}$$
(34)

With \({\widetilde{Q}} = Q_0 + \Delta Q = Q_0\,(1 + \delta _Q)\), \(\lambda _0 := \lambda (Q_0)\) and \(q_0 := {Q_0}/{m_e}\), we find

$$\begin{aligned} {\widetilde{\lambda }}= & {} \lambda (Q_0) + \Delta \lambda \approx \lambda (Q_0) + \frac{\partial ^{}{\lambda }}{\partial {Q}^{}}(Q_0)\,\Delta Q \nonumber \\= & {} \lambda (Q_0) + \frac{\partial ^{}{\lambda }}{\partial {q}^{}}\,q_0\,\delta _Q = \lambda (Q_0) + \lambda _0\,\frac{\partial ^{}{\log (\lambda )}}{\partial {q}^{}}\,q_0\,\delta _Q \nonumber \\= & {} \lambda (Q_0)\left( 1+q_0\,\frac{\partial ^{}{\log (f(q))}}{\partial {q}^{}}\,\delta _Q\right) . \end{aligned}$$
(35)

2.2.5 The leading reaction \(n + p \rightarrow d + \gamma \)

The formulas given above are the basis for the calculation of the primordial abundance variations mainly due to the dependence on the Q-values of most reactions in the BBN-network.

For the leading reaction \(n + p \rightarrow d + \gamma \) in this network it is possible to study more details, since for this reaction an accurate description for the relevant energies in the framework of the so-called pionless effective field theory [16, 17] is available. According to that work, the cross section for the capture reaction \(n + p \rightarrow d + \gamma \) is given by

$$\begin{aligned} \sigma _{np\rightarrow d\gamma }(E) = \frac{4\pi \,\alpha \,\left( \gamma ^2+p^2\right) ^3}{\gamma ^3\,M_N^4\,p} \left[ \left| {\widetilde{\chi }}_{M1}\right| ^2 + \left| {\widetilde{\chi }}_{E1}\right| ^2 \right] \, \end{aligned}$$
(36)

with \(\alpha = {e^2}/{\hbar c}\) the electromagnetic fine-structure constant and \(E={p^2}/{M_N}\) is the total kinetic energy in the CMS, with p the magnitude of the momentum of either the proton or the neutron, and \(\gamma := \sqrt{B\,M_N}\) is the “binding momentum” of the deuteron ground state.Footnote 2 The (dimensionless) electric dipole contribution is given up to N\({}^3\)LO by

$$\begin{aligned} \left| {\widetilde{\chi }}_{E1}\right| ^2= & {} \frac{\gamma ^4\,M_N^2\,p^2}{(\gamma ^2+p^2)^4} \left[ \underbrace{ 1+\gamma \,\rho _d+(\gamma \,\rho _d)^2+(\gamma \,\rho _d)^3} _{\approx \frac{1}{1-\gamma \,\rho _d}} \right. \nonumber \\{} & {} \left. \quad + \frac{\gamma \,M_N}{6\pi }\left( \frac{\gamma ^2}{3}+p^2\right) \right. \nonumber \\{} & {} \quad \left. \times \left( {}^{/{\!\!\!\pi }}C_2^{({}^3 P_0)} + 2\,{}^{/{\!\!\!\pi }}C_2^{({}^3 P_1)} + \frac{20}{3}{}^{/{\!\!\!\pi }}C_2^{({}^3 P_2)} \right) \right] , \end{aligned}$$
(37)

where \(\rho _d\) is the effective range. We use the numerical values from Ref. [16] , \(\gamma ^{-1}=4.318\,946\,\,\text {fm}\), \(\rho _d=1.764\pm 0.002\,\,\text {fm}\), \({}^{/{\!\!\!\pi }}C_2^{({}^3 P_0)}=6.53\,\,\text {fm}^4\), \({}^{/{\!\!\!\pi }}C_2^{({}^3 P_1)}=-5.91\,\,\text {fm}^4\), \({}^{/{\!\!\!\pi }}C_2^{({}^3 P_0)}=0.57\,\,\text {fm}^4\). Furthermore, the magnetic dipole contribution at NLO reads

$$\begin{aligned} \left| {\widetilde{\chi }}_{M1}\right| ^2= & {} \frac{\gamma ^4\,\kappa _1^2\,\left( 1-a_s\,\gamma \right) ^2}{ \left( 1+a_s^2\,\gamma ^2\right) \left( \gamma ^2+p^2\right) ^2} \nonumber \\{} & {} \quad \times \Bigg [ 1 + \gamma \,\rho _d - \frac{r_0}{a_s}\,\frac{\left( \gamma \,a_s+a_s^2\,p^2\right) \,a_s^2\,p^2}{\left( 1+a_s^2\,p^2\right) \left( 1-a_s\,\gamma \right) } \nonumber \\{} & {} \quad - \frac{{}^{/{\!\!\!\pi }}L_{np}}{\kappa _1}\,\frac{a_s\,M_N}{2\pi }\,\frac{\gamma ^2+p^2}{1-a_s\,\gamma } \Bigg ], \end{aligned}$$
(38)

where \(\kappa _1 = (\mu _p-\mu _n)/2\) is the nucleon isovector magnetic moment (in units of \(\mu _N = {e\,\hbar }/(M_N\,c)\)), \(a_s\) is the scattering length and \(r_0\) is the effective range in the \({}^1S_0\)-channel. Again we use the numerical values from Ref. [16] , \(a_s = -23.714\pm 0.013\,\,\text {fm}\), \(r_0 = 2.73\pm 0.03\,\,\text {fm}\), \({}^{/{\!\!\!\pi }}L_{np} = -4.513\,\,\text {fm}^2\). The resulting cross section is compared to experimental data in Fig. 1.

Fig. 1
figure 1

Radiative capture \(n + p \rightarrow d + \gamma \) cross section (in mb) (magenta, color online) as a function of the CMS kinetic energy in MeV, from [17] ; the calculated M1 (red) and E1 (blue) contributions to the cross section are also shown separately. Experimental data later than 1960 are from NNDC online [27]

Full size image

Considering only the leading contributions one finds

$$\begin{aligned} \sigma _{M1;np\rightarrow d\gamma }(p) = \frac{ \pi \,\alpha \,\left( \mu _n-\mu _p\right) ^2\,\gamma \,\left( \gamma ^2+p^2\right) \,\left( 1-a_s\,\gamma \right) ^2 }{ M_N^4\,p\,\left( 1+a_s^2\,p^2\right) }. \end{aligned}$$
(39)

With \(p=\sqrt{M_N\,E}, \gamma =\sqrt{M_N\,B_d}\) (\(B_d\) the binding energy of the deuteron) and introducing W via \(a_s=: -1/\sqrt{M_N\,W}\) this reads

$$\begin{aligned} \sigma _{M1;np\rightarrow d\gamma }(E)= & {} \pi \,\frac{\alpha }{M_N^2}\,\left( \mu _n-\mu _p\right) ^2 \nonumber \\{} & {} \times \frac{ \sqrt{B_d}\,(B_d + E)\left( \sqrt{B_d}+\sqrt{W}\right) ^2 }{ M_N\,\sqrt{E}\left( E+W\right) }. \end{aligned}$$
(40)

Likewise

$$\begin{aligned} \sigma _{E1;np\rightarrow d\gamma }(p) = \frac{4\pi \,\alpha \,p\,\gamma }{ M_N^2\,\left( \gamma ^2+p^2\right) \,(1-\gamma \,\rho _d) } \end{aligned}$$
(41)

or, with \(\rho _d =: {1}/\left( \sqrt{M_N\,R}\right) \),

$$\begin{aligned} \sigma _{E1;np\rightarrow d\gamma }(E) = 4\pi \,\frac{\alpha }{M_N^2}\, \frac{ \sqrt{E\,B_d} }{ \left( E + B_d\right) \left( 1-\sqrt{\frac{B_d}{R}}\right) }. \end{aligned}$$
(42)

The cross section for the inverse reaction can be obtained via

$$\begin{aligned} \sigma _{\gamma \,d\rightarrow np}\left( E_\gamma \right)= & {} \frac{2}{3}\,\frac{p^2}{k^2}\,\sigma _{np\rightarrow d\gamma }\left( E_\gamma -B_d\right) \nonumber \\= & {} \frac{2}{3}\, \frac{M_N c^2\,\left( E_\gamma -B\right) _d}{E_\gamma ^2}\, \sigma _{np\rightarrow d\gamma }\left( E_\gamma -B_d\right) \nonumber \\ \end{aligned}$$
(43)

with \(E_\gamma = K\) the photon energy in the rest frame of the deuteron, where we used \(k\approx K\) and

$$\begin{aligned} p^2\approx & {} M_N\,\left( k-B_d\right) \approx M_N\,\left( K-B_d\right) = M_N\,k - \gamma ^2 \nonumber \\{} & {} \quad \Leftrightarrow \,\, p^2+\gamma ^2 \approx M_N\,k \approx M_N\,K\, \end{aligned}$$
(44)

as well as the ratio of the statistical weights

$$\begin{aligned} \frac{g_p\,g_n}{g_\gamma \,g_d} = \frac{2\cdot 2}{2\cdot 3} = \frac{2}{3}. \end{aligned}$$
(45)

and

$$\begin{aligned} E = \frac{p^2}{M_N} \approx k - B_d \approx K - B_d = E_\gamma - B_d. \end{aligned}$$
(46)
Fig. 2
figure 2

Photodisintegration \(\gamma + d \rightarrow n + p\) cross section (in mb) (magenta, color online) as a function of the (laboratory) photon energy in MeV, from [17]. The calculated M1 (red) and E1 (blue) contributions to the cross section are also shown separately. Experimental data from Ref. [28]

Full size image

We thus find for the photodisintegration reaction

$$\begin{aligned}{} & {} \sigma _{M1;\gamma d\rightarrow np}(p) \nonumber \\{} & {} \quad = \frac{2\pi }{3}\,\alpha \,\frac{\left( \mu _n-\mu _p\right) ^2\,p^2\,\gamma \,\left( \gamma ^2+p^2\right) ^2\,\left( 1-a_s\,\gamma \right) ^2}{k^2\,M_N^4\,p\,\left( \gamma ^2+p^2\right) \,\left( 1+a_s^2\,p^2\right) } \nonumber \\{} & {} \quad = \frac{2\pi }{3}\,\frac{\alpha }{M_N^2}\,\left( \mu _n-\mu _p\right) ^2\, \frac{p\,\gamma \,\left( 1-a_s\,\gamma \right) ^2}{ \left( \gamma ^2+p^2\right) \,\left( 1+a_s^2\,p^2\right) } \nonumber \\{} & {} \quad = \frac{2\pi }{3}\,\frac{\alpha }{M_N^2}\,\left( \mu _n-\mu _p\right) ^2\, \frac{\sqrt{B_d}\,\sqrt{E_\gamma -B_d}\,\left( \sqrt{B_d}+\sqrt{W}\right) ^2}{E_\gamma \,\left( E_\gamma -B_d+W\right) } \nonumber \\{} & {} \quad = \sigma _{M1;\gamma d\rightarrow np}(E_\gamma ), \end{aligned}$$
(47)

where we used \(W = (M_N\,a_s^2)\). This indeed corresponds to the Bethe-Longmire zero range expression, see Eq. (56) of Ref. [29]. For the electric dipole contribution to the photodisintegration cross section one finds the zero-range expression

$$\begin{aligned}{} & {} \sigma _{E1;\gamma d\rightarrow np}(p) \nonumber \\{} & {} \quad = \frac{8\pi }{3}\,\alpha \, \frac{p^3\,\gamma \,\left( \gamma ^2+p^2\right) ^2}{k^2\,M_N^2\,\left( \gamma ^2+p^2\right) ^3 } \nonumber \\{} & {} \quad = \frac{8\pi }{3}\,\alpha \, \frac{\gamma \,p^3}{\left( \gamma ^2+p^2\right) ^3} = \frac{8\pi }{3}\,\frac{\alpha }{\gamma ^2}\,\frac{(p\,\gamma )^3}{\left( \gamma ^2+p^2\right) ^3} \nonumber \\{} & {} \quad = \frac{8\pi }{3}\,\frac{\alpha }{\gamma ^2}\, \frac{M_N^3\,B_d^3\,(1-\eta )^{\frac{3}{2}}}{M_N^3\,E_\gamma ^3} = \frac{8\pi }{3}\,\frac{\alpha }{\gamma ^2}\,\frac{(1-\eta )^{\frac{3}{2}}}{\eta ^3} \nonumber \\{} & {} \quad = \frac{8\pi }{3}\,\frac{\alpha }{M_N}\,\frac{\sqrt{B_d}\,\left( E_\gamma -B_d\right) ^{\frac{3}{2}}}{E_\gamma ^3} \nonumber \\{} & {} \quad = \sigma _{E1;\gamma d\rightarrow np}(E_\gamma ) \end{aligned}$$
(48)

where \(\gamma ^2 + p^2\approx M_N\,k \approx M_N\,K =: M_N\,E_\gamma \) and \(\eta := {E_\gamma }/{B_d}\), corresponding to the expression of Eq. (16) in [30], first derived by Bethe and Peierls. The effective range correction (see Eq. (6) in [29]) to this is given by the factor \((1-\gamma \,\rho _d)^{-1}\). The result from the N\({}^3\)LO-calculation of [17] is compared to experimental data in Fig. 2.

Therefore, for this leading reaction in the BBN-network a sufficiently accurate description of the experimental data is available. Moreover, this EFT-description allows to study the variation of the cross section due to changes in nuclear parameters, such as the deuteron binding energy \(B_d\), the \({}^1 S_0\) np scattering length \(a_s\), the corresponding effective range \(r_0\) as well as the effective range \(\rho _d\) in the deuteron channel of np-scattering. Below we shall concentrate on the dependence on \(B_d\) and \(a_s\), since these give the leading effects.

In Fig. 3 the numerically calculated rate according to Eq. (2) for the \(n + p \rightarrow d + \gamma \) reaction is shown and compared to the parameterizations used in the original version of the codes. Apart from the original NUC123 parametrisation, see [31], these curves are very consistent. In the rest of this paper, the parameterization according to a rational function fit of the form

$$\begin{aligned} f(t) = c_0,\,\frac{1+\sum _{i=1}^5 c_i\,t^i}{1+\sum _{i=1}^4 d_j\,t^j} \end{aligned}$$
(49)

to the calculated rate based on the N\({}^3\)LO-cross section is used throughout in all programmes.

From the formulas above in leading order, i.e. at very low energies, where the M1-contribution dominates, the dependence of the cross section and hence of the rate of the \(n + p \rightarrow d + \gamma \) reaction is found to be

$$\begin{aligned} \gamma _{M1;np\rightarrow d\gamma } \propto B_d^{\frac{5}{2}}\,a_s^2, \end{aligned}$$
(50)

leading to

$$\begin{aligned} \frac{\partial \log {\gamma }}{\partial \log {a_s}} = 2, \qquad \frac{\partial \log {\gamma }}{\partial \log {B_d}} = \frac{5}{2}, \end{aligned}$$
(51)

which are energy or temperature independent. However, taking into account the full N\({}^3\)LO-expressions above, this is found to vary appreciably in the BBN-relevant range \(10^{-3} \le T_9 \le 10\), with \(T_9 := T / [10^9\,\text {K}]\), leading to a rather strong suppression of the dependence at high temperatures, see Fig. 4.

Fig. 3
figure 3

The temperature dependent rate (in units of cm\({}^3\) s\({}^{-1}\)) calculated from the cross section of the \(n + p \rightarrow d + \gamma \) reaction in N\({}^3\)LO and compared to the parameterizations used in the programmes NUC123 [18] (in black, color online), PArthENoPE [23] (in magenta), AlterBBN [20] (in green) and PRIMAT [4] for which the two blue curves correspond to the lower and upper limit of the rate. The red solid curve represents a rational function fit to the red data points. \(T_9 := T / [10^9\,\text {K}]\) 

Full size image
Fig. 4
figure 4

Temperature dependence of the fractional change in the rate \(\gamma \) of the \(n + p \rightarrow d +\gamma \) reaction, due to a fractional change in \(x=a_s\) (in red, color online) or \(x=B_d\) (in blue) : \(\frac{\partial \log {\gamma }}{\partial \log {x}}\). Data points are from a numerical evaluation of Eq. (2), the thin solid lines represent a rational function fit to these data and the thick solid lines represent the powers found in the extreme low energy (or low temperature) limit. \(T_9 := T / [10^9\,\text {K}]\)

Full size image

2.2.6 Temperature dependence of the rates for the leading reactions

Such a suppression, in particular for the dependence on the binding energies, is to be expected for the other nuclear reactions also. However, for most reactions the data for the rates are given in the form of parameterizations as a function of \(T_9\) or in the form of tables. Only if the cross-sections \(\sigma (E)\), or, equivalently, the astrophysical S(E)-function is available, it is possible to study the temperature dependence of a change in the rate \(\gamma \) due to a change in the binding energy or Q-value according to Eqs. (17, 24). To this end we numerically compute the integrals in these equations and then fit the ratio of the change in the rate \(\Delta \gamma (T_9)/\Delta \gamma _0\) according to Eqs. (17, 19) for direct reactions or Eqs. (24,25) for radiative capture reactions by a rational function of the form

$$\begin{aligned} g(T_9) = \frac{1+r_1\,T_9 + r_2\,T_9^2 + r_3\,T_9^3}{1+q\,T_9}. \end{aligned}$$
(52)

This is then used in the rate equations. We do this for the leading reactions in the BBN-network, viz. the radiative capture reactions

$$\begin{aligned}{} & {} p+{}^2\text {H}\rightarrow {}^3\text {He}+\gamma , \quad p+{}^3\text {H}\rightarrow {}^4\text {He}+\gamma , \nonumber \\{} & {} \quad {}^3\text {H}+{}^4\text {He}\rightarrow {}^7\text {Li}+\gamma , \quad {}^3\text {He}+{}^4\text {He}\rightarrow {}^7\text {Be}+\gamma , \nonumber \\{} & {} \quad {}^2\text {H}+{}^4\text {He}\rightarrow {}^6\text {Li}+\gamma , \quad p+{}^7\text {Li}\rightarrow {}^4\text {He}+{}^4\text {He}+\gamma ,\nonumber \\ \end{aligned}$$
(53)

the charge exchange reactions

$$\begin{aligned} n+{}^3\text {He}\rightarrow {}^3\text {H}+p, \quad n+{}^7\text {Be}\rightarrow {}^7\text {Li}+p, \end{aligned}$$
(54)

and the other direct reactions

$$\begin{aligned}{} & {} {}^2\text {H}+{}^2\text {H}\rightarrow {}^3\text {H}+p, \quad {}^2\text {H}+{}^2\text {H}\rightarrow {}^3\text {He}+n, \nonumber \\{} & {} \quad {}^2\text {H}+{}^3\text {H}\rightarrow {}^4\text {He}+n, \quad {}^2\text {H}+{}^3\text {He}\rightarrow {}^4\text {He}+p, \nonumber \\{} & {} \quad p+{}^7\text {Li}\rightarrow {}^4\text {He}+{}^4\text {He}, \quad p+{}^6\text {Li}\rightarrow {}^3\text {He}+{}^4\text {He}, \nonumber \\{} & {} \quad {}^2\text {H}+{}^7\text {Be}\rightarrow {}^4\text {He}+{}^4\text {He}+p, \end{aligned}$$
(55)

for which parameterizations of the energy dependence of the cross section can e.g. be found in Appendix D of [32]. For some selected reactions the calculated ratios \(\Delta \gamma (T_9)/\Delta \gamma _0\) together with the rational function fit are shown in Fig. 5, showing that for temperatures \(T_9 > 0.1\) this change is indeed generally suppressed with respect to the change calculated with Eqs. (19, 25)

Fig. 5
figure 5

Temperature dependence of the change in the rate \(\Delta \gamma (T_9)/\Delta \gamma _0\) for a fractional change in the Q-value of some selected leading reactions, due to a fractional change in \(x=a_s\) or \(x=B_d\): \(\frac{\partial \log {\gamma }}{\partial \log {x}}\). Data points are from a numerical evaluation of Eqs. (17, 24); solid lines (color online) represent the rational function fits used in subsequent calculations. \(T_9 := T / [10^9\,\text {K}]\)

Full size image

3 The BBN response matrix

We estimate the linear dependence of primordial abundances \(Y_n\) on small changes in the neutron life time \(\tau _n\), the nuclear binding energies \(B_a\) and the \({}^1 S_0\) np scattering length \(a_s\), \(\partial \log {Y_n}/\partial \log {X_k}\), by calculating the abundance of the nuclide

$$\begin{aligned} n \in \left\{ {^2}\text {H}, {^3}\text {H}+{^3}\text {He}, {^4}\text {He}, {^6}\text {Li}, {^7}\text {Li}+{^7}\text {Be}, \right\} \end{aligned}$$
(56)

i.e.

$$\begin{aligned} Y_n\left( X_k\left( 1+\delta _k\right) \right) ,\qquad X_k \in \left\{ \tau _n,B_a, a_s \right\} \end{aligned}$$
(57)

for fractional changes \(\delta _k \approx {\mathcal {O}}(10^{-3})\) in the nuclear parameters \(X_k\) with the publicly available codes for BBN: A version of the Kawano code called NUC123 [18] (in FORTRAN), two more modern implementations based on this: PArthENoPE [21,22,23] (in FORTRAN) and AlterBBN [19, 20] (in C) as well as an implementation as a mathematica-notebook: PRIMAT [4]. To this end we perform a least-squares fit of a quadratic polynomial to the abundances:

$$\begin{aligned} P_k(\delta _k) := c_0\left( 1+c_1\,\delta _k + c_2\,\delta _k^2\right) , \end{aligned}$$
(58)

such that

$$\begin{aligned} \frac{\partial ^{}{}}{\partial {c_j}^{}}\left| Y_n\left( X_k\left( 1+\delta _k\right) \right) -P_k(\delta _k)\right| ^2 = 0,\quad j=0,1,2. \end{aligned}$$
(59)

Then

$$\begin{aligned} \frac{\partial ^{}{\log {Y_n}}}{\partial {\log {X_k}}^{}} \approx c_1 \end{aligned}$$
(60)

will be called an element of the (linear) nuclear BBN response matrix. It represents the (dimensionless) fractional change in the primordial abundance \(Y_n\) due to a fractional change in the nuclear parameter \(X_k\) in linear approximation. This method was preferred over a direct approximation of the (logarithmic) derivatives via finite differences, since some of the calculated abundances turned out to be rather noisy in particular when close to zero.

4 Numerical results

In what follows, we use \(\eta =6.14\times 10^{-10}\) from [37] as the baryon-to-photon density ratio, but we will also allow for variations of this parameter. In all programmes, the following modifications were made:

  • All natural constants were updated to recent values listed by CODATA [33] and PDG [36, 37];

  • Atomic mass excesses were taken from the NUBASE2020 [34] compilation; nuclear binding energies were then calculated by accounting for the atomic binding energies from [35], although this is a minor effect;

  • Reverse reaction rate constants were recalculated on the basis of the nuclear data above;

  • In NUC123 hard coded constants were substituted by their analytical expressions in terms of natural constants updated from CODATA [33] and PDG [36, 37].

In addition, and also in the primat-implementation [4], the rate of the \(n + p \rightarrow d + \gamma \) radiative capture reaction was calculated on the basis of the analytical expression for the cross section from the EFT calculation in [17], see also Sect. 2 and rational function fits of the temperature dependence and the dependencies on the deuteron binding energy and the \({}^1 S_0\) np scattering length, as explained in Sect. 3 were used.

For the fractional change in the rate due to changes in the Q-values of direct reactions we used the expression of Eqs. (19, 25) with the exception of the reactions listed in Eqs. (53, 54 and 55), where we used Eqs. (17, 24). For the Q-value dependence of the weak decay rates we used Eqs. (33, 35).

Table 1 Final abundances as number ratios \(Y_n/Y_H\) (for \({}^4\text {He}\) the mass ratio \(Y_p\)) calculated with the modified versions of the codes
Full size table

The values obtained with each of the programmes for the abundances at the end of the BBN-epoch in terms of the number ratios \(Y_{{}^2\text {H}}/Y_\text {H}\), \(Y_{{}^3\text {H}+{}^3\text {He}}/Y_\text {H}\), \(Y_{{}^6\text {Li}}/Y_\text {H}\), \(Y_{{}^7\text {Li}+{}^7\text {Be}}/Y_\text {H}\), and the mass ratio for \({}^4\text {He}\) are listed in Table 1. The discrepancy of about a factor of three in the abundance ratio of \({}^7\text {Li}+{}^7\text {Be}\) to \(\text {H}\) is known as the “\(\text {Li}\)-problem”, see [37] and references therein. Here various possible explanations of this discrepancy are discussed: e.g. systematic errors in the observed lithium-abundance and in the determination of the primordial abundance from these observations, possible issues in stellar astrophysics leading to the destruction of lithium and/or obscuring lithium from detection, uncertainties in nuclear reaction input data, fluctuations in the baryon-to-photon ratio, effects from decays of beyond-the-standard-model particles leading to non-equilibrium nucleons dissociating light elements or changes in fundamental natural constants. In spite of this unresolved issue in BBN the consistency of the cosmic microwave background observations with the determined abundances of deuterium and helium is considered in [37] to be a “non-trivial success”. Accordingly, we think that this issue is no obstacle for the study presented here.

In order to determine the sensitivity of the abundances, each of the programmes was run for fractional changes of the parameters \(\tau _n\), \(a_s\), \(B_{{}^2\text {H}}\), \(B_{{}^3\text {H}}\), \(B_{{}^3\text {He}}\), \(B_{{}^4\text {He}}\), \(B_{{}^6\text {Li}}\), \(B_{{}^7\text {Li}}\) and \(B_{{}^7\text {Be}}\) for about a dozen equidistant values in a range \([-\delta ,\delta ], \delta \approx {\mathcal {O}}(10^{-4}\)–\(10^{-3})\).

The elements of the response matrix were then determined by a polynomial fit, as explained above in Sect. 3 for the abundances of \(Y_{{}^2\text {H}}/Y_\text {H}\), \(Y_{{}^3\text {H}+{}^3\text {He}}/Y_\text {H}\), \(Y_{{}^6\text {Li}}/Y_\text {H}\), \(Y_{{}^7\text {Li}+{}^7\text {Be}}/Y_\text {H}\), and the mass ratio for \({}^4\text {He}\).

The values for the resulting response matrix elements are given and compared to some results from the literature in Table 2.

In order to illustrate the dependence on the baryon-to-photon density parameter \(\eta \) we displayed in Fig. 6 the variation of the response matrix elements for a change of \(\eta \) in the range \(5.94\times 10^{-10}\)–\(6.34\times 10^{-10}\) which corresponds to the error range quoted in [37]: \(\eta _{10} := \eta \times 10^{10} = 6.143 \pm 0.190\).

Fig. 6
figure 6

Baryon-to-photon density \(\eta \)-dependence of the transfer matrix elements \(\partial \log {Y_n}/\partial \log {X_k}\), \(n={}^2\text {H}\) (crosses in red), \({}^3\text {H}+{}^3\text {He}\) (asterisks in blue), \({}^4\text {He}\) (open squares in black), \({}^6\text {Li}\) (filled squares in magenta) and \({}^7\text {Li}+{}^7\text {Be}\) (open circles in orange; color online). For each of the programmes: a NUC123, b PArtHEnoPE, c alterBBN, d PRIMAT, the variation of the response matrix elements is shown as 9 subsequent points for \(\eta _{10} := \eta \times 10^{10} = 5.94, 5.99, 6.04, 6.09, 6.14, 6.19, 6.24, 6.29, 6.34\), the central values at 6.14 corresponding to the values listed in Table 2. For better visibility, in the panels labeled “\({}^4\text {He}\)” and “\({}^6\text {Li}\)” the values of the response matrix elements \(\partial \log {Y_{B_{{}^6\text {Li}}}}/\partial \log {X_k}\) (filled squares, in magenta) have been divided by 100. The same applies to the panels labeled “\({}^4\text {He}\)”, “\({}^7\text {Li}\)” and “\({}^7\text {Be}\)” for the response matrix elements \(\partial \log {Y_{{}^7\text {Li}+{}^7\text {Be}}}/\partial \log {X_k}\) (open circles, in orange)

Full size image
Table 2 BBN response matrix \(\partial \log {Y_n}/\partial \log {X_k}\) at \(\eta =6.14 \times 10^{-10}\) and \(\tau _n = 879.4\,\text {s}\)
Full size table

The following observations can be made:

  • Concerning the baryon-to-photon density ratio\(\eta \)-dependence : Although the final abundances at the end of the primordial nucleosynthesis do depend on \(\eta \) strong enough and, in particular the \({}^4\text {He}\) and deuteron abundances allow for estimating a rather strict bound on \(\eta \), see e.g. Fig. 24.1 in section 24 of [37] compatible with the CMB determination of the cosmic baryon density [37], the \(\eta \)-dependence of the linear response to the nuclear parameters studied here was found to be in general almost linear and of rather moderate size, see Fig. 6. Note that a conspicuous correlation between the values for the response matrix elements exists (many values being even almost identical, see Fig. 6) for the \({}^2\text {H}\) and \({}^6\text {Li}\) abundances for all dependences studied here.

  • The values found for the current best value \(\eta =6.14\times 10^{-10}\) [37] were found to be by and large consistent with those cited in [14], if the same assumptions concerning the \(a_s\)-dependence (values indicated by \({}^{(*)}\) in Table 2) and the temperature independent modification of the rates according to Eqs. (19, 25) are made (extracted from the entries indicated by \({}^{\dagger }\) in Table 2), see Table 3 . Note that in [14] a slightly different value \(\eta =6.19\times 10^ {-10}\) was used.

  • More importantly, it was found that accounting for the actual \(a_s\) dependence in the calculation of the cross section for the \(n + p \rightarrow d + \gamma \) reaction and, accordingly for a temperature dependence in the corresponding rate, in fact the linear dependence of the abundances on this scattering length is reduced with respect to the temperature independent \(a_s^2\) dependence assumed in [14] approximately by a factor of three.

  • Also, accounting for the temperature dependence in the rate when varying the bindings energies of at least the leading reactions in the nuclear BBN network, reduces the values of the response matrix elements in some cases appreciably: In particular this applies to the abundance-dependence of \({}^6\text {Li}\) in the binding energy of \({}^6\text {Li}\) (\(\approx 80 \mapsto \approx 75\)) and the abundance-dependences of \({}^7\text {Li}+{}^7\text {Be}\) on the binding energy of \({}^3\text {H}\) (\(\approx 4 \mapsto \approx 3.5\)), on the binding energy of \({}^3\text {He}\) (\(\approx 8.25 \mapsto \approx 6.75\)) and on the binding energy of \({}^7\text {Be}\) (\(\approx 100 \mapsto 87\)).

  • Furthermore, although the numbers found are roughly consistent, see e.g. the ranges listed in Tables 3 and 4, the four publicly available codes, which do differ in the number of coupled reactions treated in the BBN-network, the treatment of radiative corrections to processes as well as the specific parameterization of the nuclear reaction rates, do lead to slightly different values for the response matrix elements studied here.

    Table 3 Comparison of the range of values obtained with the four codes studied here with the results of [14]
    Full size table

    We shall therefore consider these differences, see Table 4, as an estimate of the systematic (in fact model-dependent) deviations for the numbers obtained. This is one of the main results of the present investigation. As can also be seen from Fig. 6 the largest relative deviations are found for the dependence of the \({}^7\text {Li}+{}^7\text {Be}\) abundance on the binding energy of \({}^2\text {H}\) with the programme PArtHEnoPE: 20 %. No obvious explanation for this could be found. Also the dependence of the \({}^2\text {H}\) abundance on the binding energy of \({}^4\text {He}\) with the programme alterBBN deviates from those found with the other codes. Note, however, that here an exceptional non-linear dependence on \(B_{{}^4\text {He}}\) was found; determining the logarithmic derivative only from left-sided finite differences yields an almost vanishing value, in accordance with the values found with the other programmes. The dependence of the \({}^3\text {H}+{}^3\text {He}\) abundance on the binding energy of \({}^4\text {He}\) varies between all programmes by \(\approx 8 \%\).

Table 4 Model dependence of the response matrix elements
Full size table

5 Summary and conclusion

We reexamined the response matrix elements \(\partial \log {Y_n} / \partial \log {X_k}\), i.e. the linear fractional change in the abundance \(Y_n\) of the nuclides \({}^2\text {H}\), \({}^3\text {H} + {}^3\text {He}\), \({}^4\text {He}\), \({}^6\text {Li}\) and \({}^7\text {Li}+{}^7\text {Be}\) due to a fractional change in nuclear parameters \(X_k\): the life time of the neutron \(\tau _n\), the \({}^1 S_0\) np scattering length \(a_s\) and the binding energies of \({}^2\text {H}\), \({}^3\text {H}\), \({}^3\text {He}\), \({}^4\text {He}\), \({}^6\text {Li}\), \({}^7\text {Li}\) and \({}^7\text {Be}\). In addition the dependence of these quantities on the baryon-to-photon density ratio \(\eta \) was studied. In order to obtain an estimate for the model dependence of the response matrix elements, these were determined with four publicly available codes for calculating the abundances of light elements in primordial nucleosynthesis. The calculated values were found to be by and large mutually consistent, the largest deviations were found for matrix elements that almost vanish anyway. Overall systematic deviations between the codes of a few percent do occur, however.

In the present treatment the nominal values of nuclear binding energies (and hence of nominal \(Q_0\)-values) were updated according to the most recent nuclear data bases currently available. Moreover, in contrast to previous studies, we did account for temperature dependences of the sensitivity of the rate of the leading \(n + p \rightarrow d + \gamma \) reaction on the \({}^1 S_0\) np scattering length \(a_s\), as well as that of the sensitivity of the rates of a dozen other leading reactions in the BBN-network to the Q-values of these reactions. Both effects lead to a reduction of the magnitude of the response matrix elements: the first effect to a reduction by a factor of three, the latter in some cases approximately by 10% . The \(\eta \) dependence of the response matrix elements was found to be a minor effect only.

These findings should be taken into account before making e.g. claims on bounds from primordial nucleosynthesis on more fundamental parameters, such as quark masses or coupling constants, underlying the nuclear parameters studied here. Here we shall refrain from determining such bounds, postponing that to a future publication and merely mention an important issue to be addressed prior to that. Ideally, a study of varying nuclear parameters in order to investigate their impact on abundances in BBN-nucleosynthesis should rely on accurate theoretical descriptions of at least the major reactions, such that the dependence of the cross sections of the leading reactions on nuclear parameters such as scattering lengths, effective range parameters and binding energies can be determined in detail. Presently such a description is available for the leading \(n+p \rightarrow d+ \gamma \) reaction only in the form of an accurate EFT-treatment. Therefore this was elaborated on in some detail here. A similar treatment of other reactions is the subject of current research, see e.g. the discussion of \(\alpha -\alpha \) scattering in [38]. A first application of the insight obtained here will be a reassessment of the dependence of primordial abundances on the electromagnetic fine-structure constant [39].