Bayesian analysis of capture reactions $\varvec{^3}\hbox {He}\varvec{(\alpha ,\gamma )^7}\hbox {Be}$ and $\varvec{^3}\hbox {H}\varvec{(\alpha ,\gamma )^7}\hbox {Li}$

Abstract

Bayesian analysis of the radiative capture reactions $^3\mathrm {He}(\alpha ,\gamma )^7\mathrm {Be}$ and $^3\mathrm {H}(\alpha ,\gamma )^7\mathrm {Li}$ are performed to draw inferences about the cross sections at threshold. We do a model comparison of two competing effective field theory power countings for the capture reactions. The two power countings differ in the contribution of two-body electromagnetic currents. In one power counting, two-body currents contribute at leading order, and in the other they contribute at higher orders. The former is favored for $^3\mathrm {He}(\alpha ,\gamma )^7\mathrm {Be}$ if elastic scattering data in the incoming channel is considered in the analysis. Without constraints from elastic scattering data, both the power countings are equally favored. For $^3\mathrm {H}(\alpha ,\gamma )^7\mathrm {Li}$, the first power counting with two-body current contributions at leading order is favored with or without constraints from elastic scattering data.

Appendices

Appendix A: $\varvec{s}$ and $\varvec{d}$ wave capture

The capture from initial s-wave state is given by

$$\begin{aligned} \frac{|{\mathcal {A}}(p)|}{C_0(\eta _p)}=\left| X(p) -\frac{2\pi }{\mu ^2} \frac{B(p) +\mu J_0(p) +\mu ^2 k_0 L^{(\zeta )}_{E1}}{[C_0(\eta _p)]^2 p (\cot \delta _0-i)}\right| , \end{aligned}$$

(A1)

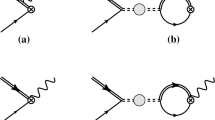
where $k_0$ is the photon energy and $L^{(\zeta )}_{E1}$ for $\zeta ={}^2P_{3/2}$ and $\zeta ={}^2P_{1/2}$ are the 2 two-body currents. We modified some definitions compared to Ref. [2] but they are equivalent expressions.

The contribution without initial state strong interaction is given by

$$\begin{aligned} X(p)= & {} 1+ \frac{2\gamma }{3}\frac{\Gamma (2+k_C/\gamma )}{C_0(\eta _p)}\nonumber \\&\times \int _0^\infty dr\ r W_{-\frac{k_C}{\gamma },\frac{3}{2}}(2\gamma r)\partial _r \left[ \frac{F_0(\eta _p)}{p r} \right] , \end{aligned}$$

(A2)

where $\gamma$ is the binding momentum of the ground or first excited state, as appropriate. The momentum $k_C=\alpha _e Z_\psi Z_\phi \mu$ is the inverse of the Bohr radius. The Coulomb expressions are

$$\begin{aligned} F_l(\eta _p,\rho )&=C_l(\eta _p)2^{-l-1}(-i)^{l+1}M_{i\eta _p, l+1/2}(2i\rho ),\nonumber \\ C_l(\eta _p)&=\frac{2^l e^{-\pi \eta _p/2}|\Gamma (l+1+i\eta _p)|}{\Gamma (2l+2)}, \end{aligned}$$

(A3)

with conventionally defined Whittaker functions $M_{k,\mu }(z)$ and $W_{k,\mu }(z)$. $F_l(\eta _p,\rho )$ is the regular Coulomb wave function.

Table 5 $^3\mathrm {He}(\alpha ,\gamma )^7\mathrm {Be}$: EFT parameters. We estimate the parameters from fits to capture data in region I ($E\lesssim 1000$ keV) and in region II ($E\lesssim 2000$ keV) as indicated. The fits that do not use elastic scattering phase shift data are indicated by the asterisk $*$ sign. We show the errors to one significant figure

Table 6 $^3\mathrm {H}(\alpha ,\gamma )^7\mathrm {Li}$: EFT parameters. The fits that do not use elastic scattering phase shift data are indicated by the asterisk $*$ sign. We show the errors to one significant figure

Fig. 9

$^3\mathrm {He}(\alpha ,\gamma )^7\mathrm {Be}$: The posteriors for the parameters $a_0$ in fm, $r_0$ in fm, $s_0$ in $\hbox {fm}^3$, $\rho _1^{(+)}$ in MeV, $\sigma _1^{(+)}$ in fm, $\rho _1^{(-)}$ in MeV, $\sigma _1^{(-)}$ in fm and $L_1^{(\pm )}$, respectively, in Model A I from 5220 samples. Parameter K (not shown) did not show strong correlation with the others. The vertical dashed lines indicate the median and the interval containing 68% of the posterior distribution around the median, Table 5

Fig. 10

$^3\mathrm {He}(\alpha ,\gamma )^7\mathrm {Be}$: The posteriors for the parameters $a_0$ in fm, $r_0$ in fm, $s_0$ in $\hbox {fm}^3$, $\rho _1^{(+)}$ in MeV, $\sigma _1^{(+)}$ in fm, $\rho _1^{(-)}$ in MeV, $\sigma _1^{(-)}$ in fm and $L_1^{(\pm )}$, respectively, in Model A II from 5816 samples. Parameter K (not shown) did not show strong correlation with the others. The vertical dashed lines indicate the median and the interval containing 68% of the posterior distribution around the median, Table 5

Fig. 11

$^3\mathrm {He}(\alpha ,\gamma )^7\mathrm {Be}$: The posteriors for the parameters $a_0$ in fm, $r_0$ in fm, $s_0$ in $\hbox {fm}^3$, $\rho _1^{(\pm )}$ in MeV and $L_1^{(\pm )}$, respectively, in Model $\hbox {A}^*$ II from 4100 samples. The vertical dashed lines indicate the median and the interval containing 68% of the posterior distribution around the median, Table 5

Fig. 12

$^3\mathrm {He}(\alpha ,\gamma )^7\mathrm {Be}$: The posteriors for the parameters $a_0$ in fm, $r_0$ in fm, $s_0$ in $\hbox {fm}^3$, $\rho _1^{(+)}$ in MeV, $\sigma _1^{(+)}$ in fm, $\rho _1^{(-)}$ in MeV, $\sigma _1^{(-)}$ in fm and $L_1^{(\pm )}$, respectively, in Model B II from 5895 samples. Parameter K (not shown) did not show strong correlation with the others. The vertical dashed lines indicate the median and the interval containing 68% of the posterior distribution around the median, Table 5

Fig. 13

$^3\mathrm {He}(\alpha ,\gamma )^7\mathrm {Be}$: The posteriors for the parameters $a_0$ in fm, $r_0$ in fm, $\rho _1^{(\pm )}$ in MeV and $L_1^{(\pm )}$, respectively, in Model $\hbox {B}^*$ II from 4573 samples. The vertical dashed lines indicate the median and the interval containing 68% of the posterior distribution around the median, Table 5

Fig. 14

$^3\mathrm {H}(\alpha ,\gamma )^7\mathrm {Li}$: The posteriors for the parameters $a_0$ in fm, $r_0$ in fm, $s_0$ in $\hbox {fm}^3$, $\rho _1^{(\pm )}$ in MeV and $L_1^{(\pm )}$, respectively, in Model A from 4153 samples. Parameter K (not shown) did not show strong correlation with the others. The vertical dashed lines indicate the median and the interval containing 68% of the posterior distribution around the median, Table 6

Fig. 15

$^3\mathrm {H}(\alpha ,\gamma )^7\mathrm {Li}$: The posteriors for the parameters $a_0$ in fm, $r_0$ in fm, $s_0$ in $\hbox {fm}^3$, $\rho _1^{(\pm )}$ in MeV and $L_1^{(\pm )}$, respectively, in Model $\hbox {A}^*$ from 2916 samples. The vertical dashed lines indicate the median and the interval containing 68% of the posterior distribution around the median, Table 6

The initial s-wave scattering in Eq. (A1) is contained in the Coulomb subtracted phase shift $\delta _0$ parameterized by the modified effective range expansion

$$\begin{aligned}{}[C_0(\eta _p)]^2 p (\cot \delta _0-i)&= -\frac{1}{a_0}+\frac{r_0}{2} p^2+\frac{s_0}{4} p^4+\cdots \nonumber \\&\quad -2k_C H(\eta _p),\nonumber \\ H(x)&= \psi (ix)+\frac{1}{2ix}-\ln (ix)\, . \end{aligned}$$

(A4)

$\psi (x)$ is the digamma function, and $\cdots$ represents terms with higher powers in $p^2$. The combination $B(p)+\mu J_0(p)$ can be evaluated as

$$\begin{aligned} B(p)+\mu J_0(p)= & {} \frac{\mu ^2}{3\pi }\frac{ip^3-\gamma ^3}{p^2+\gamma ^2}+k_C C(p)+\Delta B(p)\nonumber \\&-\frac{k_C\mu ^2}{2\pi }\left[ 2 H(\eta _p)+2\gamma _E -\frac{5}{3}+ \ln 4\pi \right] .\nonumber \\ \end{aligned}$$

(A5)

The function C(p) is given by the double integral

$$\begin{aligned} C(p)= & {} \frac{\mu ^2}{6\pi ^2(p^2+\gamma ^2)}\int _0^1dx\int _0^1dy \frac{1}{\sqrt{x(1-x)}\sqrt{1-y}}\nonumber \\&\times \left( xp^2\ln \left[ \frac{\pi }{4k_C^2} (-yp^2+(1-y)\gamma ^2/x-i\delta ) \right] \right. \nonumber \\&\left. +p^2 \ln \left[ \frac{\pi }{4k_C^2} (-yp^2-(1-y)p^2/x-i\delta ) \right] \right. \nonumber \\&\left. +x\gamma ^2\ln \left[ \frac{\pi }{4k_C^2} (y\gamma ^2+(1-y)\gamma ^2/x-i\delta ) \right] \right. \nonumber \\&\left. +\gamma ^2\ln \left[ \frac{\pi }{4k_C^2}(y\gamma ^2-(1-y) p^2/x-i\delta ) \right] \right) ,\nonumber \\ \end{aligned}$$

(A6)

which is reduced to a single integral before evaluating numerically. The function $\Delta B(p)$ is obtained from

$$\begin{aligned}&B_{{ab}}(p)=-3\int d^3 r \left[ \frac{G_C^{(1)}(-B;r',r)}{r'}\right] \Big |_{r'=0}\nonumber \\&\times \frac{\partial G_C^{(+)}(E;\varvec{r},0)}{\partial r_a}\frac{r_b}{r},\nonumber \\&\left[ \frac{G_C^{(1)}(-B;r',r)}{r'}\right] \Big |_{r'=0}=-\frac{\mu \gamma }{6\pi r} \Gamma (2+k_C/\gamma )W_{-\frac{k_C}{\gamma },\frac{3}{2}}(2\gamma r), \nonumber \\&G_C^{(+)}(E;\varvec{r},0)=-\frac{\mu }{2\pi r}\Gamma (1+i\eta _p) W_{-i\eta _p,\frac{1}{2}}(-i2 p r). \end{aligned}$$

(A7)

The integral $B_{{ab}}(p)$ is divergent at $r=0$. However, when combined with the contribution from $J(p)\delta _{{ab}}$ it is finite. Thus we make the substitution $(r_b/r)[\partial /\partial r_a]=(r_ar_b/r^2)[\partial /\partial r] \rightarrow (\delta _{ab}/3)[\partial /\partial r]$ in the integral and accordingly $B_{ab}(p)\equiv B(p)\delta _{ab}$. The finite piece $\Delta B(p)$ is obtained numerically from B(p) after subtracting the zero and single photon contributions i.e. removing terms up to order $\alpha _e^2$ [2].

The capture from initial d-wave states is given by the amplitude [2]:

$$\begin{aligned} Y(p)= & {} \frac{2\gamma }{3}\Gamma (2+k_C/\gamma )\int _0^\infty dr\ r W_{-k_C/\gamma ,3/2}(2\gamma r) \nonumber \\&\times \left( \frac{\partial }{\partial r} +\frac{3}{r}\right) \frac{F_2(\eta _p, r p)}{r p}. \end{aligned}$$

(A8)

Appendix B: Wave Function Renormalization

The wave function renormalization constant is calculated as [2]:

$$\begin{aligned} -\frac{2\pi }{h^{(\zeta )2}{{\mathcal {Z}}}^{(\zeta )}}= & {} \frac{1}{p}\frac{\partial }{\partial p} 9 [C_1(\eta _p)]^2 p^3(\cot \delta _1-i)\nonumber \\= & {} \rho _1^{(\zeta )}-4k_C\,H\left( -i\frac{k_C}{\gamma }\right) -\frac{2k_C^2}{\gamma ^3}(k_C^2-\gamma ^2)\nonumber \\&\times \left[ \psi '\left( \frac{k_C}{\gamma }\right) -\frac{\gamma ^2}{2k_C^2}-\frac{\gamma }{k_C}\right] , \end{aligned}$$

(B1)

where we used the relation

$$\begin{aligned} 9 [C_1(\eta _p)]^2 p^3(\cot \delta _1-i)= & {} 2 k_C(k_C^2-\gamma ^2)H(-i\eta _\gamma )\nonumber \\&+\frac{1}{2}\rho _1(p^2+\gamma ^2)\nonumber \\&+\frac{1}{4}\sigma _1(p^2+\gamma ^2)^2+\cdots \nonumber \\&-2 k_C(k_C^2+p^2) H(\eta _p). \end{aligned}$$

(B2)

Appendix C: Parameter Estimates

We list the parameter estimates for both $^3\mathrm {He}(\alpha ,\gamma )^7\mathrm {Be}$ and $^3\mathrm {H}(\alpha ,\gamma )^7\mathrm {Li}$ in Tables 5 and 6, respectively. For the Bayesian fits we show the median and the bounds containing 68% of the posterior distributions. Typically, a very asymmetric bound indicates either a skewed or sometimes a bi-modal distribution.

Appendix D: Parameter Correlations

We include the so called corner plots [38] in Figs 9, 10, 11, 12, 13, 14, and 15 for the parameters from the MultiNest algorithm [21], implemented in Python [22]. The plots show around 99% of the posterior distribution around the median. We include only those fits where the estimated parameter values were consistent with the EFT power-counting expectations. We set the precision in the logarithm of the evidence to 0.3. The default suggested precision is 0.5. MultiNest is an adaptive algorithm that adjusts the MCMC calls based on the desired precision. Usually, twice as many “live” points as parameters is suggested in fits [22]. We used 100–120 live points in the fits which was adequate given our fits with atmost 10 parameters. We tested the numerical stability by using a range 40–120 of live points $n_\mathrm {live}$ in MultiNest. We compared the results from MuliNest with fits from the original Nested Sampling algorithm [20] implemented with our own Fortran code. We tested with few hundred live points $n_\mathrm {live}$, using about $10^5$ MCMC steps per sample point for a sample size of about $100\times n_\mathrm {live}$ (total $10^7\times n_\mathrm {live}$ MCMC calls). The original NS algorithm is not as efficient as the adaptive algorithms as pointed out in the literature such as in Refs. [21, 34] though it provides an independent verification where we can control the parameters of MCMC simulations more directly.

Appendix E: Accuracy and Precision

The EFT power-counting comparisons performed in this work is different from the typical Bayesian model comparisons where two or more models with fixed but possibly different number of parameters are compared. In the literature, EFT calculations are considered model-independent though we call the two power-countings Model A and Model B in accordance to the practice in the field of Bayesian analysis. In the construction of an EFT, once the low-energy degrees of freedom and the low-energy symmetries are identified, no attempt is made in modeling the high-energy physics. The relevant halo EFT symmetries do not preclude considering terms in the Lagrangian with mass dimensions greater than 4. As a consequence, the EFTs are non-renormalizable field theories that contain infinitely many terms (and unknown couplings) in principle. However, in practice an expansion in a small parameter $Q/\Lambda$ where Q is a typical small momentum and $\Lambda$ some higher momentum scale is constructed. Then usually only a finite number of terms (and unknown couplings) from the Lagrangian is relevant at a given order of the expansion.

The LO contributions in Model A and Model B differ. They contain different Feynman diagrams. Thus these two theories reproduce the true value with different accuracies at LO. Higher order contributions should bring them closer to the true value (assuming they have consistent convergence properties). However, the estimate $Q/\Lambda$ from NLO contributions, for example, is too naïve. This is just a conservative estimate that does not capture the functional dependence on $p/\Lambda$ and $p/\gamma$ correctly, where p is the incoming momentum and $\gamma$ is the binding momentum. The following example demonstrates some of these ideas.

Suppose we consider the s-wave scattering of two neutral particles of mass m at low momentum $p\ll 1/R$ where R is the range of the two-particle interaction. The exact analytic form of the T-matrix is known [39,40,41], which is given by the effective range expansion as

$$\begin{aligned} T(p)&=\frac{4\pi }{m}\frac{1}{-\frac{1}{a_0}+\frac{1}{2} r_0 p^2 +\frac{1}{4} s_0 p^4+\cdots -i p}\, . \end{aligned}$$

(E1)

We can imagine a system where say $1/R=200$ MeV, $1/a_0=-10$ MeV, $1/r_0 = 30$ MeV, and the rest of the scattering parameters are of natural size given by appropriate powers of R such as $s_0=R^3$, etc. Associating $p\lesssim 70$ MeV with the low-momentum scale Q, we can use the usual pionless EFT expansion [42, 43] and construct a power counting (Model 1) where $1/|a|\sim Q$ and the rest of the scattering parameters including $r_0$ scales with appropriate powers of R. However, the size of the effective range $r_0$ is intermediate between $Q\sim 1/|a|$ and 1/R, and it is a priori not clear how one should classify it. Thus, one can construct an alternate power counting (Model 2) with $1/r_0\sim Q$. As the reader might notice, these $a_0$, $r_0$ values are not physically irrelevant as they are close to the ones for neutron–proton scattering in the $^1S_0$ channel where $a_0\approx -8.31$ MeV, $r_0\approx 72.3$ MeV. The two theories expanded to NLO gives

$$\begin{aligned} T^{(1)}(p)&=-\frac{4\pi }{m}\frac{1}{\frac{1}{a_0}+ip}\left[ 1+\frac{r_0 p^2/2}{\frac{1}{a_0}+ip}\right] , \end{aligned}$$

(E2)

for Model 1 and

$$\begin{aligned} T^{(2)}(p)&=-\frac{4\pi }{m}\frac{1}{\frac{1}{a_0}-\frac{1}{2} r_0 p^2+ip}\left[ 1+\frac{s_0p^4/4}{\frac{1}{a_0}-\frac{1}{2} r_0 p^2+ip} \right] , \end{aligned}$$

(E3)

for Model 2. The amplitudes $T^{(1)}$ and $T^{(2)}$ both scale as 1/Q at LO but they differ at non-zero momentum p. The NLO contribution in Model 1 is of relative ${\mathcal {O}}(Q/\Lambda )$ whereas in Model 2 it is ${\mathcal {O}}(Q^3/\Lambda ^3)$. Moreover, the functional dependence on p is also different at NLO.

The radiative capture reactions $^3\mathrm {He}(\alpha ,\gamma )^7\mathrm {Be}$ and $^3\mathrm {H}(\alpha ,\gamma )^7\mathrm {Li}$ at low momentum do not have a simple expansion in p, like the example above, due to the Coulomb interaction. However, the general principle still holds. Comparing the theories at the same order of the $Q/\Lambda$ expansion would not achieve the same level of accuracy since the LO contributions are different. It will also not necessarily achieve the same level of precision because the conservative estimate $Q/\Lambda$ of error from higher order corrections is too naïve. It does not capture the momentum p dependence precisely.

We want to address the question: Given two EFTs with different accuracies and precisions, how does one perform a Bayesian “model” comparison? One can make different decisions. We compare them at the same level of accuracy, which seems physically reasonable as we explain next.

EFTs with unknown couplings are undefined. Imposing renormalization conditions (matching conditions) fixes the couplings and defines the theory though in practice EFT couplings are often determined by fitting cross sections over a range of momentum. However, one still theoretically associates the couplings with renormalization conditions. Reference [44] demonstrates this in chiral perturbation theory ($\chi$PT) up to NNLO for nucleon–nucleon scattering where 6 couplings are determined from matching conditions. In the $\chi$PT calculations, the matching conditions could be imposed analytically. It is equivalent to requiring the EFT calculation to reproduce the scattering amplitude at 6 “training data” points exactly. In this case at 6 low momenta in an arbitrarily small neighborhood around the virtual pole in the $^1S_0$T-matrix [44]. The EFT calculation is then validated by predicting the phase shift and comparing with data over a range of momenta [44]. The lecture notes in Ref. [45] has further examples from particle physics on matching conditions in EFTs.

Unlike in the $\chi$PT nucleon-nucleon scattering calculation [44], in the capture reaction we do not know the analytic form of the exact capture cross section. We can only insist that the EFTs reproduce cross sections at certain low-momenta data points exactly to define the couplings and the theories. In essence we achieve the same accuracy in the two power countings by imposing the same matching conditions i.e. the EFTs reproduce the same set of training data points exactly. In particular both the EFTs reproduce the s-wave scattering length $a_0$, effective range $r_0$, and shape parameter $s_0$ exactly, which physically means we are imposing renormalization conditions on the elastic scattering amplitude and its derivatives at zero momentum. Reproducing the p-wave binding momentum $\gamma$ and effective range $\rho _1$ is a renormalization condition on the location of the pole and the residue of the T-matrix. The two-body currents are renormalization conditions to reproduce the charge radii of the ground and excited final states. Then the EFTs are validated by checking how well they reproduce the data at the higher momenta. Experimentally we only know the charge radii of the ground states of $^7\hbox {Be}$ and $^7\hbox {Li}$. However, this is not an issue in practice, since we fit the couplings to the capture cross sections over a momentum range. Alternatively, we can predict the charge radii of the excited states from the fitted two-body currents. An important requirement in deciding on the minimum number of matching conditions is that one should determine all the couplings at a given order in the expansion. For example, imposing three matching conditions in “Model A” would constrain three LO couplings but leave three other LO couplings undetermined. This is inconsistent. Working in an iterative manner, one can see that imposing six matching conditions would determine all six LO couplings in Model A, and consistently determine all couplings in Model B up to NLO (when considering both capture and phase shift data). Similarly, nine matching conditions determines all NLO couplings in Model A and all NNLO couplings in Model B capture (NLO in phase shift). Again, in practice, we determine the EFT couplings by fitting them to data over a momentum range, and then compare the two EFT power countings at the same level of accuracy.