Spherical and Planar Ball Bearings — Nonholonomic Systems with Invariant Measures

Abstract

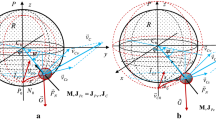
We first construct nonholonomic systems of $n$ homogeneous balls $\mathbf{B}_{1},\dots,\mathbf{B}_{n}$ with centers $O_{1},\ldots,O_{n}$ and with the same radius $r$ that are rolling without slipping around a fixed sphere $\mathbf{S}_{0}$ with center $O$ and radius $R$. In addition, it is assumed that a dynamically nonsymmetric sphere $\mathbf{S}$ of radius $R+2r$ and the center that coincides with the center $O$ of the fixed sphere $\mathbf{S}_{0}$ rolls without slipping over the moving balls $\mathbf{B}_{1},\dots,\mathbf{B}_{n}$. We prove that these systems possess an invariant measure. As the second task, we consider the limit, when the radius $R$ tends to infinity. We obtain a corresponding planar problem consisting of $n$ homogeneous balls $\mathbf{B}_{1},\dots,\mathbf{B}_{n}$ with centers $O_{1},\ldots,O_{n}$ and the same radius $r$ that are rolling without slipping over a fixed plane $\Sigma_{0}$, and a moving plane $\Sigma$ that moves without slipping over the homogeneous balls. We prove that this system possesses an invariant measure and that it is integrable in quadratures according to the Euler – Jacobi theorem.